What is quantum computing. Quantum computing versus classical: why do we need so many numbers? Classic calculations: AND, OR, NOT

Candidate of Physical and Mathematical Sciences L. FEDICHKIN (Physical and Technological Institute of the Russian Academy of Sciences.

Using the laws of quantum mechanics, it is possible to create a fundamentally new type of computer that will allow solving some problems that are inaccessible to even the most powerful modern supercomputers. The speed of many complex calculations will increase sharply; messages sent over quantum communication lines will be impossible to intercept or copy. Today, prototypes of these quantum computers of the future have already been created.

American mathematician and physicist of Hungarian origin Johann von Neumann (1903-1957).

American theoretical physicist Richard Phillips Feynman (1918-1988).

American mathematician Peter Shor, a specialist in the field of quantum computing. He proposed a quantum algorithm for fast factorization of large numbers.

Quantum bit, or qubit. States correspond to, for example, spin directions atomic nucleus up or down.

A quantum register is a chain of quantum bits. One- or two-qubit quantum gates perform logical operations on qubits.

INTRODUCTION, OR A LITTLE ABOUT INFORMATION PROTECTION

What program do you think has sold the most licenses in the world? I won’t risk insisting that I know the right answer, but I definitely know one wrong one: this Not any of the versions Microsoft Windows. The most common operating system is ahead of a modest product from RSA Data Security, Inc. - a program that implements an encryption algorithm with public key RSA, named after its authors - American mathematicians Rivest, Shamir and Adelman.

The fact is that the RSA algorithm is built into most commercial operating systems, as well as many other applications used in various devices - from smart cards to cell phones. In particular, it is also available in Microsoft Windows, which means it is certainly more widespread than this popular operating system. To detect traces of RSA, for example, in a browser Internet Explorer(a program for viewing www pages on the Internet), just open the “Help” menu, enter the “About Internet Explorer” submenu and view the list of used products from other companies. Another common browser, Netscape Navigator, also uses the RSA algorithm. In general, it is difficult to find a well-known company working in the field high technology, which would not buy a license for this program. Today, RSA Data Security, Inc. has already sold more than 450 million(!) licenses.

Why was the RSA algorithm so important?

Imagine that you need to quickly exchange a message with a person who is far away. Thanks to the development of the Internet, such exchange has become available to most people today - you just need to have a computer with a modem or network card. Naturally, when exchanging information over the network, you would like to keep your messages secret from strangers. However, it is impossible to completely protect a long communication line from eavesdropping. This means that when messages are sent, they must be encrypted, and when received, they must be decrypted. But how can you and your interlocutor agree on which key you will use? If you send the key to the cipher over the same line, an eavesdropping attacker can easily intercept it. You can, of course, transmit the key via some other communication line, for example, send it by telegram. But this method is usually inconvenient and, moreover, not always reliable: the other line can also be tapped. It’s good if you and your recipient knew in advance that you would exchange encryption, and therefore gave each other the keys in advance. But what if, for example, you want to send a confidential commercial offer to a possible business partner or buy a product you like in a new online store using a credit card?

In the 1970s, to solve this problem, encryption systems were proposed that use two types of keys for the same message: public (not requiring secrecy) and private (strictly secret). The public key is used to encrypt the message, and the private key is used to decrypt it. You send your correspondent a public key, and he uses it to encrypt his message. All an attacker who has intercepted a public key can do is encrypt his email with it and forward it to someone. But he will not be able to decipher the correspondence. You, knowing the private key (it is initially stored with you), can easily read the message addressed to you. To encrypt reply messages, you will use the public key sent by your correspondent (and he will keep the corresponding private key for himself).

This is exactly the cryptographic scheme used in the RSA algorithm, the most common public key encryption method. Moreover, to create a pair of public and private keys, the following important hypothesis is used. If there are two large ones (requiring more than a hundred decimal digits to be written) simple numbers M and K, then finding their product N=MK will not be difficult (you don’t even need to have a computer for this: a fairly careful and patient person will be able to multiply such numbers with a pen and paper). But to solve the inverse problem, that is, knowing big number N, decompose it into prime factors M and K (so-called factorization problem) - almost impossible! This is exactly the problem that an attacker will face if he decides to “hack” the RSA algorithm and read the information encrypted with it: in order to find out the private key, knowing the public one, he will have to calculate M or K.

To test the validity of the hypothesis about the practical complexity of factoring large numbers, special competitions have been and are still being held. The decomposition of just a 155-digit (512-bit) number is considered a record. The calculations were carried out in parallel on many computers for seven months in 1999. If this task were performed on a single modern personal computer, it would require approximately 35 years of computer time! Calculations show that using even a thousand modern workstations and the best computing algorithm known today, one 250-digit number can be factorized in about 800 thousand years, and a 1000-digit number in 10-25 (!) years. (For comparison, the age of the Universe is ~10 10 years.)

Therefore, cryptographic algorithms like RSA, operating on sufficiently long keys, were considered absolutely reliable and were used in many applications. And everything was fine until then ...until quantum computers appeared.

It turns out that using the laws of quantum mechanics, it is possible to build computers for which the problem of factorization (and many others!) will not be very difficult. According to estimates, quantum computer with only about 10 thousand quantum bits of memory, can factor a 1000-digit number into prime factors in just a few hours!

HOW IT ALL BEGAN?

It was not until the mid-1990s that the theory of quantum computers and quantum computing became established as new area Sciences. As is often the case with great ideas, it is difficult to pinpoint the originator. Apparently, the Hungarian mathematician J. von Neumann was the first to draw attention to the possibility of developing quantum logic. However, at that time, not only quantum, but also ordinary, classical computers had not yet been created. And with the advent of the latter, the main efforts of scientists were aimed primarily at finding and developing new elements for them (transistors, and then integrated circuits), and not at creating fundamentally different computing devices.

In the 1960s American physicist R. Landauer, who worked at IBM, tried to draw the attention of the scientific world to the fact that calculations are always a certain physical process, which means that it is impossible to understand the limits of our computing capabilities without specifying what physical implementation they correspond to. Unfortunately, at that time, the dominant view among scientists was that calculation was a kind of abstract logical procedure that should be studied by mathematicians, not physicists.

As computers became more widespread, quantum scientists came to the conclusion that it was practically impossible to directly calculate the state of an evolving system consisting of only a few dozen interacting particles, such as a methane molecule (CH 4). This is explained by the fact that in order to fully describe a complex system, it is necessary to keep in computer memory an exponentially large (in terms of the number of particles) number of variables, the so-called quantum amplitudes. A paradoxical situation has arisen: knowing the equation of evolution, knowing with sufficient accuracy all the potentials of interaction of particles with each other and the initial state of the system, it is almost impossible to calculate its future, even if the system consists of only 30 electrons in a potential well, and there is a supercomputer with RAM, the number of bits of which is equal to the number of atoms in the visible region of the Universe (!). And at the same time, to study the dynamics of such a system, you can simply conduct an experiment with 30 electrons, placing them in a given potential and initial state. This, in particular, was noted by the Russian mathematician Yu. I. Manin, who in 1980 pointed out the need to develop a theory of quantum computing devices. In the 1980s, the same problem was studied by the American physicist P. Benev, who clearly showed that a quantum system can perform calculations, as well as the English scientist D. Deutsch, who theoretically developed a universal quantum computer that is superior to its classical counterpart.

Much attention to the problem of developing quantum computers was attracted by Nobel Prize winner in physics R. Feynman, well known to regular readers of Science and Life. Thanks to his authoritative call, the number of specialists who paid attention to quantum computing increased many times over.

But still for a long time It remained unclear whether the hypothetical computing power of a quantum computer could be used to speed up the solution of practical problems. But in 1994, an American mathematician, an employee of Lucent Technologies (USA) P. Shore stunned scientific world, proposing a quantum algorithm that allows for fast factorization of large numbers (the importance of this problem was already discussed in the introduction). Compared to the best known today classical methods Shor's quantum algorithm provides multiple acceleration of calculations, and the longer the factored number, the greater the gain in speed. The fast factorization algorithm is of great practical interest for various intelligence agencies that have accumulated banks of undecrypted messages.

In 1996, Shor's colleague at Lucent Technologies L. Grover proposed a quantum algorithm quick search in an unordered database. (An example of such a database is a telephone book in which the names of subscribers are not arranged alphabetically, but in an arbitrary manner.) The task of searching, selecting the optimal element among numerous options is very often encountered in economic, military, engineering problems, V computer games. Grover's algorithm allows not only to speed up the search process, but also to approximately double the number of parameters taken into account when choosing the optimum.

The real creation of quantum computers was hampered by essentially the only serious problem - errors, or interference. The fact is that the same level of interference spoils the process of quantum computing much more intensively than classical computing. P. Shor outlined ways to solve this problem in 1995, developing a scheme for encoding quantum states and correcting errors in them. Unfortunately, the topic of error correction in quantum computers is as important as it is complex to cover in this article.

DEVICE OF A QUANTUM COMPUTER

Before we tell you how a quantum computer works, let us remember the main features of quantum systems (see also “Science and Life” No. 8, 1998; No. 12, 2000).

To understand the laws of the quantum world, one should not rely directly on everyday experience. In the usual way (in the everyday understanding), quantum particles behave only if we constantly “peep” at them, or, more strictly speaking, constantly measure the state in which they are. But as soon as we “turn away” (stop observing), quantum particles immediately move from a very specific state into several different forms at once. That is, an electron (or any other quantum object) will be partially located at one point, partially at another, partially at a third, etc. This does not mean that it is divided into slices, like an orange. Then it would be possible to reliably isolate some part of the electron and measure its charge or mass. But experience shows that after measurement the electron always turns out to be “safe and sound” at one single point, despite the fact that before that it managed to be almost everywhere at the same time. This state of an electron, when it is located at several points in space at once, is called superposition of quantum states and are usually described by the wave function, introduced in 1926 by the German physicist E. Schrödinger. The modulus of the value of the wave function at any point, squared, determines the probability of finding a particle at that point in this moment. After measuring the position of a particle, its wave function seems to shrink (collapse) to the point where the particle was detected, and then begins to spread out again. The property of quantum particles to be in many states simultaneously, called quantum parallelism, has been successfully used in quantum computing.

Quantum bit

The basic cell of a quantum computer is a quantum bit, or, for short, qubit(q-bit). This quantum particle, having two basic states, which are denoted 0 and 1 or, as is customary in quantum mechanics, and. Two values ​​of the qubit can correspond, for example, to the ground and excited states of the atom, the up and down directions of the spin of the atomic nucleus, the direction of the current in the superconducting ring, two possible positions of the electron in the semiconductor, etc.

Quantum register

The quantum register is structured almost the same as the classical one. This is a chain of quantum bits on which one- and two-bit logical operations can be performed (similar to the use of NOT, 2I-NOT, etc. operations in a classical register).

The basic states of a quantum register formed by L qubits include, as in the classical one, all possible sequences of zeros and ones of length L. There can be 2 L different combinations in total. They can be considered a record of numbers in binary form from 0 to 2 L -1 and designated. However, these basic states do not exhaust all possible values ​​of the quantum register (unlike the classical one), since there are also superposition states defined by complex amplitudes related by the normalization condition. A classical analogue for most possible values ​​of a quantum register (with the exception of basic ones) simply does not exist. The states of a classical register are just a pitiful shadow of the entire wealth of states of a quantum computer.

Imagine that an external influence is applied to the register, for example, electrical impulses are applied to a part of the space or laser beams are directed. If it is a classical register, an impulse, which can be considered as a computational operation, will change L variables. If this is a quantum register, then the same pulse can simultaneously convert to variables. Thus, a quantum register is, in principle, capable of processing information several times faster than its classical counterpart. From here it is immediately clear that small quantum registers (L<20) могут служить лишь для демонстрации отдельных узлов и принципов работы квантового компьютера, но не принесут большой практической пользы, так как не сумеют обогнать современные ЭВМ, а стоить будут заведомо дороже. В действительности квантовое ускорение обычно значительно меньше, чем приведенная грубая оценка сверху (это связано со сложностью получения большого количества амплитуд и считывания результата), поэтому практически полезный квантовый компьютер должен содержать тысячи кубитов. Но, с другой стороны, понятно, что для достижения действительного ускорения вычислений нет необходимости собирать миллионы квантовых битов. Компьютер с памятью, измеряемой всего лишь в килокубитах, будет в некоторых задачах несоизмеримо быстрее, чем классический суперкомпьютер с терабайтами памяти.

It is worth noting, however, that there is a class of problems for which quantum algorithms do not provide significant acceleration compared to classical ones. One of the first to show this was the Russian mathematician Yu. Ozhigov, who constructed a number of examples of algorithms that, in principle, cannot be accelerated by a single clock cycle on a quantum computer.

Nevertheless, there is no doubt that computers operating according to the laws of quantum mechanics are a new and decisive stage in the evolution of computing systems. All that remains is to build them.

QUANTUM COMPUTERS TODAY

Prototypes of quantum computers already exist today. True, so far it has been experimentally possible to assemble only small registers consisting of only a few quantum bits. Thus, recently a group led by American physicist I. Chang (IBM) announced the assembly of a 5-bit quantum computer. Undoubtedly, this is a great success. Unfortunately, existing quantum systems are not yet capable of providing reliable calculations, as they are either poorly controlled or very susceptible to noise. However, there are no physical restrictions on building an effective quantum computer; it is only necessary to overcome technological difficulties.

There are several ideas and proposals on how to make reliable and easily controllable quantum bits.

I. Chang develops the idea of ​​using the spins of the nuclei of some organic molecules as qubits.

Russian researcher M.V. Feigelman, working at the Institute of Theoretical Physics named after. L.D. Landau RAS, proposes to assemble quantum registers from miniature superconducting rings. Each ring plays the role of a qubit, and states 0 and 1 correspond to the direction of the electric current in the ring - clockwise and counterclockwise. Such qubits can be switched using a magnetic field.

At the Institute of Physics and Technology of the Russian Academy of Sciences, a group led by Academician K. A. Valiev proposed two options for placing qubits in semiconductor structures. In the first case, the role of a qubit is played by an electron in a system of two potential wells created by a voltage applied to mini-electrodes on the surface of the semiconductor. States 0 and 1 are the positions of the electron in one of these wells. The qubit is switched by changing the voltage on one of the electrodes. In another version, the qubit is the nucleus of a phosphorus atom embedded at a certain point of the semiconductor. States 0 and 1 - directions of nuclear spin along or against the external magnetic field. Control is carried out using the combined action of magnetic pulses of resonant frequency and voltage pulses.

Thus, research is actively underway and it can be assumed that in the very near future - in ten years - an effective quantum computer will be created.

A LOOK INTO THE FUTURE

Thus, it is quite possible that in the future, quantum computers will be manufactured using traditional methods of microelectronic technology and contain many control electrodes, reminiscent of a modern microprocessor. In order to reduce the noise level, which is critical for the normal operation of a quantum computer, the first models will apparently have to be cooled with liquid helium. It is likely that the first quantum computers will be bulky and expensive devices that will not fit on a desk and are maintained by a large staff of systems programmers and hardware adjusters in white coats. First, only government agencies will have access to them, then wealthy commercial organizations. But the era of conventional computers began in much the same way.

What will happen to classic computers? Will they die off? Hardly. Both classical and quantum computers have their own areas of application. Although, most likely, the ratio on the market will gradually shift towards the latter.

The introduction of quantum computers will not lead to the solution of fundamentally unsolvable classical problems, but will only speed up some calculations. In addition, quantum communication will become possible - the transfer of qubits over a distance, which will lead to the emergence of a kind of quantum Internet. Quantum communication will make it possible to provide a secure (by the laws of quantum mechanics) connection of everyone with each other from eavesdropping. Your information stored in quantum databases will be more reliably protected from copying than it is now. Firms producing programs for quantum computers will be able to protect them from any, including illegal, copying.

For a deeper understanding of this topic, you can read the review article by E. Riffel and V. Polak, “Fundamentals of Quantum Computing,” published in the Russian journal “Quantum Computers and Quantum Computing” (No. 1, 2000). (By the way, this is the first and so far the only journal in the world dedicated to quantum computing. Additional information about it can be found on the Internet at http://rcd.ru/qc.). Once you have mastered this work, you will be able to read scientific articles on quantum computing.

Somewhat more preliminary mathematical preparation will be required when reading the book by A. Kitaev, A. Shen, M. Vyaly “Classical and Quantum Computations” (Moscow: MTsNMO-CheRo, 1999).

A number of fundamental aspects of quantum mechanics, essential for carrying out quantum calculations, are discussed in the book by V. V. Belokurov, O. D. Timofeevskaya, O. A. Khrustalev “Quantum teleportation - an ordinary miracle” (Izhevsk: RHD, 2000).

The RCD publishing house is preparing to publish a translation of A. Steen's review on quantum computers as a separate book.

The following literature will be useful not only educationally, but also historically:

1) Yu. I. Manin. Computable and incomputable.

M.: Sov. radio, 1980.

2) J. von Neumann. Mathematical foundations of quantum mechanics.

M.: Nauka, 1964.

3) R. Feynman. Simulation of physics on computers // Quantum computer and quantum computing:

Sat. in 2 volumes - Izhevsk: RHD, 1999. T. 2, p. 96-123.

4) R. Feynman. Quantum mechanical computers

// Ibid., p. 123.-156.

See the issue on the same topic

The creation of a universal quantum computer is one of the most difficult problems of modern physics, the solution of which will radically change humanity’s ideas about the Internet and methods of information transfer, cybersecurity and cryptography, electronic currencies, artificial intelligence and machine learning systems, methods for synthesizing new materials and medicines, approaches to modeling complex physical, quantum and ultra-large (Big Data) systems.

The exponential growth of dimensionality when attempting to calculate real systems or the simplest quantum systems is an insurmountable obstacle for classical computers. However, in 1980, Yuri Manin and Richard Feynman (in 1982, but in more detail) independently put forward the idea of ​​using quantum systems for computing. Unlike classical modern computers, quantum circuits use qubits (quantum bits) for calculations, which by their nature are quantum two-level systems and make it possible to directly use the phenomenon of quantum superposition. In other words, this means that a qubit can simultaneously be in states |0> and |1>, and two interconnected qubits can simultaneously be in states |00>, |10>, |01> and |11>. It is this property of quantum systems that should provide an exponential increase in the performance of parallel computing, making quantum computers millions of times faster than the most powerful modern supercomputers.

In 1994, Peter Shor proposed a quantum algorithm for factoring numbers into prime factors. The question of the existence of an effective classical solution This problem is extremely important and is still open, while Shor’s quantum algorithm provides exponential acceleration relative to the best classical analogue. For example, a modern supercomputer in the petaflop range (10 15 operations/sec) can resolve a number with 500 decimal places in 5 billion years; a quantum computer in the megahertz range (10 6 operations/sec) would solve the same problem in 18 seconds. It is important to note that the complexity of solving this problem is the basis of the popular RSA cryptographic security algorithm, which will simply lose relevance after the creation of a quantum computer.

In 1996, Lov Grover proposed a quantum algorithm for solving the enumeration (search) problem with quadratic acceleration. Despite the fact that the acceleration of Grover's algorithm is noticeably lower than Shor's algorithm, its wide range of applications is important, and the obvious impossibility of accelerating the classic version of brute force. Today, more than 40 effective quantum algorithms are known, most of which are based on the ideas of the Shor and Grover algorithms, the implementation of which is an important step towards the creation of a universal quantum computer.

The implementation of quantum algorithms is one of the priority tasks of the Research Center for Physics and Mathematics. Our research in this area is aimed at developing multi-qubit superconducting quantum integrated circuits to create universal quantum information processing systems and quantum simulators. The basic element of such circuits is Josephson tunnel junctions, consisting of two superconductors separated by a thin barrier - a dielectric about 1 nm thick. Superconducting qubits based on Josephson junctions when cooled in dissolution cryostats to almost the temperature absolute zero(~20 mK) exhibit quantum mechanical properties, demonstrating quantization of electric charge (charge qubits), phase or flux of the magnetic field (flux qubits) depending on their design. Capacitive or inductive coupling elements, as well as superconducting coplanar resonators, are used to combine qubits into circuits, and control is carried out by microwave pulses with controlled amplitude and phase. Superconducting circuits are particularly attractive because they can be fabricated using planar mass technologies used in the semiconductor industry. At the Research Center for Physics and Mathematics, we use equipment (R&D class) from the world's leading manufacturers, specially designed and created for us, taking into account the peculiarities of the technological processes for manufacturing superconducting quantum integrated circuits.

Although the quality of superconducting qubits has improved by almost several orders of magnitude over the past 15 years, superconducting quantum integrated circuits are still very unstable compared to classical processors. Building a reliable universal multiqubit quantum computer requires solving a large number of physical, technological, architectural and algorithmic problems. The REC for Physics and Mathematics has been formed comprehensive program research and development towards the creation of multi-qubit superconducting quantum circuits, including:

• methods of formation and research of new materials and interfaces;
• design and manufacturing technology of quantum circuit elements;
• scalable fabrication of highly coherent qubits and high-quality resonators;
• tomography (characteristic measurements) of superconducting qubits;
• control of superconducting qubits, quantum switching (entanglement);
• error detection methods and error correction algorithms;
• development of multi-qubit quantum circuit architecture;
• superconducting parametric amplifiers with quantum noise level.

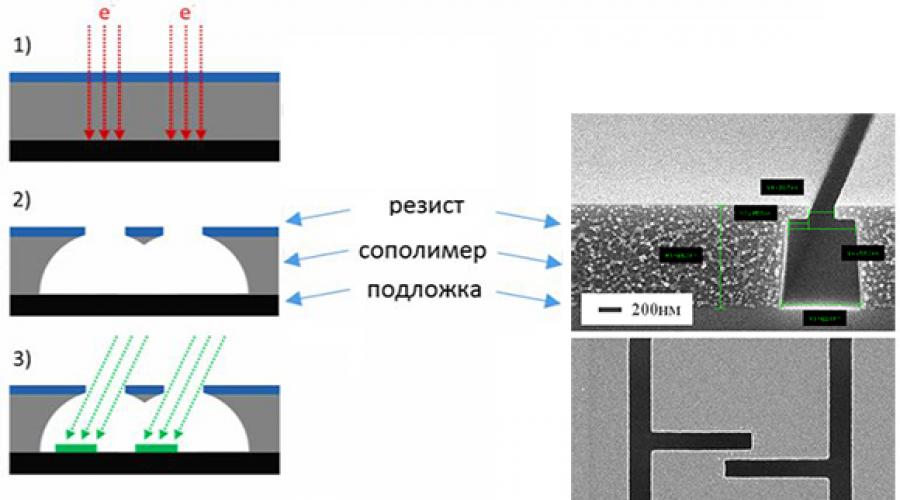
Due to their nonlinear properties with ultra-low losses (by nature) and scalability (manufactured by lithographic methods), Josephson junctions are extremely attractive for creating quantum superconducting circuits. Often, to fabricate a quantum circuit, it is necessary to form hundreds and thousands of Josephson junctions with characteristic dimensions of the order of 100 nm in a np crystal. Wherein reliable operation circuits is implemented only if the parameters of the transitions are accurately reproduced. In other words, all transitions of quantum circuits must be absolutely identical. To do this, they resort to the use of the most modern methods of electron beam lithography and subsequent high-precision shadow deposition through resistive or rigid masks.

The formation of Josephson junctions is carried out by standard ultra-high-resolution lithography methods using two-layer resistive or rigid masks. When such a two-layer mask is developed, windows are formed for the deposition of superconductor layers at such angles that the processes result in the superposition of the deposited layers. Before deposition of the second superconductor layer, a very high quality Josephson junction dielectric tunnel layer is formed. After the Josephson junctions are formed, the two-layer mask is removed. At the same time, at each stage of transition formation, a critical factor is the creation of “ideal” interfaces - even atomic contamination radically worsens the parameters of the manufactured circuits as a whole.

FMN has developed an aluminum technology for the formation of Josephson junctions Al–AlOx–Al with minimum sizes in the range of 100-500 nm and the reproducibility of transition parameters with respect to the critical current is no worse than 5%. Continuing technological research is aimed at searching for new materials, improving technological operations for forming transitions, and approaches to integration with new route technological processes and increasing the reproducibility of junction manufacturing when increasing their number to tens of thousands of pieces on a chip.

Josephson qubits (quantum two-level system or "artificial atom") are characterized by the typical splitting of the energy of the ground excited state into levels and are driven by standard microwave pulses (external adjustment of the distance between levels and eigenstates) at a splitting frequency in the gigahertz range. All superconducting qubits can be divided into charge (quantization of electric charge) and flow qubits (quantization of magnetic field or phase), and the main criteria for the quality of qubits from the point of view of quantum computing are relaxation time (T1), coherence time (T2, dephasing) and time to performing one operation. The first charge qubit was realized in the NEC laboratory (Japan) by a scientific group led by Y. Nakamura and Yu. Pashkin (Nature 398, 786–788, 1999). Over the past 15 years, the coherence times of superconducting qubits have been improved by leading research groups by nearly six orders of magnitude, from nanoseconds to hundreds of microseconds, enabling hundreds of two-qubit operations and error correction algorithms.

At REC FMS we develop, manufacture and test charge and flow qubits various designs(streaming, fluxoniums, 2D/3D transmons, X-mons, etc.) with aluminum Josephson junctions, we conduct research into new materials and methods for creating highly coherent qubits, aimed at improving the basic parameters of superconducting qubits.

The center's specialists are developing thin-film transmission lines and high-quality superconducting resonators with resonant frequencies in the range of 3-10 GHz. They are used in quantum circuits and memories for quantum computing, enabling control of individual qubits, communication between them, and readout of their states in real time. The main task here is to increase the quality factor of the structures created in the single-photon regime at low temperatures.

In order to improve the parameters of superconducting resonators, we conduct research into various types of their designs, thin film materials (aluminum, niobium, niobium nitride), film deposition methods (electron beam, magnetron, atomic layer) and the formation of topologies (explosive lithography, various etching processes ) on various substrates (silicon, sapphire) and integration various materials in one scheme.

Scientific groups from various fields of physics have long been studying the possibility of coherent interaction (communication) of quantum two-level systems with quantum harmonic oscillators. Until 2004, such interaction could only be achieved in experiments in atomic physics and quantum optics, where a single atom coherently exchanges a single photon with single-mode radiation. These experiments made a great contribution to the understanding of the mechanisms of interaction of light with matter, quantum physics, physics of coherence and decoherence, and also confirmed theoretical basis quantum computing concepts. However, in 2004, a research team led by A. Wallraff (Nature 431, 162-167 (2004)) was the first to demonstrate the possibility of coherent coupling of a solid-state quantum circuit with a single microwave photon. Thanks to these experiments and after solving a number of technological problems, principles for creating controlled solid-state two-level quantum systems were developed, which formed the basis new paradigm quantum electrodynamics circuits (QED circuits) have been actively studied in recent years.

QED circuits are extremely attractive both from the point of view of studying the features of the interaction of various elements of quantum systems and creating quantum devices for practical use. We explore different types of interaction schemes for QED circuit elements: effective communication qubits and control elements, circuit solutions for qubit entanglement, quantum nonlinearity of interaction of elements with a small number of photons, etc. These studies are aimed at developing a base of practical experimental methods for creating multi-qubit quantum integrated circuits.

The main goal of research in this direction at FMS is to develop a technology for creating a metrological, methodological and algorithmic base for implementing Shor and Grover algorithms using multiqubit quantum circuits and demonstrating quantum acceleration compared to classical supercomputers. This extremely ambitious scientific and technical task requires solving a colossal number of theoretical physical, technological, circuit design, metrological and algorithmic problems, which leading scientific groups and IT companies are currently actively working on.

Research and development in the field of quantum computing is carried out in close cooperation with leading Russian scientific teams of ISSP RAS, MISIS, MIPT, NSTU and RKTs under the management of world-famous Russian scientists.

Historical reference

Quantum computing are unthinkable without control over the quantum state of individual elementary particles. Two physicists - the Frenchman Serge Lroche and the American David Wineland - succeeded. Lrosh caught single photons in the resonator and “unhooked” them from the outside world for a long time. Wineland trapped single ions with specific quantum states and isolated them from external influences. Harosh used atoms to observe the state of the photon. Wineland used photons to change the states of ions. They managed to make progress in studying the relationship between the quantum and classical worlds. In 2012 they were awarded Nobel Prize in physics for “breakthrough experimental methods, which made it possible to measure and control individual quantum systems."

The operation of quantum computers is based on the properties of a quantum bit of information. If computing processes use P qubits, then the Hilbert state space of a quantum system has a dimension equal to 2". Under Hilbert space we will understand a dimensional vector space in which the scalar product is defined under the condition that the value tends to P to infinity.

In our case, this means that there are 2" base states, and the computer can operate on a superposition of these 2" base states.

Note that an impact on any qubit immediately leads to a simultaneous change in all 2” base states. This property is called "quantum parallelism».

Quantum computing is a unitary transformation. This means that a linear transformation is carried out with complex coefficients, keeping the sum of the squares of the transformed variables unchanged. A unitary transformation is an orthogonal transformation in which the coefficients form a unitary matrix.

Under unitary matrix we will understand the square matrix ||aj|, the product of which by the complex conjugate and transposed matrix || aJI gives the identity matrix. Numbers ajk And a ki complex. If the numbers a ik are real numbers, then the unitary matrix will be orthogonal. A certain number of qubits form the quantum register of a computer. In such a chain of quantum bits, one- and two-bit logical operations can be carried out in the same way as the operations NOT, NAND, 2 OR-HE, etc. are carried out in a classical register. (Fig. 5.49).

Specific number N registers form essentially a quantum computer. The operation of a quantum computer occurs in accordance with developed calculation algorithms.

Rice. 5.49.

NOT - boolean NOT; CNOT - controlled NOT

Qubits as information carriers have a number of interesting properties that completely distinguish them from classical bits. One of the main theses of quantum information theory is state entanglement. Suppose there are two two-level qubits A And IN, realized in the form of an atom with an electronic or nuclear spin, a molecule with two nuclear spins. Due to the interaction of two subsystems A And IN a nonlocal correlation arises that is purely quantum in nature. This correlation can be described by the mixed state density matrix

Where p i- population or probability i- state, so R ( + p 2 + p 3 + + Ra = 1-

The property of coherent quantum states to have a sum of probabilities equal to one is called entanglement, or coupling, of states. Entangled, or entangled, quantum objects are connected to each other no matter how far they are located from each other. If the state of one of the linked objects is measured, then information about the state of other objects is immediately obtained.

If two qubits are interlocked, then they are devoid of individual quantum states. They depend on each other in such a way that the measurement for one type gives “O”, and for the other - “1” and vice versa (Fig. 5.50). In this case, the maximally linked pair is said to carry one e-bit cohesion.

Entangled states are a resource in quantum computing devices, and methods for reliably generating entangled qubits must be developed to replenish the number of entangled states. One of the methods

Rice. 5.50. The maximally entangled pair of qubits scheme is an algorithmic way to obtain entangled qubits on ions in traps, nuclear spins, or a pair of photons. The process of decay of a particle in a singlet state into two particles can be very effective. In this case, pairs of particles are generated that are entangled in coordinate, momentum, or spin.

Developing a comprehensive theory of entanglement is a key goal of quantum information theory. With its help, it will be possible to get closer to solving the problems of teleportation, ultra-dense coding, cryptography, and data compression. For this purpose, quantum algorithms are being developed, including quantum Fourier transforms.

The calculation scheme on a quantum computer has the following algorithm: a system of qubits is formed, on which the initial state is recorded. Through unitary transformations, the state of the system and its subsystems changes when logical operations are performed. The process ends with the measurement of new qubit values. The role of connecting conductors of a classical computer is played by qubits, and the logical blocks of a classical computer are played by unitary transformations. This concept of a quantum processor and quantum logic gates was formulated in 1989 by David Deutsch. He then proposed a universal logic block that could be used to perform any quantum computation.

Doina-Jozhi algorithm allows you to determine “in one calculation” whether the function of a binary variable /(/?) is constant (f x (ri)= Oh, f 2 (ri) = 1 regardless P) or "balanced" (f 3 ( 0) = 0,/ 3 (1) = 1;/ 4 (0) = 1, / 4 (1) = 0).

It turned out that two basic operations are sufficient to construct any calculation. The quantum system gives a result that is correct only with some probability. But by slightly increasing the operations in the algorithm, you can bring the probability of obtaining as close as you like correct result to one. Using basic quantum operations, it is possible to simulate the operation of ordinary logic gates that make up ordinary computers.

Grover's algorithm allows us to find a solution to the equation f(x) = 1 for 0 x in O(VN) time and is intended for database lookup. Grover's quantum algorithm is obviously more efficient than any algorithm for unordered search on a classical computer.

Shor factorization algorithm allows you to determine for prime factors aub given integer M= a"Xb by using an appropriate quantum circuit. This algorithm allows you to find the factors of an A-digit integer. It can be used to estimate the computational process time. At the same time, Shor's algorithm can be interpreted as an example of a procedure for determining the energy levels of a quantum computing system.

Zalka-Wiesner algorithm allows you to simulate the unitary evolution of a quantum system P particles in almost linear time using O(n) qubits

Simon's algorithm solves the black box problem exponentially faster than any classical algorithm, including probabilistic algorithms.

Error Correction Algorithm makes it possible to increase the noise immunity of a quantum computing system that is susceptible to the destruction of fragile quantum states. The essence of this algorithm is that it does not require cloning qubits and determining their state. A quantum logic circuit is formed that is capable of detecting an error in any qubit without actually reading the individual state. For example, triplet 010 passing through such a device detects an incorrect middle bit. The device flips it over without determining the specific values ​​of any of the three bits. Thus, based on information theory and quantum mechanics, one of the fundamental algorithms arose - quantum error correction.

These problems are important for creating a quantum computer, but they fall within the purview of quantum programmers.

A quantum computer is more progressive than a classical one in a number of indicators. Most modern computers operate according to the von Neumann or Harvard scheme: P memory bits store state and are changed by the processor every time tick. In a quantum computer, a system of P qubits is in a state that is a superposition of all base states, so a change in the system affects everyone 2" basic states simultaneously. Theoretically, the new scheme can work exponentially faster than the classic one. An almost quantum database search algorithm shows a quadratic increase in power compared to classical algorithms.

From time to time we see a flurry of news about quantum computing. This topic is getting a lot of attention, with one company claiming to have the encryption algorithm you'll soon need as quantum computers render current encryption algorithms useless.

For an inquisitive person, such statements raise questions. What is quantum computing (Figure 1)? It's real? If so, how does it work? And how does this relate to cryptography? Then more personal questions arise. Could Quantum Computing Change the Way I Design? Should I study this material?

Even in artists' renderings, quantum computing elements are unlike anything in the digital hardware world.

Figure 1 – Visualization of quantum computing elements

It turns out it's not too much simple questions for studying. The relevant literature mainly falls into one of two genres. The first is intended for a general readership and treats quantum mechanics as hell: dark, possibly dangerous, and completely incomprehensible. After reading such literature, it is quite difficult to draw any conclusions.

The second genre is completely different, but equally "useful", written by experts in order to impress other experts. This genre is characterized by the use of terms such as Turing machine, Richard Feynman's name, Hilbert space and Hadamard transform, all of the above and about 75 more words, followed by a tangle of equations with unfamiliar and inexplicable terminology. Of course, you all remember well what |0> means!

Three parallel universes

One of the reasons why this topic is so complex is that quantum computing spans three disciplines with very different terminology and interests. It all started with theoretical physicists. Back in 1980, physicist Paul Benioff ( Paul Benioff) from Argonne National Laboratory described how some quantum mechanical effects could be used to implement a Turing machine. Two years later famous physicist Richard Feynman also raised the question of a computer using quantum behavior.

But the idea was picked up by a completely different group: computer scientists and mathematicians. Taking from physics the basic ideas of the quantum bit (qubit) and reversible unitary transformations (which they called quantum gates or quantiles), computer scientists studied what calculations could be performed if ideal qubits and quantum gates existed. They found cases where such supposed computers could be much faster than conventional digital computers.

This result prompted experimental physicists - the third group - to begin attempts to create physical devices, which could be close to ideal qubits and quantum gates. These were long, resource-intensive studies that still have not proven that a truly working quantum computer is physically possible. But this possibility is extremely encouraging.

Some clarifications

So what is this imaginary computer that we are interested in? Let's first clear up some misunderstandings. A quantum computer is not an ordinary computer that simulates quantum mechanical phenomena. Nor is this an ordinary digital computer, built from some transistors (from the end of Moore's Law) so tiny that they store or switch individual quanta of energy.

Instead, quantum computers are machines based on a unique behavior described by quantum mechanics, and completely different from the behavior classical systems. One of these differences is the ability of a particle or group of particles in some respect to be in only two discrete quantum basic states - let's call them 0 and 1. We will do without funny parentheses here (notations adopted in quantum theory - added by the translator). Examples of this kind can be spin electron, photon polarization or quantum dot charge.

Second, quantum computing depends on the property of superposition—the counterintuitive ability of a particle to be in some combination of both basic states 0 and 1 at the same time, until a measurement is made. Once you measure such a state, it turns into a 0 or 1, and all other information disappears. Quantum mechanics correctly describes such a combined state as the sum of two basic states, each of which is multiplied by some complex factor. Full size of these coefficients is always equal to 1. Such a state can be represented as a unit vector starting at the origin and ending somewhere on a sphere called the Bloch sphere, which is shown in Figure 2. The key point here is that the square (modulus - added by the translator) of the complex coefficient for the base state 0 represents the probability that as a result of the measurement the qubit will be found in the base state 0, similarly for the base state 1. And when you make a measurement, you will always get or exactly state 0, or exactly state 1.

Figure 2 – Bloch sphere – one of the ways to visualize quantum superposition in a qubit

This (superposition property - added by translator) is important because it allows the qubit to be in both states 0 and 1 at the same time. Therefore, a register consisting of n qubits can simultaneously “contain” all possible binary numbers n bits long. This allows a quantum computer to perform a single operation not just on one n-bit integer, but on all possible n-bit integers at once—very significant parallelism as n increases.

Third, quantum computing depends on the ability of a quantum gate to change these coefficients, and therefore the probability of measuring any given number, in a predictable manner. If you start with a state in which all the coefficients in all qubits are equal, and then measure all the qubits in a register, you are equally likely to find any string of bits between a string of all zeros and a string of all ones, inclusive. But by running this initial state through a carefully chosen sequence of quantum gates, a quantum computer can change these coefficients so that the state you are most likely to measure as an output is the result of some calculation, for example it is very likely that you measure the bits of a number that is a perfect square.

Computer on paper

But what does all this have to do with real computing? To answer this question, we must shift our attention from theoretical physicists to computer scientists and mathematicians. To get practical results, we must be able to map the qubit register into a specific superposition of states. We need quantum gates, possibly wires and some kind of output devices.

All this is easy for computer scientists - they can simply assume that these ideas have already been implemented in real life. However, they will have to make concessions to quantum mechanics. To avoid breaking the laws of quantum physics, computer scientists must require quantum gates to be reversible—you can put the result at the output and get the correct input values ​​at the input. And they insist that quantum gates must be unitary transformations. According to matrix algebra, this means that when you put a qubit state through a quantum gate, the state you get will be either 0 or 1 when measured, and the sum of the probabilities of the squares (modules - added by translator) of these coefficients will remain equal unit.

Note that these quantum gates, even in theory, are very different from ordinary logic gates. For example, most Boolean functions are not invertible. It is impossible to output the input data from a NAND gate unless the output is 0. And of course, logic gates only work with ones and zeros (states 1 and 0), while quantum gates work by rotating a vector inside a Bloch sphere . In fact, there is nothing in common between them except the name.

Computer scientists have discovered that a very small set of quantum gates is sufficient to emulate a Turing machine—just a set of single-input quantum gates and one two-input quantum gate. The most commonly used example of a two-input quantum gate is the “controlled NOT” (CNOT). This reversible function either flips the vector state of a qubit or leaves it unchanged, depending on the state of the second qubit. It's more like a quantum XOR analogy.

Possible benefits

We still haven't answered the question of how all this can be used. The answer is that if you connect enough quantum gates together in a suitable manner, and if you can prepare input qubits representing all possible numbers in your input data domain, then at the output of the quantum gate array you can, in theory, measure the bits that represent the values ​​of some useful function.

Let's give an example. In 1994, mathematician Peter Shor, at Bell Labs, developed an algorithm for factoring very large numbers using quantum routines. This factorization is a vital problem in applied mathematics because there is no analytical solution: the only way is trial and error, and you can only make the algorithm faster by choosing the appropriate trial numbers more skillfully. Accordingly, when you make the input number very large, the amount of trial and error becomes enormous. It is no coincidence that this is the basis of cryptography algorithms like RSA. RSA and elliptic curve ciphers are difficult to break, especially because it is so difficult to factor huge numbers.

Shor's algorithm combined some traditional calculations with two quantum functions that directly speed up the algorithm in the trial and error part, essentially trying all possible numbers at the same time, a demonstration of the algorithm is shown in Figure 3. One of these quantum functions performs modular exponentiation, and the other performs a quantum version of the fast Fourier transform (FFT). For reasons that only a mathematician could love, if we were to introduce a set of n qubits prepared so that together they represent all possible binary numbers up to length n, then in quantum gates the different states in a superposition cancel each other out - like the interference of two coherent light rays - and we are left with a certain structure of states in the output register.

Figure 3 – Shor's algorithm depends on quantum routines for modular exponentiation and FFT operations. (image courtesy of Tyson Williams)

This procedure does not produce a prime factor - it is only an intermediate step that allows one to calculate a possible prime factor. This calculation is done by measuring the qubits—note that we are in the realm of possibility, but not precision, of measuring the most likely state of each qubit—and then doing a lot of routine calculations on a regular processor (CPU) to make sure the result is correct.

All of this may seem hopelessly complicated and impossible. But the ability of quantum exponentiation and quantum FFT to work simultaneously with all possible powers of 2 to find the largest prime factor makes Shor's algorithm faster than conventional calculations for large numbers, even when using rather slow theoretical quantum routines.

Shor's algorithm is a shining example of quantum computing because it is both unlike conventional computing and potentially extremely important. But he is not alone. The US National Institute of Standards and Technology (NIST) maintains a large library of quantum computing algorithms in its Quantum Algorithms Zoo, at math.nist.gov/quantum/zoo/.

Are these algorithms just math exercises? It's too early to say for sure. But in practice, researchers have actually created laboratory quantum calculators with several working qubits. These machines have successfully factored the number 15 (first done at IBM in 2001), predictably producing 3 and 5, and the current world record is 21 (done by a multi-institution team in 2012). So for small numbers the idea works. The suitability of this approach for large numbers can only be tested in the future on machines with more qubits. And this brings the issue to a practical level.

Path to Realization

To create functional quantum computing devices, it is necessary to go through a number of implementation stages. We must build working qubits - not just five, but thousands. We must organize a structure of quantum gates and the equivalent of wires - unless we can get the gates to act directly on the state in the input quantum register. All this complex tasks, and the timetable for their resolution is unpredictable.

Unfortunately, the problems are related not so much to the novelty of the problems, but to the laws of quantum mechanics and classical physics. Perhaps the most important and least familiar of these is called decoherence. The role of a qubit is to hold a physical object—such as an ion, a packet of photons, or an electron—in place so that we can influence it and ultimately measure a quantized quantity such as charge or spin. For this quantity to behave in a quantum rather than classical manner, we must be able to restrict its state to a superposition of two pure base states, which we called 0 and 1.

But the nature of quantum systems is such that it links them to the things around them, greatly increasing the number of possible underlying states. Physicists call this blurring of pure states decoherence. An analogy could be a coherent laser beam in a light guide, scattered by inhomogeneities in the material and smeared from the superposition of two modes into completely incoherent light. The goal of creating a physical qubit is to prevent decoherence for as long as possible.

In practice, this means that even a single qubit is a complex laboratory instrument, perhaps using lasers or high-frequency radio transmitters, precisely controlled electric and magnetic fields, exact dimensions, special materials and possibly cryogenic cooling. Its use is essentially a complex experimental procedure. Even with all these efforts, today this “as long as possible” is measured in tens of microseconds. Thus, you have very little time to perform quantum calculations before your qubits lose their coherence. That is, before the information disappears.

Today, these limitations preclude the possibility of large quantum registers or computations that require more than a few microseconds. However, research is currently underway in microelectronics to create much more extensive arrays of qubits and quantum gates.

However, this work itself is somewhat disjointed because it is not yet certain which physical phenomenon to use to store quantum states. There are qubit designs that quantize the polarization of photons, the charge of electrons trapped in quantum dots, the net spin of supercooled ions in a trap, charge in a device called a transmon, and several other approaches.

The type of qubit you choose will naturally determine the quantum gate implementation. For example, you can use the interaction of radio pulses with internal spins in molecules in a trap, or the interaction of beam splitters with photon modes in waveguides. Obviously, the essence of the matter lies deep in the field of experimental physics. And, as already mentioned, the implementation of qubits or quantum gates requires the use of a large number of different equipment, from digital logic to lasers or radio transmitters, antennas, to cryogenic coolers.

The implementation of a qubit also depends on how the state of the qubit is measured. You may need an ultra-sensitive photometer or bolometer, a resistive bridge, or some other incredibly sensitive device to measure the qubits and force the superposition state into the ground state. And on top of that, this process of measuring the state of a qubit introduces another problem unfamiliar to traditional computing: getting the wrong answer.

Doubts

There are two main types of problems with extracting the ground state from a qubit. First, you are measuring a quantum superposition, not a classical quantity. Assuming the qubit remains coherent, you will get one or the other of the base states, but you cannot be sure in advance which one you will get: you can only be sure that the probability of you getting a particular state will be the square (modulus – added by the translator) of the coefficient of this state in superposition. If you measure a qubit in exactly the same state a hundred times, you will get a distribution of zeros and ones that converges to the squares of the coefficients.

So you don't know whether the baseline state you measured in some trial actually has the highest probability. Once you've read the quantum output register, measuring the bits, thereby setting them all to their base states, you have three options. You may doubt that you have the right answer and move on. You can check with traditional calculations, like Shor's algorithm does, to see if the number you thought was actually the correct solution. Or, you can repeat the calculation a large number of times, sequentially or in parallel, and take the most frequently occurring result. You can also organize your calculations so that the answer is a probability distribution of the underlying states rather than a specific binary number. In this case, repetition is also necessary.

This is true even for a theoretically perfect quantum computer. But the actual implementation has one more problem: good old classic noise. Even if everything goes well, there is no decoherence of the qubits, and the calculation is designed to produce an answer with a very high probability, you are still observing qubits while trying to measure very, very small physical quantities. The noise is still there. Again, the only solution is to either detect the error by further calculations, or to perform the calculations so many times that you are willing to accept any remaining uncertainty as a result. The concept of a guaranteed correct answer is alien to the very essence of quantum computing.

If all this doesn't paint a rosy picture of the future of quantum computing, then it's something to be taken very seriously. The search is underway best choice to implement qubits, although the answer may depend on the algorithm. Microelectronics scientists are working to miniaturize quantum components using new materials and structures that would enable the creation of very large arrays of quantum computing devices that could be mass-produced like traditional processor chips. Computer scientists are developing prototype assemblers and compilers that can translate an algorithm into the layout of quantum registers and quantum gates in a particular technology.

Is it worth it? Here's one fact. Shore calculated that a modest hybrid—that is, quantum plus conventional—computer could crack the powerful RSA encryption algorithm faster than a conventional computer could encrypt it. Similar results have been found for problems such as sorting and untangling other similar complex math problems. So, there is enough promise in this area to keep researchers excited. But it would be nice to see all this while still alive.

Today I would like to begin publishing a series of notes about this burning topic, on which my new book was recently published, namely an introduction to understanding the quantum computational model. I thank my good friend and colleague Alexander for the opportunity to post guest posts on this topic on his blog.

I have tried to make this short note as simple as possible from the point of view of understanding for the untrained reader who, however, would like to understand what quantum computing is. However, the reader is required to have a basic understanding of computer science. Well, a general mathematical education wouldn’t fit either :). There are no formulas in the article, everything is explained in words. However, you all can ask me questions in the comments and I will try to explain as best I can.

What is quantum computing?

Let's start with the fact that quantum computing is a new, very fashionable topic, which is developing by leaps and bounds in several directions (while in our country, like any fundamental science, it remains in disrepair and is left to a few scientists sitting in their ivory towers ). And now they are already talking about the appearance of the first quantum computers (D-Wave, but this is not a universal quantum computer), new quantum algorithms are published every year, quantum programming languages ​​are created, the shadowy genius of the International Business Machines in secret underground laboratories produces quantum calculations on dozens of qubits.

What is it? Quantum computing is a computing model that differs from the Turing and von Neumann models and is expected to be more efficient for some tasks. At least, problems have been found for which the quantum computing model gives polynomial complexity, while for the classical computing model there are no known algorithms that would have a complexity lower than exponential (but, on the other hand, it has not yet been proven that such algorithms do not exist ).

How can this be? It's simple. The quantum computing model is based on several fairly simple rules for transforming input information, which provide massive parallelization of computing processes. In other words, you can evaluate the value of a function for all its arguments at the same time (and this will be a single function call). This is achieved by special preparation of input parameters and a special type of function.

Lighter Prots teaches that all this is syntactic manipulation with mathematical symbols, behind which, in fact, there is no meaning. There is a formal system with rules for transforming input into output, and this system allows, through the consistent application of these rules, to obtain output from input data. All this ultimately comes down to multiplying a matrix and a vector. Yes Yes Yes. The entire quantum computing model is based on one simple operation - multiplying a matrix by a vector, resulting in another vector as the output.

The luminary Halikaarn, in contrast, teaches that there is an objective physical process that performs the specified operation, and only the existence of which determines the possibility of massive parallelization of function calculations. The fact that we perceive this as multiplying a matrix by a vector is just our less than perfect way of reflecting objective reality in our minds.

We are in our scientific laboratory In the name of the luminaries Prots and Halikaarn, we combine these two approaches and say that the quantum computing model is a mathematical abstraction that reflects an objective process. In particular, the numbers in vectors and matrices are complex, although this does not increase the computational power of the model at all (it would be just as powerful with real numbers), but complex numbers were chosen because an objective physical process was found that carries out such transformations, as the model describes, and in which complex numbers are used. This process is called the unitary evolution of a quantum system.

The quantum computing model is based on the concept of a qubit. This is essentially the same as a bit in classical information theory, but a qubit can take on multiple values ​​at the same time. They say that a qubit is in a superposition of its states, that is, the value of a qubit is a linear combination of its base states, and the coefficients of the base states are precisely complex numbers. The basic states are the values ​​0 and 1, known from classical information theory (in quantum computing they are usually denoted |0> and |1>).

It’s not very clear yet what the trick is. And here’s the trick. The superposition of one qubit is written as A|0> + B|1>, where A and B are some complex numbers, the only constraint on which is that the sum of the squares of their moduli must always be equal to 1. What if we consider two qubits? Two bits can have 4 possible values: 00, 01, 10 and 11. It is reasonable to assume that the two qubits represent a superposition of four base values: A|00> + B|01> + C|10> + D|11>. And so it is. The three qubits are a superposition of eight basic values. In other words, a quantum register of N qubits simultaneously stores 2N complex numbers. Well, from a mathematical point of view, this is a 2N-dimensional vector in a complex-valued space. This is what achieves the exponential power of the quantum computing model.

Next is a function that is applied to the input data. Since the input is now a superposition of all possible values ​​of the input argument, the function must be converted to accept such a superposition and process it. Here, too, everything is more or less simple. Within the quantum computing model, each function is a matrix subject to one constraint: it must be Hermitian. This means that when this matrix is ​​multiplied by its Hermitian conjugate, the identity matrix should be obtained. The Hermitian conjugate matrix is ​​obtained by transposing the original matrix and replacing all its elements with their complex conjugates. This limitation follows from the previously mentioned limitation on the quantum register. The fact is that if such a matrix is ​​multiplied by the vector of a quantum register, the result is a new quantum register, the sum of the squares of the moduli of complex-valued coefficients for the quantum states of which is always equal to 1.

It is shown that any function can be transformed in a special way into such a matrix. Also shown. that any Hermitian matrix can be expressed by the tensor product of a small set of basis matrices representing basic logical operations. Everything here is approximately the same as in the classical computational model. This is a more complex topic that is beyond the scope of this review article. That is, now the main thing to understand is that any function can be expressed in the form of a matrix suitable for use within the quantum computing model.

What happens next? Here we have an input vector, which is a superposition various options values ​​of the function input parameter. There is a function in the form of a Hermitian matrix. The quantum algorithm is a matrix-vector multiplication. The result is a new vector. What kind of nonsense is this?

The fact is that in the quantum computing model there is another operation called measurement. We can measure a vector and get a specific qubit value from it. That is, the superposition collapses into a specific value. And the probability of obtaining one or another value is equal to the square of the modulus of the complex-valued coefficient. And now it’s clear why the sum of squares should be equal to 1, since during the measurement some specific value will always be obtained, and therefore the sum of the probabilities of obtaining them is equal to one.

So what happens? Having N qubits, you can simultaneously process 2N complex numbers. And the output vector will contain the results of processing all these numbers simultaneously. This is the power of the quantum computing model. But you can only get one value, and it can be different each time depending on the probability distribution. This is a limitation of the quantum computing model.

The essence of the quantum algorithm is as follows. An equally probable superposition of all possible values ​​of the input parameter is created. This superposition is fed to the function input. Further, based on the results of its execution, a conclusion is drawn about the properties of this function. The fact is that we cannot get all the results, but we can completely draw conclusions about the properties of the function. And the next section will show some examples.

In the vast majority of sources on quantum computing, the reader will find descriptions of several algorithms, which, in fact, are usually used to demonstrate the power of the computational model. Here we will also briefly and superficially look at such algorithms (two of them, which demonstrate different basic principles of quantum computing). Well, for a detailed acquaintance with them, I again refer to my new book.

Deutsch's algorithm

This is the first algorithm that has been developed to demonstrate the essence and effectiveness of quantum computing. The problem that this algorithm solves is completely divorced from reality, but it can be used to show basic principle, which forms the basis of the model.

So, let there be some function that receives one bit as input and returns one bit as output. Honestly, there could only be 4 such functions. Two of them are constant, meaning one always returns 0, and the other always returns 1. The other two are balanced, meaning they return 0 and 1 in equal numbers of cases. Question: how can you determine in one call to this function whether it is constant or balanced?

Obviously, this cannot be done in the classical computational model. You need to call the function twice and compare the results. But in the quantum computing model this can be done, since the function will be called only once. Let's see…

As already written, we will prepare an equally probable superposition of all possible values ​​of the function’s input parameter. Since we have one qubit at the input, its equal-probability superposition is prepared using one application of the Hadamard gate (this is a special function that prepares equal-probability superpositions:). Next, the Hadamard gate is applied again, which works in such a way that if an equal-probability superposition is fed to its input, it converts it back into states |0> or |1> depending on what phase the equal-probability superposition is in. After this, the qubit is measured, and if it is equal to |0>, then the function in question is constant, and if |1>, then it is balanced.

What happens? As already mentioned, when measuring we cannot obtain all the values ​​of a function. But we can draw certain conclusions about its properties. Deutsch's problem asks about a property of a function. And this property is very simple. After all, how does it work out? If the function is constant, then modulo 2 addition of all its output values ​​always gives 0. If the function is balanced, then modulo 2 addition of all its output values ​​always gives 1. This is exactly the result we got as a result of executing the Deutsch algorithm. We do not know exactly what value the function returned from an equally probable superposition of all input values. We only know that this is also a superposition of results, and if we now transform this superposition in a special way, then unambiguous conclusions will be drawn about the property of the function.

Something like that.

Grover's algorithm

Another algorithm, which shows a quadratic gain compared to the classical computational model, solves a problem that is closer to reality. This is Grover's algorithm, or, as Love Grover himself calls it, the algorithm for finding a needle in a haystack. This algorithm is based on another principle underlying quantum computing, namely amplification.

We have already mentioned a certain phase that a quantum state within a qubit may have. There is no phase as such in the classical model; it is something new within the framework of quantum computing. The phase can be understood as the sign of the coefficient of a quantum state in superposition. Grover's algorithm is based on the fact that a specially prepared function changes the phase of the state |1>.

Grover's algorithm solves the inverse problem. If you have an unordered set of data in which you need to find one element that satisfies the search criterion, Grover's algorithm will help you do this more efficiently than simple brute force. If simple enumeration solves the problem in O(N) function calls, then Grover’s algorithm effectively finds a given element in O(√N) function calls.

Grover's algorithm consists of the following steps:

1. Initialization of the initial state. Again, an equal-probability superposition of all input qubits is prepared.

2. Applying Grover Iteration. This iteration consists of sequential application of the search function (it determines the search criterion for the element) and a special diffusion gate. The diffusion gate changes the coefficients of quantum states, rotating them around the average. This produces amplification, that is, an increase in the amplitude of the desired value. The trick is that it is necessary to apply iteration a certain number of times (√2 n), otherwise the algorithm will return the wrong results.

3. Measurement. After measuring the input quantum register, the desired result is likely to be obtained. If it is necessary to increase the reliability of the answer, then the algorithm is run several times and the cumulative probability of the correct answer is calculated.

The interesting thing about this algorithm is that it allows you to solve an arbitrary problem (for example, any of the NP-complete class), providing, albeit not exponential, but a significant increase in efficiency compared to the classical computational model. A future article will show how this can be done.

However, it can no longer be said that scientists continue to sit in their ivory tower. Despite the fact that many quantum algorithms are developed for some strange and incomprehensible Mathan-like problems (for example, determining the order of an ideal of a finite ring), a number of quantum algorithms have already been developed that solve very applied problems. First of all, these are tasks in the field of cryptography (compromising various cryptographic systems and protocols). Next are typical mathematical problems on graphs and matrices, and such problems have a very wide range of application. Well, there are a number of approximation and emulation algorithms that use the analog component of the quantum computing model.