Координатный метод нахождения угла между прямыми. Метод координат в пространстве: формулы и комментарии репетитора

Координатный метод нахождения угла между прямыми. Метод координат в пространстве: формулы и комментарии репетитора
Координатный метод нахождения угла между прямыми. Метод координат в пространстве: формулы и комментарии репетитора
22.09.2019

В данной статье на примере решения задачи C2 из ЕГЭ разобран способ нахождения с помощью метода координат. Напомним, что прямые являются скрещивающи-мися, если они не лежат в одной плоскости. В частности, если одна прямая лежит в плоскости, а вторая прямая пересекает эту плоскость в точке, которая не лежит на первой прямой, то такие прямые являются скрещивающимися (см. рисунок).

Для нахождения расстояния между скрещивающимися прямыми необходимо:

  1. Провести через одну из скрещивающихся прямых плоскость, которая параллельна другой скрещивающейся прямой.
  2. Опустить перпендикуляр из любой точки второй прямой на полученную плоскость. Длина этого перпендикуляра будет являться искомым расстоянием между прямыми.

Разберем данный алгоритм подробнее на примере решения задачи C2 из ЕГЭ по математике.

Расстояние между прямыми в пространстве

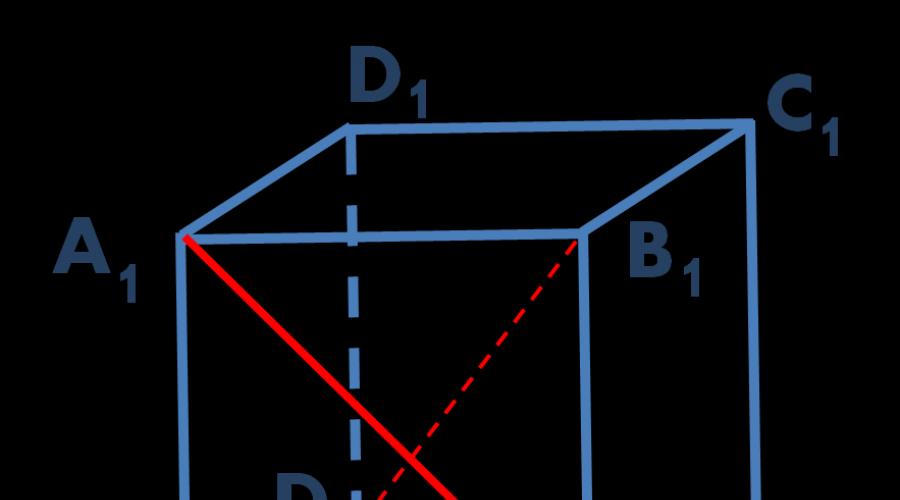
Задача. В единичном кубе ABCDA 1 B 1 C 1 D 1 найдите расстояние между прямыми BA 1 и DB 1 .

Рис. 1. Чертеж к задаче

Решение. Через середину диагонали куба DB 1 (точку O ) проведем прямую, параллельную прямой A 1 B . Точки пересечения данной прямой с ребрами BC и A 1 D 1 обозначаем соответственно N и M . Прямая MN лежит в плоскости MNB 1 и параллельна прямой A 1 B , которая в этой плоскости не лежит. Это означает, что прямая A 1 B параллельна плоскости MNB 1 по признаку параллельности прямой и плоскости (рис. 2).

Рис. 2. Искомое расстояние между скрещивающимися прямыми равно расстоянию от любой точки выделенной прямой до изображенной плоскости

Ищем теперь расстояние от какой-нибудь точки прямой A 1 B до плоскости MNB 1 . Это расстояние по определению будет являться искомым расстоянием между скрещивающимися прямыми.

Для нахождения этого расстояния воспользуемся методом координат. Введем прямоугольную декартову систему координат таким образом, чтобы ее начало совпало с точкой B, ось X была направлена вдоль ребра BA , ось Y — вдоль ребра BC , ось Z — вдоль ребра BB 1 (рис. 3).

Рис. 3. Прямоугольную декартову систему координат выберем так, как показано на рисунке

Находим уравнение плоскости MNB 1 в данной системе координат. Для этого определяем сперва координаты точек M , N и B 1: Полученные координаты подставляем в общее уравнение прямой и получаем следующую систему уравнений:

Из второго уравнения системы получаем из третьего получаем после чего из первого получаем Подставляем полученные значения в общее уравнение прямой:

Замечаем, что иначе плоскость MNB 1 проходила бы через начало координат. Делим обе части этого уравнения на и получаем:

Расстояние от точки до плоскости определяется по формуле.

Использование метода координат при вычислении угла

между плоскостями

Наиболее общий метод нахождения угла между плоскостями - метод координат (иногда - с привлечением векторов). Его можно использовать тогда, когда испробованы все остальные. Но бывают ситуации, в которых метод координат имеет смысл применять сразу же, а именно тогда, когда система координат естественно связана с многогранником, указанным в условии задачи, т.е. явно просматриваются три попарно перпендикулярные прямые, на которых можно задать оси координат. Такими многогранниками являются прямоугольный параллелепипед и правильная четырехугольная пирамида. В первом случае система координат может быть задана выходящими из одной вершины ребрами (рис.1), во втором - высотой и диагоналями основания (рис. 2)

Применение метода координат состоит в следующем.

Вводится прямоугольная система координат в пространстве. Желательно ввести ее «естественным» образом - «привязать» к тройке попарно перпендикулярных прямых, имеющих общую точку.

Для каждой из плоскостей, угол между которыми ищется, составляется уравнение. Проще всего составить такое уравнение, зная координаты трех точек плоскости, не лежащих на одной прямой.

Уравнение плоскости в общем виде имеет вид Ах + By + Cz + D = 0.

Коэффициенты А, В, С в этом уравнении являются координатами нормального вектора плоскости (вектора, перпендикулярного плоскости). Определяем затем длины и скалярное произведение нормальных векторов к плоскостям, угол между которыми ищется. Если координаты этих векторов (А 1 , В 1 ; С 1 ) и (А 2 ; В 2 ; С 2 ), то искомый угол вычисляется по формуле

Замечание. Необходимо помнить, что угол между векторами (в отличие от угла между плоскостями) может быть тупым, и чтобы избежать возможной неопределенности, в числителе правой части формулы стоит модуль.

Решите методом координат такую задачу.

Задача 1. Дан куб ABCDA 1 B 1 C 1 D 1 . Точка К - середина ребра AD, точка L - середина ребра CD. Чему равен угол между плоскостями А 1 KL и A 1 AD?

Решение . Пусть начало системы координат находится в точке А, а оси координат идут вдоль лучей AD, АВ, АА 1 (рис. 3). Ребро куба примем равным 2 (удобно делить пополам). Тогда координаты точек A 1 , К, L таковы: А 1 (0; 0; 2), К(1; 0; 0), L(2; 1; 0).

Рис. 3

Запишем уравнение плоскости А 1 К L в общем виде. Затем подставим в него координаты выбранных точек этой плоскости. Получим систему трех уравнений с четырьмя неизвестными:

Выразим коэффициенты А, В, С через D и придем к уравнению

Разделив обе его части на D (почему D = 0?) и домножив затем на -2, получим уравнение плоскости A 1 KL: 2х - 2 у + z - 2 = 0. Тогда нормальный вектор к этой плоскости имеет координаты (2: -2; 1) . Уравнение плоскости A 1 AD таково: y=0, а координаты нормального вектора к ней, например, (0; 2: 0) . Согласно приведенной выше формуле для косинуса угла между плоскостями получаем:

В задании С2 по математике чаще всего надо решить задачу, в которой надо определить:

  1. Расстояние между двумя точками
  2. Расстояние от точки до прямой
  3. Расстояние от точки до плоскости
  4. Расстояние между скрещивающимися прямыми
  5. Угол между двумя прямыми
  6. Угол между прямой и плоскостью
  7. Угол между плоскостями
Задачи элементарные, если следовать алгоритму решения С2 и помнить про основные тригонометрические свойства, как например свойства диагоналей или площадь поверхности многогранника. Опорные задачи вам помогут вспомнить эти основные свойства.

Теперь перейдем непосредственно к алгоритмам.

1. Для определения расстояния между двумя точками А и В используем один из двух способов:

  • Включаем АВ в некоторый треугольник и находим его длину как сторону треугольника
  • По формуле

При чем координатный метод на мой взгляд наиболее прост, надо только аккуратно определить координаты каждой точки.

2. Для определения расстояния от точки до прямой вычисляется

  • как длина отрезка перпендикуляра, если удастся включить этот отрезок в некоторый треугольник в качестве одной из высот
при помощи координатного метода используя формулы вычисления площади, в которых искомым расстоянием будет высота и

3. Расстояние от точки до плоскости равно

  • длине перпендикуляра, опущенного из этой точки на плоскость. Для этого аккуратно строим сечение, которое перпендикулярно плоскости и проходит через заданную точку. Искомое расстояние будет равно высоте полученного нового многогранника.
  • С использованием координатного метода

Уравнение находится путем подстановки координат трех точек, принадлежащих этой плоскости

  • С использованием векторного метода
Для этого надо вспомнить правила сложения и вычитания векторов, что произведение перпендикулярных векторов равно нулю.
  • Методом объемов, если имеется пирамида АВСМ, то расстояние от точки М до плоскости, содержащей треугольник АВС вычисляется по формуле
  • Методом опорных задач, которые можно посмотреть
4. Расстояние между скрещивающимися прямыми можно решить с помощью

4.1. Поэтапно-вычислительного метода:

  • построить общий перпендикуляр двух скрещивающихся прямых и найти его длину;
  • построить плоскость, содержащую одну из прямых и параллельную второй. Тогда искомое расстояние будет равно расстоянию от точки до прямой, построенной в плоскости;
  • заключить данные прямые в параллельные плоскости, проходящие через данные скрещивающиеся прямые, найти расстояние между этими плоскостями
  • построить плоскость, перпендикулярную одной из этих прямых и построить ортогональную проекцию второй прямой

4.2. Векторно-координатного метода

  • Находим координаты концов отрезка, являющегося общим перпендикуляром двух скрещивающихся прямых
  • Находим расстояние между двумя точками
4.3. Векторного метода
Задачу сводим к определению длины вектора, принадлежащего перпендикуляру являющемуся общим перпендикуляром двух скрещивающихся прямых

6. Угол между прямой и плоскостью определяется путем включения его в прямоугольный треугольник в качестве одного из острых углов, либо векторно-координаторным методом

Как определяется угол между плоскостями рассмотрим в следующем уроке. Данные алгоритмы решения С2 способствуют комплексному пониманию метода решения поставленной задачи. " В помощь школьнику журнал для школьников и их родителей". Read more: http://education-club.ru/#ixzz2IXf5GOJU

7. Угол между плоскостями (геометрический метод)

  • 1. Найти прямую, по которой пересекаются плоскости.
  • 2. Выбрать на этой прямой точку и провести к ней два перпендикуляра, лежащих в этих плоскостях. Или провести плоскость, перпендикулярную линии пересечения плоскостей.
  • 3. Найти тригонометрическую функцию угла, образованного перпендикулярами к линии пересечения плоскостей. Как правило, мы делаем это через треугольник, в который входит искомый угол.
  • 4. В ответе записать значение угла, или тригонометрической функции угла.

Угол между плоскостями. Метод координат. Задание С2

Две пересекающиеся плоскости образуют две пары равных между собой двугранных углов:

Величина двугранного угла измеряется величиной соответствующего линейного угла.

Чтобы построить линейный угол двугранного угла, нужно взять на линии пересечения плоскостей произвольную точку, и в каждой плоскости провести к этой точке луч перпендикулярно линии пересечения плоскостей. Угол, образованный этими лучами и есть линейный угол двугранного угла:

Величиной угла между плоскостями называется величина меньшегодвугранного угла.

Пусть наши плоскости и заданы уравнениями:

Косинус угла между плоскостями находится по такой формуле:

В ответе мы записываем , так как величиной угла между плоскостями называется величина меньшего двугранного угла.

В правильной четырехугольной призме со стороной основания 12 и высотой 21 на ребре взята точка М так, что . На ребре взята точка K так, что . Найдите угол между плоскостью и плоскостью .

Сделаем чертеж. Так как мы будем использовать метод координат, сразу введем систему координат: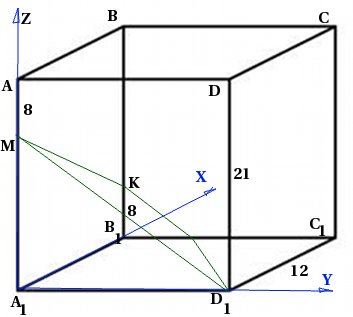

Теперь перед нами стоит задача написать уравнения плоскости и плоскости .

Подробный алгоритм нахождения уравнения плоскости по трем точкам я описывала .

После того, как мы найдем коэффициенты в уравнениях плоскости и плоскости , подставим их в формулу для нахождения косинуса угла между плоскостями, и найдем угол.

Предлагаю вам посмотреть подробное видеорешение этой задачи:


Еще одна задача от Инны Владимировны Фельдман


Видео уроки "Координатный метод решения задач с-2"

Урок 2 http://youtu.be/dKQWG8OZRGo
урок 3 http://youtu.be/ddgr0PnbFno
урок 4 http://youtu.be/n6yx2pQC0Lo
урок 5 http://youtu.be/JkWbxAw1YLI
урок 6 http://youtu.be/gybIqCMKBiI
урок 7 http://youtu.be/_LpARpYxp5g
урок 8 http://youtu.be/XJhyZQoofD8

Метод координат — весьма эффективный и универсальный способ нахождения любых углов или расстояний между стереометрическими объектами в пространстве. Если Ваш репетитор по математике имеет высокую квалификацию, то он должен это знать. В противном случае я бы советовал для «С» части сменить репетитора. Моя подготовка к ЕГЭ по математике С1-С6 обычно включает разбор основных алгоритмов и формул, описанных ниже.

Угол между прямыми а и b

Углом между прямыми в пространстве называется угол между любыми параллельными им пересекающимися прямыми. Этот угол равен углу между направляющими векторами данных прямых (или дополняет его до 180 град).

Какой алгоритм использует репетитор по математике для поиска угла?

1) Выбираем любые вектора и , имеющие направления прямых а и b (параллельные им).
2) Определяем координаты векторов и по соответствующим координатам их начал и концов (от координат конца вектора нужно отнять координаты начала).
3) Подставляем найденный координаты в формулу:
. Для нахождения самого угла, нужно найти арккосинус полученного результата.

Нормаль к плоскости

Нормалью к плоскости называется любой вектор, перпендикулярный к этой плоскости.
Как найти нормаль? Для поиска координат нормали достаточно узнать координаты любых трех точек M, N и K, лежащих в данной плоскости. По этим координатам находим координаты векторов и и требуем выполнения условий и . Приравнивая скалярные произведение векторов к нулю, составляем систему уравнений с тремя переменными, из которой можно найти координаты нормали.

Замечание репетитора по математике : Совсем не обязательно решать систему полностью, ибо достаточно подобрать хотя бы одну нормаль. Для этого можно подставить вместо какой-нибудь из ее неизвестных координат любое число (например единицу) и решить систему двух уравнений с оставшимися двумя неизвестными. Если она решений не имеет, то это значит, что в семействе нормалей нет той, у которой по выбранной переменной стоит единица. Тогда подставьте единицу вместо другой переменной (другой координаты) и решите новую систему. Если опять промахнетесь, то Ваша нормаль будет иметь единицу по последней координате, а сама она окажется параллельной какой-нибудь координатной плоскости (в таком случае ее легко найти и без системы).

Допустим, что нам заданы прямая и плоскость координатами направляющего вектора и нормали
Угол между прямой и плоскость вычисляется по следующей формуле:

Пусть и — две любые нормали к данным плоскостям. Тогда косинус угла между плоскостями равен модулю косинуса угла между нормалями:

Уравнение плоскости в пространстве

Точки, удовлетворяющие равенству образуют плоскость с нормалью . Коэффициент отвечает за величину отклонения (параллельного сдвига) между двумя плоскостями с одной и той же заданной нормалью . Для того, чтобы написать уравнение плоскости нужно сначала найти ее нормаль (как это описано выше), а затем подставить координаты любой точки плоскости вместе с координатами найденной нормали в уравнение и найти коэффициент .

МОУ средняя общеобразовательная школа №13

Метод координат


2008
План:


  1. Введение


  3. Суть метода координат

  4. Системы метода координат

  5. Основные формулы метода координат

  6. Задачи разного уровня сложности на тему «Метод координат»
(с подробными решениями)

  1. Заключение

  2. Список используемой литературы

Введение

В геометрии применяются различные методы решения задач - это синтетический (чисто геометрический) метод, метод преобразований, векторный, метод координат и другие. Они занимают различное положение в школе. Основным методом считается синтетический, а из других наиболее высокое положение занимает метод координат потому, что он тесно связан с алгеброй. Изящество синтетического метода достигается с помощью интуиции, догадок, дополнительных построений. Координатный метод этого не требует: решение задач во многом алгоритмизировано, что в большинстве случаев упрощает поиск и само решение задачи.

Метод координат - способ определять положение точки или тела с помощью чисел или других символов .

Система координат - комплекс определений, реализующий метод координат, т.е. способ определять положение точки или тела с помощью чисел или других символов.

Придавая геометрическим исследованиям алгебраический характер, метод координат переносит в геометрию наиболее важную особенность алгебры - единообразие способов решения задач. Если в арифметике и элементарной геометрии приходится, как правило, искать для каждой задачи особый путь решения, то в алгебре и аналитической геометрии решения проводятся по общему для всех задач плану, легко приспособляемому к любой задаче. Перенесение в геометрию свойственных алгебре и поэтому обладающих большой общностью способов решения задач составляет главную ценность метода координат. Другое достоинство метода координат состоит в том, что его применение избавляет от необходимости прибегать к наглядному представлению сложных пространственных изображений.

Цели изучения метода координат

Можно выделить следующие цели изучения метода координат в школьном курсе геометрии:


  • дать учащимся эффективный метод решения задач и доказательства ряда теорем;

  • показать на основе этого метода тесную связь алгебры и геометрии;

  • способствовать развитию вычислительной и графической культуры учащихся.

Суть метода координат

Сущность метода координат как метода решения задач состоит в том, что, задавая фигуры уравнениями и выражая в координатах различные геометрические соотношения, мы можем решать геометрическую задачу средствами алгебры. Обратно, пользуясь координатами, можно истолковывать алгебраические и аналитические соотношения и факты геометрически и таким образом применять геометрию к решению алгебраических задач.

Метод координат - это универсальный метод.

В отношении школьного курса геометрии можно сказать, что в некоторых случаях метод координат дает возможность строить доказательства и решать многие задачи более рационально, красиво, чем чисто геометрическими способами. Метод координат связан, правда, с одной геометрической сложностью. Одна и та же задача получает различное аналитическое представление в зависимости от того или иного выбора системы координат. И только достаточный опыт позволяет выбирать систему координат наиболее целесообразно.


Системы координат:
1. Прямоугольная (Декартова)система координат (Декарт Рене (1596-1650))

Родился в Турине в зажиточной дворянской семье. Через несколько дней от чахотки умерла его мать, выходила и сохранила ему жизнь кормилица. В 8 лет Рене отдали на полное попечение в одну из лучших иезуитских коллегий. С детства Декарт любил решать задачи и все свое свободное время посвящал изучению математики. Декарт изучал философию, математику, физику, астрономию, филологию. Декарт впервые показал, как можно применить математику для наглядного изображения и математического анализа для самых разнообразных явлений природы и общества.

В его работах впервые появляются:


  1. переменные величины

  2. строгие законы геометрии переведены на алгебраический язык

  3. предложено изображать связи между явлениями природы кривыми линиями, а записывать их алгебраическими выражениями

  4. введены латинские буквы постоянных и переменных величин, а также обозначения степеней
2.Косоугольная система координат отличается от прямоугольной тем, что ее оси не перпендикулярны. Координаты точки определяются как в прямоугольной системе координат по прямым параллельным осям.

3. Полярная система координат . Полярные координаты точки определяются следующим образом: на плоскости задается числовой луч ОХ. Начало луча, точка О, называется полюсом, а ось ОХ – полярной осью. Для определения положения точки М в полярной системе координат указывают расстояние от полюса до этой точки и направление, в котором она находится. Расстояние от точки до полюса называется полярным радиусом точки и обозначается буквой (произносится “ро”).

Направление задается углом поворота от луча ОХ до луча ОМ

Метод координат

формулы

Длина вектора по его координатам

Формула для нахождения координат середины отрезка

Расстояние между двумя точками

Уравнение окружности ,(центр окружности
,радиус r)

Уравнение прямой
, при условии
(уравнением прямой в прямоугольной системе координат является уравнение первой степени)

Каждая прямая задается уравнением. При этом числа a,b,c определяются для каждой прямой однозначно с точностью до пропорциональности (если умножить их на одно и то же число
, то полученное уравнение
будет определять ту же прямую).

Расстояние от точки
до прямой m
,равно

Расстояние от точки
до плоскости
, равно

Вывод формулы
.

Опустим из точки
перпендикуляр АВ на плоскость , заданную уравнением
.Пусть
- точка пересечения этого перпендикуляра с плоскостью . Тогда
- расстояние от точки
до плоскости .Поскольку вектор перпендикулярен плоскости ,он коллинеарен вектору
.Это означает, что
,если
, или
,если
, то есть
.Перепишем это равенство в координатах: .Но точка
, поэтому
и
=
.
(теорема Стюарта)

Если дан треугольник АВС и на его основании точка D , лежащая между точками В и С, то справедливо равенство:

Доказательство:

Выберем систему координат как показано на рисунке.

В выбранной системе координат вершины треугольника АВС будут иметь следующие координаты:

A(x 1 ;y 1 ), B(x 2 ;0), C(0;0) и точка D(x 3 ;0) .

Вычислим все величины, входящие в равенство :

Подставим все эти значения в левую часть равенства:

что и требовалось доказать.

Задача 1. Найти расстояние от точки А(-1,3,0) до плоскости , заданной уравнением x -3y -2z +5=0.

Решение. По формуле
получаем:

.

Ответ:
.


Задача 2 . Векторы и взаимно перпендикулярны, а вектор образует с каждым из них угол 60˚. Зная что
, вычислить скалярное произведение

Решение. По свойству скалярного произведения раскроем скобки:

=

Из определения скалярного произведения получаем:
(так как и перпендикулярны);

Подставляя эти значения в выражение
=, находим скалярное произведение:
=0 – 50+9 12 -120=-62

Ответ:
=0 – 50+9 12 -120=-62
Задача 3 .Дан квадрат ABCD со стороной а . Определите расстояние между серединой отрезка АМ , где М – середина ВС , и точкой N на стороне CD , делящей ее так, что CN:ND=3:1 .

Решение:


Выберем систему координат как показано на рисунке.

Тогда точки M и N , согласно условию, будут иметь координаты:

соответственно.

Так как Е – середина АМ , то ее координаты будут следующими:

Значит, Е .

Найдем расстояние между точками E и N :

Ответ: ЕN =


Задача 4 .Дан куб АВСDA1B1C1D1 с ребрами длины 1.На его боковом ребре АА 1 взята точка Е так, что
.НА ребре ВС взята точка F так, что
Через центр куба и точки Е и F проведена плоскость .Найти расстояние от вершины В до плоскости .

Решение.

Введем систему координат с центром в вершине В.Тогда
Найдем уравнение плоскости . Пусть это уравнение . Заметим, что не проходит через начало координат, поэтому
и уравнение можно разделить на D; получим следующее уравнение:
или ax + by + cz +1=0

Для определения неизвестных коэффициентов a, b и c подставим в уравнение ax + by + cz +1=0 координаты трех точек Е, F и О, удовлетворяющие этому уравнению (так как эти точки лежат в плоскости ).Получим систему уравнений:
Преобразуем систему, умножив первое уравнение на 3,второе на 4,а третье на -6 и сложив первое уравнение с третьим получаем
, b=-4,
.Итак уравнение плоскости имеет вид:

5x + 8y - 9z – 2 =0. Теперь находим расстояние от точки В1(0,0,1) до плоскости
.

Ответ:
.


Задача 5 .Основанием треугольной пирамиды SАВС является равносторонний треугольник АВС, сторона которого равна 4.Известно также, что АS=ВS =
, а CS=3.Найдите площадь сферы, описанной около этой пирамиды.