Parametr bilan bog'liq muammolar (grafik yechim) Kirish. Grafik usul yordamida parametr bilan bog'liq masalalarni yechish rejasi. Parametrli tenglamalarni echishning grafik usuli

Parametrli tenglamalar haqli ravishda eng ko'plardan biri hisoblanadi murakkab vazifalar maktab matematikasi kursida. Aynan shunday vazifalar yildan-yilga bitta vazifa bo'yicha B va C tipidagi vazifalar ro'yxatiga kiradi. davlat imtihoni Yagona davlat imtihoni. Biroq, parametrlarga ega bo'lgan ko'p sonli tenglamalar orasida grafik tarzda osongina echilishi mumkin bo'lganlar ham bor. Keling, bir nechta muammolarni hal qilish misolida ushbu usulni ko'rib chiqaylik.

|x 2 – 2x – 3| tenglama bo'lgan a sonining butun qiymatlari yig'indisini toping. = a to'rtta ildizga ega.

Yechim.

Muammoning savoliga javob berish uchun, keling, bir koordinata tekisligida funktsiyalar grafiklarini tuzamiz

y = |x 2 – 2x – 3| va y = a.

Birinchi funksiyaning grafigi y = |x 2 – 2x – 3| y = x 2 – 2x – 3 parabola grafigidan grafikning Ox o‘qi ostida joylashgan qismini x o‘qiga nisbatan simmetrik tarzda ko‘rsatish orqali olinadi. Grafikning x o'qi ustida joylashgan qismi o'zgarishsiz qoladi.

Keling, buni bosqichma-bosqich qilaylik. y = x 2 – 2x – 3 funksiyaning grafigi parabola bo‘lib, uning shoxlari yuqoriga yo‘naltirilgan. Uning grafigini qurish uchun biz cho'qqining koordinatalarini topamiz. Buni x 0 = -b/2a formulasi yordamida amalga oshirish mumkin. Shunday qilib, x 0 = 2/2 = 1. Parabolaning ordinata o'qi bo'ylab cho'qqisining koordinatasini topish uchun x 0 ning natijaviy qiymatini ko'rib chiqilayotgan funktsiya tenglamasiga almashtiramiz. Biz y 0 = 1 – 2 – 3 = -4 ekanligini olamiz. Demak, parabolaning uchi koordinatalariga (1; -4) ega.

Keyinchalik, koordinata o'qlari bilan parabola shoxlarining kesishish nuqtalarini topishingiz kerak. Parabola shoxlarining abtsissa o'qi bilan kesishgan nuqtalarida funksiyaning qiymati nolga teng. Shuning uchun biz x 2 – 2x – 3 = 0 kvadrat tenglamani yechamiz. Uning ildizlari kerakli nuqtalar bo'ladi. Vyeta teoremasi bo'yicha bizda x 1 = -1, x 2 = 3 bor.

Parabola shoxlarining ordinata o'qi bilan kesishgan nuqtalarida argumentning qiymati nolga teng. Shunday qilib, y = -3 nuqta parabola shoxlarining y o'qi bilan kesishgan nuqtasidir. Olingan grafik 1-rasmda ko'rsatilgan.

y = |x 2 – 2x – 3| funksiyaning grafigini olish uchun grafikning abtsissa ostida joylashgan qismini x o'qiga nisbatan simmetrik ravishda aks ettiramiz. Olingan grafik 2-rasmda ko'rsatilgan.

y = a funktsiyaning grafigi abscissa o'qiga parallel bo'lgan to'g'ri chiziqdir. U 3-rasmda tasvirlangan. Rasmdan foydalanib, agar a (0; 4) intervalga tegishli bo'lsa, grafiklarning to'rtta umumiy nuqtasi (va tenglamaning to'rtta ildizi) borligini aniqlaymiz.

Olingan intervaldan a sonining butun qiymatlari: 1; 2; 3. Muammoning savoliga javob berish uchun ushbu sonlarning yig'indisini topamiz: 1 + 2 + 3 = 6.

Javob: 6.

|x 2 – 4|x| tenglamasi bo'lgan a sonining butun qiymatlarining o'rtacha arifmetik qiymatini toping. – 1| = a oltita ildizga ega.

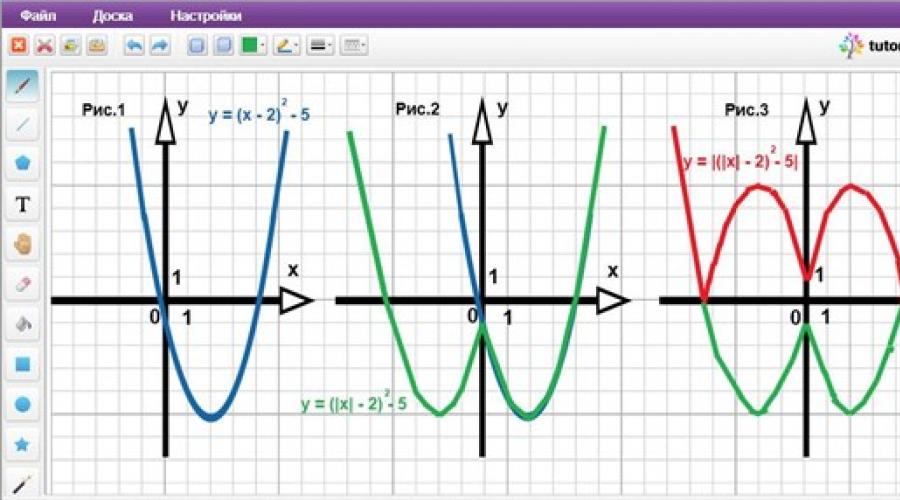
y = |x 2 – 4|x| funksiya grafigini tuzishdan boshlaylik – 1|. Buning uchun a 2 = |a| tengligidan foydalanamiz 2 va funktsiyaning o'ng tomonida yozilgan submodulli ifodada to'liq kvadratni tanlang:

x 2 – 4|x| – 1 = |x| 2 – 4|x| - 1 = (|x| 2 – 4|x| + 4) – 1 – 4 = (|x |– 2) 2 – 5.

Shunda asl funksiya y = |(|x| – 2) 2 – 5| ko‘rinishga ega bo‘ladi.

Ushbu funktsiyaning grafigini qurish uchun biz funktsiyalarning ketma-ket grafiklarini tuzamiz:

1) y = (x – 2) 2 – 5 – (2; -5) koordinatali nuqtada tepasi bo‘lgan parabola; (1-rasm).

2) y = (|x| – 2) 2 – 5 – 1-qadamda tuzilgan parabolaning ordinata o‘qining o‘ng tomonida joylashgan qismi Oy o‘qining chap tomonida simmetrik tarzda aks ettirilgan; (2-rasm).

3) y = |(|x| – 2) 2 – 5| – 2-bandda tuzilgan grafikning x o‘qidan pastda joylashgan qismi yuqoriga qarab x o‘qiga nisbatan simmetrik tarzda ko‘rsatiladi. (3-rasm).

Olingan chizmalarni ko'rib chiqaylik:

y = a funktsiyaning grafigi abscissa o'qiga parallel bo'lgan to'g'ri chiziqdir.

Rasmdan foydalanib, funksiyalar grafiklari oltita umumiy nuqtaga ega degan xulosaga kelamiz (tenglama oltita ildizga ega), agar a (1; 5) oralig'iga tegishli bo'lsa.

Buni quyidagi rasmda ko'rish mumkin:

a parametrining butun qiymatlarining o'rtacha arifmetik qiymatini topamiz:

(2 + 3 + 4)/3 = 3.

Javob: 3.

blog.site, materialni to'liq yoki qisman nusxalashda asl manbaga havola talab qilinadi.

Ushbu usulning imkoniyatlarini to'liq ochib berish uchun biz muammolarning asosiy turlarini ko'rib chiqamiz.

Parametrli masalalarni grafik usulda yechishda bilim va ko'nikmalarni tekshirish uchun namunaviy topshiriqlar (koordinata tekisligi)

1-mashq.

Qanday qadriyatlardaa= tenglamaning ikkita ildizi bormi?

Yechim.

Keling, ekvivalent tizimga o'tamiz:

Koordinata tekisligidagi bu sistema (;) egri chiziqni aniqlaydi. Bu parabolik yoyning barcha nuqtalari (va faqat ular) dastlabki tenglamani qanoatlantiradigan koordinatalarga ega ekanligi aniq. Shuning uchun, parametrning har bir sobit qiymati uchun tenglama yechimlari soni, bu parametr qiymatiga mos keladigan gorizontal chiziq bilan egri chiziqning kesishish nuqtalari soniga teng.

Shubhasiz, ko'rsatilgan chiziqlar grafikni ikkita nuqtada kesishganda, bu ikkita ildizga ega bo'lgan dastlabki tenglamaga teng.

Javob: da.

Vazifa 2.

Tizim qaysi a ning barcha qiymatlarini toping o‘ziga xos yechimga ega.

Yechim.

Keling, asl tizimni ushbu shaklda qayta yozamiz:

Ushbu tizimning barcha yechimlari (shaklning juftlari) lyuklash orqali rasmda ko'rsatilgan maydonni hosil qiladi. Berilgan tizim uchun yagona yechim talabi grafik tilga quyidagicha tarjima qilinadi: gorizontal chiziqlar hosil bo'lgan mintaqa bilan faqat bitta umumiy nuqtaga ega bo'lishi kerak. Buni faqat to'g'ri ko'rish osonva belgilangan talabni qondirish.

Javob: yoki.

Hozirgina muhokama qilingan ikkita vazifa ilgari berilganlarga nisbatan aniqroq tavsiyalar berishga imkon beradi:

parametrni o'zgaruvchi orqali ifodalashga harakat qiling, ya'ni shaklning tengliklarini oling, keyin

funksiya grafigini tekislikda chizing.

Vazifa 3.

Qanday qadriyatlardaA tenglamaning uchta ildizi bormi?

Yechim.

Bizda ... bor

Ushbu to'plamning grafigi "burchak" va parabolaning birlashuvidir. Shubhasiz, faqat to'g'ri chiziq hosil bo'lgan birikmani uchta nuqtada kesib o'tadi.

Javob: .

Izoh: Odatda parametr hisobga olinadi sobit, lekin noma'lum raqam sifatida. Ayni paytda, rasmiy nuqtai nazardan, parametr o'zgaruvchidir va muammoda mavjud bo'lgan boshqalarga "teng". Shakl parametrining bunday ko'rinishida funktsiyalar bir emas, balki ikkita o'zgaruvchi bilan aniqlanadi.

Vazifa 4.

Barcha parametr qiymatlarini toping, buning uchun tenglama bitta yechimga ega.

Yechim.

Kasr nolga teng bo'ladi, agar kasrning numeratori nolga teng bo'lsa va maxraji nolga teng bo'lmasa.

Ildizlarni topish kvadratik trinomial:

Olingan tizimdan foydalanib, dastlabki tenglamaning grafigini qurish oson. Aynan ushbu grafikdagi "teshilishlar" ning mavjudligi va = bo'lganda tenglama noyob echimga ega bo'lishiga imkon beradi. Bu qaror qabul qilishda hal qiluvchi omil.

Javob: Va.

Vazifa 5.

Qaysi parametr qiymatlarida,A tenglama yagona yechimga ega.

Yechim.

Dastlabki tenglamaga ekvivalent sistemani yozamiz

Bu erdan olamiz

Grafik quramiz va o'qlarga perpendikulyar to'g'ri chiziqlar chizamizA .

Tizimning dastlabki ikkita tengsizligi soyalash orqali ko'rsatilgan nuqtalar to'plamini belgilaydi va bu to'plam giperbolalarni va o'z ichiga olmaydi.

Keyin segment va nur, segment va chiziqlar mos ravishda yotadigan nur va , asl tenglamaning grafigi. Bitta yechim bo'lsa, 2 bo'ladi< < или < или = .

Javob : 2 < < или < или = .

Vazifa 6.

Barcha parametr qiymatlarini topingA , buning uchun tenglama

aniq ikki xil yechimga ega

Yechim.

Ikkita tizim to'plamini ko'rib chiqing

Agar , Bu.

Agar < , Bu.

Bu yerdan

yoki

Parabola va to'g'ri chiziq ikkita umumiy nuqtaga ega:A (-2; - 2), IN(-1; -1) va, IN - birinchi parabolaning tepasi,D - ikkinchisining tepasi. Shunday qilib, dastlabki tenglamaning grafigi rasmda ko'rsatilgan.

To'liq ikki xil yechim bo'lishi kerak. Bu yoki bilan amalga oshiriladi.

Javob: yoki.

Vazifa 7.

Har biri uchun tenglama bo'lgan barcha raqamlar to'plamini toping

faqat ikki xil ildizga ega.

Yechim.

Keling, ushbu tenglamani shaklda qayta yozamiz

Bu shart bilan tenglamaning ildizlari.

Keling, ushbu tenglamaning grafigini tuzamiz. IN Ushbu holatda Ordinata o'qiga o'zgaruvchini belgilash orqali grafikni qurish qulay. Bu erda biz javobni vertikal to'g'ri chiziqlar bilan "o'qiymiz", biz bu tenglamaning faqat ikki xil ildizga ega ekanligini aniqlaymiz = -1 yoki yoki.

Nuqtali chiziqlar shundan dalolat beradi.

Javob: da = -1 yoki yoki.

Vazifa 8.

Buning uchun tengsizlikning yechimlari to'plami intervalni o'z ichiga oladi.

Yechim.

Keling, dastlabki tenglamaga ekvivalent bo'lgan ikkita tizim to'plamini yozamiz:

yoki

Birinchi tizimga yechim yo'q ekanA segmentga kiritilishi mumkin emas, keyin biz ikkinchi tizim uchun kerakli tadqiqotlarni amalga oshiramiz.

Bizda ... bor

belgilaylik . Keyin sistemaning ikkinchi tengsizligi shaklni oladi< - va koordinata tekisligida rasmda ko'rsatilgan to'plamni aniqlaydi.

Rasmdan foydalanib, biz hosil bo'lgan to'plam abtsissalari intervalning barcha qiymatlari orqali o'tadigan barcha nuqtalarni o'z ichiga olganligini aniqlaymiz.

Keyin, bu yerdan.

Javob : .

Vazifa 9.

Tizimni qondiradigan yagona raqam mavjud bo'lgan barcha manfiy bo'lmagan raqamlarni toping

Yechim.

Bizda ... bor

Koordinata tekisligidagi birinchi tenglama vertikal chiziqlar turkumini belgilaydi. To'g'ri chiziqlar va tekisliklarni to'rtta maydonga bo'ling. Ulardan ba'zilari tengsizlik tizimining echimlari. Har bir hududdan test punkti olib, aynan qaysilarini aniqlash mumkin. Nuqtasi tengsizlikni qanoatlantiradigan mintaqa uning yechimidir (bu texnika bir o'zgaruvchili tengsizliklarni yechishda intervallar usuli bilan bog'liq). To'g'ri chiziqlar qurish

Masalan, nuqtani olamiz va uni tengsizlikni qanoatlantiradigan nuqtalar Koordinatalariga almashtiramiz.

Biz ikkita maydonni olamiz (I) va ( II), lekin shartga ko'ra, biz faqat maydonni olamiz (I). To'g'ri chiziqlar qurish , k .

Shunday qilib, asl tizim nurlar ustida yotgan barcha nuqtalar (va faqat ular) tomonidan qondiriladi va chizmada qalin chiziqlar bilan ta'kidlangan (ya'ni, biz ma'lum bir sohada nuqtalarni quramiz).

Endi biz tuzatilgandan so'ng noyobni topishimiz kerak. Biz o'qni kesib o'tadigan parallel chiziqlar quramiz. va chiziq bilan kesishgan bir nuqta qaerda bo'lishini toping.

Rasmdan biz yechimning o'ziga xosligi talabiga erishilganligini aniqlaymiz, agar (allaqachon 2 ball uchun),

chiziqlarning kesishish nuqtasining ordinatasi qayerda va,

qayerda - chiziqlarning kesishish nuqtasining ordinatasi va.

Shunday qilib, olamiz< .

Javob: < .

10-topshiriq.

Parametrning qaysi qiymatlarida tizim yechimlarga ega?

Yechim.

Keling, faktorlarga ajratamiz chap tomoni tizim tengsizliklari, bizda mavjud

Biz to'g'ri chiziqlar quramiz va ... Biz rasmda sistemaning tengsizligini qanoatlantiradigan tekislikning nuqtalari to'plamini soya qilib ko'rsatamiz.

Biz giperbolani quramiz = .

U holda giperbolaning tanlangan yoylarining abssissalari dastlabki sistemaning yechimlari hisoblanadi.M , P , N , Q - tugun nuqtalari. Keling, ularning abscissalarini topamiz.

Ballar uchun P , Q bizda ... bor

Javobni yozish uchun qoladi: yoki.

Javob: yoki.

11-topshiriq.

Moduldagi tengsizlikning har qanday yechimi ikki () dan oshmaydigan barcha qiymatlarni toping.

Yechim .

Keling, ushbu tengsizlikni ushbu shaklda qayta yozamiz. va = tenglamalarining grafiklarini tuzamiz.

"Intervallar usuli" dan foydalanib, biz asl tengsizlikning yechimi soyali maydonlar bo'lishini aniqlaymiz.

Endi hududni quraylik va uning qaysi qismi soyali maydonga tushishini ko'ring.

Bular. endi, agar biron bir qo'zg'almas qiymat uchun hosil bo'lgan maydon bilan kesishgan to'g'ri chiziq faqat abtsissalari shartni qanoatlantiradigan nuqtalarni bersa. < 2, keyin kerakli parametr qiymatlaridan biridir.

Shunday qilib, biz buni ko'ramiz.

Javob: .

12-topshiriq.

Parametrning qaysi qiymatlari uchun tengsizlikning yechimlari to'plami to'rttadan ko'p bo'lmagan butun qiymatlarni o'z ichiga oladi?

Yechim.

Keling, bu tengsizlikni shaklga aylantiraylik. Bu tengsizlik ikki tizimning birikmasiga teng

yoki

Ushbu to'plamdan foydalanib, biz asl tengsizlikning yechimini tasvirlaymiz.

Qayerga to'g'ri chiziqlar chizamiz. Keyin belgilangan to'plamdan to'rtta nuqtadan ko'p bo'lmagan chiziq chiziqlarni kesib o'tadigan qiymat kerakli bo'ladi. Shunday qilib, biz u yoki yoki ekanligini ko'ramiz.

Javob: yoki yoki.

13-topshiriq.

Qaysi parametr qiymatlaridaA yechim tizimiga ega

Yechim.

Kvadrat uchburchakning ildizlari va.

Keyin

Biz to'g'ri chiziqlar quramiz va ...

"Intervallar" usuli yordamida biz tizim tengsizligi (soyali maydon) yechimini topamiz.

Aylananing markazining boshi va radiusi 2 bo'lgan soyali maydonga to'g'ri keladigan qismi bu tizimning yechimi bo'ladi. .

Biz qiymatlarni tizimdan topamiz

va ning ma'nosi tizimdan.

Javob:

14-topshiriq.

Parametr qiymatlariga qarabA > tengsizlikni yeching.

Yechim.

Keling, ushbu tengsizlikni shaklda qayta yozamiz va funktsiyani ko'rib chiqamiz, modullarni kengaytirib, biz quyidagicha yozamiz:

Biz jadval tuzmoqdamiz. Grafik koordinata tekisligini ikki mintaqaga ajratadi. t (0;0) ni olib, asl tengsizlikka almashtirsak, 0 > 1 ni olamiz va shuning uchun yuqorida joylashgan grafik sohasida asl tengsizlik qondiriladi.

To'g'ridan-to'g'ri raqamdan biz quyidagilarni olamiz:

echimlar yo'q;

da ;

da.

Javob: echimlar yo'q;

da ;

da.

15-topshiriq.

Tengsizliklar tizimi mos keladigan parametrning barcha qiymatlarini toping

faqat bittasi bilan qanoatlanadi.

Yechim.

Keling, ushbu tizimni ushbu shaklda qayta yozamiz:

Keling, ushbu tizim tomonidan belgilangan hududni quraylik.

1) , parabolaning tepasi.

2) - nuqtalardan o'tuvchi to'g'ri chiziq va.

Yechimning yagonaligi talabi grafik tilga quyidagicha tarjima qilinadi: hosil bo'lgan maydonga ega gorizontal chiziqlar faqat bitta umumiy nuqtaga ega bo'lishi kerak. Belgilangan talab to'g'ri chiziqlar bilan qondiriladi va bu erda parabola va to'g'ri chiziqning kesishish nuqtasining ordinatasi.

Keling, qiymatni topamiz:

= (uchun mos emas vazifaning ma'nosi),

Ordinatni topish:

Javob: ,

16-topshiriq.

Barcha parametr qiymatlarini topingA, buning ostida tengsizliklar tizimi

faqat bitta x uchun javob beradi.

Yechim .

Parabolalarni tuzamiz va oxirgi sistemaning yechimini soya qilib ko'rsatamiz.

1) , .

2) , .

Rasmda masalaning sharti yoki bo'lganda qanoatlanishi ko'rsatilgan.

Javob: yoki.

17-topshiriq.

Qaysi qiymatlar uchun tenglama aniq uchta ildizga ega?

Yechim.

Bu tenglama to'plamga teng

Aholi grafigi parabola va burchak grafiklarining birikmasidir.

Chiziqlar hosil bo'lgan birlashmani uchta nuqtada kesib o'tadi.

Javob: da.

18-topshiriq.

Qaysi qiymatlar uchun tenglama aniq uchta yechimga ega?

Yechim.

Keling, bu tenglamaning chap tomonini aylantiramiz. ga nisbatan kvadrat tenglamani olamiz.

Biz tenglamani olamiz

Bu jamiga teng

Parabola grafiklarining birlashuvi populyatsiya uchun yechimdir.

Parabolalarning kesishish ordinata nuqtalarini toping:

Biz rasmdan kerakli ma'lumotlarni o'qiymiz: bu tenglama yoki da uchta yechimga ega

Javob: da yoki

19-topshiriq.

Parametrga qarab, tenglamaning ildizlari sonini aniqlang

Yechim .

Bu tenglamani a ga nisbatan kvadratik deb hisoblang.

,

.

Biz umumiylikni olamiz

Aholi tenglamalarining grafiklarini tuzamiz va masalada berilgan savolga javob beramiz.

Javob:: yechim yo'q;

: bitta yechim;

: ikkita yechim;

yoki: uchta yechim;

yoki: to'rtta yechim.

Vazifa 20.

Tizimda nechta yechim bor?

Yechim.

Ko'rinib turibdiki, tizimning ikkinchi tenglamasining ildizlari soni tizimning o'zi yechimlari soniga teng.

Bizda ... bor, .

Ushbu tenglamani kvadrat tenglama sifatida ko'rib, biz to'plamni olamiz.

Endi koordinata tekisligiga kirish vazifani soddalashtiradi. Tenglamani yechish orqali kesishish nuqtalarining koordinatalarini topamiz

Bu yerdan

Parabolalarning uchlari va.

Javob:: to'rtta yechim;

: ikkita yechim;

: bitta yechim;

: yechim yo'q.

Vazifa 21.

Tenglama faqat ikkita aniq ildizga ega bo'lgan parametrning barcha haqiqiy qiymatlarini toping. Bu ildizlarni yozing.

Yechim .

Qavslar ichida kvadrat uch a’zoning ildizlarini topamiz:

Bu tenglamaning yechimlari to‘plamini koordinata tekisligida grafiklar tuzib, quyidagi shart bilan tasvirlaylik.

Rasmdan kerakli ma'lumotlarni o'qiymiz. Demak, bu tenglamaning (va) va (va) da ikki xil ildizi bor.

Javob: da (va) va

da (va).

Vazifa 2 2 .

Tengsizliklar tizimini yeching:

Yechim.

Tekislikda parabola va to'g'ri chiziqlar grafiklarini tuzamiz.

Soyali maydondagi barcha nuqtalar tizimning yechimidir. Keling, qurilgan maydonni ikki qismga ajratamiz.

Agar shunday bo'lsa, unda hech qanday yechim yo'q.

Agar, u holda soyali maydon nuqtalarining abssissasi to'g'ri chiziq nuqtalarining abssissasidan katta bo'ladi, lekin parabolaning abssissasidan (tenglamaning katta ildizi) kichik bo'ladi.

Uni to‘g‘ri chiziqli tenglama orqali ifodalaymiz:

Keling, tenglamaning ildizlarini topamiz:

Keyin.

Agar shunday bo'lsa, unda.

Javob: va 1 uchun yechimlar yo'q;

da;

da.

23-topshiriq.

Tengsizliklar sistemasini yeching

Yechim.

– parabolaning tepasi.

Parabolaning tepasi.

Parabolalarning kesishish nuqtalarining abtsissalarini toping:

Soyali maydon tizimning yechimidir. Keling, uni ikki qismga ajratamiz.

Parabola tenglamalarida biz ularni quyidagicha ifodalaymiz:

Keling, yozamiz javob:

agar va bo'lsa, unda echimlar yo'q;

agar, keyin< ;

agar, keyin.

24-topshiriq.

Qaysi qiymatlarda va tenglama yechimlari yo'qmi?

Yechim.

Tenglama tizimga ekvivalent

Keling, tizimning ko'plab echimlarini tuzamiz.

Parabolaning uchta bo'lagi bu tenglamaning yechimidir.

Keling, qaysi birini topamiz va uni istisno qilamiz.

Demak, hech qanday yechim yo'q;

yechimlar bo'lmaganda;

(eslatma: qolganlari uchunAbir yoki ikkita yechim mavjud).

Javob: ; .

Vazifa 25.

Parametrning qaysi haqiqiy qiymatlari uchun shartlarni qondiradigan kamida bittasi mavjud:

Yechim.

Tengsizlikni grafik usulda “interval usuli” yordamida yechib, grafik tuzamiz. Keling, grafikning qaysi qismi tengsizlikni yechish uchun tuzilgan maydonga tushishini ko'rib chiqamiz va tegishli qiymatlarni topamiz.A.

To'g'ri chiziqlarning grafiklarini quramiz va

Ular koordinata tekisligini 4 ta hududga ajratadilar.

Oxirgi tengsizlikni interval usuli yordamida grafik tarzda yechamiz.

Soyali maydon uning yechimidir. Parabola grafigining bir qismi shu sohaga to'g'ri keladi. Intervalda; (shartga ko'ra, tizimning tengsizligi qat'iy) berilgan tizimning shartlarini qondiradigan mavjud.

Javob:

Vazifa 26.

Parametrning barcha qiymatlarini toping, ularning har biri uchun tengsizlikning yechimlari to'plami tengsizlikning bitta yechimini o'z ichiga olmaydi.

Yechim.

Keling, tengsizlikning yechimlari to'plamini (“interval usulidan foydalangan holda”) tuzamiz. Keyin biz kerakli parametr qiymatlarining "chiziq" ni quramizq ko'rsatilgan hududlarning hech biri "chiziq" ga tegishli bo'lmaganlar

Javob: yoki.

Vazifa 27.

Parametrning qaysi qiymatlari uchun tenglama yagona yechimga ega?

Yechim.

Kasrning sonini koeffitsientlarga ajratamiz.

Ushbu tenglama tizimga teng:

Koordinata tekisligida aholining grafigini tuzamiz.

yoki

– chiziqlarning kesishish nuqtasi va. Aholi grafigi to'g'ri chiziqlar birlashmasidan iborat.

Grafik nuqtalarini abtsissalar bilan "teshib tashlang".

Biz to'g'ri chiziqlar chizamiz va grafik bilan kesishgan bir nuqta borligini ko'ramiz.

Ko'rinib turibdiki, faqat ushbu tenglama uchun yoki yagona yechim bor.

Javob: yoki.

Vazifa 28.

Parametrning qaysi haqiqiy qiymatlari uchun tengsizliklar tizimi yechimga ega emas?

Yechim.

Soyali mintaqaning tekis nuqtalari to'plami ushbu tengsizliklar tizimini qanoatlantiradi.

Biz to'g'ri chiziqlar quramiz. Rasmdan aniqlaymizki, qachon ( giperbola va to'g'ri chiziqning kesishish nuqtasining abssissasi), to'g'ri chiziqlar soyali maydonni kesib o'tmaydi.

Javob: da.

Vazifa 29.

Qaysi parametr qiymatlaridaA tizim o'ziga xos yechimga ega.

Yechim.

Keling, shunga o'xshash tizimga o'tamiz.

Koordinata tekisligida biz mos ravishda parabolalar va parabolalarning cho'qqilarining grafiklarini tuzamiz, nuqta va.

Tenglamani yechish orqali parabolalarning kesishish nuqtalarining abssissalarini hisoblaylik

Soyali maydon tengsizliklar tizimining yechimidir. To'g'ridan-to'g'ri va

soyali maydon bilan bitta umumiy nuqtaga ega.

Javob: da i.

Vazifa 30.

Tengsizlikni yeching:

Yechim.

Parametrga qarab, biz qiymatni topamiz.

Tengsizlikni “interval usuli” yordamida yechamiz.

Keling, parabolalarni quraylik

: .

Parabolalarning kesishish nuqtasining koordinatalarini hisoblaymiz:

Soyali mintaqadagi nuqtalar bu tengsizlikni qondiradi. To'g'ri chiziq chizib, biz bu maydonni uch qismga ajratamiz.

1) Agar bo'lsa, unda echimlar yo'q.

2) Agar, u holda tenglamada uni orqali ifodalaymiz:

Shunday qilib, hududdaI bizda ... bor.

Agar shunday bo'lsa, qarang:

a) mintaqa II .

orqali tenglamada ifodalaymiz.

Kichikroq ildiz

Kattaroq ildiz.

Shunday qilib, mintaqada II bizda ... bor.

b) hudud III : .

Javob: yechimlar bo'lmaganda;

da

da, .

Adabiyot:

Galitskiy M. L., Goldman A. M., Zvavich L. I. 8-9 sinflar uchun algebra masalalari to'plami: Qo'llanma matematikani chuqur o'rganadigan maktablar va sinflar o'quvchilari uchun - 2-nashr. – M.: Ta’lim, 1994 yil.

P. I. Gornshteyn, V. B. Polonskiy, M. S. Yakir. Parametrlar bilan bog'liq muammolar. 3-nashr, kengaytirilgan va qayta ko'rib chiqilgan. – M.: Ilexa, Xarkov: Gimnaziya, 2003 yil.

Faddeev D.K. Algebra 6 – 8. – M.: Ta’lim, 1983 (b – ka matematika o‘qituvchisi).

A. X. Shaxmeyster. Parametrli tenglamalar va tengsizliklar. B. G. Ziv tomonidan tahrirlangan. S - Peterburg. Moskva. 2004 yil.

V. V. Amelkin, V. L. Rabtsevich. Parametrlar bilan bog'liq muammolar Minsk "Asar", 2002 yil.

A. X. Shaxmeister. Yagona davlat imtihonidagi parametrlar bilan bog'liq muammolar. Moskva universiteti nashriyoti, Neva MTsNMOdagi CheRo.

TO parametrli vazifalar masalan, chiziqli va kvadrat tenglamalar yechimlarini izlashni o'z ichiga olishi mumkin umumiy ko'rinish, parametr qiymatiga qarab mavjud bo'lgan ildizlar soni uchun tenglamani o'rganish.

Batafsil ta'riflar bermasdan, quyidagi tenglamalarni misol sifatida ko'rib chiqing:

y = kx, bu erda x, y o'zgaruvchilar, k - parametr;

y = kx + b, bu erda x, y - o'zgaruvchilar, k va b - parametrlar;

ax 2 + bx + c = 0, bu erda x - o'zgaruvchilar, a, b va c - parametr.

Parametrli tenglamani (tengsizlik, tizim) yechish, qoida tariqasida, yechish demakdir cheksiz to'plam tenglamalar (tengsizliklar, tizimlar).

Parametrli vazifalarni ikki turga bo'lish mumkin:

A) shart shunday deydi: tenglamani yeching (tengsizlik, tizim) - bu parametrning barcha qiymatlari uchun barcha echimlarni toping. Agar kamida bitta holat o'rganilmagan bo'lsa, bunday yechimni qoniqarli deb hisoblash mumkin emas.

b) tenglama (tengsizlik, tizim) ma'lum xususiyatlarga ega bo'lgan parametrning mumkin bo'lgan qiymatlarini ko'rsatish talab qilinadi. Masalan, uning bitta yechimi bor, yechimlari yo'q, oraliqga tegishli yechimlari bor va hokazo.Bunday topshiriqlarda qaysi parametr qiymatida kerakli shart qanoatlantirilishini aniq ko'rsatish kerak.

Parametr noma'lum sobit raqam bo'lib, o'ziga xos ikkilikka ega. Avvalo, taxmin qilingan mashhurlik parametrni raqam sifatida qabul qilish kerakligini ko'rsatishini hisobga olish kerak. Ikkinchidan, parametrni manipulyatsiya qilish erkinligi uning noaniqligi bilan cheklangan. Masalan, parametr o'z ichiga olgan ifodaga bo'lish yoki bunday ifodadan juft daraja ildizini olish operatsiyalari dastlabki tadqiqotni talab qiladi. Shuning uchun, parametr bilan ishlashda ehtiyot bo'lish kerak.

Masalan, ikkita -6a va 3a raqamlarini solishtirish uchun siz uchta holatni ko'rib chiqishingiz kerak:

1) a manfiy son bo'lsa -6a 3a dan katta bo'ladi;

2) a = 0 bo'lgan holatda -6a = 3a;

3) -6a 3a dan kichik bo'ladi, agar a musbat son 0 bo'lsa.

Yechim javob bo'ladi.

kx = b tenglama berilgan bo'lsin. Bu tenglama bir o'zgaruvchiga ega cheksiz sonli tenglamalar uchun qisqa shakldir.

Bunday tenglamalarni yechishda quyidagi holatlar bo'lishi mumkin:

1. k nolga teng bo'lmagan istalgan haqiqiy son va b R dan istalgan son bo'lsin, u holda x = b/k.

2. k = 0 va b ≠ 0 bo'lsin, dastlabki tenglama 0 x = b ko'rinishini oladi. Shubhasiz, bu tenglama hech qanday yechimga ega emas.

3. K va b nolga teng sonlar bo'lsin, u holda biz 0 x = 0 tenglikka ega bo'lamiz. Uning yechimi har qanday haqiqiy sondir.

Ushbu turdagi tenglamani yechish algoritmi:

1. Parametrning “nazorat” qiymatlarini aniqlang.

2. Birinchi xatboshida aniqlangan parametr qiymatlari uchun x uchun dastlabki tenglamani yeching.

3. Birinchi xatboshida tanlanganlardan farq qiluvchi parametr qiymatlari uchun x uchun dastlabki tenglamani yeching.

4. Javobni quyidagi shaklda yozishingiz mumkin:

1) ... uchun (parametr qiymatlari), tenglamaning ildizlari bor ...;

2) ... uchun (parametr qiymatlari), tenglamada ildiz yo'q.

1-misol.

|6 – x| parametrli tenglamani yeching = a.

Yechim.

Bu erda a ≥ 0 ekanligini ko'rish oson.

6-modul qoidasiga ko'ra x = ±a, biz x ni ifodalaymiz:

Javob: x = 6 ± a, bu erda a ≥ 0.

2-misol.

a(x – 1) + 2(x – 1) = 0 tenglamani x o‘zgaruvchisiga nisbatan yeching.

Yechim.

Qavslarni ochamiz: ah – a + 2x – 2 = 0

Keling, tenglamani yozamiz standart shakl: x(a + 2) = a + 2.

Agar a + 2 ifodasi nolga teng bo'lmasa, ya'ni a ≠ -2 bo'lsa, bizda x = (a + 2) / (a ​​+ 2) yechim mavjud, ya'ni. x = 1.

Agar a + 2 nolga teng bo'lsa, ya'ni. a = -2, u holda biz 0 x = 0 to'g'ri tenglikka egamiz, shuning uchun x har qanday haqiqiy sondir.

Javob: a ≠ -2 uchun x = 1 va a = -2 uchun x € R.

3-misol.

x o'zgaruvchiga nisbatan x/a + 1 = a + x tenglamani yeching.

Yechim.

Agar a = 0 bo'lsa, u holda tenglamani a + x = a 2 + ax yoki (a – 1)x = -a(a – 1) ko'rinishga o'tkazamiz. a = 1 uchun oxirgi tenglama 0 x = 0 ko'rinishga ega, shuning uchun x har qanday raqamdir.

Agar a ≠ 1 bo'lsa, oxirgi tenglama x = -a ko'rinishini oladi.

Ushbu yechimni koordinata chizig'ida tasvirlash mumkin (1-rasm)

Javob: a = 0 uchun yechimlar mavjud emas; x - a = 1 bo'lgan istalgan raqam; a ≠ 0 va a ≠ 1 uchun x = -a.

Grafik usul

Parametrli tenglamalarni echishning yana bir usulini ko'rib chiqaylik - grafik. Bu usul juda tez-tez ishlatiladi.

4-misol.

a parametriga qarab ||x| tenglama nechta ildizga ega – 2| = a?

Yechim.

Grafik usul yordamida yechish uchun y = ||x| funksiyalarning grafiklarini tuzamiz – 2| va y = a (2-rasm).

Chizmada y = a to'g'ri chiziqning joylashishi va ularning har biridagi ildizlar sonining mumkin bo'lgan holatlari aniq ko'rsatilgan.

Javob: agar a bo'lsa tenglamaning ildizlari bo'lmaydi< 0; два корня будет в случае, если a >2 va a = 0; a = 2 holatda tenglama uchta ildizga ega bo'ladi; to'rtta ildiz - 0 da< a < 2.

5-misol.

2|x| tenglama qanday bo'lsa + |x – 1| = a bitta ildizga egami?

Yechim.

y = 2|x| funksiyalarning grafiklarini tasvirlaymiz + |x – 1| va y = a. y = 2|x| uchun + |x – 1|, modullarni interval usuli yordamida kengaytirib, biz quyidagilarni olamiz:

(-3x + 1, x da< 0,

y = (x + 1, 0 ≤ x ≤ 1 uchun,

(3x – 1, x > 1 uchun.

Yoniq 3-rasm Ko'rinib turibdiki, a = 1 bo'lgandagina tenglama bitta ildizga ega bo'ladi.

Javob: a = 1.

6-misol.

|x + 1| tenglamaning yechimlari sonini aniqlang + |x + 2| = a parametriga qarab a?

Yechim.

y = |x + 1| funksiyaning grafigi + |x + 2| singan chiziq bo'ladi. Uning uchlari (-2; 1) va (-1; 1) nuqtalarda joylashgan bo'ladi. (4-rasm).

Javob: agar a parametri bittadan kichik bo'lsa, tenglamaning ildizlari bo'lmaydi; agar a = 1 bo'lsa, tenglamaning yechimi [-2 oraliqdagi cheksiz sonlar to'plamidir; -1]; agar a parametrining qiymatlari birdan katta bo'lsa, tenglama ikkita ildizga ega bo'ladi.

Hali ham savollaringiz bormi? Parametrli tenglamalarni echishni bilmayapsizmi?
Repetitordan yordam olish uchun ro'yxatdan o'ting.
Birinchi dars bepul!

veb-sayt, materialni to'liq yoki qisman nusxalashda manbaga havola talab qilinadi.

a parametrining har bir qiymati uchun a tengsizlikni yechish | 2 x + a | ≤ x + 2 |2x+a| \leq x+2 .

Birinchidan, yordamchi masalani hal qilaylik. Bu tengsizlikni ikkita o'zgaruvchisi x x va a bo'lgan tengsizlik deb hisoblaymiz va koordinatalari tengsizlikni qanoatlantiradigan barcha nuqtalarni x O a xOa koordinata tekisligiga chizamiz.

Agar 2 x + a ≥ 0 2x+a \geq 0 (ya’ni a = - 2 x a=-2x va undan yuqori to‘g‘ri chiziqda) bo‘lsa, 2 x + a ≤ x + 2 ⇔ a ≤ 2 - x 2x+ a ni olamiz. \leq x+2 \Chapga o'q a \leq 2-x .

To'plam rasmda ko'rsatilgan. o'n bir.

Endi ushbu chizma yordamida asl masalani yechaylik. Agar a a ni tuzatsak, u holda gorizontal to'g'ri chiziqni olamiz a = const a = \textrm(const) . X x qiymatlarini aniqlash uchun siz ushbu chiziqning kesishish nuqtalarining abssissasini tengsizlikning echimlari to'plami bilan topishingiz kerak. Masalan, a = 8 a=8 bo'lsa, u holda tengsizlikning yechimlari yo'q (to'g'ri chiziq to'plamni kesib o'tmaydi); a = 1 a=1 bo'lsa, u holda yechimlar [ - 1 segmentidan barcha x x ; 1 ] [-1;1] va boshqalar. Shunday qilib, uchta variant mumkin.

1) Agar $$a>4$$ bo'lsa, unda hech qanday yechim yo'q.

2) a = 4 a=4 bo'lsa, x = - 2 x=-2 bo'ladi.

JAVOB

$$a da

a = 4 a=4 uchun - x = - 2 x=-2 ;

$$a>4$$ uchun - hech qanday yechim yo'q.

$$3-|x-a| tengsizligi bo'lgan a a parametrining barcha qiymatlarini toping > x^2$$ a) kamida bitta yechimga ega; b) kamida bitta ijobiy yechimga ega.

Tengsizlikni $$3-x^2 > |x-a)$$ ko'rinishda qayta yozamiz. X O y xOy tekislikda chap va o‘ng qismlarning grafiklarini tuzamiz. Chapdagi grafik cho‘qqisi (0; 3) (0;3) nuqtada bo‘lgan shoxlari pastga qaragan paraboladir. Grafik x o'qini (± 3 ; 0) nuqtalarda kesib o'tadi (\pm \sqrt(3);0) . O'ng tomonning grafigi x o'qi ustidagi uchi bilan burchak bo'lib, uning tomonlari koordinata o'qlariga nisbatan 45 ° 45^(\circ) burchak ostida yuqoriga yo'naltirilgan. Cho'qqining abssissasi x = a x=a nuqtadir.

a) Tengsizlik kamida bitta yechimga ega bo'lishi uchun parabola hech bo'lmaganda bir nuqtada y = | x - a | y=|x-a| . Bu burchakning tepasi abscissa o'qining A A va B B nuqtalari orasida joylashgan bo'lsa amalga oshiriladi (12-rasmga qarang - A A va B B nuqtalari kiritilmagan). Shunday qilib, burchak shoxlaridan biri parabolaga tepaning qaysi holatida tegishini aniqlash kerak.

Burchakning tepasi A A nuqtasida bo'lgan holatni ko'rib chiqaylik. Keyin burchakning o'ng novdasi parabolaga tegadi. Uning qiyaligi birga teng. Bu shuni anglatadiki, y = 3 - x 2 y = 3-x^2 funksiyaning teginish nuqtasida hosilasi 1 1 ga teng, ya'ni - 2 x = 1 -2x=1, qaerdan x = - 1 2 x = -\frac( 1)(2) . U holda tangens nuqtaning ordinatasi y = 3 - (1 2) 2 = 11 4 y = 3 - (\frac(1)(2))^2 = \frac(11)(4) ga teng. Burchak koeffitsienti k = 1 k=1 boʻlgan va koordinatalari (- 1 2 ; 11 4) nuqtadan oʻtuvchi toʻgʻri chiziq tenglamasi (-\frac(1)(2); \frac(11)(4) ) quyidagi * ( \^* : y - 11 4 = 1 · (x + 1 2) y - \frac{11}{4} = 1 \cdot (x+ \frac{1}{2}) , откуда y = x + 13 4 y = x + \frac{13}{4} .!}

Bu burchakning o'ng filialining tenglamasi. X o'qi bilan kesishgan nuqtaning abssissasi - 13 4 -\frac(13)(4), ya'ni A A nuqta koordinatalari A (- 13 4 ; 0) A(-\frac(13)(4) ga teng. 0); Simmetriya sababli B B nuqtasi koordinatalariga ega: B (13 4 ; 0) B(\frac(13)(4); 0) .

Bundan a ∈ (- 13 4 ; 13 4) a\in (-\frac(13)(4); \frac(13)(4)) ekanligini olamiz.

b) Agar burchakning tepasi F F va B B nuqtalari orasida joylashgan bo'lsa, tengsizlik ijobiy echimlarga ega (13-rasmga qarang). F F nuqtaning o‘rnini topish qiyin emas: agar burchak cho‘qqisi F F nuqtada bo‘lsa, uning o‘ng shoxchasi (y = x - a y = x-a tenglamasi bilan berilgan to‘g‘ri chiziq (0; 3) nuqtadan o‘tadi. ) (0;3) bu yerdan a = - 3 a=-3 va F F nuqtaning (- 3 ; 0) (-3;0) koordinatalari borligini aniqlaymiz, shuning uchun a ∈ (- 3 ; 13 4) a \da (-3; \frac(13)(4) ) .

JAVOB

a) a ∈ (- 13 4 ; 13 4) ,       a\in (-\frac(13)(4); \frac(13)(4)),\:\:\: b) a ∈ (- 3) 13 4) a \in (-3; \frac(13)(4)) ;

* {\^* Полезные формулы: !}

- \-- (x 0 ; y 0) (x_0;y_0) nuqtadan o'tuvchi va burchak koeffitsienti k k bo'lgan to'g'ri chiziq y - y 0 = k (x - x 0) y-y_0= tenglama bilan berilgan. k(x-x_0);

- \-- (x 0 ; y 0) (x_0;y_0) va (x 1 ; y 1) (x_1;y_1) nuqtalardan o'tuvchi to'g'ri chiziqning burchak koeffitsienti, bu erda x 0 ≠ x 1 x_0 \neq x_1, k = y 1 - y 0 x 1 - x 0 k = \dfrac(y_1-y_0)(x_1-x_0) formulasi bilan hisoblanadi.

Izoh. Agar y = k x + l y=kx+l to'g'ri chiziq va y = a x 2 + b x + c y = ax^2+bx+c parabola teginadigan parametrning qiymatini topish kerak bo'lsa, u holda quyidagini yozishingiz mumkin: k x + l = a x 2 + b x + c kx+l = ax^2+bx+c tenglamasi bitta yechimga ega bo'lishi sharti bilan burchak cho'qqisi bo'lgan a a parametrining qiymatlarini topishning yana bir usuli A nuqtada bo'ladi A quyidagicha: x - a = 3 - x 2 x-a = 3-x^2 to'liq bitta yechimga ega ⇔ D = 1 + 4 (a + 3) = 0 ⇔ a = - 13 4 \chap o'q D = 1 + 4(a+3) = 0 \Chapga o'q a = -\ dfrac(13)(4) .

E'tibor bering, bu tarzda chiziqning ixtiyoriy grafikga tegishi shartini yozib bo'lmaydi. Masalan, y = 3 x - 2 y = 3x - 2 to'g'ri chiziq y = x 3 y=x^3 kub parabolasiga (1 ; 1) (1;1) nuqtada tegib, uni (-) nuqtada kesib o'tadi. 2 ; - 8) (-2;-8), ya'ni x 3 = 3 x + 2 x^3 = 3x+2 tenglama ikkita yechimga ega.

a a parametrining barcha qiymatlarini toping, ularning har biri uchun tenglama (a + 1 - | x + 2 |) (x 2 + 4 x + 1 - a) = 0 (a+1-|x+2| )(x^2 +4x+1-a) = 0 a) aniq ikkita aniq ildizga ega; b) aniq uch xil ildiz.

25-misoldagi kabi bajaramiz. Bu tenglamaning yechimlari to'plamini x O a xOa tekisligida tasvirlaymiz. Bu ikkita tenglamaning kombinatsiyasiga teng:

1) a = | x + 2 | - 1 a = |x+2| -1 - shoxlari yuqoriga va tepasi nuqtada (- 2 ; - 1) (-2;-1) bo'lgan burchak.

2) a = x 2 + 4 x + 1 a = x^2 + 4x + 1 - bu shoxlari yuqoriga va tepasi (- 2 ; - 3) (-2;-3) nuqtada joylashgan parabola. Rasmga qarang. 14.

Ikki grafikning kesishish nuqtalarini topamiz. Burchakning o'ng shoxchasi y = x + 1 y=x+1 tenglama bilan berilgan. Tenglamani yechish

x + 1 = x 2 + 4 x + 1 x+1 = x^2+4x+1

x = 0 x=0 yoki x = - 3 x=-3 ekanligini topamiz. Faqat x = 0 x=0 qiymati mos keladi (chunki o'ng filial uchun x + 2 ≥ 0 x+2 \geq 0). Keyin a = 1 a=1 . Xuddi shunday, biz ikkinchi kesishish nuqtasining koordinatalarini topamiz - (- 4 ; 1) (-4; 1) .

Keling, asl muammoga qaytaylik. A = const a=\textrm(const) gorizontal chiziq tenglamaning yechimlari to‘plamini ikki nuqtada kesib o‘tadigan a a uchun tenglamaning aynan ikkita yechimi mavjud. Grafikdan bu ∈ (- 3 ; - 1) ∪ ( 1 ) a\in (-3;-1)\bigcup\(1\) uchun to'g'ri ekanligini ko'ramiz. Ishda aniq uchta yechim bo'ladi uch ochko kesishmalar, bu faqat a = - 1 a=-1 bo'lganda mumkin.

JAVOB

a) a ∈ (- 3 ; - 1) ∪ ( 1 ) ;       a\in (-3;-1)\bigcup\(1\);\:\:\: b) a = - 1 a=-1 .

$$\begin(holatlar) x^2-x-a \leq 0,\\ x^2+2x-6a \leq 0 \end(holatlar) $$

aynan bitta yechimga ega.

Tengsizliklar sistemasining yechimlarini x O a xOa tekisligida tasvirlaylik. Tizimni $$ \begin(cases) a \leq -x^2+x,\\ a \geq \dfrac(x^2+6x)(6) .\end(cases) $$ shaklida qayta yozamiz.

Birinchi tengsizlik a = - x 2 + x a = -x^2+x va undan pastda joylashgan nuqtalar bilan, ikkinchisi esa a = x 2 + 6 x 6 a = parabolada yotgan nuqtalar bilan qanoatlantiriladi. \dfrac(x^2 +6x)(6) va undan yuqori. Parabolalarning uchlari va ularning kesishish nuqtalarining koordinatalarini topamiz va keyin grafik tuzamiz. Birinchi parabolaning tepasi (1 2 ; 1 4) (\dfrac(1)(2);\dfrac(1)(4)), ikkinchi parabolaning tepasi (- 1 ; - 1 6) ( -1; -\dfrac( 1)(6)), kesishish nuqtalari (0 ; 0) (0;0) va (4 7 ; 12 49) (\dfrac(4)(7); \dfrac(12) )(49)). Tizimni qondiradigan nuqtalar to'plami rasmda ko'rsatilgan. 15. A = 0 a=0 va a = hollarda gorizontal chiziq a = const a=\textrm(const) bu to‘plam bilan aynan bitta umumiy nuqtaga ega ekanligini (bu sistemaning aynan bitta yechimga ega ekanligini bildiradi) ko‘rinadi. 1 4 a= \dfrac(1)(4) .

JAVOB

A = 0 ,  a = 1 4 a=0,\: a=\dfrac(1)(4)

Toping eng kichik qiymat parametr a a , ularning har biri uchun tizim

$$\begin(holatlar) x^2+y^2 + 3a^2 = 2y + 2\sqrt(3)ax,\\ \sqrt(3)|x|-y=4 \end(holatlar) $$

o‘ziga xos yechimga ega.

Birinchi tenglamani o'zgartiramiz, to'liq kvadratlarni ta'kidlash:

(x 2 - 2 3 a x + 3 a 2) + (y 2 - 2 y + 1) = 1 ⇔ (x - a 3) 2 + (y - 1) 2 = 1.       18 (x^2- 2\sqrt(3)ax+3a^2)+(y^2-2y+1)=1 \Chap oʻq (x-a\sqrt(3))^2+(y-1)^2 =1. \:\:\:\chap (18\o'ng)

Oldingi muammolardan farqli o'laroq, bu erda chizmani x O y xOy tekisligida tasvirlash yaxshiroqdir ("o'zgaruvchi - parametr" tekisligidagi chizma odatda bitta o'zgaruvchi va bitta parametr bilan bog'liq muammolar uchun ishlatiladi - natija tekislikdagi to'plamdir. Bu masalada biz ikkita o'zgaruvchi va parametr bilan shug'ullanamiz (x; y; a) (x; y;a) uch o'lchovli fazoda chizish qiyin ishdir vizual bo'lish). (18) tenglama markazi (a 3 ; 1) (a\sqrt(3);1) radiusi 1 bo'lgan aylanani belgilaydi. Bu doiraning markazi a ning qiymatiga bog'liq bo'lib, uning istalgan nuqtasida joylashgan bo'lishi mumkin. chiziq y = 1 y = 1.

Tizimning ikkinchi tenglamasi y = 3 | x | - 4 y = \sqrt(3)|x|-4 tomonlarini abscissa o'qiga 60 ° 60^(\circ) burchak ostida yuqoriga ko'targan holda burchakni o'rnatadi (to'g'ri chiziqning burchak koeffitsienti tangensdir. qiyalik burchagi tg 60 ° = 3 \textrm(tg )(60^(\circ)) = \sqrt(3)), cho'qqisi (0; - 4) (0;-4) nuqtada.

Bu tizim Agar aylana burchak shoxlaridan biriga tegsa, tenglamalar aynan bitta yechimga ega. Bu mumkin to'rtta holat(16-rasm): aylananing markazi A A, B B, C C, D D nuqtalaridan birida bo'lishi mumkin. Biz a a parametrining eng kichik qiymatini topishimiz kerakligi sababli bizni D D nuqtaning abssissasi qiziqtiradi. Keling, ko'rib chiqaylik to'g'ri uchburchak D H M D H M. D D nuqtadan H M HM to'g'ri chiziqgacha bo'lgan masofa aylananing radiusiga teng, shuning uchun D H = 1 DH=1. Demak, D M = D H sin 60 ° = 2 3 DM=\dfrac(DH)(\textrm(sin)(60^(\circ))) = \dfrac(2)(\sqrt(3)) . M M nuqtaning koordinatalari y = 1 y=1 va y = - 3 x - 4 y=-\sqrt(3)x-4 (burchakning chap tomoni) ikkita chiziqning kesishish nuqtasi koordinatalari sifatida topiladi. .

Biz M (- 5 3) M(-\dfrac(5)(\sqrt(3))) ni olamiz. U holda D D nuqtaning abssissasi - 5 3 - 2 3 = - 7 3 -\dfrac(5)(\sqrt(3))-\dfrac(2)(\sqrt(3))=-\dfrac( ga teng bo'ladi. 7)(\ sqrt(3)) .

Doira markazining abtsissasi a 3 a\sqrt(3) ga teng bo lgani uchun a = - 7 3 a=-\dfrac(7)(3) ga teng bo ladi.

JAVOB

A = - 7 3 a=-\dfrac(7)(3)

a a parametrining barcha qiymatlarini toping, ularning har biri uchun tizim

$$\begin(holatlar) |4x+3y| \leq 12a,\\ x^2+y^2 \leq 14ax +6ay -57a^2+16a+64 \end(holatlar) $$

aynan bitta yechimga ega.

X O y xOy tekislikdagi har bir tengsizlikning yechimlar to'plamini tasvirlaylik.

Ikkinchi tengsizlikda biz mukammal kvadratlarni tanlaymiz:

x 2 - 14 a x + 49 + y 2 - 6 a y + 9 a 2 ≤ a 2 + 16 a + 64 ⇔ (x - 7 a) 2 + (y - 3 a) 2 ≤ (a + 8) 2     (1)   (1) ) x^2-14ax+49 + y^2-6ay + 9a^2 \leq a^2 + 16a + 64 \Chap oʻq (x-7a)^2+(y-3a)^2 \leq (a+8) )^2 \:\:\:\: (19)

a + 8 = 0 a+8=0 (a = - 8 a=-8) bo'lganda (19) tengsizlik koordinatalari (7 a ; 3 a) (7a;3a), ya'ni (- 56 ; -) bo'lgan nuqtani bildiradi. 24) (-56;-24) . a ning boshqa barcha qiymatlari uchun (19) radiusning (7 a ; 3 a) (7a; 3a) nuqtasida markazlashtirilgan doirani aniqlaydi | a+8 | |a+8| .

Keling, birinchi tengsizlikni ko'rib chiqaylik.
1) manfiy a uchun uning yechimlari yo'q. Bu tizimda hech qanday yechim yo'qligini anglatadi.

2) Agar a = 0 a=0 bo'lsa, u holda 4 x + 3 y = 0 4x+3y=0 to'g'ri chiziqni olamiz. Ikkinchi tengsizlikdan radiusi 8 bo'lgan markazi (0; 0) (0; 0) bo'lgan aylana olamiz. Shubhasiz, bir nechta echim bor.

3) Agar $$a>0$$ bo'lsa, bu tengsizlik qo'sh tengsizlikka ekvivalent bo'ladi - 12 a ≤ 4 x + 3 y ≤ 12 a -12a \leq 4x+3y \leq 12a . U y = ± 4 a - 4 x 3 y=\pm 4a -\dfrac(4x)(3) , har biri 4 x + 3 y = 0 4x+ toʻgʻri chiziqqa parallel boʻlgan ikkita toʻgʻri chiziq orasidagi chiziqni belgilaydi. 3y=0 (17-rasm).

Biz $$a>0$$ ni ko'rib chiqayotganimiz uchun aylananing markazi birinchi chorakda y = 3 x 7 y = \dfrac(3x)(7) chiziqda joylashgan. Haqiqatan ham markazning koordinatalari x = 7 a x=7a , y = 3 a y=3a ; a ani ifodalab, tenglashtirib, x 7 = y 3 \dfrac(x)(7)=\dfrac(y)(3) ni olamiz, bundan y = 3 x 7 y = \dfrac(3x)(7) . Tizim aynan bitta yechimga ega boʻlishi uchun aylananing a 2 a_2 toʻgʻri chiziqqa tegishi zarur va yetarli. Bu aylana radiusi aylana markazidan a 2 a_2 to'g'ri chiziqgacha bo'lgan masofaga teng bo'lganda sodir bo'ladi. Nuqtadan chiziqgacha bo'lgan masofa formulasiga ko'ra * (\^{*} получаем, что расстояние от точки (7 a ; 3 a) (7a;3a) до прямой 4 x + 3 y - 12 a = 0 4x+3y-12a=0 равно | 4 · 7 a + 3 · 3 a - 12 a | 4 2 + 3 2 = 5 a \dfrac{|4\cdot 7a + 3\cdot 3a -12a|}{\sqrt{4^2+3^2}} = 5\left|a\right| . Приравнивая к радиусу круга, получаем 5 a = | a + 8 | 5{a} = |a+8| . Так как $$a>0$$, опускаем модули и находим, что a = 2 a=2 .!}

JAVOB

A = 2 a=2

* {\^{*} Пусть даны точка M (x 0 ; y 0) M (x_0;y_0) и прямая l l , !} tenglama bilan berilgan a x + b y + c = 0 ax+by+c=0 . U holda M M nuqtadan l l to'g'ri chiziqgacha bo'lgan masofa r = | formula bilan aniqlanadi a x 0 + b x 0 + c | a 2 + b 2 \rho = \dfrac(|ax_0+bx_0+c|)(\sqrt(a^2+b^2)) .

a a parametrining qaysi qiymatlarida tizim ishlaydi

$$\begin(holatlar) |x|+|y|=1,\\ |x+a|+|y+a|=1 \end(holatlar)$$da yechim yo'qmi?

Tizimning birinchi tenglamasi x O y xOy tekisligidagi A B C D ABCD kvadratini aniqlaydi (uni qurish uchun x ≥ 0 x\geq 0 va y ≥ 0 y\geq 0 ni hisobga oling. Keyin tenglama x + y = ko'rinishni oladi. 1 x+y=1 segmentni olamiz - birinchi chorakda yotgan x + y = 1 x+y=1, keyin esa O x Ox o'qiga nisbatan bu segmentni aks ettiramiz hosil bo'lgan to'plamni O y Oy o'qiga nisbatan aks ettiradi (18-rasmga qarang). Ikkinchi tenglama kvadratni belgilaydi P Q R S PQRS , kvadratga teng A B C D ABCD , lekin (- a ; - a) (-a;-a) nuqtada markazlashtirilgan. Shaklda. Misol tariqasida, 18-rasmda a = - 2 a=-2 uchun bu kvadrat ko'rsatilgan. Agar bu ikki kvadrat kesishmasa, tizim hech qanday yechimga ega emas.

Agar P Q PQ va B C BC segmentlari mos tushsa, ikkinchi kvadratning markazi (1; 1) (1;1) nuqtada ekanligini tushunish oson. A ning o'sha qiymatlari bizga mos keladi, ularda markaz "yuqorida" va "o'ngda", ya'ni $$a1$$ joylashgan.

JAVOB

A ∈ (- ∞ ; - 1) ∪ (1 ; + ∞) a\in (-\infty;-1)\bigcup(1;+\infty) .

Tizim uchun b b parametrining barcha qiymatlarini toping

$$\begin(holatlar) y=|b-x^2|,\\ y=a(x-b) \end(holatlar) $$

a ning istalgan qiymati uchun kamida bitta yechimga ega.

Keling, bir nechta holatlarni ko'rib chiqaylik.

1) Agar $$b2) Agar b = 0 b=0 boʻlsa, tizim $$\begin(holatlar) y=x^2,\\ y=ax .\end(holatlar) $$ koʻrinishini oladi.

Har qanday a a uchun sonlar juftligi (0 ; 0) (0;0) bu sistemaning yechimidir, shuning uchun b = 0 b=0 mos keladi.

3) Keling, $$b>0$$ ni tuzatamiz. Birinchi tenglama y = x 2 - b y=x^2-b parabolaning O x Ox o'qiga nisbatan bir qismini aks ettirish orqali olingan nuqtalar to'plami bilan qondiriladi (19a, b-rasmga qarang). Ikkinchi tenglama chiziqlar oilasini belgilaydi (almashtirish turli ma'nolar a a , (b ; 0) (b;0) nuqtadan o'tuvchi, vertikaldan tashqari, (b ; 0) (b;0) nuqtadan o'tuvchi barcha turdagi to'g'ri chiziqlarni olishingiz mumkin. Agar (b ; 0) (b;0) nuqta [ - b segmentida yotsa; b ] [-\sqrt(b);\sqrt(b)] . abscissa o'qi, keyin to'g'ri chiziq har qanday qiyalik uchun birinchi funktsiya grafigini kesib o'tadi (19a-rasm). Aks holda (19b-rasm) har qanday holatda ham bu grafikni kesib o'tmaydigan to'g'ri chiziq bo'ladi. - b ≤ b ≤ b -\sqrt(b)\leq b \leq \sqrt(b) tengsizlikni yechish va $$b>0$$ ekanligini hisobga olsak, b ∈ (0 ; 1 ] b \ ni olamiz. ichida (0;1] .

Natijalarni birlashtiramiz: $$b \in $$.

JAVOB

$$b \$$da

a ning barcha qiymatlarini toping, ularning har biri uchun f (x) = x 2 - | x - a 2 | - 3 x f(x) = x^2-|x-a^2|-3x kamida bitta maksimal nuqtaga ega.

Modulni kengaytirib, biz buni olamiz

$$f(x) = \begin(holatlar) x^2-4x+a^2, \:\:\: x\geq a^2 ,\\ x^2-2x-a^2, \:\ :\: x\leq a^2 . \end(holatlar) $$

Ikki intervalning har birida y = f (x) y=f(x) funksiyaning grafigi shoxlari yuqoriga qaragan paraboladir.

Yuqori shoxlari bo'lgan parabolalar maksimal nuqtalarga ega bo'lmasligi sababli, yagona imkoniyat maksimal nuqta bu intervallarning chegara nuqtasi - x = a 2 x=a^2 nuqtasidir. Bu nuqtada y = x 2 - 4 x + a 2 y=x^2-4x+a^2 parabolaning cho'qqisi $$x>a^2$$ oralig'iga tushsa, maksimal bo'ladi va parabola cho'qqisi y = x 2 - 2 x - a 2 y=x^2-2x-a^2 - $$x\lt a^2$$ oralig'i uchun (20-rasmga qarang). Bu shart $$2 \gt a^2$$ va $$1 \lt a^2$$ tengsizliklari bilan berilgan, ularni yechishda a ∈ (- 2 ; 1) ∪ (1 ; 2) a\in ekanligini topamiz. (-\ sqrt(2);1)\bigcup(1;\sqrt(2)) .

JAVOB

A ∈ (- 2 ; 1) ∪ (1 ; 2) a\in (-\sqrt(2);1)\bigcup(1;\sqrt(2))

a ning barcha qiymatlarini toping, ularning har biri uchun umumiy yechimlar tengsizliklar

y + 2 x ≥ a y+2x \geq a va y - x ≥ 2 a             (20) y-x \geq 2a \:\:\:\:\:\:\:\: (20)

tengsizlikning yechimlaridir

$2y-x>a+3 \:\:\:\:\:\:\:\:\: (21)$$

Vaziyatni boshqarish uchun ba'zan bitta parametr qiymatini hisobga olish foydali bo'ladi. Masalan, a = 0 a=0 uchun chizma tuzamiz. Tengsizliklar (20) (aslida biz tengsizliklar tizimi (20) bilan ishlaymiz) B A C BAC burchagi nuqtalari (21-rasmga qarang) - nuqtalar bilan qanoatlantiriladi, ularning har biri ikkala to'g'ri chiziq ustida joylashgan y = - 2 x y=-2x va y = x y =x (yoki bu satrlarda). (21) tengsizlik y = 1 2 x + 3 2 y = \dfrac(1)(2)x + \dfrac(3)(2) to'g'ri chiziq ustida joylashgan nuqtalar bilan qanoatlantiriladi. Ko'rinib turibdiki, a = 0 a=0 bo'lganda masalaning sharti qanoatlanmaydi.

a a parametri uchun boshqa qiymat qabul qilsak, nima o'zgaradi? Chiziqlarning har biri harakatlanadi va o'ziga parallel chiziqqa aylanadi, chunki chiziqlarning burchak koeffitsientlari a ga bog'liq emas. Masalaning sharti bajarilishi uchun butun B A C BAC burchagi l l to'g'ri chiziq ustida yotishi kerak. Chunki A B AB va A C AC to'g'ri chiziqlarning burchak koeffitsientlari mutlaq qiymatda kattaroqdir qiyalik to'g'ri chiziq l l, burchakning tepasi to'g'ri chiziq l l ustida yotishi zarur va etarli.

Tenglamalar sistemasini yechish

$$\begin(holatlar) y+2x=a,\\ y-x=2a, \end(holatlar)$$

A nuqtaning koordinatalarini toping (- a 3 ; 5 a 3) A(-\dfrac(a)(3);\dfrac(5a)(3)) . Ular (21) tengsizlikni qondirishi kerak, shuning uchun $$\dfrac(10a)(3)+\dfrac(a)(3) > a+3$$, bu erdan $$a>\dfrac(9)(8)$$ .

JAVOB

$$a>\dfrac(9)(8)$$