Gunohning jadval qiymatlari. Trigonometrik funktsiyalar
Sinus (), kosinus (), tangens (), kotangens () tushunchalari burchak tushunchasi bilan uzviy bog'liqdir. Bularni, birinchi qarashda, murakkab tushunchalarni (ko'pgina maktab o'quvchilarida dahshatga soladigan) yaxshi tushunish uchun va "iblis u chizilgandek dahshatli emas"ligiga ishonch hosil qilish uchun keling, keling, "shayton" dan boshlaylik. juda boshlang'ich va burchak tushunchasini tushunish.
Burchak tushunchasi: radian, daraja
Keling, rasmga qaraylik. Vektor nuqtaga nisbatan ma'lum miqdorda "aylangan". Shunday qilib, bu aylanishning boshlang'ich pozitsiyasiga nisbatan o'lchovi bo'ladi burchak.
Burchak tushunchasi haqida yana nimani bilishingiz kerak? Albatta, burchak birliklari!
Geometriyada ham, trigonometriyada ham burchakni daraja va radian bilan o'lchash mumkin.
Burchak (bir daraja) aylananing bir qismiga teng dumaloq yoy bilan qoplangan aylanadagi markaziy burchak. Shunday qilib, butun doira dumaloq yoylarning "bo'laklari" dan iborat yoki aylana tomonidan tasvirlangan burchak tengdir.

Ya'ni, yuqoridagi rasmda teng burchak ko'rsatilgan, ya'ni bu burchak aylana o'lchamidagi aylana yoyga tayanadi.
Radianlardagi burchak uzunligi aylananing radiusiga teng bo'lgan aylana yoyi bilan qoplangan doiradagi markaziy burchakdir. Xo'sh, tushundingizmi? Agar yo'q bo'lsa, keling, buni rasmdan aniqlaylik.

Shunday qilib, rasmda radianga teng burchak ko'rsatilgan, ya'ni bu burchak aylana yoyga tayanadi, uning uzunligi aylananing radiusiga teng (uzunligi uzunlikka teng yoki radius tengdir). yoy uzunligi). Shunday qilib, yoy uzunligi quyidagi formula bo'yicha hisoblanadi:
Radianlarda markaziy burchak qayerda.
Xo'sh, buni bilib, aylana tasvirlangan burchakda qancha radian borligiga javob bera olasizmi? Ha, buning uchun siz aylana formulasini eslab qolishingiz kerak. Mana u:
Xo'sh, endi bu ikki formulani o'zaro bog'laymiz va aylana tasvirlangan burchak teng ekanligini topamiz. Ya'ni, qiymatni darajalar va radyanlardagi o'zaro bog'lash orqali biz buni olamiz. Tegishli ravishda, . Ko'rib turganingizdek, "daraja" dan farqli o'laroq, "radian" so'zi olib tashlandi, chunki o'lchov birligi odatda kontekstdan aniq bo'ladi.
Qancha radian bor? Hammasi to'g'ri!
Tushundim? Keyin davom eting va uni tuzating:
Qiyinchiliklar bormi? Keyin qarang javoblar:
To'g'ri burchakli uchburchak: sinus, kosinus, tangens, burchak kotangensi
Shunday qilib, biz burchak tushunchasini aniqladik. Lekin burchakning sinusi, kosinusu, tangensi va kotangensi nima? Keling, buni aniqlaylik. Buning uchun bizga to'g'ri burchakli uchburchak yordam beradi.

To'g'ri burchakli uchburchakning tomonlari nima deyiladi? To'g'ri, gipotenuza va oyoqlar: gipotenuza to'g'ri burchakka qarama-qarshi yotgan tomon (bizning misolimizda bu tomon); oyoqlari qolgan ikkita tomon va (to'g'ri burchakka qo'shni bo'lganlar) va agar biz burchakka nisbatan oyoqlarni ko'rib chiqsak, u holda oyoq qo'shni oyoq, oyoq esa aksincha. Xo'sh, endi savolga javob beraylik: burchakning sinus, kosinus, tangensi va kotangensi nima?
Burchak sinusi- bu qarama-qarshi (uzoq) oyoqning gipotenuzaga nisbati.
Bizning uchburchakda.
Burchak kosinusi- bu qo'shni (yaqin) oyoqning gipotenuzaga nisbati.
Bizning uchburchakda.
Burchakning tangensi- bu qarama-qarshi (uzoq) tomonning qo'shni (yaqin) nisbati.
Bizning uchburchakda.
Burchak kotangensi- bu qo'shni (yaqin) oyoqning qarama-qarshi (uzoq) nisbati.
Bizning uchburchakda.
Bu ta'riflar zarur eslab qoling! Qaysi oyoqni nimaga bo'lish kerakligini eslab qolishni osonlashtirish uchun siz buni aniq tushunishingiz kerak tangens Va kotangent faqat oyoqlar o'tiradi va gipotenuz faqat ichida paydo bo'ladi sinus Va kosinus. Va keyin siz birlashmalar zanjiri bilan kelishingiz mumkin. Masalan, bu:
Kosinus → teginish → teginish → ulashgan;
Kotangent → teginish → teginish → qo‘shni.
Avvalo, sinus, kosinus, tangens va kotangens uchburchak tomonlarining nisbati bu tomonlarning uzunligiga (bir xil burchak ostida) bog'liq emasligini yodda tutishingiz kerak. Ishonma? Keyin rasmga qarab ishonch hosil qiling:

Masalan, burchakning kosinusini ko'rib chiqaylik. Ta'rifga ko'ra, uchburchakdan: , lekin uchburchakdan burchakning kosinusini hisoblashimiz mumkin: . Ko'ryapsizmi, tomonlarning uzunligi har xil, lekin bir burchakning kosinus qiymati bir xil. Shunday qilib, sinus, kosinus, tangens va kotangens qiymatlari faqat burchakning kattaligiga bog'liq.
Agar siz ta'riflarni tushunsangiz, davom eting va ularni birlashtiring!
Quyidagi rasmda ko'rsatilgan uchburchak uchun biz topamiz.

Xo'sh, tushundingizmi? Keyin o'zingizni sinab ko'ring: burchak uchun xuddi shunday hisoblang.
Birlik (trigonometrik) doira
Darajalar va radianlar tushunchalarini tushunib, biz radiusi teng bo'lgan doirani ko'rib chiqdik. Bunday doira deyiladi yagona. Bu trigonometriyani o'rganishda juda foydali bo'ladi. Shuning uchun, keling, buni biroz batafsilroq ko'rib chiqaylik.

Ko'rib turganingizdek, bu aylana Dekart koordinata tizimida qurilgan. Doira radiusi birga teng, aylananing markazi koordinatalarning boshida joylashgan bo'lsa, radius vektorining boshlang'ich pozitsiyasi o'qning musbat yo'nalishi bo'ylab o'rnatiladi (bizning misolimizda bu radius).
Doiradagi har bir nuqta ikkita raqamga to'g'ri keladi: o'q koordinatasi va o'q koordinatasi. Bu koordinata raqamlari nima? Va umuman olganda, ularning mavzuga qanday aloqasi bor? Buning uchun biz ko'rib chiqilgan to'g'ri burchakli uchburchak haqida eslashimiz kerak. Yuqoridagi rasmda siz ikkita to'g'ri burchakli uchburchakni ko'rishingiz mumkin. Uchburchakni ko'rib chiqing. U to'rtburchaklar, chunki u o'qga perpendikulyar.
Uchburchak nimaga teng? Hammasi to'g'ri. Bundan tashqari, biz bilamizki, bu birlik doirasining radiusi, ya'ni . Keling, bu qiymatni kosinus formulamizga almashtiramiz. Mana nima sodir bo'ladi:
Uchburchak nimaga teng? Xo'sh, albatta,! Ushbu formulaga radius qiymatini almashtiring va quyidagilarni oling:
Xo'sh, aylanaga tegishli nuqta qanday koordinatalarga ega ekanligini ayta olasizmi? Xo'sh, yo'qmi? Agar buni tushunsangiz va shunchaki raqamlar bo'lsa-chi? U qaysi koordinataga mos keladi? Albatta, koordinatalar! Va u qaysi koordinataga mos keladi? To'g'ri, koordinatalar! Shunday qilib, davr.

Xo'sh, nimaga teng va nimaga teng? To'g'ri, keling, tangens va kotangensning tegishli ta'riflaridan foydalanamiz va buni olamiz, a.
Agar burchak kattaroq bo'lsa-chi? Masalan, ushbu rasmdagi kabi:

Ushbu misolda nima o'zgardi? Keling, buni aniqlaylik. Buning uchun yana to'g'ri burchakli uchburchakka o'taylik. To'g'ri uchburchakni ko'rib chiqing: burchak (burchakka qo'shni sifatida). Burchak uchun sinus, kosinus, tangens va kotangensning qiymatlari qanday? To'g'ri, biz trigonometrik funktsiyalarning tegishli ta'riflariga amal qilamiz:
Ko'rib turganingizdek, burchak sinusining qiymati hali ham koordinataga to'g'ri keladi; burchak kosinusining qiymati - koordinata; va mos keladigan nisbatlarga tangens va kotangens qiymatlari. Shunday qilib, bu munosabatlar radius vektorining har qanday aylanishiga taalluqlidir.
Radius vektorining boshlang'ich pozitsiyasi o'qning ijobiy yo'nalishi bo'ylab joylashganligi allaqachon aytib o'tilgan. Hozirgacha biz bu vektorni soat sohasi farqli ravishda aylantirdik, lekin agar biz uni soat yo'nalishi bo'yicha aylantirsak nima bo'ladi? Hech qanday g'ayrioddiy narsa yo'q, siz ham ma'lum bir qiymatga ega burchakka ega bo'lasiz, lekin faqat salbiy bo'ladi. Shunday qilib, radius vektorini soat sohasi farqli ravishda aylantirganda, biz olamiz ijobiy burchaklar, va soat yo'nalishi bo'yicha aylanganda - salbiy.
Shunday qilib, biz bilamizki, radius vektorining aylana atrofida butun aylanishi yoki. Radius vektorini burish mumkinmi? Xo'sh, albatta qila olasiz! Birinchi holda, shuning uchun radius vektori bitta to'liq aylanishni amalga oshiradi va yoki pozitsiyasida to'xtaydi.
Ikkinchi holda, ya'ni radius vektori uchta to'liq aylanishni amalga oshiradi va yoki holatida to'xtaydi.
Shunday qilib, yuqoridagi misollardan xulosa qilishimiz mumkinki, bir-biridan farq qiladigan burchaklar yoki (bu erda har qanday butun son) radius vektorining bir xil holatiga mos keladi.
Quyidagi rasmda burchak ko'rsatilgan. Xuddi shu rasm burchakka mos keladi va hokazo. Ushbu ro'yxatni cheksiz davom ettirish mumkin. Bu burchaklarning barchasi umumiy formula yoki (bu yerda har qanday butun son) bilan yozilishi mumkin.

Endi, asosiy trigonometrik funktsiyalarning ta'riflarini bilib, birlik doirasidan foydalanib, qiymatlar nima ekanligiga javob berishga harakat qiling:
Mana sizga yordam beradigan birlik doirasi:

Qiyinchiliklar bormi? Keyin buni aniqlaylik. Shunday qilib, biz buni bilamiz:
Bu erdan ma'lum burchak o'lchovlariga mos keladigan nuqtalarning koordinatalarini aniqlaymiz. Keling, tartibda boshlaylik: burchak koordinatali nuqtaga to'g'ri keladi, shuning uchun:
Mavjud emas;
Bundan tashqari, xuddi shu mantiqqa rioya qilgan holda, biz burchaklar mos ravishda koordinatali nuqtalarga mos kelishini aniqlaymiz. Buni bilib, tegishli nuqtalarda trigonometrik funktsiyalarning qiymatlarini aniqlash oson. Avval o'zingiz sinab ko'ring, keyin javoblarni tekshiring.
Javoblar:
Mavjud emas
Mavjud emas
Mavjud emas
Mavjud emas
Shunday qilib, biz quyidagi jadvalni tuzishimiz mumkin:

Bu barcha qadriyatlarni eslab qolishning hojati yo'q. Birlik aylanasidagi nuqtalar koordinatalari va trigonometrik funktsiyalar qiymatlari o'rtasidagi muvofiqlikni eslash kifoya:
Ammo burchaklarning trigonometrik funktsiyalarining qiymatlari va quyidagi jadvalda keltirilgan, eslash kerak:

Qo'rqmang, endi biz sizga bitta misol keltiramiz mos keladigan qiymatlarni eslab qolish juda oddiy:
Ushbu usuldan foydalanish uchun burchakning barcha uch o'lchovi uchun sinus qiymatlarini (), shuningdek burchak tangensining qiymatini eslab qolish juda muhimdir. Ushbu qiymatlarni bilib, butun jadvalni tiklash juda oddiy - kosinus qiymatlari strelkalar bo'yicha uzatiladi, ya'ni:
Buni bilib, siz uchun qiymatlarni tiklashingiz mumkin. Numerator " " mos keladi va maxraj " " mos keladi. Kotangent qiymatlari rasmda ko'rsatilgan o'qlarga muvofiq o'tkaziladi. Agar siz buni tushunsangiz va o'qlar bilan diagrammani eslab qolsangiz, jadvaldagi barcha qiymatlarni eslab qolish kifoya qiladi.
Doiradagi nuqtaning koordinatalari
Aylanada nuqtani (uning koordinatalarini) topish mumkinmi? aylana markazining koordinatalarini, uning radiusini va burilish burchagini bilish?
Xo'sh, albatta qila olasiz! Keling, chiqaraylik nuqta koordinatalarini topishning umumiy formulasi.
Masalan, oldimizda aylana bor:

Bizga nuqta aylananing markazi ekanligi berilgan. Doira radiusi teng. Nuqtani gradusga aylantirish orqali olingan nuqtaning koordinatalarini topish kerak.
Rasmdan ko'rinib turibdiki, nuqta koordinatasi segment uzunligiga to'g'ri keladi. Segmentning uzunligi aylana markazining koordinatasiga to'g'ri keladi, ya'ni u tengdir. Segment uzunligini kosinus ta'rifi yordamida ifodalash mumkin:
Keyin biz nuqta koordinatasini olamiz.
Xuddi shu mantiqdan foydalanib, nuqta uchun y koordinata qiymatini topamiz. Shunday qilib,
Shunday qilib, umuman olganda, nuqtalarning koordinatalari formulalar bilan aniqlanadi:
Doira markazining koordinatalari,
Doira radiusi,
Vektor radiusining aylanish burchagi.
Ko'rib turganingizdek, biz ko'rib chiqayotgan birlik doirasi uchun bu formulalar sezilarli darajada kamayadi, chunki markazning koordinatalari nolga va radius birga teng:
Xo'sh, keling, aylana bo'ylab nuqtalarni topishni mashq qilib, ushbu formulalarni sinab ko'raylik?
1. Nuqtani aylantirib olingan birlik doiradagi nuqtaning koordinatalarini toping.
2. Nuqtani aylantirib olingan birlik doiradagi nuqtaning koordinatalarini toping.
3. Nuqtani aylantirib olingan birlik doiradagi nuqtaning koordinatalarini toping.
4. Nuqta aylananing markazidir. Doira radiusi teng. Dastlabki radius vektorini ga aylantirish orqali olingan nuqtaning koordinatalarini topish kerak.
5. Nuqta aylananing markazidir. Doira radiusi teng. Dastlabki radius vektorini ga aylantirish orqali olingan nuqtaning koordinatalarini topish kerak.
Aylanadagi nuqtaning koordinatalarini topishda muammo bormi?
Ushbu beshta misolni yeching (yoki ularni echishni yaxshi biling) va siz ularni topishni o'rganasiz!
1.
Siz buni sezishingiz mumkin. Ammo biz boshlang'ich nuqtaning to'liq inqilobiga nima mos kelishini bilamiz. Shunday qilib, kerakli nuqta burilish paytida bo'lgani kabi bir xil holatda bo'ladi. Buni bilib, biz nuqtaning kerakli koordinatalarini topamiz:
2. Birlik doirasi nuqtada markazlashtirilgan, ya'ni biz soddalashtirilgan formulalardan foydalanishimiz mumkin:
Siz buni sezishingiz mumkin. Biz boshlang'ich nuqtaning ikkita to'liq aylanishiga nima mos kelishini bilamiz. Shunday qilib, kerakli nuqta burilish paytida bo'lgani kabi bir xil holatda bo'ladi. Buni bilib, biz nuqtaning kerakli koordinatalarini topamiz:
Sinus va kosinus jadval qiymatlari hisoblanadi. Biz ularning ma'nolarini eslaymiz va olamiz:
Shunday qilib, kerakli nuqta koordinatalarga ega.
3. Birlik doirasi nuqtada markazlashtirilgan, ya'ni biz soddalashtirilgan formulalardan foydalanishimiz mumkin:
Siz buni sezishingiz mumkin. Keling, ushbu misolni rasmda tasvirlaymiz:

Radius o'qga teng va o'q bilan burchaklarni hosil qiladi. Kosinus va sinusning jadval qiymatlari teng ekanligini bilib, bu erda kosinus manfiy, sinus esa ijobiy qiymat olishini aniqlab, biz:
Mavzu bo'yicha trigonometrik funktsiyalarni kamaytirish formulalarini o'rganishda bunday misollar batafsilroq muhokama qilinadi.
Shunday qilib, kerakli nuqta koordinatalarga ega.
4.
Vektor radiusining burilish burchagi (shart bo'yicha)
Sinus va kosinusning tegishli belgilarini aniqlash uchun biz birlik doira va burchakni quramiz:

Ko'rib turganingizdek, qiymat, ya'ni ijobiy, qiymat esa, ya'ni salbiy. Tegishli trigonometrik funktsiyalarning jadval qiymatlarini bilib, biz quyidagilarni olamiz:
Olingan qiymatlarni formulamizga almashtiramiz va koordinatalarni topamiz:
Shunday qilib, kerakli nuqta koordinatalarga ega.
5. Ushbu muammoni hal qilish uchun biz umumiy shakldagi formulalardan foydalanamiz, bu erda
Doira markazining koordinatalari (bizning misolimizda,
Doira radiusi (shart bo'yicha)
Vektor radiusining burilish burchagi (shart bo'yicha).
Barcha qiymatlarni formulaga almashtiring va quyidagini oling:
va - jadval qiymatlari. Keling, eslaylik va ularni formulaga almashtiramiz:
Shunday qilib, kerakli nuqta koordinatalarga ega.
XULOSA VA ASOSIY FORMULALAR
Burchakning sinusi - bu qarama-qarshi (uzoq) oyoqning gipotenuzaga nisbati.
Burchakning kosinusi - qo'shni (yaqin) oyoqning gipotenuzaga nisbati.
Burchakning tangensi - qarama-qarshi (uzoq) tomonning qo'shni (yaqin) tomonga nisbati.
Burchakning kotangensi - qo'shni (yaqin) tomonning qarama-qarshi (uzoq) tomonga nisbati.
Ushbu maqola o'z ichiga oladi sinuslar, kosinuslar, tangenslar va kotangentlar jadvallari. Birinchidan, biz trigonometrik funktsiyalarning asosiy qiymatlari jadvalini, ya'ni 0, 30, 45, 60, 90, ..., 360 gradus burchaklarning sinuslari, kosinuslari, tangenslari va kotangentlari jadvalini beramiz ( 0, p/6, p/4, p/3, p/2, …, 2p radian). Shundan so'ng biz sinuslar va kosinuslar jadvalini, shuningdek V. M. Bradisning tangens va kotangentlar jadvalini beramiz va trigonometrik funktsiyalarning qiymatlarini topishda ushbu jadvallardan qanday foydalanishni ko'rsatamiz.
Sahifani navigatsiya qilish.
0, 30, 45, 60, 90, ... daraja burchaklar uchun sinuslar, kosinuslar, tangenslar va kotangentlar jadvali
Adabiyotlar ro'yxati.
- Algebra: Darslik 9-sinf uchun. o'rtacha maktab/Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovskiy - M.: Ta'lim, 1990. - 272 pp.: kasal - ISBN 5-09-002727-7
- Bashmakov M.I. Algebra va tahlilning boshlanishi: Darslik. 10-11 sinflar uchun. o'rtacha maktab - 3-nashr. - M.: Ta'lim, 1993. - 351 b.: kasal. - ISBN 5-09-004617-4.
- Algebra va tahlilning boshlanishi: Proc. 10-11 sinflar uchun. umumiy ta'lim muassasalar / A. N. Kolmogorov, A. M. Abramov, P. Dudnitsyn va boshqalar; Ed. A. N. Kolmogorov - 14-nashr - M.: Ta'lim, 2004. - 384 pp.: ISBN 5-09-013651-3.
- Gusev V. A., Mordkovich A. G. Matematika (texnika maktablariga kiruvchilar uchun qo'llanma): Proc. nafaqa.- M.; Yuqori maktab, 1984.-351 b., kasal.
- Bradis V. M. To'rt xonali matematik jadvallar: Umumiy ta'lim uchun. darslik muassasalar. - 2-nashr. - M.: Bustard, 1999.- 96 b.: kasal. ISBN 5-7107-2667-2
Maqolada biz uning qanday ko'rinishini to'liq tushunamiz trigonometrik qiymatlar jadvali, sinus, kosinus, tangens va kotangens. Trigonometrik funksiyalarning asosiy ma'nosini 0,30,45,60,90,...,360 gradus burchakdan ko'rib chiqamiz. Keling, trigonometrik funktsiyalarning qiymatlarini hisoblashda ushbu jadvallardan qanday foydalanishni ko'rib chiqaylik.
Avval ko'rib chiqaylik kosinus, sinus, tangens va kotangens jadvali 0, 30, 45, 60, 90,... daraja burchakdan. Ushbu miqdorlarning ta'rifi bizga 0 va 90 daraja burchaklar funktsiyalarining qiymatini aniqlash imkonini beradi:
sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, 00 dan kotangens aniqlanmagan bo'ladi
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, 90 0 dan tangens noaniq bo'ladi
Agar siz burchaklari 30 dan 90 darajagacha bo'lgan to'g'ri burchakli uchburchaklarni olsangiz. Biz olamiz:
sin 30 0 = 1/2, cos 30 0 = √3/2, tan 30 0 = √3/3, cos 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tan 45 0 = 1, cos 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, karyola 60 0 = √3/3
Keling, barcha olingan qiymatlarni shaklda ifodalaylik trigonometrik jadval:
Sinuslar, kosinuslar, tangenslar va kotangentlar jadvali!
Agar biz qisqartirish formulasidan foydalansak, jadvalimiz 360 gradusgacha bo'lgan burchaklar uchun qiymatlarni qo'shib ortadi. Bu shunday ko'rinadi:

Shuningdek, davriylik xususiyatlaridan kelib chiqib, agar burchaklarni 0 0 +360 0 *z .... 330 0 +360 0 *z bilan almashtirsak, jadvalni oshirish mumkin, bunda z butun sondir. Ushbu jadvalda bitta doiradagi nuqtalarga mos keladigan barcha burchaklarning qiymatini hisoblash mumkin.

Keling, jadvalni eritmada qanday ishlatishni ko'rib chiqaylik.
Hammasi juda oddiy. Bizga kerak bo'lgan qiymat bizga kerak bo'lgan hujayralarning kesishish nuqtasida joylashganligi sababli. Masalan, 60 graduslik burchakning kos qiymatini oling, jadvalda u quyidagicha ko'rinadi:

Trigonometrik funktsiyalarning asosiy qiymatlarining yakuniy jadvalida biz xuddi shu tarzda harakat qilamiz. Lekin bu jadvalda 1020 gradus burchakdan tangens qancha ekanligini bilish mumkin, u = -√3 1020 0 = 300 0 +360 0 *2 ni tekshiramiz. Keling, uni jadval yordamida topamiz.

Bradis stoli. Sinus, kosinus, tangens va kotangens uchun.
Bradis jadvallari bir necha qismlarga bo'lingan bo'lib, ular kosinus va sinus, tangens va kotangens jadvallaridan iborat - ular ikki qismga bo'lingan (tg 90 gradusgacha bo'lgan burchaklar va ctg kichik burchaklar).
Sinus va kosinus


tg burchak 00 dan boshlanib, 760 bilan tugaydi, ctg 140 dan boshlanib, 900 bilan tugaydi.


tg gacha 900 va ctg kichik burchaklar.
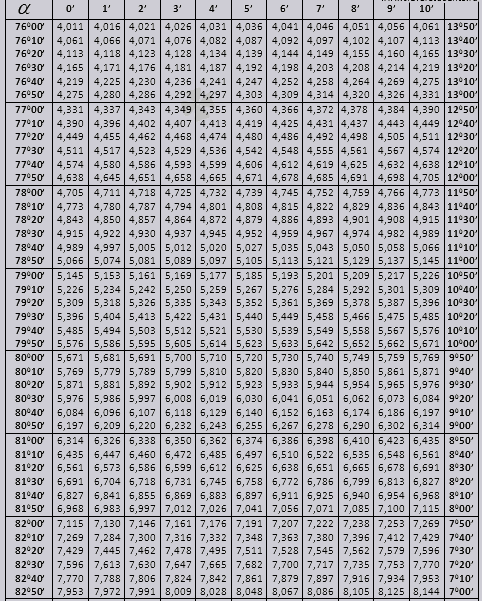

Keling, muammolarni hal qilishda Bradis jadvallaridan qanday foydalanishni aniqlaymiz.
Keling, sin belgisini topamiz (chap chetidagi ustundagi belgi) 42 daqiqa (belgi yuqori qatorda). Kesishish orqali biz belgini qidiramiz, u = 0,3040.
Daqiqa qiymatlari olti daqiqalik interval bilan ko'rsatilgan, agar bizga kerak bo'lgan qiymat aynan shu oraliqda bo'lsa, nima qilish kerak. Keling, 44 daqiqani olaylik, lekin jadvalda faqat 42 bor, biz 42 ni asos qilib olamiz va o'ng tomondagi qo'shimcha ustunlardan foydalanamiz, 2-tuzatishni olamiz va 0,3040 + 0,0006 ga qo'shamiz.
Gunoh 47 daqiqa bilan biz 48 daqiqani asos qilib olamiz va undan 1 tuzatishni ayiramiz, ya'ni 0,3057 - 0,0003 = 0,3054
Kosni hisoblashda biz gunohga o'xshash ishlaymiz, faqat jadvalning pastki qatorini asos qilib olamiz. Masalan, cos 20 0 = 0,9397
90 0 gacha bo'lgan tg burchagi va kichik burchakning karyolasi qiymatlari to'g'ri va ularda tuzatishlar yo'q. Masalan, tg 78 0 37min = 4,967 ni toping 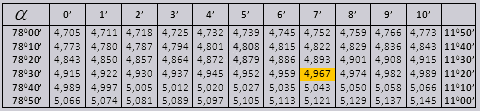
va ctg 20 0 13min = 25,83 
Xo'sh, biz asosiy trigonometrik jadvallarni ko'rib chiqdik. Umid qilamizki, bu ma'lumot siz uchun juda foydali bo'ldi. Jadvallar haqida savollaringiz bo'lsa, ularni sharhlarda yozishni unutmang!
Eslatma: Devor bamperlari devorlarni himoya qilish uchun bamper taxtasi. Havolaga rioya qiling ramkasiz devor bamperlari (http://www.spi-polymer.ru/otboyniki/) va ko'proq bilib oling.
1. Trigonometrik funktsiyalar argumenti bo'lgan elementar funksiyalardir burchak. Trigonometrik funktsiyalar to'g'ri burchakli uchburchakda tomonlar va o'tkir burchaklar o'rtasidagi munosabatlarni tavsiflaydi. Trigonometrik funktsiyalarni qo'llash sohalari juda xilma-xildir. Masalan, har qanday davriy jarayonlarni trigonometrik funktsiyalar yig'indisi (Furye seriyasi) sifatida ko'rsatish mumkin. Bu funksiyalar ko‘pincha differensial va funksional tenglamalarni yechishda paydo bo‘ladi.
2. Trigonometrik funksiyalarga quyidagi 6 ta funksiya kiradi: sinus, kosinus, tangens,kotangent, sekant Va kosekant. Bu funksiyalarning har biri uchun teskari trigonometrik funksiya mavjud.
3. Foydalanib trigonometrik funksiyalarning geometrik ta'rifini kiritish qulay birlik doirasi. Quyidagi rasmda radiusi r=1 bo‘lgan aylana ko‘rsatilgan. Aylanada M(x,y) nuqta belgilangan. OM radius vektori va Ox o'qining musbat yo'nalishi orasidagi burchak a ga teng.
4. Sinus burchak a - M(x,y) nuqtaning y ordinatasining r radiusiga nisbati:
sina=y/r.
r=1 bo‘lgani uchun sinus M(x,y) nuqtaning ordinatasiga teng bo‘ladi.
5. Kosinus burchak a - M(x,y) nuqtaning x abtsissasining r radiusiga nisbati:
cosa=x/r
6. Tangent burchak a - M(x,y) nuqtaning y ordinatasining uning x abtsissasiga nisbati:
tana=y/x,x≠0
7. Kotangent burchak a - M(x,y) nuqtaning x abssissasining y ordinatasiga nisbati:
kota=x/y,y≠0
8. Sekant burchak a - r radiusning M(x,y) nuqtaning x abscissasiga nisbati:
seca=r/x=1/x,x≠0
9. Kosekant burchak a - r radiusning M(x,y) nuqtaning y ordinatasiga nisbati:
csca=r/y=1/y,y≠0
10. Birlik aylanada x, y proyeksiyalar, M(x,y) nuqtalar va radius r to'g'ri burchakli uchburchak hosil qiladi, bunda x,y - oyoqlari, r - gipotenuza. Shunday qilib, to'g'ri burchakli uchburchakda qo'llaniladigan trigonometrik funktsiyalarning yuqoridagi ta'riflari quyidagicha tuzilgan:
Sinus burchak a - qarama-qarshi tomonning gipotenuzaga nisbati.
Kosinus burchak a - qo'shni oyoqning gipotenuzaga nisbati.
Tangent burchak a qo'shni oyoqqa qarama-qarshi oyoq deb ataladi.
Kotangent a burchakka qarama-qarshi tomonga ulashgan tomon deyiladi.
Sekant burchak a - gipotenuzaning qo'shni oyoqqa nisbati.
Kosekant burchak a - gipotenuzaning qarama-qarshi oyoqqa nisbati.
11. Sinus funksiyasining grafigi
y=sinx, aniqlash sohasi: x∈R, qiymatlar diapazoni: −1≤sinx≤1
12. Kosinus funksiyasining grafigi
y=cosx, aniqlash sohasi: x∈R, qiymatlar diapazoni: −1≤cosx≤1
13. Tangens funksiya grafigi 14. Kotangent funksiyaning grafigi 15. Sekant funksiyaning grafigi
y=tanx, domen: x∈R,x≠(2k+1)p/2, diapazon: −∞ 
y=cotx, domen: x∈R,x≠kp, diapazon: −∞ 
y=sekx, domen: x∈R,x≠(2k+1)p/2, diapazon: sekx∈(−∞,−1]∪∪)