Bir xil asosli logarifmlar yig'indisi. Asosiy logarifmik identifikatsiya. Integratsiya chegaralarini almashtirish
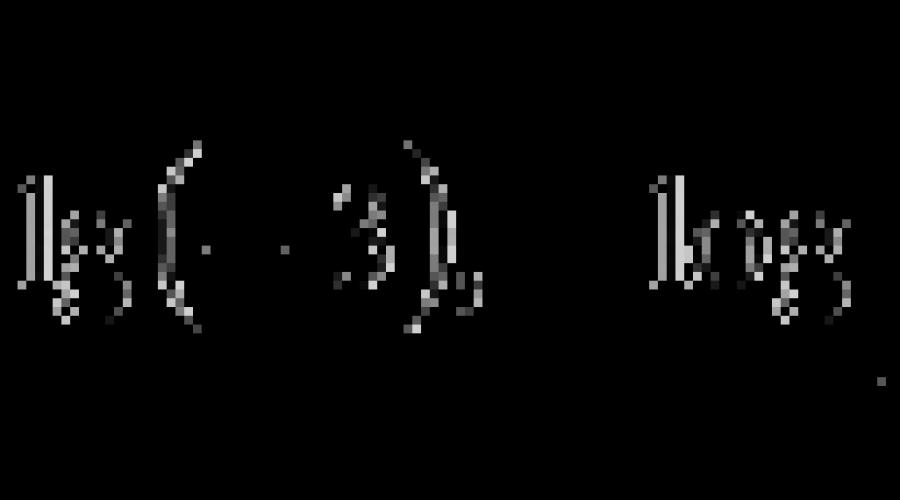
Ushbu maqolaning diqqat markazida logarifm. Bu yerda logarifmning ta’rifini beramiz, qabul qilingan yozuvni ko‘rsatamiz, logarifmalarga misollar keltiramiz, natural va o‘nlik logarifmlar haqida gapiramiz. Shundan so'ng, asosiyni ko'rib chiqaylik logarifmik identifikatsiya.
Sahifani navigatsiya qilish.
Logarifmning ta'rifi
Logarifm tushunchasi muammoni hal qilishda paydo bo'ladi ma'lum ma'noda teskari, ko'rsatkichni topish kerak bo'lganda ma'lum qiymat daraja va ma'lum asos.
Ammo so'zboshilari etarli, "logarifm nima" degan savolga javob berish vaqti keldi? Keling, tegishli ta'rifni beraylik.
Ta'rif.
b ning a asosiga logarifmi, bu erda a>0, a≠1 va b>0 ko'rsatkich bo'lib, natijada b olish uchun a sonini ko'tarish kerak.
Ushbu bosqichda biz "logarifm" so'zi darhol ikkita keyingi savolni keltirib chiqarishi kerakligini ta'kidlaymiz: "qanday raqam" va "qanday asosda". Boshqacha qilib aytadigan bo'lsak, oddiygina logarifm yo'q, faqat raqamning ba'zi bir asosga logarifmi.
Keling, darhol kiramiz logarifm yozuvi: b sonining a asosiga logarifmi odatda log a b sifatida belgilanadi. b sonining e asosiga logarifmi va 10 asosining logarifmi mos ravishda lnb va logb ning o'ziga xos maxsus belgilariga ega, ya'ni ular log e b emas, balki lnb va log 10 b emas, balki lgb deb yozadilar.
Endi biz berishimiz mumkin: .
Va yozuvlar  mantiqiy emas, chunki ularning birinchisida logarifm belgisi ostida manfiy son, ikkinchisida asosda manfiy son, uchinchisida logarifm belgisi ostida manfiy son va birlik mavjud. asos.
mantiqiy emas, chunki ularning birinchisida logarifm belgisi ostida manfiy son, ikkinchisida asosda manfiy son, uchinchisida logarifm belgisi ostida manfiy son va birlik mavjud. asos.
Endi gaplashaylik logarifmlarni o'qish qoidalari. Log a b "b ning a asosiga logarifmi" sifatida o'qiladi. Masalan, log 2 3 - 2-asosning uchta logarifmi va 2-sonli ikki nuqtaning uchdan ikki qismining logarifmi. Kvadrat ildiz beshdan. e asosining logarifmi deyiladi tabiiy logarifm, va lnb yozuvi "b ning natural logarifmini" o'qiydi. Misol uchun, ln7 - ettitaning natural logarifmi va biz uni pi ning natural logarifmi sifatida o'qiymiz. 10 ta asosiy logarifm ham maxsus nomga ega - o'nlik logarifm, va lgb "b ning o'nlik logarifmi" sifatida o'qiladi. Misol uchun, lg1 - birning o'nlik logarifmi va lg2.75 - ikki nuqtaning etti besh yuzdan birining o'nlik logarifmi.
Logarifmning ta'rifi berilgan a>0, a≠1 va b>0 shartlar haqida alohida to'xtalib o'tish joiz. Keling, ushbu cheklovlar qaerdan kelib chiqqanligini tushuntirib beraylik. Yuqorida keltirilgan logarifm ta'rifidan to'g'ridan-to'g'ri kelib chiqadigan shaklning tengligi bizga yordam beradi.
a≠1 dan boshlaylik. Har qanday daraja birga teng bo'lganligi sababli, tenglik faqat b=1 bo'lganda to'g'ri bo'lishi mumkin, lekin log 1 1 har qanday haqiqiy son bo'lishi mumkin. Bu noaniqlikni oldini olish uchun a≠1 qabul qilinadi.
a>0 shartining maqsadga muvofiqligini asoslab beramiz. a=0 bilan, logarifmning ta'rifiga ko'ra, biz faqat b=0 bilan mumkin bo'lgan tenglikka ega bo'lamiz. Ammo log 0 0 har qanday nolga teng bo'lmagan haqiqiy son bo'lishi mumkin, chunki noldan nolga teng bo'lmagan kuch nolga teng. a≠0 sharti bizga bu noaniqlikdan qochish imkonini beradi. Va qachon a<0 нам бы пришлось отказаться от рассмотрения рациональных и иррациональных значений логарифма, так как степень с рациональным и ирratsional ko'rsatkich faqat manfiy bo'lmagan asoslar uchun aniqlanadi. Shuning uchun a>0 sharti qabul qilinadi.
Nihoyat, a>0 tengsizlikdan b>0 sharti kelib chiqadi, chunki , va musbat asosli darajaning qiymati har doim musbat bo'ladi.
Ushbu fikrni yakunlash uchun, aytaylik, logarifmning belgilangan ta'rifi logarifm belgisi ostidagi raqam asosning ma'lum bir kuchi bo'lsa, darhol logarifm qiymatini ko'rsatishga imkon beradi. Haqiqatan ham, logarifmning ta'rifi, agar b=a p bo'lsa, b sonining a asosi uchun logarifmi p ga teng ekanligini aytishga imkon beradi. Ya'ni log a a p =p tengligi to'g'ri. Masalan, 2 3 =8, keyin log 2 8=3 ekanligini bilamiz. Bu haqda maqolada ko'proq gaplashamiz.
Logarifmlar, har qanday raqamlar kabi, har qanday usulda qo'shilishi, ayirilishi va o'zgartirilishi mumkin. Ammo logarifmlar aniq emasligi sababli oddiy raqamlar, bu erda qoidalar mavjud, ular deyiladi asosiy xususiyatlar.
Siz, albatta, ushbu qoidalarni bilishingiz kerak - ularsiz biron bir jiddiy logarifmik muammoni hal qilib bo'lmaydi. Bundan tashqari, ular juda oz - siz bir kunda hamma narsani o'rganishingiz mumkin. Shunday qilib, keling, boshlaylik.
Logarifmlarni qo‘shish va ayirish
Bir xil asoslarga ega ikkita logarifmni ko'rib chiqing: log a x va jurnal a y. Keyin ularni qo'shish va ayirish mumkin, va:
- jurnal a x+ jurnal a y=log a (x · y);
- jurnal a x− jurnal a y=log a (x : y).
Demak, logarifmlar yig‘indisi ko‘paytmaning logarifmiga, ayirmasi esa bo‘lakning logarifmiga teng. Eslatma: asosiy moment Bu yerga - bir xil asoslar. Agar sabablar boshqacha bo'lsa, bu qoidalar ishlamaydi!
Ushbu formulalar, hatto uning alohida qismlari hisobga olinmagan taqdirda ham logarifmik ifodani hisoblashda yordam beradi ("Logarifm nima" darsiga qarang). Misollarni ko'rib chiqing va qarang:
Jurnal 6 4 + jurnal 6 9.
Logarifmlar bir xil asosga ega bo'lgani uchun biz yig'indi formulasidan foydalanamiz:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.
Vazifa. Ifodaning qiymatini toping: log 2 48 − log 2 3.
Asoslar bir xil, biz farq formulasidan foydalanamiz:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.
Vazifa. Ifodaning qiymatini toping: log 3 135 − log 3 5.
Yana asoslar bir xil, shuning uchun bizda:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.
Ko'rib turganingizdek, asl iboralar "yomon" logarifmlardan iborat bo'lib, ular alohida hisoblanmaydi. Ammo transformatsiyalardan so'ng butunlay normal raqamlar olinadi. Ko'pchilik bu haqiqatga asoslanadi test qog'ozlari. Ha, testga o'xshash iboralar Yagona davlat imtihonida barcha jiddiylik bilan (ba'zan deyarli hech qanday o'zgarishlarsiz) taklif etiladi.
Logarifmadan ko'rsatkichni chiqarish
Endi vazifani biroz murakkablashtiramiz. Agar logarifmning asosi yoki argumenti kuch bo'lsa-chi? Keyin ushbu daraja ko'rsatkichini quyidagi qoidalarga muvofiq logarifm belgisidan chiqarish mumkin:
Buni payqash oson oxirgi qoida birinchi ikkitasini kuzatib boradi. Ammo baribir buni eslab qolish yaxshiroqdir - ba'zi hollarda bu hisob-kitoblar miqdorini sezilarli darajada kamaytiradi.
Albatta, agar logarifmning ODZiga rioya qilinsa, ushbu qoidalarning barchasi mantiqiy bo'ladi: a > 0, a ≠ 1, x> 0. Va yana bir narsa: barcha formulalarni nafaqat chapdan o'ngga, balki aksincha qo'llashni o'rganing, ya'ni. Logarifmning o'ziga logarifm belgisidan oldingi raqamlarni kiritishingiz mumkin. Bu eng ko'p talab qilinadigan narsa.
Vazifa. Ifodaning qiymatini toping: log 7 49 6 .
Keling, birinchi formuladan foydalanib, argumentdagi darajadan xalos bo'laylik:
log 7 49 6 = 6 log 7 49 = 6 2 = 12
Vazifa. Ifodaning ma'nosini toping:
[Rasm uchun sarlavha]
E'tibor bering, maxraj logarifmadan iborat bo'lib, uning asosi va argumenti aniq darajalardir: 16 = 2 4 ; 49 = 7 2. Bizda ... bor:
 [Rasm uchun sarlavha]
[Rasm uchun sarlavha] O'ylaymanki, oxirgi misol biroz tushuntirishni talab qiladi. Logarifmlar qayerga ketdi? Biz oxirgi daqiqagacha faqat maxraj bilan ishlaymiz. Biz u erda turgan logarifmning asosini va argumentini kuchlar shaklida taqdim etdik va ko'rsatkichlarni olib tashladik - biz "uch qavatli" kasrni oldik.
Endi asosiy kasrni ko'rib chiqaylik. Numerator va maxraj bir xil sonni o'z ichiga oladi: log 2 7. Log 2 7 ≠ 0 bo'lgani uchun biz kasrni kamaytirishimiz mumkin - 2/4 maxrajda qoladi. Arifmetika qoidalariga ko'ra, to'rttani hisoblagichga o'tkazish mumkin, bu bajarilgan. Natijada javob bo'ldi: 2.
Yangi poydevorga o'tish
Logarifmlarni qo'shish va ayirish qoidalari haqida gapirganda, ular faqat bir xil asoslar bilan ishlashini alohida ta'kidladim. Agar sabablar boshqacha bo'lsa-chi? Agar ular bir xil sonning aniq kuchlari bo'lmasa-chi?
Yangi poydevorga o'tish uchun formulalar yordamga keladi. Keling, ularni teorema shaklida tuzamiz:
Logarifm jurnali berilsin a x. Keyin istalgan raqam uchun c shu kabi c> 0 va c≠ 1, tenglik to'g'ri:
[Rasm uchun sarlavha]
Xususan, agar biz qo'ysak c = x, biz olamiz:
[Rasm uchun sarlavha]
Ikkinchi formuladan kelib chiqadiki, logarifmning asosi va argumenti almashtirilishi mumkin, ammo bu holda butun ifoda "aylantiriladi", ya'ni. logarifm maxrajda ko'rinadi.
Bu formulalar oddiy sonli ifodalarda kam uchraydi. Ularning qanchalik qulay ekanligini faqat logarifmik tenglamalar va tengsizliklarni yechishdagina baholash mumkin.
Biroq, yangi poydevorga o'tishdan tashqari, umuman hal qilib bo'lmaydigan muammolar mavjud. Keling, ulardan bir nechtasini ko'rib chiqaylik:
Vazifa. Ifodaning qiymatini toping: log 5 16 log 2 25.
E'tibor bering, ikkala logarifmning argumentlari aniq kuchlarni o'z ichiga oladi. Keling, ko'rsatkichlarni chiqaramiz: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;
Endi ikkinchi logarifmni “teskari” qilaylik:
[Rasm uchun sarlavha]Faktorlarni qayta tartibga solishda mahsulot o'zgarmasligi sababli, biz xotirjamlik bilan to'rt va ikkitani ko'paytirdik va keyin logarifmlar bilan ishladik.
Vazifa. Ifodaning qiymatini toping: log 9 100 lg 3.
Birinchi logarifmning asosi va argumenti aniq kuchlardir. Keling, buni yozamiz va ko'rsatkichlardan xalos bo'laylik:
[Rasm uchun sarlavha]Endi yangi bazaga o'tish orqali o'nlik logarifmdan xalos bo'laylik:
[Rasm uchun sarlavha]Asosiy logarifmik identifikatsiya
Ko'pincha yechim jarayonida raqamni berilgan asosga logarifm sifatida ko'rsatish kerak bo'ladi. Bunday holda, quyidagi formulalar bizga yordam beradi:
Birinchi holda, raqam n argumentda turgan daraja ko'rsatkichiga aylanadi. Raqam n mutlaqo hamma narsa bo'lishi mumkin, chunki bu faqat logarifm qiymati.
Ikkinchi formula aslida tarjima qilingan ta'rifdir. Bu shunday deyiladi: asosiy logarifmik identifikatsiya.
Aslida, raqam bo'lsa, nima bo'ladi b raqamni shunday kuchga ko'taring b bu kuchga raqamni beradi a? To'g'ri: siz xuddi shu raqamni olasiz a. Ushbu xatboshini yana diqqat bilan o'qing - ko'p odamlar unga yopishib olishadi.
Yangi bazaga o'tish uchun formulalar singari, asosiy logarifmik identifikatsiya ba'zan yagona mumkin bo'lgan yechimdir.
Vazifa. Ifodaning ma'nosini toping:
[Rasm uchun sarlavha]
E'tibor bering, log 25 64 = log 5 8 - oddiygina kvadratni logarifmning asosi va argumentidan oldi. Quvvatlarni bir xil asos bilan ko'paytirish qoidalarini hisobga olgan holda, biz quyidagilarni olamiz:
[Rasm uchun sarlavha]Agar kimdir bilmasa, bu yagona davlat imtihonidan olingan haqiqiy vazifa edi :)
Logarifmik birlik va logarifmik nol
Xulosa qilib aytganda, men xususiyatlar deb atash qiyin bo'lgan ikkita identifikatsiyani beraman - aksincha, ular logarifm ta'rifining oqibatlari. Ular doimo muammolarda paydo bo'ladi va ajablanarlisi shundaki, hatto "ilg'or" talabalar uchun ham muammolarni keltirib chiqaradi.
- jurnal a a= 1 - logarifmik birlik. Bir marta va umuman eslab qoling: har qanday bazaga logarifm a shu asosdan bittaga teng.
- jurnal a 1 = 0 - logarifmik nol. Baza a har qanday bo'lishi mumkin, lekin agar argument bitta bo'lsa, logarifm nolga teng! Chunki a 0 = 1 ta'rifning bevosita natijasidir.
Bu barcha xususiyatlar. Ularni amalda qo'llashni mashq qiling! Dars boshida cheat varaqini yuklab oling, uni chop eting va muammolarni hal qiling.
Ma'lumki, ifodalarni darajalar bilan ko'paytirishda ularning ko'rsatkichlari har doim qo'shiladi (a b *a c = a b+c). Bu matematik qonun Arximed tomonidan olingan bo'lib, keyinchalik 8-asrda matematik Virasen butun ko'rsatkichlar jadvalini yaratdi. Aynan ular logarifmlarning keyingi kashfiyoti uchun xizmat qilganlar. Ushbu funktsiyadan foydalanish misollarini oddiy qo'shish orqali noqulay ko'paytirishni soddalashtirish kerak bo'lgan deyarli hamma joyda topish mumkin. Agar siz ushbu maqolani o'qishga 10 daqiqa vaqt ajratsangiz, biz sizga logarifm nima ekanligini va ular bilan qanday ishlashni tushuntiramiz. Oddiy va tushunarli tilda.
Matematikada ta'rif
Logarifm quyidagi ko‘rinishdagi ifodadir: log a b=c, ya’ni har qanday manfiy bo‘lmagan (ya’ni har qanday musbat) “b” sonning “a” asosiga logarifmi “c” darajasi deb hisoblanadi. "b" qiymatini olish uchun "a" bazasini ko'tarish kerak. Logarifmni misollar yordamida tahlil qilamiz, deylik log 2 ifodasi bor 8. Javobni qanday topish mumkin? Bu juda oddiy, siz shunday quvvat topishingiz kerakki, 2 dan kerakli quvvatga qadar siz 8 ga ega bo'lasiz. Boshingizdagi ba'zi hisob-kitoblarni amalga oshirgandan so'ng, biz 3 raqamini olamiz! Va bu to'g'ri, chunki 2 dan 3 ning kuchiga javob 8 ni beradi.
Logarifmlarning turlari
Ko'pgina o'quvchilar va talabalar uchun bu mavzu murakkab va tushunarsiz ko'rinadi, lekin aslida logarifmlar unchalik qo'rqinchli emas, asosiysi ularning umumiy ma'nosini tushunish va ularning xususiyatlarini va ba'zi qoidalarini eslab qolishdir. Uchtasi bor individual turlar logarifmik ifodalar:
- Natural logarifm ln a, bu yerda asos Eyler soni (e = 2,7).
- O'nlik a, bu erda asos 10 ga teng.
- Har qanday b sonining a>1 asosiga logarifmi.
Ularning har biri hal qilinadi standart tarzda, bu logarifmik teoremalardan foydalangan holda soddalashtirish, qisqartirish va keyinchalik bitta logarifmaga qisqartirishni o'z ichiga oladi. Olish uchun to'g'ri qiymatlar logarifmlar, ularni hal qilishda ularning xususiyatlarini va harakatlar ketma-ketligini eslab qolishingiz kerak.
Qoidalar va ba'zi cheklovlar
Matematikada aksioma sifatida qabul qilingan bir qancha qoida-cheklovlar mavjud, ya'ni ular muhokama qilinmaydi va haqiqatdir. Masalan, raqamlarni nolga bo'lish mumkin emas, shuningdek, juft ildizni ajratib bo'lmaydi manfiy raqamlar. Logarifmlarning o'z qoidalari ham bor, ularga rioya qilgan holda siz hatto uzoq va sig'imli logarifmik iboralar bilan ishlashni osongina o'rganishingiz mumkin:
- “A” bazasi har doim noldan katta bo'lishi kerak va 1 ga teng bo'lmasligi kerak, aks holda ifoda o'z ma'nosini yo'qotadi, chunki "1" va "0" har qanday darajada har doim ularning qiymatlariga teng;
- a > 0 bo'lsa, a b >0 bo'lsa, "c" ham noldan katta bo'lishi kerakligi ma'lum bo'ladi.
Logarifmlarni qanday yechish mumkin?
Masalan, 10 x = 100 tenglamasining javobini topish vazifasi beriladi. Bu juda oson, biz 100 ni oladigan o'n sonni ko'tarib, kuch tanlash kerak. Bu, albatta, 10 2 =. 100.
Endi bu ifodani logarifmik shaklda ifodalaylik. Biz log 10 100 = 2 ni olamiz. Logarifmlarni echishda berilgan sonni olish uchun logarifm asosini kiritish zarur bo'lgan quvvatni topish uchun barcha amallar amalda birlashadi.
Noma'lum darajaning qiymatini aniq aniqlash uchun siz darajalar jadvali bilan ishlashni o'rganishingiz kerak. Bu shunday ko'rinadi:

Ko'rib turganingizdek, agar sizda texnik aqlingiz va ko'paytirish jadvalini bilsangiz, ba'zi eksponentlarni intuitiv ravishda taxmin qilish mumkin. Biroq uchun katta qiymatlar sizga darajalar jadvali kerak bo'ladi. Bundan hatto murakkab matematik mavzular haqida hech narsa bilmaydiganlar ham foydalanishlari mumkin. Chap ustunda raqamlar mavjud (a asosi), raqamlarning yuqori qatori a soni ko'tarilgan c kuchining qiymati. Chorrahada hujayralar javob bo'lgan raqamlar qiymatlarini o'z ichiga oladi (a c = b). Keling, masalan, 10 raqami bo'lgan birinchi katakchani olaylik va uning kvadratini olamiz, biz ikkita katakchamizning kesishmasida ko'rsatilgan 100 qiymatini olamiz. Hammasi shu qadar sodda va osonki, hatto eng haqiqiy gumanist ham tushunadi!
Tenglamalar va tengsizliklar
Ma'lum bo'lishicha, ma'lum sharoitlarda ko'rsatkich logarifmdir. Shuning uchun har qanday matematik sonli ifodalarni logarifmik tenglik sifatida yozish mumkin. Masalan, 3 4 =81 ni to'rtga teng 81 ning 3 logarifmi sifatida yozish mumkin (log 3 81 = 4). Salbiy kuchlar uchun qoidalar bir xil: 2 -5 = 1/32 biz uni logarifm sifatida yozamiz, log 2 (1/32) = -5 ni olamiz. Matematikaning eng qiziqarli bo'limlaridan biri "logarifmlar" mavzusidir. Tenglamalarning xossalarini o'rgangandan so'ng, biz quyida misollar va echimlarni ko'rib chiqamiz. Endi tengsizliklar qanday ko‘rinishini va ularni tenglamalardan qanday ajratish mumkinligini ko‘rib chiqamiz.

Quyidagi shaklning ifodasi berilgan: log 2 (x-1) > 3 - bu logarifmik tengsizlik, chunki noma'lum qiymat "x" logarifm belgisi ostida. Shuningdek, ifodada ikkita miqdor solishtiriladi: ikkita asosga kerakli sonning logarifmi uch sonidan katta.
Logarifmik tenglamalar va tengsizliklar o'rtasidagi eng muhim farq shundaki, logarifmli tenglamalar (misol - logarifm 2 x = √9) javobda bir yoki bir nechta o'ziga xos raqamli qiymatlarni nazarda tutadi, holbuki tengsizliklarni yechishda ular mintaqa sifatida aniqlanadi. qabul qilinadigan qiymatlar, va bu funksiyaning uzilish nuqtalari. Natijada, javob tenglamaning javobidagi kabi oddiy raqamlar to'plami emas, balki doimiy qator yoki raqamlar to'plamidir.

Logarifmlar haqidagi asosiy teoremalar
Logarifmning qiymatlarini topishning ibtidoiy vazifalarini hal qilishda uning xossalari noma'lum bo'lishi mumkin. Biroq, logarifmik tenglamalar yoki tengsizliklar haqida gap ketganda, birinchi navbatda, logarifmlarning barcha asosiy xususiyatlarini aniq tushunish va amalda qo'llash kerak. Tenglamalar misollarini keyinroq ko'rib chiqamiz, keling, avval har bir xususiyatni batafsil ko'rib chiqamiz;
- Asosiy identifikatsiya quyidagicha ko'rinadi: a logaB =B. Bu faqat a 0 dan katta, birga teng emas va B noldan katta bo'lganda qo'llaniladi.
- Mahsulotning logarifmini quyidagi formulada ifodalash mumkin: log d (s 1 * s 2) = log d s 1 + log d s 2. Bu holda majburiy shart: d, s 1 va s 2 > 0; a≠1. Siz bu logarifmik formulani misollar va yechim bilan isbotlashingiz mumkin. log a s 1 = f 1 va log a s 2 = f 2, keyin a f1 = s 1, a f2 = s 2 bo‘lsin. Biz s 1 * s 2 = a f1 *a f2 = a f1+f2 (xususiyatlari)ni olamiz. daraja ), so'ngra ta'rifi bo'yicha: log a (s 1 * s 2) = f 1 + f 2 = log a s1 + log a s 2, bu isbotlanishi kerak bo'lgan narsa.
- Bo'limning logarifmi quyidagicha ko'rinadi: log a (s 1/s 2) = log a s 1 - log a s 2.
- Formula ko'rinishidagi teorema qabul qiladi keyingi ko'rinish: log a q b n = n/q log a b.
Ushbu formula "logarifm darajasining xossasi" deb ataladi. Bu oddiy darajalarning xususiyatlariga o'xshaydi va bu ajablanarli emas, chunki barcha matematika tabiiy postulatlarga asoslanadi. Keling, dalilni ko'rib chiqaylik.
Log a b = t bo'lsin, a t =b chiqadi. Ikkala qismni m darajaga ko'tarsak: a tn = b n;
lekin a tn = (a q) nt/q = b n ekan, shuning uchun log a q b n = (n*t)/t, keyin log a q b n = n/q log a b. Teorema isbotlangan.
Muammolar va tengsizliklarga misollar
Logarifmlarga oid masalalarning eng keng tarqalgan turlari tenglamalar va tengsizliklarga misollardir. Ular deyarli barcha muammoli kitoblarda uchraydi va matematika imtihonlarining majburiy qismidir. Universitetga kirish yoki o'tish uchun kirish imtihonlari matematikada bunday masalalarni to'g'ri yechishni bilish kerak.

Afsuski, logarifmning noma'lum qiymatini echish va aniqlashning yagona rejasi yoki sxemasi mavjud emas, lekin har bir matematik tengsizlik yoki logarifmik tenglamaga ma'lum qoidalar qo'llanilishi mumkin. Avvalo, siz ifodani soddalashtirish yoki olib kelishi mumkinligini aniqlashingiz kerak umumiy ko'rinish. Uzunlarini soddalashtiring logarifmik ifodalar Agar ularning xususiyatlaridan to'g'ri foydalansangiz mumkin. Keling, ular bilan tezda tanishaylik.
Logarifmik tenglamalarni yechishda biz qanday turdagi logarifmga ega ekanligimizni aniqlashimiz kerak: misol ifodasi tabiiy logarifm yoki o'nlikdan iborat bo'lishi mumkin.
Mana ln100, ln1026 misollar. Ularning yechimi shundan kelib chiqadiki, ular 10 ta asosi mos ravishda 100 va 1026 ga teng bo'ladigan quvvatni aniqlashlari kerak. Tabiiy logarifmlarni yechish uchun logarifmik identifikatsiyalarni yoki ularning xususiyatlarini qo'llash kerak. Keling, har xil turdagi logarifmik masalalarni yechish misollarini ko'rib chiqaylik.

Logarifm formulalarini qanday ishlatish kerak: misollar va echimlar bilan
Shunday qilib, keling, logarifmlar haqidagi asosiy teoremalardan foydalanish misollarini ko'rib chiqaylik.
- Mahsulot logarifmining xususiyati kengaytirish zarur bo'lgan vazifalarda ishlatilishi mumkin katta ahamiyatga ega b raqamlarini oddiy omillarga aylantiring. Masalan, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Javob 9.
- log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 - ko'rib turganingizdek, logarifm kuchining to'rtinchi xususiyatidan foydalanib, biz ko'rinishidan murakkab va yechilmaydigan ifodani yechishga muvaffaq bo'ldik. Siz shunchaki bazani faktorlarga ajratib, keyin ko'rsatkich qiymatlarini logarifm belgisidan chiqarib olishingiz kerak.

Yagona davlat imtihonidan topshiriqlar
Logarifmlar ko'pincha mavjud kirish imtihonlari, ayniqsa, Yagona davlat imtihonidagi ko'plab logarifmik muammolar ( Davlat imtihoni barcha maktab bitiruvchilari uchun). Odatda, bu vazifalar nafaqat A qismida (imtihonning eng oson test qismi), balki C qismida ham (eng murakkab va hajmli vazifalar) mavjud. Imtihon aniq va talab qiladi mukammal bilim"Tabiiy logarifmlar" mavzulari.
Muammolarga misollar va yechimlar rasmiylardan olingan Yagona davlat imtihonlari variantlari. Keling, bunday vazifalar qanday hal qilinishini ko'rib chiqaylik.
Berilgan log 2 (2x-1) = 4. Yechish:
keling, ifodani biroz soddalashtirib, uni qayta yozamiz log 2 (2x-1) = 2 2, logarifmning ta'rifi bo'yicha biz 2x-1 = 2 4 ni olamiz, shuning uchun 2x = 17; x = 8,5.
- Yechim og'ir va chalkash bo'lmasligi uchun barcha logarifmlarni bir xil asosga qisqartirish yaxshidir.
- Logarifm belgisi ostidagi barcha ifodalar musbat deb ko'rsatiladi, shuning uchun logarifm belgisi ostidagi va uning asosi sifatidagi ifodaning ko'rsatkichi ko'paytiruvchi sifatida chiqarilganda, logarifm ostida qolgan ifoda musbat bo'lishi kerak.
Jamiyat rivojlanib, ishlab chiqarish murakkablashgan sari matematika ham rivojlandi. Oddiydan murakkabga o'tish. Qo'shish va ayirish usulidan foydalangan holda oddiy buxgalteriya hisobidan ularning takroriy takrorlanishi bilan biz ko'paytirish va bo'lish tushunchasiga keldik. Ko'paytirishning takroriy amalini qisqartirish ko'rsatkich tushunchasiga aylandi. Raqamlarning asosga va ko'rsatkichlar soniga bog'liqligining birinchi jadvallari 8-asrda hind matematigi Varasena tomonidan tuzilgan. Ulardan logarifmlarning paydo bo'lish vaqtini hisoblashingiz mumkin.
Tarixiy eskiz
16-asrda Yevropaning tiklanishi ham mexanikaning rivojlanishiga turtki boʻldi. T katta hajmdagi hisoblashni talab qildi ko'paytirish va bo'lish bilan bog'liq ko'p xonali raqamlar. Qadimgi stollar katta xizmat qilgan. Ular murakkab amallarni oddiyroq - qo'shish va ayirish bilan almashtirishga imkon berdi. Oldinga katta qadam 1544 yilda nashr etilgan matematik Maykl Stifelning ishi bo'lib, unda u ko'plab matematiklarning g'oyasini amalga oshirdi. Bu jadvallardan nafaqat tub sonlar ko'rinishidagi darajalar uchun, balki o'zboshimchalik bilan ratsional bo'lganlar uchun ham foydalanishga imkon berdi.
1614 yilda bu g'oyalarni ishlab chiqqan shotlandiyalik Jon Nepier birinchi marta taqdim etdi yangi atama"sonning logarifmi". Sinuslar va kosinuslarning logarifmlarini, shuningdek, tangenslarni hisoblash uchun yangi murakkab jadvallar tuzildi. Bu astronomlarning ishini ancha qisqartirdi.
Uch asr davomida olimlar tomonidan muvaffaqiyatli qo'llanilgan yangi jadvallar paydo bo'la boshladi. Oldindan ancha vaqt o'tdi yangi operatsiya algebrada u o'zining tugallangan shaklini oldi. Logarifmning ta’rifi berildi va uning xossalari o‘rganildi.
Faqat 20-asrda, kalkulyator va kompyuterning paydo bo'lishi bilan insoniyat 13-asr davomida muvaffaqiyatli ishlagan qadimiy jadvallardan voz kechdi.
 Bugun biz b ning logarifmini a asosi bo'lgan x soni deb ataymiz, ya'ni a ning b ni tashkil qiladi. Bu formula sifatida yoziladi: x = log a(b).
Bugun biz b ning logarifmini a asosi bo'lgan x soni deb ataymiz, ya'ni a ning b ni tashkil qiladi. Bu formula sifatida yoziladi: x = log a(b).
Misol uchun, log 3(9) 2 ga teng bo'ladi. Agar ta'rifga amal qilsangiz, bu aniq. Agar 3 ni 2 ning darajasiga oshirsak, biz 9 ni olamiz.
Shunday qilib, tuzilgan ta'rif faqat bitta cheklovni o'rnatadi: a va b raqamlari haqiqiy bo'lishi kerak.
Logarifmlarning turlari
Klassik ta'rif haqiqiy logarifm deb ataladi va aslida a x = b tenglamaning yechimidir. Variant a = 1 chegara chizig'idir va qiziqish uyg'otmaydi. Diqqat: har qanday kuchga 1 1 ga teng.
Logarifmning haqiqiy qiymati faqat asos va argument 0 dan katta bo'lganda aniqlanadi va asos 1 ga teng bo'lmasligi kerak.
Matematika sohasida alohida o'rin tutadi logarifmlarni o'ynang, ular bazasining o'lchamiga qarab nomlanadi:

Qoidalar va cheklovlar
Logarifmlarning asosiy xususiyati qoidadir: mahsulotning logarifmi logarifmik yig'indiga teng. log abp = log a(b) + log a(p).
Ushbu bayonotning varianti sifatida u quyidagicha bo'ladi: log c(b/p) = log c(b) - log c(p), bo'linish funktsiyasi funktsiyalarning farqiga teng.
Oldingi ikkita qoidadan shuni ko'rish oson: log a(b p) = p * log a(b).
Boshqa xususiyatlarga quyidagilar kiradi:

Izoh. Umumiy xatoga yo'l qo'ymang - yig'indining logarifmi logarifmalar yig'indisiga teng emas.
 Ko'p asrlar davomida logarifmni topish juda ko'p vaqt talab qiladigan ish edi. Matematiklar foydalangan taniqli formula Polinom kengayishining logarifmik nazariyasi:
Ko'p asrlar davomida logarifmni topish juda ko'p vaqt talab qiladigan ish edi. Matematiklar foydalangan taniqli formula Polinom kengayishining logarifmik nazariyasi:
ln (1 + x) = x — (x^2)/2 + (x^3)/3 — (x^4)/4 + … + ((-1)^(n + 1))*(( x^n)/n), bu erda n - natural son 1 dan katta, bu hisoblashning to'g'riligini belgilaydi.
Boshqa asosli logarifmlar bir asosdan ikkinchisiga o'tish teoremasi va ko'paytma logarifmining xossasi yordamida hisoblangan.
Chunki bu usul juda ko'p mehnat talab qiladi va amaliy muammolarni hal qilishda amalga oshirish qiyin, biz logarifmlarning oldindan tuzilgan jadvallaridan foydalandik, bu esa barcha ishlarni sezilarli darajada tezlashtirdi.
Ba'zi hollarda maxsus mo'ljallangan logarifm grafiklaridan foydalanilgan, bu kamroq aniqlik bergan, ammo qidiruvni sezilarli darajada tezlashtirgan. istalgan qiymat. Bir necha nuqtalar ustida tuzilgan y = log a(x) funktsiyaning egri chizig'i istalgan boshqa nuqtadagi funktsiya qiymatini topish uchun oddiy o'lchagichdan foydalanish imkonini beradi. Muhandislar uzoq vaqt Ushbu maqsadlar uchun grafik qog'oz deb ataladigan qog'oz ishlatilgan.
17-asrda birinchi yordamchi analog hisoblash sharoitlari paydo bo'ldi, bu 19-asr tugallangan ko'rinishga ega bo'ldi. Eng muvaffaqiyatli qurilma slayd qoidasi deb nomlandi. Qurilmaning soddaligiga qaramay, uning ko'rinishi barcha muhandislik hisob-kitoblari jarayonini sezilarli darajada tezlashtirdi va buni ortiqcha baholash qiyin. Hozirda bu qurilma bilan kam odam tanish.
Kalkulyatorlar va kompyuterlarning paydo bo'lishi boshqa har qanday qurilmalardan foydalanishni ma'nosiz qildi.
Tenglamalar va tengsizliklar
Logarifmlar yordamida turli xil tenglamalar va tengsizliklarni yechish uchun quyidagi formulalar qo'llaniladi:
- Bir bazadan ikkinchisiga o'tish: log a(b) = log c(b) / log c(a);
- Natijada oldingi versiya: log a (b) = 1 / log b (a).
Tengsizliklarni yechish uchun quyidagilarni bilish foydalidir:
- Logarifmning qiymati faqat asos va argument bittadan katta yoki kichik bo'lsagina ijobiy bo'ladi; agar kamida bitta shart buzilgan bo'lsa, logarifm qiymati salbiy bo'ladi.
- Agar tengsizlikning o‘ng va chap tomonlariga logarifm funksiyasi qo‘llanilsa va logarifmning asosi birdan katta bo‘lsa, tengsizlik belgisi saqlanib qoladi; aks holda u o'zgaradi.
Namuna muammolar
Keling, logarifmlar va ularning xossalarini ishlatishning bir nechta variantlarini ko'rib chiqaylik. Tenglamalarni echishga misollar:

Logarifmni bir darajaga joylashtirish variantini ko'rib chiqing:
- Masala 3. 25^log 5(3) ni hisoblang. Yechish: muammoning shartlarida yozuv quyidagiga o'xshaydi (5^2)^log5(3) yoki 5^(2 * log 5(3)). Buni boshqacha yozamiz: 5^log 5(3*2) yoki funktsiya argumenti sifatidagi raqamning kvadrati funksiyaning o'zi (5^log 5(3))^2 kvadrati sifatida yozilishi mumkin. Logarifmlarning xossalaridan foydalanib, bu ifoda 3^2 ga teng. Javob: hisoblash natijasida biz 9 ni olamiz.
Amaliy foydalanish
Sof matematik vosita bo'lib, u uzoqroq ko'rinadi haqiqiy hayot logarifm to'satdan ob'ektlarni tasvirlash uchun katta ahamiyatga ega bo'ldi haqiqiy dunyo. Undan foydalanilmagan fanni topish qiyin. Bu nafaqat tabiiy, balki to'liq amal qiladi gumanitar sohalar bilim.
Logarifmik bog'liqliklar
Raqamli bog'liqliklarga ba'zi misollar:

Mexanika va fizika
Tarixan mexanika va fizika har doim foydalanish orqali rivojlangan matematik usullar tadqiqotlar va shu bilan birga matematika, jumladan, logarifmlarning rivojlanishi uchun turtki bo'lib xizmat qildi. Fizikaning aksariyat qonunlari nazariyasi matematika tilida yozilgan. Logarifm yordamida fizik qonunlarni tavsiflashga ikkita misol keltiramiz.
Raketa tezligi kabi murakkab miqdorni hisoblash muammosini Tsiolkovskiy formulasi yordamida hal qilish mumkin, bu koinotni o'rganish nazariyasiga asos solgan:
V = I * ln (M1/M2), bu erda
- V - samolyotning oxirgi tezligi.
- I - dvigatelning o'ziga xos impulsi.
- M 1 - raketaning boshlang'ich massasi.
- M 2 - yakuniy massa.
Boshqa muhim misol - bu boshqa buyuk olim Maks Plankning termodinamikadagi muvozanat holatini baholashga xizmat qiluvchi formulasida qo'llaniladi.
S = k * ln (Ō), bu erda
- S – termodinamik xususiyat.
- k – Boltsman doimiysi.
- Ō - turli holatlarning statistik og'irligi.
Kimyo
Kimyoda logarifmlar nisbatini o'z ichiga olgan formulalardan foydalanish unchalik aniq emas. Keling, ikkita misol keltiraylik:
- Nernst tenglamasi, muhitning oksidlanish-qaytarilish potentsialining moddalarning faolligiga va muvozanat konstantasiga nisbatan sharti.
- Avtoliz indeksi va eritmaning kislotaligi kabi konstantalarni hisoblash ham bizning funktsiyamizsiz amalga oshirilmaydi.
Psixologiya va biologiya
 Va psixologiyaning bunga qanday aloqasi borligi umuman aniq emas. Ma'lum bo'lishicha, sezish kuchi bu funktsiya tomonidan qo'zg'atuvchining intensivligining teskari nisbati sifatida yaxshi tasvirlangan. pastroq qiymat intensivlik.
Va psixologiyaning bunga qanday aloqasi borligi umuman aniq emas. Ma'lum bo'lishicha, sezish kuchi bu funktsiya tomonidan qo'zg'atuvchining intensivligining teskari nisbati sifatida yaxshi tasvirlangan. pastroq qiymat intensivlik.
Keyin yuqoridagi misollar Logarifmlar mavzusi biologiyada keng qo'llanilishi endi ajablanarli emas. Logarifmik spirallarga mos keladigan biologik shakllar haqida butun jildlarni yozish mumkin edi.
Boshqa hududlar
Ko'rinadiki, dunyoning mavjudligi bu funktsiya bilan bog'liqsiz mumkin emas va u barcha qonunlarni boshqaradi. Ayniqsa, tabiat qonunlari bilan bog'liq bo'lsa geometrik progressiya. MatProfi veb-saytiga murojaat qilish arziydi va quyidagi faoliyat sohalarida bunday misollar ko'p:

Ro'yxat cheksiz bo'lishi mumkin. Ushbu funktsiyaning asosiy tamoyillarini o'zlashtirib, siz cheksiz donolik dunyosiga sho'ng'ishingiz mumkin.
Demak, bizda ikki kuch bor. Agar siz raqamni pastki qatordan olsangiz, bu raqamni olish uchun ikkitasini ko'tarishingiz kerak bo'lgan quvvatni osongina topishingiz mumkin. Misol uchun, 16 ni olish uchun siz ikkitadan to'rtinchi darajaga ko'tarishingiz kerak. Va 64 ni olish uchun siz ikkitadan oltinchi kuchga ko'tarishingiz kerak. Buni jadvaldan ko'rish mumkin.
Va endi - aslida, logarifmning ta'rifi:
X ning logarifmi asosi x ni olish uchun a ko'tarilishi kerak bo'lgan kuchdir.
Belgilanishi: log a x = b, bu erda a - asos, x - argument, b - logarifm aslida nimaga teng.
Masalan, 2 3 = 8 ⇒ log 2 8 = 3 (8 ning 2 ta logarifmi uchta, chunki 2 3 = 8). Xuddi shu muvaffaqiyat jurnali bilan 2 64 = 6, chunki 2 6 = 64.
Berilgan asosga sonning logarifmini topish amali logarifmlash deyiladi. Shunday qilib, jadvalimizga yangi qator qo'shamiz:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| log 2 2 = 1 | log 2 4 = 2 | log 2 8 = 3 | log 2 16 = 4 | log 2 32 = 5 | log 2 64 = 6 |
Afsuski, barcha logarifmlarni hisoblash oson emas. Masalan, log 2 5 ni topishga harakat qiling. 5 raqami jadvalda yo'q, lekin mantiq logarifm segmentning biron bir joyida yotishini ta'kidlaydi. Chunki 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.
Bunday raqamlar irratsional deb nomlanadi: o'nli kasrdan keyingi sonlar cheksiz yozilishi mumkin va ular hech qachon takrorlanmaydi. Agar logarifm mantiqsiz bo'lib chiqsa, uni shunday qoldirgan ma'qul: log 2 5, log 3 8, log 5 100.
Logarifm ikki o'zgaruvchiga (asosiy va argument) ega ifoda ekanligini tushunish muhimdir. Avvaliga ko'p odamlar asos qayerda va argument qayerda ekanligini chalkashtirib yuborishadi. Zerikarli tushunmovchiliklardan qochish uchun rasmga qarang:
Bizning oldimizda logarifm ta'rifidan boshqa narsa yo'q. Eslab qoling: logarifm kuchdir, dalil olish uchun asosni qurish kerak. Bu kuchga ko'tarilgan poydevor - rasmda qizil rang bilan ta'kidlangan. Ma'lum bo'lishicha, tayanch har doim pastda bo'ladi! Men o'quvchilarimga birinchi darsdayoq bu ajoyib qoidani aytaman - va hech qanday chalkashlik bo'lmaydi.
Biz ta'rifni aniqladik - faqat logarifmlarni hisoblashni o'rganish qoladi, ya'ni. "log" belgisidan xalos bo'ling. Boshlash uchun ta'rifdan ikkita muhim fakt kelib chiqishini ta'kidlaymiz:
- Argument va asos har doim noldan katta bo'lishi kerak. Bu logarifm ta'rifi kichraytirilgan ratsional ko'rsatkich bilan darajani aniqlashdan kelib chiqadi.
- Baza bittadan farq qilishi kerak, chunki har qanday darajada bitta bo'lib qoladi. Shu sababli, "ikkitasini olish uchun qanday kuchga ko'tarilishi kerak" degan savol ma'nosizdir. Bunday daraja yo'q!
Bunday cheklovlar deyiladi qabul qilinadigan qiymatlar diapazoni(ODZ). Ma’lum bo‘lishicha, logarifmning ODZ si quyidagicha ko‘rinadi: log a x = b ⇒ x > 0, a > 0, a ≠ 1.
E'tibor bering, b raqamiga cheklovlar yo'q (logarifmning qiymati). Masalan, logarifm salbiy bo'lishi mumkin: log 2 0,5 = -1, chunki 0,5 = 2 −1.
Biroq, endi biz faqat ko'rib chiqamiz raqamli ifodalar, bu erda logarifmning CVD ni bilish shart emas. Barcha cheklovlar allaqachon vazifalar mualliflari tomonidan hisobga olingan. Ammo ular ketganda logarifmik tenglamalar va tengsizliklar, DHS talablari majburiy bo'ladi. Axir, asos va dalil yuqoridagi cheklovlarga mutlaqo mos kelmaydigan juda kuchli konstruktsiyalarni o'z ichiga olishi mumkin.
Endi ko'rib chiqaylik umumiy sxema logarifmlarni hisoblash. U uch bosqichdan iborat:
- a asosini va x argumentini minimal bilan daraja sifatida ifodalang mumkin bo'lgan sabab, birdan katta. Yo'lda, o'nli kasrlardan qutulish yaxshiroqdir;
- b o'zgaruvchisi uchun tenglamani yeching: x = a b ;
- Olingan b soni javob bo'ladi.
Ana xolos! Agar logarifm mantiqsiz bo'lib chiqsa, bu birinchi bosqichda allaqachon ko'rinadi. Baza birdan katta bo'lishi talabi juda muhim: bu xato ehtimolini kamaytiradi va hisob-kitoblarni sezilarli darajada osonlashtiradi. Xuddi shu bilan o'nli kasrlar: agar siz ularni darhol oddiylarga aylantirsangiz, xatolar kamroq bo'ladi.
Keling, ushbu sxema aniq misollar yordamida qanday ishlashini ko'rib chiqaylik:
Vazifa. Logarifmni hisoblang: log 5 25
- Baza va argumentni beshning kuchi sifatida tasavvur qilaylik: 5 = 5 1 ; 25 = 5 2;
- Javobni oldik: 2.
Keling, tenglamani tuzamiz va yechamiz:
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2 ;
Vazifa. Logarifmni hisoblang:
Vazifa. Logarifmni hisoblang: log 4 64
- Baza va argumentni ikkining kuchi sifatida tasavvur qilaylik: 4 = 2 2 ; 64 = 2 6;
- Keling, tenglamani tuzamiz va yechamiz:
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3 ; - Javobni oldik: 3.
Vazifa. Logarifmni hisoblang: log 16 1
- Baza va argumentni ikkining kuchi sifatida tasavvur qilaylik: 16 = 2 4 ; 1 = 2 0;
- Keling, tenglamani tuzamiz va yechamiz:
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ; - Javobni oldik: 0.
Vazifa. Logarifmni hisoblang: log 7 14
- Asos va argumentni yettining kuchi sifatida tasavvur qilaylik: 7 = 7 1 ; 14 ni ettining kuchi sifatida ifodalab bo'lmaydi, chunki 7 1< 14 < 7 2 ;
- Oldingi paragrafdan kelib chiqadiki, logarifm hisobga olinmaydi;
- Javob o'zgarmaydi: log 7 14.
Oxirgi misol bo'yicha kichik eslatma. Raqam boshqa raqamning aniq kuchi emasligiga qanday ishonch hosil qilish mumkin? Bu juda oddiy - uni qismlarga ajratish kifoya asosiy omillar. Agar kengayish kamida ikki xil omilga ega bo'lsa, bu raqam aniq kuch emas.
Vazifa. Raqamlarning aniq darajalar ekanligini aniqlang: 8; 48; 81; 35; 14 .
8 = 2 · 2 · 2 = 2 3 - aniq daraja, chunki faqat bitta multiplikator mavjud;
48 = 6 · 8 = 3 · 2 · 2 · 2 · 2 = 3 · 2 4 - bu aniq kuch emas, chunki ikkita omil mavjud: 3 va 2;
81 = 9 · 9 = 3 · 3 · 3 · 3 = 3 4 - aniq daraja;
35 = 7 · 5 - yana aniq kuch emas;
14 = 7 · 2 - yana aniq daraja emas;
Biz o'zimizni ham ta'kidlaymiz tub sonlar har doim o'zlarining aniq darajalari.
O'nlik logarifm
Ba'zi logarifmlar shunchalik keng tarqalganki, ular maxsus nom va belgiga ega.
X ning o'nlik logarifmi 10 ta asosning logarifmi, ya'ni. X raqamini olish uchun 10 raqamini ko'tarish kerak bo'lgan kuch. Belgilanishi: lg x.
Masalan, log 10 = 1; lg 100 = 2; lg 1000 = 3 - va boshqalar.
Bundan buyon darslikda “Find lg 0.01” kabi ibora paydo bo'lganda, bilib oling: bu matn terish xatosi emas. Bu o'nlik logarifm. Ammo, agar siz ushbu belgi bilan tanish bo'lmasangiz, uni har doim qayta yozishingiz mumkin:
log x = log 10 x
Oddiy logarifmlar uchun to'g'ri bo'lgan hamma narsa o'nlik logarifmlar uchun ham to'g'ri.
Tabiiy logarifm
O'z belgisiga ega bo'lgan yana bir logarifm mavjud. Qaysidir ma'noda, bu o'nlikdan ham muhimroqdir. haqida natural logarifm haqida.
X ning natural logarifmi e asosining logarifmi, ya'ni. x sonini olish uchun e soni ko'tarilishi kerak bo'lgan kuch. Belgilanishi: ln x.
Ko'pchilik so'raydi: e raqami nima? Bu irratsional son, uning aniq qiymat topish va yozib olish mumkin emas. Men faqat birinchi raqamlarni keltiraman:
e = 2,718281828459...
Bu raqam nima va nima uchun kerakligi haqida batafsil ma'lumot bermaymiz. Esda tutingki, e tabiiy logarifmning asosi hisoblanadi:
ln x = log e x
Shunday qilib, ln e = 1; ln e 2 = 2; ln e 16 = 16 - va hokazo. Boshqa tomondan, ln 2 irratsional sondir. Umuman olganda, har qandayning natural logarifmi ratsional son mantiqsiz. Albatta, birlikdan tashqari: ln 1 = 0.
Tabiiy logarifmlar uchun oddiy logarifmlar uchun to'g'ri bo'lgan barcha qoidalar o'rinlidir.