hosila nima?
Hosila funksiyaning ta'rifi va ma'nosi

Ko'pchilik ushbu maqolani bitta o'zgaruvchining funksiyasining hosilasi va uning qo'llanilishi bo'yicha muallif kursida kutilmagan tarzda joylashtirishdan hayratda qoladi. Axir, maktabdan beri bo'lgani kabi: standart darslikda birinchi navbatda hosila ta'rifi, uning geometrik, mexanik ma'nosi berilgan. Keyinchalik, talabalar ta'rifi bo'yicha funktsiyalarning hosilalarini topadilar va, aslida, shundan keyingina ular yordamida differentsiallash texnikasini mukammallashtiradilar. hosilaviy jadvallar.

Lekin mening nuqtai nazarimga ko'ra, quyidagi yondashuv ko'proq pragmatikdir: birinchi navbatda, YAXSHI TUSHUNISH maqsadga muvofiqdir. funktsiya chegarasi va, xususan, cheksiz kichik miqdorlar. Gap shundaki hosila ta'rifi chegara tushunchasiga asoslanadi, unda yomon ko'rib chiqiladi maktab kursi. Shuning uchun yosh iste'molchilarning katta qismi bilim graniti hosilasining mohiyatini tushunmaydi. Shunday qilib, agar siz yomon yo'naltirilgan bo'lsangiz differensial hisob yoki dono miya uchun uzoq yillar ushbu yukdan muvaffaqiyatli xalos bo'ling, iltimos, boshlang funksiya chegaralari. Shu bilan birga, ularning yechimini master/eslab qoling.

Xuddi shu amaliy ma'no birinchi navbatda foydali ekanligini ta'kidlaydi hosilalarni topishni o'rganing, shu jumladan murakkab funksiyalarning hosilalari. Nazariya - bu nazariya, lekin ular aytganidek, siz doimo farqlashni xohlaysiz. Shu munosabat bilan, sanab o'tilgan asosiy darslar bilan ishlash yaxshiroqdir va ehtimol farqlash ustasi o'z harakatlarining mohiyatini anglamasdan ham.

Maqolani o'qib bo'lgach, ushbu sahifadagi materiallardan boshlashni maslahat beraman. Losmalar bilan eng oddiy muammolar, bu erda, xususan, funksiya grafigiga tegish masalasi ko'rib chiqiladi. Lekin kutishingiz mumkin. Gap shundaki, lotinning ko'pgina ilovalari uni tushunishni talab qilmaydi va nazariy dars juda kech paydo bo'lganligi ajablanarli emas - men tushuntirishim kerak bo'lganda. ortish/kamayish oraliqlari va ekstremallarni topish funktsiyalari. Bundan tashqari, u uzoq vaqt davomida bu mavzuda edi. Funktsiyalar va grafiklar”, men nihoyat uni oldinroq qo'yishga qaror qilgunimcha.

Shuning uchun, aziz choynaklar, och hayvonlar kabi lotinning mohiyatini o'zlashtirishga shoshilmang, chunki to'yinganlik ta'msiz va to'liq bo'lmaydi.

Funksiyaning ortishi, kamayishi, maksimal, minimumi haqida tushuncha

Ko'pchilik o'quv qurollari ba'zi amaliy masalalar yordamida hosila tushunchasiga olib keladi va men ham o'ylab topdim qiziqarli misol. Tasavvur qiling, biz turli yo'llar bilan borish mumkin bo'lgan shaharga sayohat qilmoqchimiz. Keling, darhol egri o'ralgan yo'llarni tashlab, faqat to'g'ri yo'llarni ko'rib chiqaylik. Biroq, to'g'ri chiziqli yo'nalishlar ham farq qiladi: siz shaharga silliq magistral bo'ylab borishingiz mumkin. Yoki tepalikli magistral bo'ylab - yuqoriga va pastga, yuqoriga va pastga. Boshqa yo'l faqat tepaga, boshqasi esa doimo pastga tushadi. Ekstremal ishqibozlar tik qoya va tik ko'tarilishli dara orqali marshrutni tanlaydilar.

Lekin sizning xohishingiz qanday bo'lishidan qat'iy nazar, hududni bilish yoki hech bo'lmaganda uning joylashgan joyini aniqlash tavsiya etiladi topografik xarita. Agar bunday ma'lumotlar etishmayotgan bo'lsa-chi? Axir, siz, masalan, silliq yo'lni tanlashingiz mumkin, ammo natijada quvnoq Finlar bilan chang'i pog'onasiga qoqilib ketishingiz mumkin. Navigator yoki hatto sun'iy yo'ldosh tasviri ishonchli ma'lumotlarni taqdim etishi haqiqat emas. Shuning uchun, matematika yordamida yo'lning relyefini rasmiylashtirish yaxshi bo'lar edi.

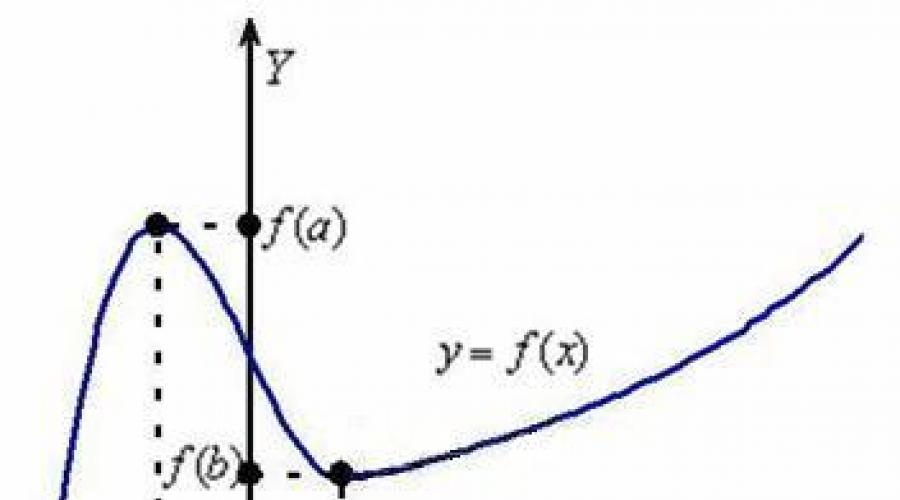
Keling, ba'zi yo'llarni ko'rib chiqaylik (yon ko'rinish):

Har holda, sizga oddiy bir haqiqatni eslataman: sayohat sodir bo'ladi chapdan o'ngga. Oddiylik uchun biz funktsiya deb faraz qilamiz davomiy ko'rib chiqilayotgan hududda.

Ushbu grafikning xususiyatlari qanday?

Intervallarda funktsiyasi ortadi, ya'ni uning har bir keyingi qiymati Ko'proq oldingi. Taxminan aytganda, taqvim mavjud pastga yuqoriga(biz tepalikka chiqamiz). Va intervalda funktsiya kamayadi- har bir keyingi qiymat Ozroq oldingi va bizning jadvalimiz yoqilgan yuqoridan pastga(biz qiyalikdan pastga tushamiz).

Keling, biz ham e'tibor beraylik yagona nuqtalar. Biz erishgan nuqtada maksimal, ya'ni mavjud qiymat eng katta (eng yuqori) bo'ladigan yo'lning bunday qismi. Xuddi shu nuqtada erishiladi eng kam, Va mavjud uning qiymati eng kichik (eng past) bo'lgan mahallasi.

Biz sinfda yanada qat'iy terminologiya va ta'riflarni ko'rib chiqamiz. funktsiyaning ekstremal qismi haqida, lekin hozircha yana bir narsani o'rganamiz muhim xususiyat: interval bilan funktsiya oshadi, lekin u ko'payadi Bilan turli tezliklarda . Va sizning e'tiboringizni tortadigan birinchi narsa - bu interval davomida grafik yuqoriga ko'tariladi ancha salqin, oraliqdan ko'ra. Matematik asboblar yordamida yo'lning tikligini o'lchash mumkinmi?

Funktsiyaning o'zgarish tezligi

G'oya shunday: keling, bir oz qiymatni olaylik ("delta x" ni o'qing), biz uni chaqiramiz argument ortishi, va keling, yo'limizning turli nuqtalarida "sinab ko'rishni" boshlaylik:

1) Eng chap nuqtaga qaraylik: masofani bosib o'tib, biz qiyalikdan balandlikka chiqamiz (yashil chiziq). Miqdor deyiladi funktsiyaning o'sishi, va ichida Ushbu holatda bu o'sish ijobiy (eksa bo'ylab qiymatlar farqi noldan katta). Keling, yo'limizning tikligining o'lchovi bo'ladigan nisbatni yarataylik. Shubhasiz, bu juda aniq raqam va ikkala o'sish ham ijobiy bo'lgani uchun .

Diqqat! Belgilanishi BIR ramz, ya'ni siz "X" dan "delta" ni "yirtib tashlay olmaysiz" va bu harflarni alohida ko'rib chiqa olmaysiz. Albatta, sharh funktsiyani oshirish belgisiga ham tegishli.

Keling, hosil bo'lgan kasrning tabiatini yanada mazmunli o'rganamiz. Keling, dastlab 20 metr balandlikda (chap qora nuqtada) bo'lamiz. Metr masofani bosib o'tib (chap qizil chiziq) biz o'zimizni 60 metr balandlikda topamiz. Keyin funktsiyaning o'sishi bo'ladi metr (yashil chiziq) va: . Shunday qilib, har bir metrda yo'lning ushbu qismi balandligi ortadi o'rtacha 4 metrga... toqqa chiqish jihozlaringizni unutdingizmi? =) Boshqacha aytganda, tuzilgan munosabat funksiyaning O'RTA O'ZGARISH TEZKI (bu holda o'sish) ni xarakterlaydi.

Eslatma : Ko'rib chiqilayotgan misolning raqamli qiymatlari faqat chizmaning nisbatlariga mos keladi.

2) Endi eng o'ngdagi qora nuqtadan bir xil masofaga boramiz. Bu erda ko'tarilish asta-sekin, shuning uchun o'sish (qizil chiziq) nisbatan kichik va oldingi holatga nisbatan nisbat juda oddiy bo'ladi. Nisbatan aytganda, metr va funktsiyaning o'sish tezligi hisoblanadi. Ya'ni, bu erda yo'lning har bir metri uchun bor o'rtacha yarim metrga ko'tarildi.

3) Tog' yonbag'rida kichik sarguzasht. Keling, tepaga qaraylik qora nuqta, ordinata o'qida joylashgan. Faraz qilaylik, bu 50 metrlik belgi. Biz yana masofani bosib o'tamiz, buning natijasida biz o'zimizni pastroq - 30 metr darajasida topamiz. Harakat amalga oshirilganligi sababli yuqoridan pastga(eksaning "qarshi" yo'nalishi bo'yicha), so'ngra final funktsiyaning o'sishi (balandligi) manfiy bo'ladi: metr (chizmadagi jigarrang segment). Va bu holatda biz allaqachon gaplashamiz pasayish darajasi Xususiyatlari: , ya'ni ushbu uchastkaning har bir metr yo'li uchun balandlik pasayadi o'rtacha 2 metrga. Beshinchi nuqtada kiyimingizga g'amxo'rlik qiling.

Keling, o'zimizga savol beraylik: "o'lchov standarti" ning qaysi qiymatidan foydalanish yaxshiroq? Bu mutlaqo tushunarli, 10 metr juda qo'pol. Yaxshi o'nlab dumlar ularga osongina mos kelishi mumkin. To'qnashuvlar bo'lishidan qat'i nazar, pastda chuqur dara bo'lishi mumkin va bir necha metrdan keyin yana tik ko'tarilish bilan uning boshqa tomoni bor. Shunday qilib, o'n metr bilan biz nisbat orqali yo'lning bunday bo'limlarining tushunarli tavsifini olmaymiz.

Yuqoridagi muhokamadan quyidagi xulosalar kelib chiqadi: Qanaqasiga kamroq qiymat , biz yo'l topografiyasini qanchalik aniq tasvirlaymiz. Bundan tashqari, quyidagi faktlar haqiqatdir:

– Har kim uchun ko'tarish nuqtalari ma'lum bir ko'tarilish chegaralariga mos keladigan qiymatni (juda kichik bo'lsa ham) tanlashingiz mumkin. Bu shuni anglatadiki, mos keladigan balandlik o'sishi ijobiy bo'lishi kafolatlanadi va tengsizlik ushbu intervallarning har bir nuqtasida funktsiyaning o'sishini to'g'ri ko'rsatadi.

- Xuddi shunday, har qanday uchun Nishab nuqtasi bu qiyalikda to'liq mos keladigan qiymat mavjud. Demak, balandlikning mos keladigan o'sishi aniq manfiy bo'lib, tengsizlik berilgan intervalning har bir nuqtasida funktsiyaning pasayishini to'g'ri ko'rsatadi.

– Funksiyaning o‘zgarish tezligi nolga teng bo‘lganda, ayniqsa qiziq holat: . Birinchidan, balandlikning nol ko'tarilishi () silliq yo'lning belgisidir. Ikkinchidan, boshqa qiziqarli vaziyatlar ham bor, ularning misollarini siz rasmda ko'rasiz. Tasavvur qiling-a, taqdir bizni burgutlar uchadigan tepalikning eng cho'qqisiga yoki qurbaqalar qichqirayotgan jarlikning tubiga olib keldi. Agar biron-bir yo'nalishda kichik bir qadam tashlasangiz, balandlikning o'zgarishi ahamiyatsiz bo'ladi va biz funktsiyaning o'zgarish tezligi aslida nolga teng deb aytishimiz mumkin. Nuqtalarda kuzatilgan rasm aynan shunday.

Shunday qilib, biz funktsiyaning o'zgarish tezligini mukammal tarzda tavsiflash uchun ajoyib imkoniyatga ega bo'ldik. Axir, matematik tahlil argumentning o'sishini nolga yo'naltirish imkonini beradi: , ya'ni uni qilish. cheksiz kichik.

Natijada, yana bir mantiqiy savol tug'iladi: yo'l va uning jadvalini topish mumkinmi? boshqa funksiya, qaysi bizga xabar berardi barcha tekis uchastkalar, ko'tarilishlar, tushishlar, cho'qqilar, vodiylar, shuningdek, yo'lning har bir nuqtasida o'sish / pasayish tezligi haqida?

hosila nima? Hosila tushunchasi.
Hosil va differentsialning geometrik ma'nosi

Iltimos, diqqat bilan o'qing va juda tez emas - material oddiy va hamma uchun ochiq! Agar ba'zi joylarda biror narsa aniq ko'rinmasa, yaxshi bo'ladi, siz har doim keyinroq maqolaga qaytishingiz mumkin. Ko'proq aytaman, barcha fikrlarni to'liq tushunish uchun nazariyani bir necha marta o'rganish foydalidir (maslahat, ayniqsa, "texnik" talabalar uchun juda muhimdir. Oliy matematika ta'lim jarayonida muhim rol o'ynaydi).

Tabiiyki, lotinning aniq ta'rifida biz uni quyidagi bilan almashtiramiz:

Biz nimaga keldik? Va biz qonunga muvofiq funktsiya uchun degan xulosaga keldik muvofiq qo'yiladi boshqa funktsiya, deb ataladi hosila funksiyasi(yoki oddiygina hosila).

hosila xarakterlaydi o'zgarish darajasi funktsiyalari Qanday qilib? Maqolaning boshidanoq g‘oya qizil ipdek davom etadi. Keling, bir narsani ko'rib chiqaylik ta'rif sohasi funktsiyalari Funktsiya berilgan nuqtada differentsiallanuvchi bo'lsin. Keyin:

1) Agar , u holda funksiya nuqtada ortadi. Va borligi aniq interval(hatto juda kichik), funktsiya o'sadigan nuqtani o'z ichiga oladi va uning grafigi "pastdan yuqoriga" ketadi.

2) Agar , u holda funksiya nuqtada kamayadi. Va funksiya pasayadigan nuqtani o'z ichiga olgan interval mavjud (grafik "yuqoridan pastga" ketadi).

3) Agar , keyin cheksiz yaqin nuqtaga yaqin joyda funksiya tezligini doimiy saqlaydi. Bu, ta'kidlanganidek, doimiy funktsiya va bilan sodir bo'ladi funktsiyaning muhim nuqtalarida, ayniqsa minimal va maksimal nuqtalarda.

Bir oz semantika. Nima ichida keng ma'noda"farqlash" fe'li nimani anglatadi? Farqlash xususiyatini ajratib ko'rsatishni anglatadi. Funktsiyani differentsiallash orqali biz uning o'zgarish tezligini funktsiyaning hosilasi shaklida "izolyatsiya qilamiz". Aytgancha, "hosil" so'zi nimani anglatadi? Funktsiya sodir bo'ldi funktsiyasidan.

Terimlar lotinning mexanik ma'nosi bilan juda muvaffaqiyatli talqin qilinadi :
Jismning koordinatalarining vaqtga bog'liq o'zgarishi qonunini va berilgan jismning harakat tezligi funksiyasini ko'rib chiqamiz. Funktsiya tana koordinatalarining o'zgarish tezligini tavsiflaydi, shuning uchun u funktsiyaning vaqtga nisbatan birinchi hosilasidir: . Agar "tana harakati" tushunchasi tabiatda mavjud bo'lmaganida, u holda bo'lmaydi hosila"tana tezligi" tushunchasi.

Jismning tezlashishi tezlikning o'zgarish tezligidir, shuning uchun: . Agar "tana harakati" va "tana tezligi" degan dastlabki tushunchalar tabiatda mavjud bo'lmaganida, u holda mavjud bo'lmaydi hosila"tananing tezlashishi" tushunchasi.

Qaror qabul qilganda turli vazifalar geometriya, mexanika, fizika va boshqa bilim sohalari ushbu funktsiyadan bir xil analitik jarayon yordamida zarur bo'ldi. y=f(x) deb nomlangan yangi funktsiyani oling hosila funksiyasi(yoki oddiygina berilgan f(x) funksiyaning hosilasi va belgisi bilan belgilanadi

Berilgan funksiyadan kelib chiqadigan jarayon f(x) yangi xususiyatga ega bo'ling f" (x), chaqirildi farqlash va u quyidagi uch bosqichdan iborat: 1) dalil keltiring x oshirish  x va funktsiyaning mos keladigan o'sishini aniqlang  y = f(x+ x) -f(x); 2) munosabat hosil qiling

3) hisoblash x doimiy va  x0, topamiz
, biz bilan belgilaymiz f" (x), go'yo natijaviy funktsiya faqat qiymatga bog'liqligini ta'kidlagandek x, bunda biz chegaraga boramiz. Ta'rif: y " =f " (x) hosilasi y=f(x) funksiya berilgan berilgan x uchun funktsiya o'sishining argument o'sishiga nisbati chegarasi deyiladi, agar argumentning o'sishi nolga moyil bo'lsa, agar, albatta, bu chegara mavjud bo'lsa, ya'ni. cheklangan. Shunday qilib,
, yoki

E'tibor bering, agar biron bir qiymatda bo'lsa x, masalan, qachon x=a, munosabat
da  x0 chekli chegaraga moyil emas, u holda bu holda ular funktsiyani aytadilar f(x) da x=a(yoki nuqtada x=a) hosilasi yo‘q yoki nuqtada differensiallanmaydi x=a.

2. Hosilning geometrik ma’nosi.

x 0 nuqtaga yaqin joyda differensiallanuvchi y = f (x) funksiya grafigini ko‘rib chiqaylik.

f(x)

Funksiya grafigidagi nuqta - A(x 0, f (x 0)) nuqtadan o‘tuvchi va grafani qandaydir B(x;f(x)) nuqtada kesib o‘tuvchi ixtiyoriy to‘g‘ri chiziqni ko‘rib chiqaylik. Bunday chiziq (AB) sekant deb ataladi. ∆ABC dan: AC = ∆x; BC =∆u; tgb=∆y/∆x.

AC ||dan beri Ox, keyin ALO = BAC = b (parallel uchun mos ravishda). Lekin ALO - AB sekantining Ox o'qining musbat yo'nalishiga moyillik burchagi. Bu tanb = k - degan ma'noni anglatadi. qiyalik to'g'ri AB.

Endi biz ∆x ni kamaytiramiz, ya'ni. ∆x→ 0. Bunda B nuqta grafik bo‘yicha A nuqtaga yaqinlashadi va AB sekant aylana oladi. AB sekantining ∆x→ 0 nuqtadagi chegaralovchi pozitsiyasi A nuqtadagi y = f (x) funktsiya grafigiga teginish deb ataladigan to'g'ri chiziq (a) bo'ladi.

Agar tgb =∆y/∆x tengligida ∆x → 0 sifatida chegaraga chiqsak, hosil bo‘ladi.
ortg =f "(x 0), chunki
-tangensning Ox o'qining musbat yo'nalishiga moyillik burchagi
, hosila ta'rifi bo'yicha. Lekin tg = k tangensning burchak koeffitsienti bo'lib, u k = tg = f "(x 0) ni bildiradi.

Shunday qilib, hosilaning geometrik ma'nosi quyidagicha:

Funktsiyaning x nuqtadagi hosilasi 0 abtsissa x nuqtada chizilgan funksiya grafigiga teginish qiyaligiga teng. 0 .

3. Hosilning fizik ma’nosi.

Nuqtaning to‘g‘ri chiziq bo‘ylab harakatini ko‘rib chiqaylik. Nuqtaning istalgan vaqtda x(t) koordinatasi berilsin. Ma'lumki (fizika kursidan) ma'lum vaqt oralig'idagi o'rtacha tezlik bu vaqt davomida bosib o'tgan masofaning vaqtga nisbatiga teng, ya'ni.

Vav = ∆x/∆t. Oxirgi tenglikdagi chegaraga ∆t → 0 sifatida o‘tamiz.

lim Vav (t) = (t 0) - t 0, ∆t → 0 vaqtidagi oniy tezlik.

va lim = ∆x/∆t = x"(t 0) (hosila ta'rifi bo'yicha).

Demak, (t) =x"(t).

Hosilning fizik ma'nosi quyidagicha: funktsiyaning hosilasiy = f(x) nuqtadax 0 funktsiyaning o'zgarish tezligif(x) nuqtadax 0

Bu hosila fizikada koordinatalarning vaqtga nisbatan maʼlum funksiyasidan tezlikni, tezlikning vaqtga nisbatan maʼlum funksiyasidan tezlanishni topish uchun ishlatiladi.

(t) = x"(t) - tezlik,

a(f) = "(t) - tezlanish, yoki

Agar aylanadagi moddiy nuqtaning harakat qonuni ma'lum bo'lsa, u holda aylanish harakati paytida burchak tezligi va burchak tezlanishini topish mumkin:

ph = ph(t) - burchakning vaqt o'tishi bilan o'zgarishi,

ō = ph"(t) - burchak tezligi,

e = ph"(t) - burchak tezlanishi yoki e = ph"(t).

Agar bir jinsli bo'lmagan tayoqning massa taqsimot qonuni ma'lum bo'lsa, unda bir jinsli bo'lmagan tayoqning chiziqli zichligini topish mumkin:

m = m(x) - massa,

x  , l - novda uzunligi,

p = m"(x) - chiziqli zichlik.

Hosildan foydalanib, elastiklik va garmonik tebranishlar nazariyasiga oid masalalar yechiladi. Shunday qilib, Guk qonuniga ko'ra

F = -kx, x - o'zgaruvchan koordinata, k - bahor elastiklik koeffitsienti. ō 2 =k/m ni qo‘yib, prujinali mayatnikning x"(t) + ō 2 x(t) = 0 differensial tenglamasini olamiz,

bu erda ō = √k/√m tebranish chastotasi (l/c), k - kamon qattiqligi (H/m).

y" + ō 2 y = 0 ko'rinishdagi tenglama garmonik tebranishlar tenglamasi (mexanik, elektr, elektromagnit) deyiladi. Bunday tenglamalarning yechimi funktsiyadir.

y = Asin(ōt + ph 0) yoki y = Acos(ōt + ph 0), bu erda

A - tebranishlar amplitudasi, ō - siklik chastotasi,

ph 0 - dastlabki bosqich.

(\large\bf funktsiyaning hosilasi)

Funktsiyani ko'rib chiqing y=f(x), intervalda ko'rsatilgan (a, b). Mayli x- intervalning istalgan sobit nuqtasi (a, b), A Dx- qiymatga ega bo'lgan ixtiyoriy raqam x+Dx intervalga ham tegishli (a, b). Bu raqam Dx argument ortishi deb ataladi.

Ta'rif. Funktsiyaning o'sishi y=f(x) nuqtada x, argument o'sishiga mos keladi Dx, raqamga qo'ng'iroq qilaylik

Dy = f(x+Dx) - f(x).

Biz bunga ishonamiz Dx ≠ 0. Berilgan belgilangan nuqtada ko'rib chiqing x bu nuqtadagi funktsiya o'sishining mos keladigan argument o'sishiga nisbati Dx

Bu munosabatni farq munosabati deb ataymiz. Qiymatidan beri x biz sobit deb hisoblaymiz, farq nisbati argumentning funktsiyasidir Dx. Bu funksiya barcha argument qiymatlari uchun aniqlanadi Dx, nuqtaning etarlicha kichik mahallasiga tegishli Dx=0, nuqtaning o'zi bundan mustasno Dx=0. Shunday qilib, biz belgilangan funktsiyaning chegarasi mavjudligi haqidagi savolni ko'rib chiqishga haqlimiz Dx → 0.

Ta'rif. Funktsiyaning hosilasi y=f(x) ma'lum bir belgilangan nuqtada x chegarasi deb ataladi Dx → 0 farq nisbati, ya'ni

Agar bu chegara mavjud bo'lsa.

Belgilanish. y'(x) yoki f'(x).

Hosilning geometrik ma'nosi: Funktsiyaning hosilasi f(x) ayni paytda x eksa orasidagi burchakning tangensiga teng ho'kiz va tegishli nuqtada ushbu funktsiya grafigiga teginish:

f'(x 0) = \tga.

Hosilning mexanik ma'nosi: Yo'lning vaqtga nisbatan hosilasi nuqtaning to'g'ri chiziqli harakati tezligiga teng:

Chiziqga teguvchi tenglama y=f(x) nuqtada M 0 (x 0 ,y 0) shaklni oladi

y-y 0 = f'(x 0) (x-x 0).

Qaysidir nuqtada egri chiziqning normali xuddi shu nuqtadagi tangensga perpendikulyar hisoblanadi. Agar f'(x 0)≠ 0, keyin normalning chiziqqa tenglamasi y=f(x) nuqtada M 0 (x 0 ,y 0) shunday yozilgan:

Funksiyaning differentsialligi tushunchasi

Funktsiyaga ruxsat bering y=f(x) ma'lum bir oraliqda aniqlanadi (a, b), x- bu oraliqdan ba'zi sobit argument qiymati, Dx- argumentning qiymati argumentning har qanday o'sishi x+Dx ∈ (a, b).

Ta'rif. Funktsiya y=f(x) berilgan nuqtada differentsiallanuvchi deb ataladi x, agar ortib borsa dy nuqtada bu funktsiya x, argument o'sishiga mos keladi Dx, shaklida ifodalanishi mumkin

Dy = A Dx +aDx,

Qayerda A- ba'zi bir raqamdan mustaqil Dx, A α - argument funktsiyasi Dx, bu da cheksiz kichikdir Dx→ 0.

Ikki cheksiz kichik funktsiyaning mahsuloti bo'lgani uchun adx dan yuqori tartibli cheksiz kichikdir Dx(3 ta cheksiz kichik funktsiyaning xossasi), u holda yozishimiz mumkin:

Dy = A Dx +o(Dx).

Teorema. Funktsiyani bajarish uchun y=f(x) ma'lum bir nuqtada farqlanishi mumkin edi x, bu nuqtada uning cheklangan hosilasi bo'lishi zarur va etarli. Qayerda A=f′(x), ya'ni

Dy = f'(x) Dx +o(Dx).

Hosilni topish operatsiyasi odatda differentsiallash deb ataladi.

Teorema. Agar funktsiya y=f(x) x, keyin bu nuqtada uzluksiz bo'ladi.

Izoh. Funksiyaning uzluksizligidan y=f(x) ayni paytda x, umuman olganda, funktsiyaning differentsialligi kuzatilmaydi f(x) ayni paytda. Masalan, funktsiya y=|x|- bir nuqtada uzluksiz x=0, lekin hosilasi yo'q.

Differensial funksiya haqida tushuncha

Ta'rif. Funktsiya farqi y=f(x) bu funktsiyaning hosilasi va mustaqil o'zgaruvchining o'sish ko'paytmasi deyiladi x:

dy = y′ Dx, df(x) = f′(x) Dx.

Funktsiya uchun y=x olamiz dy=dx=x′Dx = 1· Dx= Dx, ya'ni dx=Dx- mustaqil o'zgaruvchining differensialligi ushbu o'zgaruvchining o'sishiga teng.

Shunday qilib, biz yozishimiz mumkin

dy = y′ dx, df(x) = f′(x) dx

Differensial dy va oshirish dy funktsiyalari y=f(x) ayni paytda x, ikkalasi ham bir xil argument o'sishiga mos keladi Dx, umuman olganda, bir-biriga teng emas.

Differensialning geometrik ma'nosi: Argument oshirilganda funksiyaning differensialligi ushbu funksiya grafigiga teginish ordinatasining ortishiga teng. Dx.

Farqlash qoidalari

Teorema. Funktsiyalarning har biri bo'lsa u(x) Va v(x) ma'lum bir nuqtada farqlanadi x, keyin bu funktsiyalarning yig'indisi, farqi, mahsuloti va qismi (bo'lim sharti bilan v(x)≠ 0) bu nuqtada ham farqlanadi va formulalar quyidagilarni o'z ichiga oladi:

Murakkab funktsiyani ko'rib chiqing y=f(ph(x))≡ F(x), Qayerda y=f(u), u=ph(x). Ushbu holatda u chaqirdi oraliq argument, x - mustaqil o'zgaruvchi.

Teorema. Agar y=f(u) Va u=ph(x) argumentlarining differentsial funksiyalari, keyin hosila murakkab funktsiya y=f(ph(x)) mavjud va bu funktsiyaning oraliq argumentga nisbatan mahsulotiga va mustaqil o'zgaruvchiga nisbatan oraliq argumentning hosilasiga teng, ya'ni.

Izoh. Uch funktsiyaning superpozitsiyasi bo'lgan murakkab funktsiya uchun y=F(f(ph(x))), farqlash qoidasi shaklga ega

y' x = y' u u' v v' x,

funktsiyalari qayerda v=ph(x), u=f(v) Va y=F(u)- ularning argumentlarining differentsial funksiyalari.

Teorema. Funktsiyaga ruxsat bering y=f(x) oshadi (yoki kamayadi) va nuqtaning ba'zi qo'shnilarida uzluksizdir x 0. Bundan tashqari, ushbu funktsiya ko'rsatilgan nuqtada differentsial bo'lsin x 0 va bu nuqtada uning hosilasi f'(x 0) ≠ 0. Keyin tegishli nuqtaning ba'zi mahallalarida y 0 =f(x 0) uchun teskarisi aniqlanadi y=f(x) funktsiyasi x=f -1 (y), va belgilangan teskari funktsiya mos keladigan nuqtada farqlanadi y 0 =f(x 0) va bu nuqtada uning hosilasi uchun y formula haqiqiydir

Hosilalar jadvali

Birinchi differentsial shaklining o'zgarmasligi

Kompleks funktsiyaning differentsialini ko'rib chiqamiz. Agar y=f(x), x=ph(t)- ularning argumentlarining funktsiyalari differentsial bo'ladi, keyin funktsiyaning hosilasi y=f(ph(t)) formula bilan ifodalanadi

y' t = y' x x' t.

A-prior dy=y′ t dt, keyin olamiz

dy = y′ t dt = y′ x · x′ t dt = y′ x (x′ t dt) = y′ x dx,

dy = y' x dx.

Shunday qilib, biz isbotladik

Funktsiyaning birinchi differentsial shaklining o'zgarmaslik xususiyati: argument bo'lganda bo'lgani kabi x mustaqil o'zgaruvchidir va argument bo'lgan holatda x o'zi yangi o'zgaruvchining differentsial funksiyasi, differentsialdir dy funktsiyalari y=f(x) bu funksiyaning hosilasining argumentning differentsialiga ko‘paytmasiga teng dx.

Differensialni taxminiy hisoblarda qo'llash

Differensial ekanligini ko'rsatdik dy funktsiyalari y=f(x), umuman olganda, o'sishga teng emas dy bu funksiya. Biroq, kichiklikning yuqori tartibidagi cheksiz kichik funktsiyagacha Dx, taxminiy tenglik amal qiladi

Dy ≈ dy.

Nisbatan bu tenglik tengligining nisbiy xatosi deyiladi. Chunki Dy-dy=o(Dx), Bu nisbiy xato bu tenglik kamayganda kerakli darajada kichik bo'ladi |Dx|.

Shuni hisobga olib Dy=f(x+d x)-f(x), dy=f'(x)Dx, olamiz f(x+d x)-f(x) ≈ f′(x)Dx yoki

f(x+d x) ≈ f(x) + f'(x)Dx.

Bu taxminiy tenglik xato bilan ruxsat beradi o(Dx) funktsiyasini almashtiring f(x) nuqtaning kichik bir mahallasida x(masalan, kichik qiymatlar uchun Dx) chiziqli funksiya dalil Dx, o'ng tomonda turgan.

Yuqori tartibli hosilalar

Ta'rif. Funktsiyaning ikkinchi hosilasi (yoki ikkinchi tartibli hosilasi). y=f(x) birinchi hosilasining hosilasi deyiladi.

Funktsiyaning ikkinchi hosilasi uchun belgi y=f(x):

Ikkinchi hosilaning mexanik ma'nosi. Agar funktsiya y=f(x) harakat qonunini tavsiflaydi moddiy nuqta to'g'ri chiziqda, keyin ikkinchi hosila f″(x) harakatlanuvchi nuqtaning vaqt momentidagi tezlanishiga teng x.

Uchinchi va to'rtinchi hosilalar xuddi shunday aniqlanadi.

Ta'rif. n th lotin (yoki hosila n-chi tartib) funktsiyalari y=f(x) uning hosilasi deyiladi n-1 th hosilasi:

y (n) =(y (n-1))′, f (n) (x)=(f (n-1) (x))′.

Belgilar: y″', y IV, y V va hokazo.

B9 muammosi funksiya yoki hosila grafigini beradi, undan quyidagi miqdorlardan birini aniqlash kerak:

1. X 0 nuqtadagi hosilaning qiymati,
2. Maksimal yoki minimal ball (ekstremum ball),
3. Ortib boruvchi va kamayuvchi funksiyalarning intervallari (monotonlik oraliqlari).

Bu masalada keltirilgan funksiyalar va hosilalar doimo uzluksiz bo‘lib, yechimni ancha osonlashtiradi. Vazifa bo'limga tegishli bo'lishiga qaramasdan matematik tahlil, bu hatto eng zaif talabalarning imkoniyatlariga to'liq mos keladi, chunki bu erda chuqur nazariy bilim talab qilinmaydi.

Losmalar, ekstremum nuqtalar va monotonlik oraliqlarining qiymatini topish uchun oddiy va universal algoritmlar mavjud - ularning barchasi quyida muhokama qilinadi.

Ahmoqona xatolarga yo'l qo'ymaslik uchun B9 muammosining shartlarini diqqat bilan o'qing: ba'zida siz juda uzun matnlarga duch kelasiz, lekin muhim shartlar, qaror qabul qilish jarayoniga ta'sir qiluvchi, ozchilik bor.

Hosila qiymatini hisoblash. Ikki nuqta usuli

Agar muammoga f(x) funksiyaning grafigi qaysidir x 0 nuqtasida shu grafaga tangens berilgan bo‘lsa va bu nuqtada hosilaning qiymatini topish talab etilsa, quyidagi algoritm qo‘llaniladi:

1. Tangens grafigida ikkita "adekvat" nuqtani toping: ularning koordinatalari butun son bo'lishi kerak. Bu nuqtalarni A (x 1 ; y 1) va B (x 2 ; y 2) belgilaymiz. Koordinatalarni to'g'ri yozing - bu asosiy moment echimlar va bu erda har qanday xato noto'g'ri javobga olib keladi.
2. Koordinatalarni bilgan holda, Dx = x 2 − x 1 argumentining ortishi va Dy = y 2 − y 1 funksiyasining o‘sishini hisoblash oson.
3. Nihoyat, hosila D = Dy/Dx qiymatini topamiz. Boshqacha qilib aytganda, funktsiyaning o'sishini argumentning o'sishiga bo'lish kerak - va bu javob bo'ladi.

Yana bir bor eslatib o'tamiz: A va B nuqtalarni ko'pincha sodir bo'lganidek f(x) funksiya grafigidan emas, balki aniq tangensdan izlash kerak. Tangens chizig'i majburiy ravishda kamida ikkita bunday nuqtani o'z ichiga oladi - aks holda muammo to'g'ri shakllantirilmaydi.

A (−3; 2) va B (−1; 6) nuqtalarini ko‘rib chiqing va o‘sishlarni toping:
Dx = x 2 - x 1 = -1 - (-3) = 2; Dy = y 2 - y 1 = 6 - 2 = 4.

Hosilaning qiymati topilsin: D = Dy/Dx = 4/2 = 2.

Vazifa. Rasmda y = f(x) funksiyaning grafigi va abtsissa x 0 nuqtada unga teginish ko'rsatilgan. f(x) funksiyaning x 0 nuqtadagi hosilasi qiymatini toping.

A (0; 3) va B (3; 0) nuqtalarini ko'rib chiqing, o'sishlarni toping:
Dx = x 2 - x 1 = 3 - 0 = 3; Dy = y 2 - y 1 = 0 - 3 = -3.

Endi hosilaning qiymatini topamiz: D = Dy/Dx = -3/3 = -1.

Vazifa. Rasmda y = f(x) funksiyaning grafigi va abtsissa x 0 nuqtada unga teginish ko'rsatilgan. f(x) funksiyaning x 0 nuqtadagi hosilasi qiymatini toping.

A (0; 2) va B (5; 2) nuqtalarini ko'rib chiqing va o'sishlarni toping:
Dx = x 2 - x 1 = 5 - 0 = 5; Dy = y 2 - y 1 = 2 - 2 = 0.

Hosilaning qiymatini topish qoladi: D = Dy/Dx = 0/5 = 0.

Oxirgi misoldan biz qoidani shakllantirishimiz mumkin: agar tangens OX o'qiga parallel bo'lsa, teginish nuqtasida funktsiyaning hosilasi nolga teng. Bunday holda, siz hech narsani hisoblashingiz shart emas - shunchaki grafikaga qarang.

Maksimal va minimal ballarni hisoblash

Ba'zan B9 masalada funktsiya grafigi o'rniga hosila grafigi beriladi va funktsiyaning maksimal yoki minimal nuqtasini topish talab etiladi. Bunday vaziyatda ikki nuqtali usul foydasiz, ammo boshqa, hatto oddiyroq algoritm ham mavjud. Birinchidan, terminologiyani aniqlaymiz:

1. x 0 nuqtasi f(x) funksiyaning maksimal nuqtasi deyiladi, agar bu nuqtaning qaysidir qo'shnisida quyidagi tengsizlik bajarilsa: f(x 0) ≥ f(x).
2. x 0 nuqtasi f(x) funksiyaning minimal nuqtasi deyiladi, agar shu nuqtaning qaysidir qo'shnisida quyidagi tengsizlik bajarilsa: f(x 0) ≤ f(x).

Hosil grafigida maksimal va minimal nuqtalarni topish uchun quyidagi amallarni bajaring:

1. Barcha keraksiz ma'lumotlarni olib tashlagan holda lotin grafigini qayta chizing. Amaliyot shuni ko'rsatadiki, keraksiz ma'lumotlar faqat qaror qabul qilishga xalaqit beradi. Shuning uchun biz e'tiborga olamiz koordinata o'qi lotinning nollari - hammasi shu.
2. Nollar orasidagi intervallardagi hosila belgilarini toping. Agar biron bir x 0 nuqtasi uchun f'(x 0) ≠ 0 ekanligi ma'lum bo'lsa, u holda faqat ikkita variant mumkin: f'(x 0) ≥ 0 yoki f'(x 0) ≤ 0. Hosilning belgisi: dastlabki chizmadan aniqlash oson: agar hosilaviy grafik OX oʻqidan yuqorida joylashgan boʻlsa, u holda f'(x) ≥ 0. Va aksincha, hosila grafik OX oʻqi ostida yotsa, f'(x) ≤ 0 boʻladi.
3. Yana lotinning nol va belgilarini tekshiramiz. Belgining minusdan plyusga o'zgarishi minimal nuqtadir. Aksincha, lotin belgisi ortiqcha dan minusga o'zgartirilsa, bu maksimal nuqtadir. Hisoblash har doim chapdan o'ngga amalga oshiriladi.

Ushbu sxema faqat uzluksiz funktsiyalar uchun ishlaydi - B9 muammosida boshqalar yo'q.

Vazifa. Rasmda f(x) funksiyaning [−5 oraliqda aniqlangan hosilasining grafigi ko'rsatilgan; 5]. f(x) funksiyaning shu segmentdagi minimal nuqtasini toping.

Keling, qutulaylik keraksiz ma'lumotlar— faqat chegaralarni qoldiramiz [−5; 5] va hosila nollari x = -3 va x = 2,5. Shuningdek, biz belgilarga e'tibor qaratamiz:

Shubhasiz, x = −3 nuqtada hosilaning belgisi minusdan plyusga o'zgaradi. Bu minimal nuqta.

Vazifa. Rasmda f(x) funksiyaning [−3 oraliqda aniqlangan hosilasining grafigi ko'rsatilgan; 7]. f(x) funksiyaning shu segmentdagi maksimal nuqtasini toping.

Keling, faqat chegaralarni qoldirib, grafikni qayta chizamiz [−3; 7] va hosila nollari x = −1.7 va x = 5. Hosil boʻlgan grafikdagi hosilaning belgilarini qayd qilaylik. Bizda ... bor:

Shubhasiz, x = 5 nuqtasida lotin belgisi ortiqcha dan minusga o'zgaradi - bu maksimal nuqta.

Vazifa. Rasmda f(x) funksiyaning [−6 oraliqda aniqlangan hosilasining grafigi ko‘rsatilgan; 4]. f(x) funksiyaning [−4” segmentiga tegishli maksimal nuqtalari sonini toping; 3].

Masalaning shartlaridan kelib chiqadiki, grafikning faqat segment bilan chegaralangan qismini ko'rib chiqish kifoya [−4; 3]. Shuning uchun biz yangi grafik quramiz, unda biz faqat chegaralarni belgilaymiz [-4; 3] va uning ichidagi hosilaning nollari. Ya'ni, x = -3,5 va x = 2 nuqtalari. Biz quyidagilarni olamiz:

Bu grafikda faqat bitta maksimal nuqta x = 2. Aynan shu nuqtada hosilaning belgisi ortiqcha dan minusga o'zgaradi.

Butun son bo'lmagan koordinatali nuqtalar haqida kichik eslatma. Masalan, oxirgi masalada x = -3,5 nuqtasi ko'rib chiqildi, ammo xuddi shu muvaffaqiyat bilan biz x = -3,4 ni olishimiz mumkin. Agar muammo to'g'ri tuzilgan bo'lsa, bunday o'zgarishlar javobga ta'sir qilmasligi kerak, chunki "belgilangan yashash joyisiz" nuqtalar muammoni hal qilishda bevosita ishtirok etmaydi. Albatta, bu hiyla butun sonlar bilan ishlamaydi.

O'sish va kamayuvchi funktsiyalarning intervallarini topish

Bunday masalada maksimal va minimal nuqtalar kabi, funktsiyaning o'zi ortib yoki kamayadigan sohalarni topish uchun hosilaviy grafikdan foydalanish taklif etiladi. Birinchidan, o'sish va kamayish nima ekanligini aniqlaymiz:

1. Agar ushbu segmentning istalgan ikkita x 1 va x 2 nuqtalari uchun quyidagi fikr to'g'ri bo'lsa, f(x) funksiya segmentda ortib borayotgan deyiladi: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . Boshqacha qilib aytganda, argument qiymati qanchalik katta bo'lsa, funktsiya qiymati shunchalik katta bo'ladi.
2. f(x) funksiya, agar bu segmentning istalgan ikkita x 1 va x 2 nuqtalari uchun quyidagi fikr to'g'ri bo'lsa, segmentdagi kamayuvchi deyiladi: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Bular. yuqoriroq qiymat argument funksiyaning kichikroq qiymatiga mos keladi.

Keling, oshirish va kamaytirish uchun etarli shartlarni tuzamiz:

1. Uzluksiz f(x) funksiya segmentda ortishi uchun uning segment ichidagi hosilasi musbat bo'lishi kifoya, ya'ni. f’(x) ≥ 0.
2. Uzluksiz f(x) funksiya segmentida kamayishi uchun uning segment ichidagi hosilasi manfiy bo'lishi kifoya, ya'ni. f’(x) ≤ 0.

Keling, bu gaplarni dalilsiz qabul qilaylik. Shunday qilib, biz o'sish va pasayish oraliqlarini topish sxemasini olamiz, bu ko'p jihatdan ekstremum nuqtalarni hisoblash algoritmiga o'xshaydi:

1. Barcha keraksiz ma'lumotlarni olib tashlang. Hosilning asl grafigida bizni birinchi navbatda funksiyaning nollari qiziqtiradi, shuning uchun biz faqat ularni qoldiramiz.
2. Nol orasidagi oraliqda hosilaning belgilarini belgilang. f’(x) ≥ 0 bo’lgan joyda funksiya ortadi, f’(x) ≤ 0 bo’lsa, u kamayadi. Agar muammo x o'zgaruvchisiga cheklovlar qo'ygan bo'lsa, biz ularni qo'shimcha ravishda yangi grafikda belgilaymiz.
3. Endi biz funktsiyaning xatti-harakati va cheklovlarni bilganimizdan so'ng, muammoda talab qilinadigan miqdorni hisoblash qoladi.

Vazifa. Rasmda f(x) funksiyaning [−3 oraliqda aniqlangan hosilasining grafigi ko'rsatilgan; 7.5]. f(x) funksiyaning kamayish oraliqlarini toping. Javobingizda ushbu intervallarga kiritilgan butun sonlar yig'indisini ko'rsating.

Odatdagidek, grafikni qayta chizamiz va chegaralarni belgilaymiz [−3; 7.5], shuningdek x = -1.5 va x = 5.3 hosilasining nollari. Keyin hosila belgilarini qayd etamiz. Bizda ... bor:

(− 1,5) oraliqda hosila manfiy bo‘lgani uchun bu funksiya kamayuvchi intervaldir. Ushbu oraliq ichidagi barcha sonlarni yig'ish qoladi:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Vazifa. Rasmda [−10 oraliqda aniqlangan f(x) funksiya hosilasining grafigi ko'rsatilgan; 4]. f(x) funksiyaning ortish oraliqlarini toping. Javobingizda ulardan eng kattasining uzunligini ko'rsating.

Keling, keraksiz ma'lumotlardan xalos bo'laylik. Keling, faqat chegaralarni qoldiramiz [−10; 4] va hosilaning nollari, bu safar ulardan to‘rttasi bor edi: x = −8, x = −6, x = −3 va x = 2. Hosilning belgilarini belgilab, quyidagi rasmni olamiz:

Biz funktsiyani oshirish intervallari bilan qiziqamiz, ya'ni. f’(x) ≥ 0. Grafikda ikkita shunday interval mavjud: (−8; −6) va (−3; 2). Keling, ularning uzunligini hisoblaylik:
l 1 = - 6 - (-8) = 2;
l 2 = 2 - (−3) = 5.

Intervallarning eng kattasining uzunligini topishimiz kerakligi sababli, javob sifatida l 2 = 5 qiymatini yozamiz.

Bitta o‘zgaruvchili funktsiyaning hosilasi.

Kirish.

Haqiqiy uslubiy ishlanmalar sanoat va qurilish fakulteti talabalari uchun mo'ljallangan. Ular "Bir o'zgaruvchining funksiyalarining differentsial hisobi" bo'limida matematika kursi dasturiga bog'liq holda tuzilgan.

Ishlanmalar yagona uslubiy qo'llanmani ifodalaydi, jumladan: qisqacha nazariy ma'lumotlar; Ushbu yechimlar uchun batafsil echimlar va tushuntirishlar bilan "standart" muammolar va mashqlar; test imkoniyatlari.

Har bir paragrafning oxirida qo'shimcha mashqlar mavjud. Ishlanmalarning bunday tuzilishi ularni o'qituvchining minimal yordami bilan bo'limni mustaqil o'zlashtirish uchun qulay qiladi.

§1. Hosila tushunchasi.

Mexanik va geometrik ma'no

hosila.

Tuzama tushunchasi matematik tahlilning eng muhim tushunchalaridan biri bo'lib, u 17-asrda paydo bo'lgan. Hosila tushunchasining shakllanishi tarixan ikkita muammo bilan bog'liq: o'zgaruvchan harakat tezligi muammosi va egri chiziqqa tegish muammosi.

Bu masalalar, ularning mazmuni turlicha bo'lishiga qaramay, funktsiyada bajarilishi kerak bo'lgan bir xil matematik operatsiyaga olib keladi. Funktsiyani differentsiallash operatsiyasi deyiladi. Differensiatsiya operatsiyasining natijasi hosila deyiladi.

Demak, y=f(x) funksiyaning x0 nuqtadagi hosilasi funksiya ortishining argument ortishiga nisbatining chegarasi (agar u mavjud bo‘lsa) bo‘ladi.
da
.

Hosil odatda quyidagicha ifodalanadi:
.

Shunday qilib, ta'rifga ko'ra

Belgilar hosilalarni belgilash uchun ham ishlatiladi
.

Hosilning mexanik ma'nosi.

Agar s=s(t) moddiy nuqtaning to'g'ri chiziqli harakati qonuni bo'lsa, u holda
bu nuqtaning t vaqtidagi tezligi.

Hosilning geometrik ma'nosi.

Agar y=f(x) funksiya nuqtada hosilaga ega bo'lsa , keyin nuqtadagi funksiya grafigiga teginishning burchak koeffitsienti
teng
.

Misol.

Funktsiyaning hosilasini toping
nuqtada =2:

1) Keling, bir nuqtani beraylik =2 o'sish
. E'tibor bering, bu.

2) Funktsiyaning nuqtadagi o'sishini toping =2:

3) Funksiya ortishining argument ortishiga nisbatini yaratamiz:

da nisbat chegarasini topamiz
:

.

Shunday qilib,
.

§ 2. Ayrimlarning hosilalari

eng oddiy funktsiyalar.

Talaba xususiy funksiyalarning hosilalarini hisoblashni o‘rganishi kerak: y=x,y= va umuman = .

y=x funksiyaning hosilasi topilsin.

bular. (x)′=1.

Funktsiyaning hosilasi topilsin

Hosil

Mayli
Keyin

Quvvat funksiyasining hosilalarini ifodalashda naqshni sezish oson
n=1,2,3 bilan.

Demak,

. (1)

Bu formula har qanday haqiqiy n uchun amal qiladi.

Xususan, (1) formuladan foydalanib, bizda quyidagilar mavjud:

;

.

Misol.

Funktsiyaning hosilasini toping

.

.

Bu funksiya shakl funksiyasining alohida holatidir

da
.

Formuladan (1) foydalanib, biz bor

.

y=sin x va y=cos x funksiyalarning hosilalari.

y=sinx bo'lsin.

∆x ga bo'linadi, biz olamiz

∆x→0 chegarasiga o'tsak, biz bor

y=cosx bo'lsin.

∆x→0 chegarasiga o'tib, biz olamiz

;
. (2)

§3. Farqlashning asosiy qoidalari.

Keling, farqlash qoidalarini ko'rib chiqaylik.

Teorema1 . Agar u=u(x) va v=v(x) funksiyalar berilgan x nuqtada differentsiallansa, bu nuqtada ularning yig’indisi ham differentsiallanadi va yig’indining hosilasi hadlar hosilalari yig’indisiga teng bo’ladi. : (u+v)"=u"+v".(3 )

Isbot: y=f(x)=u(x)+v(x) funksiyani ko‘rib chiqamiz.

X argumentining ∆x ortishi u va v funksiyalarning ∆u=u(x+∆x)-u(x), ∆v=v(x+∆x)-v(x) o’sishlariga mos keladi. Shunda y funksiyasi ortadi

∆y=f(x+∆x)-f(x)=

=--=∆u+∆v.

Demak,

Demak, (u+v)"=u"+v".

Teorema2. Agar u=u(x) va v=v(x) funksiyalar berilgan x nuqtada differensiallanuvchi bo’lsa, ularning ko’paytmasi bir nuqtada differentsial bo’ladi, bu holda hosilaning hosilasi quyidagi formula bo’yicha topiladi: ( uv)"=u"v+uv". (4)

Isbot: y=uv bo‘lsin, bu yerda u va v x ning ba’zi differentsiallanuvchi funksiyalari. X ga ∆x o'sish beraylik, u holda u ∆u, v ∆v, y esa ∆y o'sishni oladi.

Bizda y+∆y=(u+∆u)(v+∆v), yoki bor

y+∆y=uv+u∆v+v∆u+∆u∆v.

Demak, ∆y=u∆v+v∆u+∆u∆v.

Bu yerdan

∆x→0 chegarasiga o'tsak va u va v ning ∆x ga bog'liq emasligini hisobga olsak, bizda shunday bo'ladi.

Teorema 3. Ikki funktsiyaning ko'paytmasining hosilasi kasrga teng bo'lib, uning maxraji bo'linuvchining kvadratiga teng bo'ladi va hisoblagich bo'linuvchining dividend hosilasining ko'paytmasi bilan bo'linuvchining ko'paytmasi o'rtasidagi farqdir. bo'luvchining hosilasi bo'yicha dividend, ya'ni.

Agar
Bu
(5)

Teorema 4. Doimiy miqdorning hosilasi nolga teng, ya'ni. agar y=C, bu erda C=const, u holda y"=0.

Teorema 5. Doimiy omil hosilaning belgisidan chiqarilishi mumkin, ya'ni. agar y=Cu(x), bu yerda S=const, u holda y"=Cu"(x).

1-misol.

Funktsiyaning hosilasini toping

.

Bu funktsiya shaklga ega
, bu erda u=x,v=cosx. Differensiatsiya qoidasini qo'llagan holda (4) topamiz

.

2-misol.

Funktsiyaning hosilasini toping

.

(5) formulani qo'llaymiz.

Bu yerga
;
.

Vazifalar.

Quyidagi funksiyalarning hosilalarini toping:

;

11)

2)
; 12)
;

3)
13)

4)
14)

5)
15)

6)
16)

7 )
17)

8)
18)

9)
19)

10)
20)