Sinus, kosinus, tangens va kotangens: trigonometriyada ta'riflar, misollar, formulalar. O'tkir burchakning sinus, kosinus, tangensi, kotangensi. Trigonometrik funktsiyalar

Trigonometriya - trigonometrik funktsiyalar va ularning geometriyada qo'llanilishini o'rganadigan matematika fanining bir tarmog'i. Trigonometriyaning rivojlanishi kunlarda boshlangan qadimgi Yunoniston. Oʻrta asrlarda bu fanning rivojlanishiga Yaqin Sharq va Hindiston olimlari muhim hissa qoʻshgan.

Ushbu maqola bag'ishlangan asosiy tushunchalar va trigonometriyaning ta'riflari. Unda asosiy trigonometrik funktsiyalarning ta'riflari muhokama qilinadi: sinus, kosinus, tangens va kotangens. Ularning ma'nosi geometriya kontekstida tushuntiriladi va tasvirlanadi.

Yandex.RTB R-A-339285-1

Dastlab argumenti burchak boʻlgan trigonometrik funksiyalarning taʼriflari toʻgʻri burchakli uchburchak tomonlari nisbati bilan ifodalangan.

Trigonometrik funktsiyalarning ta'riflari

Burchakning sinusi (sin a) - bu burchakka qarama-qarshi bo'lgan oyoqning gipotenuzaga nisbati.

Burchakning kosinusu (cos a) - qo'shni oyoqning gipotenuzaga nisbati.

Burchak tangensi (t g a) - qarama-qarshi tomonning qo'shni tomonga nisbati.

Burchak kotangenti (c t g a) - qo'shni tomonning qarama-qarshi tomoniga nisbati.

Ushbu ta'riflar uchun berilgan o'tkir burchak to'g'ri uchburchak!

Keling, misol keltiraylik.

To'g'ri burchakli C burchakli ABC uchburchakda A burchakning sinusi nisbatga teng oyoq BC gipotenuzasiga AB.

Sinus, kosinus, tangens va kotangensning ta'riflari ushbu funktsiyalarning qiymatlarini uchburchak tomonlarining ma'lum uzunliklaridan hisoblash imkonini beradi.

Esda tutish muhim!

Sinus va kosinus qiymatlari diapazoni -1 dan 1 gacha. Boshqacha qilib aytganda, sinus va kosinus -1 dan 1 gacha qiymatlarni oladi. Tangens va kotangens qiymatlari diapazoni butun son chizig'idir, ya'ni bu funksiyalar har qanday qiymatlarni qabul qilishi mumkin.

Yuqorida keltirilgan ta'riflar o'tkir burchaklarga tegishli. Trigonometriyada burilish burchagi tushunchasi kiritiladi, uning qiymati o'tkir burchakdan farqli o'laroq, 0 dan 90 gradusgacha chegaralanmaydi, gradus yoki radianda aylanish burchagi - ∞ dan + ∞ gacha bo'lgan har qanday haqiqiy son bilan ifodalanadi.

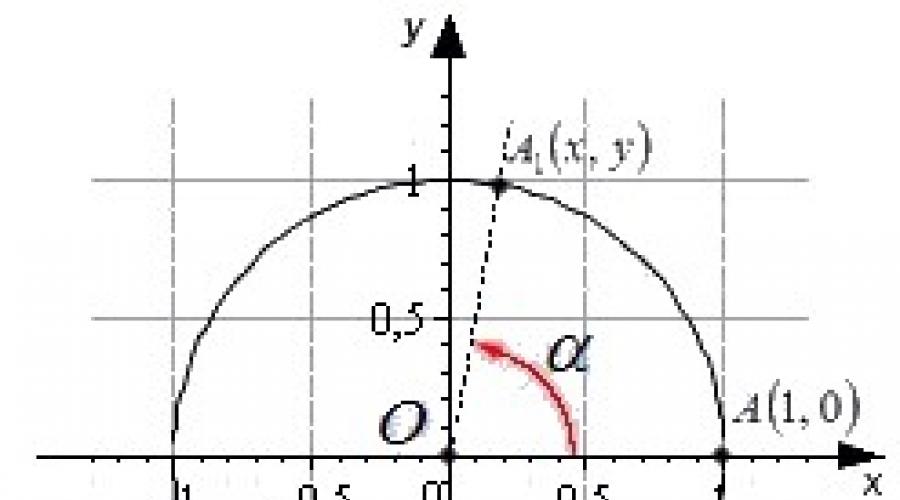
Shu nuqtai nazardan, biz ixtiyoriy kattalikdagi burchakning sinusini, kosinusini, tangensini va kotangensini aniqlashimiz mumkin. Markazi Dekart koordinata tizimining boshida joylashgan birlik doirani tasavvur qilaylik.

Koordinatalari (1, 0) bo'lgan boshlang'ich A nuqta ma'lum a burchak orqali birlik doira markazi atrofida aylanadi va A 1 nuqtaga boradi. Ta'rif A 1 (x, y) nuqtaning koordinatalari bo'yicha berilgan.

Aylanish burchagining sinus (sin).

Aylanish burchagi a sinusi A nuqtaning ordinatasi 1 (x, y). sin a = y

Aylanish burchagining kosinusu (cos).

Aylanish burchagi a kosinusu A 1 (x, y) nuqtaning abssissasidir. cos a = x

Aylanish burchagining tangensi (tg).

A burilish burchagi tangensi A 1 (x, y) nuqta ordinatasining uning abtsissasiga nisbati hisoblanadi. t g a = y x

Aylanish burchagining kotangenti (ctg).

Aylanish burchagi a kotangensi A 1 (x, y) nuqta abssissasining uning ordinatasiga nisbati hisoblanadi. c t g a = x y

Har qanday aylanish burchagi uchun sinus va kosinus aniqlanadi. Bu mantiqan to'g'ri, chunki aylanmadan keyin nuqtaning abscissa va ordinatasi istalgan burchakda aniqlanishi mumkin. Tangens va kotangens bilan vaziyat boshqacha. Aylanishdan keyin nuqta nol abscissa (0, 1) va (0, - 1) nuqtaga o'tganda tangens aniqlanmagan. Bunday hollarda t g a = y x tangensi ifodasi shunchaki ma'noga ega emas, chunki u nolga bo'linishni o'z ichiga oladi. Vaziyat kotangent bilan o'xshash. Farqi shundaki, nuqta ordinatasi nolga tushgan hollarda kotangent aniqlanmaydi.

Esda tutish muhim!

Har qanday a burchak uchun sinus va kosinus aniqlanadi.

Tangens a = 90° + 180° k, k ∈ Z (a = p 2 + p k, k ∈ Z) dan tashqari barcha burchaklar uchun aniqlanadi.

Kotangent a = 180° k, k ∈ Z (a = p k, k ∈ Z) dan tashqari barcha burchaklar uchun aniqlanadi.

Qaror qabul qilganda amaliy misollar"aylanish burchagi sinusi a" demang. "Aylanish burchagi" so'zlari shunchaki olib tashlandi, bu esa kontekstdan nima muhokama qilinayotgani allaqachon aniq ekanligini anglatadi.

Raqamlar

Aylanish burchagini emas, balki sonning sinusini, kosinusini, tangensini va kotangensini aniqlash haqida nima deyish mumkin?

Sonning sinus, kosinus, tangensi, kotangensi

Sonning sinus, kosinus, tangensi va kotangensi t-da mos ravishda sinus, kosinus, tangens va kotangensga teng bo'lgan son t radian.

Masalan, 10 p sonining sinusi sinusga teng aylanish burchagi 10 p rad.

Sonning sinusini, kosinusini, tangensini va kotangensini aniqlashning yana bir usuli mavjud. Keling, buni batafsil ko'rib chiqaylik.

Har qanday haqiqiy raqam t birlik doiradagi nuqta to'rtburchaklar Dekart koordinata tizimining boshidagi markaz bilan bog'langan. Bu nuqtaning koordinatalari orqali sinus, kosinus, tangens va kotangens aniqlanadi.

Doiradagi boshlang'ich nuqta koordinatalari (1, 0) bo'lgan A nuqtadir.

Ijobiy raqam t

Salbiy raqam t aylana bo'ylab soat sohasi farqli ravishda harakatlansa, boshlang'ich nuqtasi ketadigan nuqtaga mos keladi va yo'ldan boradi t.

Aylanadagi son bilan nuqta o‘rtasidagi bog‘lanish o‘rnatilgandan so‘ng, biz sinus, kosinus, tangens va kotangens ta’rifiga o‘tamiz.

t ning sinusi (gunohi).

Raqamning sinusi t- songa mos keladigan birlik doiradagi nuqtaning ordinatasi t. sin t = y

Kosinus (cos) t

Sonning kosinusu t- songa mos keladigan birlik aylana nuqtasining abssissasi t. cos t = x

Tangensi (tg) t

Sonning tangensi t- songa mos keladigan birlik doiradagi nuqtaning abssissasiga ordinataning nisbati t. t g t = y x = sin t cos t

Eng so'nggi ta'riflar ushbu bandning boshida berilgan ta'rifga mos keladi va unga zid kelmaydi. Raqamga mos keladigan aylanaga ishora qiling t, burchak bilan burilgandan keyin boshlang'ich nuqtasi ketadigan nuqtaga to'g'ri keladi t radian.

Burchak va son argumentning trigonometrik funktsiyalari

Burchakning har bir qiymati a bu burchakning sinusi va kosinusining ma'lum bir qiymatiga mos keladi. Xuddi a = 90 ° + 180 ° k dan boshqa barcha a burchaklar kabi, k ∈ Z (a = p 2 + p k, k ∈ Z) ma'lum bir tangens qiymatiga mos keladi. Kotangent, yuqorida aytib o'tilganidek, a = 180° k, k ∈ Z (a = p k, k ∈ Z) dan tashqari barcha a uchun aniqlanadi.

Aytishimiz mumkinki, sin a, cos a, t g a, c t g a alfa burchakning funksiyalari yoki burchak argumentining funksiyalaridir.

Xuddi shunday, sonli argumentning funktsiyalari sifatida sinus, kosinus, tangens va kotangens haqida gapirishimiz mumkin. Har bir haqiqiy raqam t sonning sinus yoki kosinusining ma'lum bir qiymatiga mos keladi t. p 2 + p · k, k ∈ Z dan boshqa barcha raqamlar tangens qiymatiga mos keladi. Xuddi shunday kotangent p · k, k ∈ Z dan boshqa barcha sonlar uchun aniqlanadi.

Trigonometriyaning asosiy funktsiyalari

Sinus, kosinus, tangens va kotangens asosiy trigonometrik funktsiyalardir.

Odatda kontekstdan trigonometrik funktsiyaning qaysi argumenti aniq bo'ladi ( burchak argumenti yoki raqamli argument) bilan shug'ullanamiz.

Keling, eng boshida berilgan ta'riflarga va 0 dan 90 darajagacha bo'lgan alfa burchagiga qaytaylik. Trigonometrik ta'riflar sinus, kosinus, tangens va kotangens to'liq mos keladi geometrik ta'riflar, to'g'ri burchakli uchburchakning tomonlar nisbati yordamida berilgan. Keling, ko'rsataylik.

To'g'ri to'rtburchaklar Dekart koordinatalari tizimida markazi bo'lgan birlik doirani olaylik. A (1, 0) boshlang'ich nuqtasini 90 gradusgacha burchakka aylantiramiz va hosil bo'lgan A 1 (x, y) nuqtadan abscissa o'qiga perpendikulyar chizamiz. Olingan to'g'ri burchakli uchburchakda A 1 O H burchak burchakka teng a burilish, oyoqning uzunligi O H A 1 (x, y) nuqtasi abssissasiga teng. Burchakka qarama-qarshi turgan oyoqning uzunligi A 1 (x, y) nuqtaning ordinatasiga teng, gipotenuzaning uzunligi esa bir ga teng, chunki u birlik doirasining radiusi.

Geometriya ta'rifiga ko'ra, a burchakning sinusi qarama-qarshi tomonning gipotenuzaga nisbatiga teng.

sin a = A 1 H O A 1 = y 1 = y

Bu shuni anglatadiki, to'g'ri burchakli uchburchakdagi o'tkir burchakning sinusini tomonlar nisbati orqali aniqlash, alfa 0 dan 90 darajagacha bo'lgan oraliqda joylashgan aylanish burchagining sinusini aniqlashga teng.

Xuddi shunday, ta'riflarning mosligini kosinus, tangens va kotangens uchun ko'rsatish mumkin.

Agar siz matnda xatolikni sezsangiz, uni belgilang va Ctrl+Enter tugmalarini bosing

Ko'rsatmalar

Birinchi variant klassik bo'lib, qog'oz, protraktor va qalam (yoki qalam) ta'rifiga ko'ra sinus burchak to'g'ri burchakli uchburchakning gipotenuzasiga qarama-qarshi tomoniga teng. Ya'ni, qiymatni hisoblash uchun burchaklaridan biri sinusi sizni qiziqtirgan burchakka teng bo'lgan to'g'ri burchakli uchburchakni qurish uchun transportyordan foydalanishingiz kerak. Keyin gipotenuzaning va qarama-qarshi oyoqning uzunligini o'lchab, ikkinchisini kerakli aniqlik bilan birinchisiga bo'ling.

Ikkinchi variant - maktab. Maktabda hamma minglab trigonometrik qiymatlarni o'z ichiga olgan "Bradis jadvallarini" eslaydi turli burchaklar. Siz qog'oz nashrini ham, uning elektron hamkasbini ham pdf formatida qidirishingiz mumkin - ular Internetda mavjud. Jadvallarni topib, qiymatni toping sinus zarur burchak qiyin bo'lmaydi.

Uchinchi variant eng maqbuldir. Agar kirish imkoningiz bo'lsa, siz standart Windows OT kalkulyatoridan foydalanishingiz mumkin. Uni kengaytirilgan rejimga o'tkazish kerak. Buning uchun menyuning "Ko'rish" bo'limida "Muhandislik" ni tanlang. Kalkulyatorning ko'rinishi o'zgaradi - xususan, trigonometrik funktsiyalarni hisoblash tugmalari paydo bo'ladi burchak, sinusini hisoblashingiz kerak. Buni klaviaturadan yoki sichqoncha kursori bilan kerakli kalkulyator tugmachalarini bosish orqali amalga oshirishingiz mumkin. Yoki shunchaki kerakli qiymatni kiritishingiz mumkin (CTRL + C va CTRL + V). Shundan so'ng, uni hisoblash kerak bo'lgan birliklarni tanlang - trigonometrik funktsiyalar uchun bu radian, daraja yoki rad bo'lishi mumkin. Bu hisoblangan qiymat kiritish maydoni ostida joylashgan uchta kalit qiymatlaridan birini tanlash orqali amalga oshiriladi. Endi “gunoh” deb belgilangan tugmani bosish orqali siz savolingizga javob olasiz.

To'rtinchi variant eng zamonaviy hisoblanadi. Internet davrida deyarli har bir yuzaga keladigan muammolarni taklif qiladigan onlayn echimlar mavjud. Foydalanuvchi uchun qulay interfeysga ega trigonometrik funktsiyalarning onlayn kalkulyatorlari yanada rivojlangan funksionallik uni umuman topa olmaydi. Ularning eng yaxshilari nafaqat individual funktsiyaning qiymatlarini, balki to'liq hisoblashni ham taklif qiladi murakkab ifodalar bir nechta funktsiyalardan.

Funksiyalar sinus va boshqalar sinus trigonometriya deb ataladigan matematika sohasiga tegishli, shuning uchun funktsiyalarning o'zi trigonometrik deb ataladi. Eng qadimgi ta'rifga ko'ra, ular to'g'ri burchakli uchburchakdagi o'tkir burchakning kattaligini uning tomonlari uzunligi nisbati orqali ifodalaydi. Qiymatlarni hisoblash sinus va hozirgi rivojlanish darajasida elektron texnologiya- yetarli oddiy vazifa.

Sizga kerak bo'ladi

• Windows kalkulyator.

Ko'rsatmalar

Hisoblash uchun foydalaning sinus va burchak - trigonometrik funktsiyalarni hisoblash ularning ko'pchiligida taqdim etiladi. Ko'pchilikda kalkulyator mavjudligini hisobga olgan holda mobil telefonlar, ba'zi bilak va boshqa mobil gadjetlar, kompyuterlar haqida gapirmasa ham, bu, ehtimol arzon yo'l hisob-kitoblar sinus A. Agar siz kompyuter dasturiy kalkulyatoridan foydalanishga qaror qilsangiz, uni asosiy OS menyusida ishga tushirish uchun havolani qidiring. Agar u Windows bo'lsa, Win tugmasini bosing, menyudan "Barcha dasturlar" ni tanlang, "Standart" bo'limiga o'ting va "Kalkulyator" qatorini bosing. Ishga tushirilgan ilovada trigonometrik funktsiyalarni hisoblash buyruqlariga kirishni ochish uchun Alt + 2 tugmalar birikmasini bosing.

Agar burchakning boshlang'ich qiymati bo'lsa sinus Siz hisoblamoqchi bo'lgan ma'lumot ichida berilgan bo'lsa, kalkulyator interfeysidagi "" yozuvi yonida joylashganligiga ishonch hosil qiling.

Sinus asosiy trigonometrik funktsiyalardan biri bo'lib, undan foydalanish faqat geometriya bilan cheklanmaydi. Muhandislik kalkulyatorlari kabi trigonometrik funktsiyalarni hisoblash uchun jadvallar har doim ham qo'lda emas va sinusni hisoblash ba'zan hal qilish uchun kerak bo'ladi. turli vazifalar. Umuman olganda, sinusni hisoblash chizish ko'nikmalarini va trigonometrik identifikatsiyalar haqidagi bilimlarni mustahkamlashga yordam beradi.

Rulet va qalam bilan o'yinlar

Oddiy vazifa: qog'ozga chizilgan burchakning sinusini qanday topish mumkin? Yechish uchun sizga oddiy o'lchagich, uchburchak (yoki kompas) va qalam kerak bo'ladi. Burchakning sinusini hisoblashning eng oddiy usuli - bu to'g'ri burchakli uchburchakning uzoq oyog'ini uzun tomoni - gipotenuzaga bo'lish. Shunday qilib, siz birinchi navbatda burchak uchidan ixtiyoriy masofada nurlardan biriga perpendikulyar chiziq chizish orqali to'g'ri burchakli uchburchak shakliga o'tkir burchakni yakunlashingiz kerak. Biz to'liq 90 ° burchakka ega bo'lishimiz kerak, buning uchun bizga ruhoniy uchburchak kerak bo'ladi.

Kompasdan foydalanish biroz aniqroq, ammo ko'proq vaqt talab etadi. Nurlardan birida siz ma'lum masofada 2 nuqtani belgilashingiz kerak, kompasda taxminan nuqtalar orasidagi masofaga teng radiusni o'rnating va bu chiziqlarning kesishmalari olinmaguncha bu nuqtalarda markazlari bo'lgan yarim doira chizing. Bizning doiralarimizning kesishish nuqtalarini bir-biri bilan bog'lab, biz burchakning nuriga qat'iy perpendikulyar olamiz, qolgan narsa chiziqni boshqa nur bilan kesishguncha uzaytirishdir;

Olingan uchburchakda burchakka qarama-qarshi tomonni va nurlarning birida uzun tomonni o'lchash uchun o'lchagichdan foydalanish kerak. Birinchi o'lchamning ikkinchisiga nisbati o'tkir burchak sinusining kerakli qiymati bo'ladi.

90° dan katta burchak uchun sinusni toping

To'g'ri burchak uchun vazifa unchalik qiyin emas. Bizni qiziqtirgan burchakning nurlaridan biri bilan toʻgʻri chiziq hosil qilish uchun chizgʻich yordamida tepadan qarama-qarshi yoʻnalishdagi nurni chizishimiz kerak. Olingan o'tkir burchakni yuqorida ta'riflanganidek davolash kerak, ular birgalikda 180 ° teskari burchak hosil qiladi.

Boshqa trigonometrik funktsiyalar yordamida sinusni hisoblash

Bundan tashqari, burchakning boshqa trigonometrik funktsiyalarining qiymatlari yoki hech bo'lmaganda uchburchak tomonlari uzunligi ma'lum bo'lsa, sinusni hisoblash mumkin. Ular bizga bu borada yordam berishadi trigonometrik identifikatsiyalar. Keling, umumiy misollarni ko'rib chiqaylik.

Burchakning ma'lum kosinusi bo'lgan sinusni qanday topish mumkin? Pifagor teoremasiga asoslangan birinchi trigonometrik o'ziga xoslik bir xil burchakdagi sinus va kosinus kvadratlarining yig'indisi birga teng ekanligini bildiradi.

Burchakning ma'lum tangensi bo'lgan sinusni qanday topish mumkin? Tangens uzoq tomonni yaqin tomonga bo'lish yoki sinusni kosinusga bo'lish orqali olinadi. Shunday qilib, sinus kosinus va tangensning mahsuloti bo'ladi va sinusning kvadrati bu mahsulotning kvadrati bo'ladi. Birinchi trigonometrik identifikatsiyaga ko'ra kvadrat kosinusni birlik va kvadrat sinus o'rtasidagi farq bilan almashtiramiz va oddiy manipulyatsiyalar orqali biz tenglamani teginish orqali kvadrat sinusni hisoblash uchun kamaytiramiz, siz sinusni hisoblaysiz; olingan natijaning ildizini chiqarib olish kerak.

Burchakning ma'lum kotangensi bo'lgan sinusni qanday topish mumkin? Kotangensning qiymatini burchakka eng yaqin bo'lgan oyog'ining uzunligini uzoqning uzunligiga bo'lish, shuningdek kosinusni sinusga bo'lish yo'li bilan hisoblash mumkin, ya'ni kotangent tangens nisbiyga teskari funktsiyadir. raqamiga 1. Sinusni hisoblash uchun tg a = 1 / ctg a formulasi yordamida tangensni hisoblashingiz va ikkinchi variantdagi formuladan foydalanishingiz mumkin. Bundan tashqari, to'g'ridan-to'g'ri formulani tangensga o'xshash qilib olishingiz mumkin, bu shunday ko'rinadi.

Uchburchakning uch tomonining sinusini qanday topish mumkin

Har qanday uchburchakning noma'lum tomoni uzunligini ikkitadan topish formulasi mavjud, shunchaki to'rtburchak emas. taniqli partiyalar qarama-qarshi burchak kosinusining trigonometrik funktsiyasidan foydalanish. U shunday ko'rinadi.

Biz trigonometriyani o'rganishni to'g'ri uchburchakdan boshlaymiz. Keling, sinus va kosinus nima ekanligini, shuningdek, o'tkir burchakning tangensi va kotangensini aniqlaymiz. Bu trigonometriyaning asoslari.

Shuni eslatib o'tamiz to'g'ri burchak 90 gradusga teng burchak hisoblanadi. Boshqacha qilib aytganda, yarim burilish burchagi.

O'tkir burchak- 90 darajadan kam.

O'tkir burchak- 90 darajadan yuqori. Bunday burchakka nisbatan "to'liq" haqorat emas, balki matematik atama :-)

Keling, to'g'ri burchakli uchburchak chizamiz. To'g'ri burchak odatda bilan belgilanadi. E'tibor bering, burchakka qarama-qarshi tomon bir xil harf bilan ko'rsatilgan, faqat kichik. Shunday qilib, qarama-qarshi tomon A burchak belgilanadi.

Burchak mos keladigan yunoncha harf bilan belgilanadi.

Gipotenuza to'g'ri burchakli uchburchakning to'g'ri burchakka qarama-qarshi tomonidir.

Oyoqlar- o'tkir burchaklarga qarama-qarshi yotgan tomonlar.

Burchakka qarama-qarshi yotgan oyoq deyiladi qarama-qarshi(burchakka nisbatan). Burchakning yon tomonlaridan birida yotadigan boshqa oyoq deyiladi qo'shni.

Sinus To'g'ri burchakli uchburchakdagi o'tkir burchak qarama-qarshi tomonning gipotenuzaga nisbati:

Kosinus To'g'ri uchburchakdagi o'tkir burchak - qo'shni oyoqning gipotenuzaga nisbati:

Tangent To'g'ri uchburchakdagi o'tkir burchak - qarama-qarshi tomonning qo'shniga nisbati:

Boshqa (ekvivalent) ta'rif: o'tkir burchakning tangensi - bu burchak sinusining uning kosinusiga nisbati:

Kotangent To'g'ri burchakli uchburchakdagi o'tkir burchak - qo'shni tomonning qarama-qarshi tomonga nisbati (yoki bir xil bo'lgan kosinusning sinusga nisbati):

Quyida sinus, kosinus, tangens va kotangens uchun asosiy munosabatlarga e'tibor bering. Muammolarni hal qilishda ular bizga foydali bo'ladi.

Keling, ulardan ba'zilarini isbotlaylik.

OK, biz ta'riflar berdik va formulalarni yozdik. Lekin nima uchun bizga hali ham sinus, kosinus, tangens va kotangens kerak?

Biz buni bilamiz har qanday uchburchak burchaklarining yig'indisi ga teng.

o'rtasidagi munosabatni bilamiz partiyalar to'g'ri uchburchak. Bu Pifagor teoremasi: .

Ma'lum bo'lishicha, uchburchakda ikkita burchakni bilib, uchinchisini topishingiz mumkin. To'g'ri burchakli uchburchakning ikki tomonini bilib, uchinchisini topishingiz mumkin. Bu shuni anglatadiki, burchaklar o'z nisbatlariga ega, tomonlar esa o'zlariga ega. Ammo agar siz to'g'ri burchakli uchburchakda bitta burchakni (to'g'ri burchakdan tashqari) va bir tomonni bilsangiz, nima qilish kerak, lekin boshqa tomonlarni topishingiz kerak?

Ilgari odamlar bu hudud va yulduzli osmon xaritalarini tuzishda duch kelgan narsadir. Axir, uchburchakning barcha tomonlarini to'g'ridan-to'g'ri o'lchash har doim ham mumkin emas.

Sinus, kosinus va tangens - ular ham deyiladi trigonometrik burchak funktsiyalari- o'rtasidagi munosabatlarni berish partiyalar Va burchaklar uchburchak. Burchakni bilib, siz maxsus jadvallar yordamida uning barcha trigonometrik funktsiyalarini topishingiz mumkin. Va uchburchak burchaklarining sinuslari, kosinuslari va tangenslarini va uning tomonlaridan birini bilib, qolgan qismini topishingiz mumkin.

Bundan tashqari, "yaxshi" burchaklar uchun sinus, kosinus, tangens va kotangens qiymatlari jadvalini tuzamiz.

Jadvaldagi ikkita qizil chiziqqa e'tibor bering. Tegishli burchak qiymatlarida tangens va kotangens mavjud emas.

Keling, FIPI vazifalar bankidan bir nechta trigonometriya masalalarini ko'rib chiqaylik.

1. Uchburchakda burchak , ga teng. Toping.

Muammo to'rt soniya ichida hal qilinadi.

Chunki , .

2. Uchburchakda burchak , , ga teng. Toping.

Pifagor teoremasidan foydalanib topamiz.

Muammo hal qilindi.

Ko'pincha muammolarda burchakli va yoki burchakli uchburchaklar mavjud. Ular uchun asosiy nisbatlarni yodda saqlang!

Burchaklari va burchakka qarama-qarshi oyog'i bo'lgan uchburchak uchun at ga teng gipotenuzaning yarmi.

Burchakli uchburchak va teng yon tomonli. Unda gipotenuza oyoqdan marta kattaroqdir.

Biz to'g'ri burchakli uchburchaklarni yechish masalalarini ko'rib chiqdik - ya'ni noma'lum tomonlar yoki burchaklarni topish. Lekin bu hammasi emas! IN Yagona davlat imtihonlari variantlari matematikada uchburchakning tashqi burchagining sinusi, kosinusu, tangensi yoki kotangensi paydo bo'ladigan ko'plab muammolar mavjud. Bu haqda keyingi maqolada batafsil.

Sinusni qanday topish mumkin?

Geometriyani o'rganish fikrlashni rivojlantirishga yordam beradi. Bu fan albatta maktabga tayyorlashga kiritiladi. Kundalik hayotda ushbu mavzu bo'yicha bilim foydali bo'lishi mumkin - masalan, kvartirani rejalashtirishda.

Tarixdan

Geometriya kursi trigonometrik funktsiyalarni o'rganuvchi trigonometriyani ham o'z ichiga oladi. Trigonometriyada biz burchaklarning sinuslari, kosinuslari, tangenslari va kotangenslarini o'rganamiz.

Lekin davom bu daqiqa Eng oddiy narsadan boshlaylik - sinus. Keling, eng birinchi tushunchani - geometriyadagi burchak sinusini batafsil ko'rib chiqaylik. Sinus nima va uni qanday topish mumkin?

"Sinus burchak" va sinusoidlar tushunchasi

Burchakning sinusi - bu qarama-qarshi tomonning qiymatlari va to'g'ri burchakli uchburchakning gipotenuzasi nisbati. Bu to'g'ridan-to'g'ri trigonometrik funktsiya bo'lib, u "sin (x)" deb yoziladi, bu erda (x) - uchburchakning burchagi.

Grafikda burchakning sinusi o'ziga xos xususiyatlarga ega sinus to'lqin bilan ko'rsatilgan. Sinus to'lqin koordinata tekisligida ma'lum chegaralar ichida joylashgan doimiy to'lqinli chiziqqa o'xshaydi. Funktsiya g'alati, shuning uchun u koordinata tekisligida 0 ga yaqin simmetrikdir (u koordinatalarning boshidan chiqadi).

Ushbu funktsiyaning ta'rif sohasi Dekart koordinata tizimida -1 dan +1 gacha bo'lgan oraliqda joylashgan. Sinus burchak funksiyasining davri 2 Pi ga teng. Bu shuni anglatadiki, har 2 Pida naqsh takrorlanadi va sinus to'lqin to'liq tsikldan o'tadi.

Sinus to'lqin tenglamasi

• sin x = a/c
• bu yerda a - uchburchak burchagiga qarama-qarshi oyoq
• c - to'g'ri burchakli uchburchakning gipotenuzasi

Burchak sinusining xossalari

1. sin(x) = - sin(x). Bu xususiyat funktsiyaning simmetrik ekanligini ko'rsatadi va agar x va (-x) qiymatlari koordinatalar tizimida har ikki yo'nalishda chizilgan bo'lsa, u holda bu nuqtalarning ordinatalari qarama-qarshi bo'ladi. Ular bir-biridan teng masofada joylashgan bo'ladi.
2. Bu funksiyaning yana bir xususiyati shundaki, [- P/2 + 2 Pn] segmentida funksiya grafigi ortadi; [P/2 + 2Pn], bu erda n har qanday butun son. Segmentda burchak sinusining grafigida pasayish kuzatiladi: [P/2 + 2Pn]; [3P/2 + 2Pn].
3. x oraliqda bo'lganda sin(x) > 0 (2Pn, P + 2Pn)
4. (x)< 0, когда х находится в диапазоне (-П+2Пn, 2Пn)

Burchak sinuslarining qiymatlari maxsus jadvallar yordamida aniqlanadi. Hisoblash jarayonini osonlashtirish uchun bunday jadvallar yaratilgan murakkab formulalar va tenglamalar. Foydalanish oson va nafaqat ma'nolarni o'z ichiga oladi vazifalari gunoh(x), balki boshqa funksiyalarning qiymatlari ham.

Bundan tashqari, ushbu funktsiyalar uchun standart qiymatlar jadvali ilovaga kiritilgan majburiy o'qish xotira uchun, ko'paytirish jadvali kabi. Bu, ayniqsa, fizikaviy va matematik jihatdan moyil bo'lgan sinflar uchun to'g'ri keladi. Jadvalda trigonometriyada ishlatiladigan asosiy burchaklarning qiymatlarini ko'rishingiz mumkin: 0, 15, 30, 45, 60, 75, 90, 120, 135, 150, 180, 270 va 360 daraja.

Shuningdek, nostandart burchaklarning trigonometrik funktsiyalari qiymatlarini belgilaydigan jadval mavjud. Foyda olish turli jadvallar, siz ba'zi burchaklarning sinusi, kosinusu, tangensi va kotangensini osongina hisoblashingiz mumkin.

Tenglamalar trigonometrik funksiyalar bilan tuziladi. Agar siz oddiy trigonometrik identifikatsiyalar va funktsiyalarning qisqarishini bilsangiz, masalan, sin (P/2 + x) = cos (x) va boshqalarni bilsangiz, bu tenglamalarni echish oson. Bunday qisqartirishlar uchun alohida jadval ham tuzilgan.

Burchakning sinusini qanday topish mumkin

Vazifa burchakning sinusini topish bo'lsa va shartga ko'ra, biz faqat burchakning kosinus, tangensi yoki kotangensiga egamiz, biz trigonometrik identifikatsiyalar yordamida kerakli narsani osongina hisoblashimiz mumkin.

• sin 2 x + cos 2 x = 1

Ushbu tenglamadan qaysi qiymat noma'lumligiga qarab sinus va kosinusni topishimiz mumkin. Biz qila olamiz trigonometrik tenglama bitta noma'lum bilan:

• sin 2 x = 1 - cos 2 x
• sin x = ± √ 1 - cos 2 x
• karavot 2 x + 1 = 1 / gunoh 2 x

Bu tenglamadan burchak kotangensining qiymatini bilib, sinusning qiymatini topish mumkin. Soddalashtirish uchun sin 2 x = y ni almashtiring va sizda oddiy tenglama mavjud. Masalan, kotangent qiymati 1 ga teng, keyin:

• 1 + 1 = 1/y
• 2 = 1/y
• 2u = 1
• y = 1/2

Endi biz o'yinchini teskari almashtirishni amalga oshiramiz:

• gunoh 2 x = ½
• sin x = 1 / √2

Standart burchak uchun kotangent qiymatini olganimiz sababli (45 0), olingan qiymatlarni jadvalda tekshirish mumkin.

Agar sizga tangens qiymat berilsa va sinusni topishingiz kerak bo'lsa, boshqa trigonometrik identifikatsiya yordam beradi:

• tg x * ctg x = 1

Bundan kelib chiqadiki:

• karavot x = 1 / tan x

Nostandart burchakning sinusini topish uchun, masalan, 240 0, burchakni qisqartirish formulalaridan foydalanish kerak. Bilamizki, p 180 0 ga mos keladi. Shunday qilib, biz tengligimizni standart burchaklar yordamida kengaytirish orqali ifodalaymiz.

• 240 0 = 180 0 + 60 0

Biz quyidagilarni topishimiz kerak: gunoh (180 0 + 60 0). Trigonometriyada kamaytirish formulalari mavjud Ushbu holatda yordam beradi. Bu formula:

• gunoh (p + x) = - gunoh (x)

Shunday qilib, 240 graduslik burchakning sinusi quyidagilarga teng:

• gunoh (180 0 + 60 0) = - gunoh (60 0) = - √3/2

Bizning holatda, x = 60 va P, mos ravishda, 180 daraja. Biz standart burchaklar funktsiyalari qiymatlari jadvalidan (-√3/2) qiymatini topdik.

Shu tarzda biz parchalanishimiz mumkin nostandart burchaklar, masalan: 210 = 180 + 30.