To'g'ri chiziq. To'g'ri chiziq tenglamasi. Ikki nuqtadan o'tuvchi chiziq tenglamasi 2 nuqta berilgan, chiziq tenglamasini toping
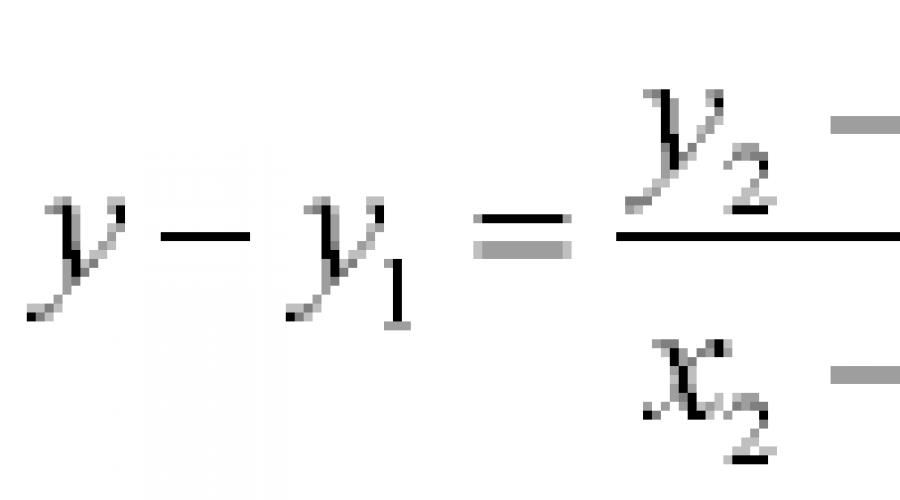
Shuningdek o'qing
Evklid geometriyasida to'g'ri chiziqning xossalari.
Istalgan nuqta orqali cheksiz ko'p to'g'ri chiziqlar o'tkazish mumkin.
Har qanday ikkita mos kelmaydigan nuqta orqali bitta to'g'ri chiziq o'tkazish mumkin.
Tekislikdagi ikkita divergent chiziq bitta nuqtada kesishadi yoki bo'ladi
parallel (avvalgisidan keyin).
Uch o'lchovli fazoda ikkita chiziqning nisbiy joylashuvi uchun uchta variant mavjud:
- chiziqlar kesishadi;
- chiziqlar parallel;
- to'g'ri chiziqlar kesishadi.
Streyt chiziq— birinchi tartibli algebraik egri chiziq: Dekart koordinata tizimidagi to‘g‘ri chiziq
tekislikda birinchi darajali tenglama (chiziqli tenglama) bilan beriladi.
To'g'ri chiziqning umumiy tenglamasi.
Ta'rif. Tekislikdagi har qanday to'g'ri chiziq birinchi tartibli tenglama bilan aniqlanishi mumkin
Ax + Wu + C = 0,
va doimiy A, B bir vaqtning o'zida nolga teng emas. Bu birinchi tartibli tenglama deyiladi umumiy
to'g'ri chiziq tenglamasi. Konstantalarning qiymatlariga qarab A, B Va BILAN Quyidagi maxsus holatlar mumkin:
. C = 0, A ≠0, B ≠ 0- to'g'ri chiziq koordinatali nuqtadan o'tadi
. A = 0, B ≠0, C ≠0 (By + C = 0)- o'qqa parallel to'g'ri chiziq Oh
. B = 0, A ≠0, C ≠ 0 (Ax + C = 0)- o'qqa parallel to'g'ri chiziq OU
. B = C = 0, A ≠0- to'g'ri chiziq o'qga to'g'ri keladi OU
. A = C = 0, B ≠0- to'g'ri chiziq o'qga to'g'ri keladi Oh
To'g'ri chiziq tenglamasi har qanday berilganga qarab turli shakllarda taqdim etilishi mumkin
boshlang'ich sharoitlar.
Nuqta va normal vektordan to'g'ri chiziq tenglamasi.
Ta'rif. Dekart to'rtburchaklar koordinatalar tizimida komponentlar (A, B) bo'lgan vektor.
tenglama bilan berilgan chiziqqa perpendikulyar
Ax + Wu + C = 0.
Misol. Nuqtadan o‘tuvchi chiziq tenglamasini toping A(1, 2) vektorga perpendikulyar (3, -1).
Yechim. A = 3 va B = -1 bilan to'g'ri chiziq tenglamasini tuzamiz: 3x - y + C = 0. C koeffitsientini topish uchun
Berilgan A nuqtaning koordinatalarini olingan ifodaga almashtiramiz: 3 - 2 + C = 0, shuning uchun
C = -1. Jami: kerakli tenglama: 3x - y - 1 = 0.
Ikki nuqtadan o'tuvchi chiziq tenglamasi.
Kosmosda ikkita nuqta berilgan bo'lsin M 1 (x 1 , y 1 , z 1) Va M2 (x 2, y 2, z 2), Keyin chiziq tenglamasi,
Ushbu nuqtalardan o'tish:
Agar maxrajlardan birortasi nolga teng bo'lsa, mos keladigan numerator nolga teng bo'lishi kerak. Yoniq
tekislikda, yuqorida yozilgan to'g'ri chiziq tenglamasi soddalashtirilgan:

Agar x 1 ≠ x 2 Va x = x 1, Agar x 1 = x 2 .
Fraksiya = k chaqirdi qiyalik Streyt.
Misol. A(1, 2) va B(3, 4) nuqtalardan o`tuvchi chiziq tenglamasini toping.
Yechim. Yuqorida yozilgan formuladan foydalanib, biz quyidagilarni olamiz:

To'g'ri chiziqning nuqta va qiyalik yordamida tenglamasi.
Agar chiziqning umumiy tenglamasi Ax + Wu + C = 0 olib kelishi:

va belgilang  , keyin hosil bo'lgan tenglama chaqiriladi
, keyin hosil bo'lgan tenglama chaqiriladi
qiyaligi k bo'lgan to'g'ri chiziq tenglamasi.
Nuqtadan to'g'ri chiziq va yo'nalish vektori tenglamasi.
Oddiy vektor orqali to'g'ri chiziq tenglamasini ko'rib chiqadigan nuqtaga o'xshatib, siz vazifani kiritishingiz mumkin
nuqtadan o'tadigan to'g'ri chiziq va to'g'ri chiziqning yo'naltiruvchi vektori.
Ta'rif. Har bir nolga teng bo'lmagan vektor (a 1 , a 2), uning tarkibiy qismlari shartni qanoatlantiradi
Aa 1 + Ba 2 = 0 chaqirdi to'g'ri chiziqning yo'naltiruvchi vektori.
Ax + Wu + C = 0.
Misol. Yo‘nalish vektori (1, -1) bo‘lgan va A(1, 2) nuqtadan o‘tuvchi to‘g‘ri chiziq tenglamasini toping.
Yechim. Biz kerakli chiziq tenglamasini quyidagi shaklda qidiramiz: Ax + By + C = 0. Ta'rifga ko'ra,
koeffitsientlar quyidagi shartlarga javob berishi kerak:
1 * A + (-1) * B = 0, ya'ni. A = B.
Keyin to'g'ri chiziq tenglamasi quyidagi ko'rinishga ega bo'ladi: Ax + Ay + C = 0, yoki x + y + C / A = 0.
da x = 1, y = 2 olamiz C/A = -3, ya'ni. zarur tenglama:
x + y - 3 = 0
To'g'ri chiziqning segmentlardagi tenglamasi.
Agar to'g'ri chiziqning umumiy tenglamasida Ax + Vu + S = 0 S≠0 bo'lsa, -S ga bo'linib, biz quyidagilarni olamiz:
 yoki qayerda
yoki qayerda

Koeffitsientlarning geometrik ma'nosi shundaki, a koeffitsienti kesishish nuqtasining koordinatasi hisoblanadi
eksa bilan to'g'ri Oh, A b- chiziqning o'q bilan kesishish nuqtasining koordinatasi OU.
Misol. To'g'ri chiziqning umumiy tenglamasi berilgan x - y + 1 = 0. Bu chiziqning segmentlardagi tenglamasini toping.
C = 1, , a = -1, b = 1.
Oddiy chiziq tenglamasi.
Agar tenglamaning ikkala tomoni bo'lsa Ax + Wu + C = 0 raqamga bo'linadi  qaysi deyiladi
qaysi deyiladi
normallashtiruvchi omil, keyin olamiz
xcosph + ysinph - p = 0 -chiziqning normal tenglamasi.
Normallashtiruvchi omilning ± belgisi shunday tanlanishi kerak m*C< 0.
R- boshdan to'g'ri chiziqqa tushirilgan perpendikulyar uzunligi;
A φ - o'qning musbat yo'nalishi bilan bu perpendikulyar tomonidan hosil qilingan burchak Oh.
Misol. Chiziqning umumiy tenglamasi berilgan 12x - 5y - 65 = 0. Har xil turdagi tenglamalarni yozish uchun talab qilinadi
bu to'g'ri chiziq.
Ushbu chiziqning segmentlardagi tenglamasi:

Bu chiziqning qiyalik bilan tenglamasi: (5 ga bo'linadi)

Chiziq tenglamasi:

cos ph = 12/13; sin ph= -5/13; p = 5.
Shuni ta'kidlash kerakki, har bir to'g'ri chiziqni segmentlarda tenglama bilan ifodalash mumkin emas, masalan, to'g'ri chiziqlar,
o'qlarga parallel yoki boshlang'ichdan o'tuvchi.
Tekislikdagi to'g'ri chiziqlar orasidagi burchak.
Ta'rif. Ikki qator berilgan bo'lsa y = k 1 x + b 1 , y = k 2 x + b 2, keyin bu chiziqlar orasidagi o'tkir burchak
sifatida belgilanadi

Ikki chiziq parallel bo'lsa k 1 = k 2. Ikki chiziq perpendikulyar
Agar k 1 = -1/ k 2 .
Teorema.
To'g'ridan-to'g'ri Ax + Wu + C = 0 Va A 1 x + B 1 y + C 1 = 0 koeffitsientlar proportsional bo'lganda parallel
A 1 = lA, B 1 = lB. Agar ham S 1 = l, keyin chiziqlar mos keladi. Ikki chiziqning kesishish nuqtasining koordinatalari
bu chiziqlar tenglamalar sistemasi yechimi sifatida topiladi.
Berilgan chiziqqa perpendikulyar berilgan nuqtadan o'tuvchi chiziq tenglamasi.
Ta'rif. Nuqtadan o'tuvchi chiziq M 1 (x 1, y 1) va chiziqqa perpendikulyar y = kx + b
tenglama bilan ifodalanadi:

Nuqtadan chiziqgacha bo'lgan masofa.
Teorema. Agar ball berilsa M(x 0, y 0), keyin to'g'ri chiziqgacha bo'lgan masofa Ax + Wu + C = 0 quyidagicha aniqlanadi:

Isbot. Nuqtaga ruxsat bering M 1 (x 1, y 1)- nuqtadan tushgan perpendikulyarning asosi M berilgan uchun
bevosita. Keyin nuqtalar orasidagi masofa M Va M 1:
![]() (1)
(1)
Koordinatalar x 1 Va 1 da tenglamalar sistemasiga yechim sifatida topish mumkin:

Tizimning ikkinchi tenglamasi berilgan M 0 nuqtadan perpendikulyar oʻtuvchi toʻgʻri chiziq tenglamasidir.
to'g'ri chiziq berilgan. Agar tizimning birinchi tenglamasini quyidagi shaklga aylantirsak:
A(x - x 0) + B(y - y 0) + Ax 0 + 0 ga + C = 0,
keyin hal qilib, biz quyidagilarni olamiz:

Ushbu ifodalarni (1) tenglamaga almashtirib, biz quyidagilarni topamiz:

Teorema isbotlangan.
Ikki ball berilsin M 1 (x 1, y 1) Va M 2 (x 2, y 2). To'g'ri chiziq tenglamasini (5) ko'rinishda yozamiz, bu erda k hali noma'lum koeffitsient:
Nuqtaidan beri M 2 berilgan chiziqqa tegishli bo'lsa, u holda uning koordinatalari (5) tenglamani qanoatlantiradi: . Bu yerdan ifodalab, (5) tenglamaga almashtirib, kerakli tenglamani olamiz:
![]()
Agar ![]() bu tenglamani yodlash uchun qulayroq shaklda qayta yozish mumkin:
bu tenglamani yodlash uchun qulayroq shaklda qayta yozish mumkin:
![]() (6)
(6)
Misol. M 1 (1,2) va M 2 (-2,3) nuqtalardan o‘tuvchi to‘g‘ri chiziq tenglamasini yozing.
Yechim. ![]() . Proportsionallik xususiyatidan foydalanib va kerakli o'zgarishlarni amalga oshirib, biz to'g'ri chiziqning umumiy tenglamasini olamiz:
. Proportsionallik xususiyatidan foydalanib va kerakli o'zgarishlarni amalga oshirib, biz to'g'ri chiziqning umumiy tenglamasini olamiz:
Ikki to'g'ri chiziq orasidagi burchak
Ikkita to'g'ri chiziqni ko'rib chiqing l 1 Va l 2:
l 1: , , Va
l 2: , ,
ph - ular orasidagi burchak (). 4-rasmdan aniq: .
 |
Bu yerdan ![]() , yoki
, yoki
(7) formuladan foydalanib, to'g'ri chiziqlar orasidagi burchaklardan birini aniqlashingiz mumkin. Ikkinchi burchak ga teng.
Misol. Ikki chiziq y=2x+3 va y=-3x+2 tenglamalar bilan berilgan. bu chiziqlar orasidagi burchakni toping.
Yechim. Tenglamalardan k 1 =2, k 2 =-3 ekanligi ayon bo`ladi. Ushbu qiymatlarni formula (7) ga almashtirib, biz topamiz
![]() . Shunday qilib, bu chiziqlar orasidagi burchak ga teng.
. Shunday qilib, bu chiziqlar orasidagi burchak ga teng.
Ikki to'g'ri chiziqning parallellik va perpendikulyarlik shartlari
To'g'ri bo'lsa l 1 Va l 2 u holda parallel bo'ladi φ=0 Va tgph=0. (7) formuladan kelib chiqadiki, , qaerdan k 2 =k 1. Shunday qilib, ikkita chiziq parallelligining sharti ularning burchak koeffitsientlarining tengligidir.
To'g'ri bo'lsa l 1 Va l 2 u holda perpendikulyar bo'ladi ph=p/2, a 2 = p/2+ a 1 . ![]() . Shunday qilib, ikkita to'g'ri chiziqning perpendikulyarligi sharti shundaki, ularning burchak koeffitsientlari kattaligi bo'yicha teskari va ishorasi bo'yicha qarama-qarshidir.
. Shunday qilib, ikkita to'g'ri chiziqning perpendikulyarligi sharti shundaki, ularning burchak koeffitsientlari kattaligi bo'yicha teskari va ishorasi bo'yicha qarama-qarshidir.
Nuqtadan chiziqgacha bo'lgan masofa
Teorema. Agar M(x 0, y 0) nuqta berilsa, Ax + B + C = 0 chiziqqa masofa quyidagicha aniqlanadi.
Isbot. M nuqtadan berilgan to‘g‘ri chiziqqa tushirilgan perpendikulyarning asosi M 1 (x 1, y 1) nuqta bo‘lsin. Keyin M va M nuqtalari orasidagi masofa 1:
x 1 va y 1 koordinatalarini tenglamalar tizimini yechish orqali topish mumkin:
Tizimning ikkinchi tenglamasi berilgan chiziqqa perpendikulyar M 0 nuqtadan o'tuvchi chiziq tenglamasidir.
Agar tizimning birinchi tenglamasini quyidagi shaklga aylantirsak:
A(x – x 0) + B(y – y 0) + Ax 0 + 0 ga + C = 0,
keyin hal qilib, biz quyidagilarni olamiz:
Ushbu ifodalarni (1) tenglamaga almashtirib, biz quyidagilarni topamiz:
Teorema isbotlangan.
Misol. Chiziqlar orasidagi burchakni aniqlang: y = -3x + 7; y = 2x + 1.
k 1 = -3; k 2 = 2 tanj= ; j = p/4.
Misol. 3x – 5y + 7 = 0 va 10x + 6y – 3 = 0 chiziqlar perpendikulyar ekanligini ko'rsating.
Biz topamiz: k 1 = 3/5, k 2 = -5/3, k 1 k 2 = -1, shuning uchun chiziqlar perpendikulyar.
Misol. A(0; 1), B(6; 5), C(12; -1) uchburchakning uchlari berilgan. C uchidan chizilgan balandlik tenglamasini toping.
AB tomonining tenglamasini topamiz: ; 4x = 6y – 6;
2x – 3y + 3 = 0;
Kerakli balandlik tenglamasi quyidagi shaklga ega: Ax + By + C = 0 yoki y = kx + b.
k=. Keyin y =. Chunki balandlik C nuqtadan o'tadi, u holda uning koordinatalari bu tenglikni qanoatlantiradi: bu erdan b = 17. Jami: .
Javob: 3x + 2y – 34 = 0.
Nuqtadan chiziqgacha bo'lgan masofa nuqtadan chiziqqa chizilgan perpendikulyar uzunligi bilan aniqlanadi.
Agar chiziq proyeksiya tekisligiga parallel bo'lsa (h | | P 1), keyin nuqtadan masofani aniqlash uchun A to'g'ri chiziqqa h nuqtadan perpendikulyarni tushirish kerak A gorizontalga h.
To'g'ri chiziq umumiy pozitsiyani egallaganida, yanada murakkab misolni ko'rib chiqaylik. Bir nuqtadan masofani aniqlash kerak bo'lsin M to'g'ri chiziqqa A umumiy pozitsiya.
Aniqlash vazifasi parallel chiziqlar orasidagi masofalar oldingisiga o'xshash tarzda hal qilinadi. Bir chiziqdan nuqta olinadi va undan boshqa chiziqqa perpendikulyar tushiriladi. Perpendikulyarning uzunligi parallel chiziqlar orasidagi masofaga teng.
Ikkinchi tartibli egri chiziq joriy Dekart koordinatalariga nisbatan ikkinchi darajali tenglama bilan aniqlangan chiziq. Umumiy holatda, Ax 2 + 2Bxy + Su 2 + 2Dx + 2Ey + F = 0,
bu yerda A, B, C, D, E, F haqiqiy sonlar va A 2 + B 2 + C 2 ≠0 raqamlaridan kamida bittasi.
Doira
Doira markazi– bu C(a,b) tekislikdagi nuqtadan teng masofada joylashgan tekislikdagi nuqtalarning geometrik joylashuvi.
Doira quyidagi tenglama bilan berilgan:
Bu yerda x,y aylanadagi ixtiyoriy nuqtaning koordinatalari, R aylananing radiusi.
Doira tenglamasining belgisi
1. X, y bilan atama mavjud emas
2. x 2 va y 2 uchun koeffitsientlar teng
Ellips
Ellips tekislikdagi nuqtalarning geometrik joylashuvi deyiladi, ularning har birining shu tekislikning berilgan ikkita nuqtasidan masofalari yig'indisi fokuslar (doimiy qiymat) deb ataladi.
Ellipsning kanonik tenglamasi:
X va y ellipsga tegishli.
a - ellipsning yarim katta o'qi
b - ellipsning yarim kichik o'qi
Ellips 2 simmetriya o'qiga ega OX va OU. Ellipsning simmetriya o'qlari uning o'qlari, ularning kesishish nuqtasi ellipsning markazidir. Fokuslar joylashgan o'q deyiladi fokus o'qi. Ellipsning o'qlari bilan kesishish nuqtasi ellipsning cho'qqisidir.
Siqish (kuchlanish) nisbati: e = s/a– ekssentriklik (ellips shaklini xarakterlaydi), u qanchalik kichik bo'lsa, ellips fokus o'qi bo'ylab kamroq cho'ziladi.
Agar ellipsning markazlari C(a, b) markazda bo'lmasa.

Giperbola
Giperbola tekislikdagi nuqtalarning geometrik joylashuvi deyiladi, masofalar farqining mutlaq qiymati, bu tekislikning ikkita berilgan nuqtasidan, fokuslar deb ataladigan har biri noldan farq qiladigan doimiy qiymatdir.
Kanonik giperbola tenglamasi
Giperbolada ikkita simmetriya o'qi mavjud:
a - simmetriyaning haqiqiy yarim o'qi
b – simmetriyaning xayoliy yarim o'qi
Giperbolaning asimptotalari:

Parabola
Parabola fokus deb ataladigan ma'lum F nuqtadan va direktrisa deb ataladigan to'g'ri chiziqdan teng masofada joylashgan tekislikdagi nuqtalarning joylashuvi.
Parabolaning kanonik tenglamasi:
U 2 =2rx, bu erda r - fokusdan direktrisagacha bo'lgan masofa (parabola parametri)
Agar parabolaning tepasi C (a, b) bo'lsa, parabolaning tenglamasi (y-b) 2 = 2r(x-a) bo'ladi.
Agar ordinata o'qi sifatida fokus o'qi olinsa, u holda parabola tenglamasi quyidagi ko'rinishga ega bo'ladi: x 2 =2qu.
Keling, misollar yordamida ikkita nuqtadan o'tuvchi chiziq uchun tenglamani qanday yaratishni ko'rib chiqaylik.
1-misol.
A(-3; 9) va B(2;-1) nuqtalardan o‘tuvchi to‘g‘ri chiziq tenglamasini yozing.
1-usul - burchak koeffitsienti bilan to'g'ri chiziq tenglamasini yaratish.
Burchak koeffitsientli to'g'ri chiziq tenglamasi shaklga ega. A va B nuqtalarning koordinatalarini to‘g‘ri chiziq tenglamasiga qo‘yib (x= -3 va y=9 - birinchi holatda, x=2 va y= -1 - ikkinchi holatda) tenglamalar sistemasiga ega bo‘lamiz. undan k va b qiymatlarini topamiz:
1 va 2- tenglamalarni a’zolar bo’yicha qo’shsak: -10=5k, shundan k= -2 hosil bo’ladi. Ikkinchi tenglamaga k= -2 qo‘yib, b ni topamiz: -1=2·(-2)+b, b=3.
Shunday qilib, y= -2x+3 kerakli tenglama hisoblanadi.
2-usul – to‘g‘ri chiziqning umumiy tenglamasini tuzamiz.
To'g'ri chiziqning umumiy tenglamasi ko'rinishga ega. A va B nuqtalarining koordinatalarini tenglamaga qo'yib, biz tizimni olamiz:
Noma'lumlar soni tenglamalar sonidan ko'p bo'lganligi sababli, tizim echilishi mumkin emas. Lekin barcha o'zgaruvchilar bitta orqali ifodalanishi mumkin. Masalan, b orqali.
Tizimning birinchi tenglamasini -1 ga ko'paytirish va ikkinchisi bilan hadlarni qo'shish orqali:
olamiz: 5a-10b=0. Demak, a=2b.
Olingan ifodani ikkinchi tenglamaga almashtiramiz: 2·2b -b+c=0; 3b+c=0; c= -3b.
ax+by+c=0 tenglamasiga a=2b, c= -3b almashtiring:
2bx+by-3b=0. Ikkala tomonni b ga bo'lish qoladi:
To'g'ri chiziqning umumiy tenglamasini burchak koeffitsientli to'g'ri chiziq tenglamasiga osongina keltirish mumkin:
3-usul - 2 nuqtadan o'tuvchi to'g'ri chiziq tenglamasini tuzing.
Ikki nuqtadan o'tuvchi chiziq tenglamasi:
![]()
Bu tenglamaga A(-3; 9) va B(2;-1) nuqtalarning koordinatalarini qo‘yaylik.
(ya'ni, x 1 = -3, y 1 =9, x 2 =2, y 2 = -1):
![]()
va soddalashtiring:
bundan 2x+y-3=0.
Maktab kurslarida burchak koeffitsienti bilan to'g'ri chiziq tenglamasi ko'pincha ishlatiladi. Lekin eng oson yo'li ikki nuqtadan o'tuvchi chiziq tenglamasi formulasini olish va ishlatishdir.
Izoh.
Agar berilgan nuqtalarning koordinatalarini almashtirganda, tenglamaning maxrajlaridan biri
![]()
nolga teng bo'lib chiqadi, keyin mos keladigan payni nolga tenglashtirish orqali kerakli tenglama olinadi.
2-misol.
Ikkita C(5; -2) va D(7;-2) nuqtalardan o‘tuvchi to‘g‘ri chiziq tenglamasini yozing.
C va D nuqtalarning koordinatalarini 2 nuqtadan o'tuvchi to'g'ri chiziq tenglamasiga almashtiramiz.
Ikki ball berilsin M(X 1 ,U 1) va N(X 2,y 2). Shu nuqtalardan o‘tuvchi chiziq tenglamasini topamiz.
Chunki bu chiziq nuqtadan o'tadi M, keyin (1.13) formulaga muvofiq uning tenglamasi shaklga ega
U – Y 1 = K(X–x 1),
Qayerda K- noma'lum burchak koeffitsienti.
Ushbu koeffitsientning qiymati kerakli to'g'ri chiziq nuqtadan o'tishi sharti bilan aniqlanadi N, ya'ni uning koordinatalari (1.13) tenglamani qanoatlantiradi.
Y 2 – Y 1 = K(X 2 – X 1),
Bu yerdan siz ushbu chiziqning qiyaligini topishingiz mumkin:
![]() ,
,
Yoki konvertatsiya qilinganidan keyin
![]() (1.14)
(1.14)
Formula (1.14) aniqlaydi Ikki nuqtadan o'tuvchi chiziq tenglamasi M(X 1, Y 1) va N(X 2, Y 2).
Maxsus holatda, ballar M(A, 0), N(0, B), A ¹ 0, B¹ 0, koordinata o'qlarida yotadi, (1.14) tenglama oddiyroq shaklga ega bo'ladi
Tenglama (1.15) chaqirdi To'g'ri chiziqning segmentlardagi tenglamasi, Bu yerga A Va B o'qlarda to'g'ri chiziq bilan kesilgan segmentlarni belgilang (1.6-rasm).

1.6-rasm
1.10-misol. Nuqtalardan o‘tuvchi chiziq tenglamasini yozing M(1, 2) va B(3, –1).
. (1.14) ga binoan, kerakli chiziqning tenglamasi shaklga ega
![]()
2(Y – 2) = -3(X – 1).
Barcha shartlarni chap tomonga o'tkazib, biz nihoyat kerakli tenglamani olamiz
3X + 2Y – 7 = 0.
1.11-misol. Nuqtadan o`tuvchi chiziq tenglamasini yozing M(2, 1) va chiziqlarning kesishish nuqtasi X+ Y - 1 = 0, X - y+ 2 = 0.
. Ushbu tenglamalarni birgalikda yechish orqali chiziqlarning kesishish nuqtasining koordinatalarini topamiz
Agar bu tenglamalarni had bo'yicha qo'shsak, biz 2 ni olamiz X+ 1 = 0, qaerdan. Topilgan qiymatni istalgan tenglamaga almashtirib, ordinataning qiymatini topamiz U:
Endi (2, 1) nuqtalardan o'tuvchi to'g'ri chiziq tenglamasini yozamiz va:
 yoki .
yoki .
Demak yoki -5( Y – 1) = X – 2.
Biz nihoyat shaklda kerakli chiziq tenglamasini olamiz X + 5Y – 7 = 0.
1.12-misol. Nuqtalardan o‘tuvchi chiziq tenglamasini toping M(2.1) va N(2,3).
(1.14) formuladan foydalanib, biz tenglamani olamiz
Bu mantiqiy emas, chunki ikkinchi maxraj nolga teng. Masala shartlaridan ko`rinib turibdiki, ikkala nuqtaning abssissalari bir xil qiymatga ega. Bu shuni anglatadiki, kerakli to'g'ri chiziq o'qga parallel OY va uning tenglamasi: x = 2.
Izoh . Agar (1.14) formuladan foydalanib chiziq tenglamasini yozishda maxrajlardan biri nolga teng bo'lib chiqsa, kerakli tenglamani mos keladigan payni nolga tenglashtirish orqali olish mumkin.
Keling, tekislikda chiziqni aniqlashning boshqa usullarini ko'rib chiqaylik.
1. Nolga teng bo'lmagan vektor berilgan chiziqqa perpendikulyar bo'lsin L, va nuqta M 0(X 0, Y 0) shu chiziqda yotadi (1.7-rasm).

1.7-rasm
belgilaylik M(X, Y) chiziqning istalgan nuqtasi L. Vektorlar va ![]() Ortogonal. Ushbu vektorlarning ortogonallik shartlaridan foydalanib, biz yoki A(X – X 0) + B(Y – Y 0) = 0.
Ortogonal. Ushbu vektorlarning ortogonallik shartlaridan foydalanib, biz yoki A(X – X 0) + B(Y – Y 0) = 0.
Biz nuqtadan o'tuvchi chiziq tenglamasini oldik M 0 vektorga perpendikulyar. Bu vektor deyiladi Oddiy vektor to'g'ri chiziqqa L. Olingan tenglamani quyidagicha qayta yozish mumkin
Oh + Vu + BILAN= 0, bu erda BILAN = –(AX 0 + tomonidan 0), (1.16),
Qayerda A Va IN– normal vektorning koordinatalari.
Chiziqning umumiy tenglamasini parametrik shaklda olamiz.
2. Tekislikdagi to'g'ri chiziqni quyidagicha aniqlash mumkin: nolga teng bo'lmagan vektor berilgan to'g'ri chiziqqa parallel bo'lsin. L va davr M 0(X 0, Y 0) bu chiziqda yotadi. Keling, yana bir ixtiyoriy nuqtani olaylik M(X, y) to‘g‘ri chiziqda (1.8-rasm).

1.8-rasm
Vektorlar va ![]() kollinear.
kollinear.
Bu vektorlarning kollinearlik shartini yozamiz: , bu yerda T– parametr deb ataladigan ixtiyoriy raqam. Bu tenglikni koordinatalarda yozamiz:
Bu tenglamalar deyiladi Parametrik tenglamalar Streyt. Ushbu tenglamalardan parametrni istisno qilaylik T:
Bu tenglamalar boshqa shaklda yozilishi mumkin
![]() . (1.18)
. (1.18)
Olingan tenglama deyiladi Chiziqning kanonik tenglamasi. Vektor deyiladi Yo'naltiruvchi vektor to'g'ri .
Izoh . If chiziqning normal vektori ekanligini ko'rish oson L, keyin uning yo'nalishi vektori beri vektor bo'lishi mumkin, ya'ni.
1.13-misol. Nuqtadan o`tuvchi chiziq tenglamasini yozing M 0(1, 1) 3-qatorga parallel X + 2U– 8 = 0.
Yechim . Vektor berilgan va kerakli chiziqlarning normal vektoridir. Nuqtadan o`tuvchi to`g`ri chiziq tenglamasidan foydalanamiz M 0 berilgan normal vektor 3( X –1) + 2(U– 1) = 0 yoki 3 X + 2u– 5 = 0. Biz kerakli chiziqning tenglamasini oldik.