Segmentdagi eng katta va eng kichikning yechimini tekshiring. Funktsiyaning eng katta va eng kichik qiymati. B15 vazifa (2014)

Keling, grafik yordamida funktsiyani qanday o'rganishni ko'rib chiqaylik. Ma'lum bo'lishicha, grafikaga qarab, bizni qiziqtirgan hamma narsani bilib olishingiz mumkin, xususan:

• funksiya doirasi
• funktsiya diapazoni
• funktsiya nollari
• ortish va pasayish davrlari
• yuqori va past nuqtalar
• segmentdagi funksiyaning eng katta va eng kichik qiymati.

Keling, terminologiyaga aniqlik kiritaylik:

Absissa nuqtaning gorizontal koordinatasi hisoblanadi.
Ordinatsiya qilish- vertikal koordinata.
abscissa- ko'pincha eksa deb ataladigan gorizontal o'q.
Y o'qi - vertikal o'q, yoki eksa.

Dalil funktsiya qiymatlari bog'liq bo'lgan mustaqil o'zgaruvchidir. Ko'pincha ko'rsatilgan.
Boshqacha qilib aytganda, biz o'zimiz tanlaymiz, funktsiya formulasida o'rniga qo'yamiz va ni olamiz.

Domen funktsiyalar - bu funktsiya mavjud bo'lgan argumentning o'sha (va faqat o'sha) qiymatlari to'plami.
Belgilangan: yoki .

Bizning rasmimizda funksiya sohasi segmentdir. Aynan shu segmentda funksiya grafigi chiziladi. Faqat shu yerda berilgan funksiya mavjud.

Funktsiya diapazoni o'zgaruvchi qabul qiladigan qiymatlar to'plamidir. Bizning rasmimizda bu segment - eng pastdan eng yuqori qiymatgacha.

Funktsiya nollari- funksiyaning qiymati nolga teng bo'lgan nuqtalar, ya'ni. Bizning rasmimizda bu nuqtalar va .

Funktsiya qiymatlari ijobiy qayerda. Bizning rasmimizda bu intervallar va .
Funktsiya qiymatlari salbiy qayerda. Bizda bu interval (yoki interval) dan to.

Eng muhim tushunchalar - oshirish va kamaytirish funktsiyalari ba'zi to'plamda. To'plam sifatida siz segment, interval, intervallar birlashmasi yoki butun son chizig'ini olishingiz mumkin.

Funktsiya ortadi

Boshqacha qilib aytganda, qancha ko'p , shuncha ko'p , ya'ni grafik o'ngga va yuqoriga boradi.

Funktsiya kamayadi to'plamda agar mavjud bo'lsa va to'plamga tegishli bo'lgan tengsizlik tengsizlikni bildiradi.

Kamayuvchi funktsiya uchun kattaroq qiymat kichikroq qiymatga mos keladi. Grafik o'ngga va pastga tushadi.

Bizning rasmimizda funktsiya oraliqda ortib boradi va intervallarda kamayadi.

Keling, nima ekanligini aniqlaylik funktsiyaning maksimal va minimal nuqtalari.

Maksimal nuqta- bu ta'rif sohasining ichki nuqtasi bo'lib, undagi funktsiyaning qiymati unga etarlicha yaqin bo'lgan barcha nuqtalardan kattaroqdir.
Boshqacha qilib aytadigan bo'lsak, maksimal nuqta - bunday nuqta, funksiyaning qiymati Ko'proq qo'shnilarga qaraganda. Bu grafikdagi mahalliy "tepalik".

Bizning rasmimizda - maksimal nuqta.

Past nuqta- ta'rif sohasining ichki nuqtasi, undagi funksiya qiymati unga etarlicha yaqin bo'lgan barcha nuqtalardan kichik bo'ladi.
Ya'ni, minimal nuqta shundayki, undagi funktsiyaning qiymati qo'shnilariga qaraganda kamroq. Grafikda bu mahalliy "teshik".

Bizning rasmimizda - minimal nuqta.

Nuqta - bu chegara. Bu ta'rif sohasining ichki nuqtasi emas va shuning uchun maksimal nuqta ta'rifiga mos kelmaydi. Axir, uning chap tomonida qo'shnilari yo'q. Xuddi shu tarzda, bizning jadvalimizda minimal nuqta bo'lishi mumkin emas.

Maksimal va minimal ballar birgalikda chaqiriladi funktsiyaning ekstremal nuqtalari. Bizning holatlarimizda bu va .

Ammo, masalan, topish kerak bo'lsa-chi funktsiya minimal kesmada? DA bu holat javob: . chunki funktsiya minimal uning minimal nuqtadagi qiymati.

Xuddi shunday, bizning funktsiyamizning maksimal qiymati . Bu nuqtada erishiladi.

Funksiyaning ekstremallari va ga teng, deyishimiz mumkin.

Ba'zan vazifalarda siz topishingiz kerak funktsiyaning eng katta va eng kichik qiymatlari ma'lum bir segmentda. Ular ekstremal holatlarga to'g'ri kelishi shart emas.

Bizning holatda eng kichik funktsiya qiymati oraliqda funktsiyaning minimaliga teng va mos keladi. Lekin uning ushbu segmentdagi eng katta qiymati ga teng. U segmentning chap uchida joylashgan.

Qanday bo'lmasin, segmentdagi uzluksiz funktsiyaning eng katta va eng kichik qiymatlari ekstremal nuqtalarda yoki segmentning uchlarida erishiladi.

mayda va chiroyli oddiy vazifa suzuvchi talaba uchun hayot chizig'i bo'lib xizmat qiladiganlar toifasidan. Tabiatda, iyul oyining o'rtalarida uyqusiragan shohlik, shuning uchun plyajda noutbuk bilan joylashish vaqti keldi. Erta tongda nazariyaning quyosh nuri tez orada amaliyotga e'tibor qaratish uchun o'ynay boshladi, uning engilligiga qaramay, qumda shisha bo'laklari bor. Shu munosabat bilan men ushbu sahifaning bir nechta misollarini vijdonan ko'rib chiqishni tavsiya qilaman. Amaliy vazifalarni hal qilish uchun siz qobiliyatga ega bo'lishingiz kerak hosilalarni toping va maqolaning materialini tushuning Funksiyaning monotonlik va ekstremallik intervallari.

Birinchidan, asosiy narsa haqida qisqacha. haqida darsda funksiya uzluksizligi Men nuqtadagi uzluksizlik va intervaldagi uzluksizlik ta'rifini berdim. Segmentdagi funksiyaning namunali xatti-harakati xuddi shunday shakllantirilgan. Funktsiya segmentda uzluksiz bo'ladi, agar:

1) intervalda uzluksiz;
2) bir nuqtada uzluksiz o'ngda va nuqtada chap.

Ikkinchi xatboshi deb atalmish bilan bog'liq bir tomonlama davomiylik bir nuqtada ishlaydi. Uning ta'rifiga bir nechta yondashuvlar mavjud, ammo men ilgari boshlangan chiziqqa sodiq qolaman:

Funktsiya bir nuqtada uzluksizdir o'ngda, agar u berilgan nuqtada aniqlangan boʻlsa va uning oʻng chegarasi berilgan nuqtadagi funksiya qiymatiga toʻgʻri kelsa: . U nuqtada uzluksizdir chap, agar ma'lum bir nuqtada aniqlangan bo'lsa va uning chap chegarasi ushbu nuqtadagi qiymatga teng bo'lsa:

Tasavvur qiling-a, yashil nuqtalar sehrli kauchuk bog'langan mixlardir:

Qo'lingizda qizil chiziqni aqliy ravishda oling. Shubhasiz, biz grafikni qanchalik yuqoriga va pastga (o'q bo'ylab) cho'zmasak ham, funktsiya saqlanib qoladi. cheklangan- tepada to'siq, pastda to'siq va mahsulotimiz maydonchada o'tlanadi. Shunday qilib, segmentda uzluksiz funksiya unga chegaralangan. Matematik tahlil jarayonida oddiy ko'rinadigan bu haqiqat aytiladi va qat'iy isbotlanadi Veyershtrasning birinchi teoremasi.... Ko'pchilik matematikada elementar gaplar zerikarli asoslanayotganidan g'azablanadi, ammo bu muhim ma'noga ega. Aytaylik, terri o'rta asrlarining ma'lum bir aholisi grafikni osmonga ko'rish chegarasidan tashqariga tortdi, bu kiritilgan. Teleskop ixtiro qilinishidan oldin, kosmosdagi cheklangan funktsiya umuman aniq emas edi! Darhaqiqat, bizni ufqdan tashqarida nima kutayotganini qayerdan bilasiz? Axir, bir paytlar Yer tekis hisoblangan, shuning uchun bugungi kunda oddiy teleportatsiya ham isbot talab qiladi =)

Ga binoan ikkinchi Veyershtras teoremasi, segmentda uzluksizfunktsiya o'z darajasiga etadi aniq yuqori chekka va uning aniq pastki chet .

Raqam ham chaqiriladi segmentdagi funksiyaning maksimal qiymati va bilan belgilanadi, va raqam - segmentdagi funksiyaning minimal qiymati belgilangan.

Bizning holatda:

Eslatma : nazariy jihatdan, yozuvlar keng tarqalgan .

Qo'pol qilib aytganda, eng yuqori qiymat grafikning eng yuqori nuqtasi, eng kichigi esa eng past nuqtasi joylashgan joyda joylashgan.

Muhim! Maqolada allaqachon ta'kidlanganidek funktsiyaning ekstremal qismi, funktsiyaning eng katta qiymati va eng kichik funktsiya qiymati – BIR XIL EMAS, nima maksimal funktsiya va funktsiya minimal. Shunday qilib, bu misolda raqam funktsiyaning minimal qiymatidir, lekin minimal qiymat emas.

Aytgancha, segmentdan tashqarida nima sodir bo'ladi? Ha, hatto toshqin ham, ko'rib chiqilayotgan muammo kontekstida bu bizni umuman qiziqtirmaydi. Vazifa faqat ikkita raqamni topishni o'z ichiga oladi va tamom!

Bundan tashqari, yechim faqat analitikdir, shuning uchun chizish kerak emas!

Algoritm sirtda yotadi va yuqoridagi rasmdan o'zini ko'rsatadi:

1) Funktsiya qiymatlarini toping tanqidiy nuqtalar, bu segmentga tegishli.

Yana bir yaxshilikni qo'lga kiriting: ekstremum uchun etarli holatni tekshirishning hojati yo'q, chunki hozirgina ko'rsatilganidek, minimal yoki maksimal mavjudligi hali kafolatlanmagan minimal yoki maksimal qiymat nima. Namoyish funktsiyasi maksimal darajaga etadi va taqdirning irodasiga ko'ra, bir xil raqam intervaldagi funktsiyaning eng katta qiymati hisoblanadi. Lekin, albatta, bunday tasodif har doim ham sodir bo'lavermaydi.

Shunday qilib, birinchi bosqichda segmentga tegishli kritik nuqtalarda funktsiya qiymatlarini ekstremal yoki yo'qligini bezovta qilmasdan hisoblash tezroq va osonroq bo'ladi.

2) Biz segmentning oxiridagi funktsiya qiymatlarini hisoblaymiz.

3) 1 va 2-bandlarda joylashgan funktsiya qiymatlari orasida biz eng kichik va eng ko'p narsani tanlaymiz. katta raqam, javobni yozing.

Biz ko'k dengiz qirg'og'ida o'tirib, sayoz suvda tovonlarga uramiz:

1-misol

Segmentdagi funksiyaning eng katta va eng kichik qiymatlarini toping

Qaror:
1) Ushbu segmentga tegishli kritik nuqtalarda funktsiyaning qiymatlarini hisoblang:

Ikkinchi kritik nuqtada funksiyaning qiymatini hisoblaymiz:

2) Segment oxiridagi funksiya qiymatlarini hisoblang:

3) "Yog'li" natijalar ko'rsatkichlar va logarifmlar bilan olingan, bu ularni solishtirishni sezilarli darajada murakkablashtiradi. Shuning uchun biz kalkulyator yoki Excel bilan qurollanamiz va taxminiy qiymatlarni hisoblab chiqamiz, buni unutmasdan:

Endi hamma narsa aniq.

Javob:

uchun kasr-ratsional misol mustaqil qaror:

6-misol

Maksimalni toping va minimal qiymat segmentdagi funktsiyalar

Segmentdagi funktsiyaning eng kichik va eng katta qiymatlarini topish jarayoni vertolyotda ob'ekt atrofida (funktsiya grafigi) ma'lum nuqtalarda uzoq masofali to'pdan o'q otish va ulardan birini tanlash bilan qiziqarli parvozni eslatadi. bu nuqtalar nazorat zarbalari uchun juda maxsus nuqtalar. Ballar ma'lum bir tarzda va ma'lum qoidalarga muvofiq tanlanadi. Qaysi qoidalar bilan? Bu haqda keyinroq gaplashamiz.

Agar funktsiya y = f(x) segmentda uzluksiz [ a, b] boʻlsa, u bu segmentga yetib boradi kamida va eng yuqori qiymatlar . Bu ham sodir bo'lishi mumkin ekstremal nuqtalar yoki segmentning oxirida. Shuning uchun, topish uchun kamida va funksiyaning eng katta qiymatlari , segmentda uzluksiz [ a, b] , siz uning barcha qiymatlarini hisoblashingiz kerak tanqidiy nuqtalar va segmentning uchlarida, so'ngra ulardan eng kichikini va eng kattasini tanlang.

Masalan, funktsiyaning maksimal qiymatini aniqlash talab qilinsin f(x) segmentida [ a, b]. Buni amalga oshirish uchun uning barcha kritik nuqtalarini [ ustida joylashganini toping. a, b] .

tanqidiy nuqta nuqta deb ataladi funksiya aniqlangan, va u hosila nolga teng yoki mavjud emas. Keyin kritik nuqtalarda funktsiyaning qiymatlarini hisoblashingiz kerak. Va nihoyat, kritik nuqtalarda va segmentning oxirida funksiya qiymatlarini solishtirish kerak ( f(a) va f(b)). Bu raqamlarning eng kattasi bo'ladi segmentdagi funksiyaning eng katta qiymati [a, b] .

Topish muammosi funktsiyaning eng kichik qiymatlari .

Biz birgalikda funktsiyaning eng kichik va eng katta qiymatlarini qidiramiz

Misol 1. Funktsiyaning eng kichik va eng katta qiymatlarini toping segmentida [-1, 2] .

Qaror. Bu funksiyaning hosilasini topamiz. Hosilni nolga () tenglashtiring va ikkita kritik nuqtani oling: va . Berilgan segmentdagi funktsiyaning eng kichik va eng katta qiymatlarini topish uchun uning segment uchlari va nuqtadagi qiymatlarini hisoblash kifoya qiladi, chunki nuqta segmentga tegishli emas [-1, 2] . Bu funksiya qiymatlari quyidagilardan iborat: , , . Bundan kelib chiqadi eng kichik funktsiya qiymati(quyidagi grafikda qizil rang bilan belgilangan), -7 ga teng, segmentning o'ng uchida - nuqtada erishiladi va eng buyuk(shuningdek, grafikda qizil), 9 ga teng, - kritik nuqtada .

Agar funktsiya ma'lum bir oraliqda uzluksiz bo'lsa va bu oraliq segment bo'lmasa (lekin, masalan, interval bo'lsa; oraliq va segment o'rtasidagi farq: intervalning chegara nuqtalari intervalga kiritilmaydi, lekin segmentning chegara nuqtalari segmentga kiritilgan), keyin funktsiya qiymatlari orasida eng kichik va eng katta bo'lmasligi mumkin. Masalan, quyidagi rasmda tasvirlangan funksiya ]-∞, +∞[ da uzluksiz va eng katta qiymatga ega emas.

Biroq, har qanday oraliq uchun (yopiq, ochiq yoki cheksiz) uzluksiz funktsiyalarning quyidagi xossasi amal qiladi.

4-misol. Funktsiyaning eng kichik va eng katta qiymatlarini toping segmentida [-1, 3] .

Qaror. Bu funksiyaning hosilasini qismning hosilasi sifatida topamiz:

.

Biz lotinni nolga tenglashtiramiz, bu bizga bitta muhim nuqtani beradi: . U [-1, 3] oraliqlariga tegishli. Berilgan segmentdagi funktsiyaning eng kichik va eng katta qiymatlarini topish uchun biz uning qiymatlarini segmentning oxirida va topilgan kritik nuqtada topamiz:

Keling, ushbu qiymatlarni taqqoslaylik. Xulosa: -5/13 ga teng, nuqtada va eng katta qiymat nuqtada 1 ga teng.

Biz birgalikda funktsiyaning eng kichik va eng katta qiymatlarini qidirishda davom etamiz

Shunday o'qituvchilar borki, ular funktsiyaning eng kichik va eng katta qiymatlarini topish mavzusida talabalarga ko'rib chiqilganlardan murakkabroq misollar keltirmaydilar, ya'ni funktsiya polinom yoki kasr, numerator bo'lgan misollar. va maxraji ko'phadlardir. Ammo biz bunday misollar bilan cheklanib qolmaymiz, chunki o'qituvchilar orasida talabalarni to'liq fikrlashga majbur qilishni yaxshi ko'radiganlar bor (hosilalar jadvali). Shuning uchun logarifm va trigonometrik funktsiyadan foydalaniladi.

Misol 6. Funktsiyaning eng kichik va eng katta qiymatlarini toping segmentida .

Qaror. Bu funksiyaning hosilasini quyidagicha topamiz mahsulotning hosilasi :

Biz lotinni nolga tenglashtiramiz, bu bitta kritik nuqtani beradi: . Bu segmentga tegishli. Berilgan segmentdagi funktsiyaning eng kichik va eng katta qiymatlarini topish uchun biz uning qiymatlarini segmentning oxirida va topilgan kritik nuqtada topamiz:

Barcha harakatlar natijasi: funktsiya minimal qiymatiga etadi, 0 ga teng, nuqtada va nuqtada va eng katta qiymat ga teng e², nuqtada.

Misol 7. Funktsiyaning eng kichik va eng katta qiymatlarini toping segmentida .

Qaror. Ushbu funktsiyaning hosilasini topamiz:

Hosilni nolga tenglashtiring:

Faqatgina muhim nuqta segmentga tegishli. Berilgan segmentdagi funktsiyaning eng kichik va eng katta qiymatlarini topish uchun biz uning qiymatlarini segmentning oxirida va topilgan kritik nuqtada topamiz:

Xulosa: funktsiya minimal qiymatiga etadi, ga teng, nuqtada va eng katta qiymat, ga teng, nuqtada.

Amaliy ekstremal masalalarda funktsiyaning eng kichik (eng katta) qiymatlarini topish, qoida tariqasida, minimal (maksimal) ni topishga to'g'ri keladi. Ammo minimal yoki maksimallarning o'zlari emas, balki ularga erishiladigan dalillarning qadriyatlari ko'proq amaliy qiziqish uyg'otadi. Amaliy muammolarni hal qilishda qo'shimcha qiyinchilik paydo bo'ladi - ko'rib chiqilayotgan hodisa yoki jarayonni tavsiflovchi funktsiyalarni kompilyatsiya qilish.

8-misol To'rtburchak asosli parallelepiped shakliga ega va tepasi ochiq bo'lgan sig'imi 4 bo'lgan tank konservalangan bo'lishi kerak. Eng kam miqdordagi material bilan qoplash uchun tankning o'lchamlari qanday bo'lishi kerak?

Qaror. Bo'lsin x- tayanch tomoni h- tank balandligi, S- qoplamasiz sirt maydoni; V- uning hajmi. Tankning sirt maydoni formula bilan ifodalanadi, ya'ni. ikki o‘zgaruvchining funksiyasi. ifodalash uchun S bitta o'zgaruvchining funksiyasi sifatida biz , qaerdan ekanligini ishlatamiz. Topilgan ifodani almashtirish h uchun formulaga kiradi S:

Keling, bu funktsiyani ekstremum uchun ko'rib chiqaylik. U hamma joyda ]0, +∞[ va da aniqlangan va farqlanadi

.

Biz hosilani nolga () tenglashtiramiz va kritik nuqtani topamiz. Bundan tashqari, da, hosilasi mavjud emas, lekin bu qiymat ta'rif sohasiga kiritilmagan va shuning uchun ekstremum nuqta bo'la olmaydi. Shunday qilib, - yagona tanqidiy nuqta. Keling, ikkinchisi yordamida ekstremum mavjudligini tekshirib ko'raylik etarli belgi. Ikkinchi hosilani topamiz. Ikkinchi hosila noldan katta bo'lganda (). Bu funktsiya minimal darajaga yetganda, degan ma'noni anglatadi . Chunki bu minimal - bu funktsiyaning yagona ekstremumi, bu uning eng kichik qiymati. Shunday qilib, tankning poydevorining yon tomoni 2 m ga teng bo'lishi kerak va uning balandligi.

9-misol Paragrafdan A, temir yo'l liniyasida joylashgan, nuqtaga Bilan, undan uzoqda l, tovarlarni tashish kerak. Og'irlik birligini temir yo'l transportida masofa birligida tashish narxi teng, avtomobil yo'lida esa teng. Qaysi nuqtaga M chiziqlar temir yo'l dan yuk tashish uchun avtomobil yo'li qurilishi kerak LEKIN ichida Bilan eng tejamkor edi AB temir yo'l to'g'ri deb taxmin qilinadi)?

Amalda, funktsiyaning eng katta va eng kichik qiymatini hisoblash uchun hosiladan foydalanish juda keng tarqalgan. Xarajatlarni minimallashtirish, foydani ko'paytirish va hisoblashni aniqlaganimizda biz ushbu amalni bajaramiz optimal yuk ishlab chiqarish uchun va hokazo, ya'ni aniqlash zarur bo'lgan hollarda optimal qiymat har qanday parametr. Bunday masalalarni to'g'ri hal qilish uchun funktsiyaning eng katta va eng kichik qiymati nima ekanligini yaxshi tushunish kerak.

Yandex.RTB R-A-339285-1

Odatda biz bu qiymatlarni x oralig'ida aniqlaymiz, bu esa o'z navbatida funktsiyaning butun doirasiga yoki uning bir qismiga mos kelishi mumkin. Bu segment bo'lishi mumkin [ a ; b ] , va ochiq interval (a ; b) , (a ; b ] , [ a ; b) , cheksiz interval (a ; b) , (a ; b ] , [ a ; b) yoki cheksiz interval - ∞ ; a , (- ∞ ; a ] , [ a ; + ∞) , (- ∞ ; + ∞) .

Ushbu maqolada biz eng katta va eng kichik qiymatlar qanday aniq hisoblanganligini tushuntiramiz. berilgan funksiya bitta o'zgaruvchi bilan y=f(x) y = f (x) .

Asosiy ta'riflar

Biz, har doimgidek, asosiy ta'riflarni shakllantirishdan boshlaymiz.

Ta'rif 1

y = f (x) funktsiyaning qaysidir x oralig'idagi eng katta qiymati m a x y = f (x 0) x ∈ X qiymati bo'lib, har qanday x x ∈ X, x ≠ x 0 qiymati uchun f (x) tengsizlikni hosil qiladi. ) ≤ f (x 0) .

Ta'rif 2

y = f (x) funktsiyaning qaysidir x oralig'idagi eng kichik qiymati m i n x ∈ X y = f (x 0) qiymati bo'lib, har qanday x ∈ X , x ≠ x 0 qiymati uchun f(X) tengsizlikni hosil qiladi. f (x) ≥ f(x0) .

Bu ta'riflar juda aniq. Bundan ham osonroq, siz buni aytishingiz mumkin: funktsiyaning eng katta qiymati uning eng kattasidir katta ahamiyatga ega abscissa x 0 da ma'lum oraliqda, eng kichiki esa x 0 da bir xil intervalda qabul qilingan eng kichik qiymatdir.

Ta'rif 3

Statsionar nuqtalar funksiya argumentining shunday qiymatlari bo'lib, uning hosilasi 0 ga aylanadi.

Nima uchun biz statsionar nuqtalar nima ekanligini bilishimiz kerak? Bu savolga javob berish uchun Ferma teoremasini esga olishimiz kerak. Bundan kelib chiqadiki, statsionar nuqta - bu differensiallanuvchi funktsiyaning ekstremumi joylashgan nuqta (ya'ni, uning mahalliy minimumi yoki maksimali). Shunday qilib, funktsiya eng kichik yoki eng katta qiymatni ma'lum bir oraliqda statsionar nuqtalardan birida oladi.

Boshqa funktsiya eng katta yoki eng kichik qiymatni funktsiyaning o'zi aniq bo'lgan va uning birinchi hosilasi mavjud bo'lmagan nuqtalarda qabul qilishi mumkin.

Ushbu mavzuni o'rganishda birinchi savol tug'iladi: barcha holatlarda berilgan oraliqda funktsiyaning maksimal yoki minimal qiymatini aniqlay olamizmi? Yo'q, agar berilgan oraliq chegaralari ta'rif sohasi chegaralariga to'g'ri keladigan bo'lsa yoki cheksiz interval bilan ishlayotgan bo'lsak, buni qila olmaymiz. Bundan tashqari, ma'lum oraliqdagi yoki cheksizlikdagi funktsiya cheksiz kichik yoki cheksiz oladi katta qadriyatlar. Bunday hollarda eng katta va/yoki eng kichik qiymatni aniqlash mumkin emas.

Grafiklardagi tasvirdan keyin bu daqiqalar yanada tushunarli bo'ladi:

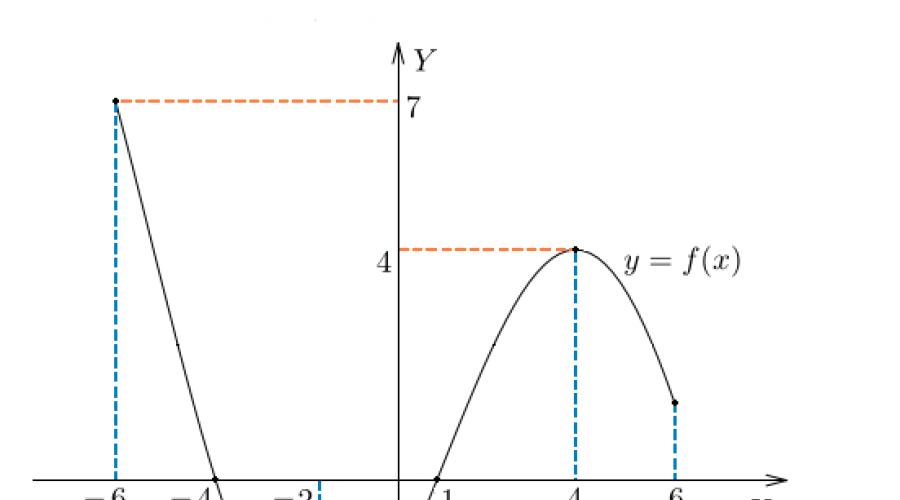
Birinchi rasm bizga [ - 6 oraliqda joylashgan statsionar nuqtalarda eng katta va eng kichik qiymatlarni (m a x y va m i n y) qabul qiluvchi funktsiyani ko'rsatadi; 6].

Keling, ikkinchi grafikda ko'rsatilgan ishni batafsil ko'rib chiqaylik. Segmentning qiymatini [ 1 ga o'zgartiramiz; 6] va biz funktsiyaning eng katta qiymatiga oraliqning o'ng chegarasida abscissa joylashgan nuqtada, eng kichiki esa statsionar nuqtada erishilishini olamiz.

Uchinchi rasmda nuqtalarning abstsissalari segmentning chegara nuqtalarini ifodalaydi [ - 3 ; 2]. Ular berilgan funksiyaning eng katta va eng kichik qiymatiga mos keladi.

Endi to'rtinchi rasmga qaraylik. Unda funksiya ochiq intervalda (- 6 ; 6) statsionar nuqtalarda m a x y (eng katta qiymat) va m i n y (eng kichik qiymat) ni oladi.

Agar [1] oraliqni olsak; 6) , u holda undagi funksiyaning eng kichik qiymatiga statsionar nuqtada erishiladi, deyishimiz mumkin. Biz maksimal qiymatni bilmaymiz. Funktsiya x = 6 intervalga tegishli bo'lsa, x 6 ga teng bo'lgan eng katta qiymatni olishi mumkin edi. Aynan shu holat 5-rasmda ko'rsatilgan.

6-chizmada bu funksiya intervalning o'ng chegarasida (- 3 ; 2 ] eng kichik qiymatga ega bo'ladi va biz eng katta qiymat haqida aniq xulosalar chiqara olmaymiz.

7-rasmda funktsiya statsionar nuqtada m a x y ga ega bo'lishini, abtsissasi 1 ga teng bo'lishini ko'ramiz. Funktsiya o'ng tarafdagi interval chegarasida minimal qiymatiga etadi. Minus cheksizlikda funksiya qiymatlari asimptotik tarzda y = 3 ga yaqinlashadi.

Agar x ∈ 2 intervalni olsak; + ∞ bo'lsa, u holda berilgan funktsiya unga eng kichik yoki eng katta qiymatni olmasligini ko'ramiz. Agar x 2 ga moyil bo'lsa, u holda funktsiyaning qiymatlari minus cheksizlikka moyil bo'ladi, chunki x = 2 to'g'ri chiziq vertikal asimptotadir. Agar abscissa plyus cheksizlikka moyil bo'lsa, u holda funktsiyaning qiymatlari asimptotik ravishda y = 3 ga yaqinlashadi. Bu 8-rasmda ko'rsatilgan holat.

Ushbu paragrafda biz ma'lum bir oraliqda funktsiyaning eng katta yoki eng kichik qiymatini topish uchun bajarilishi kerak bo'lgan harakatlar ketma-ketligini beramiz.

1. Birinchidan, funksiyaning sohasini topamiz. Shartda ko'rsatilgan segment unga kiritilgan yoki yo'qligini tekshiramiz.
2. Keling, ushbu segmentdagi birinchi hosila mavjud bo'lmagan nuqtalarni hisoblaylik. Ko'pincha ularni argumenti modul belgisi ostida yoki ichida yozilgan funktsiyalarda topish mumkin quvvat funktsiyalari, uning darajasi kasrli ratsional sondir.
3. Keyinchalik, qaysi statsionar nuqtalar berilgan segmentga tushishini aniqlaymiz. Buning uchun funktsiyaning hosilasini hisoblashingiz kerak, keyin uni 0 ga tenglashtiring va hosil bo'lgan tenglamani yeching, so'ngra tegishli ildizlarni tanlang. Agar biz bitta statsionar nuqtani olmasak yoki ular berilgan segmentga tushmasa, biz keyingi bosqichga o'tamiz.
4. Keling, funktsiya berilgan statsionar nuqtalarda (agar mavjud bo'lsa) yoki birinchi hosila mavjud bo'lmagan nuqtalarda (agar mavjud bo'lsa) qanday qiymatlarni olishini aniqlaylik yoki x = a va x uchun qiymatlarni hisoblaymiz. = b.
5. 5. Bizda funktsiya qiymatlari qatori mavjud bo'lib, ulardan endi eng kattasini va eng kichikini tanlashimiz kerak. Bu biz topishimiz kerak bo'lgan funktsiyaning eng katta va eng kichik qiymatlari bo'ladi.

Keling, muammolarni hal qilishda ushbu algoritmni qanday qilib to'g'ri qo'llashni ko'rib chiqaylik.

1-misol

Holati: y = x 3 + 4 x 2 funksiya berilgan. Uning segmentlar bo'yicha eng katta va eng kichik qiymatini aniqlang [1; 4 ] va [ - 4 ; - bir].

Qaror:

Keling, ushbu funktsiyaning domenini topishdan boshlaylik. Bunday holda, u 0 dan tashqari barcha haqiqiy sonlar to'plami bo'ladi. Boshqacha qilib aytganda, D (y) : x ∈ (- ∞ ; 0) ∪ 0 ; +∞ . Shartda ko'rsatilgan ikkala segment ham aniqlash maydoni ichida bo'ladi.

Endi kasrni differentsiallash qoidasiga ko'ra funktsiyaning hosilasini hisoblaymiz:

y "= x 3 + 4 x 2" = x 3 + 4 " x 2 - x 3 + 4 x 2" x 4 = = 3 x 2 x 2 - (x 3 - 4) 2 x x 4 = x 3 - 8 x 3

Funktsiyaning hosilasi segmentlarning barcha nuqtalarida mavjud bo'lishini bilib oldik [1; 4 ] va [ - 4 ; - bir].

Endi biz funktsiyaning statsionar nuqtalarini aniqlashimiz kerak. Buni x 3 - 8 x 3 = 0 tenglama bilan bajaramiz. Uning faqat bitta haqiqiy ildizi bor, ya'ni 2. Bu funksiyaning statsionar nuqtasi bo'ladi va birinchi segmentga tushadi [1; 4].

Keling, birinchi segmentning oxirida va berilgan nuqtada funktsiyaning qiymatlarini hisoblaylik, ya'ni. x = 1 , x = 2 va x = 4 uchun:

y(1) = 1 3 + 4 1 2 = 5 y(2) = 2 3 + 4 2 2 = 3 y(4) = 4 3 + 4 4 2 = 4 1 4

Biz funksiyaning eng katta qiymati m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 ga x = 1 da erishiladi va eng kichik m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 - x = 2 da.

Ikkinchi segment hech qanday statsionar nuqtalarni o'z ichiga olmaydi, shuning uchun biz funktsiya qiymatlarini faqat berilgan segmentning oxirida hisoblashimiz kerak:

y (- 1) = (- 1) 3 + 4 (- 1) 2 = 3

Demak, m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m i n y x ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

Javob: Segment uchun [1; 4 ] - m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 , m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 , segment uchun [ - 4 ; - 1 ] - m a x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m i n y x ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

Rasmga qarang:

O'qishdan oldin Bu yerga, biz sizga bir tomonlama chegarani va cheksizlikda chegarani qanday qilib to'g'ri hisoblashni takrorlashni maslahat beramiz, shuningdek ularni topishning asosiy usullarini o'rganamiz. Ochiq yoki cheksiz oraliqda funksiyaning eng katta va/yoki eng kichik qiymatini topish uchun biz quyidagi amallarni ketma-ket bajaramiz.

1. Avval berilgan oraliq berilgan funktsiya sohasining kichik to'plami bo'ladimi yoki yo'qligini tekshirishingiz kerak.
2. Kerakli oraliqda joylashgan va birinchi hosila mavjud bo'lmagan barcha nuqtalarni aniqlaymiz. Odatda ular argument modul belgisiga kiritilgan funksiyalar uchun va kasrli quvvat funksiyalari uchun. ratsional ko'rsatkich. Agar ushbu nuqtalar etishmayotgan bo'lsa, keyingi bosqichga o'tishingiz mumkin.
3. Endi biz qaysi statsionar nuqtalar berilgan intervalga tushishini aniqlaymiz. Birinchidan, hosilani 0 ga tenglashtiramiz, tenglamani yechib, mos ildizlarni topamiz. Agar bizda bitta statsionar nuqta bo'lmasa yoki ular berilgan intervalga tushmasa, biz darhol o'tamiz keyingi harakat. Ular interval turiga qarab belgilanadi.

• Agar interval [ a ga o'xshash bo'lsa; b) , keyin funksiyaning x = a nuqtadagi qiymatini va bir tomonlama chegara lim x → b - 0 f (x) ni hisoblashimiz kerak.
• Agar interval (a ; b ] ko'rinishga ega bo'lsa, u holda funksiyaning x = b nuqtadagi qiymatini va bir tomonlama chegara lim x → a + 0 f (x) ni hisoblashimiz kerak.
• Agar oraliq shaklga ega bo'lsa (a ; b) , u holda biz bir tomonlama chegaralarni hisoblashimiz kerak lim x → b - 0 f (x) , lim x → a + 0 f (x) .
• Agar interval [ a ga o'xshash bo'lsa; + ∞) , keyin x = a nuqtadagi qiymatni va ortiqcha cheksizlik chegarasini hisoblash kerak lim x → + ∞ f (x) .
• Agar interval (- ∞ ; b ] ga o'xshash bo'lsa, biz x = b nuqtadagi qiymatni va minus cheksizlikdagi chegarani hisoblaymiz lim x → - ∞ f (x) .
• Agar - ∞ ; b , u holda biz bir tomonlama chegara lim x → b - 0 f (x) va minus cheksizlikdagi chegarani ko'rib chiqamiz lim x → - ∞ f (x)
• Agar - ∞ ; + ∞ , keyin minus va plyus cheksizlik chegaralarini ko'rib chiqamiz lim x → + ∞ f (x) , lim x → - ∞ f (x) .

1. Oxirida siz funktsiya va chegaralarning olingan qiymatlari asosida xulosa qilishingiz kerak. Bu erda ko'plab variantlar mavjud. Demak, agar bir tomonlama chegara minus cheksizlik yoki ortiqcha cheksizlikka teng bo‘lsa, u holda funksiyaning eng kichik va eng katta qiymati haqida hech narsa deyish mumkin emasligi darhol ma’lum bo‘ladi. Quyida biz bitta odatiy misolni ko'rib chiqamiz. Batafsil tavsiflar nima ekanligini tushunishga yordam beradi. Agar kerak bo'lsa, materialning birinchi qismidagi 4 - 8 raqamlarga qaytishingiz mumkin.

Shart: y = 3 e 1 x 2 + x - 6 - 4 funksiya berilgan. Uning eng katta va eng kichik qiymatini intervallarda hisoblang - ∞ ; - 4 , - ∞ ; - 3 , (- 3 ; 1 ] , (- 3 ; 2) , [ 1 ; 2) , 2 ; + ∞, [4; +∞).

Qaror

Avvalo, funksiyaning sohasini topamiz. Kasrning maxraji kvadrat trinomial, bu 0 ga aylanmasligi kerak:

x 2 + x - 6 = 0 D = 1 2 - 4 1 (- 6) = 25 x 1 = - 1 - 5 2 = - 3 x 2 = - 1 + 5 2 = 2 ⇒ D (y) : x ∈ (- ∞ ; - 3) ∪ (- 3 ; 2) ∪ (2 ; + ∞)

Biz shartda ko'rsatilgan barcha intervallar tegishli bo'lgan funksiya doirasini oldik.

Endi funksiyani farqlaymiz va olamiz:

y "= 3 e 1 x 2 + x - 6 - 4" = 3 e 1 x 2 + x - 6 " = 3 e 1 x 2 + x - 6 1 x 2 + x - 6 " == 3 e 1 x 2 + x - 6 1 "x 2 + x - 6 - 1 x 2 + x - 6" (x 2 + x - 6) 2 = - 3 (2 x + 1) e 1 x 2 + x - 6 x 2 + x - 6 2

Demak, funktsiyaning hosilalari uning ta'rifining butun sohasida mavjud.

Keling, statsionar nuqtalarni topishga o'tamiz. Funktsiyaning hosilasi x = - 1 2 da 0 ga aylanadi. Bu (- 3 ; 1 ] va (- 3 ; 2) oraliqlarda joylashgan statsionar nuqta.

Funksiyaning x = - 4 dagi qiymatini (- ∞ ; - 4 ] oraliqda, shuningdek minus cheksizlikdagi chegarani hisoblab chiqamiz:

y (- 4) \u003d 3 e 1 (- 4) 2 + (- 4) - 6 - 4 \u003d 3 e 1 6 - 4 ≈ - 0. 456 lim x → - ∞ 3 e 1 x 2 + x - 6 = 3 e 0 - 4 = - 1

3 e 1 6 - 4 > - 1 bo'lgani uchun, u holda m a x y x ∈ (- ∞ ; - 4 ] = y (- 4) = 3 e 1 6 - 4. Bu funksiyaning eng kichik qiymatini yagona aniqlash imkonini bermaydi. Biz faqat - 1 dan pastda chegara bor degan xulosaga kelishimiz mumkin, chunki funktsiya aynan shu qiymatga minus cheksizlikda asimptotik tarzda yaqinlashadi.

Ikkinchi intervalning o'ziga xos xususiyati shundaki, u bitta statsionar nuqtaga va bitta qat'iy chegaraga ega emas. Shuning uchun biz funktsiyaning eng katta yoki eng kichik qiymatini hisoblay olmaymiz. Chegarani minus cheksizda belgilash orqali va argument chap tomonda - 3 ga moyil bo'lganligi sababli, biz faqat qiymatlar oralig'ini olamiz:

lim x → - 3 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 - 0 3 e 1 (x + 3) (x - 3) - 4 = 3 e 1 (- 3 - 0 + 3) (- 3 - 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → - ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1

Bu funktsiya qiymatlari oraliqda joylashishini anglatadi - 1 ; +∞

Funksiyaning uchinchi oraliqdagi maksimal qiymatini topish uchun x = 1 bo'lsa, x = - 1 2 statsionar nuqtadagi qiymatini aniqlaymiz. Shuningdek, argument o'ng tomonda - 3 ga moyil bo'lgan holat uchun bir tomonlama chegarani bilishimiz kerak:

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e 4 25 - 4 ≈ - 1. 444 y (1) = 3 e 1 1 2 + 1 - 6 - 4 ≈ - 1 . 644 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 - 3 + 0 + 3 (- 3 + 0 - 2) - 4 = = 3 e 1 (- 0) - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

Ma'lum bo'lishicha, funktsiya m a x y x ∈ (3 ; 1 ] = y - 1 2 = 3 e - 4 25 - 4) statsionar nuqtada eng katta qiymatni oladi. Eng kichik qiymatga kelsak, biz uni aniqlay olmaymiz. bilish, - 4 gacha bo'lgan pastki chegaraning mavjudligi.

Interval uchun (- 3 ; 2) oldingi hisoblash natijalarini olamiz va chap tomondan 2 ga moyil bo'lganda bir tomonlama chegara nimaga teng ekanligini yana bir bor hisoblaymiz:

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e - 4 25 - 4 ≈ - 1. 444 lim x → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = - 4 lim x → 2 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 - 0 + 3) (2 - 0 - 2) - 4 = = 3 e 1 - 0 - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

Demak, m a x y x ∈ (- 3 ; 2) = y - 1 2 = 3 e - 4 25 - 4 va eng kichik qiymatni aniqlash mumkin emas va funksiya qiymatlari pastdan - 4 soni bilan chegaralanadi.

Oldingi ikkita hisob-kitobda qilgan ishimizga asoslanib, biz [ 1 oraliqda ; 2) funktsiya x = 1 da eng katta qiymatni oladi va eng kichigini topish mumkin emas.

(2 ; + ∞) oraliqda funksiya na eng katta, na eng kichik qiymatga erishmaydi, ya'ni. u - 1 oraliqdan qiymatlarni oladi; +∞ .

lim x → 2 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 + 0 + 3) ) (2 + 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x - 6 - 4 = 3 e 0 - 4 = - 1

X = 4 da funksiya qiymati nimaga teng bo lishini hisoblab, m a x y x ∈ [ 4 ; + ∞) = y (4) = 3 e 1 14 - 4 va ortiqcha cheksizlikda berilgan funksiya y = - 1 chiziqqa asimptotik yaqinlashadi.

Keling, har bir hisob-kitobda olganimizni berilgan funktsiyaning grafigi bilan taqqoslaylik. Rasmda asimptotlar nuqtali chiziqlar bilan ko'rsatilgan.

Funktsiyaning eng katta va eng kichik qiymatini topish haqida gaplashmoqchi bo'lganimiz shu edi. Biz bergan harakatlar ketma-ketligi kerakli hisob-kitoblarni imkon qadar tez va sodda tarzda amalga oshirishga yordam beradi. Ammo esda tutingki, birinchi navbatda funktsiya qaysi intervallarda kamayishi va qaysilarida ko'payishini aniqlash foydali bo'ladi, shundan so'ng qo'shimcha xulosalar chiqarish mumkin. Shunday qilib, siz funktsiyaning eng katta va eng kichik qiymatini aniqroq aniqlashingiz va natijalarni asoslashingiz mumkin.

Agar siz matnda xatolikni sezsangiz, uni belgilab, Ctrl+Enter tugmalarini bosing