Berilgan trapetsiyaning maydoniga teng to‘rtburchak yasang. To'rtburchak trapezoid: barcha formulalar va misollar
To'rtburchak trapetsiyaning xossalari
- U to'rtburchak trapezoid va ikkita burchak to'g'ri bo'lishi kerak
- Ikkala to'g'ri burchak To'rtburchaklar trapezoidlar, albatta, qo'shni cho'qqilarga tegishlidir
- Ikkala to'g'ri burchak to'rtburchaklar trapezoidda ular bir xil tomonga ulashgan bo'lishi kerak
- To'rtburchak trapesiyaning diagonallari bir tomondan to'g'ri burchakli uchburchak hosil qiling
- Yon uzunligi asoslarga perpendikulyar trapetsiyaning balandligi uning balandligiga teng
- To'rtburchak trapezoidda asoslari parallel, bir tomoni asoslarga perpendikulyar, ikkinchi tomoni esa asoslarga moyil
- To'rtburchak trapezoidda ikkita burchak to'g'ri, qolgan ikkitasi o'tkir va o'tmas
Vazifa
IN to'rtburchak trapezoid eng katta tomoni asoslar yig‘indisiga teng, balandligi 12 sm. Tomonlari trapetsiya asoslariga teng bo‘lgan to‘rtburchakning maydonini toping.Yechim.
Trapetsiyani ABCD deb belgilaymiz. Trapetsiya asoslarining uzunliklarini a (kattaroq AD asosi) va b (kichikroq BC asosi) deb belgilaymiz. To'g'ri burchak bo'lsin
Tomonlari trapetsiya asoslariga teng bo'lgan to'rtburchakning maydoni teng bo'ladi.
S = ab
ABCD trapesiya ustki asosining C cho'qqisidan CK balandligini pastki poydevorga tushiramiz. Trapetsiyaning balandligi masalaning shartlaridan ma'lum. Keyin, Pifagor teoremasiga ko'ra
CK 2 + KD
Trapetsiyaning eng katta yon tomoni asoslar yig'indisiga teng bo'lgani uchun CD = a + b
Trapetsiya to'rtburchaklar shaklida bo'lgani uchun trapetsiyaning yuqori poydevoridan chizilgan balandlik pastki poydevorni ikki qismga bo'ladi.
ya'ni
12 2 + (a - b) 2 = (a + b) 2
qayerda
144 + a 2 - 2ab + b 2 = a 2 + 2ab + b 2
144 = 4ab
To'rtburchakning maydoni S = ab bo'lgani uchun (yuqoriga qarang), keyin
144 = 4S
S = 144/4 = 36
Javob: 36 sm
2 .\[(\Katta(\matn(erkin trapezoid)))\]
Ta'riflar
Trapezoid - bu ikki tomoni parallel, qolgan ikki tomoni parallel bo'lmagan qavariq to'rtburchak.
Trapetsiyaning parallel tomonlari uning asoslari, qolgan ikki tomoni esa yon tomonlari deyiladi.
Trapetsiyaning balandligi bir asosning istalgan nuqtasidan boshqa asosga tushadigan perpendikulyardir.
Teoremalar: trapetsiyaning xossalari
1) Yon tomondagi burchaklar yig'indisi \(180^\circ\) ga teng.
2) Diagonallar trapetsiyani to'rtta uchburchakka ajratadi, ulardan ikkitasi o'xshash, qolgan ikkitasi esa teng kattalikdir.
Isbot
1) Chunki \(AD\parallel BC\), keyin burchaklar \(\BAD burchagi\) va \(\burchak ABC\) bu chiziqlar va koʻndalang \(AB\) uchun bir tomonlama boʻladi, shuning uchun, \(\ burchak BAD +\ burchak ABC = 180 ^ \ aylanma \).
2) Chunki \(AD\parallel BC\) va \(BD\) sekant, keyin \(\angle DBC=\angle BDA\) ko'ndalang yotadi.
Bundan tashqari, vertikal sifatida \(\BOC burchagi=\AOD burchagi\) belgilang.
Shuning uchun, ikki burchak ostida \(\uchburchak BOC \sim \uchburchak AOD\).
Keling, buni isbotlaylik \(S_(\uchburchak AOB)=S_(\uchburchak COD)\). Trapetsiyaning balandligi \(h\) bo'lsin. Keyin \(S_(\triangle ABD)=\frac12\cdot h\cdot AD=S_(\triangle ACD)\). Keyin: \
Ta'rif
Trapetsiyaning o'rta chizig'i tomonlarning o'rta nuqtalarini bog'laydigan segmentdir.
Teorema
Trapetsiyaning o'rta chizig'i asoslarga parallel va ularning yarim yig'indisiga teng.

Isbot*
1) Keling, parallellikni isbotlaylik.

\(M\) nuqta orqali \(MN"\parallel AD\) (\(N"\CD\da)) to'g'ri chiziqni o'tkazamiz. Keyin, Thales teoremasiga ko'ra (bundan buyon \(MN"\parallel AD\parallel BC, AM=MB\)) nuqta \(N"\) - \(CD\) segmentining o'rtasi. Bu \(N\) va \(N"\) nuqtalari mos kelishini bildiradi.
2) Formulani isbotlaymiz.
Keling, \(BB"\perp AD, CC"\perp AD\) qilaylik. Mayli \(BB"\qop MN=M", CC"\qopqoq MN=N"\).

U holda, Thales teoremasi bo'yicha \(M"\) va \(N"\) mos ravishda \(BB"\) va \(CC"\) segmentlarining o'rta nuqtalaridir. Bu shuni anglatadiki, \(MM"\) \(\triangle ABB"\) ning o'rta chizig'i, \(NN"\) - \(\triangle DCC"\) ning o'rta chizig'i. Shunung uchun: \
Chunki \(MN\parallel AD\parallel BC\) va \(BB", CC"\perp AD\) , keyin \(B"M"N"C"\) va \(BM"N"C\) to'rtburchaklardir. Thales teoremasiga ko'ra, \(MN\parallel AD\) va \(AM=MB\) dan \(B"M"=M"B\) kelib chiqadi.Demak, \(B"M"N"C "\) va \(BM"N"C\) teng to'rtburchaklardir, shuning uchun \(M"N"=B"C"=BC\) .
Shunday qilib:
\ \[=\dfrac12 \left(AB"+B"C"+BC+C"D\o'ng)=\dfrac12\left(AD+BC\o'ng)\]
Teorema: ixtiyoriy trapetsiyaning xossasi
Asoslarning o'rta nuqtalari, trapetsiya diagonallarining kesishish nuqtasi va yon tomonlari kengaytmalarining kesishish nuqtasi bir xil to'g'ri chiziqda yotadi.

Isbot*
"Uchburchaklarning o'xshashligi" mavzusini o'rganganingizdan so'ng, isbot bilan tanishishingiz tavsiya etiladi.
1) \(P\) , \(N\) va \(M\) nuqtalar bir to`g`rida yotishini isbotlaylik.

\(PN\) to'g'ri chiziq chizamiz (\(P\) lateral tomonlarning kengaytmalarining kesishish nuqtasi, \(N\) \(BC\) ning o'rtasi). Uni \(AD\) tomonini \(M\) nuqtada kesishsin. \(M\) \(AD\) ning o'rta nuqtasi ekanligini isbotlaylik.
\(\triangle BPN\) va \(\triangle APM\) ni ko'rib chiqing. Ular ikkita burchakda o'xshashdir (\(\ burchak APM \) - umumiy, \ (\ burchak PAM = \ burchak PBN \) \ (AD \ parallel BC \) va \ (AB \) sekantda mos keladi). Ma'nosi: \[\dfrac(BN)(AM)=\dfrac(PN)(PM)\]
\(\triangle CPN\) va \(\triangle DPM\) ni ko'rib chiqing. Ular ikki burchakda o'xshash (\(\ burchak DPM \) - umumiy, \ (\ burchak PDM = \ burchak PCN \) \ (AD \ parallel BC \) va \ (CD \) sekantda mos keladi). Ma'nosi: \[\dfrac(CN)(DM)=\dfrac(PN)(PM)\]
Bu yerdan \(\dfrac(BN)(AM)=\dfrac(CN)(DM)\). Lekin \(BN=NC\) shuning uchun \(AM=DM\) .
2) \(N, O, M\) nuqtalar bir to'g'rida yotishini isbotlaylik.

\(N\) \(BC\) ning o'rta nuqtasi va \(O\) diagonallarning kesishish nuqtasi bo'lsin. Keling, to'g'ri chiziq chizamiz \(NO\) , u \(AD\) tomonini \(M\) nuqtada kesib o'tadi. \(M\) \(AD\) ning o'rta nuqtasi ekanligini isbotlaylik.
\(\uchburchak BNO\sim \uchburchak DMO\) ikki burchak bo'ylab (\(\angle OBN=\angle ODM\) \(BC\parallel AD\) va \(BD\) sekantda ko'ndalang yotadi; \(\burchak BON=\DOM burchagi) vertikal sifatida). Ma'nosi: \[\dfrac(BN)(MD)=\dfrac(ON)(OM)\]
Xuddi shunday \(\uchburchak CON\sim \triangle AOM\). Ma'nosi: \[\dfrac(CN)(MA)=\dfrac(ON)(OM)\]
Bu yerdan \(\dfrac(BN)(MD)=\dfrac(CN)(MA)\). Lekin \(BN=CN\) shuning uchun \(AM=MD\) .
\[(\Katta(\matn(Isosceles trapezoid)))\]
Ta'riflar
Agar burchaklaridan biri to'g'ri bo'lsa, trapezoid to'rtburchaklar deyiladi.
Agar tomonlar teng bo'lsa, trapetsiya teng yon tomonli deyiladi.
Teoremalar: teng yonli trapesiyaning xossalari
1) Teng yonli trapesiyaning asos burchaklari teng.
2) Teng yonli trapesiyaning diagonallari teng.
3) Diagonallar va asosdan tashkil topgan ikkita uchburchak teng yon tomonlardir.
Isbot
1) \(ABCD\) teng yonli trapesiyani ko'rib chiqaylik.

\(B\) va \(C\) uchlaridan mos ravishda \(BM\) va \(CN\) perpendikulyarlarni \(AD\) tomonga tushiramiz. Chunki \(BM\perp AD\) va \(CN\perp AD\) , keyin \(BM\parallel CN\) ; \(AD\parallel BC\) , keyin \(MBCN\) parallelogram, shuning uchun \(BM = CN\) .
To'g'ri uchburchaklarni ko'rib chiqing \(ABM\) va \(CDN\) . Ularning gipotenuzalari teng va \(BM\) oyog'i \(CN\) oyog'iga teng bo'lgani uchun, bu uchburchaklar teng, shuning uchun \(\DAB burchagi = \burchak CDA\) .
2) 
Chunki \(AB=CD, \burchak A=\D burchak, AD\)- umumiy, keyin birinchi belgiga ko'ra. Shuning uchun, \(AC=BD\) .
3) Chunki \(\uchburchak ABD=\uchburchak ACD\), keyin \(\burchak BDA=\burchak SAPR\) . Demak, \(\triangle AOD\) uchburchak teng yon tomonlardir. Xuddi shunday, \(\uchburchak BOC\) teng yon tomonli ekanligi isbotlangan.
Teoremalar: teng yonli trapesiya belgilari
1) Agar trapetsiyaning asos burchaklari teng bo'lsa, u teng yon tomonli bo'ladi.
2) Agar trapetsiyaning diagonallari teng bo'lsa, u teng yon tomonli bo'ladi.
Isbot
\(ABCD\) trapesiyani ko'rib chiqaylik, shundayki \(\burchak A = \D burchak\) .

Keling, rasmda ko'rsatilganidek, \(AED\) uchburchakka trapetsiyani to'ldiramiz. Chunki \(\burchak 1 = \burchak 2\) , u holda uchburchak \(AED\) teng yon tomonli va \(AE = ED\) . Burchaklar \(1\) va \(3\) parallel chiziqlar \(AD\) va \(BC\) va sekant \(AB\) uchun mos burchaklarga teng. Xuddi shunday, \(2\) va \(4\) burchaklar teng, lekin \(\burchak 1 = \burchak 2\), keyin \(\burchak 3 = \burchak 1 = \burchak 2 = \burchak 4\), shuning uchun \(BEC\) uchburchak ham teng yon tomonli va \(BE = EC\) .
Natijada \(AB = AE - BE = DE - CE = CD\), ya'ni \(AB = CD\), bu isbotlanishi kerak bo'lgan narsadir.
2) \(AC=BD\) bo'lsin. Chunki \(\uchburchak AOD\sim \uchburchak BOC\), keyin ularning o'xshashlik koeffitsientini \(k\) deb belgilaymiz. Agar \(BO=x\) bo'lsa, u holda \(OD=kx\) . Xuddi \(CO=y \Rightarrow AO=ky\) .

Chunki \(AC=BD\) , keyin \(x+kx=y+ky \O'ng ko'rsatkich x=y\) . Bu shuni anglatadiki, \(\uchburchak AOD\) teng yon tomonli va \(\angle OAD=\angle ODA\) .
Shunday qilib, birinchi belgiga ko'ra \(\uchburchak ABD=\uchburchak ACD\) (\(AC=BD, \angle OAD=\burchak ODA, AD\)- umumiy). Shunday qilib, \(AB=CD\), nima uchun.
Ushbu maqolada biz trapezoidning xususiyatlarini iloji boricha to'liq aks ettirishga harakat qilamiz. Xususan, biz gaplashamiz umumiy belgilar va trapetsiyaning xossalari, shuningdek, chizilgan trapetsiyaning xususiyatlari va trapetsiya ichiga chizilgan doira haqida. Shuningdek, biz teng yonli va to'rtburchak trapezoidning xususiyatlariga to'xtalamiz.
Muhokama qilingan xususiyatlardan foydalangan holda muammoni hal qilish misoli uni boshingizdagi joylarga ajratishga va materialni yaxshiroq eslab qolishga yordam beradi.
Trapesiya va hamma narsa
Boshlash uchun, keling, trapezoid nima ekanligini va u bilan qanday boshqa tushunchalar bog'liqligini qisqacha eslaylik.
Demak, trapezoid to'rtburchak figura bo'lib, uning ikki tomoni bir-biriga parallel (bu asoslar). Va ikkalasi parallel emas - bu tomonlar.
Trapezoidda balandlikni tushirish mumkin - poydevorlarga perpendikulyar. Markaziy chiziq va diagonallar chizilgan. Trapetsiyaning istalgan burchagidan bissektrisa chizish ham mumkin.
Haqida har xil xususiyatlar, bu barcha elementlar va ularning kombinatsiyalari bilan bog'liq, biz hozir gaplashamiz.
Trapetsiya diagonallarining xossalari
Aniqroq bo'lishi uchun, siz o'qiyotganingizda, qog'oz varag'iga ACME trapetsiyasining eskizini chizib oling va unda diagonallarni chizing.
- Agar siz diagonallarning har birining o'rta nuqtalarini topsangiz (bu nuqtalarni X va T deb ataymiz) va ularni birlashtirsangiz, siz segmentga ega bo'lasiz. Trapetsiya diagonallarining xossalaridan biri shundaki, HT segmenti o'rta chiziqda yotadi. Va uning uzunligini asoslar farqini ikkiga bo'lish orqali olish mumkin: HT = (a – b)/2.
- Bizning oldimizda bir xil trapezoid ACME. Diagonallar O nuqtada kesishadi. Keling, diagonallarning segmentlari bilan birga trapetsiya asoslari bilan tuzilgan AOE va MOK uchburchaklarini ko'rib chiqaylik. Bu uchburchaklar o'xshash. Uchburchaklarning o'xshashlik koeffitsienti k trapetsiya asoslarining nisbati orqali ifodalanadi: k = AE/KM.
AOE va MOK uchburchaklar maydonlarining nisbati k 2 koeffitsienti bilan tavsiflanadi. - Xuddi shu trapetsiya, bir xil diagonallar O nuqtada kesishadi. Faqat bu safar biz diagonallarning segmentlari trapetsiya tomonlari bilan birga hosil bo'lgan uchburchaklarni ko'rib chiqamiz. AKO va EMO uchburchaklarining maydonlari o'lchamlari bo'yicha teng - ularning maydonlari bir xil.
- Trapezoidning yana bir xususiyati diagonallarni qurishni o'z ichiga oladi. Shunday qilib, agar siz AK va ME tomonlarini kichikroq asos yo'nalishi bo'yicha davom ettirsangiz, ertami-kechmi ular ma'lum bir nuqtada kesishadi. Keyin trapezoidning asoslari o'rtasidan to'g'ri chiziq torting. U asoslarni X va T nuqtalarda kesib o'tadi.
Agar biz XT chizig'ini endi cho'zsak, u holda O trapetsiya diagonallarining kesishish nuqtasini, X va T asoslarning yon tomonlari va o'rtalarining kengaytmalari kesishgan nuqtani birlashtiradi. - Diagonallarning kesishish nuqtasi orqali biz trapetsiya asoslarini bog'laydigan segmentni chizamiz (T kichikroq KM asosida, X kattaroq AEda yotadi). Diagonallarning kesishish nuqtasi ushbu segmentni quyidagi nisbatda ajratadi: TO/OX = KM/AE.
- Endi diagonallarning kesishish nuqtasi orqali trapetsiya (a va b) asoslariga parallel bo'lgan segmentni chizamiz. Kesishish nuqtasi uni ikkita teng qismga ajratadi. Formuladan foydalanib, segment uzunligini topishingiz mumkin 2ab/(a + b).
Trapetsiyaning o'rta chizig'ining xossalari
Trapetsiyadagi o'rta chiziqni uning asoslariga parallel ravishda chizing.
- Trapezoidning o'rta chizig'ining uzunligini asoslar uzunligini qo'shib, ularni yarmiga bo'lish orqali hisoblash mumkin: m = (a + b)/2.
- Agar siz trapetsiyaning ikkala asosi orqali biron bir segmentni (masalan, balandlikni) o'tkazsangiz, o'rta chiziq uni ikkita teng qismga ajratadi.
Trapetsiyaning bissektrisa xossasi
Trapetsiyaning istalgan burchagini tanlang va bissektrisa chizing. Masalan, ACME trapesiyamizning KAE burchagini olaylik. Qurilishni o'zingiz tugatgandan so'ng, bissektrisa taglikdan (yoki rasmning o'zidan tashqaridagi to'g'ri chiziqda davom etishi) yon tomondan bir xil uzunlikdagi segmentni kesib tashlashini osongina tekshirishingiz mumkin.
Trapetsiya burchaklarining xossalari
- Yon tomonga ulashgan ikki juft burchakdan qaysi birini tanlasangiz, juftlikdagi burchaklar yig‘indisi har doim 180 0 ga teng: a + b = 180 0 va g + d = 180 0.
- Trapetsiya asoslarining o'rta nuqtalarini TX segmenti bilan bog'laymiz. Endi trapetsiya asoslaridagi burchaklarni ko'rib chiqamiz. Agar ularning birortasi uchun burchaklar yig'indisi 90 0 ga teng bo'lsa, TX segmentining uzunligini ikkiga bo'lingan tagliklar uzunligidagi farq asosida osongina hisoblash mumkin: TX = (AE – KM)/2.
- Agar trapezoid burchakning tomonlari orqali parallel chiziqlar o'tkazilsa, ular burchakning tomonlarini proportsional segmentlarga bo'linadi.
Teng yonli (teng yonli) trapesiyaning xossalari
- Teng yonli trapesiyada har qanday asosdagi burchaklar tengdir.
- Endi biz nima haqida gapirayotganimizni tasavvur qilishni osonlashtirish uchun yana trapesiya yasang. AE asosiga diqqat bilan qarang - qarama-qarshi M asosining tepasi AE ni o'z ichiga olgan chiziqning ma'lum bir nuqtasiga proyeksiyalangan. A cho'qqidan M cho'qqining proyeksiya nuqtasigacha bo'lgan masofa va teng yonli trapetsiyaning o'rta chizig'i teng.
- Teng yonli trapezoid diagonallarining xossasi haqida bir necha so'z - ularning uzunligi teng. Shuningdek, bu diagonallarning trapetsiya asosiga moyillik burchaklari bir xil.
- Faqat teng yonli trapesiya atrofida aylana tasvirlanishi mumkin, chunki to'rtburchakning qarama-qarshi burchaklarining yig'indisi 180 0 ga teng - buning uchun zaruriy shart.
- Teng yon tomonli trapesiyaning xossasi oldingi paragrafdan kelib chiqadi - agar trapezoid yaqinida aylana tasvirlanishi mumkin bo'lsa, u izoskeldir.
- Teng yonli trapezoidning xususiyatlaridan trapetsiyaning balandlik xususiyati kelib chiqadi: agar uning diagonallari to'g'ri burchak ostida kesishsa, balandlik uzunligi asoslar yig'indisining yarmiga teng bo'ladi: h = (a + b)/2.
- Yana TX segmentini trapetsiya asoslarining o'rta nuqtalari orqali o'tkazing - teng yonli trapesiyada u asoslarga perpendikulyar. Va ayni paytda TX - teng yonli trapezoidning simmetriya o'qi.
- Bu safar trapetsiyaning qarama-qarshi cho'qqisidan balandlikni kattaroq poydevorga tushiring (uni a deb ataymiz). Siz ikkita segmentni olasiz. Agar asoslarning uzunligi qo'shilsa va yarmiga bo'lingan bo'lsa, bittaning uzunligini topish mumkin: (a + b)/2. Kattaroq bazadan kichigini ayirib, hosil bo'lgan farqni ikkiga bo'lsak, ikkinchisini olamiz: (a – b)/2.
Doira ichiga chizilgan trapetsiyaning xossalari
Biz allaqachon aylana ichiga yozilgan trapezoid haqida gapirayotganimiz sababli, keling, ushbu masalaga batafsil to'xtalib o'tamiz. Xususan, aylananing markazi trapezoidga nisbatan qayerda joylashgan. Bu erda ham qalam olishga vaqt ajratish va quyida muhokama qilinadigan narsalarni chizish tavsiya etiladi. Shunday qilib, siz tezroq tushunasiz va yaxshiroq eslaysiz.
- Doira markazining joylashishi trapetsiya diagonalining uning yon tomoniga egilish burchagi bilan aniqlanadi. Misol uchun, diagonal trapezoidning tepasidan yon tomonga to'g'ri burchak ostida cho'zilishi mumkin. Bunday holda, kattaroq asos aylana markazini o'rtada kesib o'tadi (R = ½AE).
- Diagonal va yon tomonlar ham o'tkir burchak ostida uchrashishi mumkin - keyin aylananing markazi trapezoidning ichida bo'ladi.
- Cheklangan doiraning markazi trapetsiyadan tashqarida, uning katta poydevoridan tashqarida bo'lishi mumkin, agar trapetsiya diagonali va yon tomoni o'rtasida bo'lsa - to'g'ri burchak.
- ACME trapezoidining (yozilgan burchak) diagonali va katta asosi tomonidan hosil qilingan burchak uning yarmiga teng. markaziy burchak, unga mos keladi: MAE = ½MOE.
- Cheklangan aylana radiusini topishning ikkita usuli haqida qisqacha. Birinchi usul: chizilgan rasmingizga diqqat bilan qarang - nimani ko'ryapsiz? Diagonal trapezoidni ikkita uchburchakka bo'lishini osongina payqashingiz mumkin. Radiusni uchburchak tomonining qarama-qarshi burchak sinusiga nisbati ikkiga ko'paytirilganda topish mumkin. Masalan, R = AE/2*sinAME. Formulani ikkala uchburchakning istalgan tomoni uchun ham xuddi shunday yozish mumkin.
- Ikkinchi usul: trapetsiyaning diagonali, yon tomoni va asosi tomonidan hosil qilingan uchburchakning maydoni orqali aylana radiusini toping: R = AM*ME*AE/4*S AME.
Doira atrofida chizilgan trapetsiyaning xossalari
Agar bitta shart bajarilsa, aylanani trapezoidga joylashtirishingiz mumkin. Quyida u haqida ko'proq o'qing. Va birgalikda bu raqamlar kombinatsiyasi bir qator qiziqarli xususiyatlarga ega.
- Agar aylana trapezoidga chizilgan bo'lsa, uning o'rta chizig'ining uzunligini tomonlarning uzunliklarini qo'shib, olingan yig'indini yarmiga bo'lish orqali osongina topish mumkin: m = (c + d)/2.
- Doira haqida tasvirlangan ACME trapetsiyasi uchun asoslar uzunliklarining yig'indisi tomonlarning uzunliklari yig'indisiga teng: AK + ME = KM + AE.
- Trapetsiya asoslarining bu xossasidan qarama-qarshi gap kelib chiqadi: asoslar yig’indisi uning tomonlari yig’indisiga teng bo’lgan trapetsiyaga aylana chizilishi mumkin.
- Radiusi r trapetsiyaga chizilgan aylananing teginish nuqtasi yon tomonini ikki qismga ajratadi, ularni a va b deb ataymiz. Doira radiusini quyidagi formula yordamida hisoblash mumkin: r = √ab.
- Va yana bir mulk. Chalkashmaslik uchun ushbu misolni o'zingiz ham chizing. Bizda aylana bo'ylab tasvirlangan yaxshi eski ACME trapezoidi bor. U O nuqtada kesishgan diagonallarni o'z ichiga oladi. Diagonallar segmentlari va lateral tomonlari tomonidan hosil qilingan AOK va EOM uchburchaklari to'rtburchaklardir.
Bu uchburchaklarning gipotenuslarga (ya'ni, trapezoidning lateral tomonlari) tushirilgan balandliklari chizilgan doira radiuslariga to'g'ri keladi. Va trapezoidning balandligi chizilgan doira diametriga to'g'ri keladi.
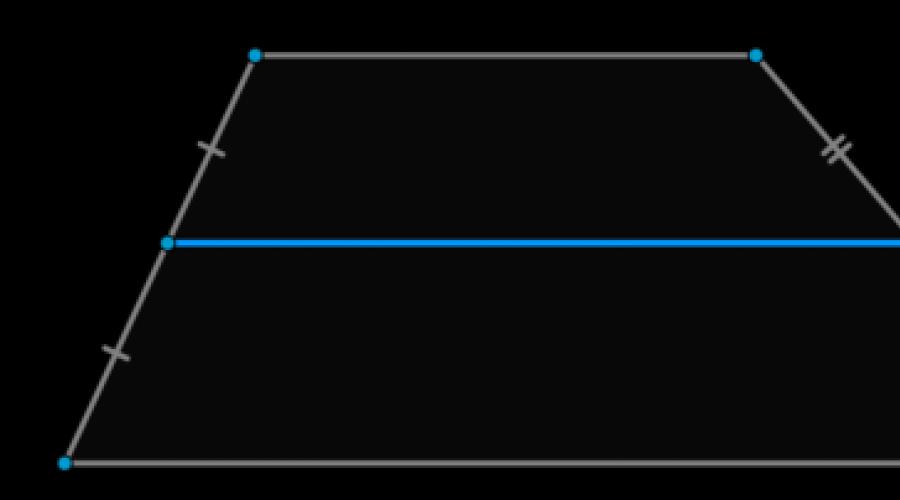
To'rtburchak trapetsiyaning xossalari
Agar burchaklaridan biri to'g'ri bo'lsa, trapetsiya to'rtburchaklar deyiladi. Va uning xususiyatlari shu holatdan kelib chiqadi.
- To'g'ri to'rtburchak trapezoidning bir tomoni uning asosiga perpendikulyar bo'ladi.
- ga ulashgan trapezoidning balandligi va lateral tomoni to'g'ri burchak, teng. Bu sizga to'rtburchaklar trapezoidning maydonini hisoblash imkonini beradi ( umumiy formula S = (a + b) * h/2) nafaqat balandlik orqali, balki to'g'ri burchakka ulashgan tomondan ham.
- To'rtburchaklar trapezoid uchun yuqorida tavsiflangan trapezoid diagonallarining umumiy xususiyatlari tegishli.
Trapetsiyaning ba'zi xossalarini isbotlash
Teng yonli trapetsiya asosidagi burchaklarning tengligi:
- Ehtimol siz allaqachon taxmin qilgandirsiz, bu erda bizga yana AKME trapesiya kerak bo'ladi - isosseles trapezoidini chizish. M cho'qqisidan AK (MT || AK) tomoniga parallel bo'lgan MT to'g'ri chiziqni o'tkazing.
Olingan to'rtburchak AKMT parallelogrammdir (AK || MT, KM || AT). ME = KA = MT bo'lgani uchun ∆ MTE teng yon tomonli va MET = MTE.
AK || MT, shuning uchun MTE = KAE, MET = MTE = KAE.
AKM = 180 0 - MET = 180 0 - KAE = KME qaerda.
Q.E.D.
Endi, teng yonli trapezoidning (diagonallarning tengligi) xususiyatiga asoslanib, buni isbotlaymiz ACME trapezoidasi teng yon tomonli:
- Boshlash uchun MX - MX || to'g'ri chiziq chizamiz KE. Biz KMHE parallelogrammasini olamiz (asosiy - MX || KE va KM || EX).
∆AMX teng yon tomonli, chunki AM = KE = MX va MAX = MEA.
MH || KE, KEA = MXE, shuning uchun MAE = MXE.
Aniqlanishicha, AKE va EMA uchburchaklari bir-biriga teng, chunki AM = KE va AE ikki uchburchakning umumiy tomonidir. Shuningdek, MAE = MXE. AK = ME degan xulosaga kelishimiz mumkin va bundan AKME trapesiya teng yon tomonli ekanligi kelib chiqadi.

Vazifani ko'rib chiqish
ACME trapesiyaning asoslari 9 sm va 21 sm, yon tomoni KA, 8 sm ga teng, kichikroq asos bilan 150 0 burchak hosil qiladi. Siz trapezoidning maydonini topishingiz kerak.
Yechish: K cho'qqisidan trapetsiyaning kattaroq asosiga balandlikni tushiramiz. Keling, trapezoidning burchaklariga qarashni boshlaylik.
AEM va KAN burchaklari bir tomonlama. Bu degani, ular jami 180 0 beradi. Shuning uchun KAN = 30 0 (trapezoidal burchaklar xususiyatiga asoslangan).
Keling, to'rtburchak ∆ANC ni ko'rib chiqaylik (menimcha, bu fikr o'quvchilarga qo'shimcha dalillarsiz ravshan). Undan biz KH trapesiya balandligini topamiz - uchburchakda bu 30 0 burchakka qarama-qarshi yotgan oyoqdir. Shuning uchun KH = ½AB = 4 sm.
Trapetsiya maydonini quyidagi formuladan foydalanib topamiz: S ACME = (KM + AE) * KN/2 = (9 + 21) * 4/2 = 60 sm 2.
Keyingi so'z
Agar siz ushbu maqolani diqqat bilan va puxta o'rgangan bo'lsangiz, qo'lingizda qalam bilan barcha berilgan xususiyatlar uchun trapezoidlarni chizish va ularni amalda tahlil qilish uchun dangasa bo'lmasangiz, materialni yaxshi o'zlashtirgan bo'lishingiz kerak edi.
Albatta, bu erda juda ko'p ma'lumotlar mavjud, turli xil va ba'zan chalkashliklar: tasvirlangan trapezoidning xususiyatlarini yozilganining xususiyatlari bilan aralashtirish unchalik qiyin emas. Ammo o'zingiz ko'rdingizki, farq juda katta.
Endi sizda hamma narsaning batafsil xulosasi bor umumiy xususiyatlar trapezoidlar. Shuningdek, teng yon tomonlar va to'rtburchaklar trapetsiyalarning o'ziga xos xususiyatlari va xususiyatlari. Test va imtihonlarga tayyorgarlik ko'rish uchun foydalanish juda qulay. O'zingiz sinab ko'ring va havolani do'stlaringiz bilan baham ko'ring!
blog.site, materialni to'liq yoki qisman nusxalashda asl manbaga havola talab qilinadi.
Miloddan avvalgi V asrda qadimgi yunon faylasufi Eleyalik Zenon o'zining mashhur aporiyalarini tuzgan, ulardan eng mashhuri "Axilles va toshbaqa" aporiyasidir. Bu qanday eshitiladi:Aytaylik, Axilles toshbaqadan o'n barobar tezroq yuguradi va undan ming qadam orqada. Bu masofani bosib o'tish uchun Axilles kerak bo'lgan vaqt ichida toshbaqa xuddi shu yo'nalishda yuz qadam sudraladi. Axilles yuz qadam yugurganda, toshbaqa yana o'n qadam sudraladi va hokazo. Jarayon infinitum davom etadi, Axilles hech qachon toshbaqaga yetib bormaydi.
Bu mulohaza barcha keyingi avlodlar uchun mantiqiy zarba bo'ldi. Aristotel, Diogen, Kant, Gegel, Gilbert... Ularning barchasi Zenon aporiyasini u yoki bu tarzda ko‘rib chiqdilar. Shok shu qadar kuchli ediki " ...munozaralar shu kungacha davom etmoqda, ilmiy jamoatchilik hali paradokslar mohiyati bo‘yicha umumiy fikrga kela olmadi... masalani o‘rganishga jalb qilindi; matematik tahlil, to'plamlar nazariyasi, yangi fizik va falsafiy yondashuvlar; ularning hech biri muammoning umumiy qabul qilingan yechimiga aylanmadi ..."[Vikipediya, "Zeno's Aporia". Hamma ularni aldashayotganini tushunadi, lekin hech kim yolg'on nimadan iboratligini tushunmaydi.
Matematik nuqtai nazardan Zenon o'z aporiyasida miqdordan ga o'tishni aniq ko'rsatdi. Ushbu o'tish doimiy o'rniga dasturni nazarda tutadi. Men tushunganimdek, o'zgaruvchan o'lchov birliklaridan foydalanish uchun matematik apparat hali ishlab chiqilmagan yoki Zenon aporiyasiga qo'llanilmagan. Odatdagi mantiqimizni qo'llash bizni tuzoqqa olib boradi. Biz fikrlash inertsiyasi tufayli o'zaro qiymatga doimiy vaqt birliklarini qo'llaymiz. Jismoniy nuqtai nazardan, bu Axilles toshbaqaga yetib olgan paytda to'liq to'xtaguncha vaqt sekinlashayotganga o'xshaydi. Vaqt to'xtasa, Axilles endi toshbaqadan o'tib keta olmaydi.
Agar biz odatdagi mantiqimizni aylantirsak, hamma narsa joyiga tushadi. Axilles bilan yuguradi doimiy tezlik. Uning yo'lining har bir keyingi qismi avvalgisidan o'n baravar qisqaroq. Shunga ko'ra, uni engish uchun sarflangan vaqt avvalgisidan o'n baravar kam. Agar biz ushbu vaziyatda "abadiylik" tushunchasini qo'llasak, "Axilles toshbaqani cheksiz tezlikda ushlaydi" deyish to'g'ri bo'ladi.
Ushbu mantiqiy tuzoqdan qanday qochish kerak? Doimiy vaqt birliklarida qoling va o'zaro birliklarga o'tmang. Zenon tilida bu shunday ko'rinadi:
Axilles ming qadam yugurishi kerak bo'lgan vaqt ichida toshbaqa xuddi shu tomonga yuz qadam sudraladi. Birinchisiga teng bo'lgan keyingi vaqt oralig'ida Axilles yana ming qadam yuguradi, toshbaqa esa yuz qadam sudraladi. Endi Axilles toshbaqadan sakkiz yuz qadam oldinda.
Bu yondashuv voqelikni mantiqiy paradokslarsiz adekvat tasvirlaydi. Ammo bu muammoning to'liq yechimi emas. Eynshteynning yorug'lik tezligining chidab bo'lmasligi haqidagi bayonoti Zenonning "Axilles va toshbaqa" aporiyasiga juda o'xshaydi. Biz bu muammoni hali o'rganishimiz, qayta o'ylab ko'rishimiz va hal qilishimiz kerak. Va yechimni cheksiz ko'p sonlarda emas, balki o'lchov birliklarida izlash kerak.
Zenonning yana bir qiziqarli aporiyasi uchadigan o'q haqida gapiradi:
Uchib yuruvchi o'q harakatsiz, chunki u har daqiqada dam oladi va har daqiqada dam bo'lgani uchun u doimo dam oladi.
Ushbu aporiyada mantiqiy paradoks juda sodda tarzda engib o'tiladi - har bir vaqtning har bir lahzasida uchuvchi o'q kosmosning turli nuqtalarida tinch holatda bo'lishini aniqlashtirish kifoya, bu aslida harakatdir. Shu o'rinda yana bir jihatga e'tibor qaratish lozim. Yo'lda avtomobilning bitta fotosuratidan uning harakatlanish faktini ham, unga bo'lgan masofani ham aniqlash mumkin emas. Mashinaning harakatlanayotganligini aniqlash uchun sizga vaqtning turli nuqtalarida bir nuqtadan olingan ikkita fotosurat kerak, ammo siz ulardan masofani aniqlay olmaysiz. Avtomobilgacha bo'lgan masofani aniqlash uchun sizga bir vaqtning o'zida kosmosning turli nuqtalaridan olingan ikkita fotosurat kerak, ammo ulardan siz harakat faktini aniqlay olmaysiz (albatta, hisob-kitoblar uchun sizga hali ham qo'shimcha ma'lumotlar kerak, trigonometriya sizga yordam beradi ). Men nimani ta'kidlamoqchiman Maxsus e'tibor, shundan iboratki, vaqtning ikki nuqtasi va kosmosdagi ikkita nuqta chalkashmaslik kerak bo'lgan turli xil narsalardir, chunki ular tadqiqot uchun turli imkoniyatlarni beradi.
Chorshanba, 4-iyul, 2018-yil
To'plam va multiset o'rtasidagi farqlar Vikipediyada juda yaxshi tasvirlangan. Ko'raylikchi.
Ko'rib turganingizdek, "to'plamda ikkita bir xil element bo'lishi mumkin emas", lekin to'plamda bir xil elementlar mavjud bo'lsa, bunday to'plam "ko'p to'plam" deb ataladi. Aqlli mavjudotlar bunday bema'ni mantiqni hech qachon tushunmaydilar. Bu "to'liq" so'zidan aqlga ega bo'lmagan gapiradigan to'tiqushlar va o'qitilgan maymunlarning darajasi. Matematiklar oddiy murabbiy sifatida harakat qilib, bizga o'zlarining bema'ni g'oyalarini targ'ib qilishadi.
Bir paytlar ko'prikni qurgan muhandislar ko'prikni sinovdan o'tkazayotganda ko'prik ostidagi qayiqda bo'lishgan. Agar ko'prik qulab tushsa, o'rtamiyona muhandis o'zi yaratgan vayronalar ostida vafot etdi. Agar ko'prik yukga bardosh bera olsa, iste'dodli muhandis boshqa ko'priklarni qurdi.
Matematiklar "menga e'tibor bering, men uydaman" yoki to'g'rirog'i, "matematika mavhum tushunchalarni o'rganadi" iborasi orqasida qanchalik yashirinmasin, ularni haqiqat bilan chambarchas bog'laydigan bitta kindik bor. Bu kindik puldir. Qo'llanilishi mumkin matematik nazariya matematiklarning o'zlariga qo'yadi.
Biz matematikani juda yaxshi o'rgandik va hozir biz kassada o'tirib, maosh beramiz. Shunday qilib, bir matematik bizga pul uchun keladi. Biz unga to'liq miqdorni hisoblaymiz va stolimizga turli xil qoziqlarga joylashtiramiz, ularga bir xil nomdagi veksellarni joylashtiramiz. Keyin biz har bir qoziqdan bitta hisob-kitobni olib, matematikaga uning "matematik ish haqi" ni beramiz. Biz matematikaga bir xil elementlari bo'lmagan to'plam bilan to'plamga teng emasligini isbotlagandagina qolgan veksellarni olishini tushuntiramiz. bir xil elementlar. Qiziq shu erda boshlanadi.
Avvalo, deputatlarning mantig‘i ishlaydi: “Buni boshqalarga ham qo‘llash mumkin, lekin menga emas!”. Keyin ular bizni bir xil nomdagi veksellar turli xil veksel raqamlariga ega ekanligiga ishontirishni boshlaydilar, ya'ni ularni bir xil elementlar deb hisoblash mumkin emas. Mayli, maoshlarni tangalarda hisoblaylik - tangalarda raqamlar yo'q. Bu erda matematik fizikani hayajon bilan eslay boshlaydi: har xil tangalar har xil miqdordagi axloqsizlikka ega, kristal tuzilishi va atomlarning joylashishi har bir tanga uchun o'ziga xosdir ...
Va endi menda eng ko'p narsa bor qiziqish so'rang: ko'p to'plam elementlari to'plam elementlariga aylanadigan chiziq qayerda va aksincha? Bunday chiziq mavjud emas - hamma narsani shamanlar hal qiladi, fan bu erda yolg'on gapirishga ham yaqin emas.
Mana qarang. Biz maydon maydoni bir xil bo'lgan futbol stadionlarini tanlaymiz. Maydonlarning maydonlari bir xil - bu bizda multiset borligini anglatadi. Ammo o'sha stadionlarning nomlariga qarasak, ko'pchilikni olamiz, chunki nomlar boshqacha. Ko'rib turganingizdek, bir xil elementlar to'plami ham to'plam, ham multisetdir. Qanday to'g'ri? Va bu erda matematik-shaman-o'tkir yengidan ko'zni chiqarib, bizga to'plam yoki multiset haqida gapira boshlaydi. Har holda, u bizni o'zining haq ekanligiga ishontiradi.
Zamonaviy shamanlar to'plamlar nazariyasi bilan qanday ishlashini, uni haqiqatga bog'lashini tushunish uchun bitta savolga javob berish kifoya: bir to'plamning elementlari boshqa to'plamning elementlaridan qanday farq qiladi? Men sizga ko'rsataman, hech qanday "bitta butun bo'lmagan" yoki "bir butun sifatida tasavvur qilib bo'lmaydigan".
Yakshanba, 18-mart, 2018-yil
Raqam raqamlarining yig'indisi - bu matematikaga hech qanday aloqasi bo'lmagan shamanlarning daf bilan raqsi. Ha, matematika darslarida bizga son raqamlari yig'indisini topish va undan foydalanish o'rgatiladi, lekin shuning uchun ular shamanlar, o'z avlodlariga o'z mahoratlari va donoliklarini o'rgatishlari kerak, aks holda shamanlar shunchaki o'lib ketadi.
Sizga dalil kerakmi? Vikipediyani oching va "Raqam raqamlari yig'indisi" sahifasini topishga harakat qiling. U mavjud emas. Matematikada biron bir raqamning raqamlari yig'indisini topish uchun ishlatiladigan formula yo'q. Axir, raqamlar biz raqamlarni yozadigan grafik belgilardir va matematika tilida vazifa quyidagicha yangraydi: "Har qanday raqamni ifodalovchi grafik belgilar yig'indisini toping." Matematiklar bu muammoni hal qila olmaydilar, ammo shamanlar buni osonlikcha hal qilishlari mumkin.
Keling, berilgan sonning raqamlari yig'indisini topish uchun nima va qanday qilishimizni aniqlaymiz. Shunday qilib, 12345 raqamiga ega bo'lamiz. Bu raqamning raqamlari yig'indisini topish uchun nima qilish kerak? Keling, barcha bosqichlarni tartibda ko'rib chiqaylik.
1. Raqamni qog'ozga yozing. Biz nima qildik? Biz raqamni grafik raqam belgisiga aylantirdik. Bu matematik operatsiya emas.
2. Olingan bitta rasmni alohida raqamlardan iborat bir nechta rasmga kesib oling. Rasmni kesish matematik operatsiya emas.
3. Alohida grafik belgilarni raqamlarga aylantirish. Bu matematik operatsiya emas.
4. Olingan raqamlarni qo'shing. Endi bu matematika.
12345 raqamining raqamlari yig'indisi 15 ga teng. Bu matematiklar foydalanadigan shamanlardan "kesish va tikish kurslari". Lekin bu hammasi emas.
Matematik nuqtai nazardan, sonni qaysi sanoq sistemasida yozishimiz muhim emas. Shunday qilib, ichida turli tizimlar Hisoblashda bir xil sonning raqamlari yig'indisi boshqacha bo'ladi. Matematikada sanoq sistemasi sonning o'ng tomonida pastki belgisi sifatida ko'rsatilgan. Katta raqam 12345 bilan men boshimni aldashni xohlamayman, keling, maqoladagi 26 raqamini ko'rib chiqaylik. Bu sonni ikkilik, sakkizlik, o‘nlik va o‘n oltilik sanoq sistemalarida yozamiz. Biz har bir qadamni mikroskop ostida ko'rib chiqmaymiz. Keling, natijani ko'rib chiqaylik.
Ko'rib turganingizdek, turli sanoq tizimlarida bir xil son raqamlari yig'indisi har xil bo'ladi. Bu natijaning matematikaga aloqasi yo'q. Bu xuddi to'rtburchakning maydonini metr va santimetrda aniqlaganingiz bilan bir xil, siz butunlay boshqacha natijalarga erishasiz.
Nol barcha sanoq tizimlarida bir xil ko'rinadi va raqamlar yig'indisiga ega emas. Bu haqiqat foydasiga yana bir dalil. Matematiklar uchun savol: matematikada raqam bo'lmagan narsa qanday qilib belgilanadi? Nima, matematiklar uchun raqamlardan boshqa hech narsa yo'q? Men shamanlar uchun ruxsat berishim mumkin, ammo olimlar uchun emas. Haqiqat faqat raqamlardan iborat emas.
Olingan natija sanoq sistemalarining sonlar uchun o'lchov birliklari ekanligiga dalil sifatida qaralishi kerak. Axir, biz raqamlarni turli o'lchov birliklari bilan taqqoslay olmaymiz. Agar bir xil miqdorning turli o'lchov birliklari bilan bir xil harakatlar olib kelsa turli natijalar ularni solishtirgandan so'ng, bu matematikaga hech qanday aloqasi yo'qligini anglatadi.
Haqiqiy matematika nima? Bu matematik operatsiya natijasi raqamning o'lchamiga, ishlatiladigan o'lchov birligiga va bu harakatni kim bajarishiga bog'liq bo'lmaganda.
Oh! Bu ayollar hojatxonasi emasmi?
- Yosh ayol! Bu jannatga ko'tarilish paytida qalblarning muqaddasligini o'rganish uchun laboratoriya! Yuqorida halo va yuqoriga o'q. Yana qanday hojatxona?
Ayol... Yuqoridagi halo va pastga o'q erkakdir.
Agar bunday dizayn san'ati asari kuniga bir necha marta ko'z o'ngingizda porlab tursa,
Shunda siz to'satdan mashinangizda g'alati belgini topsangiz ajablanarli emas:
Shaxsan men najas qilayotgan odamda minus to'rt darajani ko'rishga harakat qilaman (bitta rasm) (bir nechta rasmlarning kompozitsiyasi: minus belgisi, to'rtta raqam, darajalar belgisi). Men esa bu qizni ahmoq deb o‘ylamayman, yo‘q fizika fanidan bilimga ega. U shunchaki grafik tasvirlarni idrok etishning kuchli stereotipiga ega. Va matematiklar buni bizga doimo o'rgatadi. Mana bir misol.
1A "minus to'rt daraja" yoki "bir a" emas. Bu "pooping man" yoki o'n oltilik tizimda "yigirma olti" raqami. Ushbu sanoq tizimida doimiy ravishda ishlaydigan odamlar avtomatik ravishda raqam va harfni bitta grafik belgi sifatida qabul qiladilar.
Oldin o'rganilgan bir qator shakllarda trapezoid muammolari qiyin ko'rinmaydi. Qanaqasiga maxsus holat to'g'ri to'rtburchak trapezoid hisoblanadi. Va uning maydonini qidirayotganda, ba'zida uni allaqachon tanish bo'lgan ikkitaga bo'lish qulayroqdir: to'rtburchaklar va uchburchaklar. Biroz o'ylab ko'rsangiz, albatta yechim topasiz.
To'g'ri to'rtburchak trapetsiyaning ta'rifi va uning xossalari
Ixtiyoriy trapetsiya parallel asoslarga ega va tomonlari ularga ixtiyoriy burchakka ega bo'lishi mumkin. Agar biz to'rtburchaklar trapetsiyani ko'rib chiqsak, unda uning bir tomoni har doim asoslarga perpendikulyar bo'ladi. Ya'ni, undagi ikkita burchak 90 darajaga teng bo'ladi. Bundan tashqari, ular har doim qo'shni cho'qqilarga yoki boshqacha aytganda, bir tomonga tegishlidir.
To'g'ri to'rtburchak trapetsiyadagi boshqa burchaklar har doim o'tkir va o'tkirdir. Bundan tashqari, ularning yig'indisi har doim 180 darajaga teng bo'ladi.
Har bir diagonal kichikroq tomoni bilan to'g'ri burchakli uchburchak hosil qiladi. Va to'g'ridan-to'g'ri burchakli cho'qqidan chizilgan balandlik raqamni ikkiga bo'ladi. Ulardan biri to'rtburchak, ikkinchisi esa to'g'ri burchakli uchburchakdir. Aytgancha, bu tomon har doim trapezoidning balandligiga teng.
Taqdim etilgan formulalarda qanday belgilar qo'llaniladi?
Trapezoidni tavsiflovchi turli xil iboralarda ishlatiladigan barcha miqdorlarni darhol ko'rsatish va ularni jadvalda taqdim etish qulay:
To'rtburchak trapetsiya elementlarini tavsiflovchi formulalar
Ulardan eng oddiylari balandlik va kichikroq tomonlarga bog'liq:
To'rtburchak trapezoidning bu tomoni uchun yana bir nechta formulalar:
s = d *sina;
c = (a - b) * tan a;
c = √ (d 2 - (a - b) 2).
Birinchisi to'g'ri burchakli uchburchakdan kelib chiqadi. Va unda aytilishicha, gipotenuzaning oyog'i qarama-qarshi burchakning sinusini beradi.
Xuddi shu uchburchakda ikkinchi oyoq ikki asosning farqiga teng. Demak, burchak tangensini oyoqlarning nisbatiga tenglashtirgan gap to'g'ri.
Xuddi shu uchburchakdan Pifagor teoremasi haqidagi bilimlar asosida formulani olish mumkin. Bu qayd etilgan uchinchi ifoda.

Boshqa tomon uchun formulalarni yozishingiz mumkin. Ulardan uchtasi ham bor:
d = (a - b) /cosa;
d = c / sin a;
d = √ (c 2 + (a - b) 2).
Birinchi ikkitasi yana bir xil to'g'ri burchakli uchburchakdagi tomonlar nisbatidan olinadi, ikkinchisi esa Pifagor teoremasidan olinadi.
Hududni hisoblash uchun qanday formuladan foydalanish mumkin?
Erkin trapezoid uchun berilgan. Siz faqat balandlikning tagliklarga perpendikulyar tomoni ekanligini hisobga olishingiz kerak.
S = (a + b) * h / 2.
Bu miqdorlar har doim ham aniq ko'rsatilmaydi. Shuning uchun, to'rtburchaklar trapezoidning maydonini hisoblash uchun siz ba'zi matematik hisoblarni bajarishingiz kerak bo'ladi.

Agar diagonallarni hisoblash kerak bo'lsa-chi?
Bunday holda, ular ikkita to'g'ri burchakli uchburchak hosil qilishini ko'rishingiz kerak. Bu siz har doim Pifagor teoremasidan foydalanishingiz mumkin degan ma'noni anglatadi. Keyin birinchi diagonal quyidagicha ifodalanadi:
d1 = √ (c 2 + b 2)
yoki boshqa yo'l bilan "c" ni "h" bilan almashtiring:
d1 = √ (h 2 + b 2).
Ikkinchi diagonal uchun formulalar xuddi shunday tarzda olinadi:
d2 = √ (c 2 + b 2) yoki d 2 = √ (h 2 + a 2).
Vazifa № 1
Vaziyat. To'rtburchaklar trapetsiyaning maydoni ma'lum va 120 dm 2 ga teng. Uning balandligi 8 sm uzunlikda. Trapezoidning barcha tomonlarini hisoblash kerak. Qo'shimcha shart - bir tayanch ikkinchisidan 6 dm kichikroq.
Yechim. Bizga balandligi ma'lum bo'lgan to'rtburchaklar trapetsiya berilganligi sababli, biz darhol tomonlardan biri 8 dm, ya'ni kichikroq tomonini aytishimiz mumkin.
Endi siz boshqasini hisoblashingiz mumkin: d = √ (c 2 + (a - b) 2). Bundan tashqari, bu erda ham c tomoni, ham asoslarning farqi bir vaqtning o'zida berilgan. Ikkinchisi 6 dm ga teng, bu shartdan ma'lum. U holda d (64 + 36), ya'ni 100 ning kvadrat ildiziga teng bo'ladi. Shunday qilib, 10 dm ga teng boshqa tomon topiladi.
Bazalarning yig'indisini maydon formulasidan topish mumkin. Bu balandlikka bo'lingan maydonning ikki barobariga teng bo'ladi. Agar hisoblasangiz, 240 / 8 chiqadi. Bu asoslarning yig'indisi 30 dm ekanligini anglatadi. Boshqa tomondan, ularning farqi 6 dm. Ushbu tenglamalarni birlashtirib, ikkala asosni hisoblashingiz mumkin:
a + b = 30 va a - b = 6.
Siz a ni (b + 6) shaklida ifodalashingiz mumkin, uni birinchi tenglikka almashtiring. Keyin ma'lum bo'ladiki, 2b 24 ga teng bo'ladi. Shuning uchun oddiygina b 12 dm bo'lib chiqadi.
Keyin oxirgi tomoni a 18 dm.
Javob. To'rtburchaklar trapetsiyaning tomonlari: a = 18 dm, b = 12 dm, c = 8 dm, d = 10 dm.

Vazifa № 2
Vaziyat. To'rtburchak trapezoid berilgan. Uning katta tomoni asoslar yig'indisiga teng. Uning balandligi 12 sm uzunlikdagi to'rtburchaklar qurilgan bo'lib, uning tomonlari trapetsiya asoslariga teng. Ushbu to'rtburchakning maydonini hisoblash kerak.
Yechim. Siz qidirayotgan narsangizdan boshlashingiz kerak. Kerakli maydon a va b ko'paytmasi sifatida aniqlanadi. Bu miqdorlarning ikkalasi ham noma'lum.
Qo'shimcha tengliklardan foydalanish kerak bo'ladi. Ulardan biri shartning bayoniga asoslanadi: d = a + b. Bu tomon uchun yuqorida keltirilgan uchinchi formuladan foydalanish kerak. Bundan chiqadi: d 2 = c 2 + (a - b) 2 yoki (a + b) 2 = c 2 + (a - b) 2.
Shartdagi c o'rniga uning qiymatini - 12 qo'yish orqali o'zgartirishlar kiritish kerak. Qavslarni ochib, o'xshash atamalarni keltirgandan so'ng, 144 = 4 ab ekanligi ma'lum bo'ladi.
Yechimning boshida a*b kerakli maydonni beradi, deyilgan. Shuning uchun, oxirgi ifodada siz ushbu mahsulotni S bilan almashtirishingiz mumkin. Oddiy hisoblash maydon qiymatini beradi. S = 36 sm 2.
Javob. Kerakli maydon 36 sm 2 ni tashkil qiladi.

Vazifa № 3
Vaziyat. To'rtburchaklar trapetsiyaning maydoni 150√3 sm². O'tkir burchak 60 darajaga teng. Kichik taglik va kichikroq diagonal orasidagi burchak bir xil ma'noga ega. Biz kichikroq diagonalni hisoblashimiz kerak.
Yechim. Trapetsiya burchaklarining xususiyatlaridan uning o'tmas burchagi 120º ekanligi ma'lum bo'ladi. Keyin diagonal uni teng qismlarga ajratadi, chunki uning bir qismi allaqachon 60 daraja. Keyin bu diagonal va ikkinchi asos orasidagi burchak ham 60 daraja. Ya'ni, katta asos, qiya tomon va kichikroq diagonaldan hosil bo'lgan uchburchak teng tomonli. Shunday qilib, kerakli diagonal a ga, shuningdek yon tomoni d = a ga teng bo'ladi.
Endi biz to'g'ri burchakli uchburchakni ko'rib chiqishimiz kerak. Undagi uchinchi burchak 30 daraja. Bu uning qarshisidagi oyoq gipotenuzaning yarmiga teng ekanligini anglatadi. Ya'ni, trapezoidning kichikroq asosi kerakli diagonalning yarmiga teng: b = a/2. Undan asoslarga perpendikulyar bo'lgan tomonga teng balandlikni topishingiz kerak. Bu erda oyog'i bo'lgan tomon. Pifagor teoremasidan:
c = (a/2) * √3.
Endi qolgan barcha miqdorlarni maydon formulasiga almashtirish:
150√3 = (a + a/2) * (a/2 * √3) / 2.
Bu tenglama yechilsa, 20 ning ildizi olinadi
Javob. Kichikroq diagonalning uzunligi 20 sm.




