Ikki kesishuvchi chiziq orasidagi eng qisqa masofani aniqlang. Kesish chiziqlar orasidagi masofa - ta'rif va topish misollari

Maqsad va vazifalar:

• tarbiyaviy - talabalarda fazoviy tushunchalarni shakllantirish va rivojlantirish; kesishgan chiziqlar orasidagi masofani topishga oid masalalarni yechish malakalarini shakllantirish
• tarbiyaviy - kesishgan chiziqlar orasidagi masofani topishda yakuniy natijalarga erishish uchun iroda va qat'iyatni tarbiyalash; Matematikani o'rganishga bo'lgan muhabbat va qiziqishni uyg'otish.
• rivojlanish - o'quvchilarning mantiqiy tafakkurini, fazoviy tushunchalarini rivojlantirish, o'z-o'zini nazorat qilish ko'nikmalarini rivojlantirish.

Loyiha mavzuning quyidagi nuqtalariga mos keladi o'quv dasturi maktab mavzusi.

1. To'g'ri chiziqlarni kesib o'tish.
2. Chiziq va tekislik orasidagi parallellik belgisi
3. Fazodagi ortogonal proyeksiya.
4. Ko'p yuzlilarning hajmi.

Kirish.

Chiziqlarni kesib o'tish ajoyib!

Agar ular bo'lmasa, hayot yuz baravar qiziqroq bo'lardi. Aytish kerakki, agar stereometriyani o'rganishga arziydigan bo'lsa, u o'zaro kesishuvchi to'g'ri chiziqlarni o'z ichiga oladi. Ular juda ko'p global, qiziqarli xususiyatlarga ega: arxitekturada, qurilishda, tibbiyotda, tabiatda.

Kesishgan to'g'ri chiziqlarning o'ziga xosligi haqidagi hayratimiz sizga etkazilishini juda xohlayman. Lekin buni qanday qilish kerak?

Balki bizning loyihamiz bu savolga javob bo'lar?

Ma'lumki, kesishuvchi chiziqlar umumiy perpendikulyar uzunligi shu chiziqlar orasidagi masofaga teng.

Teorema: Ikki kesishuvchi chiziq orasidagi masofa shu chiziqlardan o'tuvchi parallel tekisliklar orasidagi masofaga teng.

Quyidagi teorema egri chiziqlar orasidagi masofa va burchakni topishning bir usulini beradi.

Kesishuvchi chiziqlar orasidagi masofa shu chiziqlardan birining unga perpendikulyar tekislikka proyeksiyasi bo'lgan nuqtadan boshqa chiziqning xuddi shu tekislikka proyeksiyasigacha bo'lgan masofaga teng.

Asosiy savol:

Kesishgan chiziqlar orasidagi masofani ularning umumiy perpendikulyarini qurmasdan topish mumkinmi?

Keling, kub bilan bog'liq muammoni ko'rib chiqaylik.

Nega kub bilan? Ha, chunki kubda barcha geometriya yashiringan, shu jumladan kesishuvchi chiziqlar geometriyasi.

Vazifa.

Kubning cheti ga teng a. Kubning ikkita qo'shni yuzlarining kesishuvchi diagonallari yotadigan chiziqlar orasidagi masofani toping.

Qo'llanilishi mumkin turli usullar ushbu muammo uchun tadqiqot.

• a-prior;
• proyeksiya usuli;
• hajm usuli;
• koordinata usuli.

Tadqiqot.

Muammoni o’rganish uslubiga ko’ra sinf guruhlarga bo’linadi. Har bir guruh oldida kesishuvchi chiziqlar orasidagi masofani topish uchun ushbu usuldan foydalanishni ko'rsatish va isbotlash vazifasi qo'yiladi. Muammoni o'rganishning yakuniy bosqichi - taqdimotlar, nashrlar yoki veb-saytlar ko'rinishidagi loyihalarni himoya qilish. Bolalar va o'qituvchi har bir guruhning loyihasini nashrlar va taqdimotlar uchun ishlab chiqilgan mezonlar bo'yicha baholash imkoniyatiga ega.

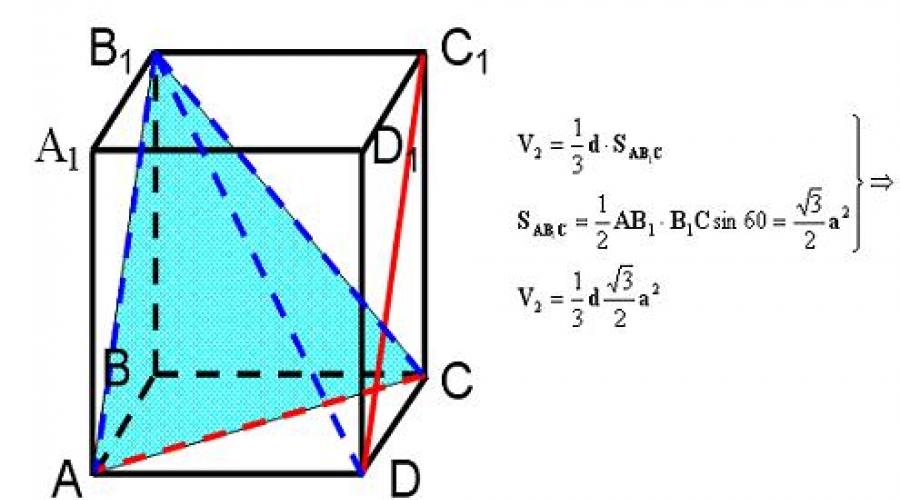
Hajmi usuli.

• piramida quring, unda ushbu piramidaning tepasidan poydevor tekisligiga tushirilgan balandlik ikkita kesishuvchi to'g'ri chiziq orasidagi kerakli masofaga teng bo'ladi;
• bu balandlik kerakli masofa ekanligini isbotlash;
• ikkitadan foydalanib, ushbu piramidaning hajmini toping;
• bu balandlikni ifodalash usullari;

Bu usul o'ziga xosligi, go'zalligi va individualligi bilan juda qiziq. Hajmi usuli fazoviy tasavvurni rivojlantirishga va raqamlarning shakli haqida aqliy g'oyalarni yaratish qobiliyatiga yordam beradi.

Qo'shimcha konstruktsiyalar natijasida biz DAB 1 C piramidasini oldik.

DAB 1 C piramidasida D cho'qqisidan AB 1 C asos tekisligiga tushirilgan balandlik AC va DC 1 kesishuvchi to'g'ri chiziqlar orasidagi kerakli masofa bo'ladi.

Keling, piramidani ko'rib chiqaylik Xulosa: Keling, bir xil piramidani ko'rib chiqaylik, lekin D nuqtasida:

V1 = V2 ekanligini hisobga olsak, biz d= olamiz

Kerakli masofa.

Proyeksiya usuli.

1. Biz kesishgan chiziqlardan biriga perpendikulyar tekislikni tanlaymiz.
2. Biz har bir to'g'ri chiziqni ushbu tekislikka proyeksiya qilamiz.
3. Proyeksiyalar orasidagi masofa kesishuvchi chiziqlar orasidagi masofa bo'ladi.

Kesishgan chiziqlar orasidagi masofani bu chiziqlarning proyeksiya tekisligiga ortogonal proyeksiyalari orasidagi masofa sifatida aniqlash mumkin.

Egri chiziqlar ta'rifidan foydalanish.

Qo'shimcha tuzilmalar: A1B, BD, AK.

A 1 O BD, OS BD

A 1 O va OS to'g'ri chiziqni kesish orqali BD

Bu bilan onlayn kalkulyator fazodagi to'g'ri chiziqlar orasidagi masofani topishingiz mumkin. Berilgan batafsil yechim tushuntirishlar bilan. Fazodagi chiziqlar orasidagi masofani hisoblash uchun chiziqlar tenglamasining turini ("kanonik" yoki "parametrik") o'rnating, katakchalarga chiziqlar tenglamalarining koeffitsientlarini kiriting va "Yechish" tugmasini bosing.

×

Ogohlantirish

Barcha hujayralar tozalansinmi?

Yopish Tozalash

Ma'lumotlarni kiritish bo'yicha ko'rsatmalar. Raqamlar butun sonlar (misollar: 487, 5, -7623 va boshqalar), oʻnli (masalan, 67., 102.54 va boshqalar) yoki kasrlar sifatida kiritiladi. Kasr a/b shaklida kiritilishi kerak, bunda a va b (b>0) butun sonlar yoki o'nlik sonlar. Misollar 45/5, 6.6/76.4, -7/6.7 va boshqalar.

Kosmosdagi chiziqlar orasidagi masofa - nazariya, misollar va echimlar

Dekart to'rtburchaklar koordinatalar tizimi berilsin Oxyz L 1 va L 2:

.

(1)

,

(2)

Qayerda M 1 (x 1 , y 1 , z 1) va M 2 (x 2 , y 2 , z 2) − to‘g‘ri chiziqlarda yotuvchi nuqtalar L 1 va L 2, a q 1 ={m 1 , p 1 , l 1) va q 2 ={m 2 , p 2 , l 2 ) – to‘g‘ri chiziqlarning yo‘nalish vektorlari L 1 va L 2, mos ravishda.

Fazodagi (1) va (2) chiziqlar mos kelishi, parallel, kesishishi yoki kesishishi mumkin. Agar fazodagi chiziqlar kesishsa yoki mos tushsa, ular orasidagi masofa nolga teng. Biz ikkita ishni ko'rib chiqamiz. Birinchisi, chiziqlar parallel, ikkinchisi - chiziqlar kesishadi. Qolganlari umumiy holatlardir. Agar parallel chiziqlar orasidagi masofani hisoblashda biz masofani nolga tenglashtirsak, demak, bu chiziqlar mos keladi. Agar kesishgan chiziqlar orasidagi masofa nolga teng bo'lsa, u holda bu chiziqlar kesishadi.

1. Fazodagi parallel chiziqlar orasidagi masofa

Keling, chiziqlar orasidagi masofani hisoblashning ikkita usulini ko'rib chiqaylik.

1-usul. Bir nuqtadan M 1 tekis L 1 samolyot chizish α , chiziqqa perpendikulyar L 2. Nuqta topish M 3 (x 3 , y 3 , y 3) tekislik kesishmalari α va tekis L 3. Aslida biz nuqtaning proyeksiyasini topamiz M 1 tekis L 2. Nuqtaning chiziqqa proyeksiyasini qanday topish mumkin, qarang. Keyin nuqtalar orasidagi masofani hisoblaymiz M 1 (x 1 , y 1 , z 1) va M 3 (x 3 , y 3 , z 3):

Misol 1. Chiziqlar orasidagi masofani toping L 1 va L 2:

Streyt L 2 nuqtadan o'tadi M 2 (x 2 , y 2 , z 2)=M

Qiymatlarni almashtirish m 2 , p 2 , l 2 , x 1 , y 1 , z 1 da (5) biz olamiz:

Chiziqning kesishish nuqtasini topamiz L 2 va samolyot α , buning uchun to'g'ri chiziqning parametrik tenglamasini tuzamiz L 2 .

Chiziqning kesishish nuqtasini topish uchun L 2 va samolyot α , o'zgaruvchilar qiymatlarini almashtiring x, y, z(7) dan (6) gacha:

Olingan qiymatni almashtirish t(7) da to'g'ri chiziqning kesishish nuqtasini olamiz L 2 va samolyot α :

Nuqtalar orasidagi masofani topish qoladi M 1 va M 3:

L 1 va L 2 teng d=7.2506.

2-usul. Chiziqlar orasidagi masofani toping L 1 va L 2 ((1) va (2) tenglamalar). Birinchidan, biz chiziqlarning parallelligini tekshiramiz L 1 va L 2. To'g'ri chiziqlarning yo'nalish vektorlari bo'lsa L 1 va L 2 tasi kollinear, ya'ni. tenglikka teng bo'ladigan l soni bo'lsa q 1 =λ q 2, keyin to'g'ri L 1 va L 2 parallel.

Parallel vektorlar orasidagi masofani hisoblashning bu usuli vektorlarning vektor mahsuloti tushunchasiga asoslanadi. Ma'lumki, vektorlarning vektor mahsulotining normasi va q 1 bu vektorlar hosil qilgan parallelogramm maydonini beradi (2-rasm). Paralelogrammning maydonini bilganingizdan so'ng, siz parallelogrammning tepasini topishingiz mumkin d, maydonni bazaga bo'lish q 1 parallelogramm.

q 1:

.

Chiziqlar orasidagi masofa L 1 va L 2 teng:

,

,

2-misol. 2-usul yordamida 1-misolni yechamiz. Chiziqlar orasidagi masofani toping

Streyt L 2 nuqtadan o'tadi M 2 (x 2 , y 2 , z 2)=M 2 (8, 4, 1) va yo'nalish vektoriga ega

q 2 ={m 2 , p 2 , l 2 }={2, −4, 8}

Vektorlar q 1 va q 2 to'g'ri chiziqli. Shuning uchun to'g'ridan-to'g'ri L 1 va L 2 parallel. Parallel chiziqlar orasidagi masofani hisoblash uchun vektorlarning vektor mahsulotidan foydalanamiz.

vektor quramiz =( x 2 −x 1 , y 2 −y 1 , z 2 −z 1 }={7, 2, 0}.

vektorlarning vektor mahsulotini hisoblab chiqamiz va q 1 . Buning uchun biz 3×3 matritsani yaratamiz, uning birinchi qatori asosiy vektorlardir i, j, k, qolgan chiziqlar esa vektorlar va elementlari bilan to'ldiriladi q 1:

Shunday qilib, vektorlarning vektor mahsulotining natijasi va q 1 vektor bo'ladi:

Javob: Chiziqlar orasidagi masofa L 1 va L 2 teng d=7.25061.

2. Kosmosda kesishuvchi chiziqlar orasidagi masofa

Dekart to'rtburchaklar koordinatalar tizimi berilsin Oxyz va bu koordinatalar sistemasida to'g'ri chiziqlar berilgan bo'lsin L 1 va L 2 ((1) va (2) tenglamalar).

To'g'ri bo'lsin L 1 va L 2 parallel emas (biz oldingi xatboshida parallel chiziqlarni muhokama qildik). Chiziqlar orasidagi masofani topish uchun L 1 va L 2 qurish kerak parallel tekisliklar α 1 va α 2 to'g'ri bo'lishi uchun L 1 samolyotda yotish α 1 a to'g'ri L 2 - samolyotda α 2. Keyin chiziqlar orasidagi masofa L 1 va L 2 tekisliklar orasidagi masofaga teng L 1 va L 2 (3-rasm).

Qayerda n 1 ={A 1 , B 1 , C 1 ) − tekislikning normal vektori α 1 . Samolyot uchun α 1 to'g'ri chiziqdan o'tdi L 1, normal vektor n 1 yo'nalish vektoriga ortogonal bo'lishi kerak q 1 tekis L 1, ya'ni. Ushbu vektorlarning skalyar mahsuloti nolga teng bo'lishi kerak:

(27)−(29) chiziqli tenglamalar tizimini uchta tenglamali va to‘rtta noma’lumli yechish. A 1 , B 1 , C 1 , D 1 va tenglamaga almashtirish

Samolyotlar α 1 va α 2 parallel, shuning uchun normal vektorlar hosil bo'ladi n 1 ={A 1 , B 1 , C 1) va n 2 ={A 2 , B 2 , C 2) bu tekisliklar kollineardir. Agar bu vektorlar teng bo'lmasa, biz (31) ni ma'lum songa ko'paytirishimiz mumkin, natijada normal vektor n 2 (30) tenglamaning normal vektoriga to'g'ri keldi.

Keyin parallel tekisliklar orasidagi masofa quyidagi formula bo'yicha hisoblanadi:

(33)

Yechim. L Streyt M 1 (x 1 , y 1 , z 1)=M 1 nuqtadan o'tadi q 1 ={m 1 , p 1 , l 1 }={1, 3, −2}.

Streyt L 2 nuqtadan o'tadi M 2 (x 2 , y 2 , z 2)=M 1 (2, 1, 4) va yo'nalish vektoriga ega q 2 ={m 2 , p 2 , l 2 }={2, −3, 7}.

2 (6, -1, 2) va yo'nalish vektoriga ega α Keling, samolyot yasaymiz L 1 chiziq orqali o'tadi L 2 .

1, to'g'ri chiziqqa parallel α Samolyotdan beri L 1 chiziqdan o'tadi M 1 (x 1 , y 1 , z 1)=M 1, keyin u ham nuqtadan o'tadi n 1 ={m 1 , p 1 , l 1 (2, 1, 4) va normal vektor α 1) samolyot q 1 tekis L 1 yo'nalish vektoriga perpendikulyar

1 . Keyin tekislik tenglamasi shartni qondirishi kerak: α Samolyotdan beri L 1 chiziqqa parallel bo'lishi kerak

2, u holda quyidagi shart bajarilishi kerak:

(40)

Keling, ushbu tenglamalarni matritsa shaklida ifodalaymiz: A 1 , B 1 , C 1 , D 1.

Ushbu maqolada Yagona davlat imtihonidan olingan C2 muammosini hal qilish misolidan foydalanib, koordinatalar usuli yordamida topish usuli tahlil qilinadi. Eslatib o'tamiz, to'g'ri chiziqlar bir tekislikda yotmasa, qiyshiq bo'ladi. Xususan, agar bitta chiziq tekislikda yotsa, ikkinchi chiziq esa bu tekislikni birinchi chiziqda yotmaydigan nuqtada kesib o'tsa, unda bunday chiziqlar kesishadi (rasmga qarang).

Topmoq kesishgan chiziqlar orasidagi masofalar zarur:

1. Boshqa kesishuvchi chiziqqa parallel bo'lgan kesishgan chiziqlardan biri orqali tekislik o'tkazing.
2. Olingan tekislikka ikkinchi chiziqning istalgan nuqtasidan perpendikulyar tushiring. Ushbu perpendikulyarning uzunligi chiziqlar orasidagi kerakli masofa bo'ladi.

Keling, matematika bo'yicha yagona davlat imtihonidan C2 muammosini hal qilish misolidan foydalanib, ushbu algoritmni batafsilroq tahlil qilaylik.

Kosmosdagi chiziqlar orasidagi masofa

Vazifa. Birlik kubida ABCDA 1 B 1 C 1 D 1 chiziqlar orasidagi masofani toping B.A. 1 va D.B. 1 .

Guruch. 1. Topshiriq uchun rasm chizish

Yechim. Kubning diagonalining o'rtasidan D.B. 1 (nuqta O) chiziqqa parallel chiziq chizamiz A 1 B. Ushbu chiziqning qirralar bilan kesishish nuqtalari Miloddan avvalgi Va A 1 D 1 mos ravishda belgilanadi N Va M. Streyt MN samolyotda yotadi MNB 1 va chiziqqa parallel A 1 B, bu tekislikda yotmaydi. Bu to'g'ri chiziq degan ma'noni anglatadi A 1 B tekislikka parallel MNB 1 to'g'ri chiziq va tekislikning parallelizmiga asoslangan (2-rasm).

Guruch. 2. Kesishgan chiziqlar orasidagi kerakli masofa tanlangan chiziqning istalgan nuqtasidan tasvirlangan tekislikgacha bo'lgan masofaga teng.

Endi biz chiziqning qaysidir nuqtasidan masofani qidiramiz A 1 B samolyotga MNB 1 . Bu masofa, ta'rifga ko'ra, o'tish chiziqlari orasidagi kerakli masofa bo'ladi.

Bu masofani topish uchun biz koordinata usulidan foydalanamiz. Keling, to'rtburchaklar dekart koordinatalar tizimini kiritaylik, shunda uning kelib chiqishi B nuqtasi, o'qi bilan mos keladi. X chekkasi bo'ylab yo'naltirilgan edi B.A., eksa Y- chekka bo'ylab Miloddan avvalgi, eksa Z- chekka bo'ylab BB 1 (3-rasm).

Guruch. 3. Rasmda ko'rsatilganidek, to'rtburchaklar Dekart koordinata tizimini tanlaymiz

Tekislik tenglamasini topish MNB Ushbu koordinatalar tizimida 1. Buning uchun birinchi navbatda nuqtalarning koordinatalarini aniqlaymiz M, N Va B 1: Olingan koordinatalarni to'g'ri chiziqning umumiy tenglamasiga almashtiramiz va quyidagi tenglamalar tizimini olamiz:

Tizimning ikkinchi tenglamasidan biz uchinchisidan olamiz, shundan so'ng biz birinchisidan olamiz Olingan qiymatlarni to'g'ri chiziqning umumiy tenglamasiga almashtiring:

Biz shuni ta'kidlaymizki, aks holda samolyot MNB 1 kelib chiqishi orqali o'tadi. Ushbu tenglamaning ikkala tomonini bo'linib, biz quyidagilarni olamiz:

Nuqtadan tekislikgacha bo'lgan masofa formula bilan aniqlanadi.

Geometriya. 11-sinf

Dars mavzusi: Kesish chiziqlar orasidagi masofa

Ter-Ovanesyan G.L., oliy toifali o'qituvchi, Soros jamg'armasi mukofoti laureati

Moskva

Keling, kesishgan chiziqlar orasidagi masofani topish masalasini ko'rib chiqaylik. Kesishgan chiziqlar orasidagi masofa bu chiziqlarga umumiy perpendikulyar uzunligi.

Bizga ABCDA 1 B 1 C 1 D 1 kub berilsin, uning cheti AB = 1 birlikka teng. AB va DC 1 to'g'ri chiziqlar orasidagi masofani topish kerak: r(AB;DC 1) - ?

Bu ikki chiziq parallel tekisliklarda yotadi: AB AA 1 B 1 B tekislikda, DC 1 D 1 DC 1 C tekislikda yotadi. Avval shu ikki tekislikka perpendikulyarni topamiz. Rasmda bunday perpendikulyarlar ko'p. Bu BC, B 1 C 1, A 1 D 1 va AD segmentidir. Bulardan faqat shu tekisliklarga perpendikulyar, shuning uchun AB va DC 1 to'g'ri chiziqlarimizga perpendikulyar bo'lgan segmentni tanlash mantiqan to'g'ri keladi, balki shu to'g'ri chiziqlardan ham o'tadi. Bunday segment AD hisoblanadi. U bir vaqtning o'zida AB to'g'ri chiziqqa perpendikulyar, chunki u AA 1 B 1 B tekislikka va DC 1 to'g'ri chiziqqa perpendikulyar, chunki u D 1 DC 1 C tekisligiga perpendikulyar. Demak, AD umumiy. AB va DC 1 kesishuvchi to'g'ri chiziqlarga perpendikulyar. Bu to'g'ri chiziqlar orasidagi masofa shu perpendikulyarning uzunligi, ya'ni AD segmentining uzunligi. Ammo AD kubning bir chekkasidir. Shuning uchun masofa 1 ga teng:

r(AB;DC 1)=AD=1

Keling, kesishgan chiziqlar orasidagi masofani topishga oid yana bir muammoni ko'rib chiqaylik, biroz murakkabroq.

Bizga yana qirrasi birga teng kub berilsin. Qarama-qarshi yuzlarning diagonallari orasidagi masofani topishingiz kerak. Ya'ni, ABCDA 1 B 1 C 1 D 1 kubi berilgan. AB cheti=1. BA 1 va DC 1 to'g'ri chiziqlar orasidagi masofani topishingiz kerak: r(A 1 B; DC 1) - ?

Bu ikki chiziq kesishadi, ya'ni masofa umumiy perpendikulyarning uzunligidir. Siz umumiy perpendikulyarni chizishingiz mumkin emas, lekin uni quyidagicha shakllantirishingiz mumkin: bu bu chiziqlar yotadigan parallel tekisliklar orasidagi perpendikulyarning uzunligi. BA 1 to'g'ri chiziq AVV 1 A 1 tekislikda, DC 1 to'g'ri chiziq D 1 DCC 1 tekislikda yotadi. Ular parallel, ya'ni ular orasidagi masofa bu to'g'ri chiziqlar orasidagi masofadir. Va kubning yuzlari orasidagi masofa chekka uzunligi. Masalan, qovurg'aning uzunligi BC. Chunki BC AVV 1 A 1 tekislikka ham, DSS 1 D 1 tekisligiga ham perpendikulyar. Bu shuni anglatadiki, shartda berilgan to'g'ri chiziqlar orasidagi masofa parallel tekisliklar orasidagi masofaga teng va 1 ga teng:

r(A 1 B;DC 1)=BC=1

Keling, kesishgan chiziqlar orasidagi masofani topishga oid yana bir muammoni ko'rib chiqaylik.

Bizga barcha qirralari ma'lum bo'lgan muntazam uchburchak prizma berilsin. Yuqori va pastki tagliklarning chekkalari orasidagi masofani topishingiz kerak. Ya'ni, bizga ABCA 1 B 1 C 1 prizmasi berilgan. Bundan tashqari, AB=3=AA 1. BC va A 1 C 1 to'g'ri chiziqlar orasidagi masofani topish kerak: r(BC;A 1 C 1) - ?

Bu chiziqlar kesishganligi sababli ular orasidagi masofa umumiy perpendikulyarning uzunligi yoki ular yotadigan parallel tekisliklarga perpendikulyar uzunligidir. Keling, bu parallel tekisliklarni topamiz.

BC toʻgʻri chiziq ABC tekislikda, A 1 C 1 toʻgʻri chiziq A 1 B 1 C 1 tekislikda yotadi. Bu ikki tekislik parallel, chunki ular prizmaning yuqori va pastki asoslaridir. Bu shuni anglatadiki, bizning to'g'ri chiziqlarimiz orasidagi masofa bu parallel tekisliklar orasidagi masofadir. Va ularning orasidagi masofa AA 1 yon chetining uzunligiga, ya'ni 3 ga teng:

r(BC;A 1 C 1)=AA 1 =3

Bunda aniq vazifa Siz nafaqat umumiy perpendikulyarning uzunligini topishingiz, balki uni qurishingiz mumkin. Buning uchun barcha yon qirralardan BC va A 1 C 1 to'g'ri chiziq bilan umumiy nuqtalari bo'lgan birini tanlaymiz. Bizning rasmimizda bu chekka CC 1. U A 1 C 1 to'g'ri chiziqqa perpendikulyar bo'ladi, chunki u yuqori asos tekisligiga perpendikulyar va BC to'g'ri chiziqqa, chunki u pastki asos tekisligiga perpendikulyar. Shunday qilib, biz nafaqat masofani topamiz, balki bu umumiy perpendikulyarni ham qurishimiz mumkin.

Bugun darsda biz kesishgan chiziqlar orasidagi umumiy perpendikulyar uzunligini qanday topishni esladik.

Men yangi Verdov faylini yaratib, bunday qiziqarli mavzuni davom ettirishimga bir daqiqa ham o'tmagan edi. Siz mehnat ruhining lahzalarini qo'lga kiritishingiz kerak, shuning uchun lirik kirish bolmaydi. Nasriy kaltaklash bo'ladi =)

Ikkita tekis bo'shliqlar mumkin:

1) chatishtirish;

2) nuqtada kesishadi;

3) parallel bo'lishi;

4) mos kelish.

1-sonli ish boshqa holatlardan tubdan farq qiladi. Ikki to'g'ri chiziq bir tekislikda yotmasa, kesishadi. Bir qo'lni yuqoriga ko'taring va boshqa qo'lni oldinga cho'zing - bu erda chiziqlarni kesib o'tishga misol. 2-4 nuqtalarda to'g'ri chiziqlar yotishi kerak bitta tekislikda.

Kosmosdagi chiziqlarning nisbiy o'rnini qanday aniqlash mumkin?

Ikkita to'g'ridan-to'g'ri bo'shliqni ko'rib chiqing:

- Streyt, nuqta bilan berilgan va yo'nalish vektori;
– nuqta va yo‘nalish vektori bilan aniqlangan to‘g‘ri chiziq.

Yaxshiroq tushunish uchun keling, sxematik chizma tuzamiz:

Chizma misol sifatida kesishuvchi to'g'ri chiziqlarni ko'rsatadi.

Ushbu to'g'ri chiziqlar bilan qanday kurashish mumkin?

Nuqtalar ma'lum bo'lgani uchun vektorni topish oson.

To'g'ri bo'lsa chatishtirish, keyin vektorlar mutanosib emas(darsga qarang Vektorlarning chiziqli (no) bog'liqligi. Vektorlar asoslari), demak, ularning koordinatalaridan tashkil topgan determinant nolga teng emas. Yoki, aslida bir xil narsa, u nolga teng bo'lmaydi: .

2-4-sonli holatlarda bizning strukturamiz bir tekislikka "tushadi" va vektorlar koplanar, va aralash mahsulot chiziqli bo'ladi bog'liq vektorlar nolga teng: .

Keling, algoritmni yanada kengaytiraylik. Keling, shunday da'vo qilaylik Shuning uchun, chiziqlar kesishadi, parallel yoki mos keladi.

Yo'nalish vektorlari bo'lsa kollinear, keyin chiziqlar parallel yoki mos keladi. Yakuniy tirnoq uchun men quyidagi texnikani taklif qilaman: bitta chiziqdagi har qanday nuqtani oling va uning koordinatalarini ikkinchi chiziq tenglamasiga almashtiring; agar koordinatalar "mos" bo'lsa, unda chiziqlar bir-biriga to'g'ri keladi, agar ular "mos kelmasa", chiziqlar parallel bo'ladi;

Algoritm oddiy, ammo amaliy misollar hali ham zarar qilmaydi:

11-misol

Ikki chiziqning o'zaro o'rnini toping

Yechim: ko'pgina geometriya masalalarida bo'lgani kabi, yechimni nuqta bo'yicha shakllantirish qulay:

1) Tenglamalardan nuqtalar va yo'nalish vektorlarini chiqaramiz:

2) vektorni toping:

Shunday qilib, vektorlar koplanardir, ya'ni chiziqlar bir tekislikda yotadi va kesishishi, parallel bo'lishi yoki mos kelishi mumkin.

4) Yo‘nalish vektorlarining kollinearligini tekshiramiz.

Ushbu vektorlarning mos keladigan koordinatalaridan tizim tuzamiz:

Kimdan hamma tenglamalar shundan kelib chiqadiki, demak, sistema izchil, vektorlarning mos koordinatalari proportsional, vektorlar esa kollineardir.

Xulosa: chiziqlar parallel yoki mos keladi.

5) Chiziqlarning umumiy nuqtalari borligini aniqlang. Birinchi chiziqqa tegishli nuqtani olaylik va uning koordinatalarini chiziq tenglamalariga almashtiramiz:

Shunday qilib, umumiy nuqtalar to'g'ri chiziqlar yo'q va ular parallel bo'lishdan boshqa tanlovi yo'q.

Javob:

Qiziqarli misol Uchun mustaqil qaror:

12-misol

Chiziqlarning o'zaro joylashishini aniqlang

Bu siz o'zingiz hal qilishingiz uchun misoldir. E'tibor bering, ikkinchi qatorda parametr sifatida harf mavjud. Mantiqiy. Umumiy holda, bu ikki xil chiziq, shuning uchun har bir satr o'z parametriga ega.

Va yana sizni misollarni o'tkazib yubormaslikni so'rayman, men taklif qilayotgan vazifalar tasodifiy emas ;-)

Kosmosdagi chiziq bilan bog'liq muammolar

Darsning yakuniy qismida men ko'rib chiqishga harakat qilaman maksimal miqdor turli vazifalar fazoviy chiziqlar bilan. Bunda hikoyaning asl tartibi kuzatiladi: avval kesishuvchi chiziqlar, keyin kesishuvchi chiziqlar bilan bog‘liq masalalarni ko‘rib chiqamiz va oxirida fazodagi parallel chiziqlar haqida gapiramiz. Biroq, shuni aytishim kerakki, ushbu darsning ba'zi vazifalari bir vaqtning o'zida chiziqlar joylashishining bir nechta holatlari uchun shakllantirilishi mumkin va shu munosabat bilan bo'limni paragraflarga bo'lish biroz o'zboshimchalik bilan amalga oshiriladi. Yana bor oddiy misollar, ko'proq bor murakkab misollar, va umid qilamanki, har bir kishi o'ziga kerak bo'lgan narsani topadi.

Chiziqlarni kesib o'tish

Shuni eslatib o'tamanki, to'g'ri chiziqlar ikkalasi ham yotadigan tekislik bo'lmasa, kesishadi. Amaliyotni o'ylab yurganimda, hayolga bir yirtqich muammo keldi va endi men sizning e'tiboringizga to'rt boshli ajdahoni taqdim etishdan xursandman:

13-misol

To'g'ri chiziqlar berilgan. Majburiy:

a) chiziqlar kesishishini isbotlash;

b) berilgan chiziqlarga perpendikulyar nuqtadan o'tuvchi chiziq tenglamalarini toping;

v) o'z ichiga olgan to'g'ri chiziq tenglamalarini tuzing umumiy perpendikulyar o'tish liniyalari;

d) chiziqlar orasidagi masofani toping.

Yechim: Yurgan kishi yo'lni egallaydi:

a) Chiziqlar kesishishini isbotlaylik. Ushbu chiziqlarning nuqtalari va yo‘nalish vektorlarini topamiz:

Vektorni topamiz:

Keling, hisoblaylik vektorlarning aralash mahsuloti:

Shunday qilib, vektorlar mutanosib emas, ya'ni chiziqlar kesishadi, bu isbotlanishi kerak bo'lgan narsadir.

Ehtimol, hamma chiziqlarni kesib o'tish uchun tekshirish algoritmi eng qisqa ekanligini payqagan.

b) nuqtadan o'tuvchi va to'g'ri chiziqlarga perpendikulyar bo'lgan chiziq tenglamalarini toping. Keling, sxematik chizma tuzamiz:

O'zgartirish uchun men to'g'ridan-to'g'ri xabar yubordim ORQADA to'g'ridan-to'g'ri, o'tish joylarida qanday qilib biroz o'chirilganiga qarang. Chorvachilikmi? Ha, umuman olganda, "de" to'g'ri chiziq asl to'g'ri chiziqlar bilan kesishadi. Garchi bu daqiqa Bizni hali bu qiziqtirmaydi, biz faqat perpendikulyar chiziq qurishimiz kerak va bu ham.

To'g'ridan-to'g'ri "de" haqida nima ma'lum? Unga tegishli nuqta ma'lum. Qo'llanma vektori yetarli emas.

Shartga ko'ra, to'g'ri chiziq to'g'ri chiziqlarga perpendikulyar bo'lishi kerak, ya'ni uning yo'nalishi vektori yo'nalish vektorlariga ortogonal bo'ladi. 9-misoldan allaqachon tanish bo'lgan holda vektor mahsulotini topamiz:

Nuqta va yo‘nalish vektoridan foydalanib “de” to‘g‘ri chiziq tenglamalarini tuzamiz:

Tayyor. Asos sifatida siz maxrajlardagi belgilarni o'zgartirishingiz va javobni shaklda yozishingiz mumkin , lekin bunga ehtiyoj yo'q.

Tekshirish uchun siz nuqta koordinatalarini hosil bo'lgan to'g'ri chiziq tenglamalariga almashtirishingiz kerak, keyin foydalaning vektorlarning skalyar mahsuloti vektor haqiqatan ham "pe one" va "pe two" yo'nalish vektorlariga ortogonal ekanligiga ishonch hosil qiling.

Umumiy perpendikulyar bo'lgan chiziq tenglamalarini qanday topish mumkin?

c) Bu muammo yanada qiyin bo'ladi. Men manikyurlar uchun bu nuqtani o'tkazib yuborishni tavsiya qilaman, analitik geometriyaga bo'lgan samimiy hamdardligingizni sovitib qo'ymoqchi emasman =) Aytgancha, ko'proq tayyor o'quvchilar ham to'xtab qolishsa yaxshi bo'lardi, haqiqat shundaki, murakkablik nuqtai nazaridan misol maqolada oxirgi joylashishi kerak, lekin taqdimot mantig'iga ko'ra u shu erda joylashgan bo'lishi kerak.

Shunday qilib, siz egri chiziqlarga umumiy perpendikulyar bo'lgan chiziq tenglamalarini topishingiz kerak.

- bu ushbu chiziqlarni bog'laydigan va ushbu chiziqlarga perpendikulyar bo'lgan segment:

Mana bizning chiroyli yigitimiz: - kesishgan chiziqlarning umumiy perpendikulyar. U yagona. Bunga o'xshash boshqasi yo'q. Ushbu segmentni o'z ichiga olgan chiziq uchun tenglamalar yaratishimiz kerak.

To'g'ridan-to'g'ri "um" haqida nima ma'lum? Uning yo'nalishi vektori ma'lum, oldingi xatboshida topilgan. Ammo, afsuski, biz "em" to'g'ri chiziqqa tegishli bitta nuqtani ham, perpendikulyarning uchlarini ham bilmaymiz - nuqtalar . Ushbu perpendikulyar chiziq ikkita asl chiziqni qayerda kesib o'tadi? Afrikadami, Antarktidadami? Vaziyatni dastlabki ko'rib chiqish va tahlil qilishdan muammoni qanday hal qilish kerakligi umuman aniq emas ... Ammo to'g'ri chiziqning parametrik tenglamalaridan foydalanish bilan bog'liq hiyla-nayrang mavjud.

Biz qarorni nuqta bo'yicha shakllantiramiz:

1) Birinchi qator tenglamalarini parametrik shaklda qayta yozamiz:

Keling, fikrni ko'rib chiqaylik. Biz koordinatalarni bilmaymiz. LEKIN. Agar nuqta berilgan chiziqqa tegishli bo'lsa, uning koordinatalari ga to'g'ri keladi, uni bilan belgilaymiz. Keyin nuqtaning koordinatalari quyidagi shaklda yoziladi:

Hayot yaxshilanmoqda, bitta noma'lum hali ham uchta noma'lum emas.

2) Xuddi shu g'azabni ikkinchi nuqtada qilish kerak. Ikkinchi qator tenglamalarini parametrik shaklda qayta yozamiz:

Agar nuqta berilgan chiziqqa tegishli bo'lsa, u holda juda aniq ma'noga ega uning koordinatalari parametrik tenglamalarni qondirishi kerak:

Yoki:

3) Vektor, oldingi topilgan vektor kabi, to'g'ri chiziqning yo'naltiruvchi vektori bo'ladi. Ikki nuqtadan vektorni qanday qurish haqida maqolada muhokama qilingan qadim zamonlar darsda Dummies uchun vektorlar. Endi farq shundaki, vektorlarning koordinatalari noma'lum parametr qiymatlari bilan yoziladi. Nima bo'libdi? Hech kim vektor boshining tegishli koordinatalarini vektor oxiri koordinatalaridan ayirishni taqiqlamaydi.

Ikki nuqta bor: .

Vektorni topish:

4) Yo'nalish vektorlari kollinear bo'lganligi sababli, bir vektor ikkinchisi orqali ma'lum "lambda" proportsionallik koeffitsienti bilan chiziqli ravishda ifodalanadi:

Yoki koordinatali:

Bu eng oddiy bo'lib chiqdi chiziqli tenglamalar tizimi uchta noma'lum bilan, masalan, standart echilishi mumkin Kramer usuli. Ammo bu erda qochish uchun imkoniyat bor oz qon, uchinchi tenglamadan biz "lambda" ni ifodalaymiz va uni birinchi va ikkinchi tenglamalarga almashtiramiz:

Shunday qilib: , va bizga "lambda" kerak emas. Parametr qiymatlari bir xil bo'lib chiqishi shunchaki baxtsiz hodisadir.

5) Osmon butunlay tozalanmoqda, keling, topilgan qiymatlarni almashtiramiz fikrlarimizga:

Yo'nalish vektori ayniqsa kerak emas, chunki uning hamkasbi allaqachon topilgan.

Uzoq safardan keyin tekshirish har doim qiziq.

:

To'g'ri tenglik olinadi.

Tenglamalarda nuqta koordinatalarini almashtiramiz :

To'g'ri tenglik olinadi.

6) Yakuniy akkord: nuqta (siz uni olishingiz mumkin) va yo‘nalish vektori yordamida to‘g‘ri chiziq tenglamalarini tuzamiz:

Asos sifatida, siz koordinatalari buzilmagan "yaxshi" nuqtani tanlashingiz mumkin, ammo bu kosmetikdir.

Kesishgan chiziqlar orasidagi masofani qanday topish mumkin?

d) Biz ajdahoning to'rtinchi boshini kesib tashladik.

Birinchi usul. Hatto yo'l emas, lekin kichik maxsus holat. Kesishgan chiziqlar orasidagi masofa ularning umumiy perpendikulyar uzunligiga teng: .

Ekstremal nuqtalar umumiy perpendikulyar oldingi xatboshida topilgan va vazifa oddiy:

Ikkinchi usul. Amalda, ko'pincha umumiy perpendikulyarning uchlari noma'lum, shuning uchun boshqa yondashuv qo'llaniladi. Parallel tekisliklarni kesishuvchi ikkita toʻgʻri chiziq orqali oʻtkazish mumkin va bu tekisliklar orasidagi masofa shu toʻgʻri chiziqlar orasidagi masofaga teng. Xususan, bu tekisliklar orasida umumiy perpendikulyar chiqib turadi.

Analitik geometriya kursida yuqoridagi mulohazalardan kelib chiqib, kesishuvchi to‘g‘ri chiziqlar orasidagi masofani topish formulasi olinadi:
("Um bir, ikkita" nuqtalarimiz o'rniga siz o'zboshimchalik bilan chiziqlarni olishingiz mumkin).

Vektorlarning aralash mahsuloti"a" bandida allaqachon topilgan: .

Vektorlarning vektor mahsuloti"be" bandida topilgan: , uning uzunligini hisoblaymiz:

Shunday qilib:

Keling, g'urur bilan kuboklarni bir qatorda namoyish qilaylik:

Javob:
A) , ya'ni to'g'ri chiziqlar kesishadi, bu isbotlanishi kerak edi;
b) ;
V) ;
G)

Chiziqlarni kesib o'tish haqida yana nima deya olasiz? Ularning o'rtasida aniq burchak mavjud. Lekin universal formula Keyingi xatboshida burchakni ko'rib chiqamiz:

Kesishgan to'g'ri bo'shliqlar, albatta, bir tekislikda yotadi:

Birinchi fikr - bor kuchingiz bilan kesishish nuqtasiga suyanish. Va men darhol o'yladim, nega o'zingizni to'g'ri istaklarni inkor etasiz?! Keling, hozir uning ustiga chiqaylik!

Fazoviy chiziqlarning kesishish nuqtasini qanday topish mumkin?

14-misol

Chiziqlarning kesishish nuqtasini toping

Yechim: Chiziqlar tenglamalarini parametrik shaklda qayta yozamiz:

Bu vazifa Ushbu darsning 7-misolida batafsil muhokama qilingan (qarang. Fazodagi chiziq tenglamalari). Aytgancha, men 12-misoldan to'g'ri chiziqlarni o'zim oldim. Men yolg'on gapirmayman, yangilarini o'ylab topishga dangasaman.

Yechim standart bo'lib, biz kesishgan chiziqlarning umumiy perpendikulyar tenglamalarini aniqlashga harakat qilganimizda allaqachon duch kelganmiz.

Chiziqlarning kesishish nuqtasi chiziqqa tegishli, shuning uchun uning koordinatalari ushbu chiziqning parametrik tenglamalarini qanoatlantiradi va ularga mos keladi. juda aniq parametr qiymati:

Ammo xuddi shu nuqta ikkinchi qatorga ham tegishli, shuning uchun:

Tegishli tenglamalarni tenglashtiramiz va soddalashtirishni amalga oshiramiz:

Qabul qildi uchlik tizimi ikkita noma'lumli chiziqli tenglamalar. Agar chiziqlar kesishsa (bu 12-misolda isbotlangan), unda tizim majburiy ravishda izchil bo'ladi va o'ziga xos echimga ega. Buni hal qilish mumkin Gauss usuli, lekin biz bunday bolalar bog'chasi fetishizmi bilan gunoh qilmaymiz, biz buni oddiyroq qilamiz: birinchi tenglamadan biz "te nol" ni ifodalaymiz va uni ikkinchi va uchinchi tenglamalarga almashtiramiz:

Oxirgi ikkita tenglama mohiyatan bir xil bo'lib chiqdi va ulardan kelib chiqadiki. Keyin:

Parametrning topilgan qiymatini tenglamalarga almashtiramiz:

Javob:

Tekshirish uchun parametrning topilgan qiymatini tenglamalarga almashtiramiz:
Tekshirish kerak bo'lgan bir xil koordinatalar olingan. Ehtiyotkor o'quvchilar nuqta koordinatalarini chiziqlarning asl kanonik tenglamalariga almashtirishlari mumkin.

Aytgancha, buning aksini qilish mumkin edi: nuqtani "es nol" orqali toping va uni "te zero" orqali tekshiring.

Mashhur matematik xurofot shunday deydi: chiziqlar kesishmasi muhokama qilinadigan joyda har doim perpendikulyarlarning hidi bor.

Berilganiga perpendikulyar bo'shliq chizig'ini qanday qurish mumkin?

(chiziqlar kesishadi)

15-misol

a) to'g'ri chiziqqa perpendikulyar nuqtadan o'tuvchi chiziq tenglamalarini yozing (chiziqlar kesishadi).

b) nuqtadan chiziqgacha bo'lgan masofani toping.

Eslatma : "chiziqlar kesishadi" bandi - ahamiyatli. Nuqta orqali
"el" to'g'ri chiziq bilan kesishadigan cheksiz sonli perpendikulyar chiziqlar chizishingiz mumkin. Yagona yechim qachon, orqali sodir bo'ladi bu nuqta perpendikulyar to'g'ri chiziq chiziladi ikki to'g'ri chiziq bilan berilgan (13-misol, "b" nuqtasiga qarang).

A) Yechim: Noma'lum qatorni bilan belgilaymiz. Keling, sxematik chizma tuzamiz:

To'g'ri chiziq haqida nima ma'lum? Shartga ko'ra, ball beriladi. To'g'ri chiziq tenglamalarini tuzish uchun yo'nalish vektorini topish kerak. Vektor bunday vektor sifatida juda mos keladi, shuning uchun biz u bilan shug'ullanamiz. Aniqroq qilib aytganda, vektorning noma'lum uchini bo'yinbog' bilan olaylik.

1) “el” toʻgʻri chiziq tenglamalaridan uning yoʻnalish vektorini chiqaramiz va tenglamalarni parametrik shaklda qayta yozamiz:

Ko'pchilik, dars paytida sehrgar uchinchi marta shlyapasidan oq oqqushni tortib olishini taxmin qilishdi. Koordinatalari noma'lum bo'lgan nuqtani ko'rib chiqing. Nuqta bo'lgani uchun uning koordinatalari "el" to'g'ri chiziqning parametrik tenglamalarini qanoatlantiradi va ular ma'lum bir parametr qiymatiga mos keladi:

Yoki bitta qatorda:

2) Shartga ko'ra, chiziqlar perpendikulyar bo'lishi kerak, shuning uchun ularning yo'nalish vektorlari ortogonaldir. Va agar vektorlar ortogonal bo'lsa, ularning skalyar mahsulot nolga teng:

Nima bo'ldi? Eng oddiy chiziqli tenglama bitta noma'lum bilan:

3) Parametrning qiymati ma'lum, nuqtani topamiz:

Va yo'nalish vektori:
.

4) To'g'ri chiziq tenglamalarini nuqta va yo'nalish vektoridan foydalanib tuzamiz :

Proportsiyaning maxrajlari kasr bo'lib chiqdi va kasrlardan xalos bo'lish to'g'ri bo'lganda aynan shunday bo'ladi. Men ularni shunchaki -2 ga ko'paytiraman:

Javob:

Eslatma : yechimning yanada qat'iy yakuni quyidagicha rasmiylashtiriladi: nuqta va yo'nalish vektoridan foydalanib to'g'ri chiziq tenglamalarini tuzamiz. . Darhaqiqat, agar vektor to'g'ri chiziqning yo'naltiruvchi vektori bo'lsa, u holda kollinear vektor ham ushbu to'g'ri chiziqning yo'naltiruvchi vektori bo'ladi.

Tekshirish ikki bosqichdan iborat:

1) chiziqlarning yo'nalish vektorlarini ortogonallik uchun tekshirish;

2) nuqtaning koordinatalarini har bir chiziq tenglamalariga almashtiramiz, ular u erda ham, u erda ham "mos" bo'lishi kerak.

HAQIDA tipik harakatlar Ko'p narsa aytilgan edi, shuning uchun men loyihani tekshirdim.

Aytgancha, men yana bir nuqtani unutdim - "el" to'g'ri chiziqqa nisbatan "en" nuqtasiga simmetrik "zyu" nuqtasini qurish. Biroq, maqolada topish mumkin bo'lgan yaxshi "tekis analog" mavjud Samolyotdagi to'g'ri chiziq bilan eng oddiy masalalar. Bu erda yagona farq qo'shimcha "Z" koordinatasida bo'ladi.

Kosmosdagi nuqtadan chiziqgacha bo'lgan masofani qanday topish mumkin?

b) Yechim: Nuqtadan chiziqgacha bo'lgan masofani topamiz.

Birinchi usul. Bu masofa perpendikulyar uzunligiga aynan teng: . Yechim aniq: agar nuqtalar ma'lum bo'lsa , Bu:

Ikkinchi usul. Amaliy masalalarda perpendikulyarning asosi ko'pincha muhrlangan sirdir, shuning uchun tayyor formuladan foydalanish yanada oqilona.

Nuqtadan chiziqgacha bo'lgan masofa quyidagi formula bilan ifodalanadi:
, bu yerda “el” to‘g‘ri chiziqning yo‘naltiruvchi vektori va – ozod berilgan chiziqqa tegishli nuqta.

1) Chiziq tenglamalaridan biz yo'nalish vektorini va eng qulay nuqtani chiqaramiz.

2) Shartdan nuqta ma'lum, vektorni keskinlashtiring:

3) Keling, topamiz vektor mahsuloti va uning uzunligini hisoblang:

4) Yo'naltiruvchi vektor uzunligini hisoblang:

5) Shunday qilib, nuqtadan chiziqgacha bo'lgan masofa: