Natural sonlar (N). Bosh va kompozit sonlar. Bo'luvchi, ko'p. Eng katta umumiy bo'luvchi, eng kichik umumiy bo'luvchi. Eng kichik umumiy ko'p va eng katta umumiy bo'luvchi Ko'paytirish. multiplikator * multiplikator = mahsulot

Natural sonlarning umumiy karralariaVabbu raqamlarning har biriga karrali sondir.

Barcha umumiy ko'paytmalarning eng kichik soni A Va b chaqirdi bu raqamlarning eng kichik umumiy karrali.

Raqamlarning eng kichik umumiy karrali A Va b Keling, K ni belgilashga rozi bo'laylik ( A, b).

Masalan, ikkita 12 va 18 raqamlari umumiy ko'paytmalari: 36, 72, 108, 144, 180 va boshqalar. 36 soni 12 va 18 sonlarining eng kichik umumiy karrali. Siz yozishingiz mumkin: K(12, 18) = 36.

Eng kam umumiy koʻplik uchun quyidagi gaplar toʻgʻri boʻladi:

1. Sonlarning eng kichik umumiy karrali A Va b

2. Sonlarning eng kichik umumiy karrali A Va b bu raqamlarning kattasidan kam emas, ya'ni. Agar a >b, keyin K( A, b) ≥ A.

3. Sonlarning har qanday umumiy karrali A Va b ularning eng kichik umumiy karrasiga bo'linadi.

Eng katta umumiy bo'luvchi

Natural sonlarning umumiy bo'luvchisi a vabberilgan sonlarning har biriga boʻluvchi boʻlgan son.

Raqamlarning barcha umumiy bo'luvchilarining eng katta soni A Va b bu sonlarning eng katta umumiy bo'luvchisi deyiladi.

Raqamlarning eng katta umumiy bo'luvchisi A Va b Keling, D ni belgilashga rozi bo'laylik ( A, b).

Misol uchun, 12 va 18 raqamlari uchun umumiy bo'linuvchilar raqamlardir: 1, 2, 3, 6. 6 raqami 12 va 18. Siz yozishingiz mumkin: D (12, 18) = 6.

1 raqami har qanday ikkita natural sonning umumiy bo'luvchisidir a Va b. Agar bu sonlarning boshqa umumiy boʻluvchilari boʻlmasa, u holda D( A, b) = 1 va raqamlar A Va b chaqiriladi o'zaro asosiy.

Masalan, 14 va 15 raqamlari nisbatan tub sonlardir, chunki D(14, 15) = 1.

Eng katta umumiy boʻluvchi uchun quyidagi gaplar toʻgʻri boʻladi:

1. Sonlarning eng katta umumiy bo‘luvchisi a Va b har doim mavjud va noyobdir.

2. Sonlarning eng katta umumiy bo‘luvchisi A Va b berilgan raqamlardan kichikroqdan oshmaydi, ya'ni. Agar a< b, Bu D(a, b) ≤ a.

3. Sonlarning eng katta umumiy bo‘luvchisi a Va b bu sonlarning har qanday umumiy boʻluvchisiga boʻlinadi.

Raqamlarning eng katta umumiy soni A Va b va ularning eng katta umumiy boʻluvchisi oʻzaro bogʻliq: sonlarning eng kichik umumiy karrali va eng katta umumiy boʻluvchining koʻpaytmasi. A Va b bu raqamlarning mahsulotiga teng, ya'ni. K( a, b)·D( a, b) = a· b.

Ushbu bayonotdan quyidagi xulosalar kelib chiqadi:

a) Ikki o'zaro tub sonning eng kichik umumiy karrali bu sonlarning ko'paytmasiga teng, ya'ni. D( a, b) = 1 => K( a, b) = a· b;

Masalan, 14 va 15 sonlarining eng kichik umumiy karralini topish uchun ularni ko'paytirish kifoya qiladi, chunki D(14, 15) = 1.

b) A oʻzaro tub sonlar koʻpaytmasiga boʻlinadi m Va n ga boʻlinishi zarur va yetarli m, va yana n.

Bu gap ikki nisbatan tub sonning koʻpaytmasi sifatida ifodalanishi mumkin boʻlgan sonlarga boʻlinish belgisidir.

c) Berilgan ikkita sonni eng katta umumiy boʻluvchiga boʻlish natijasida olingan boʻlaklar nisbatan tub sonlardir.

Bu xususiyatdan berilgan sonlarning topilgan eng katta umumiy boʻluvchisining toʻgʻriligini tekshirishda foydalanish mumkin. Masalan, 12 soni 24 va 36 sonlarining eng katta umumiy boʻluvchisi ekanligini tekshirib koʻramiz. Buning uchun oxirgi gapga koʻra 24 va 36 ni 12 ga boʻlamiz. Biz mos ravishda 2 va 3 raqamlarini olamiz. muqobildir. Demak, D(24, 36)=12.

Muammo 32. 6 ga bo‘linish testini tuzing va isbotlang.

Yechim x 6 ga bo'linadigan bo'lsa, uning 2 va 3 ga bo'linishi zarur va etarli.

Raqamga ruxsat bering x 6 ga bo'linadi. So'ngra haqiqatdan x 6 va 62, shundan kelib chiqadi x 2. Va haqiqatdan x 6 va 63, shundan kelib chiqadi x 3. Son 6 ga bo‘linishi uchun u 2 va 3 ga bo‘linishi kerakligini isbotladik.

Keling, ushbu shartning etarliligini ko'rsatamiz. Chunki x 2 va x 3, keyin x- 2 va 3 sonlarning umumiy karrali. Har qanday umumiy sonlar ularning eng kichik karrali ga bo'linadi, ya'ni x K(2;3).

D(2, 3)=1 ekan, K(2, 3)=2·3=6. Demak, x 6.

Muammo 33. 12, 15 va 60 ni shakllantirish.

Yechim. Natural son uchun x 12 ga bo'linadigan bo'lsa, 3 va 4 ga bo'linishi zarur va etarli.

Natural son uchun x 15 ga bo'linadigan bo'lsa, 3 va 5 ga bo'linishi zarur va etarli.

Natural son uchun x 60 ga bo'linadigan bo'lsa, uning 4, 3 va 5 ga bo'linishi zarur va etarli.

Muammo 34. Raqamlarni toping a Va b, agar K( a, b)=75, a· b=375.

Yechim. K formulasidan foydalanish a,b)·D( a,b)=a· b, kerakli sonlarning eng katta umumiy boʻluvchisini toping A Va b:

D( a, b) === 5.

Keyin kerakli raqamlar shaklda ifodalanishi mumkin A= 5R, b= 5q, Qayerda p Va q p va 5 q tenglikka a b = 275. Keling, 5 ni olamiz p· 5 q=375 yoki p· q=15. Hosil boʻlgan tenglamani ikkita oʻzgaruvchili tanlash yoʻli bilan yechamiz: koʻpaytmasi 15 ga teng boʻlgan nisbiy tub sonlar juftlarini topamiz. Shunday ikkita juftlik mavjud: (3, 5) va (1, 15). Shuning uchun kerakli raqamlar A Va b Ular: 15 va 25 yoki 5 va 75.

Muammo 35. Raqamlarni toping A Va b, agar D( a, b) = 7 va a· b= 1470.

Yechim. D beri ( a, b) = 7, u holda kerakli sonlar shaklda ifodalanishi mumkin A= 7R, b= 7q, Qayerda p Va q o'zaro tub sonlardir. 5-iboralarni almashtiramiz R va 5 q tenglikka a b = 1470. Keyin 7 p· 7 q= 1470 yoki p· q= 30. Ikki oʻzgaruvchili hosil boʻlgan tenglamani tanlash yoʻli bilan yechamiz: koʻpaytmasi 30 ga teng boʻlgan nisbiy tub sonlar juftlarini topamiz. Bunday juftlik toʻrtta boʻladi: (1, 30), (2, 15), (3, 10). ), (5, 6). Shuning uchun kerakli raqamlar A Va b Ular: 7 va 210, 14 va 105, 21 va 70, 35 va 42.

Muammo 36. Raqamlarni toping A Va b, agar D( a, b) = 3 va A:b= 17:14.

Yechim. Chunki a:b= 17:14, keyin A= 17R Va b= 14p, Qayerda R- sonlarning eng katta umumiy bo‘luvchisi A Va b. Demak, A= 17·3 = 51, b= 14·3 = 42.

Muammo 37. Raqamlarni toping A Va b, agar ma'lum bo'lsa, K( a, b) = 180, a:b= 4:5.

Yechim. Chunki a: b=4:5 A=4R Va b=5R, Qayerda R- sonlarning eng katta umumiy bo‘luvchisi a Va b. Keyin R·180=4 R· 5 R. Qayerda R=9. Demak, a= 36 va b=45.

Muammo 38. Raqamlarni toping A Va b, agar D( a,b)=5, K( a,b)=105.

Yechim. D beri ( a, b) K( a, b) = a· b, Bu a· b= 5 105 = 525. Bundan tashqari, kerakli raqamlar shaklda ifodalanishi mumkin A= 5R Va b= 5q, Qayerda p Va q o'zaro tub sonlardir. 5-iboralarni almashtiramiz R va 5 q tenglikka A· b= 525. Keyin 5 p· 5 q=525 yoki p· q=21. Ko'paytmasi 21 ga teng bo'lgan nisbiy tub sonlar juftlarini topamiz. Bunday ikkita juftlik mavjud: (1, 21) va (3, 7). Shuning uchun kerakli raqamlar A Va b quyidagilar: 5 va 105, 15 va 35.

Muammo 39. Raqam ekanligini isbotlang n(2n+ 1)(7n+ 1) har qanday natural uchun 6 ga boʻlinadi n.

Yechim. 6 soni kompozitdir; uni ikkita nisbatan tub sonning ko'paytmasi sifatida ko'rsatish mumkin: 6 = 2·3. Agar berilgan sonning 2 va 3 ga boʻlinishini isbotlasak, kompozit songa boʻlinish qobiliyatini tekshirishga asoslanib, u 6 ga boʻlinadi degan xulosaga kelishimiz mumkin.

Raqam ekanligini isbotlash uchun n(2n+ 1)(7n+ 1) 2 ga bo'linadi, biz ikkita imkoniyatni ko'rib chiqishimiz kerak:

1) n 2 ga bo'linadi, ya'ni. n= 2k. Keyin mahsulot n(2n+ 1)(7n+ 1) quyidagicha ko'rinadi: 2 k(4k+ 1)(14k+ 1). Ushbu mahsulot 2 ga bo'linadi, chunki birinchi omil 2 ga bo'linadi;

2) n 2 ga bo'linmaydi, ya'ni. n= 2k+ 1. Keyin mahsulot n(2n+ 1 )(7n+ 1) quyidagicha ko'rinadi: (2 k+ 1)(4k+ 3)(14k+ 8). Ushbu mahsulot 2 ga bo'linadi, chunki oxirgi omil 2 ga bo'linadi.

Ish ekanligini isbotlash uchun n(2n+ 1)(7n+ 1) 3 ga bo'linadi, uchta imkoniyatni hisobga olish kerak:

1) n 3 ga bo'linadi, ya'ni. n= 3k. Keyin mahsulot n(2n+ 1)(7n+ 1) quyidagicha ko'rinadi: 3 k(6k+ 1)(21k+ 1). Ushbu mahsulot 3 ga bo'linadi, chunki birinchi omil 3 ga bo'linadi;

2) n 3 ga bo'linganda, qolgan 1 ga teng, ya'ni. n= 3k+ 1. Keyin mahsulot n(2n+ 1)(7n+ 1) quyidagicha ko'rinadi: (3 k+ 1)(6k+ 3)(21k+ 8). Ushbu mahsulot 3 ga bo'linadi, chunki ikkinchi omil 3 ga bo'linadi;

3) n 3 ga bo'linganda, qolgan 2 ga teng, ya'ni. n= 3k+ 2. Keyin mahsulot n(2n+ 1)(7n+ 1) quyidagicha ko'rinadi: (3 k+ 2)(6k+ 5)(21k+ 15). Ushbu mahsulot 3 ga bo'linadi, chunki oxirgi omil 3 ga bo'linadi.

Shunday qilib, mahsulot ekanligi isbotlangan n(2n+ 1)(7n+ 1) 2 va 3 ga boʻlinadi. Bu 6 ga boʻlinishini bildiradi.

Mustaqil ishlash uchun mashqlar

1. Ikkita raqam berilgan: 50 va 75. To‘plamni yozing:

a) 50 sonining bo'luvchilari; b) 75 sonining bo‘luvchilari; v) berilgan sonlarning umumiy bo‘luvchilari.

50 va 75 ning eng katta umumiy boʻluvchisi nima?

2. 375 soni sonlarning umumiy karralimi: a) 125 va 75; b) 85 va 15?

3. Raqamlarni toping A Va b, agar ma'lum bo'lsa, K( a, b) = 105, a· b= 525.

4. Raqamlarni toping A Va b, agar D( a, b) = 7, a· b= 294.

5. Raqamlarni toping A Va b, agar D( a, b) = 5, a:b= 13:8.

6. Raqamlarni toping A Va b, agar ma'lum bo'lsa, K( a, b) = 224, a:b= 7:8.

7. Raqamlarni toping a Va b, agar D( a, b) = 3, K( a; b) = 915.

8. 15 ga bo‘linish testini isbotlang.

9. 1032, 2964, 5604, 8910, 7008 sonlar to‘plamidan 12 ga bo‘linuvchilarini yozing.

10. 18, 36, 45, 75 ga bo‘linish mezonlarini tuzing.

Natural sonlar to'plami = (1, 2, 3...). Ya'ni natural sonlar to'plami barcha musbat sonlar to'plamidir. Natural sonlarda qo'shish, ko'paytirish, ayirish va bo'lish amallari aniqlanadi. Ikki natural sonni qo‘shish, ko‘paytirish va ayirish natijasi butun son bo‘ladi. Ikki natural sonni bo'lish natijasi butun yoki kasr bo'lishi mumkin.

Masalan: 20: 4 = 5 - bo'linish natijasi butun son.
20: 3 = 6 2/3 - bo'linish natijasi kasrdir.
Agar bo'linish natijasi butun son bo'lsa, natural n soni m natural soniga bo'linadigan deyiladi. Bunda m soni n sonining bo‘luvchisi, n soni esa m sonining karrali deyiladi.

Birinchi misolda 20 soni 4 ga bo'linadi, 4 soni 20 ning bo'luvchisi, 20 soni esa 4 ga karrali.
Ikkinchi misolda 20 soni mos ravishda 3 soniga bo'linmaydi, bo'luvchilar va ko'paytmalar haqida gap bo'lishi mumkin emas;

Agar n sonining o‘zidan va bittadan boshqa bo‘luvchilari bo‘lmasa, tub son deyiladi. Tut sonlarga misollar: 2, 7, 11, 97 va boshqalar.
Agar n sonining o'zidan va bittadan boshqa bo'luvchilari bo'lsa, kompozitsion son deyiladi.

Har qanday natural son tub sonlar ko‘paytmasiga ajralishi mumkin va bu parchalanish omillar tartibiga qadar yagonadir. Masalan: 36=2 2 3 3 = 2 3 2 3 = 3 2 3 2 – bu kengayishlarning barchasi faqat omillar tartibida farqlanadi.

Ikkita m va n sonlarning eng katta umumiy boʻluvchisi m va n ning ham boʻluvchisi boʻlgan eng katta natural sondir. Masalan, 34 va 85 raqamlari 17 ning eng katta umumiy koeffitsientiga ega.

Ikkita m va n sonning eng kichik umumiy karrali m va n ning ham karrali eng kichik natural sondir. Masalan, 15 va 4 raqamlari 60 ning eng kichik umumiy karrali bor.

Ikki tub songa bo'linadigan natural son ularning ko'paytmasiga ham bo'linadi. Misol uchun, agar raqam 2 va 3 ga bo'linadigan bo'lsa, u 6 = 2 3 ga, agar 11 va 7 ga bo'lsa, 77 ga bo'linadi.

Misol: 6930 soni 11 - 6930: 11 = 630 ga bo'linadi va 7 - 6930 ga bo'linadi: 7 = 990. Ishonch bilan aytishimiz mumkinki, bu raqam 77 ga ham bo'linadi. Keling, tekshiramiz: 6930: 77 = 90.

n sonini tub omillarga ajratish algoritmi:

1. n sonining (1 dan tashqari) eng kichik tub bo‘luvchisini toping - a1.
2. n sonni a1 ga bo'ling, qismni n1 deb belgilang.
3. n=a1 n1.
4. n1 bilan bir xil amalni tub son olguncha bajaramiz.

Misol: 17,136 sonini tub ko‘paytmalarga ko‘paytiring

1. 1 dan boshqa eng kichik tub bo‘luvchi, bu yerda 2.

2. 17 136: 2 = 8 568;

3. 17 136 = 8 568 2.

4. 8568 sonining eng kichik tub bo‘luvchisi 2 ga teng.

5. 8 568: 2 = 4284;

6. 17 136 = 4284 2 2.

7. 4284 sonining eng kichik tub bo‘luvchisi 2 ga teng.

8. 4284: 2 = 2142;

9. 17 136 = 2142 2 2 2.

10. 2142 sonining eng kichik tub bo‘luvchisi 2 ga teng.

11. 2142: 2 = 1071;

12. 17 136 = 1071 2 2 2 2.

13. 1071 sonining eng kichik tub bo‘luvchisi 3 ga teng.

14. 1071: 3 = 357;

15. 17 136 = 357 3 2 2 2 2.

16. 357 ning eng kichik tub bo‘luvchisi 3 ga teng.

17. 357: 3 = 119;

18. 17 136 = 119 3 3 2 2 2 2.

19. 119 sonining eng kichik tub bo‘luvchisi 7 ga teng.

20. 119: 7 = 17;

21. 17 tub son bo‘lib, 17 136 = 17 7 3 3 2 2 2 2 degan ma’noni anglatadi.

Biz 17 136 sonining tub omillarga parchalanishini oldik.

Xulosa uchun kalit so'zlar:Butun sonlar. Natural sonlar ustidagi arifmetik amallar. Natural sonlarning bo‘linuvchanligi. Bosh va kompozit sonlar. Natural sonni tub ko‘paytuvchilarga ko‘paytirish. 2, 3, 5, 9, 4, 25, 10, 11 ga boʻlinish belgilari. Eng katta umumiy boʻluvchi (GCD), shuningdek, eng kichik umumiy koʻp (LCD). Qolgan bilan bo'linish.

Butun sonlar- bu ob'ektlarni hisoblash uchun ishlatiladigan raqamlar - 1, 2, 3, 4 , ... Lekin raqam 0 tabiiy emas!

Natural sonlar to'plami bilan belgilanadi N. Yozib olish "3 ∈ N" uch soni natural sonlar to‘plamiga tegishli ekanligini bildiradi va yozuv "0 ∉ N" nol soni bu to'plamga tegishli emasligini bildiradi.

O'nlik sanoq tizimi- pozitsion radiks sanoq sistemasi 10 .

Natural sonlar ustidagi arifmetik amallar

Natural sonlar uchun quyidagi amallar aniqlanadi: qo'shish, ayirish, ko'paytirish, bo'lish, eksponentatsiya, ildiz chiqarish. Birinchi to'rtta harakat arifmetik.

a, b va c natural sonlar bo'lsin

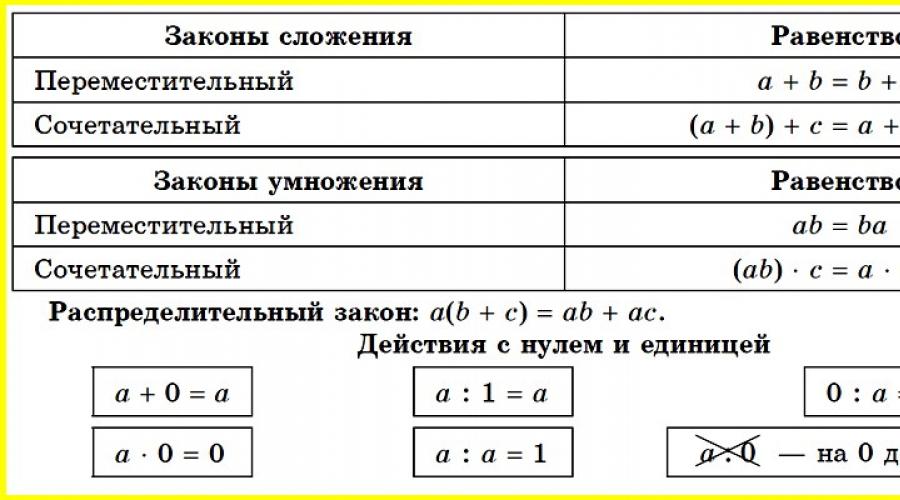
1. QO‘SHIMCHA. Muddat + muddat = summa

Qo'shish xususiyatlari
1. Kommunikativ a + b = b + a.
2. Konyunktiv a + (b + c) = (a + b) + c.
3. a + 0= 0 + a = a.

2. AYIRISH. Minuend - Subtrahend = Farq

Ayirishning xossalari
1. a - (b + c) = a - b - c sonidan yig'indini ayirish.
2. Yig'indidan sonni ayirish (a + b) - c = a + (b - c); (a + b) - c = (a - c) + b.
3. a - 0 = a.
4. a - a = 0.

3. KO‘PTIRISH. Ko'paytiruvchi * Ko'paytiruvchi = Mahsulot

Ko'paytirishning xossalari
1. Kommunikativ a*b = b*a.
2. Konyunktiv a*(b*c) = (a*b)*c.
3. 1 * a = a * 1 = a.
4. 0 * a = a * 0 = 0.
5. Tarqatish (a + b) * c = ac + bc; (a - b) * c = ac - miloddan avvalgi.

4. BO'LISH. Dividend: bo'linuvchi = qism

Bo'linish xususiyatlari
1. a: 1 = a.
2. a: a = 1. Siz nolga bo'la olmaysiz!
3. 0: a= 0.

Jarayon

1. Avvalo, qavs ichidagi amallar.
2. Keyin ko'paytirish, bo'lish.
3. Va faqat oxirida qo'shish va ayirish.

Natural sonlarning bo‘linuvchanligi. Bosh va kompozit sonlar.

Natural sonning bo'luvchisi A qaysi natural sondir A qoldiqsiz bo'linadi. Raqam 1 har qanday natural sonning bo‘luvchisidir.

Natural son deyiladi oddiy, faqat mavjud bo'lsa ikki bo'luvchi: bitta va sonning o'zi. Masalan, 2, 3, 11, 23 sonlar tub sonlardir.

Ikkidan ortiq bo'luvchiga ega bo'lgan son deyiladi kompozitsion. Masalan, 4, 8, 15, 27 raqamlari qo`shma sonlardir.

Bo'linish testi ishlaydi bir nechta raqamlar: agar omillarning kamida bittasi ma'lum bir raqamga bo'linadigan bo'lsa, mahsulot ham bu raqamga bo'linadi. Ish 24 15 77 tomonidan bo'linadi 12 , bu raqamning ko'paytmasi beri 24 tomonidan bo'linadi 12 .

Yig'indi uchun bo'linish testi (farq) raqamlar: agar har bir atama ma'lum bir songa bo'linadigan bo'lsa, unda butun yig'indi shu raqamga bo'linadi. Agar a: b Va c:b, Bu (a + c): b. Agar a: b, A c ga bo'linmaydi b, Bu a+c raqamga bo'linmaydi b.

Agar a: c Va c:b, Bu a: b. 72:24 va 24:12 ekanligiga asoslanib, biz 72:12 degan xulosaga kelamiz.

Sonni tub sonlar darajalarining ko'paytmasi sifatida ko'rsatish deyiladi sonni asosiy omillarga ajratish.

Arifmetikaning asosiy teoremasi: har qanday natural son (.dan tashqari 1 ) yoki shunday oddiy, yoki uni faqat bitta usulda faktorlarga ajratish mumkin.

Raqamni tub ko‘rsatkichlarga ajratishda bo‘linish belgilaridan foydalaniladi va bunda “ustun” belgisi qo‘llaniladi, bunda bo‘linuvchi vertikal chiziqning o‘ng tomonida joylashgan bo‘lib, bo‘linish qismi dividend ostida yoziladi.

Masalan, vazifa: sonni tub omillarga ko'paytirish 330 . Yechim:

Bo'linish belgilari 2, 5, 3, 9, 10, 4, 25 va 11.

ga bo'linish belgilari mavjud 6, 15, 45 h.k., ya'ni mahsuloti faktorlarga ajratilishi mumkin bo'lgan raqamlarga 2, 3, 5, 9 Va 10 .

Eng katta umumiy bo'luvchi

Berilgan ikkita natural sonning har biri boʻlinadigan eng katta natural son deyiladi eng katta umumiy bo'luvchi bu raqamlar ( GCD). Masalan, GCD (10; 25) = 5; va GCD (18; 24) = 6; GCD (7; 21) = 1.

Ikki natural sonning eng katta umumiy boʻluvchisi ga teng boʻlsa 1 , keyin bu raqamlar chaqiriladi o'zaro asosiy.

Eng katta umumiy bo'luvchini topish algoritmi(NOD)

GCD ko'pincha muammolarda qo'llaniladi. Masalan, bir sinf o‘quvchilariga 155 ta daftar va 62 ta ruchka teng taqsimlangan. Bu sinfda nechta o'quvchi bor?

Yechim: Bu sinfdagi o‘quvchilar sonini topish 155 va 62 sonlarining eng katta umumiy bo‘luvchisini topishga to‘g‘ri keladi, chunki daftar va ruchkalar teng bo‘lingan. 155 = 5 31; 62 = 2 31. GCD (155; 62) = 31.

Javob: Sinfda 31 o'quvchi.

Eng kichik umumiy ko'plik

Natural sonning karralari A ga bo'linadigan natural sondir A izsiz. Masalan, raqam 8 ko'paytmalari bor: 8, 16, 24, 32 , ... Har qanday natural son mavjud cheksiz ko'p sonli.

Eng kichik umumiy ko'plik(LCM) bu sonlarning karrali eng kichik natural sondir.

Eng kichik umumiy karralini topish algoritmi ( MOQ):

LCM ham ko'pincha muammolarda qo'llaniladi. Misol uchun, ikkita velosipedchi bir vaqtning o'zida bir xil yo'nalishdagi velosiped yo'li bo'ylab harakatlanishdi. Biri 1 daqiqada, ikkinchisi esa 45 soniyada aylana yasaydi. Harakat boshlanganidan so'ng ular boshidan qancha daqiqalar ichida uchrashadilar?

Yechim: Boshida yana uchrashadigan daqiqalar soniga bo'linishi kerak 1 min, shuningdek yoqilgan 45 s. 1 daqiqada = 60 s. Ya'ni, LKM ni topish kerak (45; 60). 45 = 32 5; 60 = 22 3 5. LCM (45; 60) = 22 32 5 = 4 9 5 = 180. Natijada velosipedchilar startda 180 s = 3 minutda uchrashadilar.

Javob: 3 min.

Qolgan bilan bo'linish

Agar natural son bo'lsa A natural songa bo'linmaydi b, keyin qila olasiz qoldiq bilan bo'linish. Bunday holda, olingan ko'rsatkich chaqiriladi to'liqsiz. Tenglik adolatli:

a = b n + r,

Qayerda A- bo'linadigan, b- ajratuvchi, n- to'liq bo'lmagan qism, r- qoldiq. Masalan, dividend teng bo'lsin 243 , ajratuvchi - 4 , Keyin 243: 4 = 60 (qolgan 3). Ya'ni, a = 243, b = 4, n = 60, r = 3, keyin 243 = 60 4 + 3 .

ga bo'linadigan raqamlar 2 qoldiqsizlar deyiladi hatto: a = 2n, n ∈ N.

Qolgan raqamlar chaqiriladi g'alati: b = 2n + 1, n ∈ N.

Bu mavzuning qisqacha mazmuni "Butun sonlar. Bo'linish belgilari". Davom etish uchun keyingi bosqichlarni tanlang:

• Keyingi xulosaga o'ting: