Ko'p hollarda signalning spektrini olish (hisoblash) vazifasi shunday ko'rinadi. Namuna olish chastotasi Fd bo'lgan ADC mavjud bo'lib, u T vaqtida kirish joyiga keladigan uzluksiz signalni raqamli namunalarga - N bo'laklarga aylantiradi. Keyinchalik, namunalar qatori ba'zi bir raqamli qiymatlarning N/2 hosil qiluvchi ma'lum bir dasturga kiritiladi (dasturchi Internetdan o'g'irlangan dastur yozgan bo'lsa, u Furye o'zgarishini amalga oshiradi).

Dasturning to'g'ri ishlayotganligini tekshirish uchun biz ikkita sinusoid sin(10*2*pi*x)+0,5*sin(5*2*pi*x) yig'indisi sifatida namunalar massivi hosil qilamiz va uni dasturga kiritamiz. . Dasturda quyidagilar chizilgan:

1-rasm Signal vaqti funksiyasining grafigi

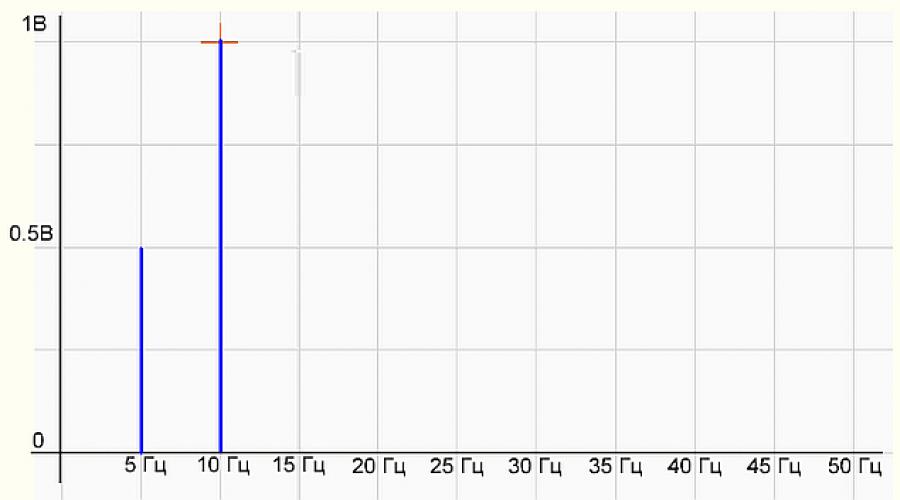
2-rasm Signal spektrining grafigi

Spektr grafigida amplitudasi 0,5 V va 10 Gts amplitudasi 1 V bo'lgan ikkita tayoq (harmonika) 5 Gts mavjud bo'lib, hamma narsa asl signal formulasi bilan bir xil. Hammasi yaxshi, yaxshi dasturchi! Dastur to'g'ri ishlaydi.

Bu shuni anglatadiki, agar biz ikkita sinusoid aralashmasidan ADC kirishiga haqiqiy signalni qo'llasak, ikkita garmonikadan iborat shunga o'xshash spektrni olamiz.

Jami, bizning haqiqiy o'lchangan signal 5 soniya davom etadi, ADC tomonidan raqamlangan, ya'ni ifodalangan diskret hisoblaydi, bor diskret davriy bo'lmagan spektr.

Matematik nuqtai nazardan, bu iborada nechta xato bor?

Endi hokimiyat qaror qildi, biz 5 soniya juda uzoq deb qaror qildik, signalni 0,5 soniyada o'lchaymiz.



3-rasm sin(10*2*pi*x)+0,5*sin(5*2*pi*x) funksiyasining 0,5 sek o‘lchov davri uchun grafigi.

4-rasm Funktsiyalar spektri

Nimadir noto'g'ri ko'rinadi! 10 Gts harmonik an'anaviy tarzda chiziladi, lekin 5 Gts tayoq o'rniga bir nechta g'alati harmonikalar paydo bo'ladi. Nima bo'layotganini bilish uchun Internetga qaraymiz ...

Ularning aytishicha, namunaning oxiriga nol qo'shishingiz kerak va spektr odatdagidek chiziladi.

Fig.5 5 soniyagacha nol qo'shildi

Fig.6 Qabul qilingan spektr

Bu hali ham 5 soniyadagidek emas. Biz nazariya bilan shug'ullanishimiz kerak. Keling, boraylik Vikipediya- bilim manbai.

2. Uzluksiz funksiya va uning Furye seriyali tasviri

Matematik jihatdan T sekund davom etgan signalimiz (0, T) segmentida aniqlangan ba'zi f(x) funksiyadir (X in). Ushbu holatda- vaqt). Bunday funktsiya har doim quyidagi shaklning harmonik funktsiyalari (sinus yoki kosinus) yig'indisi sifatida ifodalanishi mumkin:

(1), bu erda:

K - trigonometrik funktsiya raqami (garmonik komponent raqami, garmonik raqam)
T - funksiya aniqlangan segment (signal davomiyligi)
Ak - k-chi garmonik komponentning amplitudasi,
kh- k- garmonik komponentning boshlang'ich fazasi

“Funksiyani qatorlar yig‘indisi sifatida ifodalash” nimani anglatadi? Bu shuni anglatadiki, Furye seriyasining harmonik komponentlarining qiymatlarini har bir nuqtada qo'shish orqali biz ushbu nuqtada funktsiyamizning qiymatini olamiz.

(Aniqroq aytganda, qatorning f(x) funktsiyasidan ildiz o'rtacha kvadrat og'ishi nolga moyil bo'ladi, lekin o'rtacha kvadrat yaqinlashuviga qaramay, funktsiyaning Furye qatori, umuman olganda, talab qilinmaydi. unga nuqta bilan yaqinlashing. https://ru.wikipedia.org/ wiki/Fourier_Series.)

Ushbu seriyani quyidagicha yozish mumkin:

(2),
Qayerda, k- kompleks amplituda.

(1) va (3) koeffitsientlar orasidagi munosabat quyidagi formulalar bilan ifodalanadi:

E'tibor bering, Furye seriyasining ushbu uchta ko'rinishi butunlay ekvivalentdir. Ba'zan Furye qatorlari bilan ishlashda sinus va kosinuslar o'rniga xayoliy argumentning ko'rsatkichlarini qo'llash qulayroq bo'ladi, ya'ni Furye konvertatsiyasini kompleks shaklda qo'llash. Ammo biz uchun (1) formuladan foydalanish qulay, bu erda Furye seriyasi mos keladigan amplitudalar va fazalarga ega bo'lgan kosinuslar yig'indisi sifatida taqdim etiladi. Qanday bo'lmasin, haqiqiy signalning Furye o'zgarishi murakkab garmonik amplitudalarga olib keladi, deb aytish noto'g'ri. Wiki to'g'ri ta'kidlaganidek, "Fourier konvertatsiyasi (ℱ) - bu haqiqiy o'zgaruvchining bir funktsiyasini boshqa funktsiya, shuningdek, haqiqiy o'zgaruvchi bilan bog'laydigan operatsiya."

Jami:
Signallarni spektral tahlil qilishning matematik asosi Furye transformatsiyasi hisoblanadi.

Furye konvertatsiyasi (0, T) segmentida cheksiz son (cheksiz qator) yig‘indisi sifatida aniqlangan uzluksiz f(x) funksiyani (signal) tasvirlash imkonini beradi. trigonometrik funktsiyalar(0, T) segmentida ham hisobga olinadigan ma'lum amplitudalar va fazalar bilan (sinus va/yoki kosinus). Bunday qator Furye seriyasi deb ataladi.

Keling, tushunish uchun zarur bo'lgan yana bir nechta fikrlarni ta'kidlaymiz to'g'ri dastur Signalni tahlil qilish uchun Furye transformatsiyasi. Agar butun X o'qi bo'yicha Furye qatorini (sinusoidlar yig'indisini) ko'rib chiqsak, segmentdan tashqarida (0, T) Furye qatori bilan ifodalangan funktsiya bizning funktsiyamizni davriy ravishda takrorlashini ko'rishimiz mumkin.

Masalan, 7-rasmdagi grafikda asl funktsiya segmentda (-T\2, +T\2) aniqlangan va Furye qatori butun x o'qi bo'yicha aniqlangan davriy funktsiyani ifodalaydi.

Buning sababi, sinusoidlarning o'zi davriy funktsiyalardir va shunga mos ravishda ularning yig'indisi davriy funktsiya bo'ladi.

7-rasm Davriy bo'lmagan asl funktsiyani Furye qatori bilan tasvirlash

Shunday qilib:

Bizning asl funktsiyamiz uzluksiz, davriy bo'lmagan, T uzunlikdagi ma'lum bir segmentda aniqlangan.
Ushbu funktsiyaning spektri diskretdir, ya'ni u garmonik komponentlarning cheksiz qatori - Furye seriyasi shaklida taqdim etiladi.
Aslida, Furye seriyasi ba'zilarini belgilaydi davriy funktsiya, segmentida biznikiga to'g'ri keladi (0, T), lekin biz uchun bu davriylik muhim emas.

Garmonik komponentlarning davrlari asl f(x) funksiyasi aniqlangan segmentning (0, T) qiymatiga karrali. Boshqacha qilib aytganda, garmonik davrlar signalni o'lchash davomiyligiga ko'paytiriladi. Masalan, Furye qatorining birinchi garmonik davri f(x) funksiya aniqlangan T intervalga teng. Furye seriyasining ikkinchi garmonikasining davri T/2 intervaliga teng. Va hokazo (8-rasmga qarang).

8-rasm Furye seriyasining garmonik komponentlarining davrlari (chastotalari) (bu erda T = 2p)

Shunga ko'ra, harmonik komponentlarning chastotalari 1 / T ga ko'paytiriladi. Ya'ni, Fk garmonik komponentlarning chastotalari Fk= k\T ga teng, bu erda k 0 dan ∞ gacha, masalan k=0 F0=0; k=1 F1=1\T; k=2 F2=2\T; k=3 F3=3\T;… Fk= k\T (nol chastotada - doimiy komponent).

Bizning asl funktsiyamiz T=1 soniya davomida qayd etilgan signal bo'lsin. Shunda birinchi garmonikaning davri bizning signalimizning davomiyligiga teng bo'ladi T1=T=1 sek va garmonik chastota 1 Gts ga teng bo'ladi. Ikkinchi garmonikaning davri signal davomiyligi 2 ga bo'lingan (T2 = T/2 = 0,5 sek) va chastotasi 2 Gts ga teng bo'ladi. Uchinchi harmonik uchun T3=T/3 sek va chastotasi 3 Hz. Va hokazo.

Bu holda harmonikalar orasidagi qadam 1 Gts ni tashkil qiladi.

Shunday qilib, davomiyligi 1 sekund bo'lgan signal 1 Gts chastotali rezolyutsiyaga ega bo'lgan harmonik komponentlarga (spektrni olish) parchalanishi mumkin.
Ruxsatni 2 marta 0,5 Gts ga oshirish uchun siz o'lchash davomiyligini 2 marta - 2 soniyagacha oshirishingiz kerak. 10 soniya davom etadigan signal 0,1 Gts chastota o'lchamlari bilan harmonik komponentlarga (spektrni olish uchun) parchalanishi mumkin. Chastota o'lchamlarini oshirishning boshqa usullari yo'q.

Namunalar qatoriga nol qo'shish orqali signalning davomiyligini sun'iy ravishda oshirish usuli mavjud. Lekin u haqiqiy chastota o'lchamlarini oshirmaydi.

3. Diskret signallar va diskret Furye transformatsiyasi

Rivojlanish bilan raqamli texnologiya O'lchov ma'lumotlarini (signallarini) saqlash usullari ham o'zgardi. Agar ilgari signal magnitafonga yozib olinishi va uni analog shaklda lentada saqlash mumkin bo'lsa, endi signallar raqamlashtiriladi va raqamlar to'plami (namuna) sifatida kompyuter xotirasidagi fayllarda saqlanadi.

Signalni o'lchash va raqamlashtirishning odatiy sxemasi quyidagicha.

9-rasm o'lchash kanalining diagrammasi

O'lchov o'tkazgichdan kelgan signal ADC ga T vaqt oralig'ida keladi. T vaqtida olingan signal namunalari (namuna olish) kompyuterga uzatiladi va xotirada saqlanadi.

10-rasm Raqamlangan signal - T vaqtida olingan N namunalar

Signalni raqamlashtirish parametrlariga qanday talablar qo'yiladi? Kirishni o'zgartiruvchi qurilma analog signal diskret kodga ( raqamli signal) analog-raqamli konvertor (ADC, English Analog-to-digital converter, ADC) deb ataladi (Wiki).

ADC ning asosiy parametrlaridan biri maksimal namuna olish chastotasi (yoki namuna olish tezligi, inglizcha namuna tezligi) - uni namuna olishda vaqt davom etadigan signalning namuna olish tezligi. U gerts bilan o'lchanadi. ((Wiki))

Kotelnikov teoremasiga ko'ra, agar uzluksiz signal Fmax chastotasi bilan chegaralangan spektrga ega bo'lsa, uni vaqt oralig'ida olingan diskret namunalaridan to'liq va noyob tarzda qayta qurish mumkin. , ya'ni. chastotasi bilan Fd ≥ 2*Fmax, bu erda Fd - namuna olish chastotasi; Fmax - signal spektrining maksimal chastotasi. Boshqacha qilib aytganda, signalni raqamlashtirish chastotasi (ADC namuna olish chastotasi) biz o'lchamoqchi bo'lgan signalning maksimal chastotasidan kamida 2 baravar yuqori bo'lishi kerak.

Agar biz Kotelnikov teoremasi talab qilganidan past chastotali namunalar olsak nima bo'ladi?

Bunday holda, "tasdiqlash" effekti paydo bo'ladi (shuningdek, stroboskopik effekt, muare effekti deb ham ataladi), bunda yuqori chastotali signal raqamlashtirishdan so'ng, aslida mavjud bo'lmagan past chastotali signalga aylanadi. Shaklda. 11 qizil yuqori chastotali sinus to'lqin haqiqiy signaldir. Pastki chastotali ko'k sinusoid - bu namuna olish vaqtida yuqori chastotali signalning yarmidan ko'prog'i o'tish vaqti bo'lganligi sababli paydo bo'ladigan xayoliy signal.

Guruch. 11. Namuna olishning etarli darajada yuqori bo'lmagan tezligida past chastotali noto'g'ri signalning paydo bo'lishi

Yashillash effektini oldini olish uchun ADC oldiga maxsus anti-aliasing filtri qo'yiladi - past chastotali filtr (LPF), u ADC namuna olish chastotasining yarmidan past chastotalarni o'tkazadi va yuqori chastotalarni kesadi.

Signalning spektrini uning diskret namunalaridan hisoblash uchun diskret Furye konvertatsiyasi (DFT) qo'llaniladi. Yana bir bor ta'kidlaymizki, diskret signalning spektri "ta'rifi bo'yicha" Fmax chastotasi bilan chegaralanadi, bu Fd namuna olish chastotasining yarmidan kam. Demak, diskret signalning spektri spektri cheksiz bo'lishi mumkin bo'lgan uzluksiz signalning Furye qatori uchun cheksiz yig'indidan farqli o'laroq, cheklangan sonli garmonikalar yig'indisi bilan ifodalanishi mumkin. Kotelnikov teoremasiga ko'ra, garmonikaning maksimal chastotasi shunday bo'lishi kerakki, u kamida ikkita namunaga to'g'ri keladi, shuning uchun harmonikalar soni diskret signal namunalari sonining yarmiga teng. Ya'ni, agar namunada N namuna bo'lsa, u holda spektrdagi harmoniklar soni N/2 ga teng bo'ladi.

Keling, diskret Furye konvertatsiyasini (DFT) ko'rib chiqaylik.

Furye seriyalari bilan taqqoslash

Biz ularning bir-biriga to'g'ri kelishini ko'ramiz, faqat DFTdagi vaqt tabiatan diskret va harmonikalar soni N/2 bilan cheklangan - namunalar sonining yarmi.

DFT formulalari k, s o'lchamsiz butun sonli o'zgaruvchilarda yoziladi, bu erda k - signal namunalari soni, s - spektral komponentlar soni.
s qiymati T davridagi to'liq garmonik tebranishlar sonini ko'rsatadi (signal o'lchash davomiyligi). Diskret Furye transformatsiyasi harmonikaning amplitudalari va fazalarini raqamli usul yordamida topish uchun ishlatiladi, ya'ni. "kompyuterda"

Boshida olingan natijalarga qaytish. Yuqorida aytib o'tilganidek, davriy bo'lmagan funktsiyani (bizning signalimizni) Furye qatoriga kengaytirganda, natijada olingan Furye qatori T davriga ega bo'lgan davriy funktsiyaga to'g'ri keladi (12-rasm).

12-rasm Davriy funksiya f(x) davri T0, o'lchash davri T>T0

12-rasmda ko'rinib turibdiki, f(x) funksiya T0 davri bilan davriydir. Biroq, T o'lchov namunasining davomiyligi T0 funksiya davriga to'g'ri kelmasligi sababli, Furye qatori sifatida olingan funktsiya T nuqtada uzilishga ega. Natijada, bu funktsiyaning spektri o'z ichiga oladi. ko'p sonli yuqori chastotali harmoniklar. Agar T o'lchov namunasining davomiyligi T0 funktsiyasining davriga to'g'ri kelgan bo'lsa, u holda Furye konvertatsiyasidan keyin olingan spektr faqat birinchi harmonikni (namuna olish davomiyligiga teng bo'lgan sinusoidni) o'z ichiga oladi, chunki f (x) funktsiyasi. sinusoiddir.

Boshqacha qilib aytadigan bo'lsak, DFT dasturi bizning signalimiz "sinusoid bo'lagi" ekanligini "bilmaydi", lekin davriy funktsiyani ketma-ket ko'rinishda ifodalashga harakat qiladi, bu esa alohida qismlarning nomuvofiqligi tufayli uzilishga ega. sinusoid.

Natijada, spektrda harmonikalar paydo bo'ladi, ular funktsiyaning shaklini, shu jumladan bu uzilishni umumlashtirishi kerak.

Shunday qilib, bir nechta sinusoidlar yig'indisi bo'lgan signalning "to'g'ri" spektrini olish uchun turli davrlar, signalni o'lchash davri har bir sinusoidning butun sonli davrlarini o'z ichiga olishi kerak. Amalda, bu shart signalni o'lchashning etarlicha uzoq davom etishi uchun bajarilishi mumkin.

13-rasm Vites qutisi kinematik xato signalining funktsiyasi va spektriga misol

Qisqaroq vaqt bilan rasm "yomonroq" ko'rinadi:

14-rasm Rotor tebranish signalining funksiyasi va spektriga misol

Amalda, "haqiqiy komponentlar" qayerda ekanligini va komponentlarning ko'p bo'lmagan davrlari va signalni namuna olish davomiyligi yoki signal shaklidagi "sakrashlar va uzilishlar" tufayli kelib chiqadigan "artefaktlar" qayerda ekanligini tushunish qiyin bo'lishi mumkin. . Albatta, "haqiqiy komponentlar" va "artefaktlar" so'zlari biron bir sababga ko'ra tirnoq belgilariga qo'yiladi. Spektr grafigida ko'plab harmonikalarning mavjudligi bizning signalimiz aslida ulardan "ibarat" ekanligini anglatmaydi. Bu 7 raqami 3 va 4 raqamlaridan "iborat" deb o'ylash bilan bir xil. 7 raqamini 3 va 4 raqamlarining yig'indisi sifatida ifodalash mumkin - bu to'g'ri.

Shunday qilib, bizning signalimiz ... yoki aniqrog'i "bizning signalimiz" emas, balki bizning signalimizni takrorlash (namuna olish) orqali tuzilgan davriy funktsiyani ma'lum amplitudalar va fazalar bilan harmonikalar (sinus to'lqinlar) yig'indisi sifatida ko'rsatish mumkin. Ammo amaliyot uchun muhim bo'lgan ko'p hollarda (yuqoridagi raqamlarga qarang), spektrda olingan harmonikani haqiqatdan ham bog'lash mumkin. haqiqiy jarayonlar, ular tsiklik xarakterga ega va signal shakliga sezilarli hissa qo'shadi.

Ba'zi natijalar

1. ADC tomonidan raqamlashtirilgan, ya'ni diskret namunalar to'plami (N dona) bilan ifodalangan, davomiyligi T sekund bo'lgan haqiqiy o'lchangan signal harmonikalar to'plami (N/) bilan ifodalangan diskret davriy bo'lmagan spektrga ega. 2 dona).

2. Signal haqiqiy qiymatlar to'plami bilan ifodalanadi va uning spektri haqiqiy qiymatlar to'plami bilan ifodalanadi. Garmonik chastotalar ijobiydir. Matematiklar uchun spektrni manfiy chastotalar yordamida murakkab shaklda ifodalash qulayroq ekanligi "bu to'g'ri" va "bu har doim bajarilishi kerak" degani emas.

3. T vaqt oralig'ida o'lchangan signal faqat T vaqt oralig'ida aniqlanadi. Signalni o'lchashni boshlashimizdan oldin nima sodir bo'lganligi va undan keyin nima sodir bo'lishi fanga noma'lum. Va bizning holatlarimizda bu qiziq emas. Vaqt cheklangan signalning DFT "haqiqiy" spektrini beradi, ya'ni ma'lum sharoitlarda uning tarkibiy qismlarining amplitudasi va chastotasini hisoblash imkonini beradi.

Amaldagi materiallar va boshqa foydali materiallar.

Biz yuqorida ko'rib turibmizki, funktsiyalarning quvvat seriyalariga kengayishi bizga ushbu funktsiyalarning taxminiy qiymatlarini kerakli aniqlik bilan hisoblash imkonini beradi. Ammo quvvat seriyasiga (Teylor yoki Maklaurin seriyasiga) kengaytirib bo'lmaydigan ko'plab funktsiyalar mavjud, chunki funksiyalarga qo'yiladigan talablar ancha qattiq (funksiya cheksiz differensial bo'lishi kerak va hokazo). Shuning uchun, kengayish shartlari kamroq og'ir bo'lgan boshqa turdagi funktsional seriyalar ham qo'llaniladi. Bu qatorlar o'z ichiga oladi trigonometrik qator.

Ta'rif: Trigonometrik qator shaklning funktsional qatori:, (1)

Bu erda doimiy raqamlar mavjud:

Trigonometrik qator koeffitsientlari.

(1) qatorning barcha a'zolari funktsional davriy bo'lmagan va umumiy minimal davr 2p ga ega. Bundan kelib chiqadi: agar f(x) funksiya trigonometrik qatorga (1) kengaytirilsa, ya'ni. u bu qatorning yig'indisidir, u holda bu funktsiyaning o'zi faqat 2p uzunlikdagi ma'lum bir intervalda (1) qatorlar yig'indisi bo'lishi kerak.

Trigonometrik qatorlarning asosiy xossalari trigonometrik funktsiyalar tizimining asosiy xususiyatlaridan kelib chiqadi. Men bitta ta'rif bilan chiqdim.

Ta'rif: j1(x),j2(x),...,j3(x)... funksiyalarning cheksiz tizimi. segmentda aniqlangan deb ataladi bu segmentda ortogonal, agar quyidagi shartlar bajarilsa:
m¹n uchun;

har qanday n uchun.

Teorema: Trigonometrik funksiyalar sistemasi [-p,p] segmentida ortogonaldir.

Isbot: Oldingi ta'rifning 1) va 2) shartlarini tekshirish kerak.

1) Integrallarni ko'rib chiqing:

Keling, trigonometrik formulalarni qo'llaymiz:

Shubhasiz, ularning yordami bilan barcha oldingi integrallar quyidagi shakldagi integrallarga keltiriladi:
Va

Keling, ularni hisoblaylik.

;

Shunday qilib, ortogonallikning birinchi talabi qondiriladi.

2)
;

va ikkinchi talab bajariladi va hokazo.

1. Trigonometrik Furye seriyasi.

Davriy f(x) funksiyasi 2p davri bilan trigonometrik qator yig‘indisi sifatida ifodalansin.
(1).

2p uzunlikdagi ba'zi bir intervaldan barcha x uchun. Lekin S(x) qatorning yig‘indisi davriy funksiya bo‘lib, davri 2p bo‘ladi. Shuning uchun f(x) va S(x) qiymatlari butun son chizig'ida (-¥, +¥) mos keladi. Shuning uchun, 2p uzunlikdagi qandaydir intervalda, odatda [-p,p] tenglikni (1) o'rganish kifoya.

Shunday qilib, f(x) [-p,p] bo'yicha (1) qatorlar yig'indisi bo'lsin va qo'shimcha ravishda, uni haddan tashqari haddan, shuning uchun oraliq bilan integrallash mumkin, deb faraz qilaylik. Bu, masalan, (1) qator koeffitsientlarining sonli qatorlari mutlaqo yaqinlashsa, ya'ni. qator yaqinlashadi

(2).

Bunda (1) funksional qatorning mutlaq qiymatdagi shartlari (2) qatorning tegishli hadlaridan oshmaydi, bu (1) qatorning bir xil yaqinlashuvini va demak, uning bo‘lmasligi imkoniyatini bildiradi. -[-p,p] ustidan muddatli integratsiya.

Bundan a 0 koeffitsientini hisoblash uchun foydalanamiz. Keling, (1) tengsizlikning ikkala tomonini [-p,p] ga termlar bo‘yicha integrallashaylik:

Trigonometrik funktsiyalarning ortogonallik xususiyatiga ko'ra, o'ngdagi barcha integrallar birinchisidan tashqari nolga teng. Shunung uchun:
, qayerda
(3).

K /k¹0/ ni hisoblash uchun (1) ning ikkala tomonini coskx ga ko'paytiramiz. Olingan qator ham [-p,p] ga bir xilda yaqinlashadi, chunki ½coskx½£1 va uni [-p,p] dan ortiq muddatga birlashtirish mumkin.

Ortogonallikning bir xil xususiyatiga ko'ra, o'ngdagi barcha integrallar nolga teng, k ni o'z ichiga olgandan tashqari.

Keyin
. Qayerda

(4).

(1) ning ikkala tomonini sin kx ga ko'paytirib, hosil bo'lgan tenglikni ga integrallash orqali biz hosil bo'lamiz.
. Qayerda

(5).

(3)-(5) formulalar yordamida hisoblangan koeffitsientlar deyiladi

Furye koeffitsientlari f(x) funksiyasi uchun va bu koeffitsientlar bilan trigonometrik qator (1) bo'ladi Funksiyaning Furye qatori (x).

Shuni ta'kidlash kerakki, ketma-ket (1) hadlarni har doim ham birlashtirib bo'lmaydi. Shuning uchun Furye koeffitsientlarini hisoblash va Furye qatorini (1) tuzish rasmiy ravishda mumkin, ammo bu qator umuman yaqinlashishini kafolatlab bo'lmaydi; va agar u yaqinlashsa, u holda uning yig'indisi f(x) funktsiyadir. Bunday hollarda, tenglik (1) o'rniga biz "yozuvlar" haqida kelishib oldik:

funktsiyalari. Ushbu transformatsiya mavjud katta qiymat, chunki u ko'plab amaliy muammolarni hal qilish uchun ishlatilishi mumkin. Furye qatorlaridan nafaqat matematiklar, balki boshqa fanlar mutaxassislari ham foydalanadilar.

Funksiyalarning Furye qatoriga kengayishi, agar siz sinusoidal funktsiyalarni sezadigan qurilmadan foydalansangiz, tabiatda kuzatilishi mumkin bo'lgan matematik usuldir.

Bu jarayon odam tovushni eshitganda paydo bo'ladi. Inson qulog'i shunday yaratilganki, u turli chastotalardagi havo bosimining individual sinusoidal tebranishlarini sezishi mumkin, bu esa o'z navbatida odamga nutqni tanib olish va musiqa tinglash imkonini beradi.

Inson qulog'i tovushni bir butun sifatida emas, balki uning Furye seriyali komponentlari orqali qabul qiladi. Strings musiqa asbobi turli chastotali sinusoidal tebranishlar bo'lgan tovushlarni hosil qiladi. Furye seriyali yorug'likning kengayishi haqiqati kamalak bilan ifodalanadi. Insonning ko'rish qobiliyati yorug'likni turli chastotali elektromagnit tebranishlarning ba'zi tarkibiy qismlari orqali qabul qiladi.

Furye transformatsiyasi ma'lum chastotali sinusoidlarning fazasi va amplitudasini tavsiflovchi funktsiyadir. Ushbu transformatsiya energiya ta'sirida yuzaga keladigan dinamik jarayonlarni tavsiflovchi tenglamalarni echish uchun ishlatiladi. Furye seriyalari murakkab tebranish signallarida doimiy komponentlarni aniqlash muammosini hal qiladi, bu esa tajribalar, tibbiyot, kimyo va astronomiyadagi kuzatishlar natijasida olingan ma'lumotlarni to'g'ri talqin qilish imkonini berdi.

Ushbu transformatsiyaning kashfiyoti frantsuz matematigi Jan Baptiste Jozef Furyega tegishli. Keyinchalik Furye seriyasi kimning sharafiga nomlandi. Dastlab olim o'z usulini issiqlik o'tkazuvchanlik mexanizmlarini o'rganish va tushuntirishda qo'llashni topdi. Issiqlikning dastlabki tartibsiz taqsimlanishi oddiy sinusoidlar shaklida ifodalanishi mumkinligi taklif qilindi. Ularning har biri uchun haroratning minimal, maksimal va fazasi aniqlanadi. Egri chiziqning yuqori va pastki cho'qqilarini, har bir harmonikning fazasini tavsiflovchi funktsiya harorat taqsimotining ifodasidan Furye transformatsiyasi deb ataladi. Transformatsiya muallifi parchalanish usulini taklif qildi murakkab funktsiya davriy funktsiyalar yig'indisi sifatida kosinus, sinus.

Maqsad kurs ishi Furye seriyasini o'rganish va bu transformatsiyani amaliy qo'llashning dolzarbligi.

Ushbu maqsadga erishish uchun quyidagi vazifalar belgilandi:

1) trigonometrik Furye qatori tushunchasini bering;

2) Furye qatoridagi funksiyaning parchalanish shartlarini aniqlash;

3) juft va toq funksiyalarning Furye qator kengayishini ko‘rib chiqing;

4) davriy bo'lmagan funksiyaning Furye qator kengayishini ko'rib chiqing;

5) Furye qatorining amaliy qo'llanilishini ochib bering.

Tadqiqot ob'ekti: Furye qatoridagi funktsiyalarni kengaytirish.

O'rganish mavzusi: Furye seriyasi.

Tadqiqot usullari: tahlil, sintez, taqqoslash, aksiomatik usul.

1.5. Juft va toq funksiyalar uchun Furye seriyalari

Simmetrik integralni ko'rib chiqing

qaerda uzluksiz yoki bo'lakcha uzluksiz. Birinchi integralga o'zgartirish kiritamiz. Ishonamizki. Keyin

Shuning uchun, agar funktsiya juft bo'lsa, u holda (ya'ni juft funktsiyaning grafigi o'qga nisbatan simmetrik va

Agar toq funksiya bo'lsa, u holda (ya'ni, toq funktsiyaning grafigi boshiga nisbatan simmetrik bo'ladi) va

Bular. juft funktsiyaning simmetrik integrali integrallash oralig'ining yarmidan ikki baravar ko'p bo'lgan integralga, toq funksiyaning simmetrik integrali esa nolga teng.

Juft va toq funksiyalarning quyidagi ikkita xususiyatiga e’tibor bering:

1) juft va toq funksiyaning mahsuloti toq funksiyadir;

2) ikkita juft (toq) funksiyaning ko‘paytmasi juft funktsiyadir.

Bu segmentda aniqlangan va trigonometrik Furye qatoriga kengaytiriladigan juft funksiya bo'lsin. Yuqorida olingan natijalardan foydalanib, biz ushbu seriyaning koeffitsientlari quyidagi shaklga ega bo'lishini aniqlaymiz:

Agar segmentda toq funksiya aniqlangan bo'lsa va bu segmentda trigonometrik Furye qatoriga kengaytirilsa, bu qatorning koeffitsientlari quyidagi ko'rinishga ega bo'ladi:

Binobarin, segmentdagi trigonometrik Furye seriyasi shaklga ega bo'ladi

teng funksiya uchun:

(16)

g'alati funktsiya uchun:

Seriya (16) ko'p burchakli sinuslarni o'z ichiga olmaydi, ya'ni juft funktsiyaning Furye qatoriga faqat juft funktsiyalar va mustaqil atama kiradi. Seriya (17) ko'p burchakli kosinuslarni o'z ichiga olmaydi, ya'ni toq funksiyaning Furye qatoriga faqat toq funksiyalar kiradi.

Ta'rif. Qatorlar
qismlardir to'liq diapazon Furye va to'liq emas deb ataladitrigonometrik Furye qatori.

Agar funktsiya to'liq bo'lmagan trigonometrik qatorga (16) (yoki (17)) kengaytirilsa, u holda deyiladi.kosinuslarda (yoki sinuslarda) trigonometrik Furye qatoriga kengayadi.

1.6. Davriy bo'lmagan funksiyaning Furye qator kengayishi

1.6.1. Funksiyalarni Furye seriyali kengaytirish

Funksiya oraliqda berilsin va bu oraliqda Dirixle teoremasining shartlari qanoatlansin. O'zgaruvchini o'zgartirishni amalga oshiramiz. Olingan argument funksiyasi aniqlanishi uchun biz tanlagan joyni belgilaymiz. Shuning uchun biz bunga ishonamiz

Olingan funktsiyani Furye qatoriga kengaytirish mumkin:

Qayerda

Keling, teskari almashtirishni qilaylik⇒ olamiz

Qayerda

(19)

Seriya (18) – Funksiyalarning asosiy trigonometrik tizimidagi Furye qatori

Shunday qilib, agar funktsiya oraliqda berilgan bo'lsa va bu oraliqda Dirixle teoremasining shartlarini qanoatlantirsa, u holda funksiyalarning trigonometrik tizimi (20) bo'yicha uni trigonometrik Furye qatoriga (18) kengaytirish mumkinligini aniqladik.

Aniqlangan juft funksiya uchun trigonometrik Furye seriyasi shaklga ega bo'ladi

Qayerda

g'alati funktsiya uchun

Qayerda

Izoh! Ayrim masalalarda funksiyani segmentga emas, balki segmentga (20) funksiyalar tizimiga muvofiq trigonometrik Furye qatoriga kengaytirish talab qilinadi. Bunday holda, siz (19) ((15) formulalaridagi integratsiya chegaralarini o'zgartirishingiz kerak, agar bu holda bo'lsa

(23)

yoki agar

(24)

Trigonometrik Furye qatorining yig'indisi davriy davomi bo'lgan davriy funktsiyadir. berilgan funksiya. Va davriy funktsiya uchun (4) tenglik to'g'ri.

1.6.2. Funksiyalarni Furye seriyali kengaytirish

Funktsiya berilgan bo'lsin va bu oraliqda Dirixle teoremasining shartlarini qanoatlantirsin. Bunday funktsiyani Furye qatoriga ham kengaytirish mumkin. Buning uchun funktsiyani intervalgacha kengaytirish va natijada olingan funktsiyani intervalda Furye qatoriga kengaytirish kerak. Bunday holda, hosil bo'lgan qator faqat funktsiya ko'rsatilgan segmentda ko'rib chiqilishi kerak. Hisoblash qulayligi uchun funksiyani juft va toq shaklda aniqlaymiz.

1) Keling, funktsiyani intervalgacha teng ravishda kengaytiramiz, ya'ni biz yangisini quramiz. hatto funktsiya, funksiya bilan segmentga to'g'ri keladi. Binobarin, bu funksiyaning grafigi o'qga nisbatan simmetrik bo'lib, segmentdagi grafik bilan mos keladi. Formulalardan (21) foydalanib, funktsiya uchun Furye qatorining koeffitsientlarini topamiz va Furye qatorining o'zini yozamiz. Furye qatorlarining yig'indisi davriy funktsiya bo'lib, davri bilan. Bu uzluksizlikning barcha nuqtalarida funksiya bilan mos keladi.

2) Funksiyani intervalgacha toq tarzda kengaytiramiz, ya’ni yangisini tuzamiz g'alati funktsiya, funksiya bilan mos keladi. Bunday funktsiyaning grafigi koordinatalarning kelib chiqishiga nisbatan simmetrik bo'lib, segmentdagi grafik bilan mos keladi. Formulalardan (22) foydalanib, funktsiya uchun Furye qatorining koeffitsientlarini topamiz va Furye qatorining o'zini yozamiz. For Furye qatorlarining yig'indisi davriy funktsiyadir. Bu uzluksizlikning barcha nuqtalarida funksiya bilan mos keladi.

Eslatmalar!

1) Xuddi shunday, intervalda aniqlangan funksiyani Furye qatoriga kengaytirishingiz mumkin

2) Funktsiyaning segmentdagi kengayishi uning segmentga ixtiyoriy tarzda davom etishini nazarda tutganligi sababli, funktsiya uchun Furye qatori yagona bo'lmaydi.

1.6.3. Funksiyalarni Furye seriyali kengaytirish

Funksiya ixtiyoriy uzunlik segmentida berilsin va undagi Dirixle teoremasining shartlarini qanoatlantirsin.

Keyin bu funktsiyani Furye seriyasiga kengaytirish mumkin. Buning uchun funktsiyani davriy ravishda (nuqta bilan) butun son chizig'i bo'ylab davom ettirish va natijada olingan funktsiyani faqat segmentda ko'rib chiqilishi kerak bo'lgan Furye qatoriga kengaytirish kerak. Davriy funksiyalarning xossasi (3) tufayli bizda mavjud

Shuning uchun funktsiyaning natijada davom etishi uchun Furye koeffitsientlarini formulalar yordamida topish mumkin.

(25)

2. Amaliy dastur Furye seriyasi

2.1. Furye qatoridagi funksiyalarni kengaytirishga oid masalalar va ularni yechish

Intervalda berilgan funktsiyaning davriy davomi bo'lgan funktsiyani trigonometrik Furye qatoriga kengaytirish talab qilinadi. Buning uchun davriy funktsiyani Furye qatoriga kengaytirish algoritmidan foydalanish kerak.

Davriy funktsiyani Furye qatoriga kengaytirish algoritmi:

1) Berilgan funksiya va uning davriy davomi grafigini tuzing;

2) Berilgan funksiyaning davrini belgilang;

3) Funksiyaning juft, toq yoki ekanligini aniqlang umumiy ko'rinish;

4) Dirixle teoremasi shartlarini amalga oshirish imkoniyatini tekshirish;

5) Ushbu funktsiya tomonidan yaratilgan Furye qatorining rasmiy tasvirini yarating;

6) Furye koeffitsientlarini hisoblash;

7) Furye qatorining koeffitsientlaridan foydalanib, berilgan funksiya uchun Furye qatorini yozing (4-band).

1-misol. Funktsiyani intervalda Furye qatoriga kengaytiring.

Yechim:

1) Berilgan funksiya va uning davriy davomi grafigini tuzamiz.

2) Funksiyaning kengayish davri.

3) Funktsiya g'alati.

4) Funktsiya uzluksiz va monotonik, ya'ni. funktsiya Dirixlet shartlarini qondiradi.

5) Furye qatorining koeffitsientlarini hisoblaymiz.

6) Furye koeffitsientlarini formulaga almashtirib, Furye qatorini yozing.

Javob:

2-misol. Ixtiyoriy davri bo'lgan funksiyani Furye qatoriga kengaytiramiz.

Yechish: funksiya yarim oraliqda (-3;3] aniqlanadi. Funksiyaning kengayish davri, yarim davr. Funksiyani Furye qatoriga kengaytiramiz.

Funktsiyaning boshlang'ich nuqtasida uzluksiz, shuning uchun biz har bir Furye koeffitsientini ikkita integral yig'indisi sifatida ifodalaymiz.

Furye qatorining topilgan koeffitsientlarini formulaga almashtirib, Furye qatorini yozamiz.

3-misol. Funktsiyani kengaytirishorasidakosinuslardagi Furye qatorida. Seriyalar yig‘indisining grafigini tuzing.

Yechish: biz funktsiyani oraliqda teng ravishda kengaytiramiz, ya'ni intervaldagi funksiya bilan mos keladigan yangi juft funktsiyani quramiz. Funksiya uchun Furye qatorining koeffitsientlarini topamiz va Furye qatorini yozamiz. Furye qatorlarining yig'indisi davriy funktsiya bo'lib, davri bilan. Bu uzluksizlikning barcha nuqtalarida funksiya bilan mos keladi.

Funktsiya uchun trigonometrik Furye seriyasi shaklga ega bo'ladi

Furye qatorining koeffitsientlarini topamiz

Shunday qilib, koeffitsientlar topilsa, biz Furye qatorini yozishimiz mumkin

Keling, qatorlar yig'indisini chizamiz

4-misol. Segmentda aniqlangan funksiya berilgan. Funktsiyani Furye qatoriga kengaytirish mumkinligini aniqlang. Funksiyaning kengayishini Furye qatorida yozing.

Yechim:

1) da funksiyaning grafigini tuzing.

2) funksiya uzluksiz va monotonik bo‘ladi, ya’ni Dirixle teoremasiga ko‘ra, uni trigonometrik Furye qatoriga kengaytirish mumkin.

3) (1.19) formulalar yordamida Furye koeffitsientlarini hisoblang.

4) topilgan koeffitsientlar yordamida Furye qatorini yozing.

2.2. Furye qatorlarini inson faoliyatining turli sohalarida qo'llash misollari

Matematika mavjud fanlardan biridir keng qo'llanilishi amalda. Har qanday ishlab chiqarish va texnologik jarayon matematik qonunlarga asoslanadi. Ilova turli asboblar Matematik apparat sizga operatsiyalarni bajarishga qodir bo'lgan qurilmalar va avtomatlashtirilgan bloklarni loyihalash imkonini beradi; murakkab hisob-kitoblar va binolar va inshootlarni loyihalashda hisob-kitoblar.

Furye seriyalari matematiklar tomonidan geometriyada qo'llaniladisferik geometriyadan masalalar yechish; m dada atematik fizikaelastik muhitning kichik tebranishlari bo'yicha masalalarni yechish. Ammo matematikadan tashqari, Furye seriyalari fanning boshqa sohalarida ham o'z qo'llanilishini topdi.

Har kuni odamlar foydalanadi turli qurilmalar. Va ko'pincha bu qurilmalar to'g'ri ishlamaydi. Masalan, ko'p shovqin tufayli tovushni eshitish qiyin yoki faks orqali olingan tasvir noaniq. Biror kishi nosozlik sababini ovoz bilan aniqlashi mumkin. Kompyuter shuningdek, qurilma shikastlangan yoki yo'qligini tashxislashi mumkin. Ortiqcha shovqin kompyuter signalini qayta ishlash yordamida olib tashlanishi mumkin. Signal raqamli qiymatlar ketma-ketligi sifatida ifodalanadi, keyinchalik ular kompyuterga kiritiladi. Tugallagandan keyin muayyan hisob-kitoblar, Furye qatorining koeffitsientlarini oling.

Signal spektrini o'zgartirish shovqinni yozib olishni tozalash, turli yozish qurilmalari tomonidan signal buzilishini qoplash, asboblar tembrini o'zgartirish va tinglovchilarning diqqatini alohida qismlarga qaratish imkonini beradi.

Raqamli tasvirni qayta ishlashda Furye seriyasidan foydalanish quyidagi effektlarni amalga oshirishga imkon beradi: xiralashtirish, qirralarni ta'kidlash, tasvirni tiklash, badiiy effektlar (bo'rttirma)

Furye seriyasining kengayishi arxitekturada tebranish jarayonlarini o'rganishda qo'llaniladi. Masalan, loyihani yaratishda har xil turlari tuzilmalar strukturaviy elementlarning mustahkamligi, qattiqligi va barqarorligini hisoblab chiqadi.

Tibbiyotda kardiogrammalar va ultratovush apparati yordamida tibbiy ko'rik o'tkazish uchun Furye seriyasi nazariyasiga asoslangan matematik apparatdan foydalaniladi.

Signallarning statistik xususiyatlarini baholash va shovqinlarni filtrlash bo'yicha yirik hisoblash muammolari dengiz tubining uzluksiz ma'lumotlarini yozish va qayta ishlashda paydo bo'ladi. O'lchovlarni amalga oshirish va ularni qayd etishda Furye seriyasidan foydalangan holda gologramma usullari istiqbolli. Ya'ni, Furye seriyalari okeanologiya kabi fanda ham qo'llaniladi.

Matematikaning elementlari ishlab chiqarishda deyarli har bir bosqichda topiladi, shuning uchun mutaxassislar ma'lum tahlil va hisoblash vositalarini bilish va qo'llash sohasida yaxshi yo'naltirilgan bo'lishlari muhimdir..

Xulosa

Kurs ishining mavzusi Furye seriyasini o'rganishga bag'ishlangan. Ixtiyoriy funktsiyani oddiyroqlarga kengaytirish mumkin, ya'ni uni Furye qatoriga kengaytirish mumkin. Kurs ishining ko'lami bizga funktsiyani ketma-ket kengaytirishning barcha jihatlarini batafsil ochib berishga imkon bermaydi. Biroq, qo'yilgan vazifalardan Furye seriyalari haqidagi asosiy nazariyani ochish mumkin bo'lib tuyuldi.

Kurs ishi trigonometrik Furye qatori tushunchasini ochib beradi. Furye qatoridagi funksiyaning parchalanish shartlari aniqlanadi. Juft va toq funksiyalarning Furye qator kengayishi ko‘rib chiqiladi; davriy bo'lmagan funktsiyalar.

Ikkinchi bobda turli oraliqlarda berilgan funksiyalarni Furye qatoriga kengaytirishga oid ayrim misollar keltirilgan. Ushbu transformatsiya qo'llaniladigan fan sohalari tavsiflanadi.

Shuningdek, Furye qatorini tasvirlashning murakkab shakli mavjud bo‘lib, kurs ishining hajmi imkon bermagani uchun uni ko‘rib chiqish mumkin emas edi. Murakkab shakl qator algebraik jihatdan oddiy. Shuning uchun u ko'pincha fizika va amaliy hisob-kitoblarda qo'llaniladi.

Kurs ishi mavzusining ahamiyati nafaqat matematikada, balki boshqa fanlar: fizika, mexanika, tibbiyot, kimyo va boshqa ko'plab fanlarda keng qo'llanilishi bilan bog'liq.

Ma'lumotnomalar

1. Bari, N.K. Trigonometrik qator. [matn]/ N.K. Bari. - Moskva, 1961 yil. - 936 s.

2. Bermant, A.F. Qisqa kurs matematik tahlil: Universitetlar uchun darslik[matn]/ A.F. Bermant, I.G. Aramanovich. – 11-nashr, oʻchirilgan. – Sankt-Peterburg: Lan nashriyoti, 2005. – 736 p.

3. Bugrov, Ya S. Oliy matematika: Universitetlar uchun darslik: 3 jildda.[matn]/ Ya. S. Bugrov, S. M. Nikolskiy; Ed. V. A. Sadovnichiy. - 6-nashr, stereotip. - M.: Bustard, 2004. -512 b.

4. Vinogradova, I. A. Matematik tahlildagi muammolar va mashqlar: universitetlar uchun qo'llanma, pedagogika. universitetlar: soat 2 da.[matn]/ I. A. Vinogradova, S. N. Olehnik, V. A. Sadovnichiy; tomonidan tahrirlangan V.A. Sadovnichigo. – 3-nashr, rev. – M.: Bustard, 2001. – 712 b.

5. Gusak, A.A. Oliy matematika. 2 jildda T. 2. Universitet talabalari uchun darslik.[matn]/ A. A. Gusak.- 5-nashr. - Minsk: TetraSystems, 2004 yil.

6. Danko, P.E. Mashqlar va masalalarda oliy matematika: universitetlar uchun darslik: 2 soat.[matn]/ P.E. Danko, A.G. Popov, T.Ya. Kozhevnikova. Moskva: ONIX: Tinchlik va ta'lim, 2003. - 306 p.

7. Lukin, A. Kirish raqamli ishlov berish signallar (matematik asoslar) [matn]/ A. Lukin. - M., 2007. - 54 b.

8. Piskunov, N. S. Kollej talabalari uchun differentsial va integral hisoblar, 2-jild: Oʻquv qoʻllanma kollejlar va universitetlar uchun.[matn]/ N. S. Piskunov. - 13-nashr - M.: Nauka, 1985. - 432 b.

9. Rudin, U. Matematik analiz asoslari.[matn]/ U. Rudin. - 2-nashr, Trans. ingliz tilidan .- M.: Mir, 1976 .- 206 b.

10. Fikhtengolts, G. M. Matematik analiz asoslari. 2-qism.[matn]/ G. M. Fixtengolts. -6-nashr, o'chirilgan. - Sankt-Peterburg: Lan nashriyoti, 2005. - 464 p.

Orenburg, 2015 yil

1

Chiziqli signal holatida Furye seriyasini yaqinlashtirish imkoniyati uzluksiz signallar holatida funktsiyalarni qurish uchun zarur bo'lishi mumkin. davriy elementlar. Foydalanish imkoniyati bu usul yordamida ularni qurish va parchalash yakuniy miqdorlar Furye seriyalari fizika, seysmologiya va boshqalar kabi turli fanlarning ko'plab muammolarini hal qilishda qo'llaniladi. Okean to'lqinlari va quyosh faolligi jarayonlari tebranish jarayonlarining parchalanish usuli va bu transformatsiyalar bilan tavsiflangan funktsiyalar bilan ko'rib chiqiladi. Rivojlanish bilan kompyuter texnologiyasi Furye seriyalari tobora ko'proq foydalanila boshlandi murakkab vazifalar, shuningdek, shu tufayli bu o'zgarishlarni bilvosita fanlarda, masalan, tibbiyot va kimyoda qo'llash mumkin bo'ldi. Furye konvertatsiyasi ham real, ham murakkab shaklda tasvirlangan, ikkinchi taqsimot tadqiqotda yutuq yaratishga imkon berdi. tashqi makon. Ushbu ishning natijasi Furye seriyasini linearizatsiyaga qo'llashdir uzluksiz funksiya va qatorlarni funktsiyaga aniqroq kiritish uchun qator koeffitsientlar sonini tanlash. Bundan tashqari, Furye seriyasini kengaytirishdan foydalanganda, bu funksiya uzluksiz bo'lishni to'xtatadi va allaqachon etarlicha kichik qiymatlarda, ishlatiladigan funktsiyaning yaxshi yaqinlashuviga erishiladi.

Furye seriyasi

Furye konvertatsiyasi

faza spektri.

1. Alasheyeva E.A., Rogova N.V. Yupqa simli yaqinlashuvda elektrodinamika masalasini echishning raqamli usuli. Ilm va tinchlik. Xalqaro ilmiy jurnal, No 8(12), 2014. 1-jild. Volgograd. B.17-19.

2. Vorobyov N.N. Seriyalar nazariyasi. Ed. Fan, Fizika-matematika adabiyoti bosh tahririyati, M., 1979, -408 S.

3. Kalinina V.N., Pankin V.F. Matematik statistika. - M.: magistratura, 2001.

4. Zamonaviy taqdimotda R. Edvards Furye seriyasi. Ed. Dunyo. 2 jildda. 1-jild. 1985 yil. 362 bet.

5. Sigorskiy V.P. Muhandisning matematik apparati. Ed. 2-steriotipik. "Texnika", 1997 yil. – 768 b.

Ixtiyoriy funktsiyaning o'ziga xos davri bo'lgan qator shaklida tasvirlanishi Furye qatori deyiladi. Ortogonal asosda kengayish deyiladi bu qaror umumiy ma'noda. Furye seriyali funktsiyalarni kengaytirish turli xil muammolarni hal qilish uchun juda kuchli vositadir. Chunki Integratsiya, differensiatsiya, shuningdek, argument va konvolyutsiya orqali ifodani o'zgartirish paytidagi bu transformatsiyaning xususiyatlari yaxshi ma'lum va o'rganilgan. Tanish bo'lmagan odam oliy matematika, shuningdek, frantsuz olimi Furyening asarlari bilan, ehtimol, bu "seriyalar" nima ekanligini va ular nima uchun kerakligini tushunmaydi. Ushbu Furye o'zgarishi bizning hayotimizning ajralmas qismiga aylandi. U nafaqat matematiklar, balki fiziklar, kimyogarlar, shifokorlar, astronomlar, seysmologlar, okeanologlar va boshqalar tomonidan ham qo'llaniladi.

Furye seriyalari ko'plab amaliy masalalarni hal qilish uchun ishlatiladi. Furye konvertatsiyasini analitik, raqamli va boshqa usullar yordamida amalga oshirish mumkin. Okean to'lqinlari kabi jarayonlar va yorug'lik to'lqinlari Quyosh faolligi davrlari deganda har qanday tebranish jarayonlarini Furye qatoriga ajratishning raqamli usuli tushuniladi. Ushbu matematik usullardan foydalanib, siz har qanday tebranish jarayonlarini minimaldan maksimalga va orqaga siljiydigan sinusoidal komponentlar qatori sifatida ifodalovchi funktsiyalarni tahlil qilishingiz mumkin. Furye transformatsiyasi ma'lum bir chastotaga mos keladigan sinusoidlarning fazasi va amplitudasini tavsiflovchi funktsiyadir. Ushbu transformatsiya juda hal qilish uchun ishlatiladi murakkab tenglamalar, termal, yorug'lik yoki ta'siri ostida yuzaga keladigan dinamik jarayonlarni tavsiflovchi elektr energiyasi. Shuningdek, Furye seriyalari murakkab tebranish signallarida doimiy komponentlarni ajratib olish imkonini beradi, bu esa tibbiyot, kimyo va astronomiyada olingan eksperimental kuzatishlarni to'g'ri talqin qilish imkonini beradi.

Texnologiyaning o'sishi bilan, ya'ni. kompyuterning paydo bo'lishi va rivojlanishi Furye konvertatsiyasiga olib keldi yangi daraja. Bu texnika fan va texnikaning deyarli barcha sohalarida mustahkam o‘rnatilgan. Masalan, raqamli audio va video. Bu o'sishning aniq amalga oshishiga aylandi ilmiy jarayon va Furye seriyasining ilovalari. Shunday qilib, Furye seriyasi murakkab shaklda kosmik fazoni o'rganishda yutuq yaratishga imkon berdi. Bundan tashqari, u fizikani o'rganishga ta'sir ko'rsatdi yarimo'tkazgichli materiallar va plazma, mikroto'lqinli akustika, okeanografiya, radar, seysmologiya.

Quyidagi ifodadan aniqlangan davriy signalning faza spektrini ko'rib chiqing:

bu yerda belgilar va mos ravishda kvadrat qavs ichiga olingan miqdorning xayoliy va haqiqiy qismlarini bildiradi.

Agar haqiqiy doimiy qiymat K ga ko'paytirilsa, Furye seriyasining kengayishi quyidagi ko'rinishga ega bo'ladi:

(1) ifodadan kelib chiqadiki, Furye fazasi spektri quyidagi xususiyatlarga ega:

1) ning funktsiyasidir, ya'ni ga bog'liq bo'lmagan quvvat spektridan farqli o'laroq, signal vaqt o'qi bo'ylab siljishi bilan o'zgaradi;

2) K ga bog'liq emas, ya'ni u signal kuchayishi yoki zaiflashishi uchun o'zgarmasdir, quvvat spektri esa K ga bog'liq.

3) ya'ni n ning toq funksiyasi.

Eslatma. Yuqoridagi mulohazalarning geometrik talqinini hisobga olgan holda, uni quvvat spektri va faza spektri nuqtai nazaridan quyidagicha ifodalash mumkin:

Chunki

keyin (2) va (3) dan, agar amplituda (yoki quvvat spektri) va faza spektrlari ma'lum bo'lsa, uni bir ma'noda qayta qurish mumkinligi kelib chiqadi.

Keling, bir misolni ko'rib chiqaylik. Bizga funktsiya berilgan orasida

Furye seriyasining umumiy ko'rinishi:

Keling, qadriyatlarimizni almashtiramiz va olamiz:

Keling, qadriyatlarimizni almashtiramiz va olamiz.

funktsiyalari. Ushbu transformatsiya katta ahamiyatga ega, chunki u ko'plab amaliy muammolarni hal qilish uchun ishlatilishi mumkin. Furye qatorlaridan nafaqat matematiklar, balki boshqa fanlar mutaxassislari ham foydalanadilar.

Funksiyalarning Furye qatoriga kengayishi, agar siz sinusoidal funktsiyalarni sezadigan qurilmadan foydalansangiz, tabiatda kuzatilishi mumkin bo'lgan matematik usuldir.

Bu jarayon odam tovushni eshitganda sodir bo'ladi. Inson qulog'i shunday yaratilganki, u turli chastotalardagi havo bosimining individual sinusoidal tebranishlarini sezishi mumkin, bu esa o'z navbatida odamga nutqni tanib olish va musiqa tinglash imkonini beradi.

Inson qulog'i tovushni bir butun sifatida emas, balki uning Furye seriyali komponentlari orqali qabul qiladi. Musiqa asbobining torlari turli chastotali sinusoidal tebranishlar bo'lgan tovushlarni hosil qiladi. Furye seriyali yorug'likning kengayishi haqiqati kamalak bilan ifodalanadi. Insonning ko'rish qobiliyati yorug'likni turli chastotali elektromagnit tebranishlarning ba'zi tarkibiy qismlari orqali qabul qiladi.

Furye transformatsiyasi ma'lum chastotali sinusoidlarning fazasi va amplitudasini tavsiflovchi funktsiyadir. Ushbu transformatsiya energiya ta'sirida yuzaga keladigan dinamik jarayonlarni tavsiflovchi tenglamalarni echish uchun ishlatiladi. Furye seriyalari murakkab tebranish signallarida doimiy komponentlarni aniqlash muammosini hal qiladi, bu esa tajribalar, tibbiyot, kimyo va astronomiyadagi kuzatishlar natijasida olingan ma'lumotlarni to'g'ri talqin qilish imkonini berdi.

Ushbu transformatsiyaning kashfiyoti frantsuz matematigi Jan Baptiste Jozef Furyega tegishli. Keyinchalik Furye seriyasi kimning sharafiga nomlandi. Dastlab olim o'z usulini issiqlik o'tkazuvchanlik mexanizmlarini o'rganish va tushuntirishda qo'llashni topdi. Issiqlikning dastlabki tartibsiz taqsimlanishi oddiy sinusoidlar shaklida ifodalanishi mumkinligi taklif qilindi. Ularning har biri uchun haroratning minimal, maksimal va fazasi aniqlanadi. Egri chiziqning yuqori va pastki cho'qqilarini, har bir harmonikning fazasini tavsiflovchi funktsiya harorat taqsimotining ifodasidan Furye transformatsiyasi deb ataladi. Transformatsiya muallifi kosinus, sinus davriy funktsiyalar yig'indisi sifatida murakkab funktsiyani parchalash usulini taklif qildi.

Kurs ishining maqsadi Furye qatorini va ushbu transformatsiyani amaliy qo'llashning dolzarbligini o'rganishdir.

Ushbu maqsadga erishish uchun quyidagi vazifalar belgilandi:

1) trigonometrik Furye qatori tushunchasini bering;

2) Furye qatoridagi funksiyaning parchalanish shartlarini aniqlash;

3) juft va toq funksiyalarning Furye qator kengayishini ko‘rib chiqing;

4) davriy bo'lmagan funksiyaning Furye qator kengayishini ko'rib chiqing;

5) Furye qatorining amaliy qo'llanilishini ochib bering.

Tadqiqot ob'ekti: Furye qatoridagi funktsiyalarni kengaytirish.

O'rganish mavzusi: Furye seriyasi.

Tadqiqot usullari: tahlil, sintez, taqqoslash, aksiomatik usul.

1.5. Juft va toq funksiyalar uchun Furye seriyalari

Simmetrik integralni ko'rib chiqing

qaerda uzluksiz yoki bo'lakcha uzluksiz. Birinchi integralga o'zgartirish kiritamiz. Ishonamizki. Keyin

Shuning uchun, agar funktsiya juft bo'lsa, u holda (ya'ni juft funktsiyaning grafigi o'qga nisbatan simmetrik va

Agar toq funksiya bo'lsa, u holda (ya'ni, toq funktsiyaning grafigi boshiga nisbatan simmetrik bo'ladi) va

Bular. juft funktsiyaning simmetrik integrali integrallash oralig'ining yarmidan ikki baravar ko'p bo'lgan integralga, toq funksiyaning simmetrik integrali esa nolga teng.

Juft va toq funksiyalarning quyidagi ikkita xususiyatiga e’tibor bering:

1) juft va toq funksiyaning mahsuloti toq funksiyadir;

2) ikkita juft (toq) funksiyaning ko‘paytmasi juft funktsiyadir.

Bu segmentda aniqlangan va trigonometrik Furye qatoriga kengaytiriladigan juft funksiya bo'lsin. Yuqorida olingan natijalardan foydalanib, biz ushbu seriyaning koeffitsientlari quyidagi shaklga ega bo'lishini aniqlaymiz:

Agar segmentda toq funksiya aniqlangan bo'lsa va bu segmentda trigonometrik Furye qatoriga kengaytirilsa, bu qatorning koeffitsientlari quyidagi ko'rinishga ega bo'ladi:

Binobarin, segmentdagi trigonometrik Furye seriyasi shaklga ega bo'ladi

teng funksiya uchun:

(16)

g'alati funktsiya uchun:

Seriya (16) ko'p burchakli sinuslarni o'z ichiga olmaydi, ya'ni juft funktsiyaning Furye qatoriga faqat juft funktsiyalar va mustaqil atama kiradi. Seriya (17) ko'p burchakli kosinuslarni o'z ichiga olmaydi, ya'ni toq funksiyaning Furye qatoriga faqat toq funksiyalar kiradi.

Ta'rif. Qatorlar
toʻliq Furye qatorining qismlari boʻlib, toʻliqsiz deyiladitrigonometrik Furye qatori.

Agar funktsiya to'liq bo'lmagan trigonometrik qatorga (16) (yoki (17)) kengaytirilsa, u holda deyiladi.kosinuslarda (yoki sinuslarda) trigonometrik Furye qatoriga kengayadi.

1.6. Davriy bo'lmagan funksiyaning Furye qator kengayishi

1.6.1. Funksiyalarni Furye seriyali kengaytirish

Funksiya oraliqda berilsin va bu oraliqda Dirixle teoremasining shartlari qanoatlansin. O'zgaruvchini o'zgartirishni amalga oshiramiz. Olingan argument funksiyasi aniqlanishi uchun biz tanlagan joyni belgilaymiz. Shuning uchun biz bunga ishonamiz

Olingan funktsiyani Furye qatoriga kengaytirish mumkin:

Qayerda

Keling, teskari almashtirishni qilaylik⇒ olamiz

Qayerda

(19)

Seriya (18) – Funksiyalarning asosiy trigonometrik tizimidagi Furye qatori

Shunday qilib, agar funktsiya oraliqda berilgan bo'lsa va bu oraliqda Dirixle teoremasining shartlarini qanoatlantirsa, u holda funksiyalarning trigonometrik tizimi (20) bo'yicha uni trigonometrik Furye qatoriga (18) kengaytirish mumkinligini aniqladik.

Aniqlangan juft funksiya uchun trigonometrik Furye seriyasi shaklga ega bo'ladi

Qayerda

g'alati funktsiya uchun

Qayerda

Izoh! Ayrim masalalarda funksiyani segmentga emas, balki segmentga (20) funksiyalar tizimiga muvofiq trigonometrik Furye qatoriga kengaytirish talab qilinadi. Bunday holda, siz (19) ((15) formulalaridagi integratsiya chegaralarini o'zgartirishingiz kerak, agar bu holda bo'lsa

(23)

yoki agar

(24)

Trigonometrik Furye qatorining yig‘indisi davriy funksiya bo‘lib, berilgan funksiyaning davriy davomi hisoblanadi. Va davriy funktsiya uchun (4) tenglik to'g'ri.

1.6.2. Funksiyalarni Furye seriyali kengaytirish

Funktsiya berilgan bo'lsin va bu oraliqda Dirixle teoremasining shartlarini qanoatlantirsin. Bunday funktsiyani Furye qatoriga ham kengaytirish mumkin. Buning uchun funktsiyani intervalgacha kengaytirish va natijada olingan funktsiyani intervalda Furye qatoriga kengaytirish kerak. Bunday holda, hosil bo'lgan qator faqat funktsiya ko'rsatilgan segmentda ko'rib chiqilishi kerak. Hisoblash qulayligi uchun funksiyani juft va toq shaklda aniqlaymiz.

1) Funksiyani teng oraliqda kengaytiramiz, ya’ni intervaldagi funksiya bilan mos keladigan yangi juft funksiya tuzamiz. Binobarin, bu funksiyaning grafigi o'qga nisbatan simmetrik bo'lib, segmentdagi grafik bilan mos keladi. Formulalardan (21) foydalanib, funktsiya uchun Furye qatorining koeffitsientlarini topamiz va Furye qatorining o'zini yozamiz. For Furye qatorlarining yig'indisi davriy funktsiya bo'lib, davri bilan. Bu uzluksizlikning barcha nuqtalarida funksiya bilan mos keladi.

2) Funksiyani intervalgacha toq tarzda kengaytiramiz, ya’ni funksiya bilan mos keladigan yangi toq funksiya tuzamiz. Bunday funktsiyaning grafigi koordinatalarning kelib chiqishiga nisbatan simmetrik bo'lib, segmentdagi grafik bilan mos keladi. Formulalardan (22) foydalanib, funktsiya uchun Furye qatorining koeffitsientlarini topamiz va Furye qatorining o'zini yozamiz. For Furye qatorlarining yig'indisi davriy funktsiyadir. Bu uzluksizlikning barcha nuqtalarida funksiya bilan mos keladi.

Eslatmalar!

1) Xuddi shunday, intervalda aniqlangan funksiyani Furye qatoriga kengaytirishingiz mumkin

2) Funktsiyaning segmentdagi kengayishi uning segmentga ixtiyoriy tarzda davom etishini nazarda tutganligi sababli, funktsiya uchun Furye qatori yagona bo'lmaydi.

1.6.3. Funksiyalarni Furye seriyali kengaytirish

Funksiya ixtiyoriy uzunlik segmentida berilsin va undagi Dirixle teoremasining shartlarini qanoatlantirsin.

Keyin bu funktsiyani Furye seriyasiga kengaytirish mumkin. Buning uchun funktsiyani davriy ravishda (nuqta bilan) butun son chizig'i bo'ylab davom ettirish va natijada olingan funktsiyani faqat segmentda ko'rib chiqilishi kerak bo'lgan Furye qatoriga kengaytirish kerak. Davriy funksiyalarning xossasi (3) tufayli bizda mavjud

Shuning uchun funktsiyaning natijada davom etishi uchun Furye koeffitsientlarini formulalar yordamida topish mumkin.

(25)

2. Furye qatorining amaliy qo‘llanilishi

2.1. Furye qatoridagi funksiyalarni kengaytirishga oid masalalar va ularni yechish

Intervalda berilgan funktsiyaning davriy davomi bo'lgan funktsiyani trigonometrik Furye qatoriga kengaytirish talab qilinadi. Buning uchun davriy funktsiyani Furye qatoriga kengaytirish algoritmidan foydalanish kerak.

Davriy funktsiyani Furye qatoriga kengaytirish algoritmi:

1) Berilgan funksiya va uning davriy davomi grafigini tuzing;

2) Berilgan funksiyaning davrini belgilang;

3) funksiyaning juft, toq yoki umumiy ekanligini aniqlang;

4) Dirixle teoremasi shartlarini amalga oshirish imkoniyatini tekshirish;

5) Ushbu funktsiya tomonidan yaratilgan Furye qatorining rasmiy tasvirini yarating;

6) Furye koeffitsientlarini hisoblash;

7) Furye qatorining koeffitsientlaridan foydalanib, berilgan funksiya uchun Furye qatorini yozing (4-band).

1-misol. Funktsiyani intervalda Furye qatoriga kengaytiring.

Yechim:

1) Berilgan funksiya va uning davriy davomi grafigini tuzamiz.

2) Funksiyaning kengayish davri.

3) Funktsiya g'alati.

4) Funktsiya uzluksiz va monotonik, ya'ni. funktsiya Dirixlet shartlarini qondiradi.

5) Furye qatorining koeffitsientlarini hisoblaymiz.

6) Furye koeffitsientlarini formulaga almashtirib, Furye qatorini yozing.

Javob:

2-misol. Ixtiyoriy davri bo'lgan funksiyani Furye qatoriga kengaytiramiz.

Yechish: funksiya yarim oraliqda (-3;3] aniqlanadi. Funksiyaning kengayish davri, yarim davr. Funksiyani Furye qatoriga kengaytiramiz.

Funktsiyaning boshlang'ich nuqtasida uzluksiz, shuning uchun biz har bir Furye koeffitsientini ikkita integral yig'indisi sifatida ifodalaymiz.

Furye qatorining topilgan koeffitsientlarini formulaga almashtirib, Furye qatorini yozamiz.

3-misol. Funktsiyani kengaytirishorasidakosinuslardagi Furye qatorida. Seriyalar yig‘indisining grafigini tuzing.

Yechish: biz funktsiyani oraliqda teng ravishda kengaytiramiz, ya'ni intervaldagi funksiya bilan mos keladigan yangi juft funktsiyani quramiz. Funksiya uchun Furye qatorining koeffitsientlarini topamiz va Furye qatorini yozamiz. Furye qatorlarining yig'indisi davriy funktsiya bo'lib, davri bilan. Bu uzluksizlikning barcha nuqtalarida funksiya bilan mos keladi.

Funktsiya uchun trigonometrik Furye seriyasi shaklga ega bo'ladi

Furye qatorining koeffitsientlarini topamiz

Shunday qilib, koeffitsientlar topilsa, biz Furye qatorini yozishimiz mumkin

Keling, qatorlar yig'indisini chizamiz

4-misol. Segmentda aniqlangan funksiya berilgan. Funktsiyani Furye qatoriga kengaytirish mumkinligini aniqlang. Funksiyaning kengayishini Furye qatorida yozing.

Yechim:

1) da funksiyaning grafigini tuzing.

2) funksiya uzluksiz va monotonik bo‘ladi, ya’ni Dirixle teoremasiga ko‘ra, uni trigonometrik Furye qatoriga kengaytirish mumkin.

3) (1.19) formulalar yordamida Furye koeffitsientlarini hisoblang.

4) topilgan koeffitsientlar yordamida Furye qatorini yozing.

2.2. Furye qatorlarini inson faoliyatining turli sohalarida qo'llash misollari

Matematika amaliyotda keng qo'llaniladigan fanlardan biridir. Har qanday ishlab chiqarish va texnologik jarayon matematik qonunlarga asoslanadi. Turli matematik vositalardan foydalanish binolar va inshootlarni loyihalashda operatsiyalarni, murakkab hisob-kitoblarni va hisob-kitoblarni bajarishga qodir bo'lgan qurilmalar va avtomatlashtirilgan birliklarni loyihalash imkonini beradi.

Furye seriyalari matematiklar tomonidan geometriyada qo'llaniladisferik geometriyadan masalalar yechish; m dada atematik fizikaelastik muhitning kichik tebranishlari bo'yicha masalalarni yechish. Ammo matematikadan tashqari, Furye seriyalari fanning boshqa sohalarida ham o'z qo'llanilishini topdi.

Har kuni odamlar turli xil qurilmalardan foydalanadilar. Va ko'pincha bu qurilmalar to'g'ri ishlamaydi. Masalan, ko'p shovqin tufayli tovushni eshitish qiyin yoki faks orqali olingan tasvir noaniq. Biror kishi nosozlik sababini ovoz bilan aniqlashi mumkin. Kompyuter shuningdek, qurilma shikastlangan yoki yo'qligini tashxislashi mumkin. Ortiqcha shovqin kompyuter signalini qayta ishlash yordamida olib tashlanishi mumkin. Signal raqamli qiymatlar ketma-ketligi sifatida ifodalanadi, keyinchalik ular kompyuterga kiritiladi. Muayyan hisob-kitoblarni amalga oshirgandan so'ng, Furye seriyasining koeffitsientlari olinadi.

Signal spektrini o'zgartirish shovqinni yozib olishni tozalash, turli yozish qurilmalari tomonidan signal buzilishini qoplash, asboblar tembrini o'zgartirish va tinglovchilarning diqqatini alohida qismlarga qaratish imkonini beradi.

Raqamli tasvirni qayta ishlashda Furye seriyasidan foydalanish quyidagi effektlarni amalga oshirishga imkon beradi: xiralashtirish, qirralarni ta'kidlash, tasvirni tiklash, badiiy effektlar (bo'rttirma)

Furye seriyasining kengayishi arxitekturada tebranish jarayonlarini o'rganishda qo'llaniladi. Masalan, har xil turdagi tuzilmalar uchun loyihani yaratishda strukturaviy elementlarning mustahkamligi, qattiqligi va barqarorligi hisoblab chiqiladi.

Tibbiyotda kardiogrammalar va ultratovush apparati yordamida tibbiy ko'rik o'tkazish uchun Furye seriyasi nazariyasiga asoslangan matematik apparatdan foydalaniladi.

Signallarning statistik xususiyatlarini baholash va shovqinlarni filtrlash bo'yicha yirik hisoblash muammolari dengiz tubining uzluksiz ma'lumotlarini yozish va qayta ishlashda paydo bo'ladi. O'lchovlarni amalga oshirish va ularni qayd etishda Furye seriyasidan foydalangan holda gologramma usullari istiqbolli. Ya'ni, Furye seriyalari okeanologiya kabi fanda ham qo'llaniladi.

Matematikaning elementlari ishlab chiqarishda deyarli har bir bosqichda topiladi, shuning uchun mutaxassislar ma'lum tahlil va hisoblash vositalarini bilish va qo'llash sohasida yaxshi yo'naltirilgan bo'lishlari muhimdir..

Xulosa

Kurs ishining mavzusi Furye seriyasini o'rganishga bag'ishlangan. Ixtiyoriy funktsiyani oddiyroqlarga kengaytirish mumkin, ya'ni uni Furye qatoriga kengaytirish mumkin. Kurs ishining ko'lami bizga funktsiyani ketma-ket kengaytirishning barcha jihatlarini batafsil ochib berishga imkon bermaydi. Biroq, qo'yilgan vazifalardan Furye seriyalari haqidagi asosiy nazariyani ochish mumkin bo'lib tuyuldi.

Kurs ishi trigonometrik Furye qatori tushunchasini ochib beradi. Furye qatoridagi funksiyaning parchalanish shartlari aniqlanadi. Juft va toq funksiyalarning Furye qator kengayishi ko‘rib chiqiladi; davriy bo'lmagan funktsiyalar.

Ikkinchi bobda turli oraliqlarda berilgan funksiyalarni Furye qatoriga kengaytirishga oid ayrim misollar keltirilgan. Ushbu transformatsiya qo'llaniladigan fan sohalari tavsiflanadi.

Shuningdek, Furye qatorini tasvirlashning murakkab shakli mavjud bo‘lib, kurs ishining hajmi imkon bermagani uchun uni ko‘rib chiqish mumkin emas edi. Seriyaning murakkab shakli algebraik jihatdan sodda. Shuning uchun u ko'pincha fizika va amaliy hisob-kitoblarda qo'llaniladi.

Kurs ishi mavzusining ahamiyati nafaqat matematikada, balki boshqa fanlar: fizika, mexanika, tibbiyot, kimyo va boshqa ko'plab fanlarda keng qo'llanilishi bilan bog'liq.

Ma'lumotnomalar

1. Bari, N.K. Trigonometrik qator. [matn]/ N.K. Bari. - Moskva, 1961 yil. - 936 s.

2. Bermant, A.F. Matematik tahlil bo'yicha qisqa kurs: universitetlar uchun darslik[matn]/ A.F. Bermant, I.G. Aramanovich. – 11-nashr, oʻchirilgan. – Sankt-Peterburg: Lan nashriyoti, 2005. – 736 p.

3. Bugrov, Ya S. Oliy matematika: Universitetlar uchun darslik: 3 jildda.[matn]/ Ya. S. Bugrov, S. M. Nikolskiy; Ed. V. A. Sadovnichiy. - 6-nashr, stereotip. - M.: Bustard, 2004. -512 b.

4. Vinogradova, I. A. Matematik tahlildagi muammolar va mashqlar: universitetlar uchun qo'llanma, pedagogika. universitetlar: soat 2 da.[matn]/ I. A. Vinogradova, S. N. Olehnik, V. A. Sadovnichiy; tomonidan tahrirlangan V.A. Sadovnichigo. – 3-nashr, rev. – M.: Bustard, 2001. – 712 b.

5. Gusak, A.A. Oliy matematika. 2 jildda T. 2. Universitet talabalari uchun darslik.[matn]/ A. A. Gusak.- 5-nashr. - Minsk: TetraSystems, 2004 yil.

6. Danko, P.E. Mashqlar va masalalarda oliy matematika: universitetlar uchun darslik: 2 soat.[matn]/ P.E. Danko, A.G. Popov, T.Ya. Kozhevnikova. Moskva: ONIX: Tinchlik va ta'lim, 2003. - 306 p.

7. Lukin, A. Raqamli signallarni qayta ishlashga kirish (matematik asoslar) [matn]/ A. Lukin. - M., 2007. - 54 b.

8. Piskunov, N. S. Kollejlar uchun differensial va integral hisoblar, 2-jild: Kollejlar uchun darslik.[matn]/ N. S. Piskunov. - 13-nashr - M.: Nauka, 1985. - 432 b.

9. Rudin, U. Matematik analiz asoslari.[matn]/ U. Rudin. - 2-nashr, Trans. ingliz tilidan .- M.: Mir, 1976 .- 206 b.

10. Fikhtengolts, G. M. Matematik analiz asoslari. 2-qism.[matn]/ G. M. Fixtengolts. -6-nashr, o'chirilgan. - Sankt-Peterburg: Lan nashriyoti, 2005. - 464 p.

Orenburg, 2015 yil