Kurs ishi “Furye seriyalari va ularning qo'llanilishi. bu yerda k garmonik son. Furye seriyasi shunday yozilgan
Shuningdek o'qing
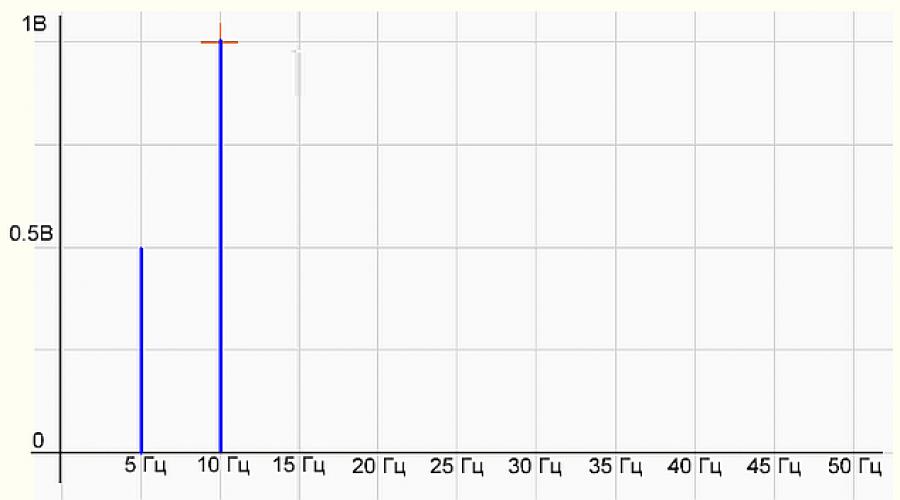
Dasturning to'g'ri ishlayotganligini tekshirish uchun biz ikkita sinusoid sin(10*2*pi*x)+0,5*sin(5*2*pi*x) yig'indisi sifatida namunalar massivi hosil qilamiz va uni dasturga kiritamiz. . Dasturda quyidagilar chizilgan:
1-rasm Signal vaqti funksiyasining grafigi

2-rasm Signal spektrining grafigi
Spektr grafigida amplitudasi 0,5 V va 10 Gts amplitudasi 1 V bo'lgan ikkita tayoq (harmonika) 5 Gts mavjud bo'lib, hamma narsa asl signal formulasi bilan bir xil. Hammasi yaxshi, yaxshi dasturchi! Dastur to'g'ri ishlaydi.
Bu shuni anglatadiki, agar biz ikkita sinusoid aralashmasidan ADC kirishiga haqiqiy signalni qo'llasak, ikkita garmonikadan iborat shunga o'xshash spektrni olamiz.
Jami, bizning haqiqiy o'lchangan signal 5 soniya davom etadi, ADC tomonidan raqamlangan, ya'ni ifodalangan diskret hisoblaydi, bor diskret davriy bo'lmagan diapazon.
Matematik nuqtai nazardan, bu iborada nechta xato bor?
Endi hokimiyat qaror qildi, biz 5 soniya juda uzoq deb qaror qildik, signalni 0,5 soniyada o'lchaymiz.

3-rasm sin(10*2*pi*x)+0,5*sin(5*2*pi*x) funksiyasining 0,5 sek o‘lchov davri uchun grafigi.

4-rasm Funktsiyalar spektri
Nimadir noto'g'ri ko'rinadi! 10 Gts harmonik odatda chiziladi, lekin 5 Gts tayoq o'rniga bir nechta g'alati harmonikalar paydo bo'ladi. Nima bo'layotganini bilish uchun Internetga qaraymiz ...
Ularning aytishicha, namunaning oxiriga nol qo'shishingiz kerak va spektr odatdagidek chiziladi.

Fig.5 5 soniyagacha nol qo'shildi

Fig.6 Qabul qilingan spektr
Bu hali ham 5 soniyadagidek emas. Biz nazariya bilan shug'ullanishimiz kerak. Keling, boraylik Vikipediya- bilim manbai.
2. Uzluksiz funksiya va uning Furye seriyali tasviri
Matematik jihatdan T sekund davom etgan signalimiz (0, T) segmentida aniqlangan ba'zi f(x) funksiyadir (X in). Ushbu holatda- vaqt). Bunday funktsiya har doim quyidagi shaklning harmonik funktsiyalari (sinus yoki kosinus) yig'indisi sifatida ifodalanishi mumkin: (1), bu erda:
(1), bu erda:
K - trigonometrik funktsiya raqami (garmonik komponent raqami, garmonik raqam)
T - funksiya aniqlangan segment (signal davomiyligi)
Ak - k-chi garmonik komponentning amplitudasi,
kh- k- garmonik komponentning boshlang'ich fazasi
“Funksiyani qatorlar yig‘indisi sifatida ifodalash” nimani anglatadi? Bu shuni anglatadiki, Furye seriyasining harmonik komponentlarining qiymatlarini har bir nuqtada qo'shish orqali biz ushbu nuqtada funktsiyamizning qiymatini olamiz.
(Aniqroq aytganda, qatorning f(x) funktsiyasidan ildiz o'rtacha kvadrat og'ishi nolga moyil bo'ladi, lekin o'rtacha kvadrat yaqinlashuviga qaramay, funktsiyaning Furye qatori, umuman olganda, talab qilinmaydi. unga nuqta bilan yaqinlashing. https://ru.wikipedia.org/ wiki/Fourier_Series.)
Ushbu seriyani quyidagicha yozish mumkin:
 (2),
(2),
Qayerda, k- kompleks amplituda.
(1) va (3) koeffitsientlar orasidagi munosabat quyidagi formulalar bilan ifodalanadi:
![]()

E'tibor bering, Furye seriyasining ushbu uchta ko'rinishi butunlay ekvivalentdir. Ba'zan Furye qatorlari bilan ishlashda sinus va kosinuslar o'rniga xayoliy argumentning ko'rsatkichlarini qo'llash qulayroq bo'ladi, ya'ni Furye konvertatsiyasidan foydalaning. murakkab shakl. Ammo biz uchun (1) formuladan foydalanish qulay, bu erda Furye seriyasi mos keladigan amplitudalar va fazalar bilan kosinus to'lqinlarining yig'indisi sifatida taqdim etiladi. Qanday bo'lmasin, haqiqiy signalning Furye o'zgarishi murakkab garmonik amplitudalarga olib keladi, deb aytish noto'g'ri. Wiki to'g'ri ta'kidlaganidek, "Fourier konvertatsiyasi (ℱ) - bu haqiqiy o'zgaruvchining bir funktsiyasini boshqa funktsiya, shuningdek, haqiqiy o'zgaruvchi bilan bog'laydigan operatsiya."
Jami:
Signallarni spektral tahlil qilishning matematik asosi Furye transformatsiyasi hisoblanadi.
Furye konvertatsiyasi (0, T) segmentida cheksiz son (cheksiz qator) yig‘indisi sifatida aniqlangan uzluksiz f(x) funksiyani (signal) tasvirlash imkonini beradi. trigonometrik funktsiyalar(0, T) segmentida ham hisobga olinadigan ma'lum amplitudalar va fazalar bilan (sinus va/yoki kosinus). Bunday qator Furye seriyasi deb ataladi.
Keling, tushunish uchun zarur bo'lgan yana bir nechta fikrlarni ta'kidlaymiz to'g'ri dastur Signalni tahlil qilish uchun Furye transformatsiyasi. Agar butun X o'qi bo'yicha Furye qatorini (sinusoidlar yig'indisini) ko'rib chiqsak, segmentdan tashqarida (0, T) Furye qatori bilan ifodalangan funktsiya bizning funktsiyamizni davriy ravishda takrorlashini ko'rishimiz mumkin.
Masalan, 7-rasmdagi grafikda asl funksiya segmentda (-T\2, +T\2) aniqlanadi va Furye qatori davriy funktsiya, butun x o'qi bo'yicha aniqlangan.
Buning sababi, sinusoidlarning o'zi davriy funktsiyalardir va shunga mos ravishda ularning yig'indisi davriy funktsiya bo'ladi.

7-rasm Davriy bo'lmagan asl funktsiyani Furye qatori bilan tasvirlash
Shunday qilib:
Bizning asl funktsiyamiz uzluksiz, davriy bo'lmagan, T uzunlikdagi ma'lum bir segmentda aniqlangan.
Ushbu funktsiyaning spektri diskretdir, ya'ni u garmonik komponentlarning cheksiz qatori - Furye seriyasi shaklida taqdim etiladi.
Darhaqiqat, Furye seriyasi (0, T) segmentida biznikiga to'g'ri keladigan ma'lum bir davriy funktsiyani belgilaydi, ammo biz uchun bu davriylik ahamiyatli emas.
Garmonik komponentlarning davrlari asl f(x) funksiyasi aniqlangan segmentning (0, T) qiymatiga karrali. Boshqacha qilib aytganda, garmonik davrlar signalni o'lchash davomiyligiga ko'paytiriladi. Masalan, Furye qatorining birinchi garmonik davri f(x) funksiya aniqlangan T intervalga teng. Furye seriyasining ikkinchi garmonikasining davri T/2 intervaliga teng. Va hokazo (8-rasmga qarang).

8-rasm Furye seriyasining garmonik komponentlarining davrlari (chastotalari) (bu erda T = 2p)
Shunga ko'ra, harmonik komponentlarning chastotalari 1 / T ga ko'paytiriladi. Ya'ni, Fk garmonik komponentlarning chastotalari Fk= k\T ga teng, bu erda k 0 dan ∞ gacha, masalan k=0 F0=0; k=1 F1=1\T; k=2 F2=2\T; k=3 F3=3\T;… Fk= k\T (nol chastotada - doimiy komponent).
Bizning asl funktsiyamiz T=1 soniya davomida qayd etilgan signal bo'lsin. Shunda birinchi garmonikaning davri bizning signalimizning davomiyligiga teng bo'ladi T1=T=1 sek va garmonik chastota 1 Gts ga teng bo'ladi. Ikkinchi garmonikaning davri signal davomiyligi 2 ga bo'lingan (T2 = T/2 = 0,5 sek) va chastotasi 2 Gts ga teng bo'ladi. Uchinchi harmonik uchun T3=T/3 sek va chastotasi 3 Hz. Va hokazo.
Bu holda harmonikalar orasidagi qadam 1 Gts ni tashkil qiladi.
Shunday qilib, davomiyligi 1 sekund bo'lgan signal 1 Gts chastotali rezolyutsiyaga ega bo'lgan harmonik komponentlarga (spektrni olish) parchalanishi mumkin.
Ruxsatni 2 marta 0,5 Gts ga oshirish uchun siz o'lchash davomiyligini 2 marta - 2 soniyagacha oshirishingiz kerak. 10 soniya davom etadigan signal 0,1 Gts chastota o'lchamlari bilan harmonik komponentlarga (spektrni olish uchun) parchalanishi mumkin. Chastota o'lchamlarini oshirishning boshqa usullari yo'q.
Namunalar qatoriga nol qo'shish orqali signalning davomiyligini sun'iy ravishda oshirish usuli mavjud. Lekin u haqiqiy chastota o'lchamlarini oshirmaydi.
3. Diskret signallar va diskret Furye transformatsiyasi
Rivojlanish bilan raqamli texnologiya O'lchov ma'lumotlarini (signallarini) saqlash usullari ham o'zgardi. Agar ilgari signal magnitafonga yozib olinishi va uni analog shaklda lentada saqlash mumkin bo'lsa, endi signallar raqamlashtiriladi va raqamlar to'plami (namuna) sifatida kompyuter xotirasidagi fayllarda saqlanadi.Signalni o'lchash va raqamlashtirishning odatiy sxemasi quyidagicha.

9-rasm o'lchash kanalining diagrammasi
O'lchov o'tkazgichdan kelgan signal ADC ga T vaqt oralig'ida keladi. T vaqtida olingan signal namunalari (namuna olish) kompyuterga uzatiladi va xotirada saqlanadi.

10-rasm Raqamlangan signal - T vaqtida olingan N namunalar
Signalni raqamlashtirish parametrlariga qanday talablar qo'yiladi? Kirishni o'zgartiruvchi qurilma analog signal diskret kodga ( raqamli signal) analog-raqamli konvertor (ADC, English Analog-to-digital converter, ADC) deb ataladi (Wiki).
ADC ning asosiy parametrlaridan biri maksimal namuna olish chastotasi (yoki namuna olish tezligi, inglizcha namuna tezligi) - uni namuna olishda vaqt davom etadigan signalning namuna olish tezligi. U Gertsda o'lchanadi. ((Wiki))
Kotelnikov teoremasiga ko'ra, agar uzluksiz signal Fmax chastotasi bilan chegaralangan spektrga ega bo'lsa, uni vaqt oralig'ida olingan diskret namunalaridan to'liq va aniq qayta qurish mumkin.  , ya'ni. chastotasi bilan Fd ≥ 2*Fmax, bu erda Fd - namuna olish chastotasi; Fmax - signal spektrining maksimal chastotasi. Boshqacha qilib aytganda, signalni raqamlashtirish chastotasi (ADC namuna olish chastotasi) biz o'lchamoqchi bo'lgan signalning maksimal chastotasidan kamida 2 baravar yuqori bo'lishi kerak.
, ya'ni. chastotasi bilan Fd ≥ 2*Fmax, bu erda Fd - namuna olish chastotasi; Fmax - signal spektrining maksimal chastotasi. Boshqacha qilib aytganda, signalni raqamlashtirish chastotasi (ADC namuna olish chastotasi) biz o'lchamoqchi bo'lgan signalning maksimal chastotasidan kamida 2 baravar yuqori bo'lishi kerak.
Agar biz Kotelnikov teoremasi talab qilganidan past chastotali namunalar olsak nima bo'ladi?
Bunday holda, "tasdiqlash" effekti paydo bo'ladi (shuningdek, stroboskopik effekt, muare effekti deb ham ataladi), bunda yuqori chastotali signal raqamlashtirishdan so'ng, aslida mavjud bo'lmagan past chastotali signalga aylanadi. Shaklda. 11 qizil yuqori chastotali sinus to'lqin haqiqiy signaldir. Pastki chastotali ko'k sinusoid - bu namuna olish vaqtida yuqori chastotali signalning yarmidan ko'prog'i o'tish vaqti bo'lganligi sababli paydo bo'ladigan xayoliy signal.

Guruch. 11. Namuna olishning etarli darajada yuqori bo'lmagan tezligida past chastotali noto'g'ri signalning paydo bo'lishi
Yashillash effektini oldini olish uchun ADC oldiga maxsus anti-aliasing filtri qo'yiladi - past chastotali filtr (LPF), u ADC namuna olish chastotasining yarmidan past chastotalarni o'tkazadi va yuqori chastotalarni kesadi.
Signalning spektrini uning diskret namunalaridan hisoblash uchun diskret Furye konvertatsiyasi (DFT) qo'llaniladi. Yana bir bor ta'kidlaymizki, diskret signalning spektri "ta'rifi bo'yicha" Fmax chastotasi bilan chegaralanadi, bu Fd namuna olish chastotasining yarmidan kam. Demak, diskret signalning spektri spektri cheksiz bo'lishi mumkin bo'lgan uzluksiz signalning Furye qatori uchun cheksiz yig'indidan farqli o'laroq, cheklangan sonli garmonikalar yig'indisi bilan ifodalanishi mumkin. Kotelnikov teoremasiga ko'ra, garmonikaning maksimal chastotasi shunday bo'lishi kerakki, u kamida ikkita namunaga to'g'ri keladi, shuning uchun harmonikalar soni diskret signal namunalari sonining yarmiga teng. Ya'ni, agar namunada N namuna bo'lsa, u holda spektrdagi harmoniklar soni N/2 ga teng bo'ladi.
Keling, diskret Furye konvertatsiyasini (DFT) ko'rib chiqaylik.

Furye seriyalari bilan taqqoslash

Biz ularning bir-biriga to'g'ri kelishini ko'ramiz, faqat DFTdagi vaqt tabiatda diskret va harmonikalar soni N/2 bilan cheklangan - namunalar sonining yarmi.
DFT formulalari k, s o'lchamsiz butun sonli o'zgaruvchilarda yoziladi, bu erda k - signal namunalari soni, s - spektral komponentlar soni.
s qiymati T davridagi to'liq garmonik tebranishlar sonini ko'rsatadi (signal o'lchash davomiyligi). Diskret Furye transformatsiyasi harmonikaning amplitudalari va fazalarini raqamli usul yordamida topish uchun ishlatiladi, ya'ni. "kompyuterda"
Boshida olingan natijalarga qaytish. Yuqorida aytib o'tilganidek, davriy bo'lmagan funktsiyani (bizning signalimizni) Furye qatoriga kengaytirganda, natijada olingan Furye qatori T davriga ega bo'lgan davriy funktsiyaga to'g'ri keladi (12-rasm).

12-rasm Davriy funksiya f(x) davri T0, o'lchash davri T>T0
12-rasmda ko'rinib turibdiki, f(x) funksiya T0 davri bilan davriydir. Biroq, T o'lchov namunasining davomiyligi T0 funksiya davriga to'g'ri kelmasligi sababli, Furye qatori sifatida olingan funktsiya T nuqtada uzilishga ega. Natijada, bu funktsiyaning spektri o'z ichiga oladi. ko'p sonli yuqori chastotali harmoniklar. Agar T o'lchov namunasining davomiyligi T0 funktsiyasining davriga to'g'ri kelgan bo'lsa, u holda Furye konvertatsiyasidan keyin olingan spektr faqat birinchi harmonikni (namuna olish davomiyligiga teng bo'lgan sinusoidni) o'z ichiga oladi, chunki f (x) funktsiyasi. sinusoiddir.
Boshqacha qilib aytadigan bo'lsak, DFT dasturi bizning signalimiz "sinusoid bo'lagi" ekanligini "bilmaydi", lekin davriy funktsiyani ketma-ket ko'rinishda ifodalashga harakat qiladi, bu esa alohida qismlarning nomuvofiqligi tufayli uzilishga ega. sinusoid.
Natijada, spektrda harmonikalar paydo bo'ladi, ular funktsiyaning shaklini, shu jumladan bu uzilishni umumlashtirishi kerak.
Shunday qilib, bir nechta sinusoidlar yig'indisi bo'lgan signalning "to'g'ri" spektrini olish uchun turli davrlar, signalni o'lchash davri har bir sinusoidning butun sonli davrlarini o'z ichiga olishi kerak. Amalda, bu shart signalni o'lchashning etarlicha uzoq davom etishi uchun bajarilishi mumkin.

13-rasm Vites qutisi kinematik xato signalining funktsiyasi va spektriga misol
Qisqaroq vaqt bilan rasm "yomonroq" ko'rinadi:

14-rasm Rotor tebranish signalining funksiyasi va spektriga misol
Amalda, "haqiqiy komponentlar" qayerda ekanligini va komponentlarning ko'p bo'lmagan davrlari va signalni namuna olish davomiyligi yoki signal shaklidagi "sakrashlar va uzilishlar" tufayli kelib chiqadigan "artefaktlar" qayerda ekanligini tushunish qiyin bo'lishi mumkin. . Albatta, "haqiqiy komponentlar" va "artefaktlar" so'zlari biron bir sababga ko'ra tirnoq belgilariga qo'yiladi. Spektr grafigida ko'plab harmonikalarning mavjudligi bizning signalimiz aslida ulardan "iborat" ekanligini anglatmaydi. Bu 7 raqami 3 va 4 raqamlaridan "iborat" deb o'ylash bilan bir xil. 7 raqamini 3 va 4 raqamlarining yig'indisi sifatida ifodalash mumkin - bu to'g'ri.
Shunday qilib, bizning signalimiz ... yoki aniqrog'i "bizning signalimiz" emas, balki bizning signalimizni takrorlash (namuna olish) orqali tuzilgan davriy funktsiyani ma'lum amplitudalar va fazalar bilan harmonikalar (sinus to'lqinlar) yig'indisi sifatida ko'rsatish mumkin. Ammo amaliyot uchun muhim bo'lgan ko'p hollarda (yuqoridagi raqamlarga qarang), spektrda olingan harmonikani haqiqatdan ham bog'lash mumkin. haqiqiy jarayonlar, ular tsiklik xarakterga ega va signal shakliga katta hissa qo'shadi.
Ba'zi natijalar
1. ADC tomonidan raqamlashtirilgan, ya'ni diskret namunalar to'plami (N dona) bilan ifodalangan, davomiyligi T sekund bo'lgan haqiqiy o'lchangan signal harmonikalar to'plami (N/) bilan ifodalangan diskret davriy bo'lmagan spektrga ega. 2 dona).2. Signal haqiqiy qiymatlar to'plami bilan ifodalanadi va uning spektri haqiqiy qiymatlar to'plami bilan ifodalanadi. Garmonik chastotalar ijobiydir. Matematiklar uchun spektrni manfiy chastotalar yordamida murakkab shaklda ifodalash qulayroq ekanligi "bu to'g'ri" va "bu har doim bajarilishi kerak" degani emas.
3. T vaqt oralig'ida o'lchangan signal faqat T vaqt oralig'ida aniqlanadi. Signalni o'lchashni boshlashimizdan oldin nima sodir bo'lganligi va undan keyin nima sodir bo'lishi fanga noma'lum. Va bizning holatlarimizda bu qiziq emas. Vaqt cheklangan signalning DFT "haqiqiy" spektrini beradi, ya'ni ma'lum sharoitlarda uning tarkibiy qismlarining amplitudasi va chastotasini hisoblash imkonini beradi.
Amaldagi materiallar va boshqa foydali materiallar.
Kirish
Funktsional qatorlarning alohida holati trigonometrik qatorlardir. Trigonometrik qatorlarni o'rganish Eyler, d'Alember, Furye va boshqalar kabi matematiklar ishlagan tovushli torning mashhur muammosiga olib keldi.
Hozirgi vaqtda trigonometrik qatorlar bilan birga quvvat seriyasi, fan va texnologiyada muhim rol o'ynaydi.
1. Trigonometrik funksiyalar sistemasi. Furye seriyasi.
Ta'rif. Funktsiyalar ketma-ketligi
1, cosx, sinx, cos2x, sin2x, … , cosnx, sinnx, …
funksiyalarning trigonometrik tizimi deyiladi.
Trigonometrik funktsiyalar tizimi uchun quyidagi tengliklar o'rinlidir:
p ∫ cos nxdx= | p ∫ sinnxdx= | p ∫ cosnx sinmxdx = 0, (n ≥ 1), | |
−π | −π | −π | |
p ∫ cosnx cosmxdx = p ∫ sinnx sinmxdx = 0, (n ≠ m ), | |||
−π | −π | ||
p ∫ cos2 nxdx = p ∫ sin2 nxdx = p , (n ≥ 1). | |||
−π | −π | ||
Ushbu tengliklardan foydalanib osongina isbotlash mumkin ma'lum formulalar trigonometriya:
cos nx sinmx = | (sin(n + m )x − sin(n − m )x ), |
||||||
cos nx cosmx = | (cos(n + m )x + cos(n - m )x ), |
||||||
sinnx sinmx = | (cos(n - m )x - cos(n + m )x ). |
||||||
Jamiyat | tenglik | chaqirdi | ortogonallik |
||||||||
trigonometrik tizim. | |||||||||||
f(x) funksiya [-p ,p ] va oraliqda integrallansin |
|||||||||||
a n = | ∫ f (x) cosnxdx ,b n = | ∫ f (x) sinnxdx, (n = 0,1,2,...). | |||||||||
−π | −π | ||||||||||
Ta'rif. | Funktsional diapazon | ||||||||||
+ ∑ (a n cosnx + b n sinx ), | |||||||||||
n= 1 | |||||||||||
a n, b n koeffitsientlari (2) formulalar bilan aniqlanadi, deyiladi
trigonometrik qator Furye funktsiyasi f(x) , va koeffitsientlarning o'zi -
Furye koeffitsientlari.
(3) qator f(x) funksiyaning trigonometrik Furye qatori ekanligi quyidagicha yoziladi:
f(x) | + ∑ (a n cosnx + b n sinx ) | |||
n= 1 | ||||
(4) qatordagi har bir atama deyiladi garmonik tebranish. Bir qator amaliy masalalarda davriy funktsiyani ketma-ket (4) ko'rinishida, ya'ni garmonik tebranishlar yig'indisi ko'rinishida ifodalash talab qilinadi.
2. Davriy funksiyalarning 2p davri bilan Furye qator kengayishi.
Ta'rif. Ular f(x) funktsiyasini aytishadi. bo'lak-bo'lak uzluksiz segmentida
Agar f(x) oraliqda uzluksiz bo'lsa, har birida f(x) funksiyaning o'ng va chap chegaralari bo'lgan chegaralangan nuqtalar bundan mustasno.
Trigonometrik qatorning yaqinlashuvi uchun yetarli shart-sharoitlarni ta’minlovchi teorema tuzamiz.
Dirixlet teoremasi. 2p davrining f(x) davriy funksiyasi shartlarni qanoatlantirsin:
1) f (x) va f ′ (x) [-p ,p ] oraliqda parcha-parcha uzluksiz;
2) agar x=c f(x) funksiyaning uzilish nuqtasi bo'lsa, u holda
f (c )= 1 2 (f (c - 0)+ f (c + 0)).
Shunda f(x) funksiyaning trigonometrik Furye qatori f(x) ga yaqinlashadi, ya’ni tenglik bajariladi.
f(x)= | + ∑ (a n cosnx + b n sinnx ), | |||
n= 1 | ||||
bu yerda a n, b n koeffitsientlari (2) formulalar bilan aniqlanadi.
Isbot. Tenglik (4) saqlanib qolsin va (4) qatorlar davr bo'yicha integratsiyani qabul qilsin. Tenglikda (4) koeffitsientlar topilsin. Buning uchun (4) tenglikning ikkala tomonini cosnx ga ko'paytiramiz va uni -p dan p gacha bo'lgan oraliqda integrallaymiz; trigonometrik sistemaning ortogonalligi tufayli biz n ni olamiz. Xuddi shunday, sinnxga ko'paytirib, integrallashda b n ni olamiz.
3. Juft va toq funksiyalarning Furye qatori.
Xulosa 1 (juft funktsiya uchun Furye seriyasi). Mayli hatto funktsiya f(x)
Dirixle teoremasining shartlarini qanoatlantiradi.
f(x)= | + ∑ a n kosnx, | |||||||
n= 1 | ||||||||
p ∫ cosnxdx , (n = 0,1,2,3,...). | ||||||||
Xulosa 2 (toq funksiya uchun Furye seriyasi). Mayli g'alati funktsiya f(x) Dirixle teoremasining shartlarini qanoatlantiradi.
Keyin quyidagi Furye seriyasining kengayishi sodir bo'ladi:
f (x )= ∑ b n sinnx , | ||||||
n= 1 | ||||||
p ∫ f(x) sin nxdx. | ||||||
1 va 2 xulosalarni isbotlash uchun quyidagi lemmadan foydalanamiz, bu geometrik jihatdan aniq (integral - maydon).
Lemma. [-a,a] oraliqda ikkita integrallanuvchi funksiya berilgan bo‘lsin: juft g(x) funksiya va toq funksiya h(x).
Keyin tenglik to'g'ri bo'ladi
∫ a g(x) dx= 2 ∫ a g(x) dx, | ∫ a h(x) dx= 0. |
|
−a | −a |
|
1-misol. f(x)=x, (x [-p ,p ] funksiyasini Furye qatoriga kengaytiring.
Funktsiya g'alati bo'lgani uchun (8) va (7) formulalarga muvofiq biz quyidagilarga ega bo'lamiz:
2p | n+12 |
|||||||||||||
b n= | ∫0 | x sin nxdx= − | ∫0 | xd cos nx=− | cosp n = (− 1) | |||||||||
(− 1) | n+1 | |||||||||||||
x = 2 ∑ | sin nx ,x ]− p ,p [. | |||||||||||||
n= 1 | ||||||||||||||
x=±p nuqtalarda bu qatorning yig'indisi nolga teng.
(9) qatordagi x = p 2 ni o'rnatib, biz shartli yaqinlashuvchi qatorni olamiz
(− 1) | n+1 | |||||||||||||||
= ∑ | 1 − | + ... | ||||||||||||||
2n+1 | ||||||||||||||||
n= 0 | ||||||||||||||||
Mashqlar |
||||||||||||||||
1. Davriy funksiya f (x) davri 2p ni Furye qatoriga kengaytiring |
||||||||||||||||
0 ≤ x ≤ p, |
||||||||||||||||
f(x)= | −p ≤x<0. |
|||||||||||||||
2. 2p davrli f (x) funksiyani Furye qatoriga kengaytiring |
||||||||||||||||
−p ≤x ≤0, |
||||||||||||||||
0 < x < π , |
||||||||||||||||
f(x) = x | ||||||||||||||||
x = p. |
||||||||||||||||
f(x)= | ||||||||||||||||
−p ≤x<π , |
||||||||||||||||
f(x)= | ||||||||||||||||
x = p. |
||||||||||||||||
f(x)=x.
−p ≤x<0, |
|||
f(x)= | 0 ≤ x ≤ p . |
||
−1 |
|||
7. [0,p] oraliqdagi funksiyani kosinuslardagi trigonometrik Furye qatoriga kengaytiring.
0 ≤x ≤ | |||
f(x)= |
< x ≤ π .
8. Segmentga yoying
0 ≤x ≤ | ||||||
f(x)= | ||||||
< x ≤π . |
||||||
p−x | ||||||
f(x)=2x.
f(x) = masalan.
Dars mavzusi bo'yicha test savollari:
1. Furye seriyasining ta'rifini eslang.
2. Furye funksional qatorining yaqinlashuvini aniqlang.
Xulosa.
Kirish.
Furye qatori trigonometrik qatorlar nazariyasining muhim qismini tashkil qiladi. Furye seriyasi birinchi marta J. Furyening (1807) issiqlik o'tkazuvchanligi muammolarini o'rganishga bag'ishlangan asarlarida paydo bo'ldi. Keyinchalik Furye seriyalari ham nazariy, ham amaliy matematikada keng tarqaldi. Shunday qilib, "Matematik fizika tenglamalari" mavzusini o'rganishda Furye seriyalaridan issiqlik tenglamasi, turli xil boshlang'ich va chegaraviy shartlarga ega to'lqin tenglamalari echimlarini topish uchun foydalaniladi. Funksiyalarning keng sinfiga qo'llaniladigan integral Furye transformatsiyasi ham keng tarqaldi.
Matematik fizikaning ko'pgina masalalarida, xususan silindrsimon mintaqa uchun potentsial nazariyaning chegaraviy masalalarida o'zgaruvchilarni ajratishda ular Bessel tenglamalari deb ataladigan echimga keladi.
F.Bessel birinchi bo`lib bu tipdagi tenglamalar yechimini tizimli o`rgangan bo`lsada, undan oldinroq ular D.Bernulli, L.Eyler, J.Lagranj asarlarida uchragan.
1. Har qanday davr 2L bo'lgan Furye qator funktsiyalari.
Har qanday davrdagi 2L funktsiyalari Furye seriyasiga kengaytirilishi mumkin. Quyidagi teorema amal qiladi.
Teorema. 2L davrining f(x) davriy funksiyasi [-L,L] oraliqdagi Dirixle teoremasining shartlarini qanoatlantirsin.
Keyin [-L,L] oralig'ida Furye seriyasining kengayishi mavjud
pnx | p nx), | ||||||||||||||
f(x)= | ∑ (a n cos | ||||||||||||||
n= 1 | |||||||||||||||
a n = | f(x)cos | p nx dx, | b n= | f(x)sin | p nx dx | ||||||||||
L - ∫ L | L - ∫ L | ||||||||||||||
(n = 0,1,2,...)
Isbot. Funktsiyani ko'rib chiqing
g(y)=f( | −p ≤y ≤p, | ||||||||||||||||||
Dirixlet teoremasi qo'llaniladi. Shunung uchun | |||||||||||||||||||
g(y)= | + ∑ (a n qulay + b n gunohkor), | ||||||||||||||||||
n= 1 | |||||||||||||||||||
p ∫f ( | )cos nydy, | π∫ | )sin nydy. | ||||||||||||||||
−π | −π | ||||||||||||||||||
tenglik (12) | almashtirish x = | Keling, kerakli narsani olamiz |
|||||||||||||||||
(10) va (11) tengliklari.
Izoh. Agar f(x) funksiya [-L,L] oraliqda juft bo'lsa, uning
Furye seriyasida faqat erkin atama a 2 0 va kosinuslar bo'ladi, agar
f(x) toq funksiya bo'lsa, uning Furye qatori faqat sinuslarni o'z ichiga oladi. 2-misol. 2-davrli f(x) funksiyani Furye qatoriga kengaytiring
[-1,1] segment f(x)=| formula bilan berilgan x| .
Chunki f(x)=| funksiyasi x| | Hatto, keyin b n = 0, | 2 ∫ 1 | xdx = 1, |
||||||||||
0, n = 2m, |
|||||||||||||
an = 2 ∫ xcos p nxdx= | |||||||||||||
((− 1) | − 1)= | N = 2m + 1. |
|||||||||||
Demak,
cosp (2m + 1)x | |||||||||||||||||||
X R. | |||||||||||||||||||
(2m + 1) | |||||||||||||||||||
m= 1 | |||||||||||||||||||
x=0 da (14) formula quyidagini beradi: | |||||||||||||||||||
p 2 | +… | ||||||||||||||||||
2. Davriy bo'lmagan funksiyalarning Furye qatori.
Davriy bo'lmagan f(x) funksiya [-L,L] oraliqda aniqlansin. Uni trigonometrik qatorga kengaytirish uchun biz ushbu segmentda tuzamiz
g(x)=f(x) da -L | |||||
davriy bo'lmagan funksiya | f(x) talab qilinadi | tanishtirish | |||
Furye ]0,L[ oraliqda. Buning uchun 2L davrining g(x) davriy funksiyasini tuzamiz
f(x), 0< x < L ,g (x ) = f 1((x ),− L < x < 0.
Chunki f 1 (x) funksiyani son-sanoqsiz sonlarda tanlash mumkin
yo‘llar bilan (g(x) Dirixlet teoremasining shartlarini qanoatlantirsa), u holda Furye qatorlarining cheksiz to‘plamini olamiz.
g(x) funksiyasi uchun.
Xususan, g(x) funksiyani juft yoki toq qilib tanlash mumkin.
Keling, davriy bo'lmagan f(x) funksiya qandaydir ]a,b[ oralig'ida aniqlansin. Ushbu funktsiyani taqdim etish uchun
Furye qatori, f 1 (x) bilan ixtiyoriy davriy funktsiyani quramiz
2L≥ b-a davri f(x) funksiyasi bilan ]a,b[ oraliqlariga to‘g‘ri keladi va biz uni Furye qatoriga kengaytiramiz.
3. Furye qatorining murakkab shakli.
Eyler formulalari yordamida (10) qator va uning koeffitsientlarini (11) aylantiramiz
(ō n = p L n )
cosō n x = | e iō n x+ e - iō n x | sinō n x = | e iō n x− e - iō n x | ||
Natijada biz seriyani olamiz
f (x) = ∑ cn ei ō n x | |||||
n =−∞ | |||||
imkoniyatlar bilan | |||||
c n= | ∫L | f (x )e - i ō n x dx ,n = 0,± 1,± 2,..., | |||
−L | |||||
qaysi deyiladi murakkab shakldagi trigonometrik Furye qatori
2L davrining f(x) funksiyalari.
Quyidagi terminologiya, ayniqsa elektrotexnika va radiotexnika sohasida qabul qilinadi. e i ō n x ifodalar garmoniklar deyiladi,
ō n raqamlari chaqiriladi to'lqin raqamlari f(x) funksiyalari. To'lqinlar to'plami
raqamlar chaqiriladi diskret spektr. Koeffitsientlar (16) deyiladi murakkab amplituda.
Spektral tahlil koeffitsientlarning xossalarini o'rganish bilan shug'ullanadi (16). 3-misol. Trigonometrik Furye qatorini kompleks shaklda toping
f(x)=e ax , (a≠ 0) funksiyalari L=p bilan.
(15) va (16) formulalar:
shap | |||||||||||||||||||||||
n ∑ =−∞ | (− 1)e | ||||||||||||||||||||||
a-in | |||||||||||||||||||||||
Odatdagi Furye seriyasiga o'tsak, biz quyidagilarni olamiz: | |||||||||||||||||||||||
shap | 2 shap | (− 1)n (a cosnx − n sinnx ) | |||||||||||||||||||||
n= 1 | |||||||||||||||||||||||
Xususan, x=0 uchun biz quyidagilarga ega bo'lamiz: | |||||||||||||||||||||||
(− 1) | |||||||||||||||||||||||
2 ashap | |||||||||||||||||||||||
n= 1 | a+n | ||||||||||||||||||||||
Mashqlar |
|||||||||||||||||||||||
Davriy f (x) funksiyani 2p davri bilan Furye qatoriga kengaytiring |
|||||||
0 ≤ x ≤ p, |
|||||||
x = p. |
|||||||
3. [ − 1,1] oraliqda ko‘rsatilgan funksiyani tenglama bo‘yicha Furye qatoriga kengaytiring. |
|||||||
4. Funksiyani Furye qatoriga kengaytiring | f(x)= | ||||||
−p ≤x<π , |
|||||||
f(x)= | |||||||
x = p. |
|||||||
5. Funksiyani [0,1] oraliqda sinuslarga kengaytiring.
f(x)=x.
6. Funksiyaning Furye koeffitsientlarini toping f(x) trigonometrik qator
−p ≤x<0, |
|||||
f(x)= | 0 ≤ x ≤ p . |
||||
−1 |
|||||
7. [0,p] oraliqda kosinuslarda trigonometrik Furye qatoriga kengaytiring. |
|||||
0 ≤x ≤ | |||||
f(x)= | |||||
< x ≤ π .
8. Segmentga yoying[ 0,p ] 2 da kosinuslarda trigonometrik Furye qatoriga
0 ≤x ≤ | ||||||
f(x)= | ||||||
< x ≤π . |
||||||
p−x | ||||||
9. [0,1] oraliqda funksiyani trigonometrik Furye qatoriga kengaytiring
f(x)=2x.
10. [ − 1,1] oraliqda funktsiyani trigonometrik Furye qatoriga kengaytiring.
f(x) = masalan.
Xulosa.
Ma'ruzada turli oraliqlardagi davriy funktsiyalarning Furye qatori ko'rib chiqildi. Furye konvertatsiyasi ko'rib chiqilib, matematik fizikaning ko'plab masalalarida o'zgaruvchilarni ajratishda yuzaga keladigan Bessel tenglamasining yechimi olinadi.
Kirish.
Ma'ruzada Furye integraliga olib keladigan Furye seriyasining cheklovchi holati muhokama qilinadi. Furye integrali uchun formulalar juft va toq funksiyalar uchun yoziladi. Turli ilovalarda Furye integrali qanday rol o'ynashi qayd etilgan. Furye integrali kompleks shaklda ifodalanadi, bu Furye qatorining kompleks tasviriga o'xshaydi.
Transformatsiya va teskari Furye transformatsiyasi, kosinus va sinus Furye transformatsiyasi uchun formulalar olinadi. Matematik fizika va elektrotexnika muammolariga Furye konvertatsiyasini qo'llash haqida ma'lumot berilgan.
1.Furye integrali Furye qatorining cheklovchi holati sifatida
f(x) funksiya cheksiz oraliqda aniqlansin
]-∞ ,∞ [ va u boʻyicha absolyut integral boʻladi, yaʼni konvergent integral mavjud.
∞ ∫ f(x) dx.
f(x)= | + ∑ (a n cosō n x + b n sinō n x ), | ||||||||||||||
n= 1 | |||||||||||||||
a n = | ∫ f (x) cosō n xdx ,b n = | ∫ f(x)sin ō n xdx, | |||||||||||||
−L | −L | ||||||||||||||
(2) koeffitsientlarni (1) qatorga almashtirib, biz quyidagilarni olamiz: | |||||||||||||||
f(x)= | ∫ f(t)dt+ | ∑ ((∫ f (t) cosō n tdt ) cosō n x + (∫ f (t) sinō n tdt ) sinō n x )) | |||||||||||||
−L | Ln=1 | −L | −L | ||||||||||||
L→ formula (3) shaklini olganligini isbotsiz ko'rsatamiz |
|||||||||||||||
f(x)= | ∫(∫ | f (t) cosō tdt) cosʼn xd ō + | ∫ (∫ f (t) sinō tdt ) sinō xd ō . | ||||||||||||
0 −∞ | |||||||||||||||
(4) formuladagi o'ngdagi ifoda deyiladi Furye integrali f(x) funksiyasi uchun. Tenglik (4) funksiya uzluksiz bo'lgan barcha nuqtalar uchun amal qiladi. Uzluksizlik nuqtalarida (4) formulaning chap tomonidagi f(x) bilan almashtirilishi kerak
Furye seriyalari va ularning aloqa texnologiyasida qo'llanilishi
| Parametr nomi | Ma'nosi |
| Maqola mavzusi: | Furye seriyalari va ularning aloqa texnologiyasida qo'llanilishi |
| Rubrika (tematik toifa) | Ta'lim |
Uzluksiz signalning ortogonal qatorlarga parchalanishi
Ma’ruza 6. Uzluksiz kanal
Qayta tiklash sifati mezonlari.
Quyidagi mezonlar mavjud:
1) Eng katta og'ish mezoni
Bu erda: ruxsat etilgan qayta qurish xatosi, - maksimal qiymat - joriy yaqinlashish xatosi.
Shu bilan birga, dastlabki signaldagi har qanday o'zgarishlar, shu jumladan qisqa muddatli emissiyalar qayd etilishiga ishonch bor.
2) SKZ mezoni. bu erda: - qo'shimcha CS yaqinlashish xatosi, - CS yaqinlashish xatosi.
3) Integral mezon
Namuna olish davri uchun maksimal o'rtacha qiymat aniqlanadi.
4) Ehtimoliy mezon
Ruxsat etilgan daraja o'rnatiladi, P qiymati - joriy yaqinlashish xatosi qandaydir o'ziga xos qiymatga bog'liq emasligi ehtimoli.
Ma'ruza maqsadi: uzluksiz kanal bilan tanishish
a) uzluksiz signalni ortogonal qatorlarga parchalash;
b) Furye qatorlari va ularning aloqa texnologiyasida qo'llanilishi;
c) Kotelnikov teoremasi (Shennonning asosiy teoremasi);
d) uzluksiz kanalning sig'imi;
e) NKS modeli.
Aloqa nazariyasida signallarni ifodalash uchun funktsiyalarni ortogonal qatorlarga kengaytirishning ikkita maxsus holati keng qo'llaniladi: trigonometrik funktsiyalarda kengayish va shakl funktsiyalarida kengayish. sinx/x. Birinchi holda, signalning oddiy Furye seriyasi ko'rinishidagi spektral tasvirini, ikkinchi holatda esa V.A. Kotelnikov.
Amaliy nuqtai nazardan signalni ifodalashning eng oddiy shakli ba'zi elementar funktsiyalarning chiziqli birikmasidir
Umuman olganda, signal murakkab tebranish bo'lib, bu murakkab funktsiyani ifodalashni juda muhim qiladi s(t), signalni oddiy funksiyalar orqali aniqlash.
Chiziqli tizimlarni o'rganishda signalning bunday ko'rinishi juda qulaydir. Bu superpozitsiya tamoyilidan foydalangan holda ko'plab muammolarni echishni qismlarga bo'lish imkonini beradi. Masalan, chiziqli tizimning chiqishidagi signalni aniqlash uchun tizimning har bir elementar ta'sirga ps k (t) munosabati hisoblab chiqiladi, so'ngra a k ga mos keladigan koeffitsientlarga ko'paytiriladigan natijalar osonlikcha hisoblab chiqiladi va ular soniga bog'liq emas edi. summaning shartlari. Ushbu talablar ortogonal funktsiyalar to'plami bilan to'liq qondiriladi.
Funktsiyalar ps 1 (t), ps 2 (t), . . . . , ps n (t) . (6.2)
Intervalda berilganlar ortogonal deb ataladi,
agar da. (6.3)
Signallarni spektral tahlil qilishning asosi vaqt funktsiyalarini Furye seriyasi yoki integral shaklida tasvirlashdir. Dirixlet shartini qanoatlantiradigan har qanday davriy signal s(t) trigonometrik funksiyalarda qator sifatida ifodalanishi kerak.
Vaqt oralig'idagi signalning o'rtacha qiymatini ifodalovchi a 0 miqdori odatda doimiy komponent deb ataladi. Bu formula bo'yicha hisoblanadi
Furye seriyasini yozishning murakkab shakli juda qulay
Kattalik A k murakkab amplituda bo'lib, u formula bo'yicha topiladi
(6.8) va (6.9) munosabatlari bir juft diskret Furye transformlarini tashkil qiladi. Shuni ta'kidlash kerakki, Furye seriyasi nafaqat davriy signalni, balki chekli davomiylikdagi har qanday signalni ham ifodalashi mumkin. Ikkinchi holda, signal S(t) butun vaqt o'qi bo'ylab davriy ravishda uzaytiriladi deb taxmin qilinadi. Bunday holda, (6.4) yoki (6.8) tenglik signalni faqat uning davomiyligi (-) oralig'ida ifodalaydi. T/2, T/2). Vaqt oralig'ida belgilangan tasodifiy signal (yoki shovqin) (- T/2, T/2), Furye qatori bilan ham ifodalanishi kerak
Qayerda a k Va b k tasodifiy o'zgaruvchilar (fluktuatsion shovqin uchun - normal taqsimot bilan mustaqil tasodifiy).
Furye seriyalari va ularning aloqa texnologiyasida qo'llanilishi - tushunchasi va turlari. "Furye seriyalari va ularning aloqa texnologiyalarida qo'llanilishi" toifasining tasnifi va xususiyatlari 2017, 2018 yil.
1Chiziqli signal holatida Furye seriyasini taxmin qilish qobiliyati uzluksiz davriy elementlarda funktsiyalarni qurish uchun zarurdir. Furye qatorining chekli yig'indilaridan foydalangan holda ularni qurish va parchalash uchun ushbu usuldan foydalanish imkoniyati turli fanlarning, masalan, fizika, seysmologiya va boshqalarning ko'plab muammolarini hal qilishda qo'llaniladi. Okean to'lqinlari va quyosh faolligi jarayonlari tebranish jarayonlarining parchalanish usuli va bu transformatsiyalar bilan tavsiflangan funktsiyalar bilan ko'rib chiqiladi. Kompyuter texnologiyalarining rivojlanishi bilan Furye seriyalari tobora murakkab masalalarda qo'llanila boshlandi va shu tufayli bu o'zgarishlardan tibbiyot va kimyo kabi bilvosita fanlarda foydalanish mumkin bo'ldi. Furye konvertatsiyasi ham haqiqiy, ham murakkab shaklda tasvirlangan, ikkinchi taqsimot kosmosni o'rganishda yutuq yaratishga imkon berdi. Ushbu ishning natijasi Furye qatorlarini uzluksiz funktsiyani linearizatsiya qilishda qo'llash va qatorni funktsiyaga aniqroq joylashtirish uchun qator koeffitsientlari sonini tanlashdir. Bundan tashqari, Furye seriyasini kengaytirishdan foydalanganda, bu funktsiya uzluksiz bo'lishni to'xtatadi va allaqachon etarlicha kichik qiymatlarda, ishlatilgan funktsiyaning yaxshi yaqinlashishiga erishiladi.
Furye seriyasi
Furye konvertatsiyasi
faza spektri.
1. Alasheyeva E.A., Rogova N.V. Yupqa simli yaqinlashuvda elektrodinamika masalasini echishning raqamli usuli. Ilm va tinchlik. Xalqaro ilmiy jurnal, No 8(12), 2014. 1-jild. Volgograd. B.17-19.
2. Vorobyov N.N. Seriyalar nazariyasi. Ed. Fan, Fizika-matematika adabiyoti bosh tahririyati, M., 1979, -408 S.
3. Kalinina V.N., Pankin V.F. Matematik statistika. - M.: Oliy maktab, 2001 yil.
4. Zamonaviy taqdimotda R. Edvards Furye seriyasi. Ed. Dunyo. 2 jildda. 1-jild. 1985 yil. 362 bet.
5. Sigorskiy V.P. Muhandisning matematik apparati. Ed. 2-steriotipik. "Texnika", 1997 yil. – 768 b.
Ixtiyoriy funktsiyaning o'ziga xos davri bo'lgan qator shaklida tasvirlanishi Furye qatori deyiladi. Umumiy shakldagi bu yechim ortogonal asosda kengayish deb ataladi. Furye seriyali funktsiyalarni kengaytirish turli xil muammolarni hal qilish uchun juda kuchli vositadir. Chunki Integratsiya, differensiatsiya, shuningdek, argument va konvolyutsiya orqali ifodani o'zgartirish paytidagi bu transformatsiyaning xususiyatlari yaxshi ma'lum va o'rganilgan. Oliy matematika, shuningdek, frantsuz olimi Furye asarlari bilan tanish bo'lmagan odam, ehtimol, bu "seriyalar" nima ekanligini va ular nima uchun kerakligini tushunmaydi. Ushbu Furye o'zgarishi bizning hayotimizning ajralmas qismiga aylandi. U nafaqat matematiklar, balki fiziklar, kimyogarlar, shifokorlar, astronomlar, seysmologlar, okeanologlar va boshqalar tomonidan ham qo'llaniladi.
Furye seriyalari ko'plab amaliy masalalarni hal qilish uchun ishlatiladi. Furye konvertatsiyasini analitik, raqamli va boshqa usullar yordamida amalga oshirish mumkin. Okean to'lqinlari va yorug'lik to'lqinlari kabi quyosh faollik davrlari kabi jarayonlar har qanday tebranish jarayonlarini Furye seriyasiga ajratishning raqamli usuliga ishora qiladi. Ushbu matematik usullardan foydalanib, siz har qanday tebranish jarayonlarini minimaldan maksimalga va orqaga siljiydigan sinusoidal komponentlar qatori sifatida ifodalovchi funktsiyalarni tahlil qilishingiz mumkin. Furye transformatsiyasi ma'lum bir chastotaga mos keladigan sinusoidlarning fazasi va amplitudasini tavsiflovchi funktsiyadir. Ushbu transformatsiya issiqlik, yorug'lik yoki elektr energiyasi ta'sirida yuzaga keladigan dinamik jarayonlarni tavsiflovchi juda murakkab tenglamalarni echish uchun ishlatiladi. Shuningdek, Furye seriyalari murakkab tebranish signallarida doimiy komponentlarni ajratib olish imkonini beradi, bu esa tibbiyot, kimyo va astronomiyada olingan eksperimental kuzatishlarni to'g'ri talqin qilish imkonini beradi.
Texnologiyaning o'sishi bilan, ya'ni. Kompyuterning paydo bo'lishi va rivojlanishi Furye transformatsiyasini yangi bosqichga olib chiqdi. Ushbu texnika fan va texnologiyaning deyarli barcha sohalarida mustahkam o'rnatilgan. Masalan, raqamli audio va video. Bu ilmiy jarayonning o'sishi va Furye seriyasini qo'llashning aniq amalga oshishiga aylandi. Shunday qilib, Furye seriyasi murakkab shaklda kosmosni o'rganishda yutuq yaratishga imkon berdi. Bundan tashqari, u yarimo'tkazgich materiallari va plazma fizikasini, mikroto'lqinli akustikani, okeanografiyani, radarni, seysmologiyani o'rganishga ta'sir ko'rsatdi.
Quyidagi ifodadan aniqlangan davriy signalning faza spektrini ko'rib chiqing:

bu yerda belgilar va mos ravishda kvadrat qavs ichiga olingan miqdorning xayoliy va haqiqiy qismlarini bildiradi.
Agar haqiqiy doimiy qiymat K ga ko'paytirilsa, Furye seriyasining kengayishi quyidagi ko'rinishga ega bo'ladi:

(1) ifodadan kelib chiqadiki, Furye fazasi spektri quyidagi xususiyatlarga ega:
1) ning funktsiyasidir, ya'ni ga bog'liq bo'lmagan quvvat spektridan farqli o'laroq, signal vaqt o'qi bo'ylab siljishi bilan o'zgaradi;
2) K ga bog'liq emas, ya'ni signalning kuchayishi yoki zaiflashishi uchun o'zgarmasdir, quvvat spektri esa K ga bog'liq.
3) ![]() ya'ni n ning toq funksiyasi.
ya'ni n ning toq funksiyasi.
Eslatma. Yuqoridagi mulohazalarning geometrik talqinini hisobga olgan holda, uni quvvat spektri va faza spektri nuqtai nazaridan quyidagicha ifodalash mumkin:
Chunki

keyin (2) va (3) dan, agar amplituda (yoki quvvat spektri) va faza spektrlari ma'lum bo'lsa, uni bir ma'noda qayta qurish mumkinligi kelib chiqadi.
Keling, bir misolni ko'rib chiqaylik. Bizga funktsiya berilgan ![]() orasida
orasida
Furye seriyasining umumiy ko'rinishi:


Keling, qadriyatlarimizni almashtiramiz va olamiz:

Keling, qadriyatlarimizni almashtiramiz va olamiz.
Furye seriyasi quyidagicha yozilgan:
, bu yerda k garmonik son.
Ushbu seriya uchun Furye koeffitsientlari quyidagi formulalar yordamida topiladi:


Davriy signallar Furye seriyasi bilan quyidagi shaklda ifodalanadi:
, bu erda asosiy chastota;
Bu erda koeffitsientlar formulalar yordamida hisoblanadi:


Furye seriyasini yozishning yana bir shakli ko'pincha ishlatiladi:
![]() , Qayerda:
, Qayerda:
![]() - amplituda k th harmonika; - boshlang'ich bosqich
- amplituda k th harmonika; - boshlang'ich bosqich
Hisoblash qulayligi uchun Furye seriyasi murakkab shaklda yozilgan:


Grafik vaqt va chastotani ko'rsatish
Davriy signal spektri
 vaqtinchalik tasvir
vaqtinchalik tasvir
|
 ASF chastotasi tasviri
ASF chastotasi tasviri
PSFga o'xshash, faqat fazalar ham salbiy bo'lishi mumkinligini hisobga olgan holda.
Bunday spektr diskret yoki chiziq deb ataladi, u davriy signalga xosdir.
To'rtburchak impulslar ketma-ketligi spektri
Impulslarning nosimmetrik joylashishini ko'rib chiqing

![]()
, ish aylanishi qayerda.

Sinusning nol nuqtalarini topamiz:
![]() Birinchi nol nuqtasi to'rtburchaklar impulslar ketma-ketligining spektri uchun eng muhim hisoblanadi.
Birinchi nol nuqtasi to'rtburchaklar impulslar ketma-ketligining spektri uchun eng muhim hisoblanadi.
![]()
To'rtburchak impulslarning ASF ketma-ketligi:

ō 1 ō 2 2p/t u 4p/t u
Energiyaning asosiy ulushi 0 dan birinchi nol nuqtasigacha (energiyaning taxminan 90%) joylashgan harmonikalar tomonidan amalga oshiriladi. Signal energiyasining 90% i to'plangan bu chastota mintaqasi (chastota) signalning spektral kengligi deb ataladi.
To'rtburchak puls uchun spektr kengligi .
Har qanday raqamli signal uzatish oddiy analogdan ko'ra ko'proq spektrni talab qiladi.
To'rtburchak impulslarning PSF ketma-ketligi:
 agar quyosh(x)>0 bo'lsa, u holda r k =0
agar quyosh(x)>0 bo'lsa, u holda r k =0
agar gunoh (x)<0, то r k = p
Pulsning davomiyligi va davrining spektr turiga ta'siri
Agar muddat kamaysa, asosiy chastota o'zgarmaydi, nol nuqtalari o'ngga o'tadi. Ko'proq komponentlar asosiy energiya to'plangan birinchi nol nuqtasiga etadi. Texnik jihatdan ular spektr kengayib borayotganini ta'kidlashadi.
Agar pulsning davomiyligi oshsa, u holda spektr torayadi.
Agar takrorlash davri oshsa, asosiy chastota kamayadi. Agar takrorlash davri kamaysa, asosiy chastota ortadi.
Pulsning holatini yoki kelib chiqishini o'zgartirish
Bu ASF ga ta'sir qilmaydi, faqat fazalar spektri o'zgaradi. Buni kechikish teoremasi asosida aks ettirish mumkin:

![]()
| |
O'zgartirilgan signalning faza spektri N=4:

Davriy signallar bilan sxemalarni hisoblash tushunchasi
Hisoblash usuli:
1. Davriy signalning kompleks spektri aniqlanadi;
2. Spektr eng muhim harmoniklarni qoldirib, baholanadi (birinchi mezon: maksimal garmonik amplitudaning 0,1 dan kam bo'lgan barchalari kesiladi);
Har bir komponentdan oqim va kuchlanish alohida hisoblab chiqiladi. Siz murakkab hisoblash usulidan foydalanishingiz mumkin.

I 0 = 0
![]()

![]()
![]()
![]()
Harmonik bo'lmagan funktsiyani uning samarali qiymati bilan baholash mumkin, ya'ni. davr uchun o'rtacha ildiz kvadrati:



Davriy bo'lmagan signal spektri haqida tushuncha
Davriy bo'lmagan signallar eng muhimi, chunki ular ma'lumotni olib yuradi. Davriy signallar axborotni uzatish uchun xizmat ko'rsatish signallari bo'lib, yangi ma'lumotlarni olib yurmaydi. Shuning uchun davriy bo'lmagan signallarning spektrlari haqida savol tug'iladi. Siz ularni davriy signallardan chegaraga o'tish, davrni cheksizlikka yo'naltirish orqali olishga harakat qilishingiz mumkin (). Bitta signal qoladi. Bitta signal spektrining kompleks amplitudasini topamiz: da.
, 
Davriy bo'lmagan signalni cheksiz kichik amplitudali va chastotasi cheksiz kichik qiymatlar bilan farq qiluvchi garmonik komponentlarning cheksiz yig'indisiga bo'linishi mumkin - Bu diskret emas, balki davriy bo'lmagan signalning uzluksiz spektri deb ataladi. Hisob-kitoblar uchun murakkab bo'lmagan amplitudalar va amplitudalarning kompleks spektral zichligi tushunchasi - chastota birligi uchun amplituda qiymati qo'llaniladi.
 Bu to'g'ridan-to'g'ri Furye konvertatsiyasi (ikki tomonlama).
Bu to'g'ridan-to'g'ri Furye konvertatsiyasi (ikki tomonlama).