To'g'ri chiziqlar orasidagi burchakni topishning koordinata usuli. Kosmosdagi koordinatalar usuli: formulalar va repetitor izohlari

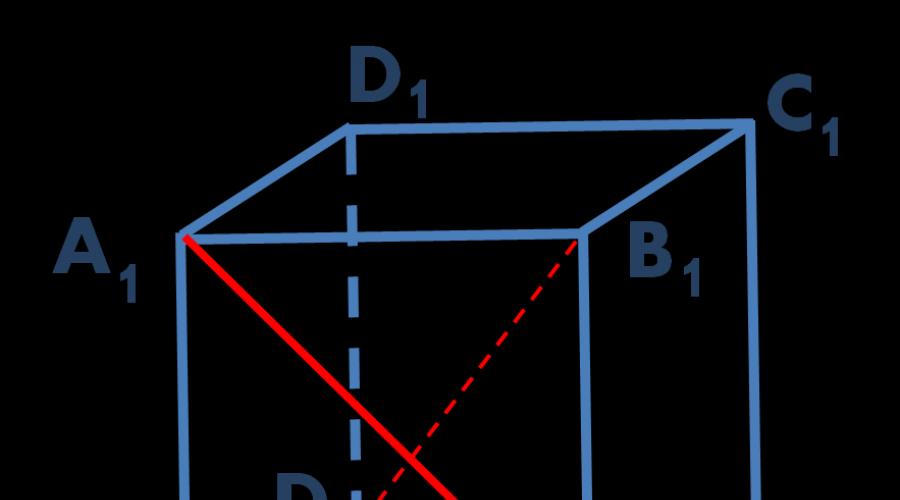
Ushbu maqolada Yagona davlat imtihonidan olingan C2 muammosini hal qilish misolidan foydalanib, koordinatalar usuli yordamida topish usuli tahlil qilinadi. Eslatib o'tamiz, to'g'ri chiziqlar bir tekislikda yotmasa, qiyshiq bo'ladi. Xususan, agar bitta chiziq tekislikda yotsa, ikkinchi chiziq esa bu tekislikni birinchi chiziqda yotmaydigan nuqtada kesib o'tsa, unda bunday chiziqlar kesishadi (rasmga qarang).

Topmoq kesishgan chiziqlar orasidagi masofalar zarur:

1. Boshqa kesishuvchi chiziqqa parallel bo'lgan kesishgan chiziqlardan biri orqali tekislik o'tkazing.
2. Olingan tekislikka ikkinchi chiziqning istalgan nuqtasidan perpendikulyar tushiring. Ushbu perpendikulyarning uzunligi chiziqlar orasidagi kerakli masofa bo'ladi.

Keling, matematika bo'yicha yagona davlat imtihonidan C2 muammosini hal qilish misolidan foydalanib, ushbu algoritmni batafsilroq tahlil qilaylik.

Kosmosdagi chiziqlar orasidagi masofa

Vazifa. Birlik kubida ABCDA 1 B 1 C 1 D 1 chiziqlar orasidagi masofani toping B.A. 1 va D.B. 1 .

Guruch. 1. Topshiriq uchun rasm chizish

Yechim. Kubning diagonalining o'rtasidan D.B. 1 (nuqta O) chiziqqa parallel chiziq chizamiz A 1 B. Ushbu chiziqning qirralar bilan kesishish nuqtalari Miloddan avvalgi Va A 1 D 1 mos ravishda belgilanadi N Va M. Streyt MN samolyotda yotadi MNB 1 va chiziqqa parallel A 1 B, bu tekislikda yotmaydi. Bu to'g'ri chiziq degan ma'noni anglatadi A 1 B tekislikka parallel MNB 1 to'g'ri chiziq va tekislikning parallelizmiga asoslangan (2-rasm).

Guruch. 2. Kesishgan chiziqlar orasidagi kerakli masofa tanlangan chiziqning istalgan nuqtasidan tasvirlangan tekislikgacha bo'lgan masofaga teng.

Endi biz chiziqning qaysidir nuqtasidan masofani qidiramiz A 1 B samolyotga MNB 1 . Bu masofa, ta'rifga ko'ra, o'tish chiziqlari orasidagi kerakli masofa bo'ladi.

Bu masofani topish uchun biz koordinata usulidan foydalanamiz. Keling, to'rtburchaklar dekart koordinatalar tizimini kiritaylik, shunda uning kelib chiqishi B nuqtasi, o'qi bilan mos keladi. X chekkasi bo'ylab yo'naltirilgan edi B.A., eksa Y- chekka bo'ylab Miloddan avvalgi, eksa Z- chekka bo'ylab BB 1 (3-rasm).

Guruch. 3. Rasmda ko'rsatilganidek, to'rtburchaklar Dekart koordinata tizimini tanlaymiz

Tekislik tenglamasini topish MNB Ushbu koordinatalar tizimida 1. Buning uchun birinchi navbatda nuqtalarning koordinatalarini aniqlaymiz M, N Va B 1: Olingan koordinatalarni to'g'ri chiziqning umumiy tenglamasiga almashtiramiz va quyidagi tenglamalar tizimini olamiz:

Tizimning ikkinchi tenglamasidan biz uchinchisidan olamiz, shundan so'ng biz birinchisidan olamiz Olingan qiymatlarni to'g'ri chiziqning umumiy tenglamasiga almashtiring:

Biz shuni ta'kidlaymizki, aks holda samolyot MNB 1 kelib chiqishi orqali o'tadi. Ushbu tenglamaning ikkala tomonini bo'linib, biz quyidagilarni olamiz:

Nuqtadan tekislikgacha bo'lgan masofa formula bilan aniqlanadi.

Burchakni hisoblashda koordinata usulidan foydalanish

samolyotlar orasida

Ko'pchilik umumiy usul burchakni topishtekisliklar o'rtasida - koordinata usuli (ba'zan vektorlar yordamida). Qolganlarning hammasi sinab ko'rilganda foydalanish mumkin. Ammo koordinata usulini darhol qo'llash mantiqiy bo'lgan holatlar mavjud, ya'ni koordinatalar tizimi tabiiy ravishda muammo bayonotida ko'rsatilgan ko'pburchak bilan bog'liq bo'lsa, ya'ni. Uchta juft perpendikulyar chiziqlar aniq ko'rinadi, ularda koordinata o'qlarini ko'rsatish mumkin. Bunday ko'p yuzlilar kubsimon va muntazam to'rtburchak piramida. Birinchi holda, koordinatalar tizimi bir cho'qqidan cho'zilgan qirralar bilan aniqlanishi mumkin (1-rasm), ikkinchisida - poydevorning balandligi va diagonallari (2-rasm).

Koordinata usulining qo'llanilishi quyidagicha.

Kosmosdagi to'rtburchaklar koordinatalar tizimi kiritiladi. Uni "tabiiy" tarzda kiritish tavsiya etiladi - uni umumiy nuqtaga ega bo'lgan juft perpendikulyar chiziqlar uchligiga "bog'lash".

Orasidagi burchak qidirilayotgan har bir tekislik uchun tenglama tuziladi. Bunday tenglamani yaratishning eng oson yo'li tekislikdagi bir chiziqda yotmaydigan uchta nuqtaning koordinatalarini bilishdir.

In tekislik tenglamasi umumiy ko'rinish kabi ko'rinadi Ax + By + Cz + D = 0.

A, B koeffitsientlari, Bu tenglamadagi C lar tekislikning normal vektorining (tekislikka perpendikulyar vektor) koordinatalaridir. Keyin tekisliklarga normal vektorlarning uzunligi va skalyar mahsulotini aniqlaymiz, ular orasidagi burchak qidiriladi. Agar bu vektorlarning koordinatalari(A 1, B 1; C 1) va (A 2; B 2; C 2). ), keyin kerakli burchakformula bo'yicha hisoblanadi

Izoh. Shuni esda tutish kerakki, vektorlar orasidagi burchak (tekisliklar orasidagi burchakdan farqli o'laroq) noaniq bo'lishi mumkin va mumkin bo'lgan noaniqlikni oldini olish uchun formulaning o'ng tomonidagi numerator modulni o'z ichiga oladi.

Bu masalani koordinata usuli yordamida yeching.

Masala 1. ABCDA 1 B 1 C 1 D 1 kubi berilgan. K nuqta AD chetining o'rtasi, L nuqtasi CD chetining o'rtasi. A tekisliklar orasidagi burchak nimaga teng? 1 KL va A 1 AD?

Yechim . Koordinatalar sistemasining kelib chiqishi nuqtada bo'lsin A, va koordinata o'qlari nurlar bo'ylab boradi AD, AB, AA 1 (3-rasm). Keling, kubning chetini 2 ga teng qilib olaylik (uni yarmiga bo'lish qulay). Keyin nuqtalarning koordinatalari A 1 , K, L quyidagicha: A 1 (0; 0; 2), K(1; 0; 0), L(2; 1; 0).

Guruch. 3

Keling, tekislikning tenglamasini yozamiz 1 K L umuman. Keyin bu tekislikning tanlangan nuqtalarining koordinatalarini unga almashtiramiz. Biz to'rtta noma'lumli uchta tenglama tizimini olamiz:

Koeffitsientlarni ifodalaylik A, B, C dan Dgacha va biz tenglamaga kelamiz

Ikkala qismga bo'lish D (nima uchun D = 0?) va keyin -2 ga ko'paytirsak, biz tekislik tenglamasini olamiz A 1 KL: 2x - 2 y + z - 2 = 0. U holda bu tekislikning normal vektori koordinatalariga ega (2: -2; 1). Tekislik tenglamasi 1 AD: y=0, va unga normal vektorning koordinatalari, masalan, (0; 2: 0). Samolyotlar orasidagi burchak kosinusining yuqoridagi formulasiga ko'ra, biz quyidagilarni olamiz:

Matematika bo'yicha C2 topshirig'ida, ko'pincha siz aniqlashingiz kerak bo'lgan muammoni hal qilishingiz kerak:

1. Ikki nuqta orasidagi masofa
2. Nuqtadan chiziqgacha bo'lgan masofa
3. Nuqtadan tekislikgacha bo'lgan masofa
4. Kesish chiziqlar orasidagi masofa
5. Ikki to'g'ri chiziq orasidagi burchak
6. To'g'ri chiziq va tekislik orasidagi burchak
7. Samolyotlar orasidagi burchak

Agar siz C2 yechim algoritmiga rioya qilsangiz va asosiy narsalarni eslab qolsangiz, vazifalar elementardir trigonometrik xususiyatlar, masalan, diagonallarning xususiyatlari yoki ko'pburchakning sirt maydoni. Asosiy vazifalar ushbu asosiy xususiyatlarni eslab qolishingizga yordam beradi.

Endi to'g'ridan-to'g'ri algoritmlarga o'tamiz.

1. Ikki A va B nuqtalari orasidagi masofani aniqlash uchun biz ikkita usuldan birini qo'llaymiz:

• Biz AB ni qandaydir uchburchakka kiritamiz va uning uzunligini uchburchakning tomoni sifatida topamiz
• Formulaga ko'ra

Bundan tashqari, koordinata usuli, mening fikrimcha, siz har bir nuqtaning koordinatalarini diqqat bilan aniqlashingiz kerak.

2. Nuqtadan chiziqgacha bo'lgan masofani aniqlash uchun hisoblang

• perpendikulyar segmentning uzunligi sifatida, agar bu segmentni balandliklardan biri sifatida biron bir uchburchakka kiritish mumkin bo'lsa

maydonni hisoblash uchun formulalar yordamida koordinata usulini qo'llash, unda kerakli masofa balandlik va bo'ladi

3. Nuqtadan tekislikgacha bo'lgan masofa

• bu nuqtadan tekislikka tushgan perpendikulyar uzunligi. Buning uchun ehtiyotkorlik bilan tekislikka perpendikulyar bo'lgan va o'tib ketadigan qismni quramiz berilgan nuqta. Kerakli masofa hosil bo'lgan yangi ko'pburchakning balandligiga teng bo'ladi.
• Koordinata usulidan foydalanish

Tenglama shu tekislikka tegishli uchta nuqtaning koordinatalarini almashtirib topiladi

• Vektor usulidan foydalanish

Buning uchun vektorlarni qo'shish va ayirish qoidalarini eslab qolish kerak, perpendikulyar vektorlarning mahsuloti nolga teng.

• Ovoz balandligi usulidan foydalanib, agar ABCM piramidasi bo'lsa, u holda M nuqtadan ABC uchburchagi joylashgan tekislikgacha bo'lgan masofa formula bo'yicha hisoblanadi.

• Ko'rish mumkin bo'lgan mos yozuvlar masalalari usulidan foydalanish

4. O'tish chiziqlari orasidagi masofa yordamida hal qilinishi mumkin

4.1. Bosqichma-bosqich hisoblash usuli:

• kesishuvchi ikkita chiziqning umumiy perpendikulyarini qurish va uning uzunligini topish;
• chiziqlardan birini o'z ichiga olgan va ikkinchisiga parallel bo'lgan tekislikni qurish. Keyin kerakli masofa nuqtadan tekislikda qurilgan to'g'ri chiziqgacha bo'lgan masofaga teng bo'ladi;
• ma'lumotlarni to'g'ridan-to'g'ri ichiga kiriting parallel tekisliklar, bu kesishuvchi chiziqlardan o'tib, bu tekisliklar orasidagi masofani toping
• shu chiziqlardan biriga perpendikulyar tekislik yasang va ikkinchi chiziqning ortogonal proyeksiyasini tuzing.

4.2. Vektor koordinatalari usuli

• Kesishgan ikkita chiziqqa umumiy perpendikulyar boʻlgan segment uchlarining koordinatalarini toping.
• Ikki nuqta orasidagi masofani topish

4.3. Vektor usuli
Ikki qiyshiq chiziqning umumiy perpendikulyariga tegishli vektor uzunligini aniqlash masalasini qisqartiramiz.

6. To'g'ri chiziq va tekislik orasidagi burchak tarkibiga kiritish orqali aniqlanadi to'g'ri uchburchak biri sifatida o'tkir burchaklar, yoki vektor-koordinatsiya usuli bilan

Samolyotlar orasidagi burchak qanday aniqlanishini keyingi darsda ko'rib chiqamiz. C2 ni hal qilish uchun ushbu algoritmlar muammoni hal qilish usulini har tomonlama tushunishga yordam beradi. "Maktab o'quvchilari va ularning ota-onalari uchun maktab o'quvchilariga yordam berish uchun jurnal". Batafsil: http://education-club.ru/#ixzz2IXf5GOJU

7. Samolyotlar orasidagi burchak(geometrik usul)

• 1. Tekisliklar kesishgan to‘g‘ri chiziqni toping.
• 2. Shu to`g`rida biror nuqtani tanlang va unga shu tekisliklarda yotgan ikkita perpendikulyar chizing. Yoki tekisliklarning kesishish chizig'iga perpendikulyar tekislik chizing.
• 3. Tekisliklarning kesishish chizig‘iga perpendikulyarlar hosil qilgan burchakning trigonometrik funksiyasini toping. Qoida tariqasida, biz buni kerakli burchakni o'z ichiga olgan uchburchak orqali qilamiz.
• 4. Javobingizdagi burchakning qiymatini yozing yoki trigonometrik funktsiya burchak.

Samolyotlar orasidagi burchak. Koordinata usuli. Vazifa C2

Ikkita kesishuvchi tekislik ikki juft teng dihedral burchak hosil qiladi:

Dihedral burchakning kattaligi mos keladigan chiziqli burchakning kattaligi bilan o'lchanadi.

Ikki burchakli burchakning chiziqli burchagini qurish uchun tekisliklarning kesishish chizig'idan ixtiyoriy nuqtani olish kerak va har bir tekislikda bu nuqtaga tekisliklarning kesishish chizig'iga perpendikulyar nurni chizish kerak. Bu nurlar hosil qilgan burchak dihedral burchakning chiziqli burchagidir:

Tekisliklar orasidagi burchakning kattaligi dihedraldan kichik burchakning kattaligidir.

Bizning tekisliklarimiz tenglamalar bilan aniqlansin:

Tekisliklar orasidagi burchakning kosinusi quyidagi formula bilan topiladi:

Javobda biz yozamiz , chunki tekisliklar orasidagi burchakning qiymati kichikroq dihedral burchakning qiymati.

O'ngda to'rtburchak prizma tayanch tomoni 12 va balandligi 21 ga teng, chetiga M nuqta olinadi, shunda . K nuqta chetiga shunday olinadi. Tekislik bilan tekislik orasidagi burchakni toping.

Keling, rasm chizamiz. Koordinatalar usulini qo'llaganimiz sababli, biz darhol koordinatalar tizimini kiritamiz: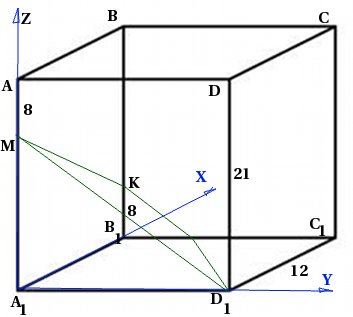

Endi oldimizda tekislik va tekislik tenglamalarini yozish vazifasi turibdi.

Men uch nuqtadan foydalanib, tekislik tenglamasini topishning batafsil algoritmini tasvirlab berdim.

Tekislik va tekislik tenglamalarida koeffitsientlarni topgandan so'ng, ularni formulaga almashtirib, tekisliklar orasidagi burchakning kosinusini topamiz va burchakni topamiz.

Men sizga ushbu muammoni hal qilishning batafsil videosini ko'rishni taklif qilaman:

Inna Vladimirovna Feldmanning yana bir topshirig'i

Video darslar "S-2 masalalarini echishning koordinatali usuli"

2-dars http://youtu.be/dKQWG8OZRGo
3-dars http://youtu.be/ddgr0PnbFno
4-dars http://youtu.be/n6yx2pQC0Lo
5-dars http://youtu.be/JkWbxAw1YLI
6-dars http://youtu.be/gybIqCMKBiI
7-dars http://youtu.be/_LpARpYxp5g
8-dars http://youtu.be/XJhyZQoofD8

Koordinata usuli juda samarali va universal usul fazodagi stereometrik jismlar orasidagi istalgan burchak yoki masofani topish. Agar sizning matematika o'qituvchingiz yuqori malakali bo'lsa, u buni bilishi kerak. Aks holda, men "C" qismi uchun repetitorni o'zgartirishni maslahat beraman. C1-C6 matematika bo'yicha Yagona davlat imtihoniga tayyorgarligim odatda quyida tavsiflangan asosiy algoritmlar va formulalar tahlilini o'z ichiga oladi.

a va b chiziqlar orasidagi burchak

Kosmosdagi chiziqlar orasidagi burchak ularga parallel bo'lgan har qanday kesishgan chiziqlar orasidagi burchakdir. Bu burchak burchakka teng bu to'g'ri chiziqlarning yo'nalish vektorlari o'rtasida (yoki uni 180 darajaga to'ldiradi).

Matematika o'qituvchisi burchakni topish uchun qanday algoritmdan foydalanadi?

1) Istalgan vektorni tanlang va a va b to'g'ri chiziqlarning yo'nalishlariga ega (ularga parallel).
2) Vektorlarning koordinatalarini ularning boshlanishi va oxirlarining tegishli koordinatalaridan foydalanib aniqlaymiz (boshlanish koordinatalarini vektor oxiri koordinatalaridan ayirish kerak).
3) Topilgan koordinatalarni formulaga almashtiring:
. Burchakning o'zini topish uchun siz natijaning yoy kosinusini topishingiz kerak.

Oddiy samolyot

Tekislikka normal - bu tekislikka perpendikulyar bo'lgan har qanday vektor.
Oddiylikni qanday topish mumkin? Normalning koordinatalarini topish uchun berilgan tekislikda yotgan har qanday uchta M, N va K nuqtalarning koordinatalarini bilish kifoya. Ushbu koordinatalardan foydalanib, biz vektorlarning koordinatalarini topamiz va shartlar bajarilishini talab qilamiz. Vektorlarning skalyar ko‘paytmasini nolga tenglashtirib, biz uchta o‘zgaruvchili tenglamalar sistemasini tuzamiz, undan normal koordinatalarni topish mumkin.

Matematika o'qituvchisi eslatmasi : Tizimni to'liq hal qilishning hojati yo'q, chunki kamida bitta normalni tanlash kifoya. Buning uchun uning istalgan noma'lum koordinatalari o'rniga istalgan raqamni (masalan, bitta) almashtirish va qolgan ikkita noma'lum bilan ikkita tenglama tizimini yechish mumkin. Agar uning yechimlari bo'lmasa, bu normalar oilasida tanlangan o'zgaruvchida qiymati bitta bo'lgan hech kim yo'qligini anglatadi. Keyin birini boshqa o'zgaruvchiga (boshqa koordinata) almashtiring va hal qiling yangi tizim. Agar siz yana o'tkazib yuborsangiz, sizning normangiz oxirgi koordinatada bo'ladi va uning o'zi qandaydir koordinata tekisligiga parallel bo'lib chiqadi (bu holda uni tizimsiz topish oson).

Faraz qilaylik, bizga yo'nalish vektori va normal koordinatalari bo'lgan to'g'ri chiziq va tekislik berilgan.
To'g'ri chiziq va tekislik orasidagi burchak quyidagi formula bo'yicha hisoblanadi:

Bu tekisliklar uchun har qanday ikkita normal bo'lsin va bo'lsin. U holda tekisliklar orasidagi burchakning kosinusu normalar orasidagi burchak kosinusining moduliga teng bo'ladi:

Kosmosdagi tekislik tenglamasi

Tenglikni qanoatlantiruvchi nuqtalar normal bilan tekislik hosil qiladi. Koeffitsient bir xil normal berilgan ikkita tekislik orasidagi og'ish (parallel siljish) miqdori uchun javobgardir. Tekislik tenglamasini yozish uchun avvalo uning normalini topish kerak (yuqorida ko'rsatilgandek), so'ngra tekislikdagi istalgan nuqtaning koordinatalarini topilgan normalning koordinatalari bilan birga tenglamaga almashtirib, koeffitsientni toping.

MOU o'rtacha umumta'lim maktabi №13

Koordinata usuli

2008
Reja:

1. 
   Kirish
2. 
   
3. 
   Koordinatalar usulining mohiyati
4. 
   Koordinatali usullar tizimlari
5. 
   Koordinata usulining asosiy formulalari
6. 
   "Koordinata usuli" mavzusidagi turli darajadagi murakkablikdagi muammolar

(batafsil yechimlar bilan)

1. 
   Xulosa
2. 
   Bibliografiya

Kirish

Geometriyada ishlatiladi turli usullar masalani yechish sintetik (sof geometrik) usul, transformatsiya usuli, vektor usuli, koordinata usuli va boshqalar. Ular maktabda turli lavozimlarni egallaydilar. Asosiy usul sintetik deb hisoblanadi va boshqalardan koordinata usuli eng yuqori o'rinni egallaydi, chunki u algebra bilan chambarchas bog'liq. Sintetik usulning nafisligi sezgi, taxminlar va qo'shimcha konstruktsiyalar yordamida erishiladi. Koordinata usuli buni talab qilmaydi: muammolarni hal qilish asosan algoritmik bo'lib, ko'p hollarda muammoning o'zini izlash va hal qilishni soddalashtiradi.

Koordinata usuli- nuqta yoki tananing o'rnini raqamlar yoki boshqa belgilar yordamida aniqlash usuli.

Koordinatalar tizimi- koordinata usulini amalga oshiradigan ta'riflar to'plami, ya'ni. raqamlar yoki boshqa belgilar yordamida nuqta yoki tananing o'rnini aniqlash usuli.

Geometrik tadqiqotlarga algebraik xususiyat berib, koordinata usuli eng ko'p uzatadi muhim xususiyat algebra - masalalar yechish usullarining bir xilligi. Agar arifmetik va elementar geometriyada, qoida tariqasida, har bir masalani hal qilishning maxsus yo'lini izlash kerak bo'lsa, algebra va analitik geometriyada echimlar barcha masalalar uchun umumiy bo'lgan, har qanday masalaga oson moslashtiriladigan reja bo'yicha amalga oshiriladi. Algebraga xos bo'lgan va shuning uchun geometriyaga katta umumiylikka ega bo'lgan masalalarni yechish usullarini ko'chirish koordinata usulining asosiy qiymati hisoblanadi. Koordinata usulining yana bir afzalligi shundaki, uni qo'llash murakkab fazoviy tasvirlarning vizual tasviriga murojaat qilish zaruratini yo'q qiladi.

Koordinata usulini o'rganishning vazifalari

Maktab geometriya kursida koordinatalar usulini o'rganish uchun quyidagi maqsadlarni ajratib ko'rsatishimiz mumkin:

• 
  talabalarga berish samarali usul masalalar yechish va bir qator teoremalarni isbotlash;
• 
  bu usul asosida algebra va geometriyaning chambarchas bog‘liqligini ko‘rsatish;
• 
  talabalarning hisoblash va grafik madaniyatini rivojlantirishga hissa qo'shish.

Koordinatalar usulining mohiyati

Koordinata usulining masalalarni yechish usuli sifatidagi mohiyati shundan iboratki, tenglamalar bilan raqamlarni ko'rsatish va koordinatalarda turli geometrik munosabatlarni ifodalash orqali biz algebra yordamida geometrik masalani yechishimiz mumkin. Aksincha, koordinatalardan foydalanib, algebraik va analitik munosabatlar va faktlarni geometrik talqin qilish va shu tariqa geometriyani algebraik masalalarni yechishda qo‘llash mumkin.

Koordinata usuli universal usul hisoblanadi.

Nisbatan maktab kursi Geometriyada shuni aytishimiz mumkinki, ba'zi hollarda koordinata usuli isbotlarni qurish va ko'plab muammolarni sof geometrik usullardan ko'ra oqilona va chiroyli hal qilish imkonini beradi. Biroq, koordinata usuli bitta geometrik murakkablik bilan bog'liq. Xuddi shu muammo koordinata tizimining ma'lum bir tanloviga qarab boshqa analitik tasvirni oladi. Va faqat etarli tajriba sizga eng mos keladigan koordinata tizimini tanlash imkonini beradi.

Koordinata tizimlari:
1. To'rtburchak (kartezian) koordinatalar tizimi (Dekart Rene (1596-1650))

Turinda badavlat zodagonlar oilasida tug'ilgan. Bir necha kundan keyin onasi iste'moldan vafot etdi va uning hamshirasi chiqib, hayotini saqlab qoldi. 8 yoshida Rene eng yaxshi yezuit kollejlaridan biriga to'liq g'amxo'rlik qildi. Bolaligidan Dekart muammolarni hal qilishni yaxshi ko'rardi bo'sh vaqt o‘zini matematika faniga bag‘ishladi. Dekart falsafa, matematika, fizika, astronomiya va filologiyani o‘rgangan. Dekart birinchi bo'lib matematikani tasavvur qilish uchun qanday ishlatish mumkinligini ko'rsatdi matematik tahlil turli xil tabiiy va ijtimoiy hodisalar uchun.

Uning asarlarida birinchi marta quyidagilar uchraydi:

1. 
   o'zgaruvchilar
2. 
   geometriyaning qat'iy qonunlari algebraik tilga tarjima qilinadi
3. 
   tabiat hodisalari o'rtasidagi bog'lanishlarni egri chiziqlar bilan tasvirlash va ularni algebraik ifodalarda yozish taklif qilindi.
4. 
   Konstantalarning lotin harflari va o'zgaruvchilar, shuningdek, daraja belgilari

2.Egri koordinatalar tizimi to'rtburchakdan o'qlari perpendikulyar emasligi bilan farq qiladi. Nuqtaning koordinatalari to'g'ri parallel o'qlar bo'ylab to'rtburchaklar koordinatalar tizimidagi kabi aniqlanadi.

3. Polar koordinatalar tizimi . Nuqtaning qutb koordinatalari quyidagicha aniqlanadi: tekislikda OX sonli nur aniqlangan. Nurning boshlanishi O nuqta qutb, OX o'qi qutb o'qi deb ataladi. M nuqtaning qutb koordinata sistemasidagi o'rnini aniqlash uchun qutbdan shu nuqtagacha bo'lgan masofani va uning joylashgan yo'nalishini ko'rsating. Nuqtadan qutbgacha bo'lgan masofa nuqtaning qutb radiusi deb ataladi va harf bilan belgilanadi. ("roh" deb talaffuz qilinadi).

Yo'nalish OX nuridan OM nuriga aylanish burchagi bilan o'rnatiladi

Koordinata usuli

formulalar

Vektor uzunligi uning koordinatalari asosida

Segmentning o'rta nuqtasining koordinatalarini topish formulasi

Ikki nuqta orasidagi masofa

Doira tenglamasi, (doira markazi
, radius r)

Chiziq tenglamasi
, shartiga ko'ra
(to'rtburchaklar koordinatalar sistemasidagi to'g'ri chiziq tenglamasi birinchi darajali tenglamadir)

Har bir to'g'ri chiziq tenglama bilan berilgan. Qayerda a,b,c raqamlari Har bir to'g'ri chiziq uchun proportsionallikka qadar yagona aniqlanadi (agar siz ularni bir xil songa ko'paytirsangiz).
, keyin hosil bo'lgan tenglama
xuddi shu qatorni belgilaydi).

Nuqtadan masofa
to'g'ri chiziqqa m
, teng

Nuqtadan masofa
samolyotga
, teng

Formulaning kelib chiqishi
.

Keling, nuqtadan to'xtaylik
tekislikka perpendikulyar AB , tenglama bilan berilgan
.Ket
- bu perpendikulyarning tekislik bilan kesishish nuqtasi . Keyin
- nuqtadan masofa
samolyotga .Vektor tekislikka perpendikulyar bo'lgani uchun , vektorga to'g'ri keladi
.Bu degani
,Agar
, yoki
,Agar
, ya'ni
.Bu tenglikni koordinatalarda qayta yozamiz: .Lekin gap
, Shunung uchun
Va
=
.
(Styuart teoremasi)

Agar ABC uchburchagi berilgan bo'lsa va unga asoslanadi D , B va C nuqtalari orasida yotgan bo'lsa, tenglik to'g'ri bo'ladi:

Isbot:

Keling, rasmda ko'rsatilgandek koordinatalar tizimini tanlaymiz.

Tanlangan koordinatalar tizimida uchburchakning uchlari ABC quyidagi koordinatalarga ega bo'ladi:

A(x 1 ;y 1 ), B(x 2 ;0), C(0;0) va davr D (x 3 ;0) .

Tenglikka kiritilgan barcha miqdorlarni hisoblaymiz:

Keling, ushbu qiymatlarning barchasini almashtiramiz chap tomoni tenglik:

Q.E.D.

Vazifa 1. A(-1,3,0) nuqtadan tekislikgacha bo'lgan masofani toping , tenglama bilan berilgan x -3y -2z +5=0.

Yechim. Formulaga ko'ra
olamiz:

.

Javob:
.

Muammo 2. Vektorlar Va o'zaro perpendikulyar va vektor ularning har biri bilan 60˚ burchak hosil qiladi. Buni bilish
, skalyar hosilani hisoblang

Yechim. Skayar mahsulotning xususiyatidan foydalanib, qavslarni ochamiz:

=

Skayar mahsulotning ta'rifidan biz quyidagilarni olamiz:
(chunki Va perpendikulyar);

Ushbu qiymatlarni ifodaga almashtirish
=, skalyar hosilani topamiz:
=0 – 50+9 12 -120=-62

Javob:
=0 – 50+9 12 -120=-62
Muammo 3.Kvadrat berilgan A B C D tomoni bilan A . Segmentning o'rtasi orasidagi masofani aniqlang AM , Qayerda M - o'rtada Quyosh , va nuqta N yon tomonda CD , uni shunday bo'lish CN:ND=3:1 .

Yechim:

Keling, rasmda ko'rsatilgandek koordinatalar tizimini tanlaymiz.

Keyin nuqtalar M Va N , shartga ko'ra, koordinatalarga ega bo'ladi:

mos ravishda.

Chunki E - o'rtada AM , u holda uning koordinatalari quyidagicha bo'ladi:

Ma'nosi, E .

Nuqtalar orasidagi masofani topamiz E Va N :

Javob: EN =

Muammo 4 Kenarlari uzunligi 1 boʻlgan ABCDA1B1C1D1 kubi berilgan. E nuqta uning yon chetiga AA 1 dan olingan.
.F nuqta BC chetida shunday olinadi
Kubning markazi va E va F nuqtalari orqali tekislik o'tkaziladi .B cho'qqidan tekislikgacha bo'lgan masofani toping .

Yechim.

Markazi B cho'qqisida bo'lgan koordinatalar tizimini joriy qilaylik
Keling, tekislikning tenglamasini topamiz . Bu tenglama bo'lsin. e'tibor bering, bu kelib chiqishi orqali o'tmaydi, shuning uchun
va tenglamani D ga bo'lish mumkin; quyidagi tenglamani olamiz:
yoki ax + by + cz +1=0

Noma'lum a, b va c koeffitsientlarini aniqlash uchun ax + ga + cz +1=0 tenglamaga ushbu tenglamani qanoatlantiradigan uchta E, F va O nuqtaning koordinatalarini qo'yamiz (chunki bu nuqtalar tekislikda yotadi). ).Tenglamalar sistemasini olamiz:
Birinchi tenglamani 3 ga, ikkinchisini 4 ga, uchinchisini -6 ga ko'paytirib, birinchi tenglamani uchinchisi bilan qo'shib, tizimni o'zgartiramiz.
, b=-4,
.Demak, tekislik tenglamasi quyidagi shaklga ega:

5x + 8y - 9z – 2 =0. Endi B1(0,0,1) nuqtadan tekislikgacha bo'lgan masofani topamiz
.

Javob:
.

Muammo 5.Baza uchburchak piramida SABC teng yonli ABC uchburchagi bo'lib, uning tomoni 4 ga teng. Bundan tashqari, AS = BS = ekanligi ma'lum.
, va CS=3.Ushbu piramida atrofida chegaralangan sharning maydonini toping.