Onlayn vektorlar tizimining chiziqli bog'liqligini o'rganing. Vektorlar sistemasining chiziqli bog'liqligi. Kollinear vektorlar
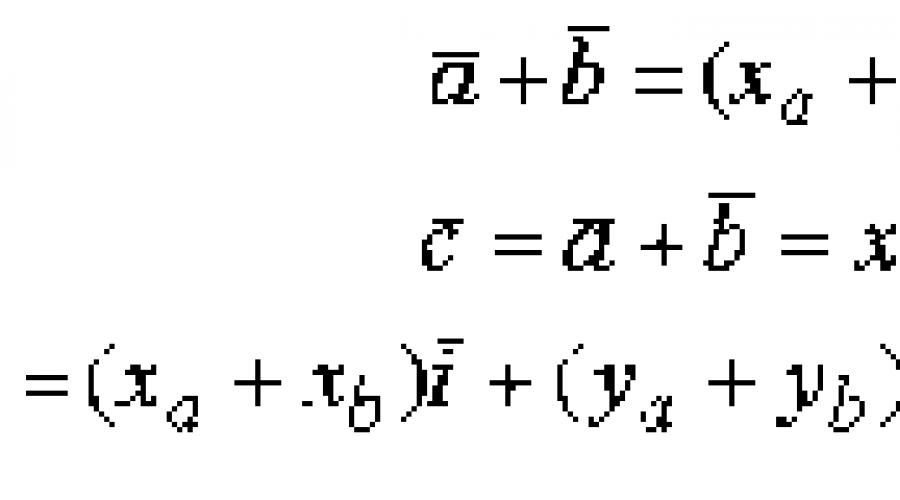
Shuningdek o'qing
Vektorlar, ularning xossalari va ular bilan harakatlari
Vektorlar, vektorlar bilan amallar, chiziqli vektor fazosi.
Vektorlar cheklangan miqdordagi haqiqiy sonlarning tartiblangan to'plamidir.
Amallar: 1.Vektorni songa ko‘paytirish: lambda*vektor x=(lamda*x 1, lambda*x 2 ... lambda*x n).(3.4, 0, 7)*3=(9, 12,0.21)
2. Vektorlarni qo'shish (bir xil vektor fazoga tegishli) vektor x + vektor y = (x 1 + y 1, x 2 + y 2, ... x n + y n,)
3. Vektor 0=(0,0…0)---n E n – n o‘lchovli (chiziqli fazo) vektor x + vektor 0 = vektor x
Teorema. n ta vektorli sistema, n o'lchovli chiziqli fazo chiziqli bog'liq bo'lishi uchun vektorlardan biri boshqalarning chiziqli birikmasi bo'lishi zarur va etarli.
Teorema. Hodisalarning n o‘lchovli chiziqli fazosining n+ 1-vektorlarining har qanday to‘plami. chiziqli bog'liq.
Vektorlarni qo'shish, vektorlarni raqamlarga ko'paytirish. Vektorlarni ayirish.
Ikki vektor yig'indisi vektorning boshidan oxirigacha yo'naltirilgan vektor bo'lib, boshi vektorning oxiriga to'g'ri keladi. Agar vektorlar bazis birlik vektorlarida kengayishlari bilan berilgan bo'lsa, vektorlarni qo'shganda ularga mos keladigan koordinatalar qo'shiladi.
Keling, buni Dekart koordinata tizimi misolida ko'rib chiqaylik. Mayli
Keling, buni ko'rsataylik

3-rasmdan ko'rinib turibdiki ![]()

Har qanday chekli vektorlar yig‘indisini ko‘pburchak qoidasi yordamida topish mumkin (4-rasm): chekli vektorlar yig‘indisini qurish uchun har bir keyingi vektorning boshini oldingisining oxiri bilan birlashtirish kifoya. va birinchi vektorning boshini oxirgi vektorning oxiri bilan bog'lovchi vektorni tuzing.

Vektor qo'shish operatsiyasining xususiyatlari:
Bu ifodalarda m, n sonlardir.
Vektorlar orasidagi farq vektor deyiladi, ikkinchi a'zo yo'nalishi bo'yicha vektorga qarama-qarshi, lekin uzunligi bo'yicha unga teng.

Shunday qilib, vektorlarni ayirish amali qo'shish amali bilan almashtiriladi
Boshlanishi A nuqtada va oxiri (x1, y1, z1) nuqtada bo'lgan vektor A nuqtaning radius vektori deyiladi va oddiygina belgilanadi. Uning koordinatalari A nuqtaning koordinatalariga to'g'ri kelganligi sababli uning birlik vektorlarda kengayishi ko'rinishga ega.

A(x1, y1, z1) nuqtadan boshlanib, B(x2, y2, z2) nuqtada tugaydigan vektorni quyidagicha yozish mumkin. ![]()
bu yerda r 2 B nuqtaning radius vektori; r 1 - A nuqtaning radius vektori.
Shuning uchun birlik vektorlarda vektorning kengayishi shaklga ega
Uning uzunligi A va B nuqtalari orasidagi masofaga teng
KO'PTIRISH
Shunday qilib, vaziyatda samolyot muammosi a = (ax; ay) vektorning b soniga ko'paytmasi formula bo'yicha topiladi
a b = (ax b; ay b)
Misol 1. a = (1; 2) vektorining 3 ga ko‘paytmasini toping.
3 a = (3 1; 3 2) = (3; 6)
Demak, fazoviy masalada a = (ax; ay; az) vektorining b soniga ko‘paytmasi formula bo‘yicha topiladi.
a b = (ax b; ay b; az b)
1-misol. a = (1; 2; -5) vektorining 2 ga ko‘paytmasini toping.
2 a = (2 1; 2 2; 2 (-5)) = (2; 4; -10)
Vektorlarning nuqta mahsuloti va ![]() vektorlar orasidagi burchak qayerda; bo'lsa, u holda
vektorlar orasidagi burchak qayerda; bo'lsa, u holda
Skayar mahsulotning ta'rifidan kelib chiqadiki ![]()
bu erda, masalan, vektorning vektor yo'nalishi bo'yicha proyeksiyasining kattaligi.
Skalar kvadrat vektor:
Nuqta mahsulotining xususiyatlari:
![]()
![]()
![]()
![]()
Koordinatalarda nuqta mahsuloti
Agar ![]()
![]() Bu
Bu ![]()
Vektorlar orasidagi burchak
Vektorlar orasidagi burchak - bu vektorlarning yo'nalishlari orasidagi burchak (eng kichik burchak).
O'zaro mahsulot (Ikki vektorning o'zaro mahsuloti.) - bu ikki omildan tuzilgan tekislikka perpendikulyar bo'lgan psevdovektor bo'lib, bu uch o'lchovli Evklid fazosida vektorlar ustidan "vektorlarni ko'paytirish" ikkilik operatsiyasining natijasidir. Mahsulot kommutativ ham, assotsiativ ham emas (u antikommutativ) va vektorlarning nuqta mahsulotidan farq qiladi. Ko'pgina muhandislik va fizika muammolarida siz ikkita mavjudga perpendikulyar vektorni qurishingiz kerak - vektor mahsuloti bu imkoniyatni beradi. O'zaro ko'paytma vektorlarning perpendikulyarligini "o'lchash" uchun foydalidir - ikkita vektorning kesishgan ko'paytmasining uzunligi, agar ular perpendikulyar bo'lsa, ularning uzunliklari mahsulotiga teng bo'ladi va vektorlar parallel yoki antiparallel bo'lsa, nolga kamayadi.
O'zaro mahsulot faqat uch o'lchovli va etti o'lchovli bo'shliqlarda aniqlanadi. Vektor mahsulotining natijasi, xuddi skalar mahsulot kabi, Evklid fazosining metrikasiga bog'liq.
Uch o'lchovli to'rtburchaklar koordinatalar tizimidagi koordinatalardan skalyar mahsulot vektorlarini hisoblash formulasidan farqli o'laroq, o'zaro mahsulot formulasi to'rtburchaklar koordinatalar tizimining yo'nalishiga yoki boshqacha aytganda, uning "xiralligiga" bog'liq.
Vektorlarning kollinearligi.
Ikki nolga teng bo'lmagan (0 ga teng bo'lmagan) vektorlar, agar ular parallel yoki bir xil to'g'ri chiziqda yotsa, ular kollinear deyiladi. Qabul qilinadigan, ammo tavsiya etilmaydigan sinonim "parallel" vektorlardir. Kollinear vektorlar bir xil yo'naltirilgan ("ko'p yo'nalishli") yoki qarama-qarshi yo'naltirilgan bo'lishi mumkin (ikkinchi holatda ular ba'zan "antikollinear" yoki "antiparallel" deb ataladi).
Vektorlarning aralash mahsuloti ( a, b, c)- a vektorning skalyar ko'paytmasi va b va c vektorlarning vektor ko'paytmasi:
(a,b,c)=a ⋅(b ×c)
u ba'zan vektorlarning uch nuqtali mahsuloti deb ataladi, aftidan, natija skaler (aniqrog'i, psevdoskalar) bo'ladi.
Geometrik ma'no: Aralash mahsulotning moduli son jihatdan vektorlar hosil qilgan parallelepiped hajmiga teng. (a,b,c) .
Xususiyatlari
Aralash bo'lak uning barcha argumentlariga nisbatan skew-simmetrik: ya'ni. e. har qanday ikki omilni qayta tartibga solish mahsulot belgisini o'zgartiradi. Bundan kelib chiqadiki, o'ng dekart koordinata tizimidagi Aralash mahsulot (ortonormal asosda) vektorlardan tashkil topgan matritsaning determinantiga teng va:
Chap kartezian koordinata tizimidagi aralash mahsulot (ortonormal asosda) vektorlardan tashkil topgan matritsaning determinantiga teng va minus belgisi bilan olinadi:
Ayniqsa,
Agar ikkita vektor parallel bo'lsa, u holda har qanday uchinchi vektor bilan ular nolga teng aralash mahsulot hosil qiladi.
Agar uchta vektor chiziqli bog'liq bo'lsa (ya'ni, koplanar, bir tekislikda yotsa), unda ularning aralash mahsuloti nolga teng.
Geometrik ma'no - aralash mahsulot tomonidan mutlaq qiymat vektorlar hosil qilgan parallelepiped hajmiga teng (rasmga qarang) va; belgi vektorlarning bu uchligi o'ng yoki chap qo'l ekanligiga bog'liq.
Vektorlarning mutanosibligi.
Uch vektor (yoki undan ko'p) koplanar deyiladi, agar ular umumiy kelib chiqishiga keltirilsa, bir tekislikda yotsa.
Tegishlilik xossalari
Agar kamida bittasi bo'lsa uchta vektor- nolga teng bo'lsa, uchta vektor ham koplanar hisoblanadi.
Bir juft kollinear vektorni o'z ichiga olgan uchlik vektorlar koplanardir.
Koplanar vektorlarning aralash mahsuloti. Bu uchta vektorning mutanosibligi uchun mezondir.
Koplanar vektorlar chiziqli bog'liqdir. Bu ham mutanosiblik mezoni hisoblanadi.
3 o'lchovli fazoda 3 ta tekis bo'lmagan vektor asosni tashkil qiladi
Chiziqli bog'liq va chiziqli mustaqil vektorlar.
Chiziqli qaram va mustaqil vektor sistemalar.Ta'rif. Vektor sistemasi deyiladi chiziqli bog'liq, agar bu vektorlarning nol vektoriga teng bo'lgan kamida bitta notrivial chiziqli birikmasi mavjud bo'lsa. Aks holda, ya'ni. agar berilgan vektorlarning faqat arzimas chiziqli birikmasi nol vektorga teng bo'lsa, vektorlar deyiladi chiziqli mustaqil.
Teorema (chiziqli bog'liqlik mezoni). Chiziqli fazodagi vektorlar sistemasi chiziqli bog'liq bo'lishi uchun bu vektorlardan kamida bittasi boshqalarning chiziqli birikmasi bo'lishi zarur va etarli.
1) Agar vektorlar orasida kamida bitta nol vektor bo'lsa, u holda vektorlarning butun tizimi chiziqli bog'liqdir.
Aslida, agar, masalan, , deb faraz qilsak, bizda notrivial chiziqli birikma mavjud.▲
2) Agar vektorlar orasidan ba'zilari chiziqli bog'liq tizimni tashkil qilsa, u holda butun tizim chiziqli bog'liqdir.
Haqiqatan ham, , vektorlari chiziqli bog'liq bo'lsin. Bu nol vektorga teng bo'lmagan trivial chiziqli birikma mavjudligini anglatadi. Ammo keyin, taxmin qilish kerak ![]() , biz nol vektorga teng bo'lmagan notrivial chiziqli birikmani ham olamiz.
, biz nol vektorga teng bo'lmagan notrivial chiziqli birikmani ham olamiz.
2. Asos va o‘lcham. Ta'rif. Chiziqli mustaqil vektorlar tizimi ![]() vektor fazosi deyiladi asos bu fazoning har qanday vektorini ushbu tizim vektorlarining chiziqli birikmasi sifatida ifodalash mumkin bo'lsa, ya'ni. Har bir vektor uchun haqiqiy sonlar mavjud
vektor fazosi deyiladi asos bu fazoning har qanday vektorini ushbu tizim vektorlarining chiziqli birikmasi sifatida ifodalash mumkin bo'lsa, ya'ni. Har bir vektor uchun haqiqiy sonlar mavjud ![]() tenglik shunday bo'ladiki, bu tenglik deyiladi vektor parchalanishi asos va raqamlarga ko'ra
tenglik shunday bo'ladiki, bu tenglik deyiladi vektor parchalanishi asos va raqamlarga ko'ra ![]() chaqiriladi vektorning bazisga nisbatan koordinatalari(yoki asosda) .
chaqiriladi vektorning bazisga nisbatan koordinatalari(yoki asosda) .
Teorema (asosga nisbatan kengayishning o'ziga xosligi to'g'risida). Kosmosdagi har bir vektor bazaga kengaytirilishi mumkin yagona yo'l bilan, ya'ni. asosdagi har bir vektorning koordinatalari aniq belgilanadi.
Vazifa 1. Vektorlar sistemasi chiziqli mustaqil ekanligini aniqlang. Vektorlar tizimi ustunlari vektorlarning koordinatalaridan iborat bo'lgan tizim matritsasi bilan belgilanadi.
 .
.
Yechim. Chiziqli birikma bo'lsin  nolga teng. Ushbu tenglikni koordinatalarda yozib, biz quyidagi tenglamalar tizimini olamiz:
nolga teng. Ushbu tenglikni koordinatalarda yozib, biz quyidagi tenglamalar tizimini olamiz:
 .
.
Bunday tenglamalar tizimi uchburchak deyiladi. Uning faqat bitta yechimi bor  . Shuning uchun vektorlar
. Shuning uchun vektorlar  chiziqli mustaqil.
chiziqli mustaqil.
Vazifa 2. Uning chiziqli ekanligini aniqlang mustaqil tizim vektorlar.
 .
.
Yechim. Vektorlar  chiziqli mustaqil (1-masalaga qarang). Vektor vektorlarning chiziqli birikmasi ekanligini isbotlaylik
chiziqli mustaqil (1-masalaga qarang). Vektor vektorlarning chiziqli birikmasi ekanligini isbotlaylik  . Vektor kengayish koeffitsientlari
. Vektor kengayish koeffitsientlari  tenglamalar sistemasidan aniqlanadi
tenglamalar sistemasidan aniqlanadi
 .
.
Ushbu tizim, uchburchak kabi, o'ziga xos echimga ega.
Shuning uchun vektorlar sistemasi  chiziqli bog'liq.
chiziqli bog'liq.
Izoh. 1-masaladagi kabi turdagi matritsalar deyiladi uchburchak , va 2-muammoda - pog'onali uchburchak . Vektorlar tizimining chiziqli bog'liqligi haqidagi savol, agar bu vektorlarning koordinatalaridan tashkil topgan matritsa pog'onali uchburchak bo'lsa, oson hal qilinadi. Agar matritsada bo'lmasa maxsus turi, keyin foydalaning elementar string konvertatsiyalari , ustunlar orasidagi chiziqli munosabatlarni saqlab, uni qadam-uchburchak shaklga qisqartirish mumkin.
Elementar transformatsiyalar chiziqlar matritsalar (EPS) matritsadagi quyidagi amallar deyiladi:
1) satrlarni qayta tartibga solish;
2) qatorni nolga teng bo‘lmagan songa ko‘paytirish;
3) ixtiyoriy songa ko'paytiriladigan satrga boshqa satr qo'shish.
Vazifa 3. Maksimal chiziqli mustaqil quyi tizimni toping va vektorlar tizimining darajasini hisoblang
 .
.
Yechim. Keling, EPS yordamida tizimning matritsasini bosqichli uchburchak shaklga keltiraylik. Protsedurani tushuntirish uchun o'zgartiriladigan matritsaning raqami bilan chiziqni belgi bilan belgilaymiz. O'qdan keyingi ustun yangi matritsa satrlarini olish uchun bajarilishi kerak bo'lgan konvertatsiya qilinayotgan matritsa satrlaridagi amallarni bildiradi.

 .
.
Shubhasiz, natijada olingan matritsaning dastlabki ikkita ustuni chiziqli mustaqil, uchinchi ustun ularning chiziqli kombinatsiyasi, to'rtinchisi esa birinchi ikkitasiga bog'liq emas. Vektorlar  asosiy deyiladi. Ular tizimning maksimal chiziqli mustaqil quyi tizimini tashkil qiladi
asosiy deyiladi. Ular tizimning maksimal chiziqli mustaqil quyi tizimini tashkil qiladi  , tizimning darajasi esa uchta.
, tizimning darajasi esa uchta.
Bazis, koordinatalar
Vazifa 4. Koordinatalari shartni qanoatlantiradigan geometrik vektorlar to‘plamida shu asosdagi vektorlarning bazis va koordinatalarini toping.  .
.
Yechim. Toʻplam koordinatadan oʻtuvchi tekislikdir. Tekislikdagi ixtiyoriy bazis ikkita kollinear bo'lmagan vektordan iborat. Tanlangan asosdagi vektorlarning koordinatalari mos keladigan tizimning yechimi bilan aniqlanadi chiziqli tenglamalar.
Ushbu muammoni hal qilishning yana bir yo'li bor, agar siz koordinatalar yordamida asosni topishingiz mumkin.
Koordinatalar  bo'shliqlar tekislikdagi koordinatalar emas, chunki ular munosabat bilan bog'langan
bo'shliqlar tekislikdagi koordinatalar emas, chunki ular munosabat bilan bog'langan  , ya'ni ular mustaqil emas. Mustaqil o'zgaruvchilar va (ular erkin deb ataladi) tekislikdagi vektorni yagona aniqlaydi va shuning uchun ularni koordinatalar sifatida tanlash mumkin. Keyin asos
, ya'ni ular mustaqil emas. Mustaqil o'zgaruvchilar va (ular erkin deb ataladi) tekislikdagi vektorni yagona aniqlaydi va shuning uchun ularni koordinatalar sifatida tanlash mumkin. Keyin asos  erkin o'zgaruvchilar to'plamida yotgan va ularga mos keladigan vektorlardan iborat
erkin o'zgaruvchilar to'plamida yotgan va ularga mos keladigan vektorlardan iborat  Va
Va  , ya'ni .
, ya'ni .
Vazifa 5. Fazodagi toq koordinatalari bir-biriga teng bo‘lgan barcha vektorlar to‘plamida shu asosdagi vektorlarning bazis va koordinatalarini toping.
Yechim. Oldingi masalada bo'lgani kabi, kosmosdagi koordinatalarni tanlaylik.
Chunki  , keyin erkin o'zgaruvchilar
, keyin erkin o'zgaruvchilar  dan vektorni yagona aniqlang va shuning uchun koordinatalar. Tegishli asos vektorlardan iborat.
dan vektorni yagona aniqlang va shuning uchun koordinatalar. Tegishli asos vektorlardan iborat.
Vazifa 6. Shaklning barcha matritsalari to‘plamida shu asosdagi vektorlarning bazis va koordinatalarini toping  , Qayerda
, Qayerda  - ixtiyoriy raqamlar.
- ixtiyoriy raqamlar.
Yechim. Har bir matritsa quyidagi shaklda noyob tarzda ifodalanadi:
Bu munosabat vektorning bazisga nisbatan kengayishidir  koordinatalari bilan
koordinatalari bilan  .
.
Vazifa 7. Vektorlar sistemasining chiziqli korpusining o‘lchami va asosini toping
 .
.
Yechim. EPS dan foydalanib, biz matritsani tizim vektorlarining koordinatalaridan bosqichli uchburchak shaklga aylantiramiz.


 .
.
Ustunlar  oxirgi matritsalar chiziqli mustaqil va ustunlar
oxirgi matritsalar chiziqli mustaqil va ustunlar  ular orqali chiziqli ifodalangan. Shuning uchun vektorlar
ular orqali chiziqli ifodalangan. Shuning uchun vektorlar  asos hosil qiladi
asos hosil qiladi  , Va
, Va  .
.
Izoh. Asos  noaniq tanlanadi. Masalan, vektorlar
noaniq tanlanadi. Masalan, vektorlar  asosini ham tashkil etadi
asosini ham tashkil etadi  .
.
a 1 = { 3, 5, 1 , 4 }, a 2 = { –2, 1, -5 , -7 }, a 3 = { -1, –2, 0, –1 }.
Yechim. qidirmoqdalar umumiy qaror tenglamalar tizimlari
a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ
Gauss usuli. Buning uchun biz ushbu bir hil tizimni koordinatalarda yozamiz:
Tizim matritsasi
Ruxsat etilgan tizim quyidagi shaklga ega: ![]() (r A = 2, n= 3). Tizim kooperativ va noaniq. Uning umumiy yechimi ( x 2 - erkin o'zgaruvchi): x 3 = 13x 2 ; 3x 1 – 2x 2 – 13x 2 = 0 => x 1 = 5x 2 => X o =. Masalan, nolga teng bo'lmagan xususiy yechimning mavjudligi vektorlar ekanligini ko'rsatadi a
1 , a
2 , a
3
chiziqli bog'liq.
(r A = 2, n= 3). Tizim kooperativ va noaniq. Uning umumiy yechimi ( x 2 - erkin o'zgaruvchi): x 3 = 13x 2 ; 3x 1 – 2x 2 – 13x 2 = 0 => x 1 = 5x 2 => X o =. Masalan, nolga teng bo'lmagan xususiy yechimning mavjudligi vektorlar ekanligini ko'rsatadi a
1 , a
2 , a
3
chiziqli bog'liq.
2-misol.
Yo'qligini bilib oling bu tizim chiziqli bog'liq yoki chiziqli mustaqil vektorlar:
1. a 1 = { -20, -15, - 4 }, a 2 = { –7, -2, -4 }, a 3 = { 3, –1, –2 }.
Yechim. Bir jinsli tenglamalar tizimini ko'rib chiqaylik a 1 x 1 + a 2 x 2 + a 3 x 3 = Θ
yoki kengaytirilgan shaklda (koordinatalar bo'yicha)

Tizim bir hil. Agar u degenerativ bo'lmasa, unda o'ziga xos echim bor. Bir hil tizimda nol (arzimas) yechim mavjud. Bu shuni anglatadiki, bu holda vektorlar tizimi mustaqildir. Agar tizim buzilgan bo'lsa, u nolga teng bo'lmagan echimlarga ega va shuning uchun u bog'liqdir.
Biz tizimni degeneratsiya uchun tekshiramiz:
 = –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.
= –80 – 28 + 180 – 48 + 80 – 210 = – 106 ≠ 0.
Tizim degenerativ emas va shuning uchun vektorlar a 1 , a 2 , a 3 chiziqli mustaqil.
Vazifalar. Berilgan vektorlar sistemasi chiziqli bog'liqmi yoki chiziqli mustaqil ekanligini aniqlang:
1. a 1 = { -4, 2, 8 }, a 2 = { 14, -7, -28 }.
2. a 1 = { 2, -1, 3, 5 }, a 2 = { 6, -3, 3, 15 }.
3. a 1 = { -7, 5, 19 }, a 2 = { -5, 7 , -7 }, a 3 = { -8, 7, 14 }.
4. a 1 = { 1, 2, -2 }, a 2 = { 0, -1, 4 }, a 3 = { 2, -3, 3 }.
5. a 1 = { 1, 8 , -1 }, a 2 = { -2, 3, 3 }, a 3 = { 4, -11, 9 }.
6. a 1 = { 1, 2 , 3 }, a 2 = { 2, -1 , 1 }, a 3 = { 1, 3, 4 }.
7. a 1 = {0, 1, 1 , 0}, a 2 = {1, 1 , 3, 1}, a 3 = {1, 3, 5, 1}, a 4 = {0, 1, 1, -2}.
8. a 1 = {-1, 7, 1 , -2}, a 2 = {2, 3 , 2, 1}, a 3 = {4, 4, 4, -3}, a 4 = {1, 6, -11, 1}.
9. Vektorlar sistemasi chiziqli bog‘liq bo‘lishini isbotlang, agar u quyidagilardan iborat bo‘lsa:
a) ikkita teng vektor;
b) ikkita proportsional vektor.
Ta'rif. Vektorlarning chiziqli birikmasi a 1 , ..., a n koeffitsientlari x 1 , ..., x n vektor deyiladi.
x 1 a 1 + ... + x n a n.
ahamiyatsiz, agar barcha koeffitsientlar x 1 , ..., x n nolga teng bo'lsa.
Ta'rif. ahamiyatsiz, agar x 1, ..., x n koeffitsientlarining kamida bittasi nolga teng bo'lmasa.
chiziqli mustaqil, agar bu vektorlarning nol vektoriga teng bo'lmagan notrivial birikmasi bo'lmasa.
Ya'ni, a 1, ..., a n vektorlari x 1 a 1 + ... + x n a n = 0 bo'lsa, faqat x 1 = 0, ..., x n = 0 bo'lganda chiziqli mustaqildir.
Ta'rif. a 1, ..., a n vektorlari deyiladi chiziqli bog'liq
, agar bu vektorlarning nol vektoriga teng bo'lmagan trivial birikmasi mavjud bo'lsa.
Uchta chiziqli bog'liq vektorlar koplanardir. (Uchta koplanar vektor chiziqli bog'liqdir.)
n o'lchovli vektorlar uchun.
Chiziqli bog'liq vektorlarning xossalari:
2 va 3 o'lchovli vektorlar uchun. Ikki chiziqli bog'liq vektorlar
- kollinear. (Kollinear vektorlar chiziqli bog'liqdir.)
3 o'lchovli vektorlar uchun.
n + 1 vektorlar har doim chiziqli bog'liqdir.
Vektorlarning chiziqli bog'liqligi va chiziqli mustaqilligi masalalariga misollar:
1-misol. a = (3; 4; 5), b = (-3; 0; 5), c = (4; 4; 4), d = (3; 4; 0) vektorlarining chiziqli mustaqilligini tekshiring. .
Yechim:
Vektorlar chiziqli bog'liq bo'ladi, chunki vektorlarning o'lchami vektorlar sonidan kamroq.
1-misol. a = (3; 4; 5), b = (-3; 0; 5), c = (4; 4; 4), d = (3; 4; 0) vektorlarining chiziqli mustaqilligini tekshiring. .
| 2-misol. a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 1) vektorlarining chiziqli mustaqilligini tekshiring. | |
| x 1 + x 2 = 0 | |
| x 1 + 2x 2 - x 3 = 0 |
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 1 | 0 |
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 1 - 0 | 0 - 0 | 0 | -1 | 1 | 0 |
x 1 + x 3 = 0
| ~ | 1 - 0 | 1 - 1 | 0 - (-1) | 0 - 0 | ~ | 1 | 0 | 1 | 0 | ||||
| 0 | 1 | -1 | 0 | 0 | 1 | -1 | 0 | ||||||
| 0 + 0 | -1 + 1 | 1 + (-1) | 0 + 0 | 0 | 0 | 0 | 0 |
birinchi qatordan ikkinchisini olib tashlang; uchinchi qatorga ikkinchi qator qo'shing:
Ushbu yechim tizimning ko'plab echimlarga ega ekanligini ko'rsatadi, ya'ni x 1, x 2, x 3 raqamlari qiymatlarining nolga teng bo'lmagan kombinatsiyasi mavjud bo'lib, a, b, c vektorlarining chiziqli birikmasi teng bo'ladi. nol vektor, masalan:
A + b + c = 0
ya'ni a, b, c vektorlari chiziqli bog'liqdir. Javob:
a, b, c vektorlari chiziqli bog'liqdir.
1-misol. a = (3; 4; 5), b = (-3; 0; 5), c = (4; 4; 4), d = (3; 4; 0) vektorlarining chiziqli mustaqilligini tekshiring. . 3-misol. a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 2) vektorlarining chiziqli mustaqilligini tekshiring.
Ushbu vektorlarning chiziqli birikmasi nol vektorga teng bo'lgan koeffitsientlarning qiymatlarini topamiz.x 1 a + x 2 b + x 3 c 1 = 0
| 2-misol. a = (1; 1; 1), b = (1; 2; 0), c = (0; -1; 1) vektorlarining chiziqli mustaqilligini tekshiring. | |
| x 1 + x 2 = 0 | |
| Bu vektor tenglamani chiziqli tenglamalar sistemasi sifatida yozish mumkin |
x 1 + 2x 3 = 0
| 1 | 1 | 0 | 0 | ~ | ||
| 1 | 2 | -1 | 0 | |||
| 1 | 0 | 2 | 0 |
Bu sistemani Gauss usuli yordamida yechamiz
| ~ | 1 | 1 | 0 | 0 | ~ | 1 | 1 | 0 | 0 | ~ | ||||
| 1 - 1 | 2 - 1 | -1 - 0 | 0 - 0 | 0 | 1 | -1 | 0 | |||||||
| 1 - 1 | 0 - 1 | 2 - 0 | 0 - 0 | 0 | -1 | 2 | 0 |
ikkinchi qatordan birinchisini ayirish; uchinchi qatordan birinchisini ayirish: