To'g'ri chiziq va tekislik orasidagi burchak ta'rifini shakllantirish. To'g'ri chiziq va tekislik orasidagi burchak: ta'rifi, topishga misollar
Maxfiyligingizni saqlash biz uchun muhim. Shu sababli, biz sizning ma'lumotlaringizdan qanday foydalanishimiz va saqlashimizni tavsiflovchi Maxfiylik siyosatini ishlab chiqdik. Iltimos, maxfiylik amaliyotlarimizni ko'rib chiqing va savollaringiz bo'lsa, bizga xabar bering.
Shaxsiy ma'lumotlarni to'plash va ulardan foydalanish
Shaxsiy ma'lumotlar ma'lum bir shaxsni aniqlash yoki unga murojaat qilish uchun ishlatilishi mumkin bo'lgan ma'lumotlarni anglatadi.
Biz bilan bog'langaningizda istalgan vaqtda shaxsiy ma'lumotlaringizni taqdim etishingiz so'ralishi mumkin.
Quyida biz to'plashimiz mumkin bo'lgan shaxsiy ma'lumotlar turlari va bunday ma'lumotlardan qanday foydalanishimiz mumkinligiga ba'zi misollar keltirilgan.
Biz qanday shaxsiy ma'lumotlarni yig'amiz:
- Saytda so'rov yuborganingizda, biz sizning ismingiz, telefon raqamingiz, manzilingiz kabi turli xil ma'lumotlarni to'plashimiz mumkin Elektron pochta va hokazo.
Shaxsiy ma'lumotlaringizdan qanday foydalanamiz:
- Biz tomonidan yig'ilgan Shaxsiy ma'lumot bizga siz bilan bog'lanish va noyob takliflar, aktsiyalar va boshqa tadbirlar va bo'lajak voqealar haqida sizni xabardor qilish imkonini beradi.
- Vaqti-vaqti bilan biz sizning shaxsiy ma'lumotlaringizdan muhim xabarlar va xabarlarni yuborish uchun foydalanishimiz mumkin.
- Shaxsiy ma'lumotlardan audit, ma'lumotlarni tahlil qilish va boshqalar kabi ichki maqsadlarda ham foydalanishimiz mumkin turli tadqiqotlar biz taqdim etayotgan xizmatlarni yaxshilash va sizga xizmatlarimiz bo'yicha tavsiyalar berish uchun.
- Agar siz sovrinlar o'yinida, tanlovda yoki shunga o'xshash aksiyada ishtirok etsangiz, biz siz taqdim etgan ma'lumotlardan bunday dasturlarni boshqarish uchun foydalanishimiz mumkin.
Ma'lumotni uchinchi shaxslarga oshkor qilish
Biz sizdan olingan ma'lumotlarni uchinchi shaxslarga oshkor etmaymiz.
Istisnolar:
- Zarur hollarda qonun hujjatlariga muvofiq sud tartibi, V sud va/yoki ommaviy so'rovlar yoki so'rovlar asosida davlat organlari rossiya Federatsiyasi hududida - shaxsiy ma'lumotlaringizni oshkor qiling. Shuningdek, biz siz haqingizdagi ma'lumotlarni oshkor qilishimiz mumkin, agar bunday oshkor qilish xavfsizlik, huquqni muhofaza qilish yoki boshqa sog'liqni saqlash maqsadlari uchun zarur yoki mos ekanligini aniqlasak. muhim holatlar.
- Qayta tashkil etish, qo'shilish yoki sotilgan taqdirda, biz to'plagan shaxsiy ma'lumotlarni tegishli vorisi uchinchi shaxsga o'tkazishimiz mumkin.
Shaxsiy ma'lumotlarni himoya qilish
Shaxsiy ma'lumotlaringizni yo'qotish, o'g'irlash va noto'g'ri foydalanish, shuningdek ruxsatsiz kirish, oshkor qilish, o'zgartirish va yo'q qilishdan himoya qilish uchun ma'muriy, texnik va jismoniy ehtiyot choralarini ko'ramiz.
Shaxsiy hayotingizni kompaniya darajasida hurmat qilish
Shaxsiy ma'lumotlaringiz xavfsizligini ta'minlash uchun biz maxfiylik va xavfsizlik standartlarini xodimlarimizga yetkazamiz va maxfiylik amaliyotlarini qat'iy tatbiq qilamiz.
To'g'ri chiziq va tekislik orasidagi burchak ta'rifini takrorlaymiz.
Ta'rif. To'g'ri chiziq bilan bu to'g'ri chiziqni kesib o'tuvchi va unga perpendikulyar bo'lmagan tekislik orasidagi burchak, toʻgʻri chiziq va uning tekislikka proyeksiyasi orasidagi burchak.
Bu tekislikni kesib o'tuvchi va unga perpendikulyar bo'lmagan g tekislik va a chiziq berilgan bo'lsin.
a to'g'ri chiziq bilan g tekislik orasidagi burchakni quramiz:
- a to'g'ri chiziqning biz uchun qulay bo'lgan istalgan nuqtasidan g tekislikka perpendikulyar tushiramiz;
- Qiya va perpendikulyar asoslar nuqtalari orqali b to'g'ri chiziq o'tkazamiz. b chiziq a chiziqning g tekislikka proyeksiyasi;
- a va b to'g'ri chiziqlar orasidagi o'tkir burchak a to'g'ri chiziq va g tekislik orasidagi burchak, ya'ni. ∠(a;b)= ∠(a;g) , bu yerda ∠(a;b) - a va b chiziqlar orasidagi burchak; ∠(a;g) - a to'g'ri chiziq va g tekislik orasidagi burchak.
Koordinatalar usuli yordamida muammolarni hal qilish uchun biz quyidagilarni yodda tutishimiz kerak:

3. Yo‘nalish vektori ( a 1 ; b 1 ; c 1 ) va normal vektorning koordinatalari ma’lum bo‘lsa.
(a; b; c), keyin a to'g'ri chiziq va g tekislik orasidagi burchak biz hozir hosil qiladigan formuladan foydalanib hisoblanadi.
To'g'ri chiziqlar orasidagi burchakni topish formulasini bilamiz:
; (1)
∠(s; a) = 90°-∠(a; b), keyin cos∠(s;a)=cos (90°-∠(a;b))=sin ∠(a;b) ; (2)
(1) va (2) dan => ; (3)  , bu yerda m va n vektorlar orasidagi burchak; (4)
, bu yerda m va n vektorlar orasidagi burchak; (4)
Biz (4) ni (3) ga almashtiramiz va hokazo. ∠(a;b)= ∠(a;g), u holda biz quyidagilarni olamiz:

4. Agar normal vektorning koordinatalari noma'lum bo'lsa, u holda tekislik tenglamasini bilishimiz kerak.
To'rtburchaklar koordinatalar sistemasidagi har qanday tekislik tenglama bilan berilishi mumkin
ax + by + cz + d = 0,
bu erda a, b, c koeffitsientlarining kamida bittasi noldan farq qiladi. Ushbu koeffitsientlar normal vektorning koordinatalari bo'ladi, ya'ni. (a; b; c).
Koordinata usulida to‘g‘ri chiziq va tekislik orasidagi burchakni topish masalalarini yechish algoritmi:
- Biz chizma qilamiz, unda biz to'g'ri chiziq va tekislikni belgilaymiz;
- Biz to'rtburchaklar koordinata tizimini joriy qilamiz;
- Yo'nalish vektorining koordinatalarini uning boshi va oxiri koordinatalaridan topamiz;
- Oddiy vektorning tekislikka koordinatalarini toping;
- Olingan ma'lumotlarni to'g'ri chiziq va tekislik orasidagi burchak sinusining formulasiga almashtiramiz;
- Burchakning o'zi qiymatini toping.
Muammoni ko'rib chiqaylik:
1. ABCDA 1 B 1 C 1 D 1 kubida AC 1 to‘g‘ri chiziq bilan BDD 1 tekislik orasidagi burchak tangensini toping..
Yechim:

1. Koordinatalar koordinata sistemasini koordinatalar koordinatalari koordinatalari D nuqtada keltiramiz.
2. AC 1 yo‘nalish vektorining koordinatalarini toping. Buning uchun birinchi navbatda A va C 1 nuqtalarining koordinatalarini aniqlang:
A(0; 1; 0);
C 1 (1; 0; 1).
{1; -1; 1}.
3. BB 1 D 1 tekislikka normal vektorning koordinatalarini toping. Buning uchun tekislikning bir tekisda yotmaydigan uchta nuqtasining koordinatalarini topamiz va tekislikning tenglamasini tuzamiz:
D(0; 0; 0);
D 1 (0; 0; 1);
B(1; 1; 0);
D: a⋅0+b⋅0+c⋅0+d=0;
D 1: a⋅0+b⋅0+c⋅1+d=0;
B: a⋅1+b⋅1+c⋅0+d=0.
Tenglamaga almashtiramiz: a⋅x+(-a)⋅y+0⋅z+0 = 0;
a⋅x-a⋅y = 0; |:a
x-y = 0.
Shunday qilib, BDD 1 tekisligining normal vektori koordinatalarga ega:
{1;-1; 0}.
4. Keling, sinusni topamiz AC 1 to'g'ri chiziq va BDD 1 tekisligi o'rtasida:

5. Asosiy trigonometrik identifikatsiyadan foydalanamiz va AC 1 to‘g‘ri chiziq va BDD 1 tekislik orasidagi burchakning kosinusini topamiz:

6. AC 1 to‘g‘ri chiziq va BDD 1 tekislik orasidagi burchak tangensini toping:
Javob: .
2. Barcha qirralari 1 ga teng bo‘lgan SABCD to‘rtburchakli muntazam piramidada BD to‘g‘ri chiziq bilan SBC tekisligi orasidagi burchak sinusini toping.
Yechim:

1. Koordinatalar koordinatalari koordinatalari koordinatalari B nuqtada joylashgan to‘rtburchaklar sistemasini kiritamiz.
2. BD yo‘nalish vektorining koordinatalarini toping. Buning uchun avval B va D nuqtalarining koordinatalarini aniqlang:

3. Normal vektorning SBC tekisligiga koordinatalarini toping. Buning uchun tekislikning bir to'g'ri chiziqda yotmaydigan uchta nuqtasining koordinatalarini topamiz va SBC tekisligining tenglamasini tuzamiz:

S nuqtaning koordinatalarini qanday oldingiz?
S nuqtadan ABC asos tekisligiga perpendikulyar tushiriladi. Kesishish nuqtasi O deb belgilandi. O nuqta S nuqtaning ABC tekisligiga proyeksiyasidir. Uning x va y koordinatalari S nuqtaning dastlabki ikkita koordinatalari bo'ladi.

Piramidaning balandligini bilib, biz S nuqtaning uchinchi koordinatasini topdik (z o'qi bo'ylab)
SOB uchburchagi to'rtburchaklardir, shuning uchun Pifagor teoremasiga ko'ra:

Tekis tenglama ax+by+cz+d=0. Nuqtalarning koordinatalarini ushbu tenglamaga almashtiramiz:

Biz uchta tenglama tizimini oldik:

Keling, tenglamaga almashtiramiz:

Shunday qilib, SBD tekisligiga normal vektor koordinatalarga ega:
 .
.
4. BD to‘g‘ri chiziq bilan SBD tekislik orasidagi sinusni toping.
Shaklni tekislikka proyeksiyalash tushunchasi
Chiziq va tekislik orasidagi burchak tushunchasini kiritish uchun, avvalo, ixtiyoriy figuraning tekislikka proyeksiyasi kabi tushunchani tushunishingiz kerak.
Ta'rif 1
Bizga $A$ ixtiyoriy nuqta berilsin. $A_1$ nuqta $A$ nuqtadan $\alpha $ tekisligiga chizilgan perpendikulyar asos bo'lsa, $A$ nuqtaning $\alpha $ tekislikka proyeksiyasi deyiladi (1-rasm).
Rasm 1. Nuqtaning tekislikka proyeksiyasi
Ta'rif 2
Bizga $F$ ixtiyoriy raqam berilsin. $F_1$ figurasi $F$ figurasining barcha nuqtalarining $\alfa $ tekisligiga proyeksiyalaridan tashkil topgan $F$ figurasining $\alpha $ tekisligiga proyeksiyasi deyiladi (2-rasm).

Shakl 2. Shaklning tekislikka proyeksiyasi
Teorema 1
To'g'ri chiziq tekisligiga perpendikulyar bo'lmagan proyeksiya to'g'ri chiziqdir.
Isbot.
Bizga $\alpha $ tekislik va unga perpendikulyar emas, balki uni kesib o'tuvchi $d$ to'g'ri chiziq berilsin. $d$ to'g'rida $M$ nuqtani tanlaymiz va uning $H$ proyeksiyasini $\alpha $ tekisligiga chizamiz. $(MH)$ to'g'ri chiziq orqali $\beta $ tekisligini chizamiz. Shubhasiz, bu tekislik $\alpha $ tekisligiga perpendikulyar bo'ladi. Ular $m$ to'g'ri chiziq bo'ylab kesishsin. $d$ chiziqning $M_1$ ixtiyoriy nuqtasini ko'rib chiqamiz va u orqali $(MH)$ to'g'risiga parallel $(M_1H_1$) chiziq o'tkazamiz (3-rasm).

3-rasm.
$\beta $ tekisligi $\alpha $ tekisligiga perpendikulyar boʻlgani uchun $M_1H_1$ $m$ toʻgʻrisiga perpendikulyar boʻladi, yaʼni $H_1$ nuqta $M_1$ nuqtaning tekislikka proyeksiyasidir. $\alfa $. $M_1$ nuqtani tanlashning o'zboshimchaligi tufayli $d$ chizig'ining barcha nuqtalari $m$ chizig'iga proyeksiyalanadi.
Shunga o'xshash tarzda mulohaza yuritish. Teskari tartibda $m$ chiziqdagi har bir nuqta $d$ chiziqdagi istalgan nuqtaning proyeksiyasi ekanligini bilib olamiz.
Bu $d$ chizig'i $m$ chizig'iga proyeksiyalanganligini bildiradi.
Teorema isbotlangan.
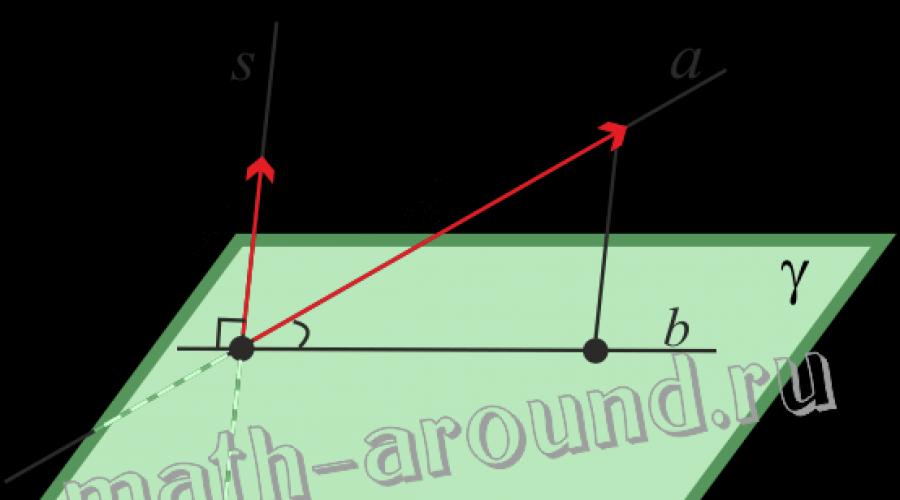
To'g'ri chiziq va tekislik orasidagi burchak tushunchasi
Ta'rif 3
Tekislikni kesib o'tuvchi to'g'ri chiziq va uning bu tekislikka proyeksiyasi orasidagi burchak to'g'ri chiziq bilan tekislik orasidagi burchak deyiladi (4-rasm).
4-rasm. To'g'ri chiziq va tekislik orasidagi burchak
Keling, bu erda bir nechta eslatma qilaylik.
Eslatma 1
Agar chiziq tekislikka perpendikulyar bo'lsa. Keyin to'g'ri chiziq va tekislik orasidagi burchak $90^\circ$ bo'ladi.
Eslatma 2
Agar chiziq parallel yoki tekislikda yotsa. U holda to'g'ri chiziq va tekislik orasidagi burchak $0^\circ$ bo'ladi.
Namuna muammolar
1-misol
Bizga $ABCD$ parallelogrammasi va parallelogramm tekisligida yotmaydigan $M$ nuqta berilsin. $B$ nuqta $M$ nuqtaning parallelogramm tekisligiga proyeksiyasi bo'lsa, $AMB$ va $MBC$ uchburchaklar to'g'ri burchakli ekanligini isbotlang.
Isbot.
Keling, rasmda muammoli holatni tasvirlaymiz (5-rasm).

5-rasm.
$B$ nuqta $M$ nuqtaning $(ABC)$ tekislikka proyeksiyasi bo'lgani uchun $(MB)$ to'g'ri chiziq $(ABC)$ tekislikka perpendikulyar bo'ladi. 1-mulohazaga ko'ra, $(MB)$ to'g'ri chiziq va $(ABC)$ tekislik orasidagi burchak $90^\circ$ ga teng ekanligini aniqlaymiz. Shuning uchun
\[\angle MBC=MBA=(90)^0\]
Bu $AMB$ va $MBC$ uchburchaklari toʻgʻri burchakli uchburchaklar ekanligini anglatadi.
2-misol
$\alpha $ samolyoti berilgan. Bu tekislikka $\varphi $ burchak ostida segment chizilgan, uning boshlanishi shu tekislikda yotadi. Ushbu segmentning proektsiyasi segmentning o'zi yarmiga teng. $\varphi$ qiymatini toping.
Yechim.
6-rasmni ko'rib chiqing.

6-rasm.
Shartga ko'ra, bizda bor
$BCD$ uchburchak to'g'ri burchakli bo'lgani uchun, kosinus ta'rifiga ko'ra
\ \[\varphi =arccos\frac(1)(2)=(60)^0\]
"A olish" video kursi muvaffaqiyat uchun zarur bo'lgan barcha mavzularni o'z ichiga oladi Yagona davlat imtihonidan o'tish matematikadan 60-65 ball. Matematika bo'yicha yagona davlat imtihonining 1-13-sonli barcha topshiriqlarini to'liq bajaring. Matematika bo'yicha asosiy yagona davlat imtihonini topshirish uchun ham javob beradi. Agar siz Yagona davlat imtihonini 90-100 ball bilan topshirmoqchi bo'lsangiz, 1-qismni 30 daqiqada va xatosiz hal qilishingiz kerak!
10-11-sinflar uchun, shuningdek, o'qituvchilar uchun yagona davlat imtihoniga tayyorgarlik kursi. Matematika bo'yicha yagona davlat imtihonining 1-qismini (birinchi 12 ta masala) va 13-muammoni (trigonometriya) hal qilish uchun kerak bo'lgan hamma narsa. Va bu Yagona davlat imtihonida 70 balldan oshadi va na 100 ball to'plagan talaba, na gumanitar fanlar talabasi ularsiz qila olmaydi.
Barcha kerakli nazariya. Tezkor usullar Yagona davlat imtihonining echimlari, tuzoqlari va sirlari. FIPI vazifalar bankining 1-qismining barcha joriy vazifalari tahlil qilindi. Kurs 2018 yilgi Yagona davlat imtihonining talablariga to'liq javob beradi.
Kurs 5 tadan iborat katta mavzular, har biri 2,5 soat. Har bir mavzu noldan, sodda va tushunarli tarzda berilgan.
Yuzlab yagona davlat imtihon topshiriqlari. So'z muammolari va ehtimollar nazariyasi. Muammolarni hal qilish uchun oddiy va eslab qolish oson algoritmlar. Geometriya. Yagona davlat imtihonining barcha turlari nazariyasi, ma'lumotnomasi, tahlili. Stereometriya. Ayyor nayranglar echimlar, foydali cheat varaqlari, fazoviy tasavvurni rivojlantirish. Trigonometriya noldan muammoga 13. Tiklash o'rniga tushunish. Murakkab tushunchalarning aniq tushuntirishlari. Algebra. Ildizlar, darajalar va logarifmlar, funksiya va hosila. Yechim uchun asos murakkab vazifalar Yagona davlat imtihonining 2 qismi.
Maqola to'g'ri chiziq va tekislik orasidagi burchakni aniqlash bilan boshlanadi. Ushbu maqolada to'g'ri chiziq va tekislik orasidagi burchakni koordinata usuli yordamida qanday topish mumkinligi ko'rsatilgan. Misollar va muammolarning echimlari batafsil muhokama qilinadi.
Yandex.RTB R-A-339285-1
Birinchidan, fazodagi to'g'ri chiziq tushunchasini va tekislik tushunchasini takrorlash kerak. To'g'ri chiziq va tekislik orasidagi burchakni aniqlash uchun bir nechta yordamchi ta'riflar kerak. Keling, ushbu ta'riflarni batafsil ko'rib chiqaylik.
Ta'rif 1
To'g'ri chiziq va tekislik kesishadi agar ularda bitta bo'lsa umumiy nuqta, ya'ni to'g'ri chiziq va tekislikning kesishish nuqtasidir.
Tekislikni kesib o'tuvchi to'g'ri chiziq tekislikka perpendikulyar bo'lishi mumkin.
Ta'rif 2
To'g'ri chiziq tekislikka perpendikulyar bu tekislikda joylashgan har qanday chiziqqa perpendikulyar bo'lganda.

Ta'rif 3
M nuqtaning tekislikka proyeksiyasi g nuqtaning o'zi, agar u yotsa berilgan samolyot, yoki tekislikning g tekislikka tegishli bo'lmasligi sharti bilan M nuqtadan o'tuvchi g tekislikka perpendikulyar chiziq bilan kesishish nuqtasidir.

Ta'rif 4
a chiziqning tekislikka proyeksiyasi g - berilgan chiziqning barcha nuqtalarining tekislikka proyeksiyalari to'plami.

Bundan g tekislikka perpendikulyar chiziq proyeksiyasi kesishish nuqtasiga ega ekanligini bilib olamiz. a chiziqning proyeksiyasi g tekislikka tegishli va a chiziq bilan tekislikning kesishish nuqtasidan o'tuvchi chiziq ekanligini aniqlaymiz. Keling, quyidagi rasmga qaraylik.

Yoniq bu daqiqa to'g'ri chiziq va tekislik orasidagi burchak ta'rifini shakllantirish uchun barcha kerakli ma'lumotlar va ma'lumotlarga egamiz
Ta'rif 5
To'g'ri chiziq va tekislik orasidagi burchak bu to'g'ri chiziq va uning bu tekislikka proyeksiyasi orasidagi burchak deyiladi va to'g'ri chiziq unga perpendikulyar emas.
Yuqorida keltirilgan burchakning ta'rifi chiziq va tekislik orasidagi burchak ikki kesishuvchi to'g'ri chiziq orasidagi burchak, ya'ni berilgan chiziq bilan birga uning tekislikka proyeksiyasi degan xulosaga kelishga yordam beradi. Bu ularning orasidagi burchak har doim o'tkir bo'lishini anglatadi. Keling, quyidagi rasmni ko'rib chiqaylik.

To'g'ri chiziq va tekislik o'rtasida joylashgan burchak to'g'ri, ya'ni 90 gradusga teng deb hisoblanadi, lekin parallel to'g'ri chiziqlar orasida joylashgan burchak aniqlanmagan. Uning qiymati nolga teng qabul qilingan holatlar mavjud.
To'g'ri chiziq va tekislik orasidagi burchakni topish zarur bo'lgan masalalarni hal qilishda ko'plab o'zgarishlar mavjud. Yechimning o'zi vaziyat bo'yicha mavjud ma'lumotlarga bog'liq. Yechimning tez-tez hamrohlari raqamlar, kosinuslar, sinuslar, burchaklar tangenslarining o'xshashligi yoki tengligi belgilaridir. Koordinata usuli yordamida burchakni topish mumkin. Keling, buni batafsil ko'rib chiqaylik.
Agar uch oʻlchamli fazoga O x y z toʻgʻri burchakli koordinatalar sistemasi kiritilsa, unda g tekislikni M nuqtada kesib oʻtuvchi a toʻgʻri chiziq koʻrsatilgan va u tekislikka perpendikulyar emas. Berilgan to'g'ri chiziq va tekislik o'rtasida joylashgan a burchakni topish kerak.
Avval siz koordinata usuli yordamida to'g'ri chiziq va tekislik orasidagi burchakning ta'rifini qo'llashingiz kerak. Keyin biz quyidagilarni olamiz.
O x y z koordinata sistemasida to'g'ri chiziqning fazodagi tenglamalariga va to'g'ri chiziqning fazodagi yo'naltiruvchi vektoriga to'g'ri keladigan a to'g'ri chiziq ko'rsatilgan bo'lib, u erda tekislik va normal tenglama mos keladi; samolyot vektori. U holda a → = (a x, a y, a z) berilgan a chiziqning yo‘nalish vektori, n → (n x, n y, n z) esa g tekislik uchun normal vektor bo‘ladi. Agar a to'g'ri chiziqning yo'nalish vektori va g tekislikning normal vektorining koordinatalari bor deb tasavvur qilsak, ularning tenglamalari ma'lum, ya'ni shart bilan aniqlangan bo'lsa, a vektorlarini aniqlash mumkin bo'ladi. → va n → tenglama asosida.
Burchakni hisoblash uchun to'g'ri chiziq va normal vektorning yo'naltiruvchi vektorining mavjud koordinatalari yordamida ushbu burchakning qiymatini olish uchun formulani o'zgartirish kerak.
a to'g'ri chiziqning g tekislik bilan kesishgan nuqtasidan boshlab a → va n → vektorlarini chizish kerak. Ushbu vektorlarning berilgan chiziqlar va tekisliklarga nisbatan joylashishining 4 ta varianti mavjud. Quyidagi rasmga qarang, unda barcha 4 ta variant ko'rsatilgan.

Bu yerdan a → va n → vektorlari orasidagi burchak a → , n → ^ deb belgilanishi va o'tkir ekanligini aniqlaymiz, u holda to'g'ri chiziq va tekislik o'rtasida joylashgan kerakli burchak a to'ldiriladi, ya'ni ifodani olamiz. a → , n → ^ = 90 ° - a ko'rinishidagi. Qachon shart bo'yicha a →, n → ^ > 90 ° bo'lsa, bizda →, n → ^ = 90 ° + a bo'ladi.
Bu erdan biz kosinuslarni olamiz teng burchaklar teng bo'lsa, oxirgi tengliklar tizim shaklida yoziladi
cos a → , n → ^ = cos 90 ° - a , a → , n → ^< 90 ° cos a → , n → ^ = cos 90 ° + α , a → , n → ^ >90°
Ifodalarni soddalashtirish uchun qisqartirish formulalaridan foydalanish kerak. Keyin cos a → , n → ^ = sin a , a → , n → ^ ko‘rinishdagi tengliklarni olamiz.< 90 ° cos a → , n → ^ = - s i n α , a → , n → ^ >90°
O'zgartirishlarni amalga oshirgandan so'ng, tizim sin a = cos a → , n → ^ , a → , n → ^ ko'rinishini oladi.< 90 ° sin α = - cos a → , n → ^ , a → , n → ^ >90 ° ⇔ sin a = cos a → , n → ^ , a → , n → ^ > 0 sin a = - cos a → , n → ^ , a → , n → ^< 0 ⇔ ⇔ sin α = cos a → , n → ^
Bundan to'g'ri chiziq bilan tekislik orasidagi burchakning sinusi to'g'ri chiziqning yo'naltiruvchi vektori bilan berilgan tekislikning normal vektori orasidagi burchak kosinusining moduliga teng ekanligini olamiz.
Ikki vektor hosil qilgan burchakni topish bo'limida bu burchak vektorlarning skalyar ko'paytmasining qiymatini va bu uzunliklarning ko'paytmasini olishi aniqlandi. To'g'ri chiziq va tekislikning kesishishi natijasida olingan burchak sinusini hisoblash jarayoni formula bo'yicha amalga oshiriladi.
sin a = cos a → , n → ^ = a → , n → ^ a → n → = a x n x + a y n y + a z n z a x 2 + a y 2 + a z 2 n x 2 + n y 2 + n z 2
Bu shuni anglatadiki, o'zgartirilgandan keyin to'g'ri chiziq va tekislikning yo'naltiruvchi vektori va tekislikning normal vektori koordinatalari bo'lgan tekislik orasidagi burchakni hisoblash formulasi
a = a r c sin a → , n → ^ a → n → = a r c sin a x n x + a y n y + a z n z a x 2 + a y 2 + a z 2 n x 2 + n y 2 + n z 2
Ma'lum sinus bilan kosinusni topish asosiyni qo'llash orqali joizdir trigonometrik identifikatsiya. To'g'ri chiziq va tekislikning kesishishi hosil bo'ladi o'tkir burchak. Bu shuni ko'rsatadiki, uning qiymati musbat son bo'ladi va uni hisoblash cos a = 1 - sin a formulasidan amalga oshiriladi.
Keling, materialni birlashtirish uchun bir nechta shunga o'xshash misollarni hal qilaylik.
1-misol
x 3 = y + 1 - 2 = z - 11 6 to'g'ri chiziq va 2 x + z - 1 = 0 tekislik hosil qilgan burchakning burchagi, sinusi, kosinusini toping.
Yechim
Yo'nalish vektorining koordinatalarini olish uchun fazodagi to'g'ri chiziqning kanonik tenglamalarini ko'rib chiqish kerak. Keyin a → = (3, - 2, 6) x 3 = y + 1 - 2 = z - 11 6 to'g'ri chiziqning yo'nalish vektori ekanligini olamiz.
Oddiy vektorning koordinatalarini topish uchun tekislikning umumiy tenglamasini ko'rib chiqish kerak, chunki ularning mavjudligi oldida mavjud koeffitsientlar bilan aniqlanadi. tenglamaning o‘zgaruvchilari. Keyin 2 x + z - 1 = 0 tekislik uchun normal vektor n → = (2, 0, 1) ko'rinishga ega ekanligini topamiz.
To'g'ri chiziq va tekislik orasidagi burchakning sinusini hisoblashga o'tish kerak. Buning uchun a → va b → vektorlarning koordinatalarini berilgan formulaga almashtirish kerak. Biz shaklning ifodasini olamiz
sin a = cos a → , n → ^ = a → , n → ^ a → n → = a x n x + a y n y + a z n z a x 2 + a y 2 + a z 2 n x 2 + n y 2 + n z 2 = = - 32 ) 0 + 6 1 3 2 + (- 2) 2 + 6 2 2 2 + 0 2 + 1 2 = 12 7 5
Bu yerdan biz kosinusning qiymatini va burchakning o'zi qiymatini topamiz. Biz olamiz:
cos a = 1 - sin a = 1 - 12 7 5 2 = 101 7 5
Javob: sin a = 12 7 5, cos a = 101 7 5, a = a r c cos 101 7 5 = a r c sin 12 7 5.
2-misol
A B → = 1, 0, 2, A C → = (- 1, 3, 0), A D → = 4, 1, 1 vektorlarining qiymatlari yordamida qurilgan piramida mavjud. A D to‘g‘ri chiziq bilan A B C tekislik orasidagi burchakni toping.
Yechim
Kerakli burchakni hisoblash uchun to'g'ri chiziqning yo'naltiruvchi vektori va tekislikning normal vektorining koordinatalariga ega bo'lish kerak. A D to'g'ri chiziq uchun yo'nalish vektori A D → = 4, 1, 1 koordinatalariga ega.
A B C tekisligiga tegishli n → normal vektor A B → va A C → vektoriga perpendikulyar. Bu A B C tekislikning normal vektorini ko'rib chiqish mumkinligini anglatadi vektor mahsuloti A B → va A C → vektorlari. Buni formuladan foydalanib hisoblaymiz va olamiz:
n → = A B → × A C → = i → j → k → 1 0 2 - 1 3 0 = - 6 · i → - 2 · j → + 3 · k → ⇔ n → = (- 6 , - 2 , 3 )
To'g'ri chiziq va tekislikning kesishishi natijasida hosil bo'lgan kerakli burchakni hisoblash uchun vektorlarning koordinatalarini almashtirish kerak. shaklning ifodasini olamiz:
a = a r c sin A D → , n → ^ A D → · n → = a r c sin 4 · - 6 + 1 · - 2 + 1 · 3 4 2 + 1 2 + 1 2 · - 6 2 + - 2 2 + 3 2 = a r c sin 23 21 2
Javob: a r c sin 23 21 2 .
Agar siz matnda xatolikni sezsangiz, uni belgilang va Ctrl+Enter tugmalarini bosing