Agar x y tenglamalar sistemasining yechimi. Tenglamalar tizimi. Misollar bilan batafsil nazariya (2019)

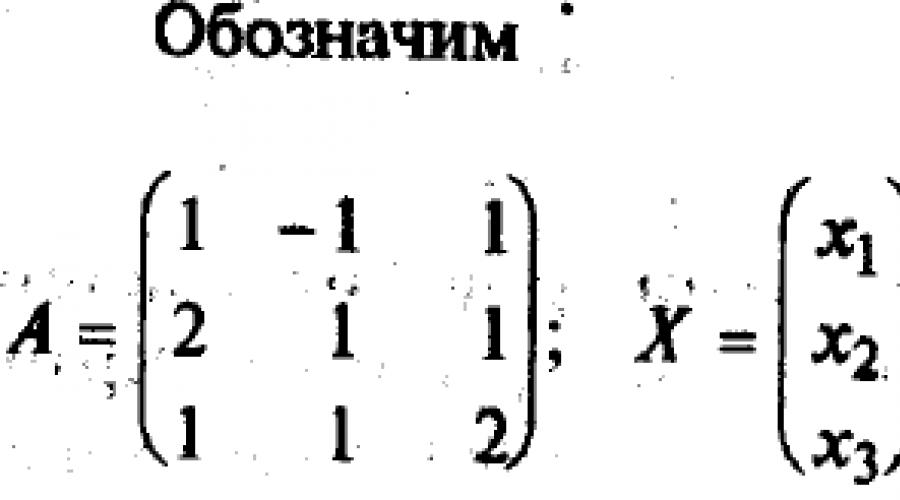
Keling, birinchi navbatda tenglamalar soni o'zgaruvchilar soniga teng bo'lgan holatni ko'rib chiqaylik, ya'ni. m = n. U holda sistemaning matritsasi kvadrat bo'lib, uning determinanti sistemaning determinanti deyiladi.

Teskari matritsa usuli

AX = B tenglamalar tizimini umumiy shaklda ko'rib chiqaylik, buzilmagan kvadrat matritsa A. Bu holda, A -1 teskari matritsa mavjud. Ikkala tomonni chap tomonda A -1 ga ko'paytiramiz. Biz A -1 AX = A -1 B ni olamiz. Demak, EX = A -1 B va

Oxirgi tenglik bunday tenglamalar sistemalarining yechimlarini topish uchun matritsa formulasidir. Ushbu formuladan foydalanish teskari matritsa usuli deb ataladi

Masalan, quyidagi tizimni hal qilish uchun ushbu usuldan foydalanamiz:

;

Tizimni yechish oxirida siz topilgan qiymatlarni tizim tenglamalariga almashtirish orqali tekshirishingiz mumkin. Bunda ular haqiqiy tengliklarga aylanishi kerak.

Ko'rib chiqilgan misol uchun biz tekshiramiz:

Kramer formulalari yordamida kvadrat matritsali chiziqli tenglamalar tizimini yechish usuli

n= 2 bo‘lsin:

Agar birinchi tenglamaning ikkala tomonini 22 ga, ikkinchisining ikkala tomonini (-a 12) ga ko‘paytirsak va natijada hosil bo‘lgan tenglamalarni qo‘shsak, u holda tizimdan x 2 o‘zgaruvchini chiqarib tashlagan bo‘lamiz. Xuddi shunday, siz x 1 o'zgaruvchisini yo'q qilishingiz mumkin (birinchi tenglamaning ikkala tomonini (-a 21) va ikkinchisining ikkala tomonini 11 ga ko'paytirish orqali). Natijada biz tizimni olamiz:

Qavs ichidagi ifoda tizimning determinantidir

belgilaylik

Keyin tizim quyidagi shaklni oladi:

Olingan sistemadan kelib chiqadiki, agar sistemaning determinanti 0 bo'lsa, sistema izchil va aniq bo'ladi. Uning yagona yechimini formulalar yordamida hisoblash mumkin:

Agar = 0, a 1 0 va/yoki  2 0 bo‘lsa, tizim tenglamalari 0*x 1 = 2 va/yoki 0*x 1 = 2 ko‘rinishini oladi. Bunday holda, tizim mos kelmaydigan bo'ladi.

= 1 = 2 = 0 bo'lganda, tizim izchil va noaniq bo'ladi (cheksiz ko'p echimlarga ega bo'ladi), chunki u quyidagi shaklni oladi:

Kramer teoremasi(Biz dalilni o'tkazib yuboramiz). Agar  tenglamalar sistemasi matritsasining determinanti nolga teng bo'lmasa, u holda sistema formulalar bilan aniqlangan yagona yechimga ega bo'ladi:

,

Bu yerda  j - A matritsadan j-ustunni erkin hadlar ustuni bilan almashtirish orqali olingan matritsaning aniqlovchisi.

Yuqoridagi formulalar deyiladi Kramer formulalari.

Misol tariqasida, teskari matritsa usuli yordamida ilgari echilgan tizimni echish uchun ushbu usuldan foydalanamiz:

Ko'rib chiqilgan usullarning kamchiliklari:

1) muhim mehnat zichligi (determinantlarni hisoblash va teskari matritsani topish);

2) cheklangan qamrov (kvadrat matritsali tizimlar uchun).

Haqiqiy iqtisodiy vaziyatlar ko'pincha tenglamalar va o'zgaruvchilar soni sezilarli bo'lgan va o'zgaruvchilardan ko'ra ko'proq tenglamalar mavjud bo'lgan tizimlar tomonidan modellashtiriladi.

Gauss usuli (o'zgaruvchilarni ketma-ket yo'q qilish usuli)

Bu usul m sistemani yechish uchun ishlatiladi chiziqli tenglamalar n o'zgaruvchisi bilan umumiy ko'rinish. Uning mohiyati kengaytirilgan matritsaga ekvivalent o'zgartirishlar tizimini qo'llashdan iborat bo'lib, uning yordamida tenglamalar tizimi uning echimlarini topish oson bo'lgan shaklga aylantiriladi (agar mavjud bo'lsa).

Bu tizim matritsasining yuqori chap qismi bosqichli matritsa bo'ladigan ko'rinishdir. Bunga darajani aniqlash uchun qadam matritsasini olishda qo'llanilgan bir xil usullar yordamida erishiladi. Bunday holda, kengaytirilgan matritsaga elementar o'zgarishlar qo'llaniladi, bu esa ekvivalent tenglamalar tizimini olish imkonini beradi. Shundan so'ng kengaytirilgan matritsa quyidagi shaklni oladi:

Bunday matritsani olish deyiladi to'g'ri Gauss usuli.

Tegishli tenglamalar tizimidan o'zgaruvchilarning qiymatlarini topish deyiladi teskari Gauss usuli. Keling, ko'rib chiqaylik.

E'tibor bering, oxirgi (m - r) tenglamalar quyidagi shaklda bo'ladi:

Agar raqamlardan kamida bittasi bo'lsa
nolga teng bo'lmasa, mos keladigan tenglik noto'g'ri bo'ladi va butun tizim mos kelmaydi.

Shuning uchun, har qanday qo'shma tizim uchun
. Bunday holda, o'zgaruvchilarning har qanday qiymatlari uchun oxirgi (m - r) tenglamalar 0 = 0 identifikatsiyalari bo'ladi va tizimni echishda ularni e'tiborsiz qoldirish mumkin (shunchaki mos keladigan qatorlarni olib tashlang).

Shundan so'ng, tizim quyidagicha ko'rinadi:

Avval r=n bo'lgan holatni ko'rib chiqamiz. Keyin tizim quyidagi shaklni oladi:

Tizimning oxirgi tenglamasidan x r ni yagona tarzda topish mumkin.

X r ni bilgan holda, biz undan x r -1 ni aniq ifodalashimiz mumkin. Keyin oldingi tenglamadan x r va x r -1 ni bilib, biz x r -2 va hokazolarni ifodalashimiz mumkin. x 1 gacha.

Shunday qilib, bu holda tizim birgalikda va aniqlangan bo'ladi.

Endi r bo'lgan holatni ko'rib chiqing Asosiy(asosiy) va qolganlari - asosiy bo'lmagan(asosiy bo'lmagan, bepul). Tizimning oxirgi tenglamasi quyidagicha bo'ladi:

Ushbu tenglamadan biz x r asosiy o'zgaruvchini asosiy bo'lmaganlar bilan ifodalashimiz mumkin:

Oxirgidan oldingi tenglama quyidagicha ko'rinadi:

Olingan ifodani unga x r o‘rniga qo‘yish orqali x r -1 asosiy o‘zgaruvchini asosiy bo‘lmaganlar bilan ifodalash mumkin bo‘ladi. Va hokazo. variablex 1 ga. Tizim yechimini olish uchun siz asosiy bo'lmagan o'zgaruvchilarni ixtiyoriy qiymatlarga tenglashtirishingiz va keyin olingan formulalar yordamida asosiy o'zgaruvchilarni hisoblashingiz mumkin. Shunday qilib, bu holda tizim izchil va noaniq bo'ladi (cheksiz miqdordagi echimlarga ega).

Masalan, tenglamalar tizimini yechamiz:

Biz asosiy o'zgaruvchilar to'plamini chaqiramiz asos tizimlari. Ular uchun koeffitsientlar ustunlari to'plamini ham chaqiramiz asos(asosiy ustunlar) yoki asosiy kichik tizim matritsalari. Barcha asosiy bo'lmagan o'zgaruvchilar nolga teng bo'lgan tizimning yechimi chaqiriladi asosiy yechim.

Oldingi misolda asosiy yechim (4/5; -17/5; 0; 0) bo'ladi (x 3 va x 4 o'zgaruvchilari (c 1 va c 2) nolga o'rnatiladi va asosiy o'zgaruvchilar x 1). va x 2 ular orqali hisoblanadi) . Asosiy bo'lmagan yechimga misol keltirish uchun x 3 va x 4 (c 1 va c 2) ni bir vaqtning o'zida nolga teng bo'lmagan ixtiyoriy sonlarga tenglashtirishimiz va ular orqali qolgan o'zgaruvchilarni hisoblashimiz kerak. Masalan, 1 = 1 va 2 = 0 bilan biz asosiy bo'lmagan yechimni olamiz - (4/5; -12/5; 1; 0). O'zgartirish orqali ikkala yechimning ham to'g'riligini tekshirish oson.

Ko'rinib turibdiki, noaniq sistemada cheksiz ko'p asosiy bo'lmagan echimlar bo'lishi mumkin. Qancha asosiy echimlar bo'lishi mumkin? O'zgartirilgan matritsaning har bir qatori bitta bazis o'zgaruvchiga mos kelishi kerak. Muammoda n ta o'zgaruvchi va r ta asosiy chiziq mavjud. Shuning uchun asosiy o'zgaruvchilarning barcha mumkin bo'lgan to'plamlari soni n ning kombinatsiyalari sonidan 2 ga oshmasligi kerak. dan kam bo'lishi mumkin , chunki tizimni o'zgaruvchilarning ushbu alohida to'plami asos bo'ladigan shaklga aylantirish har doim ham mumkin emas.

Bu qanaqa? Bu o'zgaruvchilar uchun koeffitsientlar ustunlaridan hosil bo'lgan matritsa bosqichma-bosqich va bir vaqtning o'zida r qatordan iborat bo'lgan tur. Bular. bu o'zgaruvchilar uchun koeffitsient matritsasi darajasi r ga teng bo'lishi kerak. U kattaroq bo'lishi mumkin emas, chunki ustunlar soni teng. Agar u r dan kichik bo'lib chiqsa, bu ustunlarning o'zgaruvchilarga chiziqli bog'liqligini ko'rsatadi. Bunday ustunlar asos bo'la olmaydi.

Keling, yuqorida muhokama qilingan misolda yana qanday asosiy echimlarni topish mumkinligini ko'rib chiqaylik. Buni amalga oshirish uchun har birida ikkita asosiy bo'lgan to'rtta o'zgaruvchining barcha mumkin bo'lgan kombinatsiyalarini ko'rib chiqing. Bunday kombinatsiyalar bo'ladi
, va ulardan biri (x 1 va x 2) allaqachon ko'rib chiqilgan.

Keling, x 1 va x 3 o'zgaruvchilarni olaylik. Ular uchun koeffitsientlar matritsasining darajasini topamiz:

Ikkiga teng bo'lgani uchun ular asosiy bo'lishi mumkin. Asosiy bo'lmagan x 2 va x 4 o'zgaruvchilarni nolga tenglashtiramiz: x 2 = x 4 = 0. Keyin x 1 = 4/5 – (1/5)*x 4 formulasidan x 1 = 4 kelib chiqadi. /5 va x 2 = -17/5 + x 3 - - (7/5)*x 4 = -17/5 + x 3 formulasidan x 3 = x 2 +17/5 = 17/ bo'ladi. 5. Shunday qilib, biz asosiy yechimni olamiz (4/5; 0; 17/5; 0).

Xuddi shunday, siz x 1 va x 4 - (9/7; 0; 0; -17/7) asosiy o'zgaruvchilar uchun asosiy echimlarni olishingiz mumkin; x 2 va x 4 – (0; -9; 0; 4); x 3 va x 4 – (0; 0; 9; 4).

Ushbu misoldagi x 2 va x 3 o'zgaruvchilarni asosiy sifatida qabul qilib bo'lmaydi, chunki mos keladigan matritsaning darajasi bittaga teng, ya'ni. ikkitadan kam:

.

Muayyan o'zgaruvchilardan asos yaratish mumkinmi yoki yo'qligini aniqlashning boshqa yondashuvi ham mumkin. Misolni yechishda tizim matritsasini bosqichma-bosqich shaklga o'tkazish natijasida u quyidagi shaklni oldi:

O'zgaruvchilar juftligini tanlab, ushbu matritsaning mos keladigan kichiklarini hisoblash mumkin edi. X 2 va x 3 dan tashqari barcha juftliklar uchun ular nolga teng emasligini tekshirish oson, ya'ni. ustunlar chiziqli mustaqildir. Va faqat x 2 va x 3 o'zgaruvchilari bo'lgan ustunlar uchun
, bu ularning chiziqli bog'liqligini ko'rsatadi.

Keling, yana bir misolni ko'rib chiqaylik. Keling, tenglamalar tizimini yechamiz

Shunday qilib, oxirgi matritsaning uchinchi qatoriga mos keladigan tenglama qarama-qarshidir - bu noto'g'ri tenglikka olib keldi 0 = -1, shuning uchun bu tizim mos kelmaydi.

Jordan-Gauss usuli 3 Gauss usulining ishlanmasidir. Uning mohiyati shundan iboratki, tizimning kengaytirilgan matritsasi o'zgaruvchilar koeffitsientlari satrlar yoki ustunlar 4 almashtirilishigacha (bu erda r - tizim matritsasi darajasi) bir xillik matritsasini tashkil etadigan shaklga aylanadi.

Keling, ushbu usul yordamida tizimni hal qilaylik:

Tizimning kengaytirilgan matritsasini ko'rib chiqamiz:

Ushbu matritsada biz birlik elementini tanlaymiz. Masalan, uchinchi cheklovdagi x 2 uchun koeffitsient 5 ga teng. Keling, ushbu ustundagi qolgan qatorlar noldan iborat bo'lishini ta'minlaylik, ya'ni. Keling, ustunni bitta qilaylik. Transformatsiya jarayonida biz buni chaqiramiz ustunruxsat beruvchi(etakchi, kalit). Uchinchi cheklov (uchinchi chiziq) biz ham qo'ng'iroq qilamiz ruxsat beruvchi. O'zim element, hal qiluvchi satr va ustunning kesishmasida joylashgan (bu erda bitta) ham deyiladi ruxsat beruvchi.

Birinchi qatorda endi (-1) koeffitsient mavjud. Uning o'rnida nolni olish uchun uchinchi qatorni (-1) ga ko'paytiring va natijani birinchi qatordan olib tashlang (ya'ni, birinchi qatorni uchinchi qatorga qo'shing).

Ikkinchi qator koeffitsientni o'z ichiga oladi 2. Uning o'rnida nolni olish uchun uchinchi qatorni 2 ga ko'paytiring va natijani birinchi qatordan olib tashlang.

Transformatsiyaning natijasi quyidagicha bo'ladi:

Ushbu matritsadan birinchi ikkita cheklovdan birini kesib tashlash mumkinligi aniq ko'rinadi (tegishli qatorlar proportsionaldir, ya'ni bu tenglamalar bir-biridan kelib chiqadi). Masalan, ikkinchisini kesib o'tamiz:

Shunday qilib, yangi tizim ikkita tenglamaga ega. Bitta ustun (ikkinchi) olinadi va bu erda birlik ikkinchi qatorda paydo bo'ladi. Yangi tizimning ikkinchi tenglamasi x 2 asosiy o'zgaruvchiga mos kelishini eslaylik.

Birinchi qator uchun asosiy o'zgaruvchini tanlaylik. Bu x 3 dan boshqa har qanday o'zgaruvchi bo'lishi mumkin (chunki x 3 uchun birinchi cheklov nol koeffitsientga ega, ya'ni x 2 va x 3 o'zgaruvchilar to'plami bu erda asosiy bo'lishi mumkin emas). Siz birinchi yoki to'rtinchi o'zgaruvchini olishingiz mumkin.

Keling, x 1 ni tanlaymiz. Keyin hal qiluvchi element 5 bo'ladi va birinchi qatorning birinchi ustunida bittasini olish uchun hal qiluvchi tenglamaning ikkala tomonini beshga bo'lish kerak bo'ladi.

Qolgan qatorlar (ya'ni, ikkinchi qator) birinchi ustunda nolga ega bo'lishini ta'minlaylik. Endi ikkinchi qator nol emas, balki 3 ni o'z ichiga olganligi sababli, biz ikkinchi qatordan o'zgartirilgan birinchi qatorning elementlarini 3 ga ko'paytirishimiz kerak:

Hosil boʻlgan matritsadan toʻgʻridan-toʻgʻri asosiy boʻlmagan oʻzgaruvchilarni nolga, asosiylarini esa boʻsh shartlarga mos tenglamalarda tenglashtirib, bitta asosiy yechimni olish mumkin: (0,8; -3,4; 0; 0). Bundan tashqari, asosiy o'zgaruvchilarni asosiy bo'lmaganlar orqali ifodalovchi umumiy formulalarni olishingiz mumkin: x 1 = 0,8 – 1,2 x 4; x 2 = -3,4 + x 3 + 1,6x 4. Ushbu formulalar tizimning butun cheksiz echimlarini tavsiflaydi (x 3 va x 4 ni ixtiyoriy sonlarga tenglashtirsangiz, siz x 1 va x 2 ni hisoblashingiz mumkin).

E'tibor bering, Jordan-Gauss usulining har bir bosqichida o'zgarishlarning mohiyati quyidagicha edi:

1) o'z o'rnida birlikni olish uchun ruxsat chizig'i rezolyutsiya elementiga bo'lingan;

2) boshqa barcha qatorlardan o'zgartirilgan o'lcham ayirildi, bu element o'rniga nolni olish uchun ruxsat ustunidagi berilgan qatordagi elementga ko'paytirildi.

Keling, tizimning o'zgartirilgan kengaytirilgan matritsasini yana ko'rib chiqaylik:

Bu yozuvdan ko'rinib turibdiki, A sistema matritsasining darajasi r ga teng.

Mulohaza yuritishimiz davomida biz tizim faqat va agar shunday bo'lsa, kooperativ bo'lishini aniqladik
. Bu shuni anglatadiki, tizimning kengaytirilgan matritsasi quyidagicha ko'rinadi:

Nolinchi qatorlarni tashlab, tizimning kengaytirilgan matritsasining darajasi ham r ga teng ekanligini bilib olamiz.

Kroneker-Kapelli teoremasi. Chiziqli tenglamalar tizimi, agar tizim matritsasining darajasi ushbu tizimning kengaytirilgan matritsasining darajasiga teng bo'lsa, izchil bo'ladi.

Eslatib o'tamiz, matritsaning darajasi uning chiziqli mustaqil qatorlarining maksimal soniga teng. Bundan kelib chiqadiki, agar kengaytirilgan matritsaning darajasi tenglamalar sonidan kichik bo'lsa, u holda tizim tenglamalari chiziqli bog'liq bo'lib, ulardan bir yoki bir nechtasini tizimdan chiqarib tashlash mumkin (chunki ular chiziqli boshqalarning kombinatsiyasi). Agar kengaytirilgan matritsaning darajasi tenglamalar soniga teng bo'lsa, tenglamalar tizimi chiziqli mustaqil bo'ladi.

Bundan tashqari, bir vaqtning o'zida chiziqli tenglamalar tizimlari uchun, agar matritsaning darajasi o'zgaruvchilar soniga teng bo'lsa, u holda tizim o'ziga xos echimga ega bo'ladi va agar u o'zgaruvchilar sonidan kam bo'lsa, u holda bahslashish mumkin. tizim cheksiz va cheksiz ko'p echimlarga ega.

1Masalan, matritsada beshta qator bo'lsin (asl qatorlar tartibi 12345). Biz ikkinchi qatorni va beshinchi qatorni o'zgartirishimiz kerak. Ikkinchi qator beshinchi o'rinni egallashi va "pastga siljishi" uchun biz qo'shni qatorlarni ketma-ket uch marta o'zgartiramiz: ikkinchi va uchinchi (13245), ikkinchi va to'rtinchi (13425) va ikkinchi va beshinchi (13452) ). Keyin, beshinchi qator asl matritsada ikkinchi o'rinni egallashi uchun beshinchi qatorni faqat ikkita ketma-ket o'zgartirish bilan yuqoriga "siljitish" kerak: beshinchi va to'rtinchi qatorlar (13542) va beshinchi va uchinchi qatorlar. (15342).

2n dan r gacha bo'lgan kombinatsiyalar soni ular n-elementlar to'plamining barcha turli xil r-elementlar kichik to'plamlari sonini chaqiradilar (elementlarning turli xil tarkibiga ega bo'lganlar turli to'plamlar deb hisoblanadi; tanlash tartibi muhim emas). U quyidagi formula bo'yicha hisoblanadi:
. Keling, "!" belgisining ma'nosini eslaylik. (faktorial):
0!=1.)

3 Bu usul avval muhokama qilingan Gauss usuliga qaraganda keng tarqalganligi va mohiyatan Gauss usulining oldinga va orqaga qadamlarini birlashtirgani uchun uni ba'zan ismning birinchi qismini tashlab, Gauss usuli deb ham atashadi.

4Masalan,
.

5Agar tizim matritsasida birliklar bo'lmaganda, masalan, birinchi tenglamaning ikkala tomonini ikkiga bo'lish mumkin bo'lar edi, keyin birinchi koeffitsient birlikka aylanadi; yoki shunga o'xshash

Ikkita noma’lum chiziqli tenglamalar tizimi ikki yoki undan ortiq chiziqli tenglamalar bo‘lib, ular uchun barcha umumiy yechimlarni topish zarur. Ikkita noma’lumda ikkita chiziqli tenglamalar tizimini ko‘rib chiqamiz. Ikki noma'lumli ikkita chiziqli tenglamalar tizimining umumiy ko'rinishi quyidagi rasmda keltirilgan:

(a1*x + b1*y = c1,
(a2*x + b2*y = c2

Bu erda x va y noma'lum o'zgaruvchilar, a1, a2, b1, b2, c1, c2 - ba'zi haqiqiy sonlar. Ikki noma’lumli ikkita chiziqli tenglamalar sistemasi yechimi (x,y) sonlar juftligi bo‘lib, agar bu raqamlarni sistema tenglamalariga almashtirsak, sistemaning har bir tenglamasi haqiqiy tenglikka aylanadi. Chiziqli tenglamalar sistemasini yechishning bir necha usullari mavjud. Chiziqli tenglamalar tizimini yechish usullaridan birini, ya'ni qo'shish usulini ko'rib chiqamiz.

Qo'shish usuli bilan yechish algoritmi

Ikki noma’lum chiziqli tenglamalar tizimini qo‘shish usuli yordamida yechish algoritmi.

1. Agar kerak bo'lsa, ekvivalent o'zgartirishlar yordamida ikkala tenglamadagi noma'lum o'zgaruvchilardan birining koeffitsientlarini tenglashtiring.

2. Olingan tenglamalarni qo‘shish yoki ayirish yo‘li bilan bitta noma’lum chiziqli tenglama hosil bo‘ladi

3. Bitta noma’lumli hosil bo‘lgan tenglamani yeching va o‘zgaruvchilardan birini toping.

4. Olingan ifodani sistemaning ikkita tenglamasidan istalganiga almashtiring va shu tenglamani yeching, shu bilan ikkinchi o‘zgaruvchini oling.

5. Yechimni tekshiring.

Qo'shish usuli yordamida yechimga misol

Aniqroq bo'lish uchun ikkita noma'lum chiziqli tenglamalar tizimini qo'shish usuli yordamida hal qilaylik:

(3*x + 2*y = 10;
(5*x + 3*y = 12;

O'zgaruvchilarning hech biri bir xil koeffitsientlarga ega emasligi sababli, biz y o'zgaruvchining koeffitsientlarini tenglashtiramiz. Buning uchun birinchi tenglamani uchga, ikkinchi tenglamani ikkiga ko'paytiring.

(3*x+2*y=10 |*3
(5*x + 3*y = 12 |*2

olamiz quyidagi tenglamalar tizimi:

(9*x+6*y = 30;
(10*x+6*y=24;

Endi ikkinchi tenglamadan birinchisini ayiramiz. Biz shunga o'xshash atamalarni keltiramiz va natijada chiziqli tenglamani yechamiz.

10*x+6*y - (9*x+6*y) = 24-30; x=-6;

Olingan qiymatni dastlabki tizimimizdagi birinchi tenglamaga almashtiramiz va hosil bo'lgan tenglamani yechamiz.

(3*(-6) + 2*y =10;
(2*y=28; y =14;

Natijada x=6 va y=14 sonlar juftligi hosil bo‘ladi. Biz tekshiryapmiz. Keling, almashtirishni amalga oshiramiz.

(3*x + 2*y = 10;
(5*x + 3*y = 12;

{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;

{10 = 10;
{12=12;

Ko'rib turganingizdek, biz ikkita to'g'ri tenglikni oldik, shuning uchun biz to'g'ri echimni topdik.

Iqtisodiyot sohasida turli jarayonlarni matematik modellashtirish uchun tenglamalar tizimlari keng qo'llaniladi. Masalan, ishlab chiqarishni boshqarish va rejalashtirish, logistika yo'nalishlari (transport muammosi) yoki jihozlarni joylashtirish muammolarini hal qilishda.

Tenglamalar sistemasi nafaqat matematikada, balki fizika, kimyo va biologiyada ham aholi sonini topish masalalarini yechishda qo'llaniladi.

Chiziqli tenglamalar tizimi bir nechta o'zgaruvchiga ega bo'lgan ikki yoki undan ortiq tenglamalar bo'lib, ular uchun umumiy yechim topish kerak. Bunday raqamlar ketma-ketligi, ular uchun barcha tenglamalar haqiqiy tenglikka aylanadi yoki ketma-ketlik mavjud emasligini isbotlaydi.

Chiziqli tenglama

ax+by=c ko’rinishdagi tenglamalar chiziqli deyiladi. X, y belgilari - qiymati topilishi kerak bo'lgan noma'lumlar, b, a - o'zgaruvchilarning koeffitsientlari, c - tenglamaning erkin hadi.
Tenglamani chizib yechish to‘g‘ri chiziqqa o‘xshaydi, uning barcha nuqtalari ko‘phadning yechimlaridir.

Chiziqli tenglamalar sistemalarining turlari

Eng oddiy misollar ikkita o'zgaruvchisi X va Y bo'lgan chiziqli tenglamalar tizimi hisoblanadi.

F1(x, y) = 0 va F2(x, y) = 0, bu erda F1,2 funksiyalar va (x, y) funksiya o'zgaruvchilari.

Tenglamalar tizimini yechish - bu tizim haqiqiy tenglikka aylanadigan qiymatlarni (x, y) topish yoki x va y ning mos qiymatlari mavjud emasligini aniqlashni anglatadi.

Nuqtaning koordinatalari sifatida yozilgan juft qiymatlar (x, y) chiziqli tenglamalar tizimining yechimi deb ataladi.

Agar tizimlar bitta umumiy yechimga ega bo'lsa yoki hech qanday yechim mavjud bo'lmasa, ular ekvivalent deb ataladi.

Chiziqli tenglamalarning bir jinsli sistemalari - o'ng tomoni nolga teng bo'lgan tizimlar. Agar tenglik belgisidan keyingi o'ng qism qiymatga ega bo'lsa yoki funktsiya bilan ifodalangan bo'lsa, bunday tizim geterogendir.

O'zgaruvchilar soni ikkitadan ancha ko'p bo'lishi mumkin, keyin biz uchta yoki undan ko'p o'zgaruvchiga ega chiziqli tenglamalar tizimining misoli haqida gapirishimiz kerak.

Tizimlar bilan duch kelganda, maktab o'quvchilari tenglamalar soni noma'lumlar soniga to'g'ri kelishi kerak deb o'ylashadi, ammo bu unday emas. Tizimdagi tenglamalar soni o'zgaruvchilarga bog'liq emas, ular xohlagancha ko'p bo'lishi mumkin;

Tenglamalar sistemalarini yechishning oddiy va murakkab usullari

Bunday tizimlarni yechishning umumiy analitik usuli mavjud emas, barcha usullar sonli yechimlarga asoslangan; Maktab matematikasi kursida almashtirish, algebraik qo'shish, almashtirish, shuningdek, grafik va matritsa usullari, Gauss usuli bilan yechish kabi usullar batafsil yoritilgan.

Yechish usullarini o'rgatishda asosiy vazifa tizimni to'g'ri tahlil qilishni va har bir misol uchun optimal yechim algoritmini topishni o'rgatishdir. Asosiysi, har bir usul uchun qoidalar va harakatlar tizimini yodlash emas, balki ma'lum bir usuldan foydalanish tamoyillarini tushunishdir.

7-sinf umumta’lim dasturida chiziqli tenglamalar sistemasiga misollar yechish juda oddiy va juda batafsil tushuntirilgan. Har qanday matematika darsligida ushbu bo'limga etarlicha e'tibor beriladi. Chiziqli tenglamalar sistemalariga misollarni Gauss va Kramer usuli yordamida yechish oliy ta’limning birinchi yillarida batafsil o‘rganiladi.

Tizimlarni almashtirish usuli yordamida yechish

O'zgartirish usulining harakatlari bir o'zgaruvchining qiymatini ikkinchisi bilan ifodalashga qaratilgan. Ifoda qolgan tenglamaga almashtiriladi, so'ngra u bitta o'zgaruvchili shaklga keltiriladi. Harakat tizimdagi noma'lumlar soniga qarab takrorlanadi

7-sinf chiziqli tenglamalar tizimi misoliga almashtirish usuli yordamida yechim keltiramiz:

Misoldan ko'rinib turibdiki, x o'zgaruvchisi F(X) = 7 + Y orqali ifodalangan. Natijada X o'rniga tizimning 2- tenglamasiga almashtirilgan ifoda 2-tenglamada bitta Y o'zgaruvchisini olishga yordam berdi. . Ushbu misolni yechish oson va Y qiymatini olish imkonini beradi Oxirgi qadam olingan qiymatlarni tekshirishdir.

Chiziqli tenglamalar sistemasiga misolni almashtirish usuli bilan yechish har doim ham mumkin emas. Tenglamalar murakkab bo'lishi mumkin va o'zgaruvchini ikkinchi noma'lum ko'rinishida ifodalash keyingi hisob-kitoblar uchun juda og'ir bo'ladi. Tizimda 3 dan ortiq noma'lum bo'lsa, almashtirish yo'li bilan yechish ham amaliy bo'lmaydi.

Chiziqli bir hil bo'lmagan tenglamalar sistemasiga misol yechimi:

Algebraik qo‘shish yordamida yechim

Qo'shish usulidan foydalangan holda tizimlar yechimlarini izlashda tenglamalar atama bo'yicha qo'shiladi va turli raqamlarga ko'paytiriladi. Matematik operatsiyalarning yakuniy maqsadi bitta o'zgaruvchidagi tenglamadir.

Ushbu usulni qo'llash amaliyot va kuzatishni talab qiladi. Chiziqli tenglamalar tizimini 3 yoki undan ortiq oʻzgaruvchi boʻlganda qoʻshish usuli yordamida yechish oson emas. Tenglamalar kasr va o'nli kasrlarni o'z ichiga olgan bo'lsa, algebraik qo'shish qulay.

Yechim algoritmi:

1. Tenglamaning ikkala tomonini ma'lum songa ko'paytiring. Arifmetik operatsiya natijasida o'zgaruvchining koeffitsientlaridan biri 1 ga teng bo'lishi kerak.
2. Hosil boʻlgan iborani termin boʻyicha qoʻshing va nomaʼlumlardan birini toping.
3. Qolgan o'zgaruvchini topish uchun olingan qiymatni tizimning 2-tenglamasiga almashtiring.

Yangi o'zgaruvchini kiritish orqali hal qilish usuli

Agar tizim ikkitadan ko'p bo'lmagan tenglamalar uchun echim topishni talab qilsa, yangi o'zgaruvchi kiritilishi mumkin, shuningdek, noma'lumlar soni ikkitadan oshmasligi kerak;

Usul yangi o'zgaruvchini kiritish orqali tenglamalardan birini soddalashtirish uchun ishlatiladi. Yangi tenglama kiritilgan noma'lum uchun yechiladi va olingan qiymatdan asl o'zgaruvchini aniqlash uchun foydalaniladi.

Misol shuni ko'rsatadiki, yangi t o'zgaruvchisini kiritish orqali tizimning 1-tenglamasini standart kvadrat uch a'zoga qisqartirish mumkin edi. Ko'phadni diskriminantni topib yechishingiz mumkin.

Diskriminantning qiymatini taniqli formuladan foydalanib topish kerak: D = b2 - 4*a*c, bu erda D - kerakli diskriminant, b, a, c - ko'phadning omillari. Berilgan misolda a=1, b=16, c=39, demak D=100. Agar diskriminant noldan katta bo'lsa, u holda ikkita yechim mavjud: t = -b±√D / 2*a, agar diskriminant noldan kichik bo'lsa, unda bitta yechim mavjud: x = -b / 2*a.

Olingan tizimlar uchun yechim qo'shish usuli bilan topiladi.

Tizimlarni echishning vizual usuli

3 ta tenglama tizimi uchun javob beradi. Usul koordinata o'qi bo'yicha tizimga kiritilgan har bir tenglamaning grafiklarini qurishdan iborat. Egri chiziqlarning kesishish nuqtalarining koordinatalari tizimning umumiy yechimi bo'ladi.

Grafik usul bir qator nuanslarga ega. Chiziqli tenglamalar sistemalarini vizual tarzda yechishning bir qancha misollarini ko‘rib chiqamiz.

Misoldan ko'rinib turibdiki, har bir chiziq uchun ikkita nuqta qurilgan, x o'zgaruvchisining qiymatlari o'zboshimchalik bilan tanlangan: 0 va 3. X qiymatlari asosida y uchun qiymatlar topildi: 3 va 0. Koordinatalari (0, 3) va (3, 0) bo'lgan nuqtalar grafikda belgilangan va chiziq bilan bog'langan.

Ikkinchi tenglama uchun qadamlar takrorlanishi kerak. Chiziqlarning kesishish nuqtasi tizimning yechimidir.

Quyidagi misol chiziqli tenglamalar sistemasining grafik yechimini topishni talab qiladi: 0,5x-y+2=0 va 0,5x-y-1=0.

Misoldan ko'rinib turibdiki, tizim hech qanday yechimga ega emas, chunki grafiklar parallel va butun uzunligi bo'ylab kesishmaydi.

2 va 3-misollardagi tizimlar bir-biriga o'xshash, ammo tuzilganida ularning echimlari boshqacha ekanligi ayon bo'ladi. Shuni esda tutish kerakki, tizimning yechimi bor yoki yo'qligini aytish har doim ham mumkin emas;

Matritsa va uning turlari

Matritsalar chiziqli tenglamalar tizimini ixcham yozish uchun ishlatiladi. Matritsa - bu raqamlar bilan to'ldirilgan maxsus jadval turi. n*m n - satr va m - ustunga ega.

Ustunlar va satrlar soni teng bo'lganda matritsa kvadrat hisoblanadi. Matritsa-vektor - cheksiz mumkin bo'lgan qatorlar soniga ega bo'lgan bitta ustunli matritsa. Diagonallardan biri va boshqa nol elementlari bo'ylab birlari bo'lgan matritsa identifikatsiya deb ataladi.

Teskari matritsa bu matritsa bo'lib, unga ko'paytirilganda asl matritsa birlik matritsaga aylanadi;

Tenglamalar tizimini matritsaga aylantirish qoidalari

Tenglamalar sistemasiga nisbatan tenglamalarning koeffitsientlari va erkin shartlari matritsa sonlari sifatida yoziladi, bitta tenglama matritsaning bir qatoridir;

Agar satrning kamida bitta elementi nolga teng bo'lmasa, matritsa qatori nolga teng emas deyiladi. Shuning uchun, agar tenglamalarning birortasida o'zgaruvchilar soni farq qiladigan bo'lsa, unda etishmayotgan noma'lum o'rniga nol kiritish kerak.

Matritsa ustunlari o'zgaruvchilarga qat'iy mos kelishi kerak. Bu shuni anglatadiki, x o'zgaruvchining koeffitsientlari faqat bitta ustunda yozilishi mumkin, masalan, birinchi, noma'lum y koeffitsienti - faqat ikkinchisida.

Matritsani ko'paytirishda matritsaning barcha elementlari ketma-ket songa ko'paytiriladi.

Teskari matritsani topish variantlari

Teskari matritsani topish formulasi juda oddiy: K -1 = 1 / |K|, bu erda K -1 teskari matritsa va |K| matritsaning determinanti hisoblanadi. |K| nolga teng bo'lmasligi kerak, u holda tizim yechimga ega.

Determinant ikki-ikki matritsa uchun osongina hisoblab chiqiladi, siz faqat diagonal elementlarni bir-biriga ko'paytirishingiz kerak. “Uchdan uch” varianti uchun |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 formulasi mavjud. + a 3 b 2 c 1. Siz formuladan foydalanishingiz mumkin yoki ishda ustunlar va elementlar qatorlari soni takrorlanmasligi uchun har bir satr va har bir ustundan bitta elementni olishingiz kerakligini eslashingiz mumkin.

Matritsa usuli yordamida chiziqli tenglamalar sistemasiga misollar yechish

Yechimni topishning matritsa usuli ko'p sonli o'zgaruvchilar va tenglamalarga ega tizimlarni echishda noqulay yozuvlarni kamaytirishga imkon beradi.

Misolda, a nm - tenglamalarning koeffitsientlari, matritsa - vektor x n - o'zgaruvchilar, b n - erkin shartlar.

Tizimlarni Gauss usuli yordamida yechish

Oliy matematikada Gauss usuli Kramer usuli bilan birgalikda oʻrganiladi va tizimlar yechimlarini topish jarayoni Gauss-Kramer yechim usuli deb ataladi. Bu usullar ko'p sonli chiziqli tenglamalarga ega bo'lgan tizimlarning o'zgaruvchilarini topish uchun ishlatiladi.

Gauss usuli almashtirish va algebraik qoʻshish yoʻli bilan yechimlarga juda oʻxshaydi, lekin tizimliroqdir. Maktab kursida 3 va 4 tenglamalar sistemalari uchun Gauss usuli bilan yechim qo'llaniladi. Usulning maqsadi tizimni teskari trapezoid shakliga tushirishdir. Algebraik o'zgartirishlar va almashtirishlar yordamida bitta o'zgaruvchining qiymati tizim tenglamalaridan birida topiladi. Ikkinchi tenglama 2 ta noma'lumli ifoda, 3 va 4 esa mos ravishda 3 va 4 o'zgaruvchiga ega.

Tizimni tavsiflangan shaklga keltirgandan so'ng, keyingi yechim ma'lum o'zgaruvchilarni tizim tenglamalariga ketma-ket almashtirishga tushiriladi.

7-sinf uchun maktab darsliklarida Gauss usuli bo'yicha yechimning namunasi quyidagicha tasvirlangan:

Misoldan ko'rinib turibdiki, (3) bosqichda ikkita tenglama olingan: 3x 3 -2x 4 =11 va 3x 3 +2x 4 =7. Har qanday tenglamani echish sizga x n o'zgaruvchilardan birini topishga imkon beradi.

Matnda tilga olingan 5-teoremada aytilishicha, agar tizim tenglamalaridan biri ekvivalent bilan almashtirilsa, natijada hosil bo'lgan tizim ham asl tenglamaga teng bo'ladi.

O'rta maktab o'quvchilari uchun Gauss usulini tushunish qiyin, ammo bu matematika va fizika darslarida ilg'or o'quv dasturlariga kirgan bolalarning zukkoligini rivojlantirishning eng qiziqarli usullaridan biridir.

Yozib olish qulayligi uchun hisob-kitoblar odatda quyidagicha amalga oshiriladi:

Tenglamalar va erkin atamalar koeffitsientlari matritsa shaklida yoziladi, bu erda matritsaning har bir qatori tizim tenglamalaridan biriga mos keladi. tenglamaning chap tomonini o'ngdan ajratadi. Rim raqamlari tizimdagi tenglamalar sonini bildiradi.

Birinchidan, ishlanadigan matritsani yozing, so'ngra qatorlardan biri bilan bajarilgan barcha harakatlar. Olingan matritsa "strelka" belgisidan keyin yoziladi va kerakli algebraik amallar natijaga erishilgunga qadar davom ettiriladi.

Natijada diagonallardan biri 1 ga, qolgan barcha koeffitsientlar esa nolga teng bo'lgan matritsa bo'lishi kerak, ya'ni matritsa birlik shakliga tushiriladi. Tenglamaning har ikki tomonida raqamlar bilan hisob-kitoblarni bajarishni unutmasligimiz kerak.

Ushbu yozib olish usuli unchalik qiyin emas va ko'plab noma'lum narsalarni sanab, chalg'itmaslikka imkon beradi.

Har qanday yechim usulidan bepul foydalanish ehtiyotkorlik va biroz tajribani talab qiladi. Hamma usullar ham amaliy xususiyatga ega emas. Yechimlarni topishning ba'zi usullari inson faoliyatining muayyan sohasida afzalroq, boshqalari esa ta'lim maqsadlarida mavjud.

1. O'zgartirish usuli: sistemaning istalgan tenglamasidan bir noma’lumni boshqasi orqali ifodalaymiz va uni sistemaning ikkinchi tenglamasiga almashtiramiz.

Vazifa. Tenglamalar tizimini yeching:

Yechim. Tizimning birinchi tenglamasidan biz ifodalaymiz da orqali X va uni sistemaning ikkinchi tenglamasiga almashtiring. Keling, tizimni olamiz asl nusxasiga teng.

Shunga o'xshash shartlarni keltirgandan so'ng, tizim quyidagi shaklga ega bo'ladi:

Ikkinchi tenglamadan biz topamiz: . Ushbu qiymatni tenglamaga almashtirish da = 2 - 2X, olamiz da= 3. Demak, bu sistemaning yechimi sonlar juftligidir.

2. Algebraik qo‘shish usuli: Ikki tenglamani qo'shish orqali siz bitta o'zgaruvchiga ega tenglamaga ega bo'lasiz.

Vazifa. Tizim tenglamasini yeching:

Yechim. Ikkinchi tenglamaning ikkala tomonini 2 ga ko'paytirib, biz tizimni olamiz asl nusxasiga teng. Ushbu tizimning ikkita tenglamasini qo'shib, biz tizimga kelamiz

Shunga o'xshash shartlar kiritilgandan so'ng, ushbu tizim quyidagi shaklni oladi: Ikkinchi tenglamadan biz topamiz. Ushbu qiymatni 3- tenglamaga almashtirish X + 4da= 5, olamiz , qayerda. Shuning uchun bu tizimning yechimi bir juft sondir.

3. Yangi o'zgaruvchilarni kiritish usuli: biz tizimda ba'zi takrorlanuvchi iboralarni qidirmoqdamiz, biz ularni yangi o'zgaruvchilar bilan belgilaymiz va shu bilan tizimning ko'rinishini soddalashtiramiz.

Vazifa. Tenglamalar tizimini yeching:

Yechim. Keling, ushbu tizimni boshqacha yozamiz:

Mayli x + y = u, xy = v. Keyin biz tizimni olamiz

Uni almashtirish usuli yordamida hal qilaylik. Tizimning birinchi tenglamasidan biz ifodalaymiz u orqali v va uni sistemaning ikkinchi tenglamasiga almashtiring. Keling, tizimni olamiz bular.

Tizimning ikkinchi tenglamasidan topamiz v 1 = 2, v 2 = 3.

Ushbu qiymatlarni tenglamaga almashtirish u = 5 - v, olamiz u 1 = 3,
u 2 = 2. Keyin bizda ikkita tizim mavjud

Birinchi tizimni yechishda biz ikkita juft sonni olamiz (1; 2), (2; 1). Ikkinchi tizimda hech qanday yechim yo'q.

Mustaqil ishlash uchun mashqlar

1. Tenglamalar sistemasini almashtirish usuli yordamida yeching.

Ushbu maqoladagi material tenglamalar tizimlari bilan birinchi tanishish uchun mo'ljallangan. Bu erda biz tenglamalar tizimining ta'rifi va uning echimlari bilan tanishamiz, shuningdek, tenglamalar tizimining eng keng tarqalgan turlarini ko'rib chiqamiz. Odatdagidek, biz tushuntiruvchi misollar keltiramiz.

Sahifani navigatsiya qilish.

Tenglamalar tizimi nima?

Tenglamalar sistemasini aniqlashga bosqichma-bosqich yondashamiz. Birinchidan, aytaylik, uni ikki nuqtani ko'rsatib berish qulay: birinchidan, yozuv turi, ikkinchidan, ushbu yozuvga kiritilgan ma'no. Keling, ularni navbatma-navbat ko'rib chiqamiz, so'ngra mulohazalarni tenglamalar tizimining ta'rifiga umumlashtiramiz.

Bizning oldimizda ulardan bir nechtasi bo'lsin. Masalan, ikkita 2 x+y=−3 va x=5 tenglamani olaylik. Keling, ularni bir-birining ostiga yozamiz va ularni chap tomonda jingalak qavs bilan birlashtiramiz:

Ustun shaklida joylashtirilgan va chap tomonda jingalak qavs bilan birlashtirilgan bir nechta tenglamalar bo'lgan ushbu turdagi yozuvlar tenglamalar tizimining yozuvlari hisoblanadi.

Bunday yozuvlar nimani anglatadi? Ular har bir tenglamaning yechimi bo'lgan tizim tenglamalarining barcha shunday yechimlari to'plamini aniqlaydi.

Buni boshqa so'zlar bilan ta'riflash zarar qilmaydi. Aytaylik, birinchi tenglamaning ayrim yechimlari sistemaning barcha boshqa tenglamalarining yechimlaridir. Shunday qilib, tizim yozuvi faqat ularni anglatadi.

Endi biz tenglamalar tizimining ta'rifini adekvat qabul qilishga tayyormiz.

Ta'rif.

Tenglamalar sistemalari Bir-birining ostida joylashgan, chap tomonda jingalak qavs bilan birlashtirilgan, tizimning har bir tenglamasining yechimi bo'lgan tenglamalarning barcha yechimlari to'plamini bildiruvchi yozuvlarni chaqiring.

Xuddi shunday ta'rif darslikda ham berilgan, ammo u erda umumiy holat uchun emas, balki ikkita o'zgaruvchili ikkita ratsional tenglama uchun berilgan.

Asosiy turlari

Turli xil tenglamalarning cheksiz soni borligi aniq. Tabiiyki, ular yordamida tuzilgan tenglamalar tizimlarining cheksiz soni ham mavjud. Shuning uchun tenglamalar tizimini o'rganish va ular bilan ishlash qulayligi uchun ularni o'xshash xususiyatlarga ko'ra guruhlarga bo'lish va keyin tenglamalar tizimini ko'rib chiqishga o'tish mantiqan to'g'ri keladi. individual turlar.

Birinchi bo'linish tizimga kiritilgan tenglamalar soni bo'yicha o'zini ko'rsatadi. Agar ikkita tenglama mavjud bo'lsa, biz ikkita tenglama tizimiga egamiz deb aytishimiz mumkin, agar uchta tenglama bo'lsa, uchta tenglama tizimi va hokazo. Bitta tenglama tizimi haqida gapirishning ma'nosi yo'qligi aniq, chunki bu holda, aslida, biz tizim bilan emas, balki tenglamaning o'zi bilan shug'ullanamiz.

Keyingi bo'linish tizim tenglamalarini yozishda ishtirok etadigan o'zgaruvchilar soniga asoslanadi. Agar bitta o'zgaruvchi bo'lsa, biz bitta o'zgaruvchiga ega bo'lgan tenglamalar tizimi bilan ishlaymiz (ular bitta noma'lum deb ham aytadilar), agar ikkita bo'lsa, ikkita o'zgaruvchili (ikki noma'lumli) tenglamalar tizimi bilan va hokazo. Masalan, ikki oʻzgaruvchisi x va y boʻlgan tenglamalar sistemasidir.

Bu yozuvga jalb qilingan barcha turli o'zgaruvchilar soniga ishora qiladi. Ularning barchasini bir vaqtning o'zida har bir tenglamaga kiritish shart emas, ularning kamida bitta tenglamada mavjudligi etarli; Masalan, uch oʻzgaruvchili x, y va z boʻlgan tenglamalar sistemasidir. Birinchi tenglamada x o'zgaruvchisi aniq, y va z esa yashirin (bu o'zgaruvchilar nolga ega deb taxmin qilishimiz mumkin), ikkinchi tenglamada x va z bor, lekin y o'zgaruvchisi aniq ko'rsatilmagan. Boshqacha qilib aytganda, birinchi tenglama sifatida ko'rish mumkin , ikkinchisi esa - x+0·y−3·z=0 sifatida.

Tenglamalar sistemalari bir-biridan farq qiladigan uchinchi nuqta - bu tenglamalar turi.

Maktabda tenglamalar tizimini o'rganish shundan boshlanadi ikkita o'zgaruvchili ikkita chiziqli tenglamalar tizimlari. Ya'ni, bunday tizimlar ikkita chiziqli tenglamani tashkil qiladi. Mana bir nechta misollar: Va . Ular tenglamalar sistemasi bilan ishlash asoslarini o‘rganadilar.

Murakkabroq masalalarni yechishda siz uchta noma'lumli uchta chiziqli tenglamalar tizimini ham uchratishingiz mumkin.

Keyinchalik 9-sinfda chiziqli bo'lmagan tenglamalar ikkita o'zgaruvchili ikkita tenglamalar tizimiga qo'shiladi, asosan ikkinchi darajali butun tenglamalar, kamroq - yuqori darajalar. Bu tizimlar nochiziqli tenglamalar tizimi deb ataladi, agar kerak bo'lsa, tenglamalar va noma'lumlar soni ko'rsatiladi. Keling, bunday chiziqli bo'lmagan tenglamalar tizimlariga misollarni ko'rsatamiz: Va .

Va keyin tizimlarda ham bor, masalan, . Ular, odatda, qaysi tenglamalarni ko'rsatmasdan, oddiygina tenglamalar tizimi deb ataladi. Shuni ta'kidlash kerakki, ular ko'pincha tenglamalar tizimi haqida oddiygina "tenglamalar tizimi" deyishadi va kerak bo'lganda tushuntirishlar qo'shiladi.

O'rta maktabda material o'rganilayotganda irratsional, trigonometrik, logarifmik va eksponensial tenglamalar tizimlarga kiradi: , , .

Agar universitetning birinchi kurs o‘quv dasturiga yanada chuqurroq nazar tashlasak, asosiy e’tibor chiziqli algebraik tenglamalar (SLAE) tizimlarini, ya’ni chap tomonida birinchi darajali ko‘phadlardan iborat bo‘lgan tenglamalarni o‘rganish va yechishga qaratiladi. va o'ng tomonda ma'lum raqamlar mavjud. Ammo u erda, maktabdagidan farqli o'laroq, ular endi ikkita o'zgaruvchiga ega ikkita chiziqli tenglamalarni emas, balki o'zgaruvchilarning ixtiyoriy soniga ega bo'lgan tenglamalarni oladilar, bu ko'pincha tenglamalar soniga to'g'ri kelmaydi.

Tenglamalar sistemasining yechimi nima?

“Tenglamalar tizimini yechish” atamasi to'g'ridan-to'g'ri tenglamalar tizimini anglatadi. Maktabda ikkita o'zgaruvchili tenglamalar tizimini yechish ta'rifi berilgan :

Ta'rif.

Ikki o'zgaruvchili tenglamalar tizimini yechish tizimning har bir tenglamasini to'g'ri tenglamaga aylantiradigan ushbu o'zgaruvchilarning juft qiymatlari deb ataladi, boshqacha qilib aytganda, tizimning har bir tenglamasining echimi.

Masalan, x=5, y=2 o'zgaruvchan qiymatlari juftligi (uni (5, 2) shaklida yozish mumkin) ta'rifi bo'yicha tenglamalar tizimining yechimidir, chunki x= bo'lganda tizim tenglamalari. 5, y=2 ularning o'rniga qo'yiladi, mos ravishda 5+2=7 va 5−2=3 to'g'ri sonli tengliklarga aylantiriladi. Ammo x=3, y=0 qiymatlari juftligi bu tizimning yechimi emas, chunki bu qiymatlarni tenglamalarga almashtirganda, ularning birinchisi noto'g'ri 3+0=7 tengligiga aylanadi.

Shunga o'xshash ta'riflar bitta o'zgaruvchiga ega tizimlar uchun, shuningdek, uch, to'rt va hokazo tizimlar uchun shakllantirilishi mumkin. o'zgaruvchilar.

Ta'rif.

Bitta o'zgaruvchili tenglamalar tizimini yechish sistemaning barcha tenglamalarining ildizi bo'lgan o'zgaruvchining qiymati bo'ladi, ya'ni barcha tenglamalarni to'g'ri sonli tengliklarga aylantiradi.

Keling, misol keltiraylik. Shaklning bitta o'zgaruvchisi t bo'lgan tenglamalar tizimini ko'rib chiqaylik . −2 soni uning yechimidir, chunki (−2) 2 =4 va 5·(−2+2)=0 ham haqiqiy son tenglikdir. t=1 esa sistemaning yechimi emas, chunki bu qiymat o‘rniga qo‘yilganda ikkita noto‘g‘ri tenglik 1 2 =4 va 5·(1+2)=0 bo‘ladi.

Ta'rif.

Uch, to'rt va boshqalar bilan tizimni yechish. o'zgaruvchilar uch, to'rt va boshqalar deb ataladi. o'zgaruvchilarning qiymatlari mos ravishda tizimning barcha tenglamalarini haqiqiy tenglikka aylantiradi.

Shunday qilib, ta'rifga ko'ra, x=1, y=2, z=0 o'zgaruvchilar qiymatlarining uch barobari tizimning yechimidir. , chunki 2·1=2, 5·2=10 va 1+2+0=3 haqiqiy sonli tenglikdir. Va (1, 0, 5) bu tizimning yechimi emas, chunki o'zgaruvchilarning ushbu qiymatlarini tizim tenglamalariga almashtirganda, ulardan ikkinchisi noto'g'ri tenglikka aylanadi 5·0=10, uchinchisi esa noto'g'ri tenglikka aylanadi. ham 1+0+5=3.

E'tibor bering, tenglamalar tizimlari yechimga ega bo'lmasligi mumkin, cheklangan miqdordagi echimlarga ega bo'lishi mumkin, masalan, bitta, ikkita, ... yoki cheksiz ko'p echimlarga ega bo'lishi mumkin. Mavzuni chuqurroq o'rganganingizda buni ko'rasiz.

Tenglamalar sistemasi va ularning yechimlari ta’riflarini hisobga olib, shunday xulosaga kelish mumkinki, tenglamalar sistemasining yechimi uning barcha tenglamalari yechimlari to‘plamining kesishishidir.

Xulosa qilish uchun, bu erda bir nechta tegishli ta'riflar mavjud:

Ta'rif.

qo'shma bo'lmagan, agar uning yechimlari bo'lmasa, aks holda tizim chaqiriladi qo'shma.

Ta'rif.

Tenglamalar sistemasi deyiladi noaniq, agar u cheksiz ko'p echimlarga ega bo'lsa va aniq, agar u cheklangan miqdordagi echimlarga ega bo'lsa yoki umuman bo'lmasa.

Bu atamalar, masalan, darslikda kiritilgan, lekin maktabda juda kam qo'llaniladi, ular oliy o'quv yurtlarida ko'proq eshitiladi;

Adabiyotlar ro'yxati.

1. Algebra: darslik 7-sinf uchun umumiy ta'lim muassasalar / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; tomonidan tahrirlangan S. A. Telyakovskiy. - 17-nashr. - M.: Ta'lim, 2008. - 240 b. : kasal. - ISBN 978-5-09-019315-3.
2. Algebra: 9-sinf: tarbiyaviy. umumiy ta'lim uchun muassasalar / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; tomonidan tahrirlangan S. A. Telyakovskiy. - 16-nashr. - M.: Ta'lim, 2009. - 271 b. : kasal. - ISBN 978-5-09-021134-5.
3. Mordkovich A.G. Algebra. 7-sinf. 2 soat ichida 1-qism. Umumta'lim muassasalari o'quvchilari uchun darslik / A. G. Mordkovich. - 17-nashr, qo'shimcha. - M.: Mnemosyne, 2013. - 175 b.: kasal. ISBN 978-5-346-02432-3.
4. Mordkovich A.G. Algebra. 9-sinf. 2 soat ichida 1-qism. Umumiy ta'lim muassasalari o'quvchilari uchun darslik / A. G. Mordkovich, P. V. Semenov. - 13-nashr, o'chirilgan. - M.: Mnemosyne, 2011. - 222 b.: kasal. ISBN 978-5-346-01752-3.
5. Mordkovich A.G. Algebra va matematik analizning boshlanishi. 11-sinf. 2 soat ichida 1-qism. Umumiy ta'lim muassasalari talabalari uchun darslik (profil darajasi) / A. G. Mordkovich, P. V. Semenov. - 2-nashr, o'chirilgan. - M.: Mnemosyne, 2008. - 287 b.: kasal. ISBN 978-5-346-01027-2.
6. Algebra va tahlilning boshlanishi: Proc. 10-11 sinflar uchun. umumiy ta'lim muassasalar / A. N. Kolmogorov, A. M. Abramov, P. Dudnitsyn va boshqalar; Ed. A. N. Kolmogorov - 14-nashr - M.: Ta'lim, 2004. - 384 pp.: ISBN 5-09-013651-3.
7. A. G. Kurosh. Oliy algebra kursi.
8. Ilyin V. A., Poznyak E. G. Analitik geometriya: Darslik: Universitetlar uchun. - 5-nashr. – M.: Fan. Fizmatlit, 1999. – 224 b. – (Oliy matematika va matematik fizika kursi). – ISBN 5-02-015234 – X (3-son)