Kosinus alfa nimaga teng? Ikki burchak uchun formulalar va argumentlar qo'shish. Kotangens funksiyaning grafigi, y = ctg x
Shuningdek o'qing
Markazi A nuqtada joylashgan.
a - radianlarda ifodalangan burchak.
tangent ( tan a) gipotenuza va oyoq orasidagi a burchakka bog'liq trigonometrik funktsiyadir to'g'ri uchburchak, nisbatga teng qarama-qarshi tomonning uzunligi |BC|
qo'shni oyoqning uzunligiga |AB| . kotangent () ctg a
gipotenuza va to‘g‘ri burchakli uchburchakning oyog‘i orasidagi a burchakka bog‘liq bo‘lgan trigonometrik funksiya bo‘lib, qo‘shni oyoq uzunligining nisbatiga teng |AB|
qarama-qarshi oyoq uzunligiga |BC| . Tangent Qayerda
n
.
;
;
.
- butun.
G'arb adabiyotida tangens quyidagicha ifodalanadi:
qarama-qarshi oyoq uzunligiga |BC| . Tangent Qayerda
Tangens funksiyaning grafigi, y = tan x
.
Kotangent
;
;
.
G'arb adabiyotida kotangens quyidagicha belgilanadi:

Quyidagi belgilar ham qabul qilinadi:
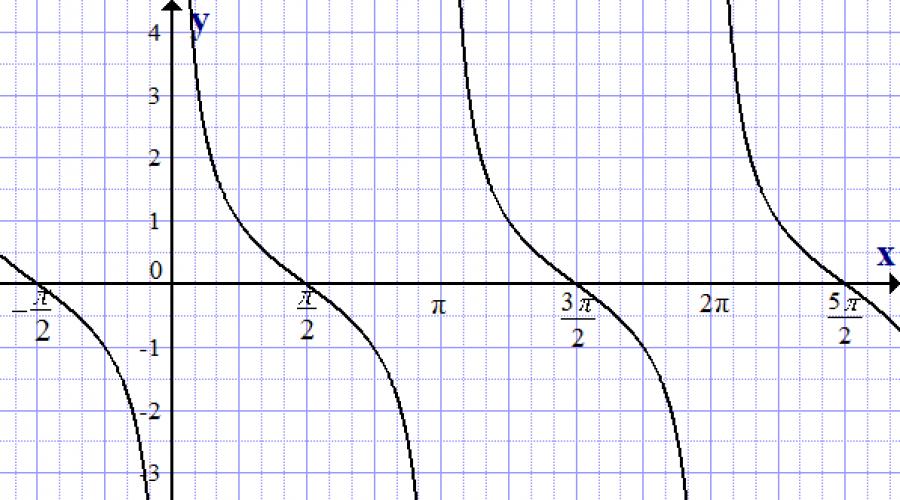
Kotangens funksiyaning grafigi, y = ctg x
Tangens va kotangensning xossalari Davriylik Funktsiyalar y = tg x va y =
ctg x
p davri bilan davriydir.
Paritet
Tangens va kotangens funksiyalari toq. Tangent Ta'rif sohalari va qadriyatlari, ortishi, kamayishi
| Tangens va kotangens funksiyalar oʻzlarining aniqlanish sohalarida uzluksizdir (uzluksizlik isbotiga qarang). Tangens va kotangensning asosiy xususiyatlari jadvalda keltirilgan ( Davriylik | Tangens va kotangens funksiyalar oʻzlarining aniqlanish sohalarida uzluksizdir (uzluksizlik isbotiga qarang). Tangens va kotangensning asosiy xususiyatlari jadvalda keltirilgan ( tg x | |
| - butun). | ||
| y= | -∞ < y < +∞ | -∞ < y < +∞ |
| Qamrov va davomiylik | - | |
| Qiymatlar diapazoni | - | |
| Ortib bormoqda | - | - |
| Pastga 0 | ||
| Ekstremal 0 | Tangens va kotangens funksiyalar oʻzlarining aniqlanish sohalarida uzluksizdir (uzluksizlik isbotiga qarang). Tangens va kotangensning asosiy xususiyatlari jadvalda keltirilgan ( 0 | - |
Nollar, y =
Ordinata o'qi bilan kesishgan nuqtalar, x =
;
;
;
;
;
Formulalar
Sinus va kosinus yordamida ifodalar
Yig'indi va ayirmadan tangens va kotangens uchun formulalar
Qolgan formulalarni, masalan, olish oson
Tangenslar mahsuloti 
Tangenslar yig‘indisi va ayirmasining formulasi
Ushbu jadvalda argumentning ma'lum qiymatlari uchun tangens va kotangentlarning qiymatlari keltirilgan.
;
;
Kompleks sonlar yordamida ifodalar
; .
.
Giperbolik funksiyalar orqali ifodalar
.
Hosilalar
Funktsiyaning x o'zgaruvchisiga nisbatan n-darajali hosila:
Tangens uchun formulalarni chiqarish > > > ; kotangent uchun > > >
Integrallar Seriyani kengaytirish Tangensning x darajasida kengayishini olish uchun siz kengayishning bir necha shartlarini olishingiz kerak. quvvat seriyasi funktsiyalar uchun gunoh x va bu ko'phadlarni bir-biriga bo'ling, .
Bu quyidagi formulalarni hosil qiladi.
da.
da. Qayerda Bn
;
;
- Bernoulli raqamlari. Ular yoki takrorlanish munosabatidan aniqlanadi:
Qayerda. 
Yoki Laplas formulasiga ko'ra:
Teskari funksiyalar
Tangens va kotangensning teskari funksiyalari mos ravishda arktangens va arkkotangensdir.
Arktangens, arctg Tangent Qayerda
, Qayerda
Arktangens, arctg Tangent Qayerda
Arkkotangent, arkktg
Foydalanilgan adabiyotlar:
I.N. Bronshteyn, K.A. Semendyaev, muhandislar va kollej talabalari uchun matematika bo'yicha qo'llanma, "Lan", 2009 yil. G. Korn, Matematika bo'yicha qo'llanma ilmiy xodimlar
- va muhandislar, 2012 yil.
- 2. Qiymatlar diapazoni: [-1;1]
- 3. Toq funksiya.
- 7. Funksiya musbat bo‘lgan intervallar: (2*pi*n; pi+2*pi*n)
- 8. Funksiya manfiy bo‘lgan intervallar: (-pi + 2*pi*n; 2*pi*n)
- 9. Ortib borayotgan intervallar: [-pi/2 +2*pi*n; pi/2 +2*pi*n]
- 10. Qisqartirilgan intervallar:
- 11. Minimal ball: -pi/2 +2*pi*n
- 12. Minimal funksiya: -1
- 13. Maksimal ball: pi/2 +2*pi*n
14. Maksimal funksiya: 1
.jpg)
- Kosinusning xossalari
- va muhandislar, 2012 yil.
- 1. Ta'rif sohasi: butun sonlar o'qi
- 3. Juft funksiya.
- 4. Eng kichik ijobiy davr: 2*pi
- 5. Funksiya grafigining Ox o'qi bilan kesishish nuqtalarining koordinatalari: (pi/2 +pi*n; 0)
- 6. Funksiya grafigining Oy o‘qi bilan kesishish nuqtalarining koordinatalari: (0;1)
- 7. Funksiya musbat bo‘lgan intervallar: (-pi/2 +2*pi*n; pi/2 +2*pi*n)
- 8. Funktsiya manfiy bo'lgan intervallar: (pi/2 +2*pi*n; 3*pi/2 +2*pi*n)
- 9. Ortib borayotgan intervallar: [-pi/2 +2*pi*n; pi/2 +2*pi*n]
- 9. Ortib borayotgan intervallar: [-pi + 2*pi*n; 2*pi*n]
- 11. Minimal ball: -pi/2 +2*pi*n
- 11. Minimal ball: pi+2*pi*n
- 13. Maksimal ball: pi/2 +2*pi*n
13. Maksimal ball: 2*pi*n
.jpg)
- Tangensning xossalari
- 2. Qiymatlar diapazoni: [-1;1]
- 1. Aniqlash maydoni: (-pi/2 +pi*n; pi/2 +pi*n)
- 5. Funksiya grafigining Ox o'qi bilan kesishish nuqtalarining koordinatalari: (pi*n; 0)
- 6. Funksiya grafigining Oy o‘qi bilan kesishish nuqtalarining koordinatalari: (0;0)
9. Funktsiya intervalgacha ortadi (-pi/2 + pi*n; pi/2 + pi*n)
.jpg)
- Kotangentning xossalari
- 1. Ta'rif sohasi: (pi*n; pi +pi*n)
- 2. Qiymatlar diapazoni: [-1;1]
- 2. Qiymat diapazoni: butun sonlar o'qi
- 4. Eng kichik ijobiy davr: pi
- 5. Funktsiya grafigining Ox o'qi bilan kesishish nuqtalarining koordinatalari: (pi/2 + pi*n; 0)
- 6. Funksiya grafigining Oy o'qi bilan kesishish nuqtalarining koordinatalari: yo'q
- 7. Funktsiya musbat bo'lgan intervallar: (pi*n; pi/2 +pi*n)
- 8. Funksiya manfiy bo‘lgan intervallar: (-pi/2 +pi*n; pi*n)
- 9. Funktsiya oraliqlarda kamayadi (pi*n; pi +pi*n)
10. Maksimal va minimal ball yo'q.
Sinus va kosinus dastlab to'g'ri burchakli uchburchaklardagi miqdorlarni hisoblash zaruratidan kelib chiqqan. Agar to'g'ri burchakli uchburchakdagi burchaklarning daraja o'lchovi o'zgarmasa, tomonlarning nisbati, bu tomonlar uzunligi qanchalik o'zgarmasin, har doim bir xil bo'lib qolishi ta'kidlandi.
Shunday qilib sinus va kosinus tushunchalari kiritildi. To'g'ri burchakli uchburchakdagi o'tkir burchakning sinusi qarama-qarshi tomonning gipotenuzaga nisbati, kosinus esa gipotenuzaga qo'shni tomonning nisbati.
Kosinuslar va sinuslar teoremalari
Ammo kosinuslar va sinuslar faqat to'g'ri burchakli uchburchaklar uchun emas, balki ko'proq uchun ishlatilishi mumkin. Har qanday uchburchakning o'tkir yoki o'tkir burchagi yoki tomonining qiymatini topish uchun kosinuslar va sinuslar teoremasini qo'llash kifoya.
Kosinus teoremasi juda oddiy: "Uchburchakning bir tomonining kvadrati boshqa ikki tomonning kvadratlari yig'indisiga, bu tomonlarning ikki baravar ko'paytmasiga va ular orasidagi burchakning kosinusiga tengdir."
Sinus teoremasining ikkita talqini mavjud: kichik va kengaytirilgan. Kichkintoyning fikriga ko'ra: "Uchburchakda burchaklar qarama-qarshi tomonlarga proportsionaldir." Ushbu teorema ko'pincha uchburchakning aylanasi xususiyati tufayli kengaytiriladi: "Uchburchakda burchaklar qarama-qarshi tomonlarga proportsionaldir va ularning nisbati aylananing diametriga tengdir."
Kompleks sonlar yordamida ifodalar
Hosila - bu argumentning o'zgarishiga nisbatan funktsiya qanchalik tez o'zgarishini ko'rsatadigan matematik vositadir. Hosilalar geometriyada va bir qator texnik fanlarda qo'llaniladi.
Muammolarni hal qilishda siz bilishingiz kerak jadval qiymatlari hosilalari trigonometrik funktsiyalar: sinus va kosinus. Sinusning hosilasi kosinus, kosinus esa sinus, lekin minus belgisi bilan.
Matematikada qo'llash
Sinuslar va kosinuslar, ayniqsa, to'g'ri burchakli uchburchaklar va ular bilan bog'liq masalalarni yechishda tez-tez ishlatiladi.
Sinuslar va kosinuslarning qulayligi texnologiyada ham namoyon bo'ladi. Burchaklar va tomonlarni kosinus va sinus teoremalari yordamida baholash oson edi, murakkab shakllar va ob'ektlarni "oddiy" uchburchaklarga bo'lishdi. Ko'pincha tomonlar nisbati va daraja o'lchovlarini hisoblash bilan shug'ullanadigan muhandislar va muhandislar jadvalsiz burchaklarning kosinuslari va sinuslarini hisoblash uchun ko'p vaqt va kuch sarfladilar.
Keyin sinuslar, kosinuslar, tangenslar va kotangentlarning minglab qiymatlarini o'z ichiga olgan Bradis jadvallari yordamga keldi. turli burchaklar. Sovet davrida ba'zi o'qituvchilar o'z shogirdlarini Bradis jadvallari sahifalarini yodlashga majbur qilishgan.
Radian - burchak kattaligi yoylar, uzunlik radiusga teng yoki 57,295779513 ° daraja.
Daraja (geometriyada) - aylananing 1/360 qismi yoki to'g'ri burchakning 1/90 qismi.
p = 3,141592653589793238462… (Pi ning taxminiy qiymati).
Burchaklar uchun kosinuslar jadvali: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| x burchak (gradusda) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x burchak (radianlarda) | 0 | p/6 | p/4 | p/3 | p/2 | 2 x p/3 | 3 x p/4 | 5 x p/6 | π | 7 x p/6 | 5 x p/4 | 4 x p/3 | 3 x p/2 | 5 x p/3 | 7 x p/4 | 11 x p/6 | 2 x p |
| chunki x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |
Muhim eslatmalar!
1. Agar formulalar o'rniga gobbledygook ni ko'rsangiz, keshingizni tozalang. Buni brauzeringizda qanday qilish kerakligi bu erda yozilgan:
2. Maqolani o'qishni boshlashdan oldin, eng ko'p bizning navigatorimizga e'tibor bering foydali resurs uchun
Sinus, kosinus, tangens, kotangens
Sinus (), kosinus (), tangens (), kotangens () tushunchalari burchak tushunchasi bilan uzviy bog'liqdir. Bularni, birinchi qarashda, murakkab tushunchalarni (ko'pgina maktab o'quvchilarida dahshatga soladigan) yaxshi tushunish uchun va "iblis u chizilgandek dahshatli emas"ligiga ishonch hosil qilish uchun keling, keling, "shayton" dan boshlaylik. juda boshlang'ich va burchak tushunchasini tushunish.
Burchak tushunchasi: radian, daraja
Keling, rasmga qaraylik. Vektor nuqtaga nisbatan ma'lum miqdorda "aylangan". Shunday qilib, bu aylanishning boshlang'ich pozitsiyasiga nisbatan o'lchovi bo'ladi burchak.
Burchak tushunchasi haqida yana nimani bilishingiz kerak? Albatta, burchak birliklari!
Geometriyada ham, trigonometriyada ham burchakni daraja va radian bilan o'lchash mumkin.
(Bir daraja) burchak deyiladi markaziy burchak aylanada, aylananing bir qismiga teng dumaloq yoyga asoslangan. Shunday qilib, butun doira dumaloq yoylarning "bo'laklari" dan iborat yoki aylana tasvirlangan burchak tengdir.

Ya'ni, yuqoridagi rasmda teng burchak ko'rsatilgan, ya'ni bu burchak aylana o'lchamidagi aylana yoyga tayanadi.
Radianlardagi burchak uzunligi aylananing radiusiga teng bo'lgan aylana yoyi bilan qoplangan doiradagi markaziy burchakdir. Xo'sh, tushundingizmi? Agar yo'q bo'lsa, keling, buni rasmdan aniqlaylik.

Demak, rasmda radianga teng burchak ko'rsatilgan, ya'ni bu burchak aylana yoyga tayanadi, uning uzunligi aylananing radiusiga teng (uzunligi uzunlik yoki radiusga teng). uzunligiga teng yoylar). Shunday qilib, yoy uzunligi quyidagi formula bo'yicha hisoblanadi:
Radianlarda markaziy burchak qayerda.
Xo'sh, buni bilib, aylana tasvirlangan burchakda qancha radian borligiga javob bera olasizmi? Ha, buning uchun siz aylana formulasini eslab qolishingiz kerak. Mana:
Xo'sh, endi bu ikki formulani o'zaro bog'laymiz va aylana tasvirlangan burchak teng ekanligini topamiz. Ya'ni, qiymatni darajalar va radyanlardagi o'zaro bog'lash orqali biz buni olamiz. Tegishli ravishda, . Ko'rib turganingizdek, "daraja" dan farqli o'laroq, "radian" so'zi olib tashlandi, chunki o'lchov birligi odatda kontekstdan aniq.
Qancha radian bor? Bu to'g'ri!
Tushundim? Keyin davom eting va uni tuzating:
Qiyinchiliklar bormi? Keyin qarang javoblar:
To'g'ri burchakli uchburchak: sinus, kosinus, tangens, burchak kotangensi
Shunday qilib, biz burchak tushunchasini aniqladik. Lekin burchakning sinusi, kosinusu, tangensi va kotangensi nima? Keling, buni aniqlaylik. Buning uchun bizga to'g'ri burchakli uchburchak yordam beradi.

To'g'ri burchakli uchburchakning tomonlari nima deyiladi? To'g'ri, gipotenuza va oyoqlar: gipotenuza to'g'ri burchakka qarama-qarshi yotgan tomon (bizning misolimizda bu tomon); oyoqlar qolgan ikkita tomon va (qo'shnilar to'g'ri burchak), va, agar biz burchakka nisbatan oyoqlarni hisobga olsak, u holda oyoq qo'shni oyoq, oyoq esa aksincha. Xo'sh, endi savolga javob beraylik: burchakning sinus, kosinus, tangensi va kotangensi nima?
Burchak sinusi- bu qarama-qarshi (uzoq) oyoqning gipotenuzaga nisbati.
Bizning uchburchakda.
Burchak kosinusi- bu qo'shni (yaqin) oyoqning gipotenuzaga nisbati.
Bizning uchburchakda.
Burchakning tangensi- bu qarama-qarshi (uzoq) tomonning qo'shni (yaqin) nisbati.
Bizning uchburchakda.
Burchak kotangensi- bu qo'shni (yaqin) oyoqning qarama-qarshi (uzoq) nisbati.
Bizning uchburchakda.
Bu ta'riflar zarur eslab qoling! Qaysi oyoqni nimaga bo'lish kerakligini eslab qolishni osonlashtirish uchun siz buni aniq tushunishingiz kerak tangens funktsiyalar uchun kotangent faqat oyoqlar o'tiradi va gipotenuz faqat ichida paydo bo'ladi sinus funktsiyalar uchun kosinus. Va keyin siz birlashmalar zanjiri bilan kelishingiz mumkin. Masalan, bu:
Kosinus → teginish → teginish → ulashgan;
Kotangent → teginish → teginish → qo‘shni.
Avvalo, sinus, kosinus, tangens va kotangens uchburchak tomonlarining nisbati bu tomonlarning uzunligiga (bir xil burchak ostida) bog'liq emasligini yodda tutishingiz kerak. Menga ishonmaysizmi? Keyin rasmga qarab ishonch hosil qiling:

Masalan, burchakning kosinusini ko'rib chiqaylik. Ta'rifga ko'ra, uchburchakdan: , lekin biz uchburchakdan burchakning kosinusini hisoblashimiz mumkin: . Ko'ryapsizmi, tomonlarning uzunligi har xil, lekin bir burchakning kosinus qiymati bir xil. Shunday qilib, sinus, kosinus, tangens va kotangens qiymatlari faqat burchakning kattaligiga bog'liq.
Agar siz ta'riflarni tushunsangiz, davom eting va ularni birlashtiring!
Quyidagi rasmda ko'rsatilgan uchburchak uchun biz topamiz.

Xo'sh, tushundingizmi? Keyin o'zingizni sinab ko'ring: burchak uchun xuddi shunday hisoblang.
Birlik (trigonometrik) doira
Darajalar va radianlar tushunchalarini tushunib, biz radiusi teng bo'lgan doirani ko'rib chiqdik. Bunday doira deyiladi yagona. Bu trigonometriyani o'rganishda juda foydali bo'ladi. Shuning uchun, keling, buni biroz batafsilroq ko'rib chiqaylik.

Ko'rib turganingizdek, bu aylana Dekart koordinata tizimida qurilgan. Doira radiusi birga teng, aylananing markazi koordinatalarning boshida joylashgan bo'lsa, radius vektorining boshlang'ich pozitsiyasi o'qning ijobiy yo'nalishi bo'ylab o'rnatiladi (bizning misolimizda bu radius).
Doiradagi har bir nuqta ikkita raqamga to'g'ri keladi: o'q koordinatasi va o'q koordinatasi. Bu koordinata raqamlari nima? Va umuman olganda, ularning mavzuga qanday aloqasi bor? Buning uchun biz ko'rib chiqilgan to'g'ri burchakli uchburchak haqida eslashimiz kerak. Yuqoridagi rasmda siz ikkita to'g'ri burchakli uchburchakni ko'rishingiz mumkin. Uchburchakni ko'rib chiqing. U to'rtburchaklar, chunki u o'qga perpendikulyar.
Uchburchak nimaga teng? Bu to'g'ri. Bundan tashqari, biz bilamizki, bu birlik doirasining radiusi, ya'ni . Keling, bu qiymatni kosinus formulamizga almashtiramiz. Mana nima sodir bo'ladi:
Uchburchak nimaga teng? Xo'sh, albatta! Ushbu formulaga radius qiymatini almashtiring va quyidagilarni oling:
Demak, nuqta qanday koordinatalarga ega ekanligini ayta olasizmi? doiraga tegishli? Xo'sh, yo'qmi? Agar buni tushunsangiz va shunchaki raqamlar bo'lsa-chi? U qaysi koordinataga mos keladi? Albatta, koordinatalar! Va u qaysi koordinataga mos keladi? To'g'ri, koordinatalar! Shunday qilib, davr.

Xo'sh, nimaga teng va nimaga teng? To'g'ri, keling, tangens va kotangensning tegishli ta'riflaridan foydalanamiz va buni olamiz, a.
Agar burchak kattaroq bo'lsa-chi? Masalan, ushbu rasmdagi kabi:

Ushbu misolda nima o'zgardi? Keling, buni aniqlaylik. Buning uchun yana to'g'ri burchakli uchburchakka o'taylik. To'g'ri uchburchakni ko'rib chiqing: burchak (burchakka qo'shni sifatida). Burchak uchun sinus, kosinus, tangens va kotangensning qiymatlari qanday? To'g'ri, biz trigonometrik funktsiyalarning tegishli ta'riflariga amal qilamiz:
Ko'rib turganingizdek, burchak sinusining qiymati hali ham koordinataga to'g'ri keladi; burchak kosinusining qiymati - koordinata; va mos keladigan nisbatlarga tangens va kotangens qiymatlari. Shunday qilib, bu munosabatlar radius vektorining har qanday aylanishiga taalluqlidir.
Radius vektorining boshlang'ich pozitsiyasi o'qning musbat yo'nalishi bo'ylab joylashganligi allaqachon aytib o'tilgan. Hozirgacha biz bu vektorni soat sohasi farqli ravishda aylantirdik, lekin agar biz uni soat yo'nalishi bo'yicha aylantirsak nima bo'ladi? Hech qanday g'ayrioddiy narsa yo'q, siz ham ma'lum bir qiymatga ega burchakka ega bo'lasiz, lekin faqat salbiy bo'ladi. Shunday qilib, radius vektorini soat sohasi farqli ravishda aylantirganda, biz olamiz ijobiy burchaklar, va soat yo'nalishi bo'yicha aylanganda - salbiy.
Shunday qilib, biz bilamizki, radius vektorining aylana atrofida butun aylanishi yoki. Radius vektorini burish mumkinmi? Xo'sh, albatta qila olasiz! Birinchi holda, shuning uchun radius vektori bitta to'liq aylanishni amalga oshiradi va yoki pozitsiyasida to'xtaydi.
Ikkinchi holda, ya'ni radius vektori uchta to'liq aylanishni amalga oshiradi va yoki holatida to'xtaydi.
Shunday qilib, yuqoridagi misollardan xulosa qilishimiz mumkinki, bir-biridan farq qiladigan burchaklar yoki (bu erda har qanday butun son) radius vektorining bir xil holatiga mos keladi.
Quyidagi rasmda burchak ko'rsatilgan. Xuddi shu rasm burchakka mos keladi va hokazo. Ushbu ro'yxatni cheksiz davom ettirish mumkin. Bu burchaklarning barchasi umumiy formula yoki (bu yerda har qanday butun son) bilan yozilishi mumkin.

Endi, asosiy trigonometrik funktsiyalarning ta'riflarini bilib, birlik doirasidan foydalanib, qiymatlar nima ekanligiga javob berishga harakat qiling:
Mana sizga yordam beradigan birlik doirasi:

Qiyinchiliklar bormi? Keyin buni aniqlaylik. Shunday qilib, biz buni bilamiz:
Bu erdan ma'lum burchak o'lchovlariga mos keladigan nuqtalarning koordinatalarini aniqlaymiz. Keling, tartibda boshlaylik: burchak koordinatali nuqtaga to'g'ri keladi, shuning uchun:
Mavjud emas;
Bundan tashqari, xuddi shu mantiqqa rioya qilgan holda, biz burchaklar mos ravishda koordinatali nuqtalarga mos kelishini aniqlaymiz. Buni bilib, tegishli nuqtalarda trigonometrik funktsiyalarning qiymatlarini aniqlash oson. Avval o'zingiz sinab ko'ring, keyin javoblarni tekshiring.
Javoblar:
Shunday qilib, biz quyidagi jadvalni tuzishimiz mumkin:

Bu barcha qadriyatlarni eslab qolishning hojati yo'q. Birlik aylanasidagi nuqtalar koordinatalari va trigonometrik funktsiyalar qiymatlari o'rtasidagi muvofiqlikni eslash kifoya:
Ammo burchaklarning trigonometrik funktsiyalarining qiymatlari va quyidagi jadvalda keltirilgan, eslash kerak:

Qo'rqmang, endi biz sizga bitta misol keltiramiz mos keladigan qiymatlarni eslab qolish juda oddiy:
Ushbu usuldan foydalanish uchun burchakning barcha uch o'lchovi uchun sinus qiymatlarini (), shuningdek burchak tangensining qiymatini eslab qolish juda muhimdir. Ushbu qiymatlarni bilib, butun jadvalni tiklash juda oddiy - kosinus qiymatlari strelkalar bo'yicha uzatiladi, ya'ni:
Buni bilib, siz uchun qiymatlarni tiklashingiz mumkin. Numerator " " mos keladi va maxraj " " mos keladi. Kotangent qiymatlari rasmda ko'rsatilgan o'qlarga muvofiq o'tkaziladi. Agar siz buni tushunsangiz va o'qlar bilan diagrammani eslab qolsangiz, jadvaldagi barcha qiymatlarni eslab qolish kifoya qiladi.
Doiradagi nuqtaning koordinatalari
Aylanada nuqtani (uning koordinatalarini) topish mumkinmi? aylana markazining koordinatalarini, uning radiusini va burilish burchagini bilish?
Xo'sh, albatta qila olasiz! Keling, chiqaraylik umumiy formula nuqtaning koordinatalarini topish uchun.
Masalan, oldimizda aylana bor:

Bizga nuqta aylananing markazi ekanligi berilgan. Doira radiusi teng. Nuqtani gradusga aylantirish orqali olingan nuqtaning koordinatalarini topish kerak.
Rasmdan ko'rinib turibdiki, nuqta koordinatasi segment uzunligiga to'g'ri keladi. Segmentning uzunligi aylana markazining koordinatasiga to'g'ri keladi, ya'ni u tengdir. Segment uzunligini kosinus ta'rifi yordamida ifodalash mumkin:
Keyin biz nuqta koordinatasini olamiz.
Xuddi shu mantiqdan foydalanib, nuqta uchun y koordinata qiymatini topamiz. Shunday qilib,
Shunday qilib, ichida umumiy ko'rinish Nuqtalarning koordinatalari quyidagi formulalar bilan aniqlanadi:
Doira markazining koordinatalari,
Doira radiusi,
Vektor radiusining burilish burchagi.
Ko'rib turganingizdek, biz ko'rib chiqayotgan birlik doirasi uchun bu formulalar sezilarli darajada kamayadi, chunki markazning koordinatalari nolga va radius birga teng:
Xo'sh, keling, aylana bo'ylab nuqtalarni topishni mashq qilib, ushbu formulalarni sinab ko'raylik?
1. Nuqtani aylantirib olingan birlik doiradagi nuqtaning koordinatalarini toping.
2. Nuqtani aylantirib olingan birlik doiradagi nuqtaning koordinatalarini toping.
3. Nuqtani aylantirib olingan birlik doiradagi nuqtaning koordinatalarini toping.
4. Nuqta aylananing markazidir. Doira radiusi teng. Dastlabki radius vektorini ga aylantirish orqali olingan nuqtaning koordinatalarini topish kerak.
5. Nuqta aylananing markazidir. Doira radiusi teng. Dastlabki radius vektorini ga aylantirish orqali olingan nuqtaning koordinatalarini topish kerak.
Aylanadagi nuqtaning koordinatalarini topishda muammo bormi?
Ushbu beshta misolni yeching (yoki ularni echishni yaxshi biling) va siz ularni topishni o'rganasiz!
XULOSA VA ASOSIY FORMULALAR
Burchakning sinusi - bu qarama-qarshi (uzoq) oyoqning gipotenuzaga nisbati.
Burchakning kosinusu - qo'shni (yaqin) oyoqning gipotenuzaga nisbati.
Burchakning tangensi - qarama-qarshi (uzoq) tomonning qo'shni (yaqin) tomonga nisbati.
Burchakning kotangensi - qo'shni (yaqin) tomonning qarama-qarshi (uzoq) tomonga nisbati.
Xo'sh, mavzu tugadi. Agar siz ushbu satrlarni o'qiyotgan bo'lsangiz, demak siz juda zo'rsiz.
Chunki odamlarning atigi 5 foizi o‘z kuchi bilan biror narsani o‘zlashtira oladi. Va agar siz oxirigacha o'qisangiz, unda siz ushbu 5% ga kirasiz!
Endi eng muhimi.
Siz ushbu mavzu bo'yicha nazariyani tushundingiz. Va takror aytaman, bu... bu shunchaki ajoyib! Siz allaqachon tengdoshlaringizning aksariyatidan yaxshiroqsiz.
Muammo shundaki, bu etarli bo'lmasligi mumkin ...
Nima uchun?
uchun muvaffaqiyatli yakunlash Yagona davlat imtihoni, kollejga byudjetga kirish uchun va eng muhimi, umrbod.
Men sizni hech narsaga ishontirmayman, faqat bitta narsani aytaman ...
Qabul qilgan odamlar yaxshi ta'lim, uni olmaganlarga qaraganda ko'proq pul ishlang. Bu statistika.
Lekin bu asosiy narsa emas.
Asosiysi, ular BAXTLI (Bunday tadqiqotlar bor). Ehtimol, ularning oldida juda ko'p ochiqlik bor ko'proq imkoniyatlar va hayot yanada yorqinroq bo'ladimi? Bilmayman...
Lekin o'zingiz o'ylab ko'ring...
Yagona davlat imtihonida boshqalardan yaxshiroq bo'lish va oxir-oqibat ... baxtli bo'lish uchun nima qilish kerak?
SHU MAVZU BO'YICHA MUAMMOLARNI YECHIB QO'L OLING.
Imtihon paytida sizdan nazariya so'ralmaydi.
Sizga kerak bo'ladi vaqtga qarshi muammolarni hal qilish.
Va agar siz ularni hal qilmagan bo'lsangiz (KO'P!), Bir joyda ahmoqona xatoga yo'l qo'yasiz yoki shunchaki vaqtingiz bo'lmaydi.
Bu xuddi sportdagidek - aniq g'alaba qozonish uchun buni ko'p marta takrorlash kerak.
To'plamni xohlagan joyingizda toping, albatta yechimlar bilan, batafsil tahlil va qaror qiling, qaror qiling, qaror qiling!
Siz bizning vazifalarimizdan foydalanishingiz mumkin (ixtiyoriy) va biz, albatta, ularni tavsiya qilamiz.
Vazifalarimizdan yaxshiroq foydalanish uchun siz hozir o'qiyotgan YouClever darsligining ishlash muddatini uzaytirishga yordam berishingiz kerak.
Qanaqasiga? Ikkita variant mavjud:
- Ushbu maqoladagi barcha yashirin vazifalarni oching -
- Darslikning barcha 99 ta maqolasidagi barcha yashirin vazifalarga kirishni oching - Darslik sotib oling - 499 rubl
Ha, bizning darsligimizda 99 ta shunday maqola bor va ulardagi barcha vazifalar va yashirin matnlarga kirish darhol ochilishi mumkin.
Barcha yashirin vazifalarga kirish saytning BUTUN muddati davomida taqdim etiladi.
Va xulosa qilib ...
Bizning vazifalarimiz sizga yoqmasa, boshqalarni toping. Faqat nazariya bilan to'xtamang.
"Tushundim" va "Men hal qila olaman" - bu mutlaqo boshqa ko'nikmalar. Sizga ikkalasi ham kerak.
Muammolarni toping va ularni hal qiling!
Trigonometriya fan sifatida Qadimgi Sharqda vujudga kelgan. Birinchidan trigonometrik nisbatlar astronomlar tomonidan aniq taqvim yaratish va yulduzlar bo'ylab harakatlanish uchun ishlab chiqilgan. Bu hisob-kitoblar sferik trigonometriya bilan bog'liq bo'lsa-da maktab kursi tekis uchburchakning tomonlari va burchaklarining nisbatlarini o'rganish.
Trigonometriya - trigonometrik funksiyalarning xossalari hamda uchburchaklarning tomonlari va burchaklari oʻrtasidagi bogʻliqliklarni oʻrganuvchi matematikaning boʻlimi.
Milodiy 1-ming yillikda madaniyat va ilm-fanning gullab-yashnashi davrida bilimlardan tarqaldi Qadimgi Sharq Gretsiyaga. Ammo trigonometriyaning asosiy kashfiyotlari Arab xalifaligi odamlarining xizmatlaridir. Xususan, turkman olimi al-Marazviy tangens va kotangens kabi funksiyalarni kiritdi va sinuslar, tangenslar va kotangentlar uchun dastlabki qiymatlar jadvallarini tuzdi. Sinus va kosinus tushunchalari hind olimlari tomonidan kiritilgan. Trigonometriyaga Evklid, Arximed, Eratosfen kabi antik davrning buyuk arboblarining asarlarida katta e'tibor berilgan.
Trigonometriyaning asosiy miqdorlari
Asosiy trigonometrik funktsiyalar raqamli argument- bular sinus, kosinus, tangens va kotangens. Ularning har biri o'z grafigiga ega: sinus, kosinus, tangens va kotangens.
Ushbu miqdorlarning qiymatlarini hisoblash uchun formulalar Pifagor teoremasiga asoslanadi. Maktab o'quvchilariga "Pifagor shimlari barcha yo'nalishlarda tengdir" formulasida ko'proq ma'lum, chunki dalil teng yonli to'g'ri burchakli uchburchak misolida keltirilgan.
Sinus, kosinus va boshqa bog'liqliklar o'rtasidagi munosabatni o'rnatadi o'tkir burchaklar va har qanday to'g'ri burchakli uchburchakning tomonlari. Keling, A burchak uchun bu miqdorlarni hisoblash formulalarini keltiramiz va trigonometrik funktsiyalar o'rtasidagi munosabatlarni kuzatamiz:

Ko'rib turganingizdek, tg va ctg teskari funktsiyalar. Agar a oyog'ini sin A va gipotenuza c ko'paytmasi, b oyog'ini cos A * c deb tasavvur qilsak, tangens va kotangens uchun quyidagi formulalarni olamiz:

Trigonometrik doira
Grafik jihatdan ko'rsatilgan miqdorlar o'rtasidagi munosabatni quyidagicha ifodalash mumkin:

Atrof, in Ushbu holatda, a burchakning barcha mumkin bo'lgan qiymatlarini ifodalaydi - 0 ° dan 360 ° gacha. Rasmdan ko'rinib turibdiki, har bir funktsiya burchakka qarab manfiy yoki ijobiy qiymat oladi. Masalan, agar a aylananing 1 va 2 choraklariga tegishli bo'lsa, ya'ni 0° dan 180° gacha bo'lgan oraliqda bo'lsa, sin a «+» belgisiga ega bo'ladi. 180° dan 360° gacha (III va IV chorak) a uchun sin a faqat manfiy qiymat bo'lishi mumkin.
Keling, qurishga harakat qilaylik trigonometrik jadvallar muayyan burchaklar uchun va miqdorlarning qiymatini toping.

30°, 45°, 60°, 90°, 180° va boshqalarga teng a qiymatlari maxsus holatlar deyiladi. Ular uchun trigonometrik funktsiyalarning qiymatlari hisoblab chiqiladi va maxsus jadvallar ko'rinishida taqdim etiladi.

Bu burchaklar tasodifan tanlanmagan. Jadvallardagi p belgisi radyanlar uchundir. Rad - aylana yoyi uzunligi uning radiusiga mos keladigan burchak. Bu qiymat radyanlarda hisoblashda universal bog'liqlikni o'rnatish uchun kiritilgan, radiusning smdagi haqiqiy uzunligi muhim emas;

Trigonometrik funktsiyalar uchun jadvallardagi burchaklar radian qiymatlariga mos keladi:

Shunday qilib, 2p to'liq aylana yoki 360 ° ekanligini taxmin qilish qiyin emas.
Trigonometrik funksiyalarning xossalari: sinus va kosinus
Sinus va kosinus, tangens va kotangensning asosiy xossalarini ko'rib chiqish va solishtirish uchun ularning funksiyalarini chizish kerak. Buni ikki o'lchovli koordinatalar tizimida joylashgan egri chiziq shaklida bajarish mumkin.
O'ylab ko'ring taqqoslash jadvali sinus va kosinusning xususiyatlari:

| Sinus to'lqini | Kosinus |
|---|---|
| y = sin x | y = cos x |
| ODZ [-1; 1] | ODZ [-1; 1] |
| sin x = 0, x = pk uchun, bu erda k s Z | cos x = 0, x = p/2 + pk uchun, bu erda k s Z |
| sin x = 1, x = p/2 + 2pk uchun, bu erda k s Z | cos x = 1, x = 2pk da, bu erda k s Z |
| sin x = - 1, x = 3p/2 + 2pk da, bu erda k s Z | cos x = - 1, x = p + 2pk uchun, bu erda k s Z |
| sin (-x) = - sin x, ya'ni funksiya toq | cos (-x) = cos x, ya'ni funksiya juft |
| funksiya davriy, eng kichik davri 2p | |
| sin x › 0, x I va II choraklarga tegishli yoki 0° dan 180° gacha (2pk, p + 2pk) | cos x › 0, x bilan I va IV choraklarga tegishli yoki 270° dan 90° gacha (- p/2 + 2pk, p/2 + 2pk) |
| sin x ‹ 0, x uchinchi va to'rtinchi choraklarga tegishli yoki 180° dan 360° gacha (p + 2pk, 2p + 2pk) | cos x ‹ 0, x 2 va 3 choraklarga tegishli yoki 90° dan 270° gacha (p/2 + 2pk, 3p/2 + 2pk) |
| [- p/2 + 2pk, p/2 + 2p] oraliqda ortadi. | [-p + 2pk, 2pk] oraliqda ortadi |
| [p/2 + 2pk, 3p/2 + 2p] oraliqlarda kamayadi | intervallarda kamayadi |
| hosila (sin x)’ = cos x | hosila (cos x)’ = - sin x |
Funksiyaning juft yoki juft emasligini aniqlash juda oddiy. Trigonometrik miqdorlarning belgilari bilan trigonometrik doirani tasavvur qilish va grafikni OX o'qiga nisbatan aqliy ravishda "katlash" kifoya. Agar belgilar bir-biriga to'g'ri kelsa, funktsiya juft, aks holda toq bo'ladi.

Radianlarning kiritilishi va sinus va kosinus to'lqinlarining asosiy xususiyatlarining ro'yxati bizga quyidagi naqshni taqdim etishga imkon beradi:

Formulaning to'g'riligini tekshirish juda oson. Misol uchun, x = p/2 uchun sinus 1 ga teng, x = 0 ning kosinasi kabi. Tekshirish jadvallarga murojaat qilish yoki berilgan qiymatlar uchun funktsiya egri chizig'ini kuzatish orqali amalga oshirilishi mumkin.
Tangensoidlar va kotangentsoidlarning xossalari
Tangens va kotangens funksiyalarning grafiklari sinus va kosinus funksiyalaridan sezilarli farq qiladi. tg va ctg qiymatlari bir-biriga o'zaro bog'liqdir.


- Y = tan x.
- Tangens x = p/2 + pk da y ning qiymatlariga intiladi, lekin ularga hech qachon etib bormaydi.
- Tangentoidning eng kichik musbat davri p dir.
- Tg (- x) = - tg x, ya'ni funksiya toq.
- Tg x = 0, x = p uchun.
- Funktsiya ortib bormoqda.
- Tg x › 0, x s uchun (pk, p/2 + pk).
- Tg x ‹ 0, x s uchun (— p/2 + pk, pk).
- Hosil (tg x)’ = 1/cos 2 x.
Keling, ko'rib chiqaylik grafik tasvir matnda quyida kotangentoidlar.

Kotangentoidlarning asosiy xususiyatlari:
- Y = karavot x.
- Sinus va kosinus funktsiyalaridan farqli o'laroq, tangentoidda Y barcha haqiqiy sonlar to'plamining qiymatlarini olishi mumkin.
- Kotangentoid x = pk da y ning qiymatlariga intiladi, lekin ularga hech qachon etib bormaydi.
- Kotangentoidning eng kichik musbat davri p ga teng.
- Ctg (- x) = - ctg x, ya'ni funksiya toq.
- Ctg x = 0, x = p/2 + pk uchun.
- Funktsiya pasaymoqda.
- Ctg x › 0, x s uchun (pk, p/2 + pk).
- Ctg x ‹ 0, x s uchun (p/2 + pk, pk).
- Hosil (ctg x)’ = - 1/sin 2 x To'g'ri