Ang batas ni Hooke ng tensyon at compression. Longitudinal at transverse deformation Pagpapasiya ng relatibong longitudinal deformation

Isaalang-alang natin ang mga deformation na nangyayari sa panahon ng pag-igting at pag-compress ng mga rod. Kapag nakaunat, tumataas ang haba ng baras at bumababa ang mga nakahalang na sukat. Kapag naka-compress, sa kabaligtaran, ang haba ng baras ay bumababa at ang mga transverse na sukat ay tumataas. Sa Fig. 2.7 ang may tuldok na linya ay nagpapakita ng deformed view ng isang stretch rod.

ℓ – haba ng baras bago ilapat ang pagkarga;

ℓ 1 – haba ng baras pagkatapos ilapat ang pagkarga;

b – nakahalang dimensyon bago ilapat ang pagkarga;

b 1 – nakahalang laki pagkatapos ng paglalagay ng load.

Absolute longitudinal strain ∆ℓ = ℓ 1 – ℓ.

Absolute transverse strain ∆b = b 1 – b.

Ang halaga ng relatibong linear deformation ε ay maaaring tukuyin bilang ratio ng absolute elongation ∆ℓ sa unang haba ng beam ℓ

Ang mga transverse deformation ay matatagpuan nang katulad

Kapag naunat, bumababa ang mga nakahalang dimensyon: ε > 0, ε′< 0; при сжатии: ε < 0, ε′ >0. Ipinapakita ng karanasan na sa panahon ng mga elastic deformation, ang transverse deformation ay palaging direktang proporsyonal sa longitudinal.

ε′ = – νε. (2.7)

Ang proportionality coefficient ν ay tinatawag Poisson's ratio o transverse strain ratio. Kinakatawan nito ang ganap na halaga ng ratio ng transverse sa longitudinal deformation sa pag-igting ng ehe

Pinangalanan ang Pranses na siyentipiko na unang nagmungkahi nito maagang XIX siglo. Ang ratio ng Poisson ay isang pare-parehong halaga para sa isang materyal sa loob ng mga limitasyon ng mga elastic deformation (ibig sabihin, mga deformation na nawawala pagkatapos maalis ang load). Para sa iba't ibang materyales Ang ratio ng Poisson ay nag-iiba sa loob ng 0 ≤ ν ≤ 0.5: para sa bakal ν = 0.28…0.32; para sa goma ν = 0.5; para sa isang plug ν = 0.

May kaugnayan sa pagitan ng stress at elastic deformation na kilala bilang Batas ni Hooke:

σ = Eε. (2.9)

Ang proportionality coefficient E sa pagitan ng stress at strain ay tinatawag na normal na elastic modulus o Young's modulus. Ang dimensyon ng E ay kapareho ng boltahe. Tulad ng ν, ang E ay nababanat pare-pareho ang materyal. Paano higit na halaga E, ang mas kaunti, ang iba pang mga bagay ay pantay, ay ang longitudinal deformation. Para sa bakal E = (2...2.2)10 5 MPa o E = (2...2.2)10 4 kN/cm 2.

Ang pagpapalit sa formula (2.9) ng halaga ng σ ayon sa formula (2.2) at ε ayon sa formula (2.5), nakakakuha tayo ng expression para sa absolute deformation

Ang produktong EF ay tinatawag ang tigas ng troso sa pag-igting at compression.

Ang mga formula (2.9) at (2.10) ay iba't ibang hugis mga talaan ng batas ni Hooke na iminungkahi sa kalagitnaan ng ika-17 siglo siglo. Modernong anyo Ang mga pag-record ng pangunahing batas na ito ng pisika ay lumitaw nang maglaon - sa simula ng ika-19 na siglo.

Ang formula (2.10) ay may bisa lamang sa mga lugar kung saan pare-pareho ang puwersa N at paninigas ng EF. Para sa isang stepped rod at isang baras na puno ng ilang pwersa, ang mga elongation ay kinakalkula sa mga seksyon na may pare-pareho ang N at F at ang mga resulta ay summed algebraically

Kung nagbabago ang mga dami na ito ayon sa isang tuluy-tuloy na batas, ang ∆ℓ ay kinakalkula ng formula

Sa ilang mga kaso, upang matiyak normal na operasyon mga makina at istruktura, ang mga sukat ng kanilang mga bahagi ay dapat mapili upang, bilang karagdagan sa kondisyon ng lakas, ang kondisyon ng higpit ay matiyak

kung saan ∆ℓ – pagbabago sa mga sukat ng bahagi;

[∆ℓ] – ang pinahihintulutang halaga ng pagbabagong ito.

Binibigyang-diin namin na ang pagkalkula ng katigasan ay palaging umaakma sa pagkalkula ng lakas.

2.4. Pagkalkula ng isang pamalo na isinasaalang-alang ang sarili nitong timbang

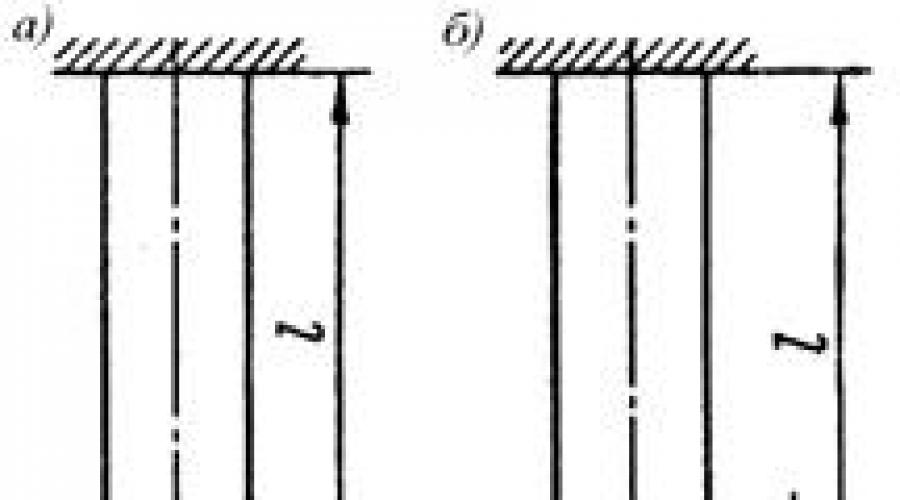
Ang pinakasimpleng halimbawa ng isang problema tungkol sa pag-unat ng isang baras na may mga parameter na nag-iiba sa haba nito ay ang problema tungkol sa pag-unat ng isang prismatic rod sa ilalim ng pagkilos ng sarili nitong timbang (Larawan 2.8a). Ang longitudinal force N x sa cross section ng beam na ito (sa layo x mula sa lower end nito) ay katumbas ng puwersa ng gravity ng pinagbabatayan na bahagi ng beam (Fig. 2.8, b), i.e.

N x = γFx, (2.14)

saan γ – volumetric na timbang materyal na pamalo.

Ang longitudinal na puwersa at stress ay nagbabago nang linear, na umaabot sa maximum sa pagkaka-embed. Ang axial displacement ng isang arbitrary na seksyon ay katumbas ng pagpahaba ng itaas na bahagi ng beam. Samakatuwid, dapat itong matukoy gamit ang formula (2.12), ang pagsasama ay isinasagawa mula sa kasalukuyang halaga x hanggang x = ℓ:

Nakuha namin ang isang expression para sa isang arbitrary na seksyon ng baras

Sa x = ℓ ang displacement ay pinakamalaki, ito ay katumbas ng pagpahaba ng baras

Ang Figure 2.8, c, d, e ay nagpapakita ng mga graph ng N x, σ x at u x

I-multiply ang numerator at denominator ng formula (2.17) sa F at makuha ang:

Ang ekspresyong γFℓ ay katumbas ng sariling bigat ng pamalo G. Samakatuwid

Ang formula (2.18) ay maaaring makuha kaagad mula sa (2.10), kung naaalala natin na ang resulta ng sariling timbang G ay dapat ilapat sa gitna ng gravity ng baras at samakatuwid ito ay nagiging sanhi ng pagpahaba lamang ng itaas na kalahati ng baras (Fig .2.8, a).

Kung ang mga tungkod, bilang karagdagan sa kanilang sariling timbang, ay puno din ng puro paayon na puwersa, kung gayon ang mga stress at deformation ay natutukoy batay sa prinsipyo ng kalayaan ng pagkilos ng mga puwersa nang hiwalay mula sa puro pwersa at mula sa kanilang sariling timbang, pagkatapos nito ang mga resulta ay idinagdag.

Ang prinsipyo ng independiyenteng pagkilos ng mga pwersa sumusunod mula sa linear deformability ng nababanat na mga katawan. Ang kakanyahan nito ay nakasalalay sa katotohanan na ang anumang halaga (stress, displacement, deformation) mula sa pagkilos ng isang pangkat ng mga puwersa ay maaaring makuha bilang kabuuan ng mga halaga na matatagpuan mula sa bawat puwersa nang hiwalay.

Isaalang-alang natin ang isang tuwid na baras ng pare-pareho ang cross-section, na mahigpit na naayos sa tuktok. Hayaang magkaroon ng haba ang baras at ma-load ng tensile force F . Ang pagkilos ng puwersang ito ay nagdaragdag sa haba ng baras ng isang tiyak na halaga Δ (Larawan 9.7, a).

Kapag ang baras ay na-compress na may parehong puwersa F ang haba ng pamalo ay mababawasan ng parehong halaga Δ (Larawan 9.7, b).

Magnitude Δ , katumbas ng pagkakaiba sa pagitan ng mga haba ng baras pagkatapos ng pagpapapangit at bago ang pagpapapangit, ay tinatawag na absolute linear deformation (pagpahaba o pagpapaikli) ng baras kapag ito ay nakaunat o naka-compress.

Ganap na linear strain ratio Δ sa orihinal na haba ng baras ay tinatawag na relatibong linear na pagpapapangit at tinutukoy ng titik ε o ε x ( nasaan ang index x ay nagpapahiwatig ng direksyon ng pagpapapangit). Kapag ang baras ay nakaunat o naka-compress, ang halaga ε ay simpleng tinatawag na relatibong longitudinal deformation ng baras. Ito ay tinutukoy ng formula:

Ang paulit-ulit na pag-aaral ng proseso ng pagpapapangit ng isang nakaunat o naka-compress na baras sa nababanat na yugto ay nakumpirma ang pagkakaroon ng isang tuwid na linya proporsyonal na pag-asa sa pagitan ng normal na stress at relative longitudinal strain. Ang pag-asa na ito ay tinatawag na batas ni Hooke at may anyo:

Magnitude E tinatawag na modulus ng longitudinal elasticity o ang modulus ng unang uri. Ito ay isang pisikal na pare-pareho (pare-pareho) para sa bawat uri ng materyal ng pamalo at nagpapakilala sa katigasan nito. Mas malaki ang halaga E , mas mababa ang magiging longitudinal deformation ng baras. Magnitude E sinusukat sa parehong mga yunit bilang boltahe, iyon ay, in Pa , MPa , at mga katulad nito. Ang mga halaga ng nababanat na modulus ay nakapaloob sa mga talahanayan ng sanggunian at literatura na pang-edukasyon. Halimbawa, ang halaga ng modulus ng longitudinal elasticity ng bakal ay kinuha katumbas ng E = 2∙10 5 MPa , at kahoy

E = 0.8∙10 5 MPa.

Kapag kinakalkula ang mga rod sa pag-igting o compression, madalas na kailangan upang matukoy ang halaga ng absolute longitudinal deformation kung ang magnitude ng longitudinal force, cross-sectional area at materyal ng rod ay kilala. Mula sa formula (9.8) makikita natin ang: . Palitan natin ang ekspresyong ito ε ang halaga nito mula sa formula (9.9). Bilang resulta nakukuha namin = . Kung gagamitin natin ang normal na formula ng stress , pagkatapos ay makuha namin ang pangwakas na pormula para sa pagtukoy ng ganap na longitudinal deformation:

Ang produkto ng modulus ng longitudinal elasticity at ang cross-sectional area ng rod ay tinatawag na katigasan kapag binanat o pinipiga.

Pag-aaral ng formula (9.10), maaari tayong gumuhit ng isang makabuluhang konklusyon: ang ganap na paayon na pagpapapangit ng isang baras sa panahon ng pag-igting (compression) ay direktang proporsyonal sa produkto ng paayon na puwersa at ang haba ng baras at inversely proporsyonal sa higpit nito.

Tandaan na ang formula (9.10) ay maaaring gamitin sa kaso kapag ang cross section ng baras at longitudinal na puwersa may mga pare-parehong halaga sa buong haba nito. Sa pangkalahatang kaso, kapag ang isang baras ay may stepwise variable stiffness at na-load kasama ang haba nito na may ilang mga puwersa, kinakailangan na hatiin ito sa mga seksyon at matukoy ang ganap na mga deformation ng bawat isa sa kanila gamit ang formula (9.10).

Ang algebraic sum ng absolute deformations ng bawat seksyon ay magiging katumbas ng absolute deformation ng buong rod, iyon ay:

Ang mga pahaba na deformation ng baras dahil sa pare-parehong pagkilos ibinahagi load kasama ang axis nito (halimbawa, mula sa pagkilos ng sarili nitong timbang), ay tinutukoy ng sumusunod na formula, na ipinakita namin nang walang patunay:

Sa kaso ng pag-igting o compression ng isang baras, bilang karagdagan sa mga longitudinal deformation, nangyayari rin ang mga transverse deformation, parehong ganap at kamag-anak. Ipahiwatig natin sa pamamagitan ng b cross-sectional na laki ng baras bago ang pagpapapangit. Kapag ang pamalo ay iniunat sa pamamagitan ng puwersa F ang laki na ito ay bababa ng Δb , na siyang ganap na transverse deformation ng baras. Ang halagang ito ay may negatibong tanda Sa panahon ng compression, sa kabaligtaran, ang ganap na transverse deformation ay magkakaroon positibong tanda(Larawan 9.8).

Isaalang-alang natin ang isang tuwid na sinag ng pare-pareho ang haba ng cross-section (Larawan 1.5), na naka-embed sa isang dulo at na-load sa kabilang dulo na may tensile force R. Sa ilalim ng puwersa R ang sinag ay pinahaba ng isang tiyak na halaga , na tinatawag na total (o absolute) elongation (absolute longitudinal deformation).

kanin. 1.5. Pagpapapangit ng sinag

Sa anumang mga punto ng sinag na isinasaalang-alang mayroong isang magkaparehong estado ng stress at, samakatuwid, ang mga linear na deformation para sa lahat ng mga punto nito ay pareho. Samakatuwid, ang halaga e ay maaaring tukuyin bilang ang ratio ng ganap na pagpahaba sa orihinal na haba ng beam, i.e.

Ang mga bar na gawa sa iba't ibang mga materyales ay humahaba nang iba. Para sa mga kaso kung saan ang mga stress sa beam ay hindi lalampas sa proporsyonalidad na limitasyon, ang sumusunod na relasyon ay itinatag sa pamamagitan ng karanasan:

saan N- longitudinal force in mga cross section kahoy; F- cross-sectional area ng beam; E- koepisyent depende sa pisikal na katangian materyal.

Isinasaalang-alang na ang normal na stress sa cross section ng beam σ = N/F nakukuha namin ε = σ/E. saan galing σ = εE.

Ang ganap na pagpahaba ng isang sinag ay ipinahayag ng formula

Ang sumusunod na pormulasyon ng batas ni Hooke ay mas pangkalahatan: ang relatibong longitudinal strain ay direktang proporsyonal sa normal na stress. Sa pormulasyon na ito, ginagamit ang batas ni Hooke hindi lamang sa pag-aaral ng tensyon at compression ng mga beam, kundi pati na rin sa ibang mga seksyon ng kurso.

Magnitude E tinatawag na elastic modulus ng unang uri. Ito ay isang pisikal na pare-pareho ng isang materyal na nagpapakilala sa katigasan nito. Mas mataas ang halaga E, ang mas kaunti, ang iba pang mga bagay ay pantay, ang paayon na pagpapapangit. Ang modulus ng elasticity ay ipinahayag sa parehong mga yunit bilang stress, i.e. sa pascals (Pa) (bakal E=2* 10 5 MPa, tanso E= 1 * 10 5 MPa).

Trabaho EF ay tinatawag na stiffness ng cross section ng beam sa pag-igting at compression.

Bilang karagdagan sa longitudinal deformation, kapag ang isang compressive o tensile force ay inilapat sa beam, ang transverse deformation ay sinusunod din. Kapag ang isang sinag ay naka-compress, ang mga nakahalang na sukat nito ay tumataas, at kapag naunat, bumababa ang mga ito. Kung ang nakahalang laki ng sinag bago ilapat ang compressive pwersa dito R italaga SA, at pagkatapos ilapat ang mga puwersang ito B - ∆B, pagkatapos ay ang halaga ∆V ay magsasaad ng ganap na transverse deformation ng beam.

Ang ratio ay ang relatibong transverse strain.

Ipinapakita ng karanasan na sa mga stress na hindi lalampas sa nababanat na limitasyon, ang relatibong transverse deformation ay direktang proporsyonal sa kamag-anak na longitudinal deformation, ngunit may kabaligtaran na tanda:

Ang proportionality coefficient q ay depende sa materyal ng troso. Ito ay tinatawag na transverse strain coefficient (o Ang ratio ng Poisson ) at ang ratio ng relatibong transverse sa longitudinal deformation, na kinuha ayon sa ganap na halaga, ibig sabihin. Ang ratio ng Poisson kasama ang elastic modulus E nailalarawan ang mga nababanat na katangian ng materyal.

Ang ratio ng Poisson ay tinutukoy sa eksperimentong paraan. Para sa iba't ibang mga materyales mayroon itong mga halaga mula sa zero (para sa cork) hanggang sa isang halaga na malapit sa 0.50 (para sa goma at paraffin). Para sa bakal, ang ratio ng Poisson ay 0.25...0.30; para sa isang bilang ng iba pang mga metal (cast iron, zinc, bronze, copper) ito

ay may mga halaga mula 0.23 hanggang 0.36.

kanin. 1.6. Beam ng variable na cross section

Ang pagpapasiya ng cross-sectional na halaga ng baras ay isinasagawa batay sa kondisyon ng lakas

kung saan ang [σ] ay ang pinahihintulutang stress.

Tukuyin natin ang longitudinal displacement δ a puntos A axis ng isang sinag na nakaunat sa pamamagitan ng puwersa P( kanin. 1.6).

Ito ay katumbas ng ganap na pagpapapangit ng bahagi ng sinag ad nakapaloob sa pagitan ng embedment at ng seksyong iginuhit sa punto d, mga. Ang longitudinal deformation ng beam ay tinutukoy ng formula

Ang formula na ito ay naaangkop lamang kapag, sa loob ng buong haba ng seksyon, ang longitudinal forces N at stiffness EF ang mga cross section ng beam ay pare-pareho. Sa kasong isinasaalang-alang, sa site ab longitudinal na puwersa N ay katumbas ng zero (hindi namin isinasaalang-alang ang patay na bigat ng beam), at sa lugar bd ito ay katumbas R, bilang karagdagan, ang cross-sectional area ng troso sa lugar ac naiiba sa cross-sectional area sa site cd. Samakatuwid, ang longitudinal deformation ng lugar ad ay dapat na matukoy bilang ang kabuuan ng mga longitudinal deformation ng tatlong mga seksyon ab, bc At CD, para sa bawat isa kung saan ang mga halaga N At EF pare-pareho sa buong haba nito:

Mga longitudinal na puwersa sa mga itinuturing na seksyon ng sinag

Kaya naman,

Katulad nito, maaari mong matukoy ang mga displacement δ ng anumang mga punto sa axis ng beam, at gamitin ang kanilang mga halaga upang bumuo ng isang diagram pahaba na paggalaw (epureδ), ibig sabihin. isang graph na naglalarawan ng pagbabago sa mga paggalaw na ito sa kahabaan ng axis ng beam.

4.2.3. Mga kondisyon ng lakas. Pagkalkula ng katigasan.

Kapag sinusuri ang mga stress ng cross-sectional area F at ang mga longitudinal na pwersa ay kilala at ang pagkalkula ay binubuo ng pagkalkula ng kinakalkula (aktwal) na mga stress σ sa mga katangiang seksyon ng mga elemento. Ang pinakamataas na boltahe na nakuha ay pagkatapos ay inihambing sa pinahihintulutang isa:

Kapag pumipili ng mga seksyon tukuyin ang mga kinakailangang lugar [F] mga cross section ng elemento (batay sa mga kilalang longitudinal forces N at pinahihintulutang diin [σ]). Mga tinatanggap na cross-sectional na lugar F dapat matugunan ang kundisyon ng lakas na ipinahayag sa ang sumusunod na anyo:

Kapag tinutukoy ang kapasidad ng pagkarga Sa pamamagitan ng kilalang halaga F at pinahihintulutang stress [σ], ang mga pinahihintulutang halaga [N] ng mga longitudinal na pwersa ay kinakalkula:

Batay sa nakuha na mga halaga [N], ang mga pinahihintulutang halaga ng mga panlabas na pag-load ay pagkatapos ay tinutukoy [ P].

Para sa kasong ito, ang kondisyon ng lakas ay may anyo

Dami mga karaniwang coefficient ang mga margin ng kaligtasan ay itinatag ng mga pamantayan. Nakasalalay sila sa klase ng istraktura (kabisera, pansamantala, atbp.), Ang nilalayon nitong buhay ng serbisyo, pagkarga (static, cyclic, atbp.), posibleng heterogeneity sa paggawa ng mga materyales (halimbawa, kongkreto), at ang uri ng pagpapapangit (tension, compression, baluktot, atbp.) at iba pang mga kadahilanan. Sa ilang mga kaso, kinakailangan upang bawasan ang kadahilanan ng kaligtasan upang mabawasan ang bigat ng istraktura, at kung minsan upang madagdagan ang kadahilanan ng kaligtasan - kung kinakailangan, isaalang-alang ang pagsusuot ng mga gasgas na bahagi ng mga makina, kaagnasan at pagkabulok ng materyal.

Ang mga halaga ng karaniwang mga kadahilanan sa kaligtasan para sa iba't ibang mga materyales, istruktura at pagkarga sa karamihan ng mga kaso ay may mga sumusunod na halaga: - 2.5...5 at - 1.5...2.5.

Sa pamamagitan ng pagsuri sa katigasan ng isang elemento ng istruktura sa isang estado ng purong tension-compression, ibig sabihin namin ang paghahanap ng sagot sa tanong: sapat ba ang mga halaga ng mga katangian ng higpit ng elemento (modulus ng pagkalastiko ng materyal)? E at cross-sectional area F), upang ang maximum ng lahat ng mga halaga ng mga displacement ng mga punto ng elemento na dulot ng panlabas na pwersa, hindi lumampas ang u max sa ilang tinukoy na halaga ng limitasyon [u]. Ito ay pinaniniwalaan na kung ang hindi pagkakapantay-pantay u max< [u] конструкция переходит в предельное состояние.

Isaalang-alang natin ang isang tuwid na sinag ng pare-pareho ang cross-section na may haba na naka-embed sa isang dulo at na-load sa kabilang dulo na may tensile force P (Fig. 8.2, a). Sa ilalim ng impluwensya ng puwersa P, ang sinag ay nagpapahaba ng isang tiyak na halaga, na tinatawag na kumpleto, o ganap, pagpahaba (absolute longitudinal deformation).

Sa anumang mga punto ng sinag na isinasaalang-alang mayroong isang magkaparehong estado ng stress at, samakatuwid, ang mga linear na pagpapapangit (tingnan ang § 5.1) para sa lahat ng mga punto nito ay pareho. Samakatuwid, ang halaga ay maaaring tukuyin bilang ang ratio ng ganap na pagpahaba sa paunang haba ng beam I, i.e. Ang linear deformation sa panahon ng tension o compression ng mga beam ay karaniwang tinatawag na relative elongation, o relative longitudinal deformation, at itinalaga.

Kaya naman,

Ang relatibong longitudinal strain ay sinusukat sa abstract units. Sumang-ayon tayo na isaalang-alang ang elongation strain bilang positibo (Fig. 8.2, a), at ang compression strain ay negatibo (Fig. 8.2, b).

Ang mas malaki ang magnitude ng puwersa na lumalawak sa sinag, mas malaki, ang iba pang mga bagay ay pantay, ang pagpahaba ng sinag; paano mas malaking lugar cross-section ng beam, mas mababa ang pagpahaba ng beam. Ang mga bar na gawa sa iba't ibang mga materyales ay humahaba nang iba. Para sa mga kaso kung saan ang mga stress sa beam ay hindi lalampas sa proporsyonalidad na limitasyon (tingnan ang § 6.1, talata 4), ang sumusunod na relasyon ay itinatag sa pamamagitan ng karanasan:

Narito ang N ay ang longitudinal force sa mga cross section ng beam; - cross-sectional area ng beam; Ang E ay isang koepisyent depende sa mga pisikal na katangian ng materyal.

Isinasaalang-alang na ang normal na stress sa cross section ng beam ay nakuha namin

Ang ganap na pagpahaba ng isang sinag ay ipinahayag ng formula

ibig sabihin, ang absolute longitudinal deformation ay direktang proporsyonal sa longitudinal force.

Sa unang pagkakataon, ang batas ng direktang proporsyonalidad sa pagitan ng mga puwersa at mga deformation ay nabuo (noong 1660). Ang mga formula (10.2)-(13.2) ay mga mathematical na expression ng batas ni Hooke para sa tensyon at compression ng isang beam.

Ang sumusunod na pormulasyon ng batas ni Hooke ay mas pangkalahatan [tingnan. formula (11.2) at (12.2)]: ang relatibong longitudinal strain ay direktang proporsyonal sa normal na stress. Sa pormulasyon na ito, ginagamit ang batas ni Hooke hindi lamang sa pag-aaral ng tensyon at compression ng mga beam, kundi pati na rin sa ibang mga seksyon ng kurso.

Ang dami E na kasama sa mga formula (10.2)-(13.2) ay tinatawag na modulus of elasticity ng unang uri (dinaglat bilang modulus of elasticity) Ang dami na ito ay isang pisikal na pare-pareho ng materyal, na nagpapakilala sa katigasan nito. Kung mas malaki ang halaga ng E, mas kaunti, ang iba pang mga bagay ay pantay, ang longitudinal deformation.

Tatawagin namin ang produkto na higpit ng cross section ng beam sa ilalim ng pag-igting at compression.

Ipinapakita ng Appendix I ang mga halaga ng elastic modulus E para sa iba't ibang mga materyales.

Ang formula (13.2) ay maaaring gamitin upang kalkulahin ang absolute longitudinal deformation ng isang seksyon ng isang beam ng haba lamang sa ilalim ng kondisyon na ang seksyon ng beam sa loob ng seksyong ito ay pare-pareho at ang longitudinal force N ay pareho sa lahat ng cross section.

Bilang karagdagan sa longitudinal deformation, kapag ang isang compressive o tensile force ay inilapat sa beam, ang transverse deformation ay sinusunod din. Kapag ang isang sinag ay naka-compress, ang mga nakahalang na sukat nito ay tumataas, at kapag naunat, bumababa ang mga ito. Kung ang transverse size ng beam bago ilapat ang compressive forces P dito ay itinalagang b, at pagkatapos ng application ng mga pwersang ito (Fig. 9.2), ang halaga ay magsasaad ng absolute transverse deformation ng beam.

Ang ratio ay ang relatibong transverse strain.

Ipinapakita ng karanasan na sa mga stress na hindi lalampas sa elastic na limitasyon (tingnan ang § 6.1, talata 3), ang relatibong transverse deformation ay direktang proporsyonal sa relatibong longitudinal deformation, ngunit may kabaligtaran na tanda:

Ang koepisyent ng proporsyonalidad sa formula (14.2) ay depende sa materyal ng beam. Tinatawag itong transverse deformation ratio, o Poisson's ratio, at ang ratio ng relatibong transverse deformation sa longitudinal deformation, na kinuha sa absolute value, i.e.

Ang ratio ng Poisson, kasama ang nababanat na modulus E, ay nagpapakilala sa mga nababanat na katangian ng materyal.

Ang halaga ng ratio ng Poisson ay tinutukoy sa eksperimentong paraan. Para sa iba't ibang mga materyales mayroon itong mga halaga mula sa zero (para sa cork) hanggang sa isang halaga na malapit sa 0.50 (para sa goma at paraffin). Para sa bakal, ang ratio ng Poisson ay 0.25-0.30; para sa isang bilang ng iba pang mga metal (cast iron, zinc, bronze, copper) mayroon itong mga halaga mula 0.23 hanggang 0.36. Ang mga tinatayang halaga ng ratio ng Poisson para sa iba't ibang mga materyales ay ibinibigay sa Appendix I.

Kapag kumikilos ang mga puwersa ng makunat sa kahabaan ng axis ng beam, tumataas ang haba nito at bumababa ang mga transverse na sukat nito. Kapag kumikilos ang mga puwersa ng compressive, nangyayari ang kabaligtaran na kababalaghan. Sa Fig. Ang Figure 6 ay nagpapakita ng isang sinag na nakaunat ng dalawang puwersa P. Bilang resulta ng pag-igting, ang sinag ay pinahaba ng isang halaga Δ l, na tinatawag na ganap na pagpahaba, at nakukuha namin ganap na transverse contraction Δа .

Ang ratio ng ganap na pagpahaba at pagpapaikli sa orihinal na haba o lapad ng sinag ay tinatawag kamag-anak na pagpapapangit. SA sa kasong ito tinatawag na relative deformation longitudinal deformation, A - relatibong transverse deformation. Ang ratio ng relatibong transverse strain sa relative longitudinal strain ay tinatawag Ang ratio ng Poisson: (3.1)

Ang ratio ng Poisson para sa bawat materyal bilang isang nababanat na pare-pareho ay tinutukoy empirically at nasa loob ng: ; para sa bakal.

Sa loob ng mga limitasyon ng nababanat na mga pagpapapangit, naitatag na ang normal na stress ay direktang proporsyonal sa kamag-anak na longitudinal na pagpapapangit. Ang dependency na ito ay tinatawag Batas ni Hooke:

, (3.2)

saan E- koepisyent ng proporsyonalidad, tinatawag modulus ng normal na pagkalastiko.