Mga katangian ng function na pinakamalaki at pinakamaliit na halaga. Paano mahanap ang pinakamaliit na halaga ng isang function

At upang malutas ito kakailanganin mo ng kaunting kaalaman sa paksa. Ang isa pang taon ng pag-aaral ay nagtatapos, ang lahat ay nais na magbakasyon, at upang mailapit ang sandaling ito, agad akong darating sa punto:

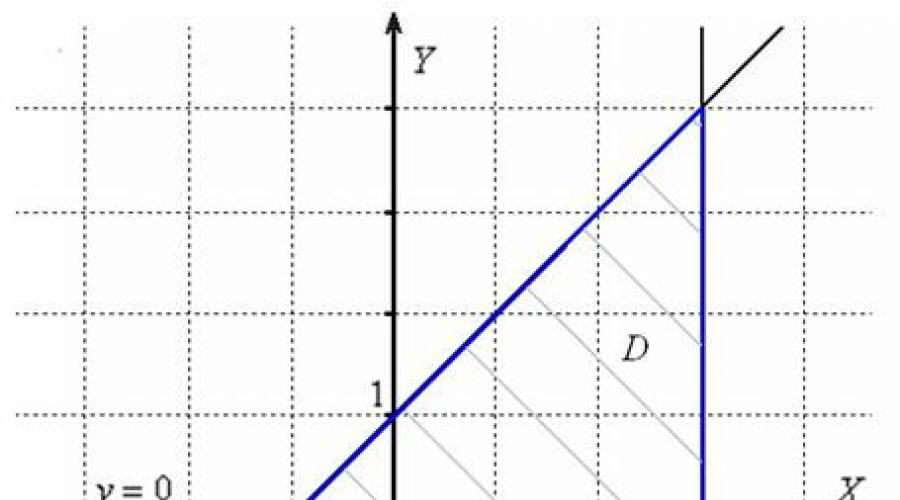
Magsimula tayo sa lugar. Ang lugar na tinutukoy sa kondisyon ay limitado sarado hanay ng mga punto sa isang eroplano. Halimbawa, ang hanay ng mga puntos na nililimitahan ng isang tatsulok, kasama ang BUONG tatsulok (kung galing mga hangganan"tusukin" kahit isang punto, pagkatapos ay hindi na isasara ang rehiyon). Sa pagsasagawa, mayroon ding mga lugar na hugis-parihaba, pabilog, at bahagyang mas malaki. kumplikadong mga hugis. Dapat tandaan na sa teorya pagsusuri sa matematika mahigpit na mga kahulugan ang ibinigay mga limitasyon, paghihiwalay, mga hangganan, atbp., ngunit sa palagay ko ay alam ng lahat ang mga konseptong ito sa isang intuitive na antas, at ngayon ay wala nang kailangan pa.

Ang isang patag na lugar ay karaniwang tinutukoy ng titik , at, bilang panuntunan, ay tinukoy nang analytical - sa pamamagitan ng ilang mga equation (hindi kinakailangang linear); mas madalas na hindi pagkakapantay-pantay. Karaniwang verbiage: "sarado na lugar na may hangganan ng mga linya."

Ang isang mahalagang bahagi ng gawain na isinasaalang-alang ay ang pagtatayo ng isang lugar sa pagguhit. Paano ito gawin? Kailangan mong iguhit ang lahat ng nakalistang linya (sa sa kasong ito 3 tuwid) at pag-aralan kung ano ang nangyari. Ang hinanap na lugar ay karaniwang bahagyang may kulay, at ang hangganan nito ay minarkahan ng makapal na linya:


Ang parehong lugar ay maaari ding itakda mga linear na hindi pagkakapantay-pantay: , na para sa ilang kadahilanan ay madalas na isinulat bilang isang enumerated list sa halip na sistema.
Dahil ang hangganan ay kabilang sa rehiyon, kung gayon ang lahat ng hindi pagkakapantay-pantay, siyempre, maluwag.

At ngayon ang kakanyahan ng gawain. Isipin na ang axis ay lalabas nang diretso patungo sa iyo mula sa pinanggalingan. Isaalang-alang ang isang function na tuloy-tuloy sa bawat isa punto ng lugar. Ang graph ng function na ito ay kumakatawan sa ilan ibabaw, at ang maliit na kaligayahan ay upang malutas ang problema ngayon hindi natin kailangang malaman kung ano ang hitsura ng ibabaw na ito. Maaari itong matatagpuan mas mataas, mas mababa, bumalandra sa eroplano - lahat ng ito ay hindi mahalaga. At ang mga sumusunod ay mahalaga: ayon sa Ang mga teorema ni Weierstrass, tuloy-tuloy V limitadong sarado lugar na naabot ng function ang pinakamalaking halaga nito (ang "pinakamataas") at ang pinakamaliit (ang "pinakamababa") mga halaga na kailangang hanapin. Ang ganitong mga halaga ay nakamit o V nakatigil na mga punto, kabilang sa rehiyonD , o sa mga puntong nasa hangganan ng lugar na ito. Ito ay humahantong sa isang simple at transparent na algorithm ng solusyon:

Halimbawa 1

Sa isang limitadong saradong lugar

Solusyon: Una sa lahat, kailangan mong ilarawan ang lugar sa pagguhit. Sa kasamaang palad, ito ay teknikal na mahirap para sa akin na gumawa ng isang interactive na modelo ng problema, at samakatuwid ay agad kong ipapakita ang panghuling paglalarawan, na nagpapakita ng lahat ng "kahina-hinalang" mga punto na natagpuan sa panahon ng pananaliksik. Karaniwang nakalista ang mga ito nang sunud-sunod habang natuklasan ang mga ito:

Batay sa preamble, ang desisyon ay maginhawang nahahati sa dalawang punto:

I) Maghanap ng mga nakatigil na puntos. Isa itong karaniwang aksyon na paulit-ulit naming isinagawa sa klase. tungkol sa extrema ng ilang variable:

Nakahanap ng nakatigil na punto nabibilang mga lugar: (markahan ito sa drawing), na nangangahulugang dapat nating kalkulahin ang halaga ng function sa isang naibigay na punto:

- tulad ng sa artikulo Ang pinakamalaki at pinakamaliit na halaga ng isang function sa isang segment, iha-highlight ko ang mahahalagang resulta nang naka-bold. Ito ay maginhawa upang subaybayan ang mga ito sa isang notebook na may lapis.

Bigyang-pansin ang aming pangalawang kaligayahan - walang saysay na suriin sapat na kondisyon para sa isang extremum. bakit naman Kahit na sa isang punto ay umabot ang function, halimbawa, lokal na minimum, pagkatapos ay HINDI ito nangangahulugang ang magiging resulta ng halaga minimal sa buong rehiyon (tingnan ang simula ng aralin tungkol sa mga walang kundisyong labis) .

Ano ang gagawin kung ang nakatigil na punto ay HINDI kabilang sa lugar? Halos wala! Dapat itong tandaan at magpatuloy sa susunod na punto.

II) Ginalugad natin ang hangganan ng rehiyon.

Dahil ang hangganan ay binubuo ng mga gilid ng isang tatsulok, ito ay maginhawa upang hatiin ang pag-aaral sa 3 subsection. Ngunit mas mahusay na huwag gawin ito kahit papaano. Mula sa aking pananaw, mas kapaki-pakinabang na isaalang-alang muna ang mga segment parallel coordinate axes, at una sa lahat, ang mga nakahiga sa mga palakol mismo. Upang maunawaan ang buong pagkakasunud-sunod at lohika ng mga aksyon, subukang pag-aralan ang pagtatapos "sa isang hininga":

1) Haharapin natin ang ilalim na bahagi ng tatsulok. Upang gawin ito, palitan nang direkta sa function:

Bilang kahalili, maaari mo itong gawin tulad nito:

Geometrically, nangangahulugan ito na ang coordinate plane (na ibinigay din ng equation)"nag-ukit" sa labas ng ibabaw isang "spatial" na parabola, na ang tuktok nito ay agad na pinaghihinalaan. Alamin natin saan siya matatagpuan:

– ang nagresultang halaga ay "bumagsak" sa lugar, at maaaring lumabas iyon sa puntong iyon (may marka sa drawing) naabot ng function ang pinakamalaki o pinakamaliit na halaga sa buong rehiyon. Sa isang paraan o iba pa, gawin natin ang mga kalkulasyon:

Ang iba pang mga "kandidato" ay, siyempre, ang mga dulo ng segment. Kalkulahin natin ang mga halaga ng function sa mga punto (may marka sa drawing):

Dito, sa pamamagitan ng paraan, maaari kang magsagawa ng isang oral mini-check gamit ang isang "nahubaran" na bersyon:

2) Upang pag-aralan ang kanang bahagi ng tatsulok, palitan ito sa function at "ayusin ang mga bagay":

Dito kami ay agad na magsasagawa ng isang magaspang na pagsusuri, "nagri-ring" sa naprosesong dulo ng segment:
, Mahusay.

Ang geometric na sitwasyon ay nauugnay sa nakaraang punto:

– ang resultang halaga ay “dumating din sa saklaw ng ating mga interes,” na nangangahulugang kailangan nating kalkulahin kung ano ang katumbas ng function sa lumitaw na punto:

Suriin natin ang pangalawang dulo ng segment:

Gamit ang function , magsagawa tayo ng control check:

3) Marahil lahat ay maaaring hulaan kung paano tuklasin ang natitirang bahagi. Pinapalitan namin ito sa pag-andar at isinasagawa ang mga pagpapasimple:

Mga dulo ng segment nasaliksik na, ngunit sa draft ay sinusuri pa rin namin kung nahanap namin nang tama ang function :
– kasabay ng resulta ng 1st subparagraph;
– kasabay ng resulta ng 2nd subparagraph.

Ito ay nananatiling malaman kung mayroong anumang bagay na kawili-wili sa loob ng segment:

- Meron! Ang pagpapalit ng tuwid na linya sa equation, nakukuha natin ang ordinate ng "kawili-wili" na ito:

Minarkahan namin ang isang punto sa pagguhit at hanapin ang kaukulang halaga ng function:

Suriin natin ang mga kalkulasyon gamit ang bersyon ng "badyet". :
, order.

At ang huling hakbang: MABUTI naming tinitingnan ang lahat ng mga "bold" na numero, inirerekomenda ko na ang mga nagsisimula ay gumawa ng isang listahan:

kung saan pipiliin namin ang pinakamalaki at pinakamaliit na halaga. Sagot Isulat natin sa istilo ng problema sa paghahanap ang pinakamalaki at pinakamaliit na halaga ng isang function sa isang segment:

Kung sakali, magko-comment ulit ako geometriko na kahulugan resulta:
– narito ang pinakamataas na punto ng ibabaw sa rehiyon;
– narito ang pinakamababang punto ng ibabaw sa lugar.

Sa nasuri na gawain, natukoy namin ang 7 "kahina-hinala" na mga punto, ngunit ang kanilang bilang ay nag-iiba sa bawat gawain. Para sa isang triangular na rehiyon, ang pinakamababang "set ng pananaliksik" ay binubuo ng tatlong puntos. Nangyayari ito kapag ang function, halimbawa, ay tumutukoy eroplano– ganap na malinaw na walang mga nakatigil na puntos, at ang pag-andar ay maaaring maabot ang pinakamataas/pinakamaliit na halaga nito lamang sa mga vertices ng tatsulok. Ngunit mayroon lamang isa o dalawang katulad na mga halimbawa - kadalasan kailangan mong harapin ang ilang uri ng ibabaw ng 2nd order.

Kung susubukan mong lutasin ang mga ganoong gawain nang kaunti, kung gayon ang mga tatsulok ay maaaring paikutin ang iyong ulo, at iyon ang dahilan kung bakit naghanda ako para sa iyo mga hindi pangkaraniwang halimbawa para maging square :))

Halimbawa 2

Hanapin ang pinakamalaki at pinakamaliit na halaga ng isang function sa isang saradong lugar na may hangganan ng mga linya

Halimbawa 3

Hanapin ang pinakamalaki at pinakamaliit na halaga ng isang function sa isang limitadong saradong lugar.

Espesyal na atensyon Bigyang-pansin ang nakapangangatwiran na pagkakasunud-sunod at pamamaraan ng pag-aaral sa hangganan ng rehiyon, pati na rin ang kadena ng mga intermediate na pagsusuri, na halos ganap na maiiwasan ang mga pagkakamali sa pagkalkula. Sa pangkalahatan, maaari mo itong lutasin sa anumang paraan na gusto mo, ngunit sa ilang mga problema, halimbawa, sa Halimbawa 2, mayroong bawat pagkakataon na gawing mas mahirap ang iyong buhay. Tinatayang sample pagtatapos ng mga takdang-aralin sa pagtatapos ng aralin.

I-systematize natin ang algorithm ng solusyon, kung hindi man sa aking kasipagan bilang isang gagamba, kahit papaano ay nawala ito sa mahabang thread ng mga komento ng unang halimbawa:

– Sa unang hakbang, bumuo kami ng isang lugar, ipinapayong lilim ito at i-highlight ang hangganan na may naka-bold na linya. Sa panahon ng solusyon, lilitaw ang mga puntos na kailangang markahan sa pagguhit.

- Maghanap ng mga nakatigil na puntos at kalkulahin ang mga halaga ng function sa kanila lamang na nabibilang sa rehiyon. I-highlight namin ang mga nagresultang halaga sa teksto (halimbawa, bilugan sila ng lapis). Kung ang isang nakatigil na punto ay HINDI kabilang sa rehiyon, pagkatapos ay markahan namin ang katotohanang ito ng isang icon o pasalita. Kung walang mga nakatigil na punto sa lahat, pagkatapos ay gumuhit kami ng isang nakasulat na konklusyon na wala sila. Sa anumang kaso, ang puntong ito ay hindi maaaring laktawan!

– Tinutuklasan namin ang hangganan ng rehiyon. Una, kapaki-pakinabang na maunawaan ang mga tuwid na linya na kahanay sa mga coordinate axes (kung meron man). Itinatampok din namin ang mga halaga ng pag-andar na kinakalkula sa mga "kahina-hinala" na mga punto. Maraming nasabi sa itaas tungkol sa pamamaraan ng solusyon at iba pa ang sasabihin sa ibaba - basahin, muling basahin, suriin ito!

– Mula sa mga napiling numero, piliin ang pinakamalaki at pinakamaliit na halaga at ibigay ang sagot. Minsan nangyayari na ang isang function ay umabot sa mga naturang halaga sa ilang mga punto nang sabay-sabay - sa kasong ito, ang lahat ng mga puntong ito ay dapat na maipakita sa sagot. Hayaan, halimbawa, at ito pala pinakamaliit na halaga. Pagkatapos ay isulat namin iyon

Ang mga huling halimbawa ay nakatuon sa iba kapaki-pakinabang na mga ideya na magiging kapaki-pakinabang sa pagsasanay:

Halimbawa 4

Hanapin ang pinakamalaki at pinakamaliit na halaga ng isang function sa isang saradong rehiyon .

Napanatili ko ang pormulasyon ng may-akda, kung saan ang lugar ay ibinigay sa anyo ng dobleng hindi pagkakapantay-pantay. Ang kundisyong ito ay maaaring isulat ng isang katumbas na sistema o sa isang mas tradisyonal na anyo para sa problemang ito:

Paalala ko sa iyo na may nonlinear nakatagpo kami ng mga hindi pagkakapantay-pantay noong , at kung hindi mo naiintindihan ang geometric na kahulugan ng notasyon, mangyaring huwag antalahin at linawin ang sitwasyon ngayon;-)

Solusyon, gaya ng dati, ay nagsisimula sa pagbuo ng isang lugar na kumakatawan sa isang uri ng "sole":

Hmm, minsan kailangan mong nguyain hindi lang ang granite ng agham...

I) Maghanap ng mga nakatigil na puntos:

Ang sistema ay pangarap ng tanga :)

Ang isang nakatigil na punto ay kabilang sa rehiyon, ibig sabihin, nasa hangganan nito.

And so, it’s okay... the lesson went well - ito ang ibig sabihin ng pag-inom ng tamang tsaa =)

II) Ginalugad natin ang hangganan ng rehiyon. Nang walang karagdagang ado, magsimula tayo sa x-axis:

1) Kung , kung gayon

Hanapin natin kung nasaan ang vertex ng parabola:
– pinahahalagahan ang gayong mga sandali – ikaw ay “natamaan” hanggang sa punto kung saan malinaw na ang lahat. Ngunit hindi pa rin namin nakakalimutan ang tungkol sa pagsuri:

Kalkulahin natin ang mga halaga ng function sa mga dulo ng segment:

2) C ibaba Alamin natin ang "ibaba" "sa isang pag-upo" - pinapalitan namin ang mga ito sa pag-andar nang walang anumang mga kumplikado, at magiging interesado lamang kami sa segment:

Kontrol:

Nagdudulot na ito ng kaunting kaguluhan sa monotonous na pagmamaneho sa kahabaan ng knurled track. Maghanap tayo ng mga kritikal na punto:

Magdesisyon tayo quadratic equation, may naaalala ka pa ba tungkol dito? ...Gayunpaman, tandaan, siyempre, kung hindi, hindi mo babasahin ang mga linyang ito =) Kung sa dalawang naunang halimbawa ang mga kalkulasyon sa mga decimal(which, by the way, is rare), tapos yung usual na naghihintay sa atin dito mga karaniwang fraction. Nahanap namin ang mga ugat ng "X" at ginagamit ang equation upang matukoy ang kaukulang mga coordinate ng "laro" ng mga punto ng "kandidato":


Kalkulahin natin ang mga halaga ng function sa mga nahanap na punto:

Suriin ang pag-andar sa iyong sarili.

Ngayon ay maingat nating pinag-aaralan ang mga napanalunang tropeo at isulat sagot:

Ito ay mga "kandidato", ito ay mga "kandidato"!

Upang malutas ito sa iyong sarili:

Halimbawa 5

Hanapin ang pinakamaliit at pinakamalaking halaga ng isang function sa isang saradong lugar

Ang isang entry na may mga kulot na braces ay ganito ang mababasa: "isang set ng mga puntos na ganoon."

Minsan sa mga ganitong halimbawa ginagamit nila Paraan ng Lagrange multiplier, Ngunit tunay na pangangailangan malabong gamitin ito. Kaya, halimbawa, kung ang isang function na may parehong lugar na "de" ay ibinigay, pagkatapos ay pagkatapos ng pagpapalit dito - na may derivative mula sa walang mga paghihirap; Bukod dito, ang lahat ay iginuhit sa "isang linya" (na may mga palatandaan) nang hindi kinakailangang isaalang-alang nang hiwalay ang itaas at mas mababang kalahating bilog. Pero, siyempre, marami pa kumplikadong mga kaso, kung saan walang Lagrange function (kung saan, halimbawa, ay ang parehong equation ng isang bilog) Mahirap makayanan – tulad ng mahirap makayanan nang walang magandang pahinga!

Magsaya sa lahat at magkita-kita tayo sa susunod na season!

Mga solusyon at sagot:

Halimbawa 2: Solusyon: Ilarawan natin ang lugar sa pagguhit:

Minsan sa mga problema B15 mayroong "masamang" mga pag-andar kung saan mahirap makahanap ng isang derivative. Dati, ito ay nangyari lamang sa panahon ng mga sample na pagsusulit, ngunit ngayon ang mga gawaing ito ay napakakaraniwan na ang mga ito ay hindi na maaaring balewalain kapag naghahanda para sa tunay na Unified State Exam.

Sa kasong ito, gumagana ang iba pang mga diskarte, ang isa ay monotone.

Ang isang function na f (x) ay sinasabing monotonically na tumataas sa segment kung para sa anumang mga puntos x 1 at x 2 ng segment na ito ang sumusunod ay:

x 1< x 2 ⇒ f (x 1) < f (x 2).

Ang isang function na f (x) ay sinasabing monotonically na bumababa sa segment kung para sa anumang mga puntos na x 1 at x 2 ng segment na ito ay may sumusunod:

x 1< x 2 ⇒ f (x 1) > f ( x 2).

Sa madaling salita, para sa pagtaas ng function, mas malaki ang x, mas malaki ang f(x). Para sa isang nagpapababang function ang kabaligtaran ay totoo: ang mas malaking x, ang mas mababa f(x).

Halimbawa, monotonically tumataas ang logarithm kung ang base a > 1, at monotonically bumababa kung 0< a < 1. Не забывайте про область mga katanggap-tanggap na halaga logarithm: x > 0.

f (x) = log a x (a > 0; a ≠ 1; x > 0)

Ang arithmetic square (at hindi lamang square) na ugat ay tumataas nang monotonically sa buong domain ng kahulugan:

Ang exponential function ay kumikilos katulad ng logarithm: tumataas ito para sa isang > 1 at bumababa para sa 0< a < 1. Но в отличие от логарифма, exponential function tinukoy para sa lahat ng numero, hindi lang x > 0:

f (x) = a x (a > 0)

Panghuli, mga degree na may negatibong exponent. Maaari mong isulat ang mga ito bilang isang fraction. Mayroon silang break point kung saan nasira ang monotony.

Ang lahat ng mga function na ito ay hindi kailanman makikita sa purong anyo. Nagdaragdag sila ng mga polynomial, fraction at iba pang kalokohan, na nagpapahirap sa pagkalkula ng derivative. Tingnan natin kung ano ang mangyayari sa kasong ito.

Mga coordinate ng parabola vertex

Kadalasan ang argumento ng function ay pinapalitan ng quadratic trinomial ng anyong y = ax 2 + bx + c. Ang graph nito ay isang karaniwang parabola kung saan kami ay interesado sa:

1. Ang mga sanga ng isang parabola ay maaaring tumaas (para sa isang > 0) o pababa (a< 0). Задают направление, в котором функция может принимать бесконечные значения;
2. Ang vertex ng isang parabola ay ang extremum point ng isang quadratic function kung saan ang function na ito ay tumatagal ng pinakamababa (para sa isang > 0) o maximum (a< 0) значение.

Ang pinakamalaking interes ay vertex ng parabola, ang abscissa ay kinakalkula ng formula:

Kaya, natagpuan namin ang extremum point ng quadratic function. Ngunit kung ang orihinal na function ay monotonic, para dito ang punto x 0 ay magiging isang extremum point din. Kaya, bumalangkas tayo ng pangunahing panuntunan:

Extremum na puntos quadratic trinomial At kumplikadong pag-andar, kung saan ito ay kasama, nag-tutugma. Samakatuwid, maaari kang maghanap ng x 0 para sa isang quadratic trinomial, at kalimutan ang tungkol sa function.

Mula sa pangangatwiran sa itaas, nananatiling hindi malinaw kung aling punto ang makukuha natin: maximum o minimum. Gayunpaman, ang mga gawain ay partikular na idinisenyo upang hindi ito mahalaga. Maghusga para sa iyong sarili:

1. Walang segment sa pahayag ng problema. Samakatuwid, hindi na kailangang kalkulahin ang f(a) at f(b). Ito ay nananatiling isaalang-alang lamang ang mga extremum point;
2. Ngunit mayroon lamang isang ganoong punto - ito ang vertex ng parabola x 0, ang mga coordinate na kung saan ay literal na kinakalkula nang pasalita at walang anumang mga derivatives.

Kaya, ang paglutas ng problema ay lubos na pinasimple at bumaba sa dalawang hakbang lamang:

1. Isulat ang equation ng parabola y = ax 2 + bx + c at hanapin ang vertex nito gamit ang formula: x 0 = −b /2a ;
2. Hanapin ang halaga ng orihinal na function sa puntong ito: f (x 0). Kung walang karagdagang kundisyon, ito ang magiging sagot.

Sa unang tingin, ang algorithm na ito at ang katwiran nito ay maaaring mukhang kumplikado. Sinadya kong hindi mag-post ng isang "hubad" na diagram ng solusyon, dahil ang walang pag-iisip na aplikasyon ng mga naturang patakaran ay puno ng mga pagkakamali.

Tingnan natin ang mga totoong problema mula sa pagsubok sa Unified State Exam sa matematika - dito matatagpuan ang pamamaraang ito nang madalas. Kasabay nito, sisiguraduhin namin na sa ganitong paraan maraming problema sa B15 ang nagiging halos oral.

Sa ilalim ng ugat ay nakatayo quadratic function y = x 2 + 6x + 13. Ang graph ng function na ito ay isang parabola na may mga sanga pataas, dahil ang coefficient a = 1 > 0.

Vertex ng parabola:

x 0 = −b /(2a ) = −6/(2 1) = −6/2 = −3

Dahil ang mga sanga ng parabola ay nakadirekta paitaas, sa puntong x 0 = −3 ang function na y = x 2 + 6x + 13 ay tumatagal sa pinakamababang halaga nito.

Ang ugat ay tumataas nang monotonically, na nangangahulugang x 0 ang pinakamababang punto ng buong function. Mayroon kaming:

Gawain. Hanapin ang pinakamaliit na halaga ng function:

y = log 2 (x 2 + 2x + 9)

Sa ilalim ng logarithm mayroong muli ng isang quadratic function: y = x 2 + 2x + 9. Ang graph ay isang parabola na may mga sanga pataas, dahil a = 1 > 0.

Vertex ng parabola:

x 0 = −b /(2a ) = −2/(2 1) = −2/2 = −1

Kaya, sa puntong x 0 = −1 ang quadratic function ay tumatagal sa pinakamababang halaga nito. Ngunit ang function na y = log 2 x ay monotoniko, kaya:

y min = y (−1) = log 2 ((−1) 2 + 2 · (−1) + 9) = ... = log 2 8 = 3

Ang exponent ay naglalaman ng quadratic function na y = 1 − 4x − x 2 . Isulat muli natin ito sa normal na anyo: y = −x 2 − 4x + 1.

Malinaw, ang graph ng function na ito ay isang parabola, mga sanga pababa (a = −1< 0). Поэтому вершина будет точкой максимума:

x 0 = −b /(2a ) = −(−4)/(2 · (−1)) = 4/(−2) = −2

Ang orihinal na function ay exponential, ito ay monotonic, samakatuwid pinakamataas na halaga ay nasa natagpuang punto x 0 = −2:

Maaaring mapansin ng isang matulungin na mambabasa na hindi namin isinulat ang hanay ng mga pinahihintulutang halaga ng ugat at logarithm. Ngunit hindi ito kinakailangan: sa loob ay may mga pag-andar na ang mga halaga ay palaging positibo.

Corollaries mula sa domain ng isang function

Minsan ang paghahanap lamang ng vertex ng parabola ay hindi sapat upang malutas ang Problema B15. Ang halaga na iyong hinahanap ay maaaring magsinungaling sa dulo ng segment, at hindi sa lahat sa matinding punto. Kung ang problema ay hindi tumukoy ng isang segment, tingnan hanay ng mga katanggap-tanggap na halaga orihinal na function. Namely:

Pakitandaan muli: ang zero ay maaaring nasa ilalim ng ugat, ngunit hindi kailanman sa logarithm o denominator ng isang fraction. Tingnan natin kung paano ito gumagana sa mga partikular na halimbawa:

Gawain. Hanapin ang pinakamalaking halaga ng function:

Sa ilalim ng ugat ay muli ang isang quadratic function: y = 3 − 2x − x 2 . Ang graph nito ay isang parabola, ngunit sumasanga pababa dahil a = −1< 0. Значит, парабола уходит на минус бесконечность, что недопустимо, поскольку арифметический parisukat na ugat ng isang negatibong numero ay hindi umiiral.

Isinulat namin ang hanay ng mga pinahihintulutang halaga (APV):

3 − 2x − x 2 ≥ 0 ⇒ x 2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; 1]

Ngayon hanapin natin ang vertex ng parabola:

x 0 = −b /(2a ) = −(−2)/(2 · (−1)) = 2/(−2) = −1

Ang puntong x 0 = −1 ay kabilang sa segment na ODZ - at ito ay mabuti. Ngayon kinakalkula namin ang halaga ng function sa punto x 0, pati na rin sa mga dulo ng ODZ:

y(−3) = y(1) = 0

Kaya, nakuha namin ang mga numero 2 at 0. Hinihiling sa amin na hanapin ang pinakamalaki - ito ang numero 2.

Gawain. Hanapin ang pinakamaliit na halaga ng function:

y = log 0.5 (6x − x 2 − 5)

Sa loob ng logarithm mayroong isang quadratic function y = 6x − x 2 − 5. Ito ay isang parabola na may mga sanga pababa, ngunit sa isang logarithm ay hindi maaaring mga negatibong numero, kaya isinulat namin ang ODZ:

6x − x 2 − 5 > 0 ⇒ x 2 − 6x + 5< 0 ⇒ (x − 1)(x − 5) < 0 ⇒ x ∈ (1; 5)

Mangyaring tandaan: ang hindi pagkakapantay-pantay ay mahigpit, kaya ang mga dulo ay hindi nabibilang sa ODZ. Naiiba nito ang logarithm mula sa ugat, kung saan ang mga dulo ng segment ay angkop sa amin.

Hinahanap namin ang vertex ng parabola:

x 0 = −b /(2a ) = −6/(2 · (−1)) = −6/(−2) = 3

Ang vertex ng parabola ay umaangkop ayon sa ODZ: x 0 = 3 ∈ (1; 5). Ngunit dahil hindi kami interesado sa mga dulo ng segment, kinakalkula namin ang halaga ng function lamang sa punto x 0:

y min = y (3) = log 0.5 (6 3 − 3 2 − 5) = log 0.5 (18 − 9 − 5) = log 0.5 4 = −2

SA praktikal na punto Mula sa isang pananaw, ang pinakamalaking interes ay ang paggamit ng derivative upang mahanap ang pinakamalaki at pinakamaliit na halaga ng isang function. Ano ang konektado dito? Pag-maximize ng kita, pagliit ng mga gastos, pagtukoy ng pinakamainam na pagkarga ng kagamitan... Sa madaling salita, sa maraming lugar ng buhay kailangan nating lutasin ang mga problema sa pag-optimize ng ilang mga parameter. At ito ang mga gawain ng paghahanap ng pinakamalaki at pinakamaliit na halaga ng isang function.

Dapat pansinin na ang pinakamalaki at pinakamaliit na halaga ng isang function ay karaniwang hinahanap sa isang tiyak na interval X, na alinman sa buong domain ng function o bahagi ng domain ng kahulugan. Ang interval X mismo ay maaaring isang segment, isang bukas na agwat , isang walang katapusang pagitan.

Sa artikulong ito ay pag-uusapan natin ang tungkol sa paghahanap ng pinakamalaki at pinakamaliit na halaga nang tahasan ibinigay na function isang variable y=f(x) .

Pag-navigate sa pahina.

Ang pinakamalaki at pinakamaliit na halaga ng isang function - mga kahulugan, mga guhit.

Tingnan natin sa madaling sabi ang mga pangunahing kahulugan.

Ang pinakamalaking halaga ng function na para sa sinuman totoo ang hindi pagkakapantay-pantay.

Ang pinakamaliit na halaga ng function y=f(x) sa pagitan ng X ay tinatawag na ganoong halaga na para sa sinuman totoo ang hindi pagkakapantay-pantay.

Ang mga kahulugang ito ay madaling maunawaan: ang pinakamalaking (pinakamaliit) na halaga ng isang function ay ang pinakamalaking (pinakamaliit) na tinatanggap na halaga sa pagitan na isinasaalang-alang sa abscissa.

Mga nakatigil na puntos– ito ang mga halaga ng argumento kung saan ang derivative ng function ay nagiging zero.

Bakit kailangan natin ng mga nakatigil na puntos kapag naghahanap ng pinakamalaki at pinakamaliit na halaga? Ang sagot sa tanong na ito ay ibinigay ng Fermat's theorem. Mula sa theorem na ito ay sumusunod na kung ang isang differentiable function ay may extremum (lokal na minimum o lokal na maximum) sa isang punto, kung gayon ang puntong ito ay nakatigil. Kaya, madalas na kinukuha ng function ang pinakamalaking (pinakamaliit) na halaga nito sa interval X sa isa sa mga nakatigil na punto mula sa interval na ito.

Gayundin, ang isang function ay kadalasang maaaring tumagal sa pinakamalaki at pinakamaliit na halaga nito sa mga punto kung saan ang unang derivative ng function na ito ay hindi umiiral, at ang function mismo ay tinukoy.

Agad nating sagutin ang isa sa mga pinakakaraniwang tanong sa paksang ito: "Palaging posible bang matukoy ang pinakamalaking (pinakamaliit) na halaga ng isang function"? Hindi, hindi palagi. Minsan ang mga hangganan ng interval X ay nag-tutugma sa mga hangganan ng domain ng kahulugan ng function, o ang interval X ay walang katapusan. At ang ilang mga pag-andar sa infinity at sa mga hangganan ng domain ng kahulugan ay maaaring tumagal sa parehong walang hanggan malaki at walang hanggan maliit na halaga. Sa mga kasong ito, walang masasabi tungkol sa pinakamalaki at pinakamaliit na halaga ng function.

Para sa kalinawan, magbibigay kami ng isang graphic na paglalarawan. Tingnan ang mga larawan at marami ang magiging mas malinaw.

Sa segment

Sa unang figure, ang function ay tumatagal ng pinakamalaking (max y) at pinakamaliit (min y) na mga halaga sa mga nakatigil na punto na matatagpuan sa loob ng segment [-6;6].

Isaalang-alang ang kaso na inilalarawan sa pangalawang figure. Baguhin natin ang segment sa . Sa halimbawang ito, ang pinakamaliit na halaga ng function ay nakakamit sa isang nakatigil na punto, at ang pinakamalaking sa punto na may abscissa na tumutugma sa kanang hangganan ng pagitan.

Sa Figure 3, ang mga boundary point ng segment [-3;2] ay ang abscissas ng mga puntos na tumutugma sa pinakamalaki at pinakamaliit na halaga ng function.

Sa isang bukas na pagitan

Sa ika-apat na figure, ang function ay tumatagal ng pinakamalaking (max y) at pinakamaliit (min y) na mga halaga sa mga nakatigil na punto na matatagpuan sa loob ng bukas na pagitan (-6;6).

Sa agwat , walang mga konklusyon ang maaaring makuha tungkol sa pinakamalaking halaga.

Sa infinity

Sa halimbawang ipinakita sa ikapitong figure, ang function ay tumatagal ng pinakamalaking halaga (max y) sa isang nakatigil na punto na may abscissa x=1, at ang pinakamaliit na halaga (min y) ay nakakamit sa kanang hangganan ng pagitan. Sa minus infinity, ang mga halaga ng function ay asymptotically lumalapit sa y=3.

Sa paglipas ng pagitan, ang function ay hindi umabot sa pinakamaliit o pinakamalaking halaga. Habang lumalapit ang x=2 mula sa kanan, ang mga value ng function ay may posibilidad na minus infinity (ang linyang x=2 ay isang vertical asymptote), at habang ang abscissa ay may posibilidad na plus infinity, ang mga value ng function ay asymptotically na lumalapit sa y=3. Ang isang graphic na paglalarawan ng halimbawang ito ay ipinapakita sa Figure 8.

Algorithm para sa paghahanap ng pinakamalaki at pinakamaliit na halaga ng tuluy-tuloy na function sa isang segment.

Sumulat tayo ng isang algorithm na nagbibigay-daan sa amin upang mahanap ang pinakamalaki at pinakamaliit na halaga ng isang function sa isang segment.

1. Hinahanap namin ang domain ng kahulugan ng function at suriin kung naglalaman ito ng buong segment.
2. Nahanap namin ang lahat ng mga punto kung saan ang unang derivative ay hindi umiiral at kung saan ay nakapaloob sa segment (kadalasan ang mga naturang punto ay matatagpuan sa mga function na may argumento sa ilalim ng modulus sign at sa mga function ng kapangyarihan na may fractional-rational exponent). Kung walang ganoong mga punto, pagkatapos ay magpatuloy sa susunod na punto.
3. Tinutukoy namin ang lahat ng mga nakatigil na punto na nasa loob ng segment. Upang gawin ito, itinutumbas namin ito sa zero, lutasin ang nagresultang equation at pumili ng angkop na mga ugat. Kung walang nakatigil na mga punto o wala sa mga ito ang nahuhulog sa segment, pagkatapos ay magpatuloy sa susunod na punto.
4. Kinakalkula namin ang mga halaga ng function sa mga napiling nakatigil na mga punto (kung mayroon man), sa mga punto kung saan ang unang derivative ay hindi umiiral (kung mayroon man), pati na rin sa x=a at x=b.
5. Mula sa nakuha na mga halaga ng pag-andar, pipiliin namin ang pinakamalaki at pinakamaliit - sila ang kinakailangang pinakamalaki at pinakamaliit na halaga ng pag-andar, ayon sa pagkakabanggit.

Suriin natin ang algorithm para sa paglutas ng isang halimbawa upang mahanap ang pinakamalaki at pinakamaliit na halaga ng isang function sa isang segment.

Halimbawa.

Hanapin ang pinakamalaki at pinakamaliit na halaga ng isang function

• sa segment;
• sa segment [-4;-1] .

Solusyon.

Ang domain ng kahulugan ng isang function ay ang buong hanay ng mga tunay na numero, maliban sa zero, iyon ay. Ang parehong mga segment ay nasa loob ng domain ng kahulugan.

Hanapin ang derivative ng function na may kinalaman sa:

Malinaw, ang derivative ng function ay umiiral sa lahat ng mga punto ng mga segment at [-4;-1].

Tinutukoy namin ang mga nakatigil na puntos mula sa equation. Ang tanging tunay na ugat ay x=2. Ang nakatigil na puntong ito ay nahuhulog sa unang bahagi.

Para sa unang kaso, kinakalkula namin ang mga halaga ng function sa mga dulo ng segment at sa nakatigil na punto, iyon ay, para sa x=1, x=2 at x=4:

Samakatuwid, ang pinakamalaking halaga ng function ay nakamit sa x=1, at ang pinakamaliit na halaga – sa x=2.

Para sa pangalawang kaso, kinakalkula namin ang mga halaga ng pag-andar lamang sa mga dulo ng segment [-4;-1] (dahil hindi ito naglalaman ng isang nakatigil na punto):

Ibinigay ang isang function na tinukoy at tuloy-tuloy sa isang tiyak na pagitan. Kailangan mong mahanap ang pinakamalaking (pinakamaliit) na halaga ng function sa pagitan na ito.

Mga teoretikal na pundasyon.
Theorem (Ikalawang Weierstrass Theorem):

Kung ang isang function ay tinukoy at tuloy-tuloy sa isang saradong agwat, pagkatapos ay maabot nito ang pinakamataas at pinakamababang halaga nito sa agwat na ito.

Maaaring maabot ng function ang pinakamalaki at pinakamaliit na halaga nito alinman sa mga panloob na punto ng pagitan o sa mga hangganan nito. Ilarawan natin ang lahat posibleng mga opsyon.

Paliwanag:
1) Naabot ng function ang pinakamalaking halaga nito sa kaliwang hangganan ng pagitan sa punto , at ang pinakamababang halaga nito sa kanang hangganan ng pagitan sa punto .
2) Naabot ng function ang pinakamalaking halaga nito sa punto (ito ang pinakamataas na punto), at ang pinakamababang halaga nito sa kanang hangganan ng pagitan sa punto.
3) Naabot ng function ang pinakamataas na halaga nito sa kaliwang hangganan ng pagitan sa punto , at ang pinakamababang halaga nito sa punto (ito ang pinakamababang punto).
4) Ang pag-andar ay pare-pareho sa pagitan, i.e. naabot nito ang pinakamababa at pinakamataas na halaga nito sa anumang punto sa pagitan, at ang minimum at maximum na mga halaga ay katumbas ng bawat isa.
5) Naabot ng function ang pinakamataas na halaga nito sa punto , at ang pinakamababang halaga nito sa punto (sa kabila ng katotohanan na ang function ay may parehong maximum at minimum sa pagitan na ito).
6) Naabot ng function ang pinakamalaking halaga nito sa isang punto (ito ang pinakamataas na punto), at ang pinakamababang halaga nito sa isang punto (ito ang pinakamababang punto).
Komento:

Ang "maximum" at "maximum value" ay magkaibang bagay. Ito ay sumusunod mula sa kahulugan ng maximum at ang intuitive na pag-unawa sa pariralang "maximum na halaga".

Algorithm para sa paglutas ng problema 2.



4) Piliin ang pinakamalaki (pinakamaliit) mula sa mga nakuhang halaga at isulat ang sagot.

Halimbawa 4:

Tukuyin ang pinakamalaki at pinakamaliit na halaga ng isang function sa segment.
Solusyon:
1) Hanapin ang derivative ng function.

2) Maghanap ng mga nakatigil na puntos (at mga puntong pinaghihinalaang extremum) sa pamamagitan ng paglutas ng equation. Bigyang-pansin ang mga punto kung saan walang two-sided finite derivative.

3) Kalkulahin ang mga halaga ng function sa mga nakatigil na punto at sa mga hangganan ng pagitan.

4) Piliin ang pinakamalaki (pinakamaliit) mula sa mga nakuhang halaga at isulat ang sagot.

Naabot ng function sa segment na ito ang pinakamalaking halaga nito sa puntong may mga coordinate .

Naabot ng function sa segment na ito ang pinakamababang halaga nito sa puntong may mga coordinate .

Maaari mong i-verify ang kawastuhan ng mga kalkulasyon sa pamamagitan ng pagtingin sa graph ng function na pinag-aaralan.


Komento: Naabot ng function ang pinakamalaking halaga nito sa pinakamataas na punto, at ang pinakamababa nito sa hangganan ng segment.

Isang espesyal na kaso.

Ipagpalagay na kailangan nating hanapin ang maximum at pinakamababang halaga ilang function sa isang pagitan. Matapos makumpleto ang unang punto ng algorithm, i.e. pagkalkula ng derivative, nagiging malinaw na, halimbawa, kailangan lamang ng mga negatibong halaga sa buong agwat na isinasaalang-alang. Tandaan na kung negatibo ang derivative, bababa ang function. Nalaman namin na bumababa ang function sa buong segment. Ang sitwasyong ito ay ipinapakita sa graph No. 1 sa simula ng artikulo.

Bumababa ang function sa segment, i.e. wala itong extrema points. Mula sa larawan makikita mo na ang function ay kukuha ng pinakamaliit na halaga sa kanang hangganan ng segment, at ang pinakamalaking halaga sa kaliwa. kung ang derivative sa pagitan ay positibo sa lahat ng dako, kung gayon ang function ay tataas. Ang pinakamaliit na halaga ay nasa kaliwang hangganan ng segment, ang pinakamalaki ay nasa kanan.

Sa artikulong ito ay pag-uusapan ko algorithm para sa paghahanap ng pinakamalaki at pinakamaliit na halaga function, minimum at maximum na mga puntos.

Mula sa teorya ay tiyak na magiging kapaki-pakinabang ito sa atin derivative table At mga panuntunan sa pagkakaiba-iba. Lahat ng ito ay nasa plato na ito:

Algorithm para sa paghahanap ng pinakamalaki at pinakamaliit na halaga.

Mas maginhawa para sa akin na magpaliwanag tiyak na halimbawa. Isaalang-alang:

Halimbawa: Hanapin ang pinakamalaking halaga ng function na y=x^5+20x^3–65x sa segment [–4;0].

Hakbang 1. Kinukuha namin ang derivative.

Y" = (x^5+20x^3–65x)" = 5x^4 + 20*3x^2 - 65 = 5x^4 + 60x^2 - 65

Hakbang 2. Paghahanap ng mga extremum point.

Extremum na punto tinatawag namin ang mga punto kung saan naabot ng function ang pinakamalaking o pinakamababang halaga nito.

Upang mahanap ang extremum point, kailangan mong i-equate ang derivative ng function sa zero (y" = 0)

5x^4 + 60x^2 - 65 = 0

Ngayon, lutasin natin ang bi quadratic equation at ang mga ugat na natagpuan ay ang aming mga extremum point.

Nilulutas ko ang mga naturang equation sa pamamagitan ng pagpapalit ng t = x^2, pagkatapos ay 5t^2 + 60t - 65 = 0.

Bawasan natin ang equation ng 5, makuha natin ang: t^2 + 12t - 13 = 0

D = 12^2 - 4*1*(-13) = 196

T_(1) = (-12 + sqrt(196))/2 = (-12 + 14)/2 = 1

T_(2) = (-12 - sqrt(196))/2 = (-12 - 14)/2 = -13

Ginagawa namin ang baligtad na pagbabago x^2 = t:

X_(1 at 2) = ±sqrt(1) = ±1
x_(3 at 4) = ±sqrt(-13) (ibinubukod namin, hindi maaaring magkaroon ng mga negatibong numero sa ilalim ng ugat, maliban kung siyempre pinag-uusapan natin ang mga kumplikadong numero)

Kabuuan: x_(1) = 1 at x_(2) = -1 - ito ang aming mga extremum point.

Hakbang 3. Tukuyin ang pinakamalaki at pinakamaliit na halaga.

Pamamaraan ng pagpapalit.

Sa kondisyon, binigyan kami ng segment [b][–4;0]. Ang puntong x=1 ay hindi kasama sa segment na ito. Kaya hindi namin ito isinasaalang-alang. Ngunit bilang karagdagan sa puntong x=-1, kailangan din nating isaalang-alang ang kaliwa at kanang mga hangganan ng ating segment, iyon ay, mga puntos -4 at 0. Upang gawin ito, pinapalitan natin ang lahat ng tatlong puntong ito sa orihinal na pag-andar. Tandaan na ang orihinal ay ang ibinigay sa kundisyon (y=x^5+20x^3–65x), sinisimulan ng ilang tao na palitan ito sa derivative...

Y(-1) = (-1)^5 + 20*(-1)^3 - 65*(-1) = -1 - 20 + 65 = [b]44
y(0) = (0)^5 + 20*(0)^3 - 65*(0) = 0
y(-4) = (-4)^5 + 20*(-4)^3 - 65*(-4) = -1024 - 1280 + 260 = -2044

Nangangahulugan ito na ang pinakamalaking halaga ng function ay [b]44 at ito ay nakakamit sa punto [b]-1, na tinatawag na pinakamataas na punto ng function sa segment [-4; 0].

Kami ay nagpasya at nakatanggap ng isang sagot, kami ay mahusay, maaari kang magpahinga. Ngunit huminto! Hindi mo ba iniisip na ang pagkalkula ng y(-4) ay kahit papaano ay napakahirap? Sa mga kondisyon ng limitadong oras, mas mahusay na gumamit ng isa pang pamamaraan, tinawag ko itong:

Sa pamamagitan ng mga pagitan ng sign constancy.

Ang mga agwat na ito ay matatagpuan para sa derivative ng function, iyon ay, para sa aming biquadratic equation.

Ginagawa ko ito ng ganito. Gumuhit ako ng nakadirekta na segment. Inilalagay ko ang mga puntos: -4, -1, 0, 1. Sa kabila ng katotohanan na ang 1 ay hindi kasama sa ibinigay na segment, dapat pa rin itong tandaan upang matukoy nang tama ang mga pagitan ng constancy ng sign. Kumuha tayo ng ilang bilang na maraming beses na mas malaki kaysa sa 1, sabihin nating 100, at isasalit ito sa ating biquadratic equation 5(100)^4 + 60(100)^2 - 65. Kahit na walang pagbibilang ng anuman, nagiging malinaw na sa puntong 100 ang may plus sign ang function. Nangangahulugan ito na para sa mga pagitan mula 1 hanggang 100 mayroon itong plus sign. Kapag dumadaan sa 1 (pumupunta kami mula kanan pakaliwa), ang function ay magbabago ng sign sa minus. Kapag dumadaan sa punto 0, ang function ay mananatili sa sign nito, dahil ito lamang ang hangganan ng segment, at hindi ang ugat ng equation. Kapag dumadaan sa -1, muling babaguhin ng function ang sign sa plus.

Mula sa teorya alam namin na kung saan ang derivative ng function ay (at iginuhit namin ito nang eksakto para dito) nagbabago ng sign mula plus hanggang minus (punto -1 sa aming kaso) umabot ang function lokal na maximum nito (y(-1)=44, gaya ng kinakalkula kanina) sa segment na ito (ito ay lohikal na naiintindihan, ang function ay tumigil sa pagtaas dahil naabot nito ang maximum at nagsimulang bumaba).

Alinsunod dito, kung saan ang derivative ng function nagbabago ng sign mula minus hanggang plus, ay nakamit lokal na minimum ng isang function. Oo, oo, natagpuan din namin ang lokal na minimum na punto ay 1, at ang y(1) ay ang pinakamababang halaga ng function sa segment, sabihin mula -1 hanggang +∞. Pakitandaan na isa lang itong LOCAL MINIMUM, ibig sabihin, minimum sa isang partikular na segment. Dahil ang totoong (global) na minimum ng function ay makakarating sa isang lugar doon, sa -∞.

Sa palagay ko, ang unang pamamaraan ay mas simple sa teorya, at ang pangalawa ay mas simple mula sa punto ng view ng mga operasyon ng aritmetika, ngunit mas kumplikado mula sa punto ng view ng teorya. Pagkatapos ng lahat, kung minsan may mga kaso kapag ang pag-andar ay hindi nagbabago ng sign kapag dumadaan sa ugat ng equation, at sa pangkalahatan maaari kang malito sa mga lokal, pandaigdigang maxima at minima, kahit na kakailanganin mong makabisado ito nang mabuti kung ikaw. planong pumasok sa isang teknikal na unibersidad (at kung bakit pa kumuha ng profile Unified State Exam at lutasin ang gawaing ito). Ngunit ang pagsasanay at pagsasanay lamang ang magtuturo sa iyo na lutasin ang mga ganitong problema minsan at para sa lahat. At maaari kang magsanay sa aming website. Dito .

Kung mayroon kang anumang mga katanungan o isang bagay na hindi malinaw, siguraduhing magtanong. Ikalulugod kong sagutin ka at gumawa ng mga pagbabago at pagdaragdag sa artikulo. Tandaan na sama-sama nating ginagawa ang site na ito!