1 aralin sa paksa

Nakumpleto:

Telegina L.B.

Layunin ng aralin:

1. ulitin ang lahat ng materyal na pinag-aralan sa mga function.
2. ipakilala ang kahulugan ng inverse proportionality at ituro kung paano buuin ang graph nito.
3. bumuo ng lohikal na pag-iisip.
4. linangin ang pansin, kawastuhan, kawastuhan.

Plano ng aralin:

1. Pag-uulit.
2. Paliwanag ng bagong materyal.
3. Minuto ng pisikal na edukasyon.
4. Pagsasama-sama.

Kagamitan: poster.

Pag-unlad ng aralin:

1. Ang aralin ay nagsisimula sa pag-uulit. Inaanyayahan ang mga mag-aaral na lutasin ang isang crossword puzzle (na inihanda nang maaga sa malaking sheet papel).

Mga tanong sa krosword:

1. Dependence sa pagitan ng mga variable, kung saan ang bawat value ng independent variable ay tumutugma sa isang value ng dependent variable. [Pag-andar].

2. Independent variable. [Argumento].

3. Ang hanay ng mga punto ng abscissa coordinate plane, na katumbas ng mga halaga ng argumento, at ang mga ordinate ay katumbas ng mga halaga ng function. [Iskedyul].

4. Function na ibinigay ng formula y=kx+b. [Linear].

5. Anong coefficient ang tawag sa isang numero? k sa formula y=kx+b? [Sulok].

6. Ano ang graph ng isang linear function? [Diretso].

7. Kung k≠0, kung gayon ang graph na y=kx+b ay nag-intersect sa axis na ito, at kung k=0, kung gayon ito ay parallel dito. Anong letra ang itinalaga ng axis na ito? [X].

8. Ang salita sa pangalan ng function na y=kx? [Proporsyonalidad].

9. Function na ibinigay ng formula y=x 2. [Quadratic].

10. Pamagat ng tsart quadratic function. [Parabola].

11. Isang titik ng alpabetong Latin, na kadalasang nagsasaad ng isang function. [Igrek].

12. Isa sa mga paraan upang tukuyin ang isang function. [Formula].

Guro : Ano ang mga pangunahing paraan ng pagtukoy ng isang function na alam natin?

(Ang isang mag-aaral ay tumatanggap ng isang gawain sa pisara: punan ang isang talahanayan ng mga halaga ng function na 12/x gamit ang ibinigay na mga halaga ng argumento nito, at pagkatapos ay i-plot ang kaukulang mga punto sa coordinate plane).

Ang iba ay sumasagot sa mga tanong ng guro: (na nakasulat nang maaga sa pisara)

1. Ano ang mga pangalan ng mga sumusunod na function na ibinigay ng mga formula: y=kx, y=kx+b, y=x 2 , y=x 3 ?

2. Tukuyin ang domain ng kahulugan ng mga sumusunod na function: y=x 2 +8, y=1/x-7, y= 4x-1/5, y=2x, y=7-5x, y=2/x, y=x 3 , y=-10/x.

Pagkatapos ay magtrabaho ang mga mag-aaral ayon sa talahanayan, na sinasagot ang mga tanong na ibinigay ng guro:

1. Aling figure mula sa talahanayan ang nagpapakita ng mga graph:

a) linear function;

b) direktang proporsyonalidad;

c) quadratic function;

d) mga function ng anyong y=kx 3 ?

2. Anong senyales ang mayroon ang koepisyent k sa mga formula ng anyong y=kx+b, na tumutugma sa mga graph sa Figures 1, 2, 4, 5 ng talahanayan?

3. Maghanap ng mga graphics sa talahanayan mga linear na function, na ang mga angular coefficient ay:

a) pantay;

b) katumbas ng magnitude at magkasalungat sa sign.

(Pagkatapos ay tinitingnan ng buong klase kung ang estudyanteng tumawag sa pisara ay wastong napunan ang talahanayan at inilagay ang mga punto sa coordinate plane).

2. Ang pagpapaliwanag ay nagsisimula sa motibasyon.

Guro: Tulad ng alam mo, inilalarawan ng bawat function ang ilang prosesong nagaganap sa mundo sa paligid natin.

Isaalang-alang, halimbawa, ang isang parihaba na may mga gilid x at y at lugar na 12 cm 2 . Alam na x*y=12, ngunit ano ang mangyayari kung sisimulan mong baguhin ang isa sa mga gilid ng parihaba, sabihin nating isang gilid na may haba x?

Haba ng gilid y ay matatagpuan mula sa formula y=12/x. Kung x dagdagan ng 2 beses, magkakaroon ito ng y=12/2x, i.e. gilid y bababa ng 2 beses. Kung ang halaga x tumaas ng 3, 4, 5... beses, pagkatapos ay ang halaga y ay bababa sa parehong halaga. Sa kabaligtaran, kung x bumaba ng ilang beses, pagkatapos y tataas ng parehong halaga. (Gumawa ayon sa talahanayan).

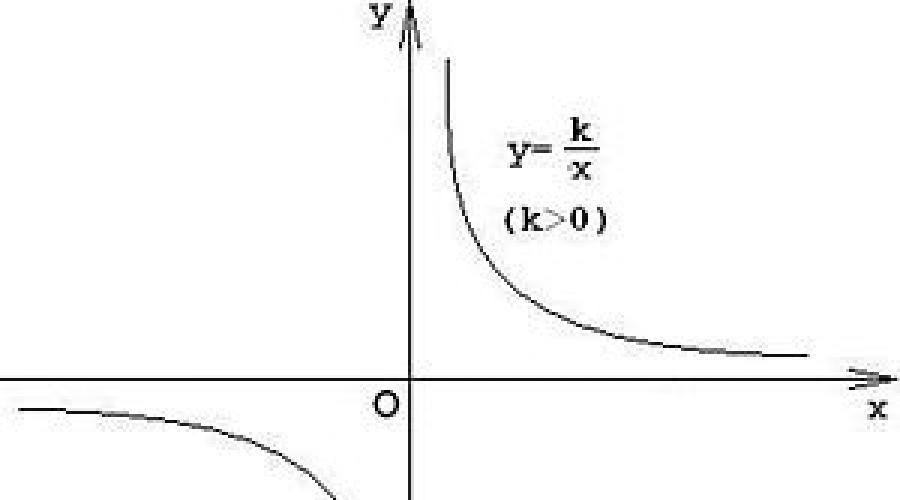
Samakatuwid, ang isang function ng form na y=12/x ay tinatawag na inverse proportionality. SA pangkalahatang pananaw ito ay nakasulat bilang y=k/x, kung saan ang k ay isang pare-pareho, at k≠0.

Ito ang paksa ng aralin ngayon, isinulat namin ito sa aming mga kuwaderno. Nagbibigay ako ng mahigpit na kahulugan. Para sa function na y=12/x, na isang espesyal na uri ng inverse proportionality, naisulat na namin ang isang bilang ng mga argumento at mga halaga ng function sa talahanayan at ilarawan ang kaukulang mga punto sa coordinate plane. Ano ang hitsura ng graph ng function na ito? Mahirap husgahan ang buong graph batay sa mga itinayong puntos, dahil ang mga punto ay maaaring konektado sa anumang paraan. Subukan nating magkasama upang makagawa ng mga konklusyon tungkol sa graph ng isang function na nagmula sa pagsasaalang-alang ng talahanayan at formula.

Mga tanong para sa klase:

1. Ano ang domain ng kahulugan ng function na y=12/x?
2. Ang mga y value ba ay positibo o negatibo kung

a) x

b) x>0?

3. Paano nagbabago ang halaga ng isang variable y na may nagbabagong halaga x?

Kaya,

1. point (0,0) ay hindi kabilang sa graph, i.e. hindi ito bumalandra sa alinman sa OX o OY axis;
2. ang graph ay nasa Ι at ΙΙΙ coordinate quarters;
3. maayos na lumalapit sa coordinate axes pareho sa Ι coordinate quarter at sa ΙΙΙ, at ito ay lumalapit sa mga axes nang mas malapit hangga't gusto.

Sa pagkakaroon ng impormasyong ito, maaari na nating ikonekta ang mga tuldok sa figure (ginagawa ito mismo ng guro sa pisara) at makita ang buong graph ng function na y=12/x. Ang resultang curve ay tinatawag na hyperbola, na sa Griyego ay nangangahulugang "pagdaraan sa isang bagay." Ang kurba na ito ay natuklasan ng mga mathematician ng sinaunang paaralang Greek noong ika-4 na siglo BC. Ang termino, hyperbole, ay ipinakilala ni Apollonius mula sa lungsod ng Pergamum (Asia Minor), na nabuhay noong ika-6-8 siglo. BC

Ngayon, sa tabi ng graph ng function na y=12/x, gagawa tayo ng graph ng function na y=-12/x. (Kumpletuhin ng mga mag-aaral ang gawaing ito sa mga kuwaderno, at isang mag-aaral sa pisara).

Sa paghahambing ng parehong mga graph, napansin ng mga mag-aaral na ang pangalawa ay sumasakop sa 2 at 4 na coordinate quarter. Bilang karagdagan, kung ang graph ng function na y=12/x ay ipinapakita nang simetriko na nauugnay sa op-amp axis, kung gayon ang graph ng function na y=-12/x ay makukuha.

Tanong: Paano nakadepende ang lokasyon ng graph ng hyperbola y=k/x sa sign at sa halaga ng coefficient k?

Ang mga mag-aaral ay kumbinsido na kung k>0, kung gayon ang graph ay matatagpuan sa Ι At ΙΙΙ coordinate quarters, at kung k

1. Ang aralin sa pisikal na edukasyon ay isinasagawa ng guro.

1. Ang pagsasama-sama ng pinag-aaralan ay nagaganap kapag nakumpleto ang Blg. 180, 185 mula sa aklat-aralin.

1. Ang aralin ay buod, mga marka, takdang-aralin: p. 8 Blg.

Aralin 2 sa paksa

"Ang inverse proportionality function at ang graph nito."

Nakumpleto:

Telegina L.B.

Layunin ng aralin:

1. pagsama-samahin ang kasanayan sa pagbalangkas ng isang function ng inverse proportionality;
2. bumuo ng interes sa paksa, lohikal na pag-iisip;
3. linangin ang pagsasarili at atensyon.

Plano ng aralin:

1. Sinusuri ang pag-unlad takdang-aralin.
2. Oral na gawain.
3. Paglutas ng problema.
4. Minuto ng pisikal na edukasyon.
5. Multi-level na independiyenteng trabaho.
6. Summing up, pagtatasa, takdang-aralin.

Kagamitan: card.

Pag-unlad ng aralin:

1. Ipapahayag ng guro ang paksa ng aralin, layunin at banghay-aralin.

Pagkatapos ay kumpletuhin ng dalawang mag-aaral ang mga nakatalagang numero ng bahay na 179, 184 sa pisara.

1. Ang natitirang mga mag-aaral ay nagtatrabaho nang harapan, na sinasagot ang mga tanong ng guro.

Mga Tanong:

• Tukuyin ang inverse proportionality function.
• Ano ang graph ng isang inverse proportionality function.
• Paano nakadepende ang lokasyon ng graph ng hyperbola y=k/x sa halaga ng coefficient k?

Quests:

1. Kabilang sa mga function na tinukoy ng mga formula ay ang mga function ng inverse proportionality:

a) y=x 2 +5, b) y=1/x, c) y= 4x-1, d) y=2x, e) y=7-5x, f) y=-11/x, g) y=x 3, h) y=15/x-2.

2. Para sa mga function ng inverse proportionality, pangalanan ang coefficient at ipahiwatig kung saang quarters matatagpuan ang graph.

3. Hanapin ang domain ng kahulugan para sa mga function ng inverse proportionality.

(Pagkatapos ay susuriin ng mga mag-aaral ang takdang-aralin ng isa't isa gamit ang lapis batay sa mga solusyon na sinuri ng guro sa mga numero sa pisara at magbigay ng marka).

Pangharap na gawain ayon sa aklat-aralin No. 190, 191, 192, 193 (oral).

1. Pagpapatupad sa mga notebook at sa pisara mula sa aklat-aralin Blg. 186(b), 187(b), 182.

4. Ang isang aralin sa pisikal na edukasyon ay isinasagawa ng guro.

5. Malayang gawain ibinigay sa tatlong pagpipilian ng iba't ibang kumplikado(ibinahagi sa mga card).

ako c. (magaan ang timbang).

Mag-plot ng graph ng inverse proportionality function y=-6/x gamit ang talahanayan:

Gamit ang graph, hanapin ang:

a) ang halaga ng y kung x = - 1.5; 2;

b) ang halaga ng x kung saan ang y = - 1; 4.

siglo ko (katamtamang kahirapan)

Mag-plot ng graph ng inverse proportionality function na y=16/x, na napunan muna ang talahanayan.

Gamit ang graph, hanapin kung anong mga halaga x y >0.

siglo ko (nadagdagan ang kahirapan)

Mag-plot ng graph ng inverse proportionality function na y=10/x-2, na napunan muna ang talahanayan.

Hanapin ang domain ng kahulugan ng function na ito.

(Ang mga mag-aaral ay naghahawak ng mga sheet na may mga ginawang graph para sa pagsubok).

6. Nagbubuod ng aralin, mga marka, takdang-aralin: Blg. 186 (a), 187 (a).

Ngayon ay titingnan natin kung anong mga dami ang tinatawag na inversely proportional, kung ano ang hitsura ng isang inverse proportionality graph, at kung paano ang lahat ng ito ay maaaring maging kapaki-pakinabang sa iyo hindi lamang sa mga aralin sa matematika, kundi pati na rin sa labas ng paaralan.

Iba't ibang sukat

Proporsyonalidad pangalanan ang dalawang dami na nakadepende sa isa't isa.

Ang pagtitiwala ay maaaring direkta at kabaligtaran. Dahil dito, ang mga ugnayan sa pagitan ng mga dami ay inilalarawan ng direkta at kabaligtaran na proporsyonalidad.

Direktang proporsyonalidad– ito ay isang relasyon sa pagitan ng dalawang dami kung saan ang pagtaas o pagbaba sa isa sa mga ito ay humahantong sa pagtaas o pagbaba sa isa pa. Yung. hindi nagbabago ang ugali nila.

Halimbawa, mas maraming pagsisikap ang ginagawa mo sa pag-aaral para sa mga pagsusulit, mas mataas ang iyong mga marka. O kung mas maraming bagay ang dadalhin mo sa paglalakad, mas mabigat ang iyong backpack na dadalhin. Yung. Ang halaga ng pagsisikap na ginugol sa paghahanda para sa mga pagsusulit ay direktang proporsyonal sa mga markang nakuha. At ang bilang ng mga bagay na nakaimpake sa isang backpack ay direktang proporsyonal sa timbang nito.

Inverse proportionality - Ito functional dependence, kung saan ang pagbaba o pagtaas ng ilang beses sa isang independiyenteng dami (ito ay tinatawag na argumento) ay nagdudulot ng proporsyonal (i.e., ang parehong bilang ng beses) na pagtaas o pagbaba sa isang nakadependeng dami (ito ay tinatawag na function).

Ilarawan natin simpleng halimbawa. Gusto mong bumili ng mansanas sa palengke. Ang mga mansanas sa counter at ang halaga ng pera sa iyong wallet ay nasa kabaligtaran na proporsyon. Yung. Kung mas maraming mansanas ang binibili mo, mas kaunting pera ang matitira sa iyo.

Function at ang graph nito

Ang inverse proportionality function ay maaaring ilarawan bilang y = k/x. kung saan x≠ 0 at k≠ 0.

Ang function na ito ay may mga sumusunod na katangian:

1. Ang domain ng kahulugan nito ay ang set ng lahat ng tunay na numero maliban sa x = 0. D(y): (-∞; 0) U (0; +∞).
2. Ang hanay ay lahat ng tunay na numero maliban y= 0. E(y): (-∞; 0) U (0; +∞) .
3. Walang maximum o minimum na mga halaga.
4. Ito ay kakaiba at ang graph nito ay simetriko tungkol sa pinagmulan.
5. Hindi pana-panahon.
6. Ang graph nito ay hindi sumasalubong sa mga coordinate axes.
7. Walang mga zero.
8. Kung k> 0 (i.e. tumataas ang argumento), bumababa nang proporsyonal ang function sa bawat pagitan nito. Kung k< 0 (т.е. аргумент убывает), функция пропорционально возрастает на каждом из своих промежутков.
9. Habang tumataas ang argumento ( k> 0) ang mga negatibong halaga ng function ay nasa pagitan (-∞; 0), at ang mga positibong halaga ay nasa pagitan (0; +∞). Kapag bumaba ang argumento ( k< 0) отрицательные значения расположены на промежутке (0; +∞), положительные – (-∞; 0).

Ang graph ng isang inverse proportionality function ay tinatawag na hyperbola. Ipinapakita ang mga sumusunod:

Mga problema sa baligtad na proporsyonalidad

Upang gawing mas malinaw, tingnan natin ang ilang mga gawain. Ang mga ito ay hindi masyadong kumplikado, at ang paglutas sa mga ito ay makakatulong sa iyong mailarawan kung ano ang kabaligtaran na proporsyonalidad at kung paano maaaring maging kapaki-pakinabang ang kaalamang ito sa iyong ordinaryong buhay.

Gawain Blg. 1. Isang sasakyan ang gumagalaw sa bilis na 60 km/h. Inabot siya ng 6 na oras bago makarating sa kanyang destinasyon. Gaano katagal aabutin niya ang parehong distansya kung siya ay gumagalaw nang doble ang bilis?

Maaari tayong magsimula sa pamamagitan ng pagsusulat ng formula na naglalarawan ng ugnayan sa pagitan ng oras, distansya at bilis: t = S/V. Sumang-ayon, ipinapaalala nito sa atin ang inverse proportionality function. At ito ay nagpapahiwatig na ang oras na ginugugol ng isang kotse sa kalsada at ang bilis kung saan ito gumagalaw ay nasa kabaligtaran na proporsyon.

Upang mapatunayan ito, hanapin natin ang V 2, na ayon sa kondisyon ay 2 beses na mas mataas: V 2 = 60 * 2 = 120 km/h. Pagkatapos ay kinakalkula namin ang distansya gamit ang formula S = V * t = 60 * 6 = 360 km. Ngayon hindi mahirap malaman ang oras t 2 na kinakailangan mula sa amin ayon sa mga kondisyon ng problema: t 2 = 360/120 = 3 oras.

Tulad ng nakikita mo, ang oras at bilis ng paglalakbay ay talagang inversely proportional: sa bilis na 2 beses na mas mataas kaysa sa orihinal na bilis, ang kotse ay gumugugol ng 2 beses na mas kaunting oras sa kalsada.

Ang solusyon sa problemang ito ay maaari ding isulat bilang isang proporsyon. Kaya gawin muna natin ang diagram na ito:

↓ 60 km/h – 6 h

↓120 km/h – x h

Ang mga arrow ay nagpapahiwatig ng isang inversely proportional na relasyon. Iminumungkahi din nila na kapag gumuhit ng isang proporsyon, ang kanang bahagi ng rekord ay dapat ibalik: 60/120 = x/6. Saan natin makukuha ang x = 60 * 6/120 = 3 oras.

Gawain Blg. 2. Ang workshop ay gumagamit ng 6 na manggagawa na maaaring kumpletuhin ang isang naibigay na dami ng trabaho sa loob ng 4 na oras. Kung ang bilang ng mga manggagawa ay hinati, gaano katagal ang mga natitirang manggagawa upang makumpleto ang parehong dami ng trabaho?

Isulat natin ang mga kondisyon ng problema sa form biswal na diagram:

↓ 6 na manggagawa – 4 na oras

↓ 3 manggagawa – x ​​h

Isulat natin ito bilang isang proporsyon: 6/3 = x/4. At makakakuha tayo ng x = 6 * 4/3 = 8 oras Kung mayroong 2 beses na mas kaunting mga manggagawa, ang mga natitira ay gugugol ng 2 beses na mas maraming oras sa paggawa ng lahat ng trabaho.

Gawain Blg. 3. May dalawang tubo na papunta sa pool. Sa pamamagitan ng isang tubo, dumadaloy ang tubig sa bilis na 2 l/s at pupunuin ang pool sa loob ng 45 minuto. Sa pamamagitan ng isa pang tubo, mapupuno ang pool sa loob ng 75 minuto. Sa anong bilis pumapasok ang tubig sa pool sa pamamagitan ng tubo na ito?

Upang magsimula, bawasan natin ang lahat ng mga dami na ibinigay sa atin ayon sa mga kondisyon ng problema sa parehong mga yunit ng pagsukat. Upang gawin ito, ipinahayag namin ang bilis ng pagpuno ng pool sa litro kada minuto: 2 l/s = 2 * 60 = 120 l/min.

Dahil ito ay sumusunod mula sa kondisyon na ang pool ay pumupuno nang mas mabagal sa pamamagitan ng pangalawang tubo, nangangahulugan ito na ang rate ng daloy ng tubig ay mas mababa. Ang proporsyonalidad ay kabaligtaran. Ipahayag natin ang hindi kilalang bilis sa pamamagitan ng x at iguhit ang sumusunod na diagram:

↓ 120 l/min – 45 min

↓ x l/min – 75 min

At pagkatapos ay binubuo namin ang proporsyon: 120/x = 75/45, mula sa kung saan x = 120 * 45/75 = 72 l/min.

Sa problema, ang bilis ng pagpuno ng pool ay ipinahayag sa litro bawat segundo; bawasan natin ang sagot na natanggap natin sa parehong form: 72/60 = 1.2 l/s.

Gawain Blg. 4. Ang isang maliit na pribadong printing house ay nagpi-print ng mga business card. Ang isang empleyado ng printing house ay nagtatrabaho sa bilis na 42 business card kada oras at nagtatrabaho sa isang buong araw - 8 oras. Kung nagtrabaho siya nang mas mabilis at nag-print ng 48 business card sa loob ng isang oras, gaano pa kaya siya makakauwi?

Sinusunod namin ang napatunayang landas at gumuhit ng isang diagram ayon sa mga kondisyon ng problema, na itinalaga ang nais na halaga bilang x:

↓ 42 business card/oras – 8 oras

↓ 48 business card/h – x h

Mayroon kaming isang inversely proportional na relasyon: ang dami ng beses na mas maraming business card ang ini-print ng isang empleyado ng isang printing house bawat oras, ang parehong bilang ng beses na mas kaunting oras na kakailanganin niya upang makumpleto ang parehong trabaho. Alam ito, gumawa tayo ng isang proporsyon:

42/48 = x/8, x = 42 * 8/48 = 7 oras.

Kaya, matapos ang trabaho sa loob ng 7 oras, ang empleyado ng bahay-imprenta ay maaaring umuwi ng isang oras nang mas maaga.

Konklusyon

Sa palagay natin, ang mga problemang ito sa kabaligtaran na proporsyonalidad ay talagang simple. Umaasa kami na ngayon ay ganoon din ang tingin mo sa kanila. At ang pangunahing bagay ay ang kaalaman tungkol sa kabaligtaran proporsyonal na pag-asa ang dami ay maaaring maging kapaki-pakinabang sa iyo nang higit sa isang beses.

Hindi lang sa math lessons and exams. Ngunit kahit na, kapag handa kang pumunta sa isang paglalakbay, mag-shopping, magpasya na kumita ng kaunting karagdagang pera sa panahon ng bakasyon, atbp.

Sabihin sa amin sa mga komento kung anong mga halimbawa ng kabaligtaran at direktang proporsyonal na relasyon ang napansin mo sa paligid mo. Hayaan itong maging isang laro. Makikita mo kung gaano ito kapana-panabik. Huwag kalimutang ibahagi ang artikulong ito sa mga social network para makapaglaro din ang mga kaibigan at kaklase mo.

website, kapag kumukopya ng materyal nang buo o bahagi, kinakailangan ang isang link sa orihinal na pinagmulan.

Entry level

Baliktad na relasyon.

Entry level.

Ngayon ay pag-uusapan natin ang tungkol sa inverse dependence, o sa madaling salita - inverse proportionality, bilang isang function. Naaalala mo ba na ang isang function ay isang tiyak na uri ng dependency? Kung hindi mo pa nababasa ang paksa, lubos kong inirerekumenda na i-drop mo ang lahat at basahin ito, dahil hindi mo maaaring pag-aralan ang anumang partikular na function nang hindi nauunawaan kung ano ito - isang function. Ito rin ay lubhang kapaki-pakinabang bago simulan ang paksang ito upang makabisado pa ang dalawa mga simpleng function

: At . Doon mo pagtitibayin ang konsepto ng isang function at matututong gumana sa mga coefficient at graph.
Kaya, naaalala mo ba kung ano ang isang function? Ulitin natin: ang function ay isang panuntunan kung saan ang bawat elemento ng isang set (argument) ay nauugnay sa isang tiyak na ( ang nag-iisa! ) elemento ng isa pang set (set ng mga value ng function). Iyon ay, kung mayroon kang isang function, nangangahulugan ito na lahat katanggap-tanggap na halaga ang isang variable (tinatawag na "argument") ay tumutugma sa isang halaga ng isang variable (tinatawag na "function"). Ano ang ibig sabihin ng "katanggap-tanggap"? Kung hindi mo masagot ang tanong na ito, bumalik sa paksang "" muli! Ang lahat ay nasa konsepto"domain ng kahulugan"

: Para sa ilang mga function, hindi lahat ng mga argumento ay pantay na kapaki-pakinabang at maaaring palitan sa mga dependency. Halimbawa, para sa isang function, hindi pinapayagan ang mga negatibong halaga ng argumento.

Function na naglalarawan ng inverse dependence

Ito ay isang function ng form kung saan.
Sa ibang paraan ito ay tinatawag na inverse proportionality: ang pagtaas sa argument ay nagdudulot ng proporsyonal na pagbaba sa function.

Tukuyin natin ang domain ng kahulugan. Ano ang maaaring katumbas nito? O, sa madaling salita, ano ang hindi maaaring katumbas nito?

Ang tanging bilang na hindi maaaring hatiin ay kung gayon:

(Ang gayong notasyon ay nangangahulugan na maaari itong maging anumang numero, maliban sa: ang tandang “ ” ay tumutukoy sa hanay ng mga tunay na numero, iyon ay, lahat ng posibleng numero; ang tandang “ ” ay tumutukoy sa pagbubukod ng isang bagay mula sa hanay na ito (katulad ng “minus ” sign), at ang isang numero sa mga kulot na bracket ay nangangahulugang isang numero lamang;

Ang hanay ng mga halaga ng pag-andar, lumalabas, ay eksaktong pareho: pagkatapos ng lahat, kung, kahit na ano pa ang hatiin natin, hindi ito gagana:

Posible rin ang ilang variation ng formula. Halimbawa, isa rin itong function na naglalarawan ng kabaligtaran na relasyon.
Tukuyin ang domain ng kahulugan at hanay ng mga halaga ng function na ito sa iyong sarili. Dapat itong magmukhang ganito:

Tingnan natin ang function na ito: . Inversely related ba ito?

Sa unang sulyap, mahirap sabihin: pagkatapos ng lahat, sa isang pagtaas, ang parehong denominator ng fraction at ang numerator ay tumataas, kaya hindi malinaw kung ang pag-andar ay bababa, at kung gayon, ito ba ay bababa nang proporsyonal? Upang maunawaan ito, kailangan nating baguhin ang expression upang walang variable sa numerator:

Sa katunayan, nakatanggap kami ng kabaligtaran na relasyon, ngunit may caveat: .

Narito ang isa pang halimbawa: .

Ito ay mas kumplikado dito: pagkatapos ng lahat, ang numerator at denominator ngayon ay tiyak na hindi magkakansela. Ngunit maaari pa rin nating subukan:

Naiintindihan mo ba ang ginawa ko? Sa numerator, idinagdag at ibinawas ko ang parehong numero (), kaya parang wala akong binago, ngunit ngayon ay may bahagi sa numerator na katumbas ng denominator. Ngayon ay hahatiin ko ang termino sa pamamagitan ng termino, iyon ay, hahatiin ko ang fraction na ito sa kabuuan ng dalawang fraction:

(at totoo, kung dadalhin mo ang nakuha ko karaniwang denominador, nakukuha lang natin ang ating paunang bahagi):

Wow! Ito ay gumagana muli kabaligtaran na relasyon, ngayon lang may naidagdag na numero dito.
Ang pamamaraang ito ay magiging lubhang kapaki-pakinabang sa amin sa ibang pagkakataon kapag gumagawa ng mga graph.

Ngayon, baguhin ang mga expression sa iyong sarili sa isang kabaligtaran na relasyon:

Mga sagot:

2. Dito kailangan mong tandaan kung paano quadratic trinomial ay factorized (ito ay inilarawan nang detalyado sa paksang ""). Hayaan akong ipaalala sa iyo na para dito kailangan mong hanapin ang mga ugat ng kaukulang quadratic equation: . Hahanapin ko sila sa salita gamit ang teorama ni Vieta: , . Paano ito ginagawa? Matututuhan mo ito sa pamamagitan ng pagbabasa ng paksa.
Kaya, nakukuha natin ang: , therefore:

3. Nasubukan mo na bang lutasin ito sa iyong sarili? Ano ang catch? Tiyak na ang katotohanan ay mayroon tayo sa numerator at sa denominator - ito ay simple. Walang problema. Kakailanganin nating bawasan ng, kaya sa numerator dapat nating alisin ito sa mga bracket (upang sa mga bracket ay makuha natin ito nang walang koepisyent):

Baliktad na graph ng relasyon

Gaya ng nakasanayan, magsimula tayo sa pinakasimpleng kaso: .
Gumawa tayo ng talahanayan:

Gumuhit tayo ng mga puntos sa coordinate plane:

Ngayon kailangan nilang maayos na konektado, ngunit paano? Makikita na ang mga punto sa kanan at kaliwang bahagi ay bumubuo ng tila hindi magkakaugnay na mga kurbadong linya. ganyan yan. Magiging ganito ang graph:

Ang graph na ito ay tinatawag na "hyperbola"(may parang "parabola" sa pangalan na yan, di ba?). Tulad ng isang parabola, ang isang hyperbola ay may dalawang sangay, ngunit hindi sila konektado sa isa't isa. Ang bawat isa sa kanila ay nagsusumikap sa mga dulo nito upang makalapit sa mga palakol at, ngunit hindi kailanman umabot sa kanila. Kung titingnan mo ang parehong hyperbole mula sa malayo, makukuha mo ang sumusunod na larawan:

Ito ay naiintindihan: dahil ang graph ay hindi maaaring tumawid sa axis. Ngunit gayundin, kaya hindi kailanman hahawakan ng graph ang axis.

Well, ngayon tingnan natin kung ano ang naiimpluwensyahan ng mga coefficient. Isaalang-alang ang mga function na ito:
:

Wow, ang ganda!
Ang lahat ng mga graph ay binuo iba't ibang kulay para mas madaling makilala sila sa isa't isa.

Kaya, ano ang dapat nating unang bigyang pansin? Halimbawa, kung ang isang function ay may minus bago ang fraction, ang graph ay binaligtad, ibig sabihin, ipinapakita ang simetriko na nauugnay sa axis.

Pangalawa: kung mas malaki ang numero sa denominator, mas "tumakas" ang graph mula sa pinanggalingan.

Paano kung ang function ay mukhang mas kumplikado, halimbawa, ?

Sa kasong ito, ang hyperbole ay magiging eksaktong kapareho ng karaniwan, ito ay magbabago nang kaunti. Isipin natin, saan?

Ano ang hindi ito mapapantayan ngayon? Tama, . Nangangahulugan ito na ang graph ay hindi makakarating sa isang tuwid na linya. Ano ang hindi ito mapapantayan? Ngayon. Nangangahulugan ito na ngayon ang graph ay magiging tuwid na linya, ngunit hindi kailanman tatawid dito. Kaya ngayon ay straight na sila at ginagampanan ang parehong papel na ginagawa nila coordinate axes para sa function. Ang mga ganitong linya ay tinatawag asymptotes(mga linyang may posibilidad ngunit hindi naaabot ng graph):

Malalaman natin ang higit pa tungkol sa kung paano binuo ang mga naturang graph sa paksa.

Ngayon subukang lutasin ang ilang mga halimbawa upang pagsamahin:

1. Ang figure ay nagpapakita ng isang graph ng isang function. Tukuyin.

2. Ipinapakita ng figure ang graph ng function. Tukuyin

3. Ipinapakita ng figure ang graph ng function. Tukuyin.

4. Ipinapakita ng figure ang graph ng function. Tukuyin.

5. Ang figure ay nagpapakita ng mga graph ng mga function at.

Piliin ang tamang ratio:

Mga sagot:

Inverse dependence sa buhay

Saan natin mahahanap ang gayong function sa pagsasanay? Maraming halimbawa. Ang pinakakaraniwan ay ang paggalaw: kung mas malaki ang bilis kung saan tayo gumagalaw, mas kaunting oras ang aabutin natin upang masakop ang parehong distansya. Sa katunayan, tandaan natin ang formula ng bilis: , where is speed, is travel time, is distance (path).

Mula dito maaari nating ipahayag ang oras:

Halimbawa:

May lalaking kasama sa trabaho average na bilis km/h, at makakarating doon sa loob ng isang oras. Ilang minuto ang gugugol niya sa parehong kalsada kung nagmamaneho siya sa bilis na km/h?

Solusyon:

Sa pangkalahatan, nalutas mo na ang mga ganitong problema sa ika-5 at ika-6 na baitang. Binubuo mo ang proporsyon:

Ibig sabihin, pamilyar na sa iyo ang konsepto ng inverse proportionality. Kaya naalala namin. At ngayon ang parehong bagay, lamang sa isang pang-adultong paraan: sa pamamagitan ng isang function.

Function (iyon ay, dependence) ng oras sa mga minuto sa bilis:

Ito ay kilala na, kung gayon:

Kailangang hanapin:

Ngayon ay gumawa ng ilang mga halimbawa mula sa buhay kung saan ang inverse proportionality ay naroroon.
Nakaisip ka ba nito? Magaling kung gagawin mo. Good luck!

REVERSE DEPENDENCE. MAIKLING TUNGKOL SA MGA PANGUNAHING BAGAY

1. Kahulugan

Function na naglalarawan ng kabaligtaran na relasyon ay isang function ng form kung saan.

Sa ibang paraan, ang function na ito ay tinatawag na inverse proportionality, dahil ang pagtaas sa argument ay nagdudulot ng proporsyonal na pagbaba sa function.

Ang tanging bilang na hindi maaaring hatiin ay kung gayon:

Ang inverse relationship graph ay isang hyperbola.

2. Coefficients, at.

Responsable para sa "pagkatagpo" at direksyon ng graph: mas malaki ang koepisyent na ito, mas matatagpuan ang hyperbola mula sa pinanggalingan, at, samakatuwid, ito ay "lumiliko" nang hindi gaanong matarik (tingnan ang figure). Ang tanda ng koepisyent ay nakakaapekto kung aling quarter ang graph ay matatagpuan sa:

• kung, kung gayon ang mga sanga ng hyperbola ay matatagpuan sa at quarters;
• kung, pagkatapos ay sa at.

x=a ay patayong asymptote, iyon ay, ang patayo kung saan ang graph ay may posibilidad.

Ang numero ay responsable para sa paglilipat ng function graph pataas sa pamamagitan ng isang halaga kung , at paglilipat nito pababa kung .

Samakatuwid, ito ay pahalang na asymptote.

Ulitin natin ang teorya tungkol sa mga function. Ang isang function ay isang panuntunan ayon sa kung saan ang bawat elemento ng isang set (argument) ay nauugnay sa isang tiyak na ( Ulitin natin: ang function ay isang panuntunan kung saan ang bawat elemento ng isang set (argument) ay nauugnay sa isang tiyak na () elemento ng isa pang set (set ng mga value ng function). Iyon ay, kung mayroong isang function \(y = f(x)\), nangangahulugan ito na para sa bawat wastong halaga ng variable \(x\)(na tinatawag na "argument") ay tumutugma sa isang halaga ng variable \(y\)(tinatawag na "function").

Function na naglalarawan ng kabaligtaran na relasyon

Ito ay isang function ng form \(y = \frac(k)(x)\), saan \(k\ne 0.\)

Ito ay isang function ng form kung saan.
Tukuyin natin ang domain ng kahulugan. Ano ang maaaring katumbas ng \(x\)? O, sa madaling salita, ano ang hindi maaaring katumbas nito?

Ang tanging numero na hindi mahahati sa ay 0, kaya \(x\ne 0.\):

\(D(y) = (- \infty ;0) \cup (0; + \infty)\)

o, ano ang pareho:

\(D(y) = R\backslash \( 0\).\)

Ang notasyong ito ay nangangahulugan na ang \(x\) ay maaaring maging anumang numero maliban sa 0: ang tanda na "R" ay tumutukoy sa hanay ng mga tunay na numero, iyon ay, lahat ng posibleng numero; ang sign na "\" ay nagpapahiwatig ng pagbubukod ng isang bagay mula sa set na ito (katulad ng "minus" sign), at ang numero 0 sa mga kulot na bracket ay nangangahulugan lamang ng numero 0; Lumalabas na mula sa lahat ng posibleng numero ay ibinubukod namin ang 0.

Ang hanay ng mga halaga ng pag-andar, lumalabas, ay eksaktong pareho: pagkatapos ng lahat, kung \(k \ne 0.\) , kung gayon kahit na ano ang hatiin natin, 0 ay hindi gagana:

\(E(y) = (- \infty ;0) \cup (0; + \infty)\)

o \(E(y) = R\backslash \( 0\).\)

Posible rin ang ilang variation ng formula \(y = \frac(k)(x)\). Halimbawa, \(y = \frac(k)((x + a))\) ay isa ring function na naglalarawan ng kabaligtaran na relasyon. Ang saklaw at saklaw ng mga halaga ng pagpapaandar na ito ay ang mga sumusunod:

\(D(y) = (- \infty ; - a) \cup (- a; + \infty)\)

\(E(y) = (- \infty ;0) \cup (0; + \infty).\)

Isaalang-alang natin halimbawa, bawasan natin ang expression sa anyo ng isang kabaligtaran na relasyon:

\(y = \frac((x + 2))((x - 3)).\)

\(y = \frac((x + 2))((x - 3)) = \frac((x - 3 + 3 + 2))((x - 3)) = \frac(((x - 3) ) + 5))((x - 3)).\)

Artipisyal naming ipinakilala ang halaga 3 sa numerator, at ngayon hinati namin ang numerator sa termino ng denominator ayon sa termino, nakukuha namin ang:

\(y = \frac(((x - 3) + 5))((x - 3)) = \frac((x - 3))((x - 3)) + \frac(5)((x - 3)) = 1 + \frac(5)((x - 3)).\)

Nakuha namin ang kabaligtaran na relasyon kasama ang numero 1.

Baliktad na graph ng relasyon

Magsimula tayo sa isang simpleng kaso \(y = \frac(1)(x).\)

Gumawa tayo ng talahanayan ng mga halaga:

Gumuhit tayo ng mga puntos sa coordinate plane:

Ikonekta ang mga tuldok, magiging ganito ang graph:

Ang graph na ito ay tinatawag na "hyperbola". Tulad ng isang parabola, ang isang hyperbola ay may dalawang sangay, ngunit hindi sila konektado sa isa't isa. Ang bawat isa sa kanila ay may posibilidad na ilipat ang mga dulo nito palapit sa mga palakol baka At Oy, ngunit hindi kailanman umabot sa kanila.

Tandaan natin ang ilang mga tampok ng function:

1. Kung ang isang function ay may minus bago ang fraction, ang graph ay binaligtad, ibig sabihin, ito ay ipinapakita nang simetriko na nauugnay sa axis baka.
2. Kung mas malaki ang numero sa denominator, mas "tumakas" ang graph mula sa pinanggalingan.

Inverse dependence sa buhay

Saan natin mahahanap ang gayong function sa pagsasanay? Maraming halimbawa. Ang pinakakaraniwan ay ang paggalaw: kung mas malaki ang bilis kung saan tayo gumagalaw, mas kaunting oras ang aabutin natin upang masakop ang parehong distansya. Tandaan natin ang formula ng bilis:

\(v = \frac(S)(t),\)

kung saan ang v ay bilis, t ay oras ng paglalakbay, S ay distansya (landas).

Mula dito maaari nating ipahayag ang oras: \(t = \frac(S)(v).\)