Propesor Stewart's Incredible Numbers epub. Stewart I. Hindi kapani-paniwalang bilang ng Propesor Stewart. Pangunahing konsepto ng numero

Nararapat kay Stewart ang pinakamataas na papuri para sa kanyang kuwento tungkol sa kung gaano kahusay, kahanga-hanga at kapaki-pakinabang ang papel ng lahat sa komunidad ng mga pandaigdigang numero. Kirkus Reviews Gumagawa si Stewart ng napakahusay na trabaho sa pagpapaliwanag ng mga kumplikadong isyu. Ang New Scientist Britain ang pinakamatalino at pinakamaraming popularizer ng matematika. Alex Bellos Tungkol saan ang aklat? Sa kanyang aklat, ang pinakasikat na British popularizer ng matematika, si Propesor Ian Stewart, ay nag-aalok ng isang kasiya-siyang pagpapakilala sa mga numerong nakapaligid sa atin, mula sa pamilyar na kumbinasyon ng mga simbolo hanggang sa mas kakaiba - mga factorial, fractals o Apéry constant. Sa landas na ito, sinabi sa atin ng may-akda ang tungkol sa mga prime number, cubic equation, ang konsepto ng zero, posibleng mga bersyon ng Rubik's cube, ang papel ng mga numero sa kasaysayan ng sangkatauhan at ang kaugnayan ng kanilang pag-aaral sa ating panahon. Sa kanyang katangiang pagpapatawa at katalinuhan, inihayag ni Stewart sa mambabasa ang kamangha-manghang mundo ng matematika. Bakit sulit na basahin ang libro Ang pinaka-kagiliw-giliw na bagay tungkol sa mga pinaka-hindi kapani-paniwalang mga numero sa kuwento ng pinakamahusay na popularizer ng matematika mula sa Britain, nagwagi ng 2015 Lewis Thomas Prize. Sinusuri ni Ian Stewart ang mga kamangha-manghang katangian ng mga numero mula zero hanggang infinity - natural, kumplikado, hindi makatwiran, positibo, negatibo, prime, composite - at ipinapakita ang kanilang kasaysayan mula sa mga kamangha-manghang pagtuklas ng mga sinaunang mathematician hanggang sa modernong estado ng agham matematika. Sa ilalim ng karanasang patnubay ng propesor, matututunan mo ang mga lihim ng mathematical code at Sudoku, Rubik's cube at musical scales, tingnan kung paano maaaring maging mas malaki ang isang infinity kaysa sa isa pa, at matutuklasan din na nakatira ka sa labing-isang dimensyon na espasyo. Ang aklat na ito ay magpapasaya sa mga mahilig sa mga numero at sa mga iniisip pa rin na hindi nila ito mahal. Tungkol sa may-akda Si Propesor Ian Stewart ay isang sikat na sikat sa mundo ng matematika at ang may-akda ng maraming kamangha-manghang mga libro, at ginawaran ng bilang ng pinakamataas na internasyonal na mga parangal sa akademya. Noong 2001 naging miyembro siya ng Royal Society of London. Emeritus Professor sa Unibersidad ng Warwick, sinasaliksik niya ang dynamics ng mga nonlinear system at isinusulong ang kaalaman sa matematika. May-akda ng pinakamabentang aklat na "The Greatest Mathematical Problems", na inilathala ng publishing house na "Alpina Non-Fiction" noong 2015. Mga pangunahing konseptoMatematika, numero, numero, bugtong, mas mataas na matematika, problema sa matematika, pananaliksik sa matematika, kasaysayan ng matematika, agham, agham.

Emeritus Professor of Mathematics sa Unibersidad ng Warwick, sikat na popularizer ng agham na si Ian Stewart, na nakatuon sa papel ng mga numero sa kasaysayan ng sangkatauhan at ang kaugnayan ng kanilang pag-aaral sa ating panahon.

Pythagorean hypotenuse

Ang mga Pythagorean triangle ay may mga tamang anggulo at integer na panig. Ang pinakasimpleng sa kanila ay may pinakamahabang bahagi ng haba 5, ang iba pa - 3 at 4. Mayroong 5 regular na polyhedra sa kabuuan. Ang isang fifth degree equation ay hindi malulutas gamit ang fifth roots - o anumang iba pang roots. Ang mga sala-sala sa isang eroplano at sa tatlong-dimensional na espasyo ay walang limang-lobed na rotational symmetry, kaya ang gayong mga simetriko ay wala sa mga kristal. Gayunpaman, maaari silang matagpuan sa mga sala-sala sa apat na dimensyon na espasyo at sa mga kagiliw-giliw na istruktura na kilala bilang mga quasicrystal.

Hypotenuse ng pinakamaliit na triple ng Pythagorean

Ang Pythagorean theorem ay nagsasaad na ang pinakamahabang bahagi ng isang right triangle (ang kilalang hypotenuse) ay nauugnay sa iba pang dalawang panig ng tatsulok na ito sa napakasimple at magandang paraan: ang parisukat ng hypotenuse ay katumbas ng kabuuan ng mga parisukat ng iba pang dalawang panig.

Ayon sa kaugalian, tinatawag namin ang teorama na ito sa pangalan ng Pythagoras, ngunit sa katunayan ang kasaysayan nito ay medyo malabo. Iminumungkahi ng mga clay tablet na alam ng mga sinaunang Babylonians ang Pythagorean theorem bago pa si Pythagoras mismo; Ang katanyagan ng nakatuklas ay dinala sa kanya ng matematikal na kulto ng mga Pythagorean, na ang mga tagasuporta ay naniniwala na ang Uniberso ay batay sa mga batas ng numero. Iniuugnay ng mga sinaunang may-akda ang iba't ibang teorema ng matematika sa mga Pythagorean - at samakatuwid ay kay Pythagoras, ngunit sa katunayan wala kaming ideya kung anong uri ng matematika ang kinasasangkutan mismo ni Pythagoras. Ni hindi natin alam kung mapapatunayan ng mga Pythagorean ang Pythagorean Theorem o kung pinaniniwalaan lang nilang totoo ito. O, malamang, mayroon silang nakakumbinsi na katibayan ng katotohanan nito, na gayunpaman ay hindi sapat para sa kung ano ang itinuturing nating ebidensya ngayon.

Mga Katibayan ng Pythagoras

Ang unang kilalang patunay ng Pythagorean theorem ay matatagpuan sa Euclid's Elements. Ito ay isang medyo masalimuot na patunay, gamit ang isang guhit na agad na makikilala ng mga Victorian schoolchildren bilang "Pythagorean na pantalon"; Ang pagguhit ay talagang katulad ng pagpapatuyo ng salawal sa isang linya. Mayroong literal na daan-daang iba pang mga patunay, karamihan sa mga ito ay ginagawang mas malinaw ang assertion.

Ang dissection ni Perigal ay isa pang puzzle proof.

Mayroon ding patunay ng theorem gamit ang pag-aayos ng mga parisukat sa isang eroplano. Marahil ito ay kung paano natuklasan ng mga Pythagorean o kanilang hindi kilalang mga nauna ang teorama na ito. Kung titingnan mo kung paano nagsasapawan ang skew square sa dalawa pang parisukat, makikita mo kung paano gupitin ang isang malaking parisukat at pagkatapos ay pagsama-samahin ang mga ito sa dalawang mas maliliit na parisukat. Maaari mo ring makita ang mga tamang tatsulok, na ang mga gilid ay nagbibigay ng mga sukat ng tatlong parisukat na kasangkot.

Mayroong mga kagiliw-giliw na patunay gamit ang mga katulad na tatsulok sa trigonometrya. Hindi bababa sa limampung magkakaibang patunay ang kilala.

Pythagorean triple

Sa teorya ng numero, ang Pythagorean theorem ay naging pinagmulan ng isang mabungang ideya: paghahanap ng mga integer na solusyon sa algebraic equation. Ang isang Pythagorean triple ay isang set ng mga integer a, b at c tulad na

a 2 + b 2 = c 2 .

Sa geometriko, ang gayong triple ay tumutukoy sa isang tamang tatsulok na may mga panig na integer.

Ang pinakamaliit na hypotenuse ng isang Pythagorean triple ay 5.

Ang iba pang dalawang panig ng tatsulok na ito ay 3 at 4. Dito

3 2 + 4 2 = 9 + 16 = 25 = 5 2 .

Ang susunod na pinakamalaking hypotenuse ay 10 dahil

6 2 + 8 2 = 36 + 64 = 100 = 10 2 .

Gayunpaman, ito ay mahalagang parehong tatsulok na may dobleng panig. Ang susunod na pinakamalaki at tunay na magkaibang hypotenuse ay 13, kung saan

5 2 + 12 2 = 25 + 144 = 169 = 13 2 .

Alam ni Euclid na mayroong walang katapusang bilang ng iba't ibang variation ng Pythagorean triplets, at nagbigay siya ng maaaring tawaging pormula para sa paghahanap ng lahat ng ito. Nang maglaon, iminungkahi ni Diophantus ng Alexandria ang isang simpleng recipe, karaniwang kapareho ng Euclidean.

Kumuha ng alinmang dalawang natural na numero at kalkulahin:

kanilang dobleng produkto;

ang pagkakaiba ng kanilang mga parisukat;

ang kabuuan ng kanilang mga parisukat.

Ang tatlong magreresultang numero ay magiging mga gilid ng Pythagorean triangle.

Kunin natin, halimbawa, ang mga numero 2 at 1. Kalkulahin natin:

dobleng produkto: 2 × 2 × 1 = 4;

pagkakaiba ng mga parisukat: 2 2 – 1 2 = 3;

kabuuan ng mga parisukat: 2 2 + 1 2 = 5,

at nakuha namin ang sikat na 3-4-5 triangle. Kung kukunin natin ang mga numero 3 at 2 sa halip, makakakuha tayo ng:

dobleng produkto: 2 × 3 × 2 = 12;

pagkakaiba ng mga parisukat: 3 2 – 2 2 = 5;

kabuuan ng mga parisukat: 3 2 + 2 2 = 13,

at makuha natin ang susunod na pinakatanyag na tatsulok 5 – 12 – 13. Subukan nating kunin ang mga numero 42 at 23 at makuha ang:

dobleng produkto: 2 × 42 × 23 = 1932;

pagkakaiba ng mga parisukat: 42 2 – 23 2 = 1235;

kabuuan ng mga parisukat: 42 2 + 23 2 = 2293,

wala pang nakarinig tungkol sa tatsulok 1235–1932–2293.

Ngunit gumagana din ang mga numerong ito:

1235 2 + 1932 2 = 1525225 + 3732624 = 5257849 = 2293 2 .

May isa pang tampok ng panuntunang Diophantine na naipahiwatig na: binigyan ng tatlong numero, maaari tayong kumuha ng isa pang di-makatwirang numero at i-multiply ang lahat ng ito. Kaya, ang isang 3–4–5 na tatsulok ay maaaring gawing 6–8–10 tatsulok sa pamamagitan ng pagpaparami ng lahat ng panig sa 2, o sa isang 15–20–25 tatsulok sa pamamagitan ng pagpaparami ng lahat sa 5.

Kung lilipat tayo sa wika ng algebra, ang panuntunan ay nasa sumusunod na anyo: hayaan ang u, v at k ay mga natural na numero. Pagkatapos ay isang kanang tatsulok na may mga gilid

Ang 2kuv at k (u 2 – v 2) ay may hypotenuse

Mayroong iba pang mga paraan ng paglalahad ng pangunahing ideya, ngunit lahat sila ay bumagsak sa inilarawan sa itaas. Binibigyang-daan ka ng pamamaraang ito na makuha ang lahat ng triple ng Pythagorean.

Regular na polyhedra

Mayroong eksaktong limang regular na polyhedra. Ang isang regular na polyhedron (o polyhedron) ay isang three-dimensional na pigura na may hangganan na bilang ng mga patag na mukha. Ang mga mukha ay nagtatagpo sa isa't isa sa mga linya na tinatawag na mga gilid; nagtatagpo ang mga gilid sa mga puntong tinatawag na vertices.

Ang kasukdulan ng Euclidean's Principia ay ang patunay na maaari lamang magkaroon ng limang regular na polyhedra, iyon ay, polyhedra kung saan ang bawat mukha ay isang regular na polygon (pantay na gilid, pantay na anggulo), lahat ng mukha ay magkapareho, at lahat ng vertices ay napapalibutan ng pantay bilang ng mga mukha na may pantay na pagitan. Narito ang limang regular na polyhedra:

tetrahedron na may apat na tatsulok na mukha, apat na vertices at anim na gilid;

cube, o hexahedron, na may 6 na parisukat na mukha, 8 vertices at 12 gilid;

octahedron na may 8 tatsulok na mukha, 6 vertices at 12 gilid;

dodecahedron na may 12 pentagonal na mukha, 20 vertices at 30 gilid;

Isang icosahedron na may 20 tatsulok na mukha, 12 vertices at 30 gilid.

Ang regular na polyhedra ay matatagpuan din sa kalikasan. Noong 1904, inilathala ni Ernst Haeckel ang mga guhit ng maliliit na organismo na kilala bilang radiolarians; marami sa kanila ay hugis tulad ng parehong limang regular polyhedra. Marahil, gayunpaman, bahagyang naitama niya ang kalikasan, at ang mga guhit ay hindi ganap na sumasalamin sa hugis ng mga tiyak na nilalang. Ang unang tatlong mga istraktura ay sinusunod din sa mga kristal. Hindi ka makakahanap ng mga dodecahedron at icosahedron sa mga kristal, bagama't minsan ay matatagpuan doon ang mga hindi regular na dodecahedron at icosahedron. Ang mga totoong dodecahedron ay maaaring mangyari bilang mga quasicrystal, na katulad ng mga kristal sa lahat ng paraan maliban na ang kanilang mga atomo ay hindi bumubuo ng isang pana-panahong sala-sala.

Maaaring maging kawili-wili ang paggawa ng mga modelo ng regular na polyhedra mula sa papel sa pamamagitan ng paggupit muna ng isang hanay ng magkakaugnay na mga mukha - ito ay tinatawag na pagbuo ng polyhedron; ang pag-unlad ay nakatiklop sa mga gilid at ang kaukulang mga gilid ay pinagdikit. Kapaki-pakinabang na magdagdag ng karagdagang glue pad sa isa sa mga tadyang ng bawat naturang pares, tulad ng ipinapakita sa Fig. 39. Kung walang ganoong plataporma, maaari kang gumamit ng adhesive tape.

Fifth degree equation

Walang algebraic formula para sa paglutas ng 5th degree equation.

Sa pangkalahatan, ganito ang hitsura ng fifth degree equation:

ax 5 + bx 4 + cx 3 + dx 2 + ex + f = 0.

Ang problema ay ang paghahanap ng formula para sa mga solusyon sa naturang equation (maaari itong magkaroon ng hanggang limang solusyon). Ang karanasan sa mga quadratic at cubic equation, pati na rin ang mga equation ng ika-apat na degree, ay nagmumungkahi na ang naturang formula ay dapat ding umiral para sa mga equation ng ikalimang degree, at, sa teorya, ang mga ugat ng ikalimang, ikatlo at ikalawang degree ay dapat lumitaw dito. Muli, maaari nating ligtas na ipagpalagay na ang gayong pormula, kung mayroon man, ay magiging napaka, napakakomplikado.

Ang pagpapalagay na ito sa huli ay naging mali. Sa katunayan, walang ganoong pormula ang umiiral; hindi bababa sa walang formula na binubuo ng mga coefficients a, b, c, d, e at f, na ginawa gamit ang karagdagan, pagbabawas, multiplikasyon at paghahati, at pagkuha ng mga ugat. Kaya mayroong isang bagay na napaka-espesyal tungkol sa numero 5. Ang mga dahilan para sa hindi pangkaraniwang pag-uugali na ito ng lima ay napakalalim, at tumagal ng maraming oras upang maunawaan ang mga ito.

Ang unang senyales ng problema ay kahit gaano kahirap ang mga mathematician na hanapin ang gayong pormula, gaano man sila katalino, palagi silang nabigo. Sa loob ng ilang panahon, naniniwala ang lahat na ang mga dahilan ay nakasalalay sa hindi kapani-paniwalang pagiging kumplikado ng formula. Ito ay pinaniniwalaan na walang sinuman ang makakaintindi ng algebra na ito nang maayos. Gayunpaman, sa paglipas ng panahon, ang ilang mga matematiko ay nagsimulang mag-alinlangan na ang gayong pormula ay umiral pa, at noong 1823 ay napatunayan ni Niels Hendrik Abel ang kabaligtaran. Walang ganyang formula. Di-nagtagal pagkatapos noon, nakahanap si Évariste Galois ng paraan upang matukoy kung ang isang equation ng isang degree o iba pa—5th, 6th, 7th, anumang uri—ay nalulusaw gamit ang ganitong uri ng formula.

Ang konklusyon mula sa lahat ng ito ay simple: ang numero 5 ay espesyal. Maaari mong lutasin ang mga algebraic equation (gamit ang nth roots para sa iba't ibang value ng n) para sa powers 1, 2, 3, at 4, ngunit hindi para sa powers 5. Dito nagtatapos ang halatang pattern.

Walang sinuman ang nagulat na ang mga equation ng degree na higit sa 5 ay kumikilos nang mas masahol pa; sa partikular, ang parehong kahirapan ay nauugnay sa kanila: walang mga pangkalahatang formula para sa paglutas ng mga ito. Hindi ito nangangahulugan na ang mga equation ay walang mga solusyon; Hindi rin ito nangangahulugan na imposibleng makahanap ng napaka-tumpak na mga halaga ng numero para sa mga solusyong ito. Ang lahat ay tungkol sa mga limitasyon ng tradisyonal na mga tool sa algebra. Ito ay nagpapaalala sa imposibilidad ng trisection ng isang anggulo gamit ang isang ruler at compass. Ang sagot ay umiiral, ngunit ang mga pamamaraan na nakalista ay hindi sapat at hindi nagpapahintulot sa amin na matukoy kung ano ito.

Crystallographic na limitasyon

Ang mga kristal sa dalawa at tatlong dimensyon ay walang 5-ray rotational symmetry.

Ang mga atomo sa isang kristal ay bumubuo ng isang sala-sala, iyon ay, isang istraktura na paulit-ulit na pana-panahon sa ilang mga independiyenteng direksyon. Halimbawa, ang pattern sa wallpaper ay paulit-ulit sa haba ng roll; bilang karagdagan, ito ay karaniwang paulit-ulit sa pahalang na direksyon, kung minsan ay may paglipat mula sa isang piraso ng wallpaper patungo sa susunod. Mahalaga, ang wallpaper ay isang dalawang-dimensional na kristal.

Mayroong 17 uri ng mga pattern ng wallpaper sa isang eroplano (tingnan ang Kabanata 17). Nag-iiba sila sa mga uri ng simetrya, iyon ay, sa mga paraan upang mahigpit na ilipat ang pattern upang ito ay namamalagi nang eksakto sa sarili nito sa orihinal na posisyon nito. Kasama sa mga uri ng simetrya, sa partikular, ang iba't ibang variant ng rotational symmetry, kung saan ang pattern ay dapat na paikutin ng isang tiyak na anggulo sa paligid ng isang tiyak na punto - ang sentro ng simetrya.

Ang pagkakasunud-sunod ng rotational symmetry ay kung gaano karaming beses ang katawan ay maaaring paikutin sa isang buong bilog upang ang lahat ng mga detalye ng pattern ay bumalik sa kanilang orihinal na mga posisyon. Halimbawa, ang 90° na pag-ikot ay ang ika-4 na order ng rotation symmetry*. Ang listahan ng mga posibleng uri ng rotational symmetry sa isang kristal na sala-sala ay muling tumuturo sa hindi pangkaraniwan ng numero 5: wala ito doon. May mga opsyon na may 2nd, 3rd, 4th at 6th order rotation symmetry, ngunit walang wallpaper pattern na may 5th order rotation symmetry. Ang rotation symmetry ng order na higit sa 6 ay wala rin sa mga kristal, ngunit ang unang paglabag sa sequence ay nangyayari pa rin sa numero 5.

Ang parehong bagay ay nangyayari sa mga crystallographic system sa tatlong-dimensional na espasyo. Dito umuulit ang sala-sala sa tatlong independiyenteng direksyon. Mayroong 219 iba't ibang uri ng symmetry, o 230 kung bibilangin natin ang mirror image ng isang disenyo bilang isang hiwalay na variant - sa kabila ng katotohanan na sa kasong ito ay walang mirror symmetry. Muli, ang mga rotational symmetries ng mga order 2, 3, 4, at 6 ay sinusunod, ngunit hindi 5. Ang katotohanang ito ay tinatawag na crystallographic confinement.

Sa four-dimensional na espasyo, umiiral ang mga sala-sala na may 5th order symmetry; Sa pangkalahatan, para sa mga sala-sala na may sapat na mataas na sukat, posible ang anumang paunang natukoy na pagkakasunud-sunod ng rotational symmetry.

Quasicrystals

Bagama't hindi posible ang 5th order rotational symmetry sa 2D o 3D lattice, maaari itong umiral sa medyo hindi gaanong regular na istruktura na kilala bilang quasicrystals. Gamit ang mga sketch ni Kepler, natuklasan ni Roger Penrose ang mga planar system na may mas pangkalahatang uri ng fivefold symmetry. Ang mga ito ay tinatawag na quasicrystals.

Ang mga quasicrystal ay umiiral sa kalikasan. Noong 1984, natuklasan ni Daniel Shechtman na ang isang haluang metal ng aluminyo at mangganeso ay maaaring bumuo ng mga quasicrystals; Sa una, binati ng mga crystallographer ang kanyang ulat na may ilang pag-aalinlangan, ngunit ang pagtuklas ay nakumpirma sa kalaunan, at noong 2011 si Shechtman ay iginawad sa Nobel Prize sa Chemistry. Noong 2009, natuklasan ng isang pangkat ng mga siyentipiko na pinamumunuan ni Luca Bindi ang mga quasicrystals sa isang mineral mula sa Russian Koryak Highlands - isang compound ng aluminyo, tanso at bakal. Ngayon ang mineral na ito ay tinatawag na icosahedrite. Sa pamamagitan ng pagsukat ng nilalaman ng iba't ibang oxygen isotopes sa mineral gamit ang mass spectrometer, ipinakita ng mga siyentipiko na ang mineral na ito ay hindi nagmula sa Earth. Nabuo ito humigit-kumulang 4.5 bilyong taon na ang nakalilipas, sa panahong nagsisimula pa lang ang solar system, at ginugol ang halos lahat ng oras nito sa asteroid belt, na umiikot sa Araw, hanggang sa binago ng ilang kaguluhan ang orbit nito at kalaunan ay dinala ito sa Earth.

Sa pagharap sa mga numero 1 hanggang 10, babalik tayo ng isang hakbang at titingnan ang 0.
Pagkatapos ay bumalik ng isa pang hakbang upang makuha ang −1.
Nagbubukas ito ng buong mundo ng mga negatibong numero para sa atin. Nagpapakita rin ng mga bagong gamit para sa mga numero.
Ngayon sila ay kailangan hindi lamang para sa pagbibilang.

0. Wala bang numero o hindi?

Ang Zero ay unang lumitaw sa mga system para sa pag-record ng mga numero at inilaan nang tumpak para sa layuning ito - para sa pag-record, iyon ay, pagtatalaga. Nang maglaon lamang ay kinilala ang zero bilang isang independiyenteng numero at pinahintulutang kunin ang lugar nito - ang lugar ng isa sa mga pangunahing bahagi ng sistema ng numero ng matematika. Gayunpaman, ang zero ay may maraming hindi pangkaraniwan, kung minsan ay kabalintunaan na mga katangian. Sa partikular, imposibleng hatiin ang anumang bagay sa 0 sa anumang makatwirang paraan at sa isang lugar sa kaibuturan, sa pinakapundasyon ng matematika, ang lahat ng mga numero ay maaaring makuha mula sa 0.

Istraktura ng sistema ng numero

Sa maraming sinaunang kultura, ang mga simbolo para sa 1, 10, at 100 ay hindi nauugnay sa bawat isa sa anumang paraan. Ang mga sinaunang Griyego, halimbawa, ay gumamit ng mga titik ng kanilang alpabeto upang kumatawan sa mga numero 1 hanggang 9, 10 hanggang 90, at 100 hanggang 900. Ang sistemang ito ay potensyal na puno ng kalituhan, bagaman kadalasan ay madaling matukoy mula sa konteksto kung ano ang eksaktong ang isang liham ay kumakatawan sa: ang aktwal na titik o numero. Ngunit, bilang karagdagan, ang gayong sistema ay nagpahirap sa mga pagpapatakbo ng aritmetika.

Ang aming paraan ng pagsulat ng mga numero, kapag ang parehong digit ay nangangahulugang magkaibang mga numero, depende sa lugar nito sa numero, ay tinatawag na positional notation (tingnan ang Kabanata 10). Ang sistemang ito ay may napakaseryosong mga pakinabang para sa pagbibilang sa papel "sa isang haligi", at ito ay kung paano, hanggang kamakailan lamang, karamihan sa mga kalkulasyon sa mundo ay isinagawa. Sa positional notation, ang pangunahing bagay na kailangan mong malaman ay ang mga pangunahing panuntunan para sa pagdaragdag at pagpaparami ng sampung simbolo 0–9. Nalalapat din ang mga pattern na ito kapag ang parehong mga numero ay nasa ibang mga posisyon.
Halimbawa,
23 + 5 = 28   230 + 50 = 280   2300 + 500 = 2800.

Gayunpaman, sa sinaunang notasyong Griyego ang unang dalawang halimbawa ay ganito ang hitsura:
κγ + ε = κη     σλ + ν = σπ,
at walang halatang pagkakatulad sa pagitan nila.

Gayunpaman, ang positional notation ay may isang karagdagang feature na partikular na lumalabas sa numerong 2015: ang pangangailangan para sa isang null na character. Sa kasong ito, sinabi niya na walang daan-daan sa bilang. Sa notasyong Griyego ay hindi na kailangan ng isang null na karakter. Sa bilang na σπ, sabihin nating, σ ay nangangahulugang 200 at π ay 80. Makatitiyak tayo na walang mga yunit sa numero dahil lamang sa walang mga simbolo ng yunit na α - θ dito. Sa halip na gamitin ang null character, hindi lang kami nagsusulat ng anumang solong character sa numero.

Kung sinubukan naming gawin ang parehong sa decimal system, ang 2015 ay magiging 215, at hindi namin masasabi kung ano ang eksaktong ibig sabihin ng numero: 215, 2150, 2105, 2015, o maaaring 2,000,150 na mga unang bersyon ng positional system gumamit ng puwang , 2 15, ngunit madaling makaligtaan ang espasyo, at ang dalawang magkasunod na puwang ay medyo mas mahabang espasyo. Kaya nagkakaroon ng kalituhan at laging madaling magkamali.

Isang Maikling Kasaysayan ng Zero

Babylon

Ang mga Babylonians ang una sa mga kultura ng mundo na gumawa ng isang simbolo na nangangahulugang "walang numero dito." Tandaan natin (tingnan ang Kabanata 10) na ang batayan ng Babylonian number system ay hindi 10 kundi 60. Sa unang bahagi ng Babylonian aritmetika, ang kawalan ng bahaging 60 2 ay ipinahiwatig ng isang espasyo, ngunit noong ika-3 siglo. BC e. nag-imbento sila ng isang espesyal na simbolo para dito. Gayunpaman, ang mga Babylonians ay tila hindi itinuturing na ang simbolo na ito ay isang tunay na numero. Bukod dito, sa dulo ng numero ang simbolo na ito ay tinanggal, at ang kahulugan nito ay kailangang hulaan mula sa konteksto.

India

Ang ideya ng positional notation ng mga numero sa isang base 10 number system ay unang lumitaw sa Lokavibhaga, isang Jain cosmological text ng 458 AD, na gumagamit din ng Shunya(ibig sabihin ay "kawalan ng laman") kung saan maglalagay kami ng 0. Noong 498, inilarawan ng sikat na Indian mathematician at astronomer na si Aryabhata ang positional system ng pagsulat ng mga numero bilang "lugar pagkatapos ng lugar, bawat isa ay 10 beses na mas malaki ang magnitude." Ang unang kilalang paggamit ng isang espesyal na simbolo para sa decimal na digit 0 ay nagsimula noong 876 sa isang inskripsiyon sa Chaturbhuja Temple sa Gwalior; ang simbolo na ito ay kumakatawan - hulaan kung ano? Maliit na bilog.

Mayan

Ang sibilisasyong Mayan sa Central America, na umabot sa tugatog nito sa isang lugar sa pagitan ng 250 at 900 AD, ay gumamit ng base-20 na sistema ng numero at may espesyal na simbolo na kumakatawan sa zero. Sa katunayan, ang pamamaraang ito ay nagsimula nang mas maaga at pinaniniwalaang naimbento ng mga Olmec (1500–400 BC). Bilang karagdagan, ang mga Mayan ay aktibong gumamit ng mga numero sa kanilang sistema ng kalendaryo, isa sa mga panuntunan kung saan tinawag na "mahabang bilang." Nangangahulugan ito ng pagbibilang ng petsa sa mga araw pagkatapos ng mythical na petsa ng paglikha, na, ayon sa modernong Western calendar, ay Agosto 11, 3114 BC. e. Sa sistemang ito, ang simbolo para sa zero ay ganap na kinakailangan, dahil kung wala ito imposibleng maiwasan ang kalabuan.

Ang zero ba ay isang numero?

Hanggang sa ika-9 na siglo. ang zero ay itinuturing na maginhawa simbolo para sa mga numerical na kalkulasyon, ngunit hindi itinuturing na isang numero sa sarili nito. Marahil dahil hindi ito ginamit sa pagbibilang.

Kung tatanungin nila kung ilang baka ang mayroon ka - at mayroon kang mga baka - ituturo mo ang bawat isa sa kanila at magbibilang: "Isa, dalawa, tatlo..." Ngunit kung wala kang anumang baka, hindi ka ituro ang ilang baka at sabihing: “Zero,” dahil wala kang dapat ituro. Dahil ang 0 ay hindi kailanman binibilang, ito ay malinaw na hindi isang numero.

Kung ang posisyon na ito ay tila kakaiba sa iyo, dapat tandaan na kahit na mas maaga ang "isa" ay hindi rin itinuturing na isang numero. Sa ilang wika, ang salitang "numero" ay nangangahulugang "maraming" o kahit na "marami". Sa halos lahat ng modernong wika ay may pagkakaiba sa pagitan ng isahan at maramihan. Ang sinaunang Griyego ay mayroon ding "dalawahan" na numero, at kapag pinag-uusapan ang tungkol sa dalawang bagay o tao, ginagamit ang mga espesyal na anyo ng mga salita. Kaya sa ganitong diwa, ang "dalawa" ay hindi rin itinuring na parehong bilang ng lahat ng iba pa. Ang parehong ay sinusunod sa maraming iba pang mga klasikal na wika at maging sa ilang mga modernong, tulad ng Scottish Gaelic o Slovenian. Ang mga bakas ng parehong mga form na ito ay makikita sa English, kung saan "pareho" ( pareho) at "lahat" ( lahat) - magkaibang salita.

Habang ang simbolo ng zero ay naging mas malawak na ginagamit, at habang ang mga numero ay nagsimulang gamitin para sa higit pa sa pagbibilang, naging malinaw na sa maraming aspeto ang zero ay kumikilos tulad ng anumang iba pang numero. Pagsapit ng ika-9 na siglo. Itinuring na ng mga Indian mathematician ang zero bilang isang tunay na numero, at hindi lamang isang simbolo na maginhawang kumakatawan sa mga puwang sa pagitan ng iba pang mga simbolo para sa kalinawan. Malayang ginamit ang Zero sa pang-araw-araw na kalkulasyon.

Sa linya ng numero, kung saan ang mga numero 1, 2, 3... ay nakasulat sa pagkakasunud-sunod mula kaliwa hanggang kanan, walang sinuman ang may problema kung saan ilalagay ang zero: sa kaliwa ng 1. Ang dahilan ay medyo halata: Ang pagdaragdag ng 1 sa anumang numero ay nagpapalipat-lipat nito ng isang hakbang sa kanan. Ang pagdaragdag ng 1 hanggang 0 ay maglilipat nito ng 1, kaya dapat ilagay ang isang 0 kung saan ang isang hakbang sa kanan ay magbibigay ng 1. Na nangangahulugang isang hakbang sa kaliwa ng isang 1.

Ang pagkilala sa mga negatibong numero sa wakas ay nakakuha ng puwesto ng zero sa serye ng mga tunay na numero. Walang nagtalo na ang 3 ay isang numero. Kung tatanggapin natin na ang −3 ay isang numero din at ang pagdaragdag ng dalawang numero ay palaging gumagawa ng isang numero, kung gayon ang resulta ng 3 + (−3) ay dapat na isang numero. At ang numero ay 0.

Mga hindi pangkaraniwang katangian

Sinabi ko "sa maraming paraan, ang zero ay kumikilos tulad ng anumang iba pang numero." Sa marami, ngunit hindi lahat. Ang Zero ay isang espesyal na numero. Dapat itong maging espesyal dahil ito ay isang solong numero na maayos na pinipiga sa pagitan ng positibo at negatibong mga numero.

Malinaw na ang pagdaragdag ng 0 sa anumang numero ay hindi magbabago sa numerong iyon. Kung mayroon akong tatlong baka at magdagdag ako ng isa pa, magkakaroon pa rin ako ng tatlong baka. Totoo, may mga kakaibang kalkulasyon tulad nito:

Ang isang pusa ay may isang buntot.
Walang pusang may walong buntot.
Samakatuwid, idinagdag:
Ang isang pusa ay may siyam na buntot.

Ang maliit na biro na ito ay gumaganap sa iba't ibang mga interpretasyon ng negasyon na "Hindi".

Mula sa espesyal na pag-aari na ito ng zero ay sumusunod na 0 + 0 = 0, na nangangahulugang −0 = 0. Ang zero ay kabaligtaran ng sarili nito. Ito lang ang numerong iyon, at eksaktong nangyayari ito dahil sa linya ng numero, ang zero ay nasa pagitan ng positibo at negatibong mga numero.

Paano ang pagpaparami? Kung isasaalang-alang natin ang multiplikasyon bilang sunud-sunod na karagdagan, kung gayon
2 × 0 = 0 + 0 = 0
3 × 0 = 0 + 0 + 0 = 0
4 × 0 = 0 + 0 + 0 + 0 = 0,
at samakatuwid
n× 0 = 0
para sa anumang numero n. Sa pamamagitan ng paraan, ito rin ay may katuturan sa mga bagay na pinansyal: kung maglagay ako ng tatlong beses na zero rubles sa aking account, pagkatapos ay sa huli ay hindi ako maglalagay ng anuman doon. Muli, ang zero ay ang tanging numero na may ganitong katangian.

Sa arithmetic m × n katumbas n × m para sa lahat ng numero n At m. Ang kasunduang ito ay nagpapahiwatig na
0 × n = 0
para sa sinuman n, sa kabila ng katotohanang hindi tayo maaaring magdagdag ng “zero times” sa pamamagitan ng n.

Ano ang mali sa dibisyon? Ang paghahati ng zero sa isang non-zero na numero ay simple at malinaw: ang resulta ay zero. Half of nothing, a third or any other part of nothing is nothing. Ngunit pagdating sa paghahati ng isang numero sa zero, ang kakaiba ng zero ay pumapasok. Ano ang, halimbawa, 1:0? Tinutukoy namin m : n parang numero q, kung saan totoo ang expression q × n = m. Kaya 1:0 ay kung ano ito q, para saan q× 0 = 1. Gayunpaman, walang ganoong numero. Anuman ang kunin natin bilang q, nakukuha namin q× 0 = 0. At hindi tayo makakakuha ng mga unit.

Ang malinaw na paraan upang malutas ang problemang ito ay tanggapin ito para sa ipinagkaloob. Ang paghahati sa pamamagitan ng zero ay ipinagbabawal dahil wala itong saysay. Sa kabilang banda, bago ipinakilala ang mga praksyon, ang expression na 1:2 ay hindi rin magkaroon ng kahulugan, kaya marahil ay hindi tayo dapat sumuko nang mabilis. Maaari naming subukang makabuo ng ilang bagong numero na magpapahintulot sa amin na hatiin sa zero. Ang problema ay ang naturang numero ay lumalabag sa mga pangunahing tuntunin ng aritmetika. Halimbawa, alam natin na 1 × 0 = 2 × 0, dahil pareho silang katumbas ng zero nang paisa-isa. Ang paghahati sa magkabilang panig ng 0, makakakuha tayo ng 1 = 2, na kung saan ay lantaran na katawa-tawa. Kaya't tila makatwiran na huwag payagan ang paghahati ng zero.

Mga numero mula sa wala

Ang konsepto ng matematika na marahil ay pinakamalapit sa konsepto ng "wala" ay matatagpuan sa set theory. marami- ito ay isang tiyak na hanay ng mga bagay sa matematika: mga numero, geometric figure, function, graph... Ang isang set ay tinukoy sa pamamagitan ng paglilista o paglalarawan ng mga elemento nito. "Ang set ng mga numero 2, 4, 6, 8" at "ang set ng mga even na numero na mas malaki sa 1 at mas mababa sa 9" ay tumutukoy sa parehong set, na maaari nating mabuo sa pamamagitan ng pag-enumerate: (2, 4, 6, 8),
kung saan ang mga kulot na braces () ay nagpapahiwatig na ang mga elemento ng isang set ay nakapaloob sa loob.

Sa paligid ng 1880, binuo ng German mathematician na si Cantor ang detalyadong set theory. Sinusubukan niyang unawain ang ilan sa mga teknikal na aspeto ng mathematical analysis na may kaugnayan sa mga breakpoint ng function - mga lugar kung saan ang isang function ay gumagawa ng mga hindi inaasahang pagtalon. Ang istraktura ng maraming mga discontinuities ay may mahalagang papel sa kanyang sagot. Sa kasong ito, hindi indibidwal na mga puwang ang mahalaga, ngunit ang kanilang kabuuan. Talagang interesado si Cantor sa walang katapusang malalaking hanay na may kaugnayan sa pagsusuri. Gumawa siya ng isang seryosong pagtuklas: nalaman niya na ang mga infinity ay hindi pareho - ang ilan sa kanila ay mas malaki, ang iba ay mas maliit (tingnan ang kabanata ℵ 0).

Tulad ng nabanggit ko sa seksyong "Ano ang isang numero?", isa pang Aleman na matematiko, si Frege, ang nakakuha ng mga ideya ni Cantor, ngunit mas interesado siya sa mga may hangganan na hanay. Naniniwala siya na sa kanilang tulong posible na malutas ang isang pandaigdigang pilosopikal na problema na may kaugnayan sa likas na katangian ng mga numero. Naisip niya kung paano nauugnay ang mga hanay sa isa't isa: halimbawa, kung gaano karaming mga tasa ang nauugnay sa maraming mga platito. Ang pitong araw ng linggo, ang pitong dwarf, at ang mga numero 1 hanggang 7 ay ganap na nakahanay sa isa't isa upang silang lahat ay tukuyin ang parehong numero.

Alin sa mga sumusunod na hanay ang dapat nating piliin na kumatawan sa bilang na pito? Si Frege, sa pagsagot sa tanong na ito, ay hindi umimik: sabay-sabay. Tinukoy niya ang numero bilang set ng lahat ng set na tumutugma sa isang naibigay na set. Sa kasong ito, walang set ang ginustong, at ang pagpili ay ginawa nang hindi malabo, at hindi random o arbitraryo. Ang aming mga simbolo at pangalan ng numero ay mga maginhawang shortcut lamang para sa mga dambuhalang set na ito. Ang numero pito ay isang set lahat mga set na katumbas ng mga gnome, at ito ay kapareho ng set ng lahat ng set na katumbas ng mga araw ng linggo o ang listahan (1, 2, 3, 4, 5, 6, 7).

Marahil ay hindi na kailangang ituro na ito ay isang napaka-eleganteng solusyon konseptwal Ang problema ay hindi nagbibigay sa amin ng anumang konkreto sa mga tuntunin ng isang makatwirang sistema para sa kumakatawan sa mga numero.

Nang iharap ni Frege ang kanyang mga ideya sa dalawang tomo na akdang The Fundamental Laws of Arithmetic (1893 at 1903), marami ang nag-isip na nalutas na niya ang problema. Ngayon alam na ng lahat kung ano ang numero. Ngunit bago ang paglalathala ng ikalawang tomo, sumulat si Bertrand Russell ng liham kay Frege na nagsasabing (paraphrase ko): “Dear Gottlob, isaalang-alang ang set ng lahat ng set na hindi naglalaman ng kanilang mga sarili.” Parang barbero sa baryo na nag-aahit ng hindi nag-aahit sa sarili; Sa gayong kahulugan, lumitaw ang isang kontradiksyon. Ang Paradox ni Russell, na tinatawag na ngayon, ay nagpakita kung gaano kapanganib ang pag-aakalang umiiral ang lahat-lahat na hanay (tingnan ang kabanata ℵ 0).

Sinubukan ng mga eksperto sa lohika sa matematika na lutasin ang problema. Ang sagot ay naging mahigpit na kabaligtaran ng "malawak na pag-iisip" ni Frege at ang kanyang patakaran sa pagsasama-sama ng lahat ng posibleng hanay sa isang bunton. Ang lansihin ay ang pumili ng eksaktong isa sa lahat ng posibleng set. Upang matukoy ang numero 2, kinakailangan na bumuo ng isang karaniwang hanay na may dalawang elemento. Upang tukuyin ang 3, maaari kang gumamit ng isang karaniwang hanay na may tatlong elemento, at iba pa. Ang lohika dito ay hindi napupunta sa mga cycle kung ang mga set na ito ay unang binuo nang hindi tahasang gumagamit ng mga numero, at pagkatapos ay magtatalaga lamang ng mga numerong simbolo at pangalan sa kanila.

Ang pangunahing problema ay ang pagpili ng mga karaniwang set na gagamitin. Kailangang tukuyin ang mga ito sa isang hindi malabo at kakaibang paraan, at ang kanilang istraktura ay kailangang kahit papaano ay nauugnay sa proseso ng pagbibilang. Ang sagot ay nagmula sa isang napaka-tiyak na hanay na kilala bilang ang walang laman na hanay.

Ang zero ay isang numero, ang batayan ng ating buong sistema ng numero. Dahil dito, maaari itong magamit upang mabilang ang mga elemento ng isang tiyak na hanay. Anong marami? Well, dapat itong isang set na walang elemento. Hindi mahirap na magkaroon ng ganoong set: hayaan ito, halimbawa, "ang set ng lahat ng mga daga na tumitimbang ng higit sa 20 tonelada bawat isa." Sa wikang matematika, nangangahulugan ito na mayroong isang set na walang iisang elemento: ang empty set. Sa matematika, madali ring makahanap ng mga halimbawa: ang hanay ng mga prime number na multiple ng 4, o ang set ng lahat ng triangles na may apat na vertices. Magkaiba ang hitsura ng mga set na ito - ang isa ay naglalaman ng mga numero, ang isa ay naglalaman ng mga tatsulok - ngunit sa katunayan sila ay parehong hanay, dahil ang mga naturang numero at tatsulok ay hindi aktwal na umiiral at ito ay imposible lamang na makilala sa pagitan ng mga hanay. Ang lahat ng mga walang laman na hanay ay naglalaman ng eksaktong parehong mga elemento: ibig sabihin, wala. Samakatuwid, ang walang laman na hanay ay natatangi. Ang simbolo para dito ay ipinakilala ng isang pangkat ng mga siyentipiko na nagtatrabaho sa ilalim ng karaniwang pseudonym na Bourbaki noong 1939, at ganito ang hitsura nito: ∅. Ang teorya ng set ay nangangailangan ng walang laman na set sa parehong paraan na kailangan ng aritmetika ang numero 0: kung isasama mo ito, ang lahat ay magiging mas simple.

Bukod dito, matutukoy natin na 0 ang walang laman na hanay.

Paano ang numero 1? Ito ay intuitively malinaw na dito kailangan namin ng isang set na binubuo ng eksaktong isang elemento, at isang natatanging isa. Well... unique ang empty set. Kaya, tinukoy namin ang 1 bilang isang set na ang tanging elemento ay ang walang laman na set: sa simbolikong wika (∅). Ito ay hindi katulad ng empty set dahil ang set na ito ay may isang elemento, samantalang ang empty set ay wala. Sumasang-ayon ako, ang nag-iisang elementong ito ay isang walang laman na hanay, nangyari ito, ngunit ang elementong ito ay naroroon pa rin sa hanay. Isipin ang set bilang isang paper bag na may mga elemento. Ang isang walang laman na hanay ay isang walang laman na pakete. Ang isang set na ang tanging elemento ay ang walang laman na set ay isang pakete na naglalaman ng isa pang walang laman na pakete. Makikita mo sa iyong sarili na hindi ito ang parehong bagay - walang anuman sa isang pakete, at mayroong isang pakete sa isa pa.

Ang pangunahing hakbang ay upang matukoy ang numero 2. Kailangan nating makakuha ng natatanging set na may dalawang elemento. Kaya bakit hindi gamitin ang dalawang set na nabanggit na natin sa ngayon: ∅ at (∅)? Samakatuwid, tinukoy namin ang 2 bilang set (∅, (∅)). At ito, ayon sa aming mga kahulugan, ay kapareho ng 0, 1.

Ngayon ang isang pangkalahatang pattern ay nagsisimula na lumitaw. Tukuyin natin ang 3 = 0, 1, 2 - isang set na may tatlong elemento na natukoy na natin. Pagkatapos 4 = 0, 1, 2, 3; 5 = 0, 1, 2, 3, 4 at iba pa. Lahat, kung titingnan mo, babalik sa bakanteng set. Halimbawa,
3 = {∅, {∅}, {∅, {∅}}}
4 = {∅, {∅}, {∅, {∅}}, {∅, {∅}, {∅, {∅}}}}.

Marahil ay hindi mo gustong makita kung ano ang hitsura ng bilang ng mga gnome.

Ang mga materyales sa gusali dito ay mga abstraction: ang walang laman na set at ang pagkilos ng pagbuo ng isang set sa pamamagitan ng pag-enumerate ng mga elemento nito. Ngunit ang paraan ng pagkakaugnay ng mga set na ito sa isa't isa ay humahantong sa paglikha ng isang mahigpit na balangkas para sa isang sistema ng numero kung saan ang bawat numero ay kumakatawan sa isang espesyal na hanay na (intuitively) ay may eksaktong bilang ng mga elemento. At hindi doon nagtatapos ang kwento. Sa pagkakaroon ng pagtukoy sa mga natural na numero, maaari tayong gumamit ng mga katulad na set theory tricks para tukuyin ang mga negatibong numero, fraction, real number (infinite decimals), complex number, at iba pa, hanggang sa pinakabagong mapanlikhang konsepto ng matematika sa quantum theory.

Kaya ngayon alam mo na ang kahila-hilakbot na sikreto ng matematika: sa pundasyon nito ay namamalagi ang kawalan.

–1. Mas mababa sa wala

Maaari bang mas mababa sa zero ang isang numero? Ang pagbibilang ng mga baka ay hindi gagawa ng anumang bagay na tulad nito, maliban kung maiisip mo ang "mga virtual na baka" na may utang ka sa isang tao. Sa kasong ito, mayroon kang natural na extension ng numerical concept na magpapadali sa buhay para sa mga algebraist at accountant. Kasabay nito, naghihintay sa iyo ang mga sorpresa: ang isang minus para sa isang minus ay nagbibigay ng isang plus. Bakit sa lupa?

Mga negatibong numero

Ang pagkakaroon ng natutunan upang magdagdag ng mga numero, nagsisimula kaming makabisado ang reverse operation: pagbabawas. Halimbawa, ang 4 − 3 sa sagot ay nagbibigay ng numero na, kapag idinagdag sa 3, ay nagbibigay ng 4. Ito ay, siyempre, 1. Ang pagbabawas ay kapaki-pakinabang dahil kung wala ito ay mahirap para sa atin, halimbawa, na malaman kung magkano ang pera aalis na kami kung sa una ay mayroon kaming 4 na rubles, ngunit gumastos kami ng 3 rubles.

Ang pagbabawas ng isang mas maliit na numero mula sa isang mas malaki ay nagdudulot ng halos walang mga problema. Kung mas kaunting pera ang ginastos namin kaysa sa aming bulsa o pitaka, kung gayon mayroon pa kaming natitira. Ngunit ano ang mangyayari kung ibawas natin ang mas malaking bilang mula sa mas maliit? Ano ang 3 − 4?

Kung mayroon kang tatlong 1 ruble na barya sa iyong bulsa, hindi mo magagawang kumuha ng apat na ganoong barya mula sa iyong bulsa at ibigay ang mga ito sa cashier sa supermarket. Ngunit ngayon, gamit ang mga credit card, kahit sino ay madaling gumastos ng pera na wala sila, hindi lamang sa kanilang bulsa, kundi pati na rin sa kanilang bank account. Kapag nangyari ito, ang isang tao ay nabaon sa utang. Sa kasong ito, ang utang ay magiging 1 ruble, hindi binibilang ang interes ng bangko. Kaya sa isang tiyak na kahulugan 3 − 4 ay katumbas ng 1, ngunit isa pa 1: isang yunit ng utang, hindi pera. Kung ang 1 ay may kabaligtaran, ito ay magiging eksaktong ganito.

Upang makilala ang utang mula sa cash, kaugalian na i-prefix ang numero na may minus sign. Sa naturang recording
3 − 4 = −1,
at maaari naming isaalang-alang na kami ay nag-imbento ng isang bagong uri ng numero: negatibo numero.

Kasaysayan ng Mga Negatibong Numero

Sa kasaysayan, ang unang pangunahing extension ng sistema ng numero ay mga fraction (tingnan ang Kabanata ½). Ang pangalawa ay mga negatibong numero. Gayunpaman, nilayon kong harapin ang mga ganitong uri ng numero sa reverse order. Ang unang kilalang pagbanggit ng mga negatibong numero ay nasa isang Chinese na dokumento mula sa Han Dynasty (202 BC - 220 AD) na tinatawag na The Art of Counting in Nine Sections (Jiu Zhang Xuan Shu).

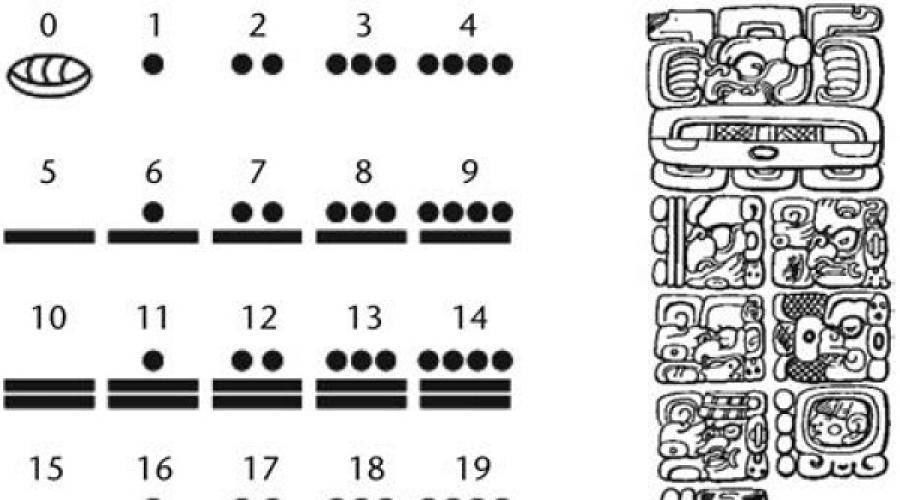
Gumamit ang aklat na ito ng pisikal na "katulong" para sa pagbibilang: pagbibilang ng mga stick. Ito ay mga maliliit na patpat na gawa sa kahoy, buto o iba pang materyal. Upang kumatawan sa mga numero, ang mga stick ay inilatag sa ilang mga hugis. Sa unit digit ng isang numero, ang pahalang na linya ay nangangahulugang "isa" at ang patayong linya ay nangangahulugang "lima". Magkamukha ang mga numero sa ika-100 na lugar. Sa sampu at libu-libong mga numero, ang mga direksyon ng mga stick ay baligtad: ang patayo ay nangangahulugang "isa", at ang pahalang ay nangangahulugang "lima". Kung saan namin ilalagay ang 0, ang mga Intsik ay nag-iwan lamang ng puwang; gayunpaman, ang espasyo ay madaling makaligtaan, kung saan ang panuntunan tungkol sa pagbabago ng mga direksyon ay nakakatulong na maiwasan ang pagkalito kung, halimbawa, walang anuman sa seksyon ng sampu. Ang pamamaraang ito ay hindi gaanong epektibo kung ang numero ay naglalaman ng ilang mga zero sa isang hilera, ngunit ito ay isang bihirang kaso.

Sa The Art of Counting in Nine Sections, ginamit din ang mga stick upang kumatawan sa mga negatibong numero, at sa napakasimpleng paraan: kulay itim ang mga ito sa halip na pula. Kaya
4 na pulang stick na binawasan ng 3 pula ay katumbas ng 1 pulang stick,
Pero
3 pulang stick na binawasan ng 4 pulang stick ay katumbas ng 1 itim na stick.

Kaya, ang itim na stick figure ay kumakatawan sa utang, at ang laki ng utang ay tumutugma sa pulang stick figure.

Kinilala rin ng mga mathematician ng India ang mga negatibong numero; bilang karagdagan, nag-compile sila ng mga pare-parehong panuntunan para sa pagsasagawa ng mga operasyong aritmetika sa kanila.

Ang manuskrito ng Bakhshali, na mula noong ika-3 siglo, ay naglalaman ng mga kalkulasyon na may mga negatibong numero, na maaaring makilala sa iba sa pamamagitan ng + sign sa mga lugar kung saan namin gagamitin -. (Maraming beses na nagbago ang mga simbolo ng matematika sa paglipas ng panahon, minsan sa paraang madali para sa atin na malito sa kanila.) Ang ideya ay kinuha ng mga Arab mathematician, at mula sa kanila ay unti-unti itong kumalat sa buong Europa. Hanggang sa ika-17 siglo Karaniwang binibigyang-kahulugan ng mga European mathematician ang negatibong sagot bilang patunay na ang problemang pinag-uusapan ay walang solusyon, ngunit naunawaan na ng Fibonacci na sa mga kalkulasyon sa pananalapi maaari silang kumatawan sa mga utang. Pagsapit ng ika-19 na siglo Ang mga negatibong numero ay hindi na natakot sa mga mathematician at nataranta sila.

Pagsulat ng mga Negatibong Numero

Sa geometriko, ito ay maginhawa upang kumatawan sa mga numero bilang mga punto sa isang linya mula kaliwa hanggang kanan at simula sa 0. Nakita na natin na ito linya ng numero mayroong natural na pagpapatuloy na may kasamang mga negatibong numero at papunta sa kabilang direksyon.

Ang pagsasagawa ng karagdagan at pagbabawas sa linya ng numero ay napaka-maginhawa at simple. Halimbawa, upang magdagdag ng 3 sa anumang numero, kailangan mong ilipat ang tatlong hakbang sa kanan. Upang ibawas ang 3, kailangan mong ilipat ang 3 hakbang sa kaliwa. Ang pagkilos na ito ay nagbibigay ng tamang resulta para sa parehong positibo at negatibong mga numero; halimbawa, kung magsisimula tayo sa −7 at magdagdag ng 3, lilipat tayo ng 3 hakbang sa kanan at makakakuha tayo ng −4. Ang mga panuntunan para sa pagsasagawa ng mga pagpapatakbo ng aritmetika para sa mga negatibong numero ay nagpapakita rin na ang pagdaragdag o pagbabawas ng negatibong numero ay nagbibigay ng parehong resulta gaya ng pagbabawas o pagdaragdag ng katumbas na positibong numero. Kaya para magdagdag ng -3 sa anumang numero, kailangan nating ilipat ang 3 hakbang sa kaliwa. Upang ibawas ang −3 mula sa anumang numero, kailangan mong ilipat ang 3 hakbang sa kanan.

Ang pagpaparami na kinasasangkutan ng mga negatibong numero ay mas kawili-wili. Kapag una nating natutunan ang tungkol sa multiplikasyon, iniisip natin ito bilang paulit-ulit na pagdaragdag. Halimbawa:
6 × 5 = 5 + 5 + 5 + 5 + 5 + 5 = 30.

Ang parehong diskarte ay nagmumungkahi na kapag nagpaparami ng 6 × −5 dapat tayong magpatuloy nang katulad:
6 × −5 = −5 + (−5) + (−5) + (−5) + (−5) + (−5) = −30.

Dagdag pa, ang isa sa mga tuntunin ng aritmetika ay nagsasaad na ang pagpaparami ng dalawang positibong numero ay nagbibigay ng parehong resulta anuman ang pagkakasunud-sunod kung saan namin kinuha ang mga numero. Kaya, 5 × 6 ay dapat ding katumbas ng 30. Ito ay, dahil
5 × 6 = 6 + 6 + 6 + 6 + 6 = 30.

Kaya't tila makatwirang gamitin ang parehong panuntunan para sa mga negatibong numero. Kung gayon ang −5 × 6 ay katumbas din ng −30.

Paano ang tungkol sa −6 × −5? Mayroong mas kaunting kalinawan sa isyung ito. Hindi tayo makakasulat nang sunud-sunod minus anim beses −5, at pagkatapos ay idagdag ang mga ito. Samakatuwid, kailangan nating patuloy na tugunan ang isyung ito. Tingnan natin kung ano ang alam na natin.

6 × 5 = 30
6 × −5 = −30
−6 × 5 = −30
−6 × −5 =?

Sa unang tingin, iniisip ng maraming tao na ang sagot ay dapat na −30. Sa sikolohikal, ito ay malamang na makatwiran: ang buong aksyon ay napuno ng espiritu ng "negatibiti," kaya ang sagot ay dapat na negatibo. Marahil ang parehong pakiramdam ay nasa likod ng stock na parirala: "Ngunit wala akong ginawa." Gayunpaman, kung ikaw wala hindi ginawa ito, na nangangahulugang dapat kang gumawa ng "wala", iyon ay isang bagay. Kung patas man ang nasabing pangungusap ay depende sa mga tuntunin ng grammar na iyong ginagamit. Ang dagdag na negasyon ay maaari ding ituring bilang isang tumitinding konstruksyon.

Sa parehong paraan, kung ano ang magiging katumbas ng −6 × −5 ay isang bagay ng kasunduan ng tao. Kapag nakabuo tayo ng mga bagong numero, walang garantiya na ang mga lumang konsepto ay mailalapat sa kanila. Kaya't maaaring magpasya ang mga mathematician na −6 × −5 = −30. Sa mahigpit na pagsasalita, maaaring napagpasyahan nila na ang pagpaparami ng -6 sa −5 ay magbubunga ng lilang hippopotamus.

Gayunpaman, mayroong ilang magandang dahilan kung bakit ang −30 ay isang hindi magandang pagpipilian sa kasong ito, at ang lahat ng mga kadahilanang ito ay tumuturo sa kabaligtaran na direksyon - patungo sa numerong 30.

Ang isang dahilan ay kung −6 × −5 = −30, kung gayon ito ay kapareho ng −6 × 5. Ang paghahati sa pareho sa −6, makuha natin ang −5 = 5, na sumasalungat sa lahat ng nasabi na natin tungkol sa mga negatibong numero .

Ang pangalawang dahilan ay dahil alam na natin: 5 + (−5) = 0. Tingnan ang number line. Ano ang limang hakbang sa kaliwa ng numero 5? Zero. Ang pag-multiply ng anumang positibong numero sa 0 ay nagbubunga ng 0, at tila makatwirang ipagpalagay na pareho ang naaangkop sa mga negatibong numero. Kaya makatuwirang isipin na −6 × 0 = 0. Samakatuwid
0 = −6 × 0 = −6 × (5 + (−5)).

Ayon sa karaniwang mga tuntunin ng aritmetika, ito ay katumbas ng
−6 × 5 + −6 × −5.

Sa kabilang banda, kung pipiliin natin ang −6 × -5 = 30, makukuha natin
0 = −6 × 0 = −6 × (5 + (−5)) = −6 × 5 + (−6) × −5 =
= −30 + 30 = 0,
at lahat ay mahuhulog sa lugar.

Ang ikatlong dahilan ay ang istraktura ng linya ng numero. Sa pamamagitan ng pagpaparami ng positibong numero sa −1, ginagawa natin ito sa katumbas na negatibong numero; ibig sabihin, iniikot namin ang buong positibong kalahati ng linya ng numero nang 180°, inililipat ito mula kanan pakaliwa. Saan dapat pumunta ang negatibong kalahati, sa teorya? Kung iiwan natin ito sa lugar, makukuha natin ang parehong problema, dahil ang −1 × −1 ay −1, na katumbas ng −1 × 1, at maaari nating tapusin na −1 = 1. Ang tanging makatwirang alternatibo ay eksaktong ito O paikutin ang negatibong bahagi ng linya ng numero sa pamamagitan ng 180°, ilipat ito mula kaliwa pakanan. Ito ay maayos dahil ang pagpaparami ngayon sa −1 ay ganap na binabaligtad ang linya ng numero, na binabaligtad ang pagkakasunud-sunod ng mga numero. Ito ay sumusunod mula dito, habang ang gabi ay sumunod sa araw, na ang isang bagong multiplikasyon sa −1 ay magpapaikot muli sa linya ng numero ng 180°. Ang pagkakasunud-sunod ng mga numero ay muling mababaligtad, at ang lahat ay babalik sa kung saan ito nagsimula. Kaya, ang −1 × −1 ay kung saan nagtatapos ang −1 kapag iniikot natin ang linya ng numero, na 1. At kung magpapasya tayo na −1 × −1 = 1, pagkatapos ay direktang sumusunod na −6 × −5 = 30.

Ang ikaapat na dahilan ay ang interpretasyon ng negatibong halaga ng pera bilang utang. Sa variant na ito, ang pag-multiply ng isang tiyak na halaga ng pera sa isang negatibong numero ay nagbibigay ng parehong resulta tulad ng pag-multiply nito sa katumbas na positibong numero, maliban na ang totoong pera ay nagiging utang. Sa kabilang panig, pagbabawas, "pag-alis" ng utang, ay may parehong epekto na parang inaalis ng bangko ang ilan sa iyong utang mula sa mga tala nito at mahalagang ibinalik sa iyo ang pera. Ang pagbabawas ng utang na 10 rubles mula sa halaga ng iyong account ay eksaktong kapareho ng pagdeposito ng 10 rubles ng iyong pera sa account na ito: habang ang halaga ng account tumataas para sa 10 rubles. Ang pinagsamang epekto ng pareho sa mga sitwasyong ito ay may posibilidad na ibalik ang balanse sa iyong bangko sa zero. Kasunod nito na ang −6 × −5 ay may parehong epekto sa iyong account gaya ng pagbabawas (pag-alis) ng utang na 5 rubles nang anim na beses, na nangangahulugang dapat nitong dagdagan ang iyong balanse sa bangko ng 30 rubles.

Ang isang pusa ay may isang buntot. Ang mga zero na pusa ay may walong buntot. (Ang isa pang pagbabasa ay "Walang pusa na may walong buntot.") Kaya nakuha natin: Ang isang pusa ay may siyam na buntot. - Tandaan ed.

Ang mundo ay binuo sa kapangyarihan ng mga numero.
Pythagoras

Kahit na sa maagang pagkabata, natututo tayong magbilang, pagkatapos ay sa paaralan nakakakuha tayo ng ideya ng walang limitasyong serye ng numero, ang mga elemento ng geometry, fractional at irrational na mga numero, at pinag-aaralan natin ang mga prinsipyo ng algebra at mathematical analysis. Ang papel ng matematika sa modernong kaalaman at modernong praktikal na aktibidad ay napakahusay.

Kung walang matematika, imposible ang pag-unlad sa physics, engineering, at organisasyon ng produksyon.
Ang numero ay isa sa mga pangunahing konsepto ng matematika, na nagpapahintulot sa isa na ipahayag ang mga resulta ng pagbibilang o pagsukat. Kailangan natin ng mga numero upang makontrol ang ating buong buhay. Pinapalibutan nila kami kahit saan: mga numero ng bahay, mga numero ng kotse, mga petsa ng kapanganakan, mga tseke...

Inamin ni Ian Stewart, isang sikat na sikat sa buong mundo ng matematika at ang may-akda ng maraming kaakit-akit na mga aklat, na ang mga numero ay nabighani sa kanya mula noong maagang pagkabata, at "hanggang ngayon siya ay nabighani sa mga numero at natututo ng higit at higit pang mga bagong katotohanan tungkol sa mga ito."

Ang mga bayani ng kanyang bagong libro ay mga numero. Ayon sa propesor sa Ingles, bawat isa sa kanila ay may kanya-kanyang sariling katangian. Ang ilan sa kanila ay may malaking papel sa maraming larangan ng matematika. Halimbawa, ang bilang na π, na nagpapahayag ng ratio ng circumference ng isang bilog sa diameter nito. Ngunit, gaya ng pinaniniwalaan ng may-akda, "kahit na ang pinakamababang bilang ay magkakaroon ng ilang hindi pangkaraniwang pag-aari." Kaya, halimbawa, imposibleng hatiin sa 0 ang lahat, at "sa isang lugar sa mismong pundasyon ng matematika, ang lahat ng mga numero ay maaaring makuha mula sa zero." Ang pinakamaliit na positive integer ay 1. Ito ang hindi mahahati na yunit ng arithmetic, ang tanging positibong numero na hindi makukuha sa pamamagitan ng pagdaragdag ng mas maliliit na positibong numero. Nagsisimula kaming magbilang mula sa 1; walang sinuman ang nahihirapan sa pagpaparami ng 1. Ang anumang numero kapag pinarami ng 1 o hinati sa 1 ay nananatiling hindi nagbabago. Ito ang tanging numero na kumikilos sa ganitong paraan.
Ang publikasyon ay bubukas na may maikling pangkalahatang-ideya ng mga numerical system. Ipinapakita ng may-akda kung paano sila nabuo sa konteksto ng pagbabago ng mga ideya ng tao tungkol sa mga numero. Kung ang kaalaman sa matematika sa malayong nakaraan ay ginamit upang malutas ang mga pang-araw-araw na problema, ang pagsasanay ngayon ay nagdudulot ng mas kumplikadong mga problema para sa matematika.
Ang bawat kabanata ng aklat ay nagsasalita tungkol sa isang "kawili-wiling numero." May mga kabanata na "0", "√2", "-1"... Ang pagbabasa ng aklat ni Ian Stewart, talagang sisimulan mong maunawaan kung gaano kahanga-hanga ang mundo ng mga numero! Siyempre, ang isang mambabasa na walang ilang kaalaman sa matematika ay maaaring mahirap maunawaan ang Hindi Kapani-paniwalang Mga Numero ni Propesor Stewart. Ang publikasyon ay para sa mga nagsusumikap na maging matalino, o gustong ipakita ang kanilang kaalaman. Ngunit, kung mahilig ka sa matematika at gusto mong matuto tungkol sa, halimbawa, super-mega large numbers o mega-small, para sa iyo ang aklat na ito.

Nararapat kay Stewart ang pinakamataas na papuri para sa kanyang kuwento tungkol sa kung gaano kahusay, kahanga-hanga at kapaki-pakinabang ang papel ng lahat sa komunidad ng mga pandaigdigang numero. Kirkus Reviews Gumagawa si Stewart ng napakahusay na trabaho sa pagpapaliwanag ng mga kumplikadong isyu. Ang New Scientist Britain ang pinakamatalino at pinakamaraming popularizer ng matematika. Alex Bellos Tungkol saan ang aklat? Sa kanyang libro