Mga natural na numero (N). Prime at composite na mga numero. Divisor, maramihan. Pinakamalaking common divisor, least common multiple. Hindi bababa sa karaniwang maramihan at pinakamalaking karaniwang divisor Multiplication. multiplier * multiplier = produkto

Mga karaniwang multiple ng natural na numeroaAtbay isang numero na isang multiple ng bawat isa sa mga numerong ito.

Pinakamaliit na bilang ng lahat ng karaniwang multiple A At b tinawag least common multiple ng mga numerong ito.

Hindi bababa sa karaniwang multiple ng mga numero A At b Sumang-ayon tayo na tukuyin ang K( A, b).

Halimbawa, ang dalawang numero na 12 at 18 ay karaniwang multiple ng: 36, 72, 108, 144, 180, atbp. Ang numerong 36 ay ang pinakamaliit na karaniwang multiple ng mga numerong 12 at 18. Maaari mong isulat ang: K(12, 18) = 36.

Para sa hindi bababa sa karaniwang maramihang ang mga sumusunod na pahayag ay totoo:

1. Hindi bababa sa karaniwang multiple ng mga numero A At b

2. Hindi bababa sa karaniwang multiple ng mga numero A At b hindi bababa sa mas malaki sa mga numerong ito, i.e. Kung isang >b, tapos K( A, b) ≥ A.

3. Anumang karaniwang multiple ng mga numero A At b hinati sa kanilang least common multiple.

Pinakamahusay na karaniwang divisor

Ang karaniwang divisor ng mga natural na numero a atbay isang numero na isang divisor ng bawat isa sa mga numerong ito.

Ang pinakamalaking bilang ng lahat ng karaniwang divisors ng mga numero A At b ay tinatawag na pinakamalaking karaniwang divisor ng mga numerong ito.

Pinakamahusay na karaniwang divisor ng mga numero A At b Sumang-ayon tayo na tukuyin ang D( A, b).

Halimbawa, para sa mga numero 12 at 18 ang karaniwang mga divisors ay ang mga numero: 1, 2, 3, 6. Ang numero 6 ay 12 at 18. Maaari mong isulat ang: D(12, 18) = 6.

Ang numero 1 ay ang karaniwang divisor ng alinmang dalawang natural na numero a At b. Kung ang mga numerong ito ay walang iba pang karaniwang divisors, kung gayon D( A, b) = 1, at ang mga numero A At b ay tinatawag kapwa prime.

Halimbawa, ang mga numero 14 at 15 ay medyo prime, dahil D(14, 15) = 1.

Para sa pinakamalaking karaniwang divisor ang mga sumusunod na pahayag ay totoo:

1. Pinakamahusay na karaniwang divisor ng mga numero a At b palaging umiiral at natatangi.

2. Pinakamahusay na karaniwang divisor ng mga numero A At b ay hindi lalampas sa mas maliit sa mga ibinigay na numero, i.e. Kung a< b, Iyon D(a, b) ≤ a.

3. Pinakamahusay na karaniwang divisor ng mga numero a At b ay nahahati ng anumang karaniwang divisor ng mga numerong ito.

Pinakamalaking common multiple ng mga numero A At b at ang kanilang pinakamalaking karaniwang divisor ay magkakaugnay: ang produkto ng hindi bababa sa karaniwang maramihang at ang pinakamalaking karaniwang divisor ng mga numero A At b katumbas ng produkto ng mga numerong ito, i.e. K( a, b)·D( a, b) = a· b.

Ang mga sumusunod na resulta ay sumusunod mula sa pahayag na ito:

a) Ang hindi bababa sa karaniwang multiple ng dalawang mutually prime na numero ay katumbas ng produkto ng mga numerong ito, i.e. D( a, b) = 1 => K( a, b) = a· b;

Halimbawa, upang mahanap ang hindi bababa sa karaniwang maramihang ng mga numero 14 at 15, sapat na upang i-multiply ang mga ito, dahil D(14, 15) = 1.

b) A hinati sa produkto ng mga numerong coprime m At n, ito ay kinakailangan at sapat na ito ay mahahati ng m, at sa n.

Ang pahayag na ito ay tanda ng divisibility sa pamamagitan ng mga numero na maaaring katawanin bilang produkto ng dalawang relatibong prime na numero.

c) Ang mga quotient na nakuha sa pamamagitan ng paghahati ng dalawang ibinigay na mga numero sa kanilang pinakamalaking karaniwang divisor ay relatibong prime number.

Maaaring gamitin ang property na ito kapag sinusuri ang kawastuhan ng nakitang pinakamalaking karaniwang divisor ng mga ibinigay na numero. Halimbawa, suriin natin kung ang numero 12 ay ang pinakamalaking karaniwang divisor ng mga numero 24 at 36. Upang gawin ito, ayon sa huling pahayag, hinahati namin ang 24 at 36 sa 12. Nakukuha namin ang mga numero 2 at 3, ayon sa pagkakabanggit, na ay medyo prime. Samakatuwid, D(24, 36)=12.

Suliranin 32. Bumuo at patunayan ang pagsubok para sa divisibility sa pamamagitan ng 6.

Solusyon x mahahati sa 6, kinakailangan at sapat na ito ay mahahati ng 2 at 3.

Hayaan ang numero x ay nahahati sa 6. Pagkatapos mula sa katotohanan na x 6 at 62, kasunod nito x 2. At mula sa katotohanan na x 6 at 63, kasunod nito x 3. Napatunayan namin na upang ang isang numero ay mahahati sa 6, ito ay dapat na mahahati ng 2 at 3.

Ipakita natin ang kasapatan ng kondisyong ito. kasi x 2 at x 3, pagkatapos x- common multiple ng mga numero 2 at 3. Anumang common multiple ng mga numero ay hinati sa kanilang hindi bababa sa maramihang, ibig sabihin x K(2;3).

Dahil D(2, 3)=1, kung gayon K(2, 3)=2·3=6. Kaya naman, x 6.

Suliranin 33. Bumalangkas sa 12, 15 at 60.

Solusyon. Upang magkaroon ng natural na numero x mahahati sa 12, kinakailangan at sapat na ito ay mahahati ng 3 at 4.

Upang magkaroon ng natural na numero x mahahati ng 15, kinakailangan at sapat na ito ay mahahati ng 3 at 5.

Upang magkaroon ng natural na numero x mahahati ng 60, kinakailangan at sapat na ito ay mahahati ng 4, 3 at 5.

Suliranin 34. Maghanap ng mga numero a At b, kung K( a, b)=75, a· b=375.

Solusyon. Gamit ang formula K( a,b)·D( a,b)=a· b, hanapin ang pinakamalaking karaniwang divisor ng mga kinakailangang numero A At b:

D( a, b) === 5.

Pagkatapos ang mga kinakailangang numero ay maaaring katawanin sa form A= 5r, b= 5q, Saan p At q p at 5 q sa pagkakapantay-pantay isang b= 275. Kunin natin ang 5 p·5 q=375 o p· q=15. Nire-solve namin ang resultang equation na may dalawang variable sa pamamagitan ng pagpili: nakahanap kami ng mga pares ng relatibong prime number na ang produkto ay katumbas ng 15. Mayroong dalawang ganoong pares: (3, 5) at (1, 15). Samakatuwid, ang mga kinakailangang numero A At b ay: 15 at 25 o 5 at 75.

Suliranin 35. Maghanap ng mga numero A At b, kung alam na D( a, b) = 7 at a· b= 1470.

Solusyon. Mula noong D( a, b) = 7, kung gayon ang mga kinakailangang numero ay maaaring katawanin sa form A= 7r, b= 7q, Saan p At q ay kapwa prime number. Palitan natin ang mga expression 5 r at 5 q sa pagkakapantay-pantay a b = 1470. Pagkatapos 7 p·7 q= 1470 o p· q= 30. Nilulutas namin ang nagresultang equation na may dalawang variable sa pamamagitan ng pagpili: nakahanap kami ng mga pares ng relatibong prime number na ang produkto ay katumbas ng 30. Mayroong apat na ganoong pares: (1, 30), (2, 15), (3, 10). ), (5, 6). Samakatuwid, ang mga kinakailangang numero A At b ay: 7 at 210, 14 at 105, 21 at 70, 35 at 42.

Suliranin 36. Maghanap ng mga numero A At b, kung alam na D( a, b) = 3 at A:b= 17:14.

Solusyon. kasi a:b= 17:14, kung gayon A= 17r At b= 14p, Saan r- pinakamalaking karaniwang divisor ng mga numero A At b. Kaya naman, A= 17·3 = 51, b= 14·3 = 42.

Suliranin 37. Maghanap ng mga numero A At b, kung alam na K( a, b) = 180, a:b= 4:5.

Solusyon. kasi a: b=4:5 tapos A=4r At b=5r, Saan r- pinakamalaking karaniwang divisor ng mga numero a At b. Pagkatapos r·180=4 r·5 r. saan r=9. Kaya naman, a= 36 at b=45.

Suliranin 38. Maghanap ng mga numero A At b, kung alam na D( a,b)=5, K( a,b)=105.

Solusyon. Mula noong D( a, b) K( a, b) = a· b, Iyon a· b= 5 105 = 525. Bilang karagdagan, ang mga kinakailangang numero ay maaaring katawanin sa form A= 5r At b= 5q, Saan p At q ay kapwa prime number. Palitan natin ang mga expression 5 r at 5 q sa pagkakapantay-pantay A· b= 525. Pagkatapos 5 p·5 q=525 o p· q=21. Nakahanap kami ng mga pares ng medyo prime na numero na ang produkto ay katumbas ng 21. Mayroong dalawang ganoong pares: (1, 21) at (3, 7). Samakatuwid, ang mga kinakailangang numero A At b ay: 5 at 105, 15 at 35.

Suliranin 39. Patunayan na ang bilang n(2n+ 1)(7n+ 1) ay nahahati sa 6 para sa anumang natural n.

Solusyon. Ang bilang na 6 ay pinagsama-sama; Kung patunayan natin na ang isang naibigay na numero ay nahahati ng 2 at 3, pagkatapos ay batay sa pagsubok ng divisibility ng isang pinagsama-samang numero maaari nating tapusin na ito ay mahahati ng 6.

Upang patunayan na ang bilang n(2n+ 1)(7n+ 1) ay nahahati sa 2, kailangan nating isaalang-alang ang dalawang posibilidad:

1) n ay nahahati sa 2, i.e. n= 2k. Pagkatapos ang produkto n(2n+ 1)(7n+ 1) magiging ganito ang hitsura: 2 k(4k+ 1)(14k+ 1). Ang produktong ito ay nahahati sa 2, dahil ang unang salik ay nahahati sa 2;

2) n ay hindi nahahati sa 2, i.e. n= 2k+ 1. Pagkatapos ang produkto n(2n+ 1 )(7n+ 1) ay magiging ganito: (2 k+ 1)(4k+ 3)(14k+ 8). Ang produktong ito ay nahahati sa 2, dahil ang huling salik ay nahahati sa 2.

Upang patunayan na ang gawain n(2n+ 1)(7n+ 1) ay nahahati sa 3, tatlong mga posibilidad ang kailangang isaalang-alang:

1) n ay nahahati sa 3, i.e. n= 3k. Pagkatapos ang produkto n(2n+ 1)(7n+ 1) magiging ganito ang hitsura: 3 k(6k+ 1)(21k+ 1). Ang produktong ito ay nahahati sa 3, dahil ang unang salik ay nahahati sa 3;

2) n Kapag hinati sa 3, ang natitira ay 1, i.e. n= 3k+ 1. Pagkatapos ang produkto n(2n+ 1)(7n+ 1) ay magiging ganito: (3 k+ 1)(6k+ 3)(21k+ 8). Ang produktong ito ay nahahati sa 3, dahil ang pangalawang kadahilanan ay nahahati sa 3;

3) n kapag hinati sa 3, ang natitira ay 2, i.e. n= 3k+ 2. Pagkatapos ang produkto n(2n+ 1)(7n+ 1) ay magiging ganito: (3 k+ 2)(6k+ 5)(21k+ 15). Ang produktong ito ay nahahati sa 3, dahil ang huling salik ay nahahati sa 3.

Kaya, ito ay napatunayan na ang produkto n(2n+ 1)(7n+ 1) ay nahahati ng 2 at 3. Nangangahulugan ito na ito ay nahahati ng 6.

Mga ehersisyo para sa malayang gawain

1. Ibinigay ang dalawang numero: 50 at 75. Isulat ang set:

a) mga divisors ng numero 50; b) mga divisors ng numero 75; c) karaniwang mga divisors ng mga ibinigay na numero.

Ano ang pinakamalaking karaniwang divisor ng 50 at 75?

2. Ang bilang na 375 ba ay isang karaniwang multiple ng mga numero: a) 125 at 75; b) 85 at 15?

3. Maghanap ng mga numero A At b, kung alam na K( a, b) = 105, a· b= 525.

4. Maghanap ng mga numero A At b, kung alam na D( a, b) = 7, a· b= 294.

5. Maghanap ng mga numero A At b, kung alam na D( a, b) = 5, a:b= 13:8.

6. Maghanap ng mga numero A At b, kung alam na K( a, b) = 224, a:b= 7:8.

7. Maghanap ng mga numero a At b, kung alam na D( a, b) = 3, K( a; b) = 915.

8. Patunayan ang pagsubok para sa divisibility sa pamamagitan ng 15.

9. Mula sa hanay ng mga numero 1032, 2964, 5604, 8910, 7008, isulat ang mga nahahati sa 12.

10. Bumuo ng pamantayan para sa divisibility ng 18, 36, 45, 75.

Ang hanay ng mga natural na numero = (1, 2, 3...). Iyon ay, ang hanay ng mga natural na numero ay ang hanay ng lahat ng positibong integer. Ang mga operasyon ng karagdagan, pagpaparami, pagbabawas at paghahati ay tinukoy sa natural na mga numero. Ang resulta ng pagdaragdag, pagpaparami at pagbabawas ng dalawang natural na numero ay isang buong numero. Ang resulta ng paghahati ng dalawang natural na numero ay maaaring alinman sa isang integer o isang fraction.

Halimbawa: 20: 4 = 5 – ang resulta ng paghahati ay isang integer.
20: 3 = 6 2/3 – ang resulta ng paghahati ay isang fraction.
Ang isang natural na bilang n ay sinasabing mahahati ng isang natural na bilang na m kung ang resulta ng paghahati ay isang integer. Sa kasong ito, ang bilang na m ay tinatawag na isang divisor ng numerong n, at ang bilang n ay tinatawag na isang multiple ng numerong m.

Sa unang halimbawa, ang bilang na 20 ay nahahati sa 4, ang 4 ay isang divisor ng 20, at ang 20 ay isang multiple ng 4.
Sa pangalawang halimbawa, ang bilang na 20 ay hindi nahahati sa numero 3 nang naaayon, maaaring walang tanong ng mga divisors at multiple.

Ang isang numero n ay tinatawag na prime kung ito ay walang divisors maliban sa kanyang sarili at isa. Mga halimbawa ng prime number: 2, 7, 11, 97, atbp.
Ang isang numero n ay tinatawag na composite kung ito ay may mga divisors maliban sa sarili nito at isa.

Anumang natural na numero ay maaaring mabulok sa isang produkto ng mga prima, at ang agnas na ito ay natatangi, hanggang sa pagkakasunud-sunod ng mga kadahilanan. Halimbawa: 36=2 2 3 3 = 2 3 2 3 = 3 2 3 2 – lahat ng mga pagpapalawak na ito ay naiiba lamang sa pagkakasunud-sunod ng mga salik.

Ang pinakamalaking karaniwang divisor ng dalawang numero na m at n ay ang pinakamalaking natural na numero na isang divisor ng parehong m at n. Halimbawa, ang mga numero 34 at 85 ay may pinakamalaking karaniwang kadahilanan na 17.

Ang hindi bababa sa karaniwang multiple ng dalawang numero na m at n ay ang pinakamaliit na natural na numero na isang multiple ng parehong m at n. Halimbawa, ang mga numerong 15 at 4 ay may hindi bababa sa karaniwang maramihang 60.

Ang isang natural na numero, na nahahati sa dalawang pangunahing numero, ay nahahati din sa kanilang produkto. Halimbawa, kung ang isang numero ay nahahati sa 2 at 3, kung gayon ito ay mahahati ng 6 = 2 3, kung sa pamamagitan ng 11 at 7, pagkatapos ay sa pamamagitan ng 77.

Halimbawa: ang numerong 6930 ay nahahati sa 11 - 6930: 11 = 630, at nahahati ng 7 - 6930: 7 = 990. Ligtas nating masasabi na ang numerong ito ay nahahati din ng 77. Suriin natin: 6930: 77 = 90.

Algorithm para sa pag-decomposing ng numero n sa pangunahing mga kadahilanan:

1. Hanapin ang pinakamaliit na prime divisor ng numero n (maliban sa 1) - a1.
2. Hatiin ang bilang n sa a1, na nagsasaad ng quotient bilang n1.
3. n=a1 n1.
4. Ginagawa namin ang parehong operasyon sa n1 hanggang makakuha kami ng isang prime number.

Halimbawa: I-factor ang bilang na 17,136 sa prime factor

1. Ang pinakamaliit na prime divisor maliban sa 1, dito 2.

2. 17 136: 2 = 8 568;

3. 17 136 = 8 568 2.

4. Ang pinakamaliit na prime divisor ng 8568 ay 2.

5. 8 568: 2 = 4284;

6. 17 136 = 4284 2 2.

7. Ang pinakamaliit na prime divisor ng 4284 ay 2.

8. 4284: 2 = 2142;

9. 17 136 = 2142 2 2 2.

10. Ang pinakamaliit na prime divisor ng 2142 ay 2.

11. 2142: 2 = 1071;

12. 17 136 = 1071 2 2 2 2.

13. Ang pinakamaliit na prime divisor ng 1071 ay 3.

14. 1071: 3 = 357;

15. 17 136 = 357 3 2 2 2 2.

16. Ang pinakamaliit na prime divisor ng 357 ay 3.

17. 357: 3 = 119;

18. 17 136 = 119 3 3 2 2 2 2.

19. Ang pinakamaliit na prime divisor ng 119 ay 7.

20. 119: 7 = 17;

21. Ang 17 ay isang prime number, na nangangahulugang 17 136 = 17 7 3 3 2 2 2 2.

Nakuha namin ang agnas ng numerong 17,136 sa pangunahing mga kadahilanan.

Mga pangunahing salita ng buod:Mga natural na numero. Mga operasyon sa aritmetika sa mga natural na numero. Divisibility ng mga natural na numero. Prime at composite na mga numero. Pag-factor ng natural na numero sa prime factor. Mga palatandaan ng divisibility ng 2, 3, 5, 9, 4, 25, 10, 11. Greatest common divisor (GCD), pati na rin ang least common multiple (LCD). Dibisyon na may natitira.

Mga natural na numero- ito ay mga numero na ginagamit upang mabilang ang mga bagay - 1, 2, 3, 4 , ... Ngunit ang bilang 0 ay hindi natural!

Ang hanay ng mga natural na numero ay tinutukoy ng N. Itala "3 ∈ N" nangangahulugan na ang numerong tatlo ay kabilang sa hanay ng mga natural na numero, at ang notasyon "0 ∉ N" nangangahulugan na ang numerong zero ay hindi kabilang sa set na ito.

Sistema ng desimal na numero- positional radix number system 10 .

Mga operasyon sa aritmetika sa mga natural na numero

Para sa mga natural na numero ang mga sumusunod na aksyon ay tinukoy: karagdagan, pagbabawas, pagpaparami, paghahati, exponentiation, pagkuha ng ugat. Ang unang apat na aksyon ay aritmetika.

Hayaang maging natural na mga numero ang a, b at c

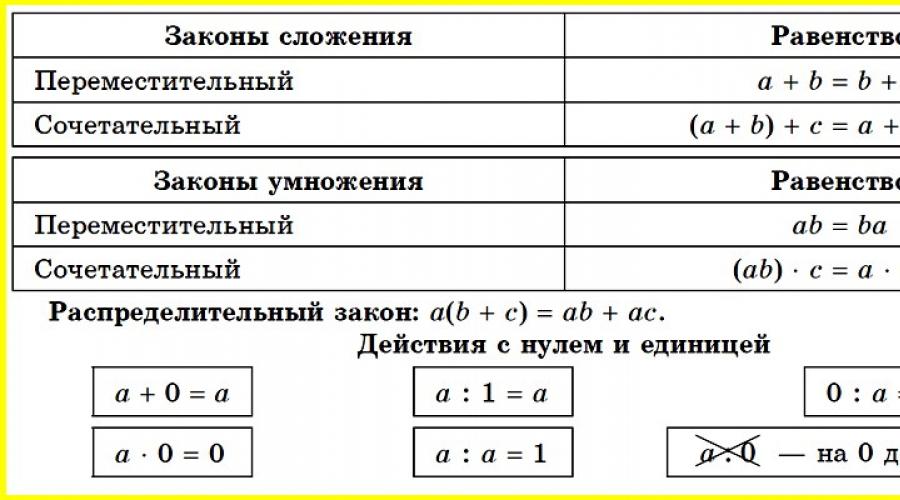
1. DAGDAG. Termino + Termino = Sum

Mga katangian ng karagdagan
1. Komunikatibo a + b = b + a.
2. Pang-ugnay na a + (b + c) = (a + b) + c.
3. a + 0= 0 + a = a.

2. SUBTRACT. Minuend - Subtrahend = Pagkakaiba

Mga Katangian ng Pagbabawas
1. Pagbabawas ng kabuuan mula sa bilang na a - (b + c) = a - b - c.
2. Pagbabawas ng numero mula sa kabuuan (a + b) - c = a + (b - c); (a + b) - c = (a - c) + b.
3. a - 0 = a.
4. a - a = 0.

3. MULTIPLICATION. Multiplier * Multiplier = Produkto

Mga Katangian ng Multiplikasyon
1. Komunikatibo a*b = b*a.
2. Pang-ugnay na a*(b*c) = (a*b)*c.
3. 1 * a = a * 1 = a.
4. 0 * a = a * 0 = 0.
5. Distributive (a + b) * c = ac + bc; (a - b) * c = ac - bc.

4. DIBISYON. Dibidendo: Divisor = Quotient

Mga katangian ng dibisyon
1. a: 1 = a.
2. a: a = 1. Hindi mo maaaring hatiin sa zero!
3. 0: a= 0.

Pamamaraan

1. Una sa lahat, ang mga aksyon sa panaklong.
2. Pagkatapos multiplication, division.
3. At sa dulo lamang ng karagdagan at pagbabawas.

Divisibility ng mga natural na numero. Prime at composite na mga numero.

Divisor ng isang natural na numero A ay ang natural na bilang kung saan A hinati nang walang natitira. Numero 1 ay isang divisor ng anumang natural na numero.

Ang natural na numero ay tinatawag simple lang, kung mayroon lang dalawa divisor: isa at ang numero mismo. Halimbawa, ang mga numero 2, 3, 11, 23 ay mga pangunahing numero.

Ang isang numero na may higit sa dalawang divisors ay tinatawag pinagsama-sama. Halimbawa, ang mga numero 4, 8, 15, 27 ay pinagsama-samang mga numero.

Pagsusulit sa divisibility gumagana ilang mga numero: kung hindi bababa sa isa sa mga kadahilanan ay nahahati sa isang tiyak na numero, kung gayon ang produkto ay mahahati din sa numerong ito. Trabaho 24 15 77 hinati ng 12 , dahil ang multiplier ng numerong ito 24 hinati ng 12 .

Pagsusuri sa divisibility para sa isang kabuuan (pagkakaiba) mga numero: kung ang bawat termino ay nahahati sa isang tiyak na numero, ang buong kabuuan ay hinati sa numerong ito. Kung a: b At c: b, Iyon (a + c): b. Paano kung a: b, A c hindi mahahati ng b, Iyon a+c hindi nahahati sa isang numero b.

Kung a: c At c: b, Iyon a: b. Batay sa katotohanan na 72:24 at 24:12, napagpasyahan namin na 72:12.

Ang representasyon ng isang numero bilang isang produkto ng mga kapangyarihan ng mga pangunahing numero ay tinatawag pag-factor ng isang numero sa prime factor.

Pangunahing Teorama ng Arithmetic: anumang natural na numero (maliban 1 ) o ay simple lang, o maaari itong i-factor sa isang paraan lamang.

Kapag nabubulok ang isang numero sa mga pangunahing kadahilanan, ang mga palatandaan ng divisibility ay ginagamit at ang "haligi" na notasyon ay ginagamit Sa kasong ito, ang divisor ay matatagpuan sa kanan ng patayong linya, at ang quotient ay nakasulat sa ilalim ng dibidendo.

Halimbawa, gawain: i-factor ang isang numero sa prime factor 330 . Solusyon:

Mga palatandaan ng divisibility sa 2, 5, 3, 9, 10, 4, 25 at 11.

May mga palatandaan ng divisibility sa 6, 15, 45 atbp., iyon ay, sa mga numero na ang produkto ay maaaring i-factorize 2, 3, 5, 9 At 10 .

Pinakamahusay na karaniwang divisor

Ang pinakamalaking natural na bilang kung saan ang bawat isa sa dalawang ibinigay na natural na mga numero ay nahahati ay tinatawag pinakamalaking karaniwang divisor ang mga numerong ito ( GCD). Halimbawa, GCD (10; 25) = 5; at GCD (18; 24) = 6; GCD (7; 21) = 1.

Kung ang pinakamalaking karaniwang divisor ng dalawang natural na numero ay katumbas ng 1 , pagkatapos ay tatawagin ang mga numerong ito kapwa prime.

Algorithm para sa paghahanap ng pinakamalaking karaniwang divisor(NOD)

Ang GCD ay kadalasang ginagamit sa mga problema. Halimbawa, 155 kuwaderno at 62 panulat ang hinati nang pantay sa pagitan ng mga mag-aaral sa isang klase. Ilang estudyante ang nasa klase na ito?

Solusyon: Ang paghahanap ng bilang ng mga mag-aaral sa klase na ito ay bumaba sa paghahanap ng pinakamalaking karaniwang divisor ng mga numero 155 at 62, dahil ang mga notebook at panulat ay hinati nang pantay. 155 = 5 31; 62 = 2 31. GCD (155; 62) = 31.

Sagot: 31 mag-aaral sa klase.

Hindi bababa sa karaniwang maramihang

Multiple ng isang natural na numero A ay isang natural na numero na nahahati ng A walang bakas. Halimbawa, numero 8 ay may maramihang: 8, 16, 24, 32 , ... Anumang natural na numero ay may walang katapusang maraming multiple.

Hindi bababa sa karaniwang maramihang(LCM) ay ang pinakamaliit na natural na numero na isang multiple ng mga numerong ito.

Algorithm para sa paghahanap ng hindi bababa sa karaniwang maramihang ( NOC):

Madalas ding ginagamit ang LCM sa mga problema. Halimbawa, dalawang siklista ang sabay na nagsimula sa isang cycle track sa parehong direksyon. Ang isa ay gagawa ng bilog sa loob ng 1 minuto, at ang isa naman sa loob ng 45 segundo. Sa anong minimum na bilang ng minuto pagkatapos ng pagsisimula ng kilusan sila magkikita sa simula?

Solusyon: Ang bilang ng mga minuto pagkatapos na magkita silang muli sa simula ay dapat hatiin sa 1 min, pati na rin sa 45 s. Sa 1 min = 60 s. Ibig sabihin, kailangang hanapin ang LCM (45; 60). 45 = 32 5; 60 = 22 3 5. LCM (45; 60) = 22 32 5 = 4 9 5 = 180. Ang resulta ay magkikita ang mga siklista sa simula sa 180 s = 3 min.

Sagot: 3 min.

Dibisyon na may natitira

Kung natural na numero A ay hindi nahahati sa natural na numero b, pagkatapos ay magagawa mo paghahati sa natitira. Sa kasong ito, ang resultang quotient ay tinatawag hindi kumpleto. Ang pagkakapantay-pantay ay patas:

a = b n + r,

saan A- mahahati, b- divider, n- hindi kumpletong quotient, r- natitira. Halimbawa, hayaang pantay ang dibidendo 243 , divider - 4 , Pagkatapos 243: 4 = 60 (natitira 3). Iyon ay, a = 243, b = 4, n = 60, r = 3, pagkatapos 243 = 60 4 + 3 .

Mga numero na nahahati sa 2 walang natitira, ay tinatawag kahit: a = 2n, n ∈ N.

Ang natitirang mga numero ay tinatawag kakaiba: b = 2n + 1, n ∈ N.

Ito ay isang buod ng paksa “Mga natural na numero. Mga palatandaan ng divisibility". Upang magpatuloy, piliin ang mga susunod na hakbang:

• Pumunta sa susunod na buod: