Pang-agham na bulletin ng internasyonal na mag-aaral. Mga problemang kinasasangkutan ng pagpapalawak ng mga function sa serye ng Fourier at ang kanilang solusyon. Hanapin natin ang mga zero point ng sine

20.09.2019

Basahin din

Independiyenteng pagtatasa ng kalidad ng mga kondisyon para sa pagsasagawa ng mga aktibidad na pang-edukasyon Independiyenteng pagtatasa ng kalidad ng trabaho ng mga organisasyong pang-edukasyon

Impormasyon sa pakikipag-ugnayan ng MPGU admissions committee

Talambuhay ni Feklin Sergey Ivanovich

Russian Federation Federal State Budgetary Educational Institution ng Mas Mataas na Edukasyon "State University of Management Registration ng huling qualifying work

Tunay na tawag ng mga espiritu. Hindi ka maaaring magpatawag ng mga espiritu. Ritual na may Ouija board at platito

Sa maraming mga kaso, ang gawain ng pagkuha (pagkalkula) ng spectrum ng isang signal ay ganito ang hitsura. Mayroong isang ADC na, na may dalas ng sampling Fd, nagko-convert ng tuluy-tuloy na signal na dumarating sa input nito sa oras ng T sa mga digital na sample - N piraso. Susunod, ang hanay ng mga sample ay pinapakain sa isang tiyak na programa na gumagawa ng N/2 ng ilang mga numerong halaga (ang programmer na ninakaw sa internet sumulat ng isang programa, tinitiyak na ginagawa nito ang pagbabago ng Fourier).

Upang suriin kung gumagana nang tama ang programa, bubuo kami ng isang hanay ng mga sample bilang kabuuan ng dalawang sinusoid sin(10*2*pi*x)+0.5*sin(5*2*pi*x) at ipasok ito sa programa . Iginuhit ng programa ang mga sumusunod:

Fig.1 Graph ng signal time function

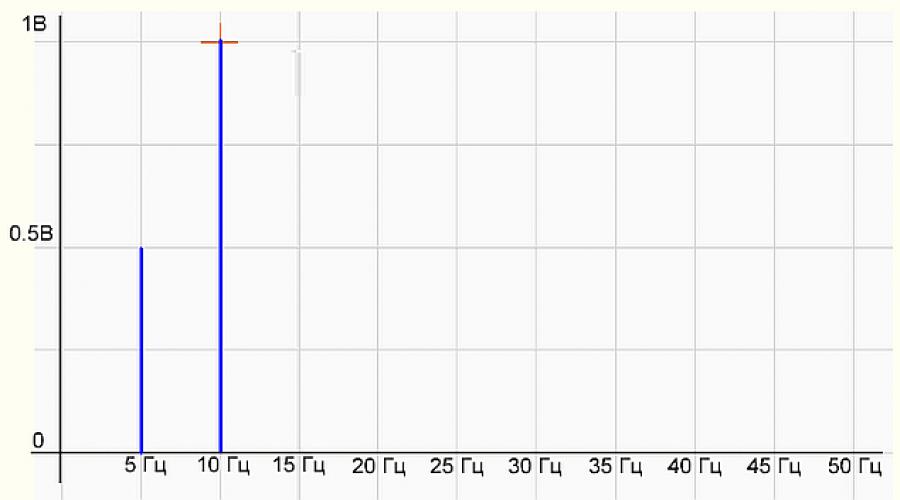
Fig.2 Signal spectrum graph

Sa spectrum graph mayroong dalawang stick (harmonics) 5 Hz na may amplitude na 0.5 V at 10 Hz na may amplitude na 1 V, ang lahat ay pareho sa formula ng orihinal na signal. Maayos ang lahat, mahusay na programmer! Ang programa ay gumagana nang tama.

Nangangahulugan ito na kung mag-aplay tayo ng isang tunay na signal mula sa pinaghalong dalawang sinusoid sa input ng ADC, makakakuha tayo ng katulad na spectrum na binubuo ng dalawang harmonika.

Kabuuan, ang aming totoo sinusukat na signal tumatagal ng 5 segundo, na-digitize ng ADC, ibig sabihin, kinakatawan discrete binibilang, may discrete non-periodic spectrum.

Mula sa isang mathematical point of view, gaano karaming mga error ang mayroon sa pariralang ito?

Ngayon ang mga awtoridad ay nagpasya, napagpasyahan namin na ang 5 segundo ay masyadong mahaba, sukatin natin ang signal sa loob ng 0.5 segundo.

Fig.3 Graph ng function na sin(10*2*pi*x)+0.5*sin(5*2*pi*x) para sa panahon ng pagsukat na 0.5 sec

Fig.4 Function spectrum

Parang may hindi tama! Ang 10 Hz harmonic ay karaniwang iginuhit, ngunit sa halip na ang 5 Hz stick, maraming kakaibang harmonic ang lilitaw. Tumingin kami sa Internet upang makita kung ano ang nangyayari...

Well, sinasabi nila na kailangan mong magdagdag ng mga zero sa dulo ng sample at ang spectrum ay iguguhit bilang normal.

Fig.5 Nagdagdag ng mga zero hanggang 5 segundo

Fig.6 Nakatanggap ng spectrum

Hindi pa rin ito katulad noong 5 segundo. Kailangan nating harapin ang teorya. Tara na sa Wikipedia- pinagmumulan ng kaalaman.

2. Continuous function at ang representasyon ng seryeng Fourier nito

Sa matematika, ang aming signal na may tagal na T segundo ay ilang function na f(x) na tinukoy sa segment (0, T) (X sa sa kasong ito- oras). Ang ganitong function ay maaaring palaging kinakatawan bilang isang kabuuan ng mga harmonic function (sine o cosine) ng form:

(1), kung saan:

K - trigonometric function number (harmonic component number, harmonic number)
T - segment kung saan tinukoy ang function (tagal ng signal)
Ang Ak ay ang amplitude ng k-th harmonic component,
θk- paunang yugto ng k-th harmonic component

Ano ang ibig sabihin ng "kumakatawan sa isang function bilang kabuuan ng isang serye"? Nangangahulugan ito na sa pamamagitan ng pagdaragdag ng mga halaga ng mga harmonic na bahagi ng serye ng Fourier sa bawat punto, nakukuha namin ang halaga ng aming function sa puntong ito.

(Higit na mahigpit, ang root-mean-square deviation ng serye mula sa function na f(x) ay magiging zero, ngunit sa kabila ng root-mean-square convergence, ang Fourier series ng isang function, sa pangkalahatan, ay hindi kinakailangan na mag-converge dito sa pointwise. Tingnan ang https://ru.wikipedia.org/ wiki/Fourier_Series.)

Ang seryeng ito ay maaari ding isulat bilang:

(2),
saan, k-th complex amplitude.

Ang ugnayan sa pagitan ng mga coefficient (1) at (3) ay ipinahayag ng mga sumusunod na formula:

Tandaan na ang lahat ng tatlong representasyong ito ng seryeng Fourier ay ganap na katumbas. Minsan, kapag nagtatrabaho sa serye ng Fourier, mas maginhawang gumamit ng mga exponents ng haka-haka na argumento sa halip na mga sine at cosine, iyon ay, gamitin ang Fourier transform sa kumplikadong anyo. Ngunit ito ay maginhawa para sa amin na gumamit ng formula (1), kung saan ang serye ng Fourier ay ipinakita bilang isang kabuuan ng mga cosine wave na may kaukulang mga amplitude at phase. Sa anumang kaso, hindi tama na sabihin na ang Fourier transform ng isang tunay na signal ay magreresulta sa mga kumplikadong harmonic amplitude. Tulad ng sinabi ng Wiki nang tama, "Ang Fourier transform (ℱ) ay isang operasyon na nag-uugnay ng isang function ng isang tunay na variable sa isa pang function, isang tunay na variable din."

Kabuuan:
Ang mathematical na batayan para sa spectral analysis ng mga signal ay ang Fourier transform.

Binibigyang-daan ka ng Fourier transform na kumatawan sa tuluy-tuloy na function f(x) (signal), na tinukoy sa segment (0, T) bilang kabuuan ng isang walang katapusang numero (walang katapusan na serye) trigonometriko function(sine at/o cosine) na may ilang partikular na amplitude at phase, na isinasaalang-alang din sa segment (0, T). Ang nasabing serye ay tinatawag na seryeng Fourier.

Tandaan natin ang ilang higit pang mga punto, kung saan kinakailangan ang pag-unawa tamang aplikasyon Fourier transforms para sa signal analysis. Kung isasaalang-alang natin ang seryeng Fourier (ang kabuuan ng sinusoids) sa buong X-axis, makikita natin na sa labas ng segment (0, T) ang function na kinakatawan ng seryeng Fourier ay pana-panahong uulitin ang ating function.

Halimbawa, sa graph ng Fig. 7, ang orihinal na function ay tinukoy sa segment (-T\2, +T\2), at ang Fourier series ay kumakatawan sa isang periodic function na tinukoy sa buong x-axis.

Nangyayari ito dahil ang mga sinusoid mismo ay mga pana-panahong pag-andar, at naaayon ang kanilang kabuuan ay magiging isang pana-panahong pag-andar.

Fig.7 Representasyon ng isang non-periodic na orihinal na function ng isang Fourier series

kaya:

Ang aming orihinal na function ay tuloy-tuloy, hindi pana-panahon, na tinukoy sa isang partikular na segment ng haba T.
Ang spectrum ng function na ito ay discrete, iyon ay, ito ay ipinakita sa anyo ng isang walang katapusang serye ng mga harmonic na bahagi - ang Fourier series.
Sa katunayan, ang seryeng Fourier ay tumutukoy sa ilan pana-panahong pag-andar, kasabay ng sa amin sa segment (0, T), ngunit para sa amin ang periodicity na ito ay hindi makabuluhan.

Ang mga panahon ng mga harmonic na bahagi ay multiple ng halaga ng segment (0, T) kung saan tinukoy ang orihinal na function na f(x). Sa madaling salita, ang mga harmonic period ay multiple ng tagal ng pagsukat ng signal. Halimbawa, ang panahon ng unang harmonic ng seryeng Fourier ay katumbas ng interval T kung saan tinukoy ang function na f(x). Ang panahon ng ikalawang harmonic ng seryeng Fourier ay katumbas ng pagitan ng T/2. At iba pa (tingnan ang Fig. 8).

Fig.8 Mga panahon (mga frequency) ng mga harmonic na bahagi ng seryeng Fourier (dito T = 2π)

Alinsunod dito, ang mga frequency ng mga harmonic na bahagi ay multiple ng 1/T. Iyon ay, ang mga frequency ng mga harmonic na sangkap na Fk ay katumbas ng Fk= k\T, kung saan ang k ay mula 0 hanggang ∞, halimbawa k=0 F0=0; k=1 F1=1\T; k=2 F2=2\T; k=3 F3=3\T;… Fk= k\T (sa zero frequency - constant component).

Hayaang ang aming orihinal na function ay isang signal na naitala sa T=1 seg. Pagkatapos ang panahon ng unang harmonic ay magiging katumbas ng tagal ng aming signal T1=T=1 sec at ang harmonic frequency ay magiging 1 Hz. Ang panahon ng pangalawang harmonic ay magiging katumbas ng tagal ng signal na hinati sa 2 (T2=T/2=0.5 sec) at ang frequency ay magiging 2 Hz. Para sa ikatlong harmonic T3=T/3 sec at ang frequency ay 3 Hz. At iba pa.

Ang hakbang sa pagitan ng mga harmonika sa kasong ito ay 1 Hz.

Kaya, ang isang signal na may tagal na 1 segundo ay maaaring mabulok sa mga harmonic na bahagi (pagkuha ng spectrum) na may frequency resolution na 1 Hz.
Upang taasan ang resolution ng 2 beses sa 0.5 Hz, kailangan mong taasan ang tagal ng pagsukat ng 2 beses - hanggang 2 segundo. Ang signal na tumatagal ng 10 segundo ay maaaring mabulok sa mga harmonic na bahagi (upang makakuha ng spectrum) na may frequency resolution na 0.1 Hz. Walang ibang mga paraan upang taasan ang resolution ng dalas.

Mayroong isang paraan upang artipisyal na taasan ang tagal ng isang signal sa pamamagitan ng pagdaragdag ng mga zero sa hanay ng mga sample. Ngunit hindi nito pinapataas ang aktwal na resolusyon ng dalas.

3. Mga discrete signal at discrete Fourier transform

Sa pag-unlad digital na teknolohiya Ang mga paraan ng pag-iimbak ng data ng pagsukat (mga signal) ay nagbago din. Kung dati ang isang senyas ay maaaring i-record sa isang tape recorder at naka-imbak sa tape sa analog form, ngayon ang mga signal ay digitized at naka-imbak sa mga file sa memorya ng computer bilang isang set ng mga numero (mga sample).

Ang karaniwang pamamaraan para sa pagsukat at pag-digitize ng signal ay ang mga sumusunod.

Fig.9 Diagram ng channel ng pagsukat

Ang signal mula sa pagsukat ng transduser ay dumarating sa ADC sa isang yugto ng panahon na T. Ang mga sample ng signal (sampling) na nakuha sa panahon ng T ay ipinadala sa computer at nakaimbak sa memorya.

Fig. 10 Digitized signal - N sample na natanggap sa panahon ng T

Ano ang mga kinakailangan para sa mga parameter ng pag-digitize ng signal? Isang device na nagko-convert ng input analog signal sa discrete code ( digital signal) ay tinatawag na analog-to-digital converter (ADC, English Analog-to-digital converter, ADC) (Wiki).

Ang isa sa mga pangunahing parameter ng ADC ay ang maximum sampling frequency (o sampling rate, English sample rate) - ang sampling rate ng isang time-continuous signal kapag sina-sample ito. Ito ay sinusukat sa hertz. ((Wiki))

Ayon sa theorem ni Kotelnikov, kung ang isang tuluy-tuloy na signal ay may spectrum na limitado ng frequency Fmax, maaari itong ganap at natatanging muling itayo mula sa mga discrete sample nito na kinuha sa mga agwat ng oras. , ibig sabihin. na may frequency Fd ≥ 2*Fmax, kung saan ang Fd ay ang sampling frequency; Fmax - maximum na dalas ng signal spectrum. Sa madaling salita, dapat na hindi bababa sa 2 beses na mas mataas ang signal digitization frequency (ADC sampling frequency) kaysa sa maximum frequency ng signal na gusto nating sukatin.

Ano ang mangyayari kung kukuha tayo ng mga sample na may mas mababang dalas kaysa sa kinakailangan ng teorem ni Kotelnikov?

Sa kasong ito, nangyayari ang "aliasing" na epekto (kilala rin bilang stroboscopic effect, moiré effect), kung saan ang isang high-frequency na signal, pagkatapos ng digitization, ay nagiging isang low-frequency na signal, na talagang wala. Sa Fig. Ang 11 red high frequency sine wave ay isang tunay na signal. Ang isang asul na sinusoid ng isang mas mababang dalas ay isang gawa-gawang signal na lumitaw dahil sa ang katunayan na sa panahon ng sampling oras higit sa kalahati ng isang panahon ng mataas na dalas signal ay may oras upang pumasa.

kanin. 11. Ang paglitaw ng isang maling signal ng mababang dalas sa isang hindi sapat na mataas na rate ng sampling

Upang maiwasan ang epekto ng aliasing, isang espesyal na anti-aliasing na filter ang inilalagay sa harap ng ADC - isang low-pass filter (LPF), na nagpapasa ng mga frequency sa ibaba ng kalahati ng frequency sampling ng ADC, at pinuputol ang mas matataas na frequency.

Upang makalkula ang spectrum ng isang signal mula sa mga discrete sample nito, ginagamit ang discrete Fourier transform (DFT). Tandaan nating muli na ang spectrum ng isang discrete signal “by definition” ay nililimitahan ng frequency Fmax, na mas mababa sa kalahati ng sampling frequency Fd. Samakatuwid, ang spectrum ng isang discrete signal ay maaaring katawanin ng kabuuan ng isang may hangganan na bilang ng mga harmonika, sa kaibahan sa walang katapusang kabuuan para sa Fourier series ng isang tuloy-tuloy na signal, ang spectrum nito ay maaaring walang limitasyon. Ayon sa teorama ni Kotelnikov, ang maximum na dalas ng isang harmonic ay dapat na tulad na ito ay nagkakahalaga ng hindi bababa sa dalawang sample, samakatuwid ang bilang ng mga harmonic ay katumbas ng kalahati ng bilang ng mga sample ng isang discrete signal. Iyon ay, kung mayroong N sample sa sample, kung gayon ang bilang ng mga harmonika sa spectrum ay magiging katumbas ng N/2.

Isaalang-alang natin ngayon ang discrete Fourier transform (DFT).

Paghahambing sa serye ng Fourier

Nakikita namin na nag-tutugma sila, maliban na ang oras sa DFT ay discrete sa kalikasan at ang bilang ng mga harmonika ay limitado ng N/2 - kalahati ng bilang ng mga sample.

Ang mga formula ng DFT ay isinusulat sa mga variable na walang sukat na integer k, s, kung saan ang k ay ang mga bilang ng mga sample ng signal, s ang mga bilang ng mga spectral na bahagi.
Ipinapakita ng value na s ang bilang ng kumpletong harmonic oscillations sa panahon ng T (tagal ng pagsukat ng signal). Ang discrete Fourier transform ay ginagamit upang mahanap ang mga amplitude at phase ng harmonics gamit ang isang numerical na paraan, i.e. "sa computer"

Pagbabalik sa mga resulta na nakuha sa simula. Tulad ng nabanggit sa itaas, kapag pinalawak ang isang non-periodic function (aming signal) sa isang Fourier series, ang resultang Fourier series ay aktwal na tumutugma sa isang periodic function na may period T (Fig. 12).

Fig. 12 Periodic function f(x) na may period T0, na may measurement period T>T0

Gaya ng makikita sa Fig. 12, ang function na f(x) ay periodic na may period T0. Gayunpaman, dahil sa katotohanan na ang tagal ng sample ng pagsukat na T ay hindi tumutugma sa panahon ng function na T0, ang function na nakuha bilang isang serye ng Fourier ay may discontinuity sa punto T. Bilang resulta, ang spectrum ng function na ito ay maglalaman isang malaking bilang ng mga high-frequency na harmonika. Kung ang tagal ng sample ng pagsukat na T ay nag-tutugma sa panahon ng function na T0, kung gayon ang spectrum na nakuha pagkatapos ng Fourier transform ay maglalaman lamang ng unang harmonic (sinusoid na may panahon na katumbas ng tagal ng sampling), dahil ang function na f(x) ay isang sinusoid.

Sa madaling salita, ang programa ng DFT ay "hindi alam" na ang aming signal ay isang "piraso ng isang sinusoid", ngunit sinusubukang kumatawan sa isang pana-panahong pag-andar sa anyo ng isang serye, na may isang discontinuity dahil sa hindi pagkakapare-pareho ng mga indibidwal na piraso ng ang sinusoid.

Bilang resulta, lumilitaw ang mga harmonika sa spectrum, na dapat magbuod ng hugis ng function, kasama ang discontinuity na ito.

Kaya, upang makuha ang "tamang" spectrum ng isang signal na ang kabuuan ng ilang mga sinusoid na may iba't ibang panahon, kinakailangan na ang panahon ng pagsukat ng signal ay naglalaman ng isang integer na bilang ng mga panahon ng bawat sinusoid. Sa pagsasagawa, ang kundisyong ito ay maaaring matugunan para sa isang sapat na mahabang tagal ng pagsukat ng signal.

Fig. 13 Halimbawa ng function at spectrum ng gearbox kinematic error signal

Sa mas maikling tagal, ang larawan ay magiging "mas masahol pa":

Fig. 14 Halimbawa ng function at spectrum ng isang rotor vibration signal

Sa pagsasagawa, maaaring mahirap maunawaan kung nasaan ang "mga tunay na bahagi" at nasaan ang "mga artifact" na dulot ng hindi maraming yugto ng mga bahagi at ang tagal ng pagsa-sample ng signal o "paglukso at pagkasira" sa hugis ng signal . Siyempre, ang mga salitang "tunay na sangkap" at "mga artifact" ay inilalagay sa mga panipi para sa isang dahilan. Ang pagkakaroon ng maraming harmonic sa spectrum graph ay hindi nangangahulugan na ang aming signal ay aktwal na "binubuo" ng mga ito. Ito ay kapareho ng pag-iisip na ang numero 7 ay "binubuo" ng mga numero 3 at 4. Ang numero 7 ay maaaring kinakatawan bilang ang kabuuan ng mga numero 3 at 4 - ito ay tama.

Kaya ang aming signal... o sa halip ay hindi kahit na ang "aming signal", ngunit ang isang periodic function na binubuo sa pamamagitan ng pag-uulit ng aming signal (sampling) ay maaaring katawanin bilang isang kabuuan ng harmonics (sine waves) na may ilang mga amplitude at phase. Ngunit sa maraming mga kaso na mahalaga para sa pagsasanay (tingnan ang mga figure sa itaas), posible talagang iugnay ang mga harmonika na nakuha sa spectrum sa tunay na proseso, na likas na paikot at gumagawa ng malaking kontribusyon sa hugis ng signal.

Ilang resulta

1. Ang isang tunay na sinusukat na signal na may tagal na T segundo, na na-digitize ng isang ADC, iyon ay, kinakatawan ng isang set ng mga discrete sample (N piraso), ay may discrete non-periodic spectrum, na kinakatawan ng isang set ng harmonics (N/ 2 piraso).

2. Ang signal ay kinakatawan ng isang hanay ng mga tunay na halaga at ang spectrum nito ay kinakatawan ng isang hanay ng mga tunay na halaga. Ang mga Harmonic frequency ay positibo. Ang katotohanan na mas maginhawa para sa mga mathematician na kumatawan sa spectrum sa kumplikadong anyo gamit ang mga negatibong frequency ay hindi nangangahulugan na "ito ay tama" at "ito ay dapat palaging gawin."

3. Ang isang signal na sinusukat sa isang agwat ng oras T ay tinutukoy lamang sa isang agwat ng oras T. Ano ang nangyari bago namin sinimulan ang pagsukat ng signal, at kung ano ang mangyayari pagkatapos noon, ay hindi alam ng agham. At sa aming kaso, hindi ito kawili-wili. Ang DFT ng isang signal na limitado sa oras ay nagbibigay ng "totoong" spectrum nito, sa kahulugan na, sa ilalim ng ilang mga kundisyon, pinapayagan nito ang isa na kalkulahin ang amplitude at dalas ng mga bahagi nito.

Mga materyales na ginamit at iba pang kapaki-pakinabang na materyales.

Nakikita namin sa itaas na ang pagpapalawak ng mga function sa serye ng kapangyarihan ay nagbibigay-daan sa amin upang makalkula ang tinatayang mga halaga ng mga function na ito na may kinakailangang katumpakan. Ngunit maraming mga pag-andar na hindi maaaring mapalawak sa serye ng kapangyarihan (serye ng Taylor o Maclaurin), dahil ang mga kinakailangan para sa mga pag-andar ay medyo mahigpit (ang pag-andar ay dapat na walang hanggan na pagkakaiba-iba, atbp.). Samakatuwid, ang iba pang mga uri ng functional series ay ginagamit din, ang mga kondisyon para sa agnas kung saan ay hindi gaanong mabigat. Kasama sa mga row na ito serye ng trigonometriko.

Kahulugan: Serye ng trigonometric functional na serye ng form:, (1)

kung saan may mga pare-parehong numero na tinatawag na:

Mga coefficient ng serye ng trigonometric.

Ang lahat ng miyembro ng series (1) ay functional non-periodic at may karaniwang minimum na panahon na 2p. Ito ay sumusunod: kung ang function na f(x) ay pinalawak sa isang trigonometric series (1), i.e. ito ang kabuuan ng seryeng ito, kung gayon ang function na ito mismo ay dapat na kabuuan ng serye (1) lamang sa isang tiyak na pagitan ng haba na 2p.

Ang mga pangunahing katangian ng trigonometriko serye ay sumusunod mula sa mga pangunahing katangian ng sistema ng trigonometriko function. Nakaisip ako ng isang kahulugan.

Kahulugan: Walang katapusang sistema ng mga function j1(x),j2(x),...,j3(x)... tinukoy sa isang segment ay tinatawag orthogonal sa segment na ito, kung ang mga sumusunod na kondisyon ay natutugunan:
para sa m¹n;

para sa anumang n.

Teorama: Ang sistema ng trigonometriko function ay orthogonal sa segment [-p,p].

Patunay: Kinakailangang suriin ang mga kondisyon 1) at 2) ng nakaraang kahulugan.

1) Isaalang-alang ang mga integral:

Ilapat natin ang mga trigonometric formula:

Malinaw, sa kanilang tulong, ang lahat ng mga nakaraang integral ay nabawasan sa mga integral ng form:
At

Kalkulahin natin ang mga ito.

;

Kaya, ang unang pangangailangan ng orthogonality ay matutugunan.

2)
;

at ang pangalawang pangangailangan ay natupad, atbp.

Trigonometric Fourier series.

Hayaang kinakatawan ang periodic function na f(x) na may period 2p bilang kabuuan ng isang trigonometric series
(1).

para sa lahat ng x mula sa ilang pagitan ng haba na 2p. Ngunit ang kabuuan ng seryeng S(x) ay isang periodic function na may panahon na 2p. Samakatuwid, ang mga halaga ng f(x) at S(x) ay nag-tutugma sa buong linya ng numero (-¥, +¥). Samakatuwid, sapat na upang pag-aralan ang pagkakapantay-pantay (1) sa ilang pagitan ng haba na 2p, kadalasan [-p,p] .

Kaya, hayaan ang f(x) ang kabuuan ng serye (1) sa [-p,p] at, bilang karagdagan, ipagpalagay na maaari itong isama ang termino sa pamamagitan ng termino samakatuwid sa pagitan. Ito, halimbawa, ay posible kung ang numerical na serye ng mga coefficient ng serye (1) ay ganap na nagtatagpo, i.e. nagtatagpo ang mga serye

(2).

Sa kasong ito, ang mga tuntunin ng functional series (1) sa absolute value ay hindi lalampas sa kaukulang termino ng series (2), na nagpapahiwatig ng pare-parehong convergence ng serye (1), at, samakatuwid, ang posibilidad ng hindi nito -term integration sa ibabaw ng [-p,p].

Ginagamit namin ito upang kalkulahin ang koepisyent a 0 . Isama natin ang magkabilang panig ng hindi pagkakapantay-pantay (1) sa loob ng [-p,p]:

Ang lahat ng integral sa kanan, ayon sa orthogonality property ng trigonometriko function, ay katumbas ng zero maliban sa una. kaya naman:
, saan
(3).

Upang kalkulahin ang isang k /k¹0/ pinaparami namin ang magkabilang panig ng (1) sa coskx. Ang resultang serye ay magkakaugnay din sa [-p,p], dahil ½coskx½£1 at maaari itong isama ang termino sa pamamagitan ng termino sa ibabaw ng [-p,p].

Sa pamamagitan ng parehong pag-aari ng orthogonality, lahat ng integral sa kanan ay katumbas ng zero maliban sa isa na naglalaman ng k.

Pagkatapos
. saan

(4).

Ang pagpaparami ng magkabilang panig ng (1) sa sin kx at pagsasama-sama ng nagresultang pagkakapantay-pantay sa pamamagitan ng , nakukuha natin
. saan

(5).

Ang mga coefficient na kinakalkula gamit ang mga formula (3)-(5) ay tinatawag

Fourier coefficients para sa function na f(x), at ang trigonometric series (1) na may mga coefficient na ito ay Fourier series ng function (x).

Dapat tandaan na hindi laging posible na pagsamahin ang serye (1) termino sa pamamagitan ng termino. Samakatuwid, ito ay pormal na posibleng kalkulahin ang Fourier coefficients at i-compile ang Fourier series (1), ngunit hindi ito magagarantiyahan na ang seryeng ito ay nagtatagpo sa lahat; at kung ito ay nagtatagpo, ang kabuuan nito ay isang function na f(x). Sa ganitong mga kaso, sa halip na pagkakapantay-pantay (1) kami ay sumang-ayon sa "sulat":

mga function. Ang pagbabagong ito ay may malaking halaga, dahil magagamit ito sa paglutas ng maraming praktikal na problema. Ang serye ng Fourier ay ginagamit hindi lamang ng mga mathematician, kundi pati na rin ng mga espesyalista sa iba pang mga agham.

Ang pagpapalawak ng mga function sa isang seryeng Fourier ay isang mathematical technique na maaaring maobserbahan sa kalikasan kung gagamit ka ng isang device na nakakaramdam ng sinusoidal function.

Ang prosesong ito nangyayari kapag ang isang tao ay nakarinig ng isang tunog. Ang tainga ng tao ay idinisenyo sa paraang madarama nito ang mga indibidwal na sinusoidal na pagbabagu-bago sa presyon ng hangin ng iba't ibang mga frequency, na, naman, ay nagpapahintulot sa isang tao na makilala ang pagsasalita at makinig sa musika.

Ang tainga ng tao ay hindi nakakakita ng tunog sa kabuuan, ngunit sa pamamagitan ng mga bahagi ng seryeng Fourier nito. Mga string instrumentong pangmusika gumagawa ng mga tunog na sinusoidal vibrations ng iba't ibang frequency. Ang katotohanan ng pagpapalawak ng liwanag ng serye ng Fourier ay kinakatawan ng isang bahaghari. Nakikita ng paningin ng tao ang liwanag sa pamamagitan ng ilan sa mga bahagi nito ng iba't ibang frequency ng electromagnetic oscillations.

Ang Fourier transform ay isang function na naglalarawan sa phase at amplitude ng sinusoids ng isang tiyak na frequency. Ang pagbabagong ito ay ginagamit upang malutas ang mga equation na naglalarawan ng mga dinamikong proseso na lumitaw sa ilalim ng impluwensya ng enerhiya. Ang serye ng Fourier ay malulutas ang problema ng pagtukoy ng mga pare-parehong bahagi sa kumplikadong mga oscillatory signal, na naging posible upang wastong bigyang-kahulugan ang data na nakuha mula sa mga eksperimento, mga obserbasyon sa medisina, kimika at astronomiya.

Ang pagtuklas ng pagbabagong ito ay pag-aari ng Pranses na matematiko na si Jean Baptiste Joseph Fourier. Sa karangalan kung kanino pinangalanan ang seryeng Fourier. Sa una, natagpuan ng siyentipiko ang aplikasyon ng kanyang pamamaraan sa pag-aaral at pagpapaliwanag ng mga mekanismo ng thermal conductivity. Iminungkahi na ang paunang hindi regular na pamamahagi ng init ay maaaring katawanin sa anyo ng mga simpleng sinusoid. Para sa bawat isa kung saan matutukoy ang minimum, maximum at phase ng temperatura. Ang function na naglalarawan sa upper at lower peak ng curve, ang phase ng bawat harmonic ay tinatawag na Fourier transform mula sa expression ng temperature distribution. Ang may-akda ng pagbabago ay nagmungkahi ng isang paraan ng agnas kumplikadong pag-andar bilang isang kabuuan ng mga periodic function na cosine, sine.

Layunin gawaing kurso ay ang pag-aaral ng seryeng Fourier at ang kaugnayan ng praktikal na aplikasyon ng pagbabagong ito.

Upang makamit ang layuning ito, ang mga sumusunod na gawain ay binuo:

1) ibigay ang konsepto ng isang trigonometric Fourier series;

2) tukuyin ang mga kondisyon para sa pagkabulok ng isang function sa isang serye ng Fourier;

3) isaalang-alang ang pagpapalawak ng serye ng Fourier ng pantay at kakaibang mga function;

4) isaalang-alang ang pagpapalawak ng serye ng Fourier ng isang non-periodic function;

5) ihayag ang praktikal na aplikasyon ng seryeng Fourier.

Layunin ng pag-aaral: pagpapalawak ng mga function sa serye ng Fourier.

Paksa ng pag-aaral: Fourier series.

Mga pamamaraan ng pananaliksik: pagsusuri, synthesis, paghahambing, pamamaraan ng axiomatic.

1.5. Fourier series para sa even at odd na function

Isaalang-alang ang simetriko integral

kung saan ay tuloy-tuloy o piecewise tuloy-tuloy sa. Gumawa tayo ng pagbabago sa unang integral. Naniniwala kami. Pagkatapos

Samakatuwid, kung pantay ang function, kung gayon (i.e. ang graph ng even function ay simetriko tungkol sa at axis

Kung ay isang kakaibang function, kung gayon (ibig sabihin, ang graph ng isang kakaibang function ay simetriko tungkol sa pinagmulan) at

Yung. ang simetriko integral ng kahit na function ay katumbas ng dalawang beses ang integral sa kalahati ng integration interval, at ang simetriko integral ng isang kakaibang function ay katumbas ng zero.

Pansinin ang sumusunod na dalawang katangian ng even at odd na function:

1) ang produkto ng isang even function at isang kakaiba ay isang kakaibang function;

2) ang produkto ng dalawang even (odd) function ay isang even function.

Hayaan ang isang pantay na function na tinukoy at napapalawak sa segment na ito sa isang trigonometric Fourier series. Gamit ang mga resultang nakuha sa itaas, nalaman namin na ang mga coefficient ng seryeng ito ay magkakaroon ng anyo:

Kung ang isang kakaibang function ay tinukoy sa isang segment at lumalawak sa segment na ito sa isang trigonometric Fourier series, ang mga coefficient ng seryeng ito ay magkakaroon ng form:

Dahil dito, magkakaroon ng anyo ang trigonometric Fourier series sa segment

para sa pantay na function:

(16)

para sa kakaibang function:

Ang serye (16) ay hindi naglalaman ng mga sine ng maraming anggulo, iyon ay, ang Fourier series ng isang even function ay kinabibilangan lamang ng even functions at isang independent term. Ang serye (17) ay hindi naglalaman ng mga cosine ng maraming anggulo, iyon ay, ang Fourier series ng isang kakaibang function ay kinabibilangan lamang ng mga kakaibang function.

Kahulugan. Mga hilera
ay mga bahagi buong saklaw Fourier at tinatawag na hindi kumpletotrigonometric Fourier series.

Kung ang isang function ay pinalawak sa isang hindi kumpletong serye ng trigonometriko (16) (o (17)), kung gayon ito ay sinasabinglumalawak sa isang trigonometric Fourier series sa mga cosine (o sines).

1.6. Fourier series na pagpapalawak ng isang non-periodic function

1.6.1. Fourier serye pagpapalawak ng mga function sa

Hayaang maibigay ang isang function sa isang pagitan at matugunan ang mga kondisyon ng Dirichlet theorem sa pagitan na ito. Magsagawa tayo ng variable na pagbabago. Hayaan kung saan namin pipiliin upang ang resultang function ng argument ay tinukoy sa. Samakatuwid, naniniwala kami na

Ang resultang function ay maaaring mapalawak sa isang serye ng Fourier:

saan

Gumawa tayo ng reverse replacement⇒ Nakukuha namin

saan

(19)

Serye (18) – Fourier series sa pangunahing trigonometric system ng mga function

Kaya, nalaman namin na kung ang isang function ay ibinigay sa isang pagitan at natutugunan ang mga kondisyon ng Dirichlet theorem sa pagitan na ito, kung gayon maaari itong palawakin sa isang trigonometric Fourier series (18) ayon sa trigonometric system of functions (20).

Ang trigonometric Fourier series para sa pantay na function na tinukoy sa ay magkakaroon ng form

saan

para sa kakaibang function

saan

Magkomento! Sa ilang mga problema, kinakailangan na palawakin ang isang function sa isang trigonometric Fourier series ayon sa sistema ng mga function (20) hindi sa isang segment, ngunit sa isang segment. Sa kasong ito, kailangan mo lamang baguhin ang mga limitasyon ng pagsasama sa mga formula (19) ((15), kung, iyon ay, sa kasong ito

(23)

o kung

(24)

Ang kabuuan ng isang trigonometric Fourier series ay isang periodic function na may period, na isang periodic continuation ibinigay na function. At para sa isang pana-panahong paggana ang pagkakapantay-pantay (4) ay totoo.

1.6.2. Fourier serye pagpapalawak ng mga function sa

Hayaang maibigay ang function at matugunan ang mga kondisyon ng Dirichlet theorem sa pagitan na ito. Ang ganitong function ay maaari ding palawakin sa isang seryeng Fourier. Upang gawin ito, ang function ay dapat na pahabain sa pagitan at ang resultang function ay pinalawak sa isang seryeng Fourier sa pagitan. Sa kasong ito, ang resultang serye ay dapat isaalang-alang lamang sa segment kung saan tinukoy ang function. Para sa kaginhawaan ng mga kalkulasyon, tutukuyin namin ang function sa isang pantay at kakaibang paraan.

1) Palawakin natin ang function sa pagitan sa isang pantay na paraan, iyon ay, gagawa tayo ng bago kahit function, coinciding sa segment na may function. Dahil dito, ang graph ng function na ito ay simetriko tungkol sa axis at tumutugma sa graph sa segment. Gamit ang mga formula (21), hahanapin natin ang mga coefficient ng seryeng Fourier para sa function at isulat ang mismong serye ng Fourier. Ang kabuuan ng seryeng Fourier para sa ay isang periodic function, na may period. Ito ay magkakasabay sa paggana sa lahat ng punto ng pagpapatuloy.

2) Palawakin natin ang function sa pagitan sa kakaibang paraan, ibig sabihin, gagawa tayo ng bago kakaibang function, kasabay ng function. Ang graph ng naturang function ay simetriko tungkol sa pinagmulan ng mga coordinate at tumutugma sa graph sa segment. Gamit ang mga formula (22), hahanapin natin ang mga coefficient ng seryeng Fourier para sa function at isulat ang seryeng Fourier mismo. Ang kabuuan ng seryeng Fourier para sa ay isang periodic function na may period. Ito ay magkakasabay sa paggana sa lahat ng punto ng pagpapatuloy.

Mga Tala!

1) Katulad nito, maaari mong palawakin ang isang function na tinukoy sa pagitan sa isang serye ng Fourier

2) Dahil ipinapalagay ng pagpapalawak ng isang function sa isang segment ang pagpapatuloy nito sa segment sa isang arbitrary na paraan, ang Fourier series para sa function ay hindi magiging kakaiba.

1.6.3. Fourier serye pagpapalawak ng mga function sa

Hayaang ibigay ang function sa isang arbitrary na bahagi ng haba at matugunan ang mga kondisyon ng Dirichlet theorem dito.

Pagkatapos ang function na ito ay maaaring palawakin sa isang seryeng Fourier. Upang gawin ito, ang function ay dapat na pana-panahon (na may isang tuldok) na ipagpatuloy sa buong linya ng numero at ang resultang function ay dapat na palawakin sa isang seryeng Fourier, na dapat isaalang-alang lamang sa segment. Dahil sa ari-arian (3) ng mga pana-panahong pag-andar, mayroon tayo

Samakatuwid, ang Fourier coefficients para sa nagresultang pagpapatuloy ng function ay matatagpuan gamit ang mga formula

(25)

2. Praktikal na Aplikasyon Fourier serye

2.1. Mga problemang kinasasangkutan ng pagpapalawak ng mga function sa serye ng Fourier at ang kanilang solusyon

Kinakailangang palawakin sa isang trigonometric Fourier series ang isang function na isang pana-panahong pagpapatuloy ng isang function na ibinigay sa isang interval. Upang gawin ito, kinakailangan na gumamit ng isang algorithm para sa pagpapalawak ng isang periodic function sa isang serye ng Fourier.

Algorithm para sa pagpapalawak ng periodic function sa isang Fourier series:

1) Bumuo ng isang graph ng isang ibinigay na function at ang pana-panahong pagpapatuloy nito;

2) Itakda ang panahon ng ibinigay na function;

3) Tukuyin kung ang function ay even, odd o pangkalahatang pananaw;

4) Suriin ang pagiging posible ng mga kondisyon ng Dirichlet theorem;

5) Lumikha ng isang pormal na representasyon ng seryeng Fourier na nabuo ng function na ito;

6) Kalkulahin ang Fourier coefficients;

7) Isulat ang seryeng Fourier para sa isang naibigay na function, gamit ang mga coefficient ng seryeng Fourier (item 4).

Halimbawa 1. Palawakin ang function sa isang seryeng Fourier sa pagitan.

Solusyon:

1) Bumuo tayo ng isang graph ng ibinigay na function at ang pana-panahong pagpapatuloy nito.

2) Panahon ng pagpapalawak ng function.

3) Ang pag-andar ay kakaiba.

4) Ang function ay tuloy-tuloy at monotoniko, i.e. natutugunan ng function ang mga kondisyon ng Dirichlet.

5) Kalkulahin natin ang mga coefficient ng seryeng Fourier.

6) Isulat ang Fourier series sa pamamagitan ng pagpapalit ng Fourier coefficients sa formula

Sagot:

Halimbawa 2. Palawakin natin ang isang function na may arbitrary na panahon sa isang seryeng Fourier.

Solusyon: ang function ay tinukoy sa kalahating pagitan (-3;3]. Panahon ng pagpapalawak ng function, kalahating panahon. Palawakin natin ang function sa isang seryeng Fourier

Sa pinanggalingan, ang function ay hindi nagpapatuloy, kaya kakatawanin namin ang bawat Fourier coefficient bilang isang kabuuan ng dalawang integral.

Isulat natin ang seryeng Fourier sa pamamagitan ng pagpapalit ng mga natagpuang coefficient ng seryeng Fourier sa formula.

Halimbawa 3. Palawakin ang isang functionsa pagitansa seryeng Fourier sa mga cosine. Bumuo ng isang graph ng kabuuan ng serye.

Solusyon: pinapalawak namin ang function sa pagitan sa isang pantay na paraan, iyon ay, bumuo kami ng bagong even function na tumutugma sa function sa interval. Hanapin natin ang mga coefficient ng seryeng Fourier para sa function at isulat ang seryeng Fourier. Ang kabuuan ng seryeng Fourier para sa ay isang periodic function, na may period. Ito ay magkakasabay sa paggana sa lahat ng punto ng pagpapatuloy.

Ang trigonometric Fourier series para sa function ay magkakaroon ng form

Hanapin natin ang mga coefficient ng seryeng Fourier

Kaya, kapag natagpuan ang mga coefficient, maaari nating isulat ang seryeng Fourier

I-plot natin ang kabuuan ng serye

Halimbawa 4. Ibinigay ang isang function na tinukoy sa segment . Alamin kung ang function ay maaaring palawakin sa isang seryeng Fourier. Isulat ang pagpapalawak ng function sa isang seryeng Fourier.

Solusyon:

1) bumuo ng isang graph ng function sa .

2) ang function ay tuloy-tuloy at monotoniko sa , iyon ay, ayon sa Dirichlet's theorem, maaari itong palawakin sa isang trigonometric Fourier series.

3) kalkulahin ang Fourier coefficients gamit ang mga formula (1.19).

4) isulat ang seryeng Fourier gamit ang mga nakitang coefficient.

2.2. Mga halimbawa ng aplikasyon ng serye ng Fourier sa iba't ibang larangan ng aktibidad ng tao

Ang matematika ay isa sa mga agham na mayroon malawak na aplikasyon sa pagsasanay. Ang anumang proseso ng produksyon at teknolohikal ay batay sa mga batas sa matematika. Aplikasyon iba't ibang instrumento Ang mathematical apparatus ay nagpapahintulot sa iyo na magdisenyo ng mga device at mga automated na unit na may kakayahang magsagawa ng mga operasyon, kumplikadong mga kalkulasyon at mga kalkulasyon sa disenyo ng mga gusali at istruktura.

Fourier series ay ginagamit ng mga mathematician sa geometry kapagpaglutas ng mga problema sa spherical geometry; sa mathematic physics sapaglutas ng mga problema sa maliliit na vibrations ng elastic media. Ngunit bukod sa matematika, natagpuan ng serye ng Fourier ang kanilang aplikasyon sa iba pang larangan ng agham.

Araw-araw ginagamit ng mga tao iba't ibang mga aparato. At kadalasan ang mga device na ito ay hindi gumagana ng maayos. Halimbawa, ang tunog ay mahirap marinig dahil sa maraming ingay, o ang imahe na natanggap sa pamamagitan ng fax ay hindi malinaw. Ang isang tao ay maaaring matukoy ang sanhi ng isang malfunction sa pamamagitan ng tunog. Maaari ding masuri ng computer kung nasira ang device. Maaaring alisin ang sobrang ingay gamit ang computer signal processing. Ang signal ay kinakatawan bilang isang pagkakasunud-sunod ng mga digital na halaga, na pagkatapos ay ipinasok sa computer. Nang matapos ilang mga kalkulasyon, makuha ang mga coefficient ng seryeng Fourier.

Ang pagpapalit ng signal spectrum ay nagbibigay-daan sa iyo na i-clear ang pag-record ng ingay, mabayaran ang pagbaluktot ng signal ng iba't ibang recording device, baguhin ang mga timbre ng mga instrumento, at ituon ang atensyon ng mga tagapakinig sa mga indibidwal na bahagi.

Sa digital image processing, ang paggamit ng Fourier series ay nagbibigay-daan para sa mga sumusunod na effect: blurring, emphasizing edges, image restoration, artistic effects (embossing)

Ang pagpapalawak ng serye ng Fourier ay ginagamit sa arkitektura sa pag-aaral ng mga proseso ng oscillatory. Halimbawa, kapag gumagawa ng isang proyekto iba't ibang uri kinakalkula ng mga istruktura ang lakas, katigasan at katatagan ng mga elemento ng istruktura.

Sa gamot, upang magsagawa ng medikal na pagsusuri sa tulong ng mga cardiograms at isang ultrasound machine, ginagamit ang isang mathematical apparatus, na batay sa teorya ng serye ng Fourier.

Ang malalaking problema sa computational ng pagtatasa ng mga istatistikal na katangian ng mga signal at pag-filter ng ingay ay lumitaw kapag nagre-record at nagpoproseso ng tuluy-tuloy na data sa ilalim ng dagat. Kapag gumagawa ng mga sukat at nire-record ang mga ito, ang mga holographic na pamamaraan gamit ang serye ng Fourier ay nangangako. Iyon ay, ang serye ng Fourier ay ginagamit din sa isang agham gaya ng oceanology.

Ang mga elemento ng matematika ay matatagpuan sa produksyon sa halos bawat hakbang, kaya mahalaga para sa mga espesyalista na malaman at maging mahusay na nakatuon sa larangan ng aplikasyon ng ilang mga tool sa pagsusuri at pagkalkula.

Konklusyon

Ang paksa ng gawaing kurso ay nakatuon sa pag-aaral ng serye ng Fourier. Ang isang arbitrary na function ay maaaring palawakin sa mas simple, iyon ay, maaari itong palawakin sa isang serye ng Fourier. Ang saklaw ng gawaing kurso ay hindi nagpapahintulot sa amin na ihayag nang detalyado ang lahat ng aspeto ng serye ng pagpapalawak ng isang function. Gayunpaman, mula sa mga gawaing ginawa, tila posible na ipakita ang pangunahing teorya tungkol sa serye ng Fourier.

Ang gawaing kurso ay nagpapakita ng konsepto ng isang trigonometric Fourier series. Ang mga kundisyon para sa pagkabulok ng isang function sa isang seryeng Fourier ay tinutukoy. Isinasaalang-alang ang mga pagpapalawak ng serye ng Fourier ng pantay at kakaibang mga function; mga di-pana-panahong pag-andar.

Ang ikalawang kabanata ay nagbibigay lamang ng ilang mga halimbawa ng pagpapalawak ng mga function na ibinigay sa iba't ibang mga pagitan sa Fourier series. Inilalarawan ang mga lugar ng agham kung saan ginagamit ang pagbabagong ito.

Mayroon ding isang kumplikadong anyo ng representasyon ng seryeng Fourier, na hindi maaaring isaalang-alang dahil ang dami ng gawaing kurso ay hindi pinapayagan. Komplikadong anyo ang serye ay algebraically simple. Samakatuwid, madalas itong ginagamit sa pisika at inilapat na mga kalkulasyon.

Ang kahalagahan ng paksa ng gawaing kurso ay dahil sa ang katunayan na ito ay malawakang ginagamit hindi lamang sa matematika, ngunit sa iba pang mga agham: pisika, mekanika, medisina, kimika at marami pang iba.

Mga sanggunian

1. Bari, N.K. Serye ng trigonometric. [text]/ N.K. Bari. - Moscow, 1961. - 936 s.

2. Bermant, A.F. Maikling kurso pagsusuri sa matematika: aklat-aralin para sa mga unibersidad[text]/ A.F. Bermant, I.G. Aramanovic. – 11th ed., nabura. – St. Petersburg: Publishing House “Lan”, 2005. – 736 p.

3. Bugrov, Ya. S. Higher mathematics: Textbook para sa mga unibersidad: Sa 3 volume.[text]/ Ya. S. Bugrov, S. M. Nikolsky; Ed. V. A. Sadovnichy. - Ika-6 na ed., stereotype. - M.: Bustard, 2004. -512 p.

4. Vinogradova, I. A. Mga problema at pagsasanay sa pagsusuri sa matematika: isang manwal para sa mga unibersidad, pedagogical. unibersidad: Sa 2 o'clock.[text]/ I. A. Vinogradova, S. N. Olehnik, V. A. Sadovnichy; inedit ni V.A. Sadovnichigo. – 3rd ed., rev. – M.: Bustard, 2001. – 712 p.

5. Gusak, A.A. Mas mataas na matematika. Sa 2 tomo T. 2. Teksbuk para sa mga mag-aaral sa unibersidad.[text]/ A. A. Gusak.– ika-5 ed. – Minsk: TetraSystems, 2004.

6. Danko, P.E. Mas mataas na matematika sa mga pagsasanay at problema: aklat-aralin para sa mga unibersidad: 2 oras.[text]/ P.E. Danko, A.G. Popov, T.Ya. Kozhevnikova. Moscow: ONIX: Kapayapaan at Edukasyon, 2003. – 306 p.

7. Lukin, A. Panimula sa digital processing signal (mathematical foundations) [text]/ A. Lukin. - M., 2007. - 54 p.

8. Piskunov, N. S. Differential at integral calculus para sa mga mag-aaral sa kolehiyo, vol. Tutorial para sa mga kolehiyo at unibersidad.[text]/ N. S. Piskunov. - Ika-13 na ed. - M.: Nauka, 1985. - 432 p.

9. Rudin, U. Fundamentals of mathematical analysis.[text]/ U. Rudin. - 2nd ed., Trans. mula sa Ingles .- M.: Mir, 1976 .- 206 p.

10. Fikhtengolts, G. M. Mga Batayan ng pagsusuri sa matematika. Bahagi 2.[text]/ G. M. Fikhtengolts. -6th ed., nabura. - St. Petersburg: Lan Publishing House, 2005. – 464 p.

Orenburg, 2015

Ang posibilidad ng pagtatantya ng serye ng Fourier sa kaso ng isang linear na signal ay maaaring kailanganin para sa pagbuo ng mga function sa kaso ng mga hindi tuloy-tuloy na signal. pana-panahong elemento. Posibilidad ng paggamit ang pamamaraang ito upang bumuo at mabulok ang mga ito gamit mga huling halaga Fourier series na ginagamit sa paglutas ng maraming problema ng iba't ibang agham, tulad ng physics, seismology, at iba pa. Ang mga proseso ng pagtaas ng tubig sa karagatan at aktibidad ng solar ay isinasaalang-alang ng paraan ng agnas ng mga proseso ng oscillatory at ang mga pag-andar na inilarawan ng mga pagbabagong ito. Sa pag-unlad teknolohiya ng kompyuter Ang serye ng Fourier ay nagsimulang magamit para sa higit pa at higit pa kumplikadong mga gawain, at salamat din dito, naging posible na gamitin ang mga pagbabagong ito sa mga hindi direktang agham, tulad ng medisina at kimika. Ang Fourier transform ay inilarawan sa parehong tunay at kumplikadong anyo, ang pangalawang pamamahagi ay naging posible upang makagawa ng isang pambihirang tagumpay sa pananaliksik kalawakan. Ang resulta ng gawaing ito ay ang aplikasyon ng serye ng Fourier sa linearization hindi tuloy-tuloy na pag-andar at pagpili ng bilang ng mga coefficient ng serye para sa mas tumpak na pagpapataw ng serye sa function. Bukod dito, kapag ginagamit ang pagpapalawak ng serye ng Fourier, function na ito huminto sa pagiging hindi nagpapatuloy at nasa sapat na maliit na halaga, ang isang mahusay na pagtatantya ng function na ginamit ay nakakamit.

Fourier serye

Fourier na pagbabago

phase spectrum.

1. Alasheyeva E.A., Rogova N.V. Numerical na paraan para sa paglutas ng problema ng electrodynamics sa thin-wire approximation. Agham at kapayapaan. Internasyonal siyentipikong journal, No. 8(12), 2014. Tomo 1. Volgograd. P.17-19.

2. Vorobyov N.N. Teorya ng serye. Ed. Agham, Pangunahing tanggapan ng editoryal ng pisikal at matematikal na panitikan, M., 1979, -408 S.

3. Kalinina V.N., Pankin V.F. Mga istatistika ng matematika. - M.: graduate School, 2001.

4. R. Edwards Fourier serye sa modernong pagtatanghal. Ed. mundo. Sa 2 volume. Tomo 1. 1985. 362 pp.

5. Sigorsky V.P. Mathematical apparatus ng engineer. Ed. 2nd stereotypical. "Technique", 1997. – 768 p.

Ang representasyon ng isang arbitrary na function na may isang tiyak na panahon sa anyo ng isang serye ay tinatawag na isang seryeng Fourier. Ang isang pagpapalawak sa isang orthogonal na batayan ay tinatawag desisyong ito sa pangkalahatang tuntunin. Ang pagpapalawak ng mga function ng serye ng Fourier ay isang medyo makapangyarihang tool para sa paglutas ng iba't ibang mga problema. kasi Ang mga katangian ng pagbabagong ito sa panahon ng integrasyon, pagkakaiba-iba, pati na rin ang paglilipat ng ekspresyon sa pamamagitan ng argumento at convolution ay kilala at pinag-aralan. Isang taong hindi pamilyar mas mataas na matematika, pati na rin sa mga gawa ng Pranses na siyentipiko na si Fourier, malamang na hindi mauunawaan kung ano ang mga "serye" na ito at kung ano ang kailangan nito. Ang pagbabagong ito ng Fourier ay naging napakahalaga sa ating buhay. Ginagamit ito hindi lamang ng mga mathematician, kundi pati na rin ng mga physicist, chemist, doktor, astronomer, seismologist, oceanographer at marami pang iba.

Ang Fourier series ay ginagamit upang malutas ang maraming inilapat na problema. Ang pagbabagong Fourier ay maaaring isagawa gamit ang analytical, numerical at iba pang mga pamamaraan. Mga proseso tulad ng pagtaas ng tubig sa karagatan at liwanag na alon sa mga cycle ng solar activity ay tumutukoy sa numerical na paraan ng pag-decomposing ng anumang oscillatory na proseso sa isang Fourier series. Gamit ang mga mathematical technique na ito, maaari mong pag-aralan ang mga function, na kumakatawan sa anumang oscillatory na proseso bilang isang serye ng mga sinusoidal na bahagi na lumilipat mula sa minimum hanggang sa maximum at pabalik. Ang Fourier transform ay isang function na naglalarawan sa phase at amplitude ng sinusoids na tumutugma sa isang tiyak na frequency. Ang pagbabagong ito ay ginagamit upang malutas ang napaka kumplikadong mga equation, na naglalarawan ng mga dynamic na proseso na nagmumula sa ilalim ng impluwensya ng thermal, liwanag o enerhiyang elektrikal. Gayundin, ginagawang posible ng serye ng Fourier na ihiwalay ang mga pare-parehong bahagi sa mga kumplikadong oscillatory signal, na ginagawang posible na wastong bigyang-kahulugan ang mga eksperimentong obserbasyon na nakuha sa medisina, kimika at astronomiya.

Sa paglago ng teknolohiya, i.e. ang pagdating at pag-unlad ng computer ay nagdala sa Fourier transform sa bagong antas. Ang diskarteng ito matatag na itinatag sa halos lahat ng larangan ng agham at teknolohiya. Ang isang halimbawa ay digital audio at video. Na naging malinaw na pagsasakatuparan ng paglago prosesong pang-agham at mga aplikasyon ng serye ng Fourier. Kaya, ang seryeng Fourier sa isang kumplikadong anyo ay naging posible upang makagawa ng isang pambihirang tagumpay sa pag-aaral ng kalawakan. Bilang karagdagan, naimpluwensyahan nito ang pag-aaral ng pisika mga materyales ng semiconductor at plasma, microwave acoustics, oceanography, radar, seismology.

Isaalang-alang ang phase spectrum ng isang periodic signal na tinutukoy mula sa sumusunod na expression:

kung saan ang mga simbolo at ayon sa pagkakabanggit ay tumutukoy sa mga haka-haka at tunay na bahagi ng dami na nakapaloob sa mga square bracket.

Kung pinarami ng isang tunay na pare-parehong halaga K, ang pagpapalawak ng serye ng Fourier ay may sumusunod na anyo:

Mula sa expression (1) sumusunod na ang phase Fourier spectrum ay may mga sumusunod na katangian:

1) ay isang function ng , ibig sabihin, sa kaibahan sa power spectrum, na hindi nakadepende sa , nagbabago ito habang lumilipat ang signal sa axis ng oras;

2) ay hindi nakasalalay sa K, iyon ay, ito ay invariant sa signal amplification o attenuation, habang ang power spectrum ay isang function ng K.

3) ibig sabihin, ito ay isang kakaibang tungkulin ng n.

Tandaan. Isinasaalang-alang ang geometric na interpretasyon ng mga pagsasaalang-alang sa itaas, maaari itong ipahayag sa mga tuntunin ng spectrum ng kapangyarihan at phase spectrum tulad ng sumusunod:

Since

pagkatapos ay mula sa (2) at (3) ito ay sumusunod na ito ay maaaring reconstructed unambiguously kung ang amplitude (o kapangyarihan spectrum) at phase spectra ay kilala.

Tingnan natin ang isang halimbawa. Binigyan kami ng function sa pagitan

Pangkalahatang view ng seryeng Fourier:

Palitan natin ang ating mga halaga at makuha natin:

Palitan natin ang ating mga halaga at makuha.

mga function. Napakahalaga ng pagbabagong ito dahil magagamit ito sa paglutas ng maraming praktikal na problema. Ang serye ng Fourier ay ginagamit hindi lamang ng mga mathematician, kundi pati na rin ng mga espesyalista sa iba pang mga agham.

Ang pagpapalawak ng mga function sa isang seryeng Fourier ay isang mathematical technique na maaaring maobserbahan sa kalikasan kung gagamit ka ng isang device na nakakaramdam ng sinusoidal function.

Ang prosesong ito ay nangyayari kapag ang isang tao ay nakarinig ng isang tunog. Ang tainga ng tao ay idinisenyo sa paraang madarama nito ang mga indibidwal na sinusoidal na pagbabagu-bago sa presyon ng hangin ng iba't ibang mga frequency, na, naman, ay nagpapahintulot sa isang tao na makilala ang pagsasalita at makinig sa musika.

Ang tainga ng tao ay hindi nakakakita ng tunog sa kabuuan, ngunit sa pamamagitan ng mga bahagi ng seryeng Fourier nito. Ang mga string ng isang instrumentong pangmusika ay gumagawa ng mga tunog na sinusoidal vibrations ng iba't ibang mga frequency. Ang katotohanan ng pagpapalawak ng liwanag ng serye ng Fourier ay kinakatawan ng isang bahaghari. Nakikita ng paningin ng tao ang liwanag sa pamamagitan ng ilan sa mga bahagi nito ng iba't ibang frequency ng electromagnetic oscillations.

Ang pagtuklas ng pagbabagong ito ay pag-aari ng Pranses na matematiko na si Jean Baptiste Joseph Fourier. Sa karangalan kung kanino pinangalanan ang seryeng Fourier. Sa una, natagpuan ng siyentipiko ang aplikasyon ng kanyang pamamaraan sa pag-aaral at pagpapaliwanag ng mga mekanismo ng thermal conductivity. Iminungkahi na ang paunang hindi regular na pamamahagi ng init ay maaaring katawanin sa anyo ng mga simpleng sinusoid. Para sa bawat isa kung saan matutukoy ang minimum, maximum at phase ng temperatura. Ang function na naglalarawan sa upper at lower peak ng curve, ang phase ng bawat harmonic ay tinatawag na Fourier transform mula sa expression ng temperature distribution. Ang may-akda ng pagbabagong-anyo ay iminungkahi ng isang paraan para sa decomposing isang kumplikadong function bilang isang kabuuan ng periodic function cosine, sine.

Ang layunin ng gawaing kurso ay pag-aralan ang serye ng Fourier at ang kaugnayan ng praktikal na aplikasyon ng pagbabagong ito.