Aling function ang tinatawag na even at odd. Function study

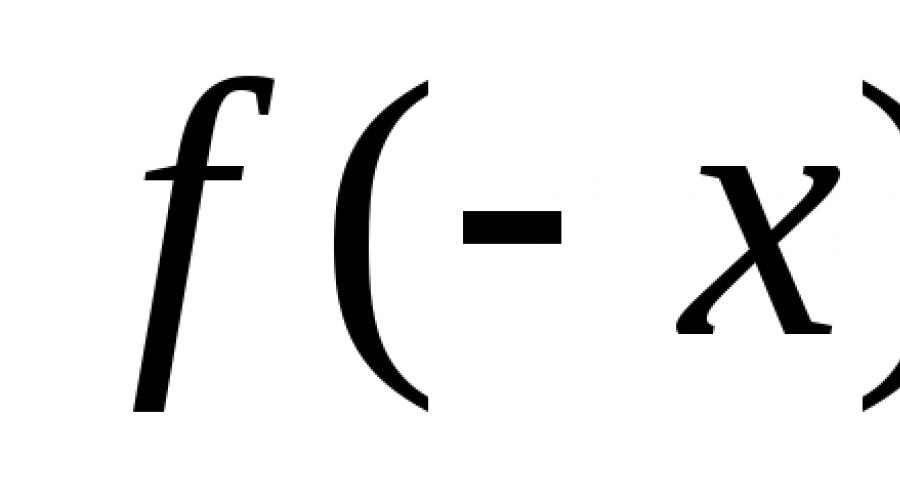
Ang pagiging even at oddness ng isang function ay isa sa mga pangunahing katangian nito, at ang parity ay tumatagal ng isang kahanga-hangang bahagi kurso sa paaralan sa matematika. Ito ay higit na tinutukoy ang pag-uugali ng function at lubos na pinapadali ang pagbuo ng kaukulang graph.

Tukuyin natin ang parity ng function. Sa pangkalahatan, ang pag-andar sa ilalim ng pag-aaral ay isinasaalang-alang kahit na para sa magkasalungat na mga halaga ng independiyenteng variable (x) na matatagpuan sa domain ng kahulugan nito, ang kaukulang mga halaga ng y (function) ay naging pantay.

Bigyan natin ng mas mahigpit na kahulugan. Isaalang-alang ang ilang function na f (x), na tinukoy sa domain na D. Ito ay magiging kahit na para sa anumang puntong x na matatagpuan sa domain ng kahulugan:

• -x (kabaligtaran) ay nasa saklaw din na ito,

• f(-x) = f(x).

Mula sa kahulugan sa itaas ay sumusunod sa kondisyong kinakailangan para sa domain ng kahulugan ng naturang function, ibig sabihin, symmetry na may paggalang sa punto O, na kung saan ay ang pinagmulan ng mga coordinate, dahil kung ang ilang punto b ay nakapaloob sa domain ng kahulugan ng isang even function, kung gayon ang kaukulang punto b ay nasa domain na ito. Mula sa itaas, samakatuwid, ang sumusunod na konklusyon ay sumusunod: kahit function ay may simetriko na anyo na may paggalang sa ordinate axis (Oy).

Paano matukoy ang parity ng isang function sa pagsasanay?

Hayaang tukuyin ito gamit ang formula h(x)=11^x+11^(-x). Kasunod ng algorithm na direktang sumusunod sa kahulugan, sinusuri muna namin ang domain ng kahulugan nito. Malinaw, ito ay tinukoy para sa lahat ng mga halaga ng argumento, iyon ay, ang unang kondisyon ay nasiyahan.

Ang susunod na hakbang ay upang palitan ang kabaligtaran na halaga (-x) para sa argumento (x).
Nakukuha namin:
h(-x) = 11^(-x) + 11^x.
Dahil ang karagdagan ay nakakatugon sa commutative (commutative) na batas, malinaw na h(-x) = h(x) at ang ibinigay na functional dependence- kahit.

Suriin natin ang parity ng function na h(x)=11^x-11^(-x). Kasunod ng parehong algorithm, nakukuha natin na h(-x) = 11^(-x) -11^x. Ang pagkuha ng minus, sa dulo mayroon kami
h(-x)=-(11^x-11^(-x))=- h(x). Samakatuwid, ang h(x) ay kakaiba.

Sa pamamagitan ng paraan, dapat itong alalahanin na may mga pag-andar na hindi maiuri ayon sa mga pamantayang ito ay tinatawag na hindi kahit na o kakaiba.

Kahit na ang mga pag-andar ay may ilang mga kagiliw-giliw na katangian:

• bilang resulta ng pagdaragdag ng mga katulad na function, nakakakuha sila ng kahit isa;
• bilang isang resulta ng pagbabawas ng naturang mga function, ang isang kahit na isa ay nakuha;
• kahit, gayundin kahit;
• bilang isang resulta ng pagpaparami ng dalawang ganoong mga pag-andar, ang isang kahit isa ay nakuha;
• bilang isang resulta ng pagpaparami ng kakaiba at kahit na mga pag-andar, isang kakaiba ang nakuha;
• bilang isang resulta ng paghahati ng kakaiba at kahit na mga pag-andar, isang kakaiba ang nakuha;
• ang derivative ng naturang function ay kakaiba;
• Kung i-square mo ang isang kakaibang function, makakakuha ka ng even one.

Ang parity ng isang function ay maaaring gamitin upang malutas ang mga equation.

Upang malutas ang isang equation tulad ng g(x) = 0, kung saan kaliwang bahagi Ang equation ay isang pantay na pag-andar, ito ay sapat na upang mahanap ang mga solusyon nito para sa mga di-negatibong halaga ng variable. Ang mga resultang ugat ng equation ay dapat isama sa kabaligtaran na mga numero. Isa sa mga ito ay napapailalim sa pag-verify.

Matagumpay din itong ginagamit upang malutas mga hindi karaniwang gawain may parameter.

Halimbawa, mayroon bang anumang halaga ng parameter a kung saan ang equation na 2x^6-x^4-ax^2=1 ay magkakaroon ng tatlong ugat?

Kung isasaalang-alang natin na ang variable ay pumapasok sa equation sa kahit na mga kapangyarihan, kung gayon malinaw na ang pagpapalit ng x ng - x ibinigay na equation hindi magbabago. Ito ay sumusunod na kung ang isang tiyak na numero ay ang ugat nito, kung gayon ang kabaligtaran na numero ay ang ugat din. Ang konklusyon ay halata: ang mga ugat ng isang equation na naiiba sa zero ay kasama sa hanay ng mga solusyon nito "sa mga pares".

Malinaw na ang numero mismo ay hindi 0, iyon ay, ang bilang ng mga ugat ng naturang equation ay maaari lamang maging pantay at, natural, para sa anumang halaga ng parameter hindi ito maaaring magkaroon ng tatlong ugat.

Ngunit ang bilang ng mga ugat ng equation na 2^x+ 2^(-x)=ax^4+2x^2+2 ay maaaring kakaiba, at para sa anumang halaga ng parameter. Sa katunayan, madaling suriin na ang hanay ng mga ugat ng equation na ito ay naglalaman ng mga solusyon "sa pares". Suriin natin kung ang 0 ay isang ugat. Kapag pinalitan natin ito sa equation, makakakuha tayo ng 2=2. Kaya, bilang karagdagan sa mga "ipinares", ang 0 ay isang ugat din, na nagpapatunay ng kanilang kakaibang numero.

Pati function.

Kahit na ay isang function na ang sign ay hindi nagbabago kapag ang sign ay nagbago x.

x pinanghahawakan ang pagkakapantay-pantay f(–x) = f(x). Lagda x hindi nakakaapekto sa tanda y.

Ang graph ng even function ay simetriko tungkol sa coordinate axis (Larawan 1).

Mga halimbawa ng pantay na function:

y=cos x

y = x 2

y = –x 2

y = x 4

y = x 6

y = x 2 + x

Paliwanag:
Kunin natin ang function y = x 2 o y = –x 2 .
Para sa anumang halaga x positibo ang function. Lagda x hindi nakakaapekto sa tanda y. Ang graph ay simetriko tungkol sa coordinate axis. Ito ay isang pantay na function.

Kakaibang function.

Kakaiba ay isang function na ang sign ay nagbabago kapag ang sign ay nagbabago x.

Sa madaling salita, para sa anumang halaga x pinanghahawakan ang pagkakapantay-pantay f(–x) = –f(x).

Ang graph ng isang kakaibang function ay simetriko na may kinalaman sa pinagmulan (Larawan 2).

Mga halimbawa ng kakaibang function:

y= kasalanan x

y = x 3

y = –x 3

Paliwanag:

Kunin natin ang function na y = – x 3 .
Lahat ng kahulugan sa magkakaroon ito ng minus sign. Iyon ay isang tanda x nakakaimpluwensya sa tanda y. Kung ang independent variable ay isang positibong numero, kung gayon ang function ay positibo, kung ang independent variable ay negatibong numero, kung gayon ang pag-andar ay negatibo: f(–x) = –f(x).
Ang graph ng function ay simetriko tungkol sa pinagmulan. Ito ay isang kakaibang function.

Mga katangian ng even at odd na function:

TANDAAN:

Hindi lahat ng function ay pantay o kakaiba. May mga function na hindi sumusunod sa naturang gradation. Halimbawa, ang root function sa = √X ay hindi nalalapat sa alinman sa kahit o kakaibang mga function (Larawan 3). Kapag naglilista ng mga katangian ng naturang mga pag-andar, dapat magbigay ng angkop na paglalarawan: ni kahit na o kakaiba.

Mga pana-panahong pag-andar.

Tulad ng alam mo, ang periodicity ay ang pag-uulit ng ilang mga proseso sa isang tiyak na agwat. Ang mga function na naglalarawan sa mga prosesong ito ay tinatawag mga pana-panahong pag-andar. Ibig sabihin, ito ay mga function kung saan ang mga graph ay may mga elemento na umuulit sa ilang mga numerical interval.

Ang isang function ay tinatawag na even (odd) kung para sa alinman at ang pagkakapantay-pantay

.

Ang graph ng pantay na function ay simetriko tungkol sa axis
.

Ang graph ng isang kakaibang function ay simetriko tungkol sa pinagmulan.

Halimbawa 6.2. Suriin kung ang isang function ay even o odd

1)
; 2)
; 3)
.

Solusyon.

1) Tinutukoy ang function kung kailan
. Hahanapin natin
.

Yung.
. Ibig sabihin, function na ito ay pantay.

2) Tinutukoy ang function kung kailan

Yung.
. Kaya, ang function na ito ay kakaiba.

3) ang function ay tinukoy para sa , ibig sabihin. Para sa

,
. Samakatuwid ang pag-andar ay hindi kahit na o kakaiba. Tawagin natin itong function ng general form.

3. Pag-aaral ng function para sa monotonicity.

Function
ay tinatawag na pagtaas (pagbaba) sa isang tiyak na pagitan kung sa pagitan ng bawat isa mas mataas na halaga ang argument ay tumutugma sa isang mas malaki (mas maliit) na halaga ng function.

Ang mga function na tumataas (bumababa) sa isang tiyak na pagitan ay tinatawag na monotonic.

Kung ang function
naiba sa pagitan
at may positive (negative) derivative
, pagkatapos ay ang function
tumataas (bumababa) sa pagitan na ito.

Halimbawa 6.3. Maghanap ng mga pagitan ng monotonicity ng mga function

1)
; 3)
.

Solusyon.

1) Ang function na ito ay tinukoy sa buong linya ng numero. Hanapin natin ang derivative.

Ang derivative ay katumbas ng zero kung
At
. Ang domain ng kahulugan ay ang number axis, na hinati ng mga tuldok
,
sa pagitan. Alamin natin ang tanda ng derivative sa bawat pagitan.

Sa pagitan
ang derivative ay negatibo, ang function ay bumababa sa pagitan na ito.

Sa pagitan
ang derivative ay positibo, samakatuwid, ang function ay tumataas sa pagitan na ito.

2) Ang function na ito ay tinukoy kung
o

.

Tinutukoy namin ang tanda ng quadratic trinomial sa bawat pagitan.

Kaya, ang domain ng kahulugan ng function

Hanapin natin ang derivative
,
, Kung
, ibig sabihin.
, Ngunit
. Tukuyin natin ang tanda ng derivative sa mga pagitan
.

Sa pagitan
ang derivative ay negatibo, samakatuwid, ang function ay bumababa sa pagitan
. Sa pagitan
ang derivative ay positibo, ang function ay tumataas sa pagitan
.

4. Pag-aaral ng function sa extremum.

Dot
tinatawag na maximum (minimum) point ng function
, kung mayroong ganoong kapitbahayan ng punto para yan sa lahat
mula sa kapitbahayan na ito ang hindi pagkakapantay-pantay

.

Ang pinakamataas at pinakamababang punto ng isang function ay tinatawag na extremum point.

Kung ang function
sa punto ay may extremum, kung gayon ang derivative ng function sa puntong ito ay katumbas ng zero o wala (isang kinakailangang kondisyon para sa pagkakaroon ng isang extremum).

Ang mga punto kung saan ang derivative ay zero o hindi umiiral ay tinatawag na kritikal.

5. Sapat na mga kondisyon para sa pagkakaroon ng isang extremum.

Panuntunan 1. Kung sa panahon ng paglipat (mula kaliwa hanggang kanan) sa pamamagitan ng kritikal na punto derivative
binabago ang sign mula “+” hanggang “–”, pagkatapos ay sa punto function
may maximum; kung mula sa "–" hanggang sa "+", kung gayon ang pinakamababa; Kung
ay hindi nagbabago ng tanda, pagkatapos ay walang extremum.

Panuntunan 2. Hayaan sa punto
unang derivative ng isang function
katumbas ng zero
, at ang pangalawang derivative ay umiiral at iba sa zero. Kung
, Iyon – pinakamataas na punto, kung
, Iyon – pinakamababang punto ng function.

Halimbawa 6.4 . I-explore ang maximum at minimum na function:

1)
; 2)
; 3)
;

4)
.

Solusyon.

1) Ang function ay tinukoy at tuloy-tuloy sa pagitan
.

Hanapin natin ang derivative
at lutasin ang equation
, ibig sabihin.
.Mula dito
- mga kritikal na puntos.

Alamin natin ang tanda ng derivative sa mga pagitan,
.

Kapag dumadaan sa mga puntos
At
ang derivative ay nagbabago ng sign mula “–” hanggang “+”, samakatuwid, ayon sa panuntunan 1
- pinakamababang puntos.

Kapag dumadaan sa isang punto
ang derivative ay nagbabago ng sign mula “+” hanggang “–”, kaya
- pinakamataas na punto.

,
.

2) Ang function ay tinukoy at tuloy-tuloy sa pagitan
. Hanapin natin ang derivative
.

Nang malutas ang equation
, hahanapin natin
At
- mga kritikal na puntos. Kung ang denominator
, ibig sabihin.
, kung gayon ang derivative ay hindi umiiral. Kaya,
- ikatlong kritikal na punto. Alamin natin ang sign ng derivative sa pagitan.

Samakatuwid, ang function ay may pinakamababa sa punto
, maximum sa mga puntos
At
.

3) Ang isang function ay tinukoy at tuloy-tuloy kung
, ibig sabihin. sa
.

Hanapin natin ang derivative

.

Maghanap tayo ng mga kritikal na punto:

Mga kapitbahayan ng mga puntos
hindi nabibilang sa domain ng kahulugan, samakatuwid hindi sila extremums. Kaya, suriin natin ang mga kritikal na punto
At
.

4) Ang function ay tinukoy at tuloy-tuloy sa pagitan
. Gamitin natin ang panuntunan 2. Hanapin ang derivative
.

Maghanap tayo ng mga kritikal na punto:

Hanapin natin ang pangalawang derivative
at tukuyin ang tanda nito sa mga punto

Sa mga punto
may minimum na function.

Sa mga punto
may maximum ang function.

Ang mga graph ng even at odd na function ay may mga sumusunod na feature:

Kung ang isang function ay pantay, ang graph nito ay simetriko tungkol sa ordinate. Kung ang isang function ay kakaiba, ang graph nito ay simetriko tungkol sa pinagmulan.

Solusyon. Isaalang-alang ang function: \(f\left(x \right)=\left|x \right|\) at palitan ang kabaligtaran \(-x \) sa halip na \(x \). Bilang resulta ng mga simpleng pagbabagong nakuha natin: $$f\left(-x \right)=\left|-x \right|=\left|x \right|=f\left(x \right)$$ Sa ibang salita, kung papalitan ang argumento ng kabaligtaran na tanda, hindi magbabago ang function.

Nangangahulugan ito na ang function na ito ay pantay, at ang graph nito ay magiging simetriko na may kinalaman sa ordinate axis ( patayong axis). Ang graph ng function na ito ay ipinapakita sa figure sa kaliwa. Nangangahulugan ito na kapag gumagawa ng isang graph, maaari ka lamang gumuhit ng kalahati, at ang pangalawang bahagi (sa kaliwa ng vertical axis, gumuhit ng simetriko sa kanang bahagi). Sa pamamagitan ng pagtukoy sa simetrya ng isang function bago simulan ang pag-plot ng graph nito, maaari mong lubos na pasimplehin ang proseso ng pagbuo o pag-aaral ng function. Kung mahirap magsagawa ng pangkalahatang pagsusuri, magagawa mo ito nang mas simple: palitan ang parehong mga halaga ng iba't ibang mga palatandaan sa equation. Halimbawa -5 at 5. Kung magkapareho ang mga halaga ng function, maaari tayong umasa na magiging pantay ang function. Mula sa isang matematikal na punto ng view, ang diskarte na ito ay hindi ganap na tama, ngunit mula sa isang praktikal na punto ng view ito ay maginhawa. Upang madagdagan ang pagiging maaasahan ng resulta, maaari mong palitan ang ilang mga pares ng mga kabaligtaran na halaga.

Solusyon. Suriin natin ang katulad ng sa nakaraang halimbawa: $$f\left(-x \right)=x\left|-x \right|=-x\left|x \right|=-f\left(x \right ) $$ Nangangahulugan ito na ang orihinal na function ay kakaiba (ang tanda ng function ay nagbago sa kabaligtaran).

Konklusyon: ang function ay simetriko tungkol sa pinagmulan. Maaari kang bumuo lamang ng isang kalahati, at iguhit ang pangalawang simetriko. Ang ganitong uri ng simetrya ay mas mahirap iguhit. Nangangahulugan ito na tinitingnan mo ang tsart mula sa kabilang panig ng sheet, at kahit nakabaligtad. O magagawa mo ito: kunin ang iginuhit na bahagi at paikutin ito sa paligid ng pinanggalingan ng 180 degrees counterclockwise.

Solusyon. Gawin natin ang parehong pagsusuri para sa pagbabago ng tanda tulad ng sa nakaraang dalawang halimbawa. $$f\left(-x \right)=\left(-x \right)^3+\left(-x \right)^2=-x^2+x^2$$ Bilang resulta, nakukuha namin na: $$f\left(-x \right)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$ At ito ibig sabihin, na ang function ay hindi kahit na o kakaiba.

Konklusyon: ang function ay hindi simetriko alinman sa paggalang sa pinagmulan o sa gitna ng coordinate system. Nangyari ito dahil ito ang kabuuan ng dalawang function: even at odd. Ang parehong sitwasyon ay mangyayari kung ibawas mo ang dalawang magkaibang function. Ngunit ang pagpaparami o paghahati ay hahantong sa ibang resulta. Halimbawa, ang produkto ng isang even at isang odd na function ay gumagawa ng isang kakaibang function. O ang quotient ng dalawang kakaibang numero ay humahantong sa isang even function.

Itago ang Palabas

Mga pamamaraan para sa pagtukoy ng isang function

Hayaang ibigay ang function ng formula: y=2x^(2)-3. Sa pamamagitan ng pagtatalaga ng anumang mga halaga sa independiyenteng variable na x, maaari mong kalkulahin, gamit ang formula na ito, ang mga kaukulang halaga ng dependent variable y. Halimbawa, kung x=-0.5, kung gayon, gamit ang formula, makikita natin na ang katumbas na halaga ng y ay y=2 \cdot (-0.5)^(2)-3=-2.5.

Ang pagkuha ng anumang halaga na kinuha ng argumentong x sa formula y=2x^(2)-3, maaari mong kalkulahin ang isang halaga lamang ng function na tumutugma dito. Ang function ay maaaring kinakatawan bilang isang talahanayan:

Gamit ang talahanayang ito, makikita mo na para sa halaga ng argumento −1 ang halaga ng function na −3 ay tumutugma; at ang halaga x=2 ay tumutugma sa y=0, atbp. Mahalaga rin na malaman na ang bawat halaga ng argumento sa talahanayan ay tumutugma lamang sa isang halaga ng function.

Higit pang mga function ang maaaring tukuyin gamit ang mga graph. Gamit ang isang graph, itinatag kung aling halaga ng function ang nauugnay sa isang tiyak na halaga x. Kadalasan, ito ay magiging isang tinatayang halaga ng function.

Kahit at kakaibang pag-andar

Ang function ay kahit function, kapag f(-x)=f(x) para sa alinmang x mula sa domain ng kahulugan. Ang ganitong function ay magiging simetriko tungkol sa Oy axis.

Ang function ay kakaibang function, kapag f(-x)=-f(x) para sa anumang x mula sa domain ng kahulugan. Ang ganitong function ay magiging simetriko tungkol sa pinagmulan O (0;0) .

Ang function ay hindi man lang, ni kakaiba at tinatawag function pangkalahatang pananaw , kapag wala itong simetrya tungkol sa axis o pinanggalingan.

Suriin natin ang sumusunod na function para sa parity:

f(x)=3x^(3)-7x^(7)

D(f)=(-\infty ; +\infty) na may simetriko na domain ng kahulugan na nauugnay sa pinagmulan. f(-x)= 3 \cdot (-x)^(3)-7 \cdot (-x)^(7)= -3x^(3)+7x^(7)= -(3x^(3)-7x^(7))= -f(x).

Nangangahulugan ito na ang function na f(x)=3x^(3)-7x^(7) ay kakaiba.

Pana-panahong pag-andar

Ang function na y=f(x) , sa domain kung saan ang equality f(x+T)=f(x-T)=f(x) hold para sa alinmang x, ay tinatawag pana-panahong pag-andar na may tuldok T \neq 0 .

Inuulit ang graph ng isang function sa anumang segment ng x-axis na may haba na T.

Ang mga pagitan kung saan positibo ang function, iyon ay, f(x) > 0, ay mga segment ng abscissa axis na tumutugma sa mga punto ng function graph na nasa itaas ng abscissa axis.

f(x) > 0 on (x_(1); x_(2)) \cup (x_(3); +\infty)

Mga agwat kung saan negatibo ang function, ibig sabihin, f(x)< 0 - отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.

f(x)< 0 на (-\infty; x_(1)) \cup (x_(2); x_(3))

Limitadong pag-andar

Bounded mula sa ibaba Nakaugalian na tumawag sa isang function na y=f(x), x \in X kapag mayroong numerong A kung saan ang hindi pagkakapantay-pantay na f(x) \geq A ay humahawak para sa alinmang x \in X .

Isang halimbawa ng function na naka-bound mula sa ibaba: y=\sqrt(1+x^(2)) since y=\sqrt(1+x^(2)) \geq 1 para sa anumang x .

Bounded mula sa itaas ang isang function na y=f(x), x \in X ay tinatawag kapag mayroong isang numero B kung saan ang hindi pagkakapantay-pantay na f(x) \neq B ay humahawak para sa anumang x \in X .

Isang halimbawa ng isang function na nakatali sa ibaba: y=\sqrt(1-x^(2)), x \in [-1;1] since y=\sqrt(1+x^(2)) \neq 1 para sa anumang x \in [-1;1] .

Limitado Nakaugalian na tumawag sa isang function na y=f(x), x \in X kapag mayroong isang numerong K > 0 kung saan ang hindi pagkakapantay-pantay \left | f(x)\kanan | \neq K para sa alinmang x \in X .

Halimbawa limitadong pag-andar: y=\sin x ay limitado sa buong numero ng axis, dahil \kaliwa | \sin x \kanan | \neq 1.

Ang pagtaas at pagbaba ng function

Nakaugalian na magsalita ng isang function na tumataas sa pagitan na isinasaalang-alang bilang pagtaas ng function pagkatapos, kapag ang isang mas malaking halaga ng x ay tumutugma sa isang mas malaking halaga ng function y=f(x) . Kasunod nito na ang pagkuha ng dalawang di-makatwirang halaga ng argumento x_(1) at x_(2) mula sa pagitan na isinasaalang-alang, na may x_(1) > x_(2) , ang magiging resulta ay y(x_(1)) > y(x_(2)).

Ang isang function na bumababa sa pagitan na isinasaalang-alang ay tinatawag nagpapababa ng function kapag ang isang mas malaking halaga ng x ay tumutugma sa isang mas maliit na halaga ng function na y(x) . Kasunod nito, ang pagkuha mula sa pagitan na isinasaalang-alang ang dalawang arbitrary na halaga ng argumento x_(1) at x_(2) , at x_(1) > x_(2) , ang magiging resulta ay y(x_(1))< y(x_{2}) .

Function Roots Nakaugalian na tawagan ang mga punto kung saan ang function na F=y(x) ay nag-intersect sa abscissa axis (nakuha ang mga ito sa pamamagitan ng paglutas ng equation na y(x)=0).

a) Kung para sa x > 0 ang isang even function ay tumataas, pagkatapos ay bumababa ito para sa x< 0

b) Kapag ang isang even function ay bumaba sa x > 0, pagkatapos ay tumataas ito sa x< 0

c) Kapag tumaas ang kakaibang function sa x > 0, tataas din ito sa x< 0

d) Kapag ang isang kakaibang function ay bumaba para sa x > 0, pagkatapos ay bababa din ito para sa x< 0

Extrema ng function

Pinakamababang punto ng function Ang y=f(x) ay karaniwang tinatawag na isang puntong x=x_(0) na ang kapitbahayan ay magkakaroon ng iba pang mga punto (maliban sa puntong x=x_(0)), at para sa kanila ang hindi pagkakapantay-pantay na f(x) > f ay magiging nasiyahan (x_(0)) . y_(min) - pagtatalaga ng function sa min point.

Pinakamataas na punto ng function Ang y=f(x) ay karaniwang tinatawag na isang puntong x=x_(0) na ang kapitbahayan ay magkakaroon ng iba pang mga punto (maliban sa puntong x=x_(0)), at para sa kanila ang hindi pagkakapantay-pantay na f(x) ay masisiyahan.< f(x^{0}) . y_{max} - обозначение функции в точке max.

Prerequisite

Ayon sa teorama ni Fermat: f"(x)=0 kapag ang function na f(x) na naiba sa puntong x_(0) ay magkakaroon ng extremum sa puntong ito.

Sapat na kondisyon

1. Kapag ang derivative ay nagbago ng sign mula plus hanggang minus, kung gayon ang x_(0) ang magiging pinakamababang punto;
2. x_(0) - ay magiging pinakamataas na punto lamang kapag ang derivative ay nagbago ng sign mula minus hanggang plus kapag dumadaan sa nakatigil na punto x_(0) .

Ang pinakamalaki at pinakamaliit na halaga ng isang function sa isang pagitan

Mga hakbang sa pagkalkula:

1. Hinahanap ang derivative f"(x);
2. Ang mga nakatigil at kritikal na punto ng function ay matatagpuan at ang mga kabilang sa segment ay pinili;
3. Ang mga halaga ng function na f(x) ay matatagpuan sa nakatigil at kritikal na mga punto at dulo ng segment. Ang mas maliit sa mga resulta na nakuha ay magiging pinakamababang halaga mga function, at higit pa - ang pinakamalaki.