Ang artikulong ito ay nagbibigay ng ideya kung paano isulat ang equation ng isang eroplanong dumadaan ibinigay na punto tatlong-dimensional na espasyo patayo sa isang ibinigay na linya. Suriin natin ang algorithm sa itaas gamit ang halimbawa ng paglutas ng mga tipikal na problema.

Yandex.RTB R-A-339285-1

Paghahanap ng equation ng isang eroplanong dumadaan sa isang ibinigay na punto sa espasyo na patayo sa isang linya

Hayaan ang isang three-dimensional na espasyo at isang rectangular coordinate system O x y z na ibigay sa loob nito. Ibinibigay din ang punto M 1 (x 1, y 1, z 1), ang tuwid na linya a at ang eroplanong α na dumadaan sa puntong M 1 patayo sa tuwid na linya a. Kinakailangang isulat ang equation ng eroplanong α.

Bago magpatuloy upang malutas ang problemang ito, alalahanin natin ang geometry theorem mula sa programa para sa mga baitang 10 - 11, na nagbabasa:

Kahulugan 1

Ang isang solong eroplano ay dumadaan sa isang ibinigay na punto sa tatlong-dimensional na espasyo at patayo sa isang ibinigay na linya.

Ngayon isaalang-alang kung paano hanapin ang equation ng solong eroplanong ito na dumadaan sa panimulang punto at patayo sa ibinigay na linya.

Posibleng isulat ang pangkalahatang equation ng isang eroplano kung ang mga coordinate ng isang punto na kabilang sa eroplanong ito ay kilala, pati na rin ang mga coordinate ng normal na vector ng eroplano.

Sa pamamagitan ng kondisyon ng problema, binibigyan tayo ng mga coordinate x 1, y 1, z 1 ng punto M 1 kung saan dumadaan ang eroplano α. Kung matukoy natin ang mga coordinate ng normal na vector ng eroplano α, pagkatapos ay maisusulat natin ang nais na equation.

Ang normal na vector ng eroplanong α, dahil ito ay di-zero at nasa linyang a, patayo sa eroplanong α, ay magiging anumang nagdidirekta na vector ng linya a. Kaya, ang problema sa paghahanap ng mga coordinate ng normal na vector ng eroplano α ay binago sa problema ng pagtukoy ng mga coordinate ng nagdidirekta na vector ng tuwid na linya a .

Ang pagpapasiya ng mga coordinate ng nagdidirekta na vector ng tuwid na linya a ay maaaring isagawa iba't ibang pamamaraan: depende sa opsyon ng pagtukoy ng tuwid na linya a sa mga paunang kondisyon. Halimbawa, kung ang linya a sa kondisyon ng problema ay ibinibigay ng mga canonical equation ng form

x - x 1 a x = y - y 1 a y = z - z 1 a z

o parametric equation ng form:

x = x 1 + a x λ y = y 1 + a y λ z = z 1 + a z λ

pagkatapos ang nagdidirekta na vector ng tuwid na linya ay magkakaroon ng mga coordinate a x, a y at a z. Sa kaso kapag ang tuwid na linya a ay kinakatawan ng dalawang puntos na M 2 (x 2, y 2, z 2) at M 3 (x 3, y 3, z 3), kung gayon ang mga coordinate ng vector ng direksyon ay matutukoy bilang (x3 - x2, y3 - y2 , z3 – z2).

Kahulugan 2

Algorithm para sa paghahanap ng equation ng isang eroplanong dumadaan sa isang naibigay na punto na patayo sa isang naibigay na linya:

Tukuyin ang mga coordinate ng nagdidirekta na vector ng tuwid na linya a: a → = (a x, a y, a z) ;

Tinukoy namin ang mga coordinate ng normal na vector ng eroplanong α bilang mga coordinate ng nagdidirekta na vector ng tuwid na linya a:

n → = (A , B , C) , kung saan A = a x , B = a y , C = a z;

Isinulat namin ang equation ng eroplano na dumadaan sa puntong M 1 (x 1, y 1, z 1) at pagkakaroon ng normal na vector n→=(A, B, C) sa anyong A (x - x 1) + B (y - y 1) + C (z - z 1) = 0. Ito ang magiging kinakailangang equation ng isang eroplano na dumadaan sa isang ibinigay na punto sa espasyo at patayo sa isang partikular na linya.

Ang resultang pangkalahatang equation ng eroplano: Ang A (x - x 1) + B (y - y 1) + C (z - z 1) \u003d 0 ay ginagawang posible na makuha ang equation ng eroplano sa mga segment o ang normal na equation ng eroplano.

Lutasin natin ang ilang halimbawa gamit ang algorithm na nakuha sa itaas.

Halimbawa 1

Ang isang puntong M 1 (3, - 4, 5) ay ibinibigay, kung saan ang eroplano ay dumadaan, at ang eroplanong ito ay patayo sa coordinate line O z.

Desisyon

ang direction vector ng coordinate line O z ang magiging coordinate vector k ⇀ = (0 , 0 , 1) . Samakatuwid, ang normal na vector ng eroplano ay may mga coordinate (0 , 0 , 1) . Isulat natin ang equation ng isang eroplanong dumadaan sa isang ibinigay na punto M 1 (3, - 4, 5) na ang normal na vector ay may mga coordinate (0, 0, 1):

A (x - x 1) + B (y - y 1) + C (z - z 1) = 0 ⇔ ⇔ 0 (x - 3) + 0 (y - (- 4)) + 1 (z - 5) = 0 ⇔ z - 5 = 0

Sagot: z - 5 = 0 .

Isaalang-alang ang isa pang paraan upang malutas ang problemang ito:

Halimbawa 2

Ang isang eroplanong patayo sa linyang O z ay bibigyan ng isang hindi kumpletong pangkalahatang equation ng eroplano ng anyong С z + D = 0 , C ≠ 0 . Tukuyin natin ang mga halaga ng C at D: ang mga kung saan ang eroplano ay dumaan sa isang naibigay na punto. Palitan ang mga coordinate ng puntong ito sa equation C z + D = 0 , nakukuha namin ang: C · 5 + D = 0 . Yung. ang mga numero, C at D ay nauugnay sa pamamagitan ng - D C = 5 . Ang pagkuha ng C \u003d 1, nakukuha namin ang D \u003d - 5.

Ipalit ang mga halagang ito sa equation C z + D = 0 at kunin ang kinakailangang equation para sa isang eroplanong patayo sa linyang O z at dumadaan sa puntong M 1 (3, - 4, 5) .

Magmumukha itong: z - 5 = 0.

Sagot: z - 5 = 0 .

Halimbawa 3

Sumulat ng equation para sa isang eroplanong dumadaan sa pinanggalingan at patayo sa linyang x - 3 = y + 1 - 7 = z + 5 2

Desisyon

Batay sa mga kondisyon ng problema, maaari itong mapagtatalunan na ang gabay na vector ng isang tuwid na linya ay maaaring kunin bilang isang normal na vector n → ng isang naibigay na eroplano. Kaya: n → = (- 3 , - 7 , 2) . Isulat natin ang equation ng isang eroplanong dumadaan sa puntong O (0, 0, 0) at pagkakaroon ng normal na vector n → \u003d (- 3, - 7, 2) :

3 (x - 0) - 7 (y - 0) + 2 (z - 0) = 0 ⇔ - 3 x - 7 y + 2 z = 0

Nakuha namin ang kinakailangang equation para sa eroplano na dumadaan sa pinanggalingan patayo sa ibinigay na linya.

Sagot:- 3x - 7y + 2z = 0

Halimbawa 4

Dahil sa isang rectangular coordinate system O x y z sa tatlong-dimensional na espasyo, naglalaman ito ng dalawang puntos A (2 , - 1 , - 2) at B (3 , - 2 , 4) . Ang eroplanong α ay dumadaan sa puntong A patayo sa linyang AB. Kinakailangang buuin ang equation ng eroplanong α sa mga segment.

Desisyon

Ang eroplanong α ay patayo sa linyang A B, pagkatapos ay ang vector A B → ang magiging normal na vector ng eroplanong α. Ang mga coordinate ng vector na ito ay tinutukoy bilang ang pagkakaiba sa pagitan ng kaukulang mga coordinate ng mga puntos B (3, - 2, 4) at A (2, - 1, - 2):

A B → = (3 - 2 , - 2 - (- 1) , 4 - (- 2)) ⇔ A B → = (1 , - 1 , 6)

Ang pangkalahatang equation ng eroplano ay isusulat sa sumusunod na anyo:

1 x - 2 - 1 y - (- 1 + 6 (z - (- 2)) = 0 ⇔ x - y + 6 z + 9 = 0

Ngayon binubuo namin ang nais na equation ng eroplano sa mga segment:

x - y + 6 z + 9 = 0 ⇔ x - y + 6 z = - 9 ⇔ x - 9 + y 9 + z - 3 2 = 1

Sagot:x - 9 + y 9 + z - 3 2 = 1

Dapat ding tandaan na may mga problema na ang pangangailangan ay isulat ang equation ng isang eroplanong dumadaan sa isang naibigay na punto at patayo sa dalawa. binigay na mga eroplano. Sa pangkalahatan, ang solusyon sa problemang ito ay ang pagsulat ng isang equation para sa isang eroplanong dumadaan sa isang naibigay na punto na patayo sa isang linya, dahil dalawang intersecting na eroplano ang tumutukoy sa isang tuwid na linya.

Halimbawa 5

Ang isang parihabang coordinate system O x y z ay ibinigay, sa loob nito ay isang punto M 1 (2, 0, - 5) . Ang mga equation ng dalawang eroplano 3 x + 2 y + 1 = 0 at x + 2 z - 1 = 0 ay ibinibigay din, na bumabagtas sa tuwid na linya a . Kinakailangang bumuo ng isang equation para sa isang eroplanong dumadaan sa puntong M 1 patayo sa linya a.

Desisyon

Tukuyin natin ang mga coordinate ng nagdidirekta na vector ng tuwid na linya a . Ito ay patayo sa parehong normal na vector n 1 → (3 , 2 , 0) ng eroplano n → (1 , 0 , 2) at ang normal na vector 3 x + 2 y + 1 = 0 ng eroplano x + 2 z - 1 = 0 .

Pagkatapos ay kukunin namin ang nagdidirekta na vector α → tuwid na linya a produkto ng vector mga vector n 1 → at n 2 → :

a → = n 1 → × n 2 → = i → j → k → 3 2 0 1 0 2 = 4 i → - 6 j → - 2 k → ⇒ a → = (4 , - 6 , - 2 )

Kaya, ang vector n → = (4, - 6, - 2) ang magiging normal na vector ng eroplano na patayo sa linya a. Isinulat namin ang nais na equation ng eroplano:

4 (x - 2) - 6 (y - 0) - 2 (z - (- 5)) = 0 ⇔ 4 x - 6 y - 2 z - 18 = 0 ⇔ ⇔ 2 x - 3 y - z - 9 = 0

Sagot: 2 x - 3 y - z - 9 = 0

Kung may napansin kang pagkakamali sa text, mangyaring i-highlight ito at pindutin ang Ctrl+Enter

13. Anggulo sa pagitan ng mga eroplano, distansya mula sa isang punto hanggang sa isang eroplano.

Hayaang magsalubong ang mga eroplanong α at β sa linya c.
Ang anggulo sa pagitan ng mga eroplano ay ang anggulo sa pagitan ng mga patayo sa linya ng kanilang intersection, na iginuhit sa mga eroplanong ito.

Sa madaling salita, sa eroplano α gumuhit kami ng isang linya na patayo sa c. Sa eroplano β - linya b, patayo din sa c. Anggulo sa pagitan ng mga eroplanong α at β katumbas ng anggulo sa pagitan ng mga linya a at b.

Tandaan na kapag ang dalawang eroplano ay nagsalubong, apat na sulok ang aktwal na nabuo. Nakikita mo sila sa larawan? Bilang anggulo sa pagitan ng mga eroplanong sinasakyan namin maanghang iniksyon.

Kung ang anggulo sa pagitan ng mga eroplano ay 90 degrees, kung gayon ang mga eroplano patayo,

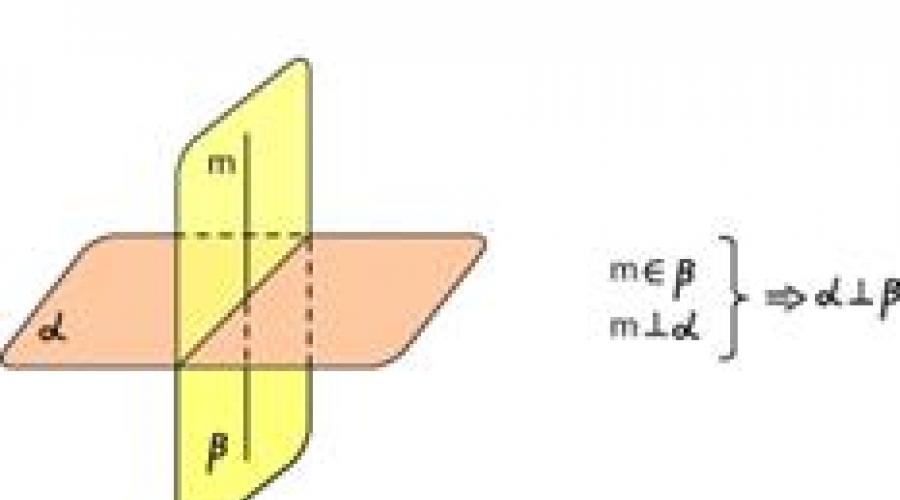
Ito ang kahulugan ng perpendicularity ng mga eroplano. Kapag nilulutas ang mga problema sa stereometry, ginagamit din namin tanda ng perpendicularity ng mga eroplano:

Kung ang eroplanong α ay dumaan sa patayo sa eroplanong β, kung gayon ang mga eroplanong α at β ay patayo.

ituro ang distansya ng eroplano

Isaalang-alang ang isang puntong T na ibinigay ng mga coordinate nito:

T \u003d (x 0, y 0, z 0)

Isaalang-alang din ang eroplanong α na ibinigay ng equation:

Ax + By + Cz + D = 0

Pagkatapos ang distansya L mula sa puntong T sa eroplano α ay maaaring kalkulahin ng formula:

Sa madaling salita, pinapalitan natin ang mga coordinate ng punto sa equation ng eroplano, at pagkatapos ay hatiin ang equation na ito sa haba ng normal na vector n sa eroplano:

Ang resultang numero ay ang distansya. Tingnan natin kung paano gumagana ang teorama na ito sa pagsasanay.

Nakuha na natin ang mga parametric equation ng isang tuwid na linya sa isang eroplano, makuha natin ang mga parametric equation ng isang tuwid na linya, na ibinigay sa isang rectangular coordinate system sa tatlong-dimensional na espasyo.

Hayaang maayos ang isang rectangular coordinate system sa tatlong-dimensional na espasyo Oxyz. Tukuyin natin ang isang tuwid na linya a(tingnan ang seksyon kung paano tukuyin ang isang tuwid na linya sa espasyo) sa pamamagitan ng pagtukoy sa nagdidirekta na vector ng isang tuwid na linya at ang mga coordinate ng ilang punto sa linya . Magsisimula tayo sa mga data na ito kapag nag-compile ng mga parametric equation ng isang tuwid na linya sa espasyo.

Hayaan ang isang arbitrary na punto sa tatlong-dimensional na espasyo. Kung ibawas natin mula sa mga coordinate ng punto M kaukulang mga coordinate ng punto M 1, pagkatapos ay makukuha natin ang mga coordinate ng vector (tingnan ang artikulo sa paghahanap ng mga coordinate ng vector sa pamamagitan ng mga coordinate ng mga punto ng pagtatapos at simula nito), iyon ay, .

Malinaw, ang hanay ng mga punto ay tumutukoy sa isang linya a kung at kung ang mga vectors at ay collinear.

Isulat natin ang kailangan at sapat na kondisyon para maging collinear ang mga vector at : , nasaan ang ilang totoong numero. Ang resultang equation ay tinatawag vector-parametric equation ng isang tuwid na linya sa rectangular coordinate system Oxyz sa tatlong-dimensional na espasyo. Ang vector-parametric equation ng isang tuwid na linya sa coordinate form ay may anyo at kumakatawan parametric equation ng tuwid na linya a. Ang pangalan na "parametric" ay hindi sinasadya, dahil ang mga coordinate ng lahat ng mga punto ng linya ay tinukoy gamit ang parameter .

Magbigay tayo ng isang halimbawa ng mga parametric equation ng isang tuwid na linya sa isang rectangular coordinate system Oxyz sa kalawakan: . Dito

15. Anggulo sa pagitan ng isang tuwid na linya at isang eroplano. Ang punto ng intersection ng isang linya na may isang eroplano.

Anumang equation ng unang degree na may paggalang sa mga coordinate x, y, z

Ax + By + Cz +D = 0 (3.1)

tumutukoy sa isang eroplano, at kabaliktaran: anumang eroplano ay maaaring katawanin ng equation (3.1), na tinatawag na equation ng eroplano.

Vector n(A, B, C) orthogonal sa eroplano ay tinatawag normal na vector mga eroplano. Sa equation (3.1), ang mga coefficient A, B, C ay hindi katumbas ng 0 sa parehong oras.

Mga espesyal na kaso ng equation (3.1):

1. D = 0, Ax+By+Cz = 0 - ang eroplano ay dumadaan sa pinanggalingan.

2. C = 0, Ax+By+D = 0 - ang eroplano ay parallel sa Oz axis.

3. C = D = 0, Ax + By = 0 - ang eroplano ay dumadaan sa Oz axis.

4. B = C = 0, Ax + D = 0 - ang eroplano ay parallel sa Oyz plane.

Coordinate plane equation: x = 0, y = 0, z = 0.

Ang isang tuwid na linya sa espasyo ay maaaring ibigay:

1) bilang isang linya ng intersection ng dalawang eroplano, i.e. sistema ng mga equation:

A 1 x + B 1 y + C 1 z + D 1 = 0, A 2 x + B 2 y + C 2 z + D 2 = 0; (3.2)

2) ang dalawang puntos nito M 1 (x 1, y 1, z 1) at M 2 (x 2, y 2, z 2), pagkatapos ay ang tuwid na linya na dumadaan sa kanila ay ibinibigay ng mga equation:

3) ang puntong M 1 (x 1 , y 1 , z 1) na kabilang dito, at ang vector a(m, n, p), s collinear. Pagkatapos ang tuwid na linya ay tinutukoy ng mga equation:

. (3.4)

Tinatawag ang mga equation (3.4). canonical equation ng linya.

Vector a tinawag gabayan ang vector nang tuwid.

Nakukuha namin ang mga parametric na equation ng tuwid na linya sa pamamagitan ng equating bawat isa sa mga relasyon (3.4) na may parameter na t:

x \u003d x 1 + mt, y \u003d y 1 + nt, z \u003d z 1 + pt. (3.5)

Paglutas ng sistema (3.2) bilang isang sistema linear na equation medyo hindi kilala x at y, dumating tayo sa mga equation ng tuwid na linya sa projection o sa pinababang mga equation ng tuwid na linya:

x = mz + a, y = nz + b. (3.6)

Mula sa mga equation (3.6) ang isa ay maaaring pumasa sa canonical equation, paghahanap z mula sa bawat equation at equating ang mga resultang halaga:

.

Ang isa ay maaaring pumasa mula sa mga pangkalahatang equation (3.2) patungo sa mga canonical na equation sa ibang paraan, kung ang isa ay makakahanap ng anumang punto ng linyang ito at ang vector ng direksyon nito n= [n 1 , n 2], saan n 1 (A 1 , B 1 , C 1) at n 2 (A 2 , B 2 , C 2) - mga normal na vector ng mga ibinigay na eroplano. Kung isa sa mga denominador m,n o R sa mga equation (3.4) ay lumalabas na katumbas ng zero, kung gayon ang numerator ng kaukulang fraction ay dapat itakda na katumbas ng zero, i.e. sistema

ay katumbas ng isang sistema ; tulad ng isang linya ay patayo sa x-axis.

Sistema ay katumbas ng sistemang x = x 1 , y = y 1 ; ang tuwid na linya ay parallel sa Oz axis.

Halimbawa 1.15. Isulat ang equation ng eroplano, alam na ang punto A (1, -1,3) ay nagsisilbing base ng patayo na iginuhit mula sa pinanggalingan hanggang sa eroplanong ito.

Desisyon. Sa pamamagitan ng kondisyon ng problema, ang vector OA Ang (1,-1,3) ay isang normal na vector ng eroplano, kung gayon ang equation nito ay maaaring isulat bilang
x-y+3z+D=0. Ang pagpapalit sa mga coordinate ng puntong A(1,-1,3) na kabilang sa eroplano, makikita natin ang D: 1-(-1)+3×3+D = 0 Þ D = -11. Kaya x-y+3z-11=0.

Halimbawa 1.16. Sumulat ng isang equation para sa isang eroplanong dumadaan sa Oz axis at bumubuo ng isang anggulo na 60 degrees sa 2x+y-z-7=0 na eroplano.

Desisyon. Ang eroplanong dumadaan sa Oz axis ay ibinibigay ng equation na Ax+By=0, kung saan ang A at B ay hindi naglalaho sa parehong oras. Huwag hayaan si B
ay 0, A/Bx+y=0. Ayon sa formula para sa cosine ng anggulo sa pagitan ng dalawang eroplano

.

Pagpapasya quadratic equation 3m 2 + 8m - 3 = 0, hanapin ang mga ugat nito
m 1 = 1/3, m 2 = -3, kung saan makakakuha tayo ng dalawang eroplano 1/3x+y = 0 at -3x+y = 0.

Halimbawa 1.17. Isulat ang mga canonical equation ng tuwid na linya:
5x + y + z = 0, 2x + 3y - 2z + 5 = 0.

Desisyon. Ang mga canonical equation ng tuwid na linya ay may anyo:

saan m, n, p- mga coordinate ng nagdidirekta na vector ng tuwid na linya, x1, y1, z1- mga coordinate ng anumang punto na kabilang sa linya. Ang tuwid na linya ay tinukoy bilang ang linya ng intersection ng dalawang eroplano. Upang makahanap ng isang punto na kabilang sa isang tuwid na linya, ang isa sa mga coordinate ay naayos (ang pinakamadaling paraan ay ilagay, halimbawa, x=0) at ang resultang sistema ay nalutas bilang isang sistema ng mga linear na equation na may dalawang hindi alam. Kaya, hayaan ang x=0, pagkatapos y + z = 0, 3y - 2z+ 5 = 0, kung saan y=-1, z=1. Natagpuan namin ang mga coordinate ng point M (x 1, y 1, z 1) na kabilang sa linyang ito: M (0,-1,1). Ang direktang vector ng isang tuwid na linya ay madaling mahanap, alam ang mga normal na vector ng orihinal na mga eroplano n 1 (5,1,1) at n 2(2,3,-2). Pagkatapos

Ang mga canonical equation ng linya ay: x/(-5) = (y + 1)/12 =
= (z - 1)/13.

Halimbawa 1.18. Sa sinag na tinukoy ng mga eroplanong 2x-y+5z-3=0 at x+y+2z+1=0, hanapin ang dalawang patayong eroplano, na ang isa ay dumadaan sa puntong M(1,0,1).

Desisyon. Ang equation ng sinag na tinukoy ng mga eroplanong ito ay u(2x-y+5z-3) + v(x+y+2z+1)=0, kung saan ang u at v ay hindi naglalaho sa parehong oras. Muli naming isinusulat ang beam equation tulad ng sumusunod:

(2u + v)x + (- u + v)y + (5u + 2v)z - 3u + v = 0.

Upang pumili ng isang eroplano na dumadaan sa punto M mula sa sinag, pinapalitan namin ang mga coordinate ng punto M sa equation ng sinag. Nakukuha namin ang:

(2u+v)×1 + (-u + v)×0 + (5u + 2v)×1 -3u + v =0, o v = - u.

Pagkatapos ay makikita natin ang equation ng eroplano na naglalaman ng M sa pamamagitan ng pagpapalit ng v = - u sa beam equation:

u(2x-y +5z - 3) - u(x + y +2z +1) = 0.

kasi u¹0 (kung hindi man v=0, at ito ay sumasalungat sa kahulugan ng isang sinag), pagkatapos ay mayroon tayong equation ng eroplanong x-2y+3z-4=0. Ang pangalawang eroplano na kabilang sa sinag ay dapat na patayo dito. Isinulat namin ang kondisyon para sa orthogonality ng mga eroplano:

(2u + v)×1 + (v - u)×(-2) + (5u + 2v)×3 = 0, o v = - 19/5u.

Samakatuwid, ang equation ng pangalawang eroplano ay may anyo:

u(2x -y+5z - 3) - 19/5 u(x + y +2z +1) = 0 o 9x +24y + 13z + 34 = 0

Equation ng eroplano. Paano magsulat ng isang equation para sa isang eroplano?
Mutual na pag-aayos ng mga eroplano. Mga gawain

Ang spatial geometry ay hindi mas kumplikado kaysa sa "flat" na geometry, at ang aming mga flight sa kalawakan ay nagsisimula sa artikulong ito. Upang maunawaan ang paksa, dapat magkaroon ng isang mahusay na pag-unawa sa mga vector, bilang karagdagan, ito ay kanais-nais na maging pamilyar sa geometry ng eroplano - magkakaroon ng maraming pagkakatulad, maraming mga pagkakatulad, kaya ang impormasyon ay mas mahusay na matutunaw. Sa isang serye ng aking mga aralin, ang 2D na mundo ay nagbubukas sa isang artikulo Equation ng isang tuwid na linya sa isang eroplano. Ngunit ngayon ay umalis na si Batman sa flat screen TV at naglulunsad mula sa Baikonur Cosmodrome.

Magsimula tayo sa mga guhit at simbolo. Sa eskematiko, ang eroplano ay maaaring iguhit bilang isang paralelogram, na nagbibigay ng impresyon ng espasyo:

Ang eroplano ay walang hanggan, ngunit mayroon tayong pagkakataon na ilarawan ang isang piraso lamang nito. Sa pagsasagawa, bilang karagdagan sa paralelogram, ang isang hugis-itlog o kahit isang ulap ay iginuhit din. Para sa mga teknikal na kadahilanan, mas maginhawa para sa akin na ilarawan ang eroplano sa ganitong paraan at sa posisyong ito. Mga totoong eroplano, na isasaalang-alang natin praktikal na mga halimbawa, ay maaaring ayusin ayon sa gusto mo - isiping kunin ang drawing sa iyong mga kamay at i-twist ito sa espasyo, na nagbibigay sa eroplano ng anumang slope, anumang anggulo.

Notasyon: kaugalian na magtalaga ng mga eroplano sa maliliit na letrang Griyego, tila upang hindi malito ang mga ito diretso sa eroplano o kasama tuwid sa kalawakan. Sanay na akong gumamit ng sulat . Sa pagguhit, ito ay ang titik na "sigma", at hindi isang butas sa lahat. Bagaman, isang holey na eroplano, ito ay tiyak na napaka nakakatawa.

Sa ilang mga kaso, madaling gamitin ang parehong mga letrang Griyego na may mga subscript para magtalaga ng mga eroplano, halimbawa, .

Malinaw na ang eroplano ay natatanging tinutukoy ng tatlong magkakaibang mga punto na hindi nakahiga sa parehong tuwid na linya. Samakatuwid, ang mga tatlong-titik na pagtatalaga ng mga eroplano ay medyo popular - ayon sa mga punto na kabilang sa kanila, halimbawa, atbp. Kadalasan ang mga titik ay nakapaloob sa panaklong: , upang hindi malito ang eroplano sa isa pang geometric na pigura.

Para sa mga may karanasang mambabasa, ibibigay ko menu ng shortcut:

• Paano magsulat ng isang equation para sa isang eroplano gamit ang isang punto at dalawang vectors?
• Paano magsulat ng isang equation para sa isang eroplano gamit ang isang punto at isang normal na vector?

at hindi kami mangungulit sa mahabang paghihintay:

Pangkalahatang equation ng eroplano

Ang pangkalahatang equation ng eroplano ay may anyo , kung saan ang mga coefficient ay sabay-sabay na hindi zero.

Ang isang bilang ng mga teoretikal na kalkulasyon at praktikal na mga problema ay wasto kapwa para sa karaniwang orthonormal na batayan at para sa affine na batayan space (kung mantika ang langis, bumalik sa aralin Linear (hindi) dependence ng mga vectors. Batayang vector). Para sa pagiging simple, ipagpalagay namin na ang lahat ng mga kaganapan ay nangyayari sa isang orthonormal na batayan at isang Cartesian rectangular coordinate system.

At ngayon magsanay tayo ng kaunting spatial na imahinasyon. Okay lang kung masama ka, ngayon bubuuin natin ng kaunti. Kahit na ang paglalaro sa nerbiyos ay nangangailangan ng pagsasanay.

Sa pinaka-pangkalahatang kaso, kapag ang mga numero ay hindi katumbas ng zero, ang eroplano ay nag-intersect sa lahat ng tatlong coordinate axes. Halimbawa, tulad nito:

Uulitin ko muli na ang eroplano ay nagpapatuloy nang walang katiyakan sa lahat ng direksyon, at mayroon tayong pagkakataon na ilarawan ang bahagi lamang nito.

Isaalang-alang ang pinakasimpleng equation ng mga eroplano:

Paano maintindihan ang equation na ito? Isipin ito: "Z" LAGING, para sa anumang mga halaga ng "X" at "Y" ay katumbas ng zero. Ito ang equation ng "katutubong" coordinate plane. Sa katunayan, pormal na ang equation ay maaaring muling isulat tulad ng sumusunod: , mula sa kung saan malinaw na nakikita na wala kaming pakialam, kung anong mga halaga ang kinuha ng "x" at "y", mahalaga na ang "z" ay katumbas ng zero.

Katulad nito:
ay ang equation ng coordinate plane ;
ay ang equation ng coordinate plane.

Palubhain natin ang problema nang kaunti, isaalang-alang ang isang eroplano (dito at higit pa sa talata ay ipinapalagay natin na ang mga numerical coefficient ay hindi katumbas ng zero). Isulat muli natin ang equation sa anyo: . Paano ito maintindihan? Ang "X" ay LAGING, para sa anumang halaga ng "y" at "z" ay katumbas ng isang tiyak na numero. Ang eroplanong ito ay parallel sa coordinate plane. Halimbawa, ang isang eroplano ay parallel sa isang eroplano at dumadaan sa isang punto.

Katulad nito:
- ang equation ng eroplano, na parallel sa coordinate plane;
- ang equation ng isang eroplano na parallel sa coordinate plane.

Magdagdag ng mga miyembro: . Ang equation ay maaaring muling isulat tulad nito: , ibig sabihin, ang "Z" ay maaaring maging anuman. Ano ang ibig sabihin nito? Ang "X" at "Y" ay konektado sa pamamagitan ng isang ratio na gumuhit ng isang tiyak na tuwid na linya sa eroplano (makikilala mo equation ng isang tuwid na linya sa isang eroplano?). Dahil ang Z ay maaaring maging anuman, ang linyang ito ay "ginagaya" sa anumang taas. Kaya, ang equation ay tumutukoy sa isang eroplanong parallel sa coordinate axis

Katulad nito:
- ang equation ng eroplano, na parallel sa coordinate axis;
- ang equation ng eroplano, na parallel sa coordinate axis.

Kung ang mga libreng termino ay zero, ang mga eroplano ay direktang dadaan sa mga kaukulang axes. Halimbawa, ang klasikong "direktang proporsyonalidad":. Gumuhit ng isang tuwid na linya sa eroplano at i-multiply ito sa isip pataas at pababa (dahil ang "z" ay anuman). Konklusyon: ang eroplano na ibinigay ng equation ay dumadaan sa coordinate axis.

Tinatapos namin ang pagsusuri: ang equation ng eroplano dumadaan sa pinanggalingan. Buweno, dito ay medyo halata na ang punto ay nakakatugon sa ibinigay na equation.

At, sa wakas, ang kaso na ipinapakita sa pagguhit: - ang eroplano ay kaibigan sa lahat ng mga coordinate axes, habang ito ay palaging "pumuputol" ng isang tatsulok na maaaring matatagpuan sa alinman sa walong octants.

Mga linear na hindi pagkakapantay-pantay sa espasyo

Upang maunawaan ang impormasyon, kailangang pag-aralan nang mabuti linear inequalities sa eroplano dahil maraming bagay ang magkakatulad. Ang talata ay magiging isang maikling pangkalahatang-ideya na may ilang mga halimbawa, dahil ang materyal ay medyo bihira sa pagsasanay.

Kung ang equation ay tumutukoy sa isang eroplano, kung gayon ang mga hindi pagkakapantay-pantay
magtanong kalahating espasyo. Kung ang hindi pagkakapantay-pantay ay hindi mahigpit (ang huling dalawa sa listahan), kung gayon ang solusyon ng hindi pagkakapantay-pantay, bilang karagdagan sa kalahating espasyo, ay kasama ang eroplano mismo.

Halimbawa 5

Hanapin ang unit na normal na vector ng eroplano .

Desisyon: Ang unit vector ay isang vector na ang haba ay isa. Tukuyin natin ang vector na ito sa pamamagitan ng . Ito ay lubos na malinaw na ang mga vector ay collinear:

Una, tinanggal namin ang normal na vector mula sa equation ng eroplano: .

Paano mahanap ang unit vector? Upang mahanap ang unit vector, kailangan mo bawat vector coordinate na hinati sa haba ng vector.

Isulat muli natin ang normal na vector sa anyo at hanapin ang haba nito:

Ayon sa itaas:

Sagot:

Suriin: , na kinakailangan upang suriin.

Malamang napansin iyon ng mga mambabasa na maingat na nag-aral sa huling talata ng aralin ang mga coordinate ng unit vector ay eksaktong mga direksyon cosine ng vector:

Lumihis tayo mula sa disassembled na problema: kapag binigyan ka ng arbitrary non-zero vector, at sa pamamagitan ng kundisyon na kinakailangan upang mahanap ang mga direksyon ng cosine nito (tingnan ang mga huling gawain ng aralin Tuldok na produkto ng mga vector), pagkatapos ikaw, sa katunayan, ay nakahanap din ng isang unit vector collinear sa ibinigay na isa. Sa katunayan, dalawang gawain sa isang bote.

Ang pangangailangan upang mahanap ang isang yunit ng normal na vector arises sa ilang mga problema ng mathematical analysis.

Nalaman namin ang pangingisda ng normal na vector, ngayon sasagutin namin ang kabaligtaran na tanong:

Paano magsulat ng isang equation para sa isang eroplano gamit ang isang punto at isang normal na vector?

Ang matibay na pagtatayo ng isang normal na vector at isang punto ay kilala ng isang darts target. Mangyaring iunat ang iyong kamay at pumili ng isang arbitrary na punto sa espasyo, halimbawa, isang maliit na pusa sa isang sideboard. Malinaw, sa pamamagitan ng puntong ito, maaari kang gumuhit ng isang solong eroplano na patayo sa iyong kamay.

Ang equation ng isang eroplano na dumadaan sa isang punto na patayo sa vector ay ipinahayag ng formula:

Unang antas

Mga coordinate at vector. Komprehensibong gabay (2019)

Sa artikulong ito, ikaw at ako ay magsisimula ng talakayan ng isang "magic wand" na magbibigay-daan sa iyo na bawasan ang maraming problema sa geometry sa simpleng aritmetika. Ang "wand" na ito ay maaaring gawing mas madali ang iyong buhay, lalo na kapag nakakaramdam ka ng kawalan ng katiyakan sa pagbuo ng mga spatial figure, mga seksyon, atbp. Ang lahat ng ito ay nangangailangan ng isang tiyak na imahinasyon at praktikal na mga kasanayan. Ang pamamaraan, na sisimulan naming isaalang-alang dito, ay magbibigay-daan sa iyo na mag-abstract ng halos ganap mula sa lahat ng uri ng geometric na mga konstruksyon at pangangatwiran. Ang pamamaraan ay tinatawag "paraan ng coordinate". Sa artikulong ito, isasaalang-alang natin ang mga sumusunod na tanong:

1. Coordinate na eroplano
2. Mga puntos at vector sa eroplano
3. Pagbuo ng isang vector mula sa dalawang puntos
4. Haba ng vector (distansya sa pagitan ng dalawang puntos).
5. Mga coordinate sa gitna
6. Produkto ng tuldok ng mga vector
7. Anggulo sa pagitan ng dalawang vector

Sa palagay ko nahulaan mo na kung bakit ang paraan ng coordinate ay tinatawag na? Totoo na nakakuha ito ng ganoong pangalan, dahil hindi ito gumagana sa mga geometric na bagay, ngunit sa kanilang mga numerical na katangian (coordinate). At ang pagbabagong-anyo mismo, na ginagawang posible na lumipat mula sa geometry patungo sa algebra, ay binubuo sa pagpapakilala ng isang coordinate system. Kung ang orihinal na figure ay flat, kung gayon ang mga coordinate ay dalawang-dimensional, at kung ang figure ay tatlong-dimensional, kung gayon ang mga coordinate ay tatlong-dimensional. Sa artikulong ito, isasaalang-alang lamang natin ang dalawang-dimensional na kaso. At ang pangunahing layunin ng artikulo ay ituro sa iyo kung paano gumamit ng ilang mga pangunahing pamamaraan ng pamamaraan ng coordinate (kung minsan ay nagiging kapaki-pakinabang ang mga ito kapag nilulutas ang mga problema sa planimetry sa bahagi B ng Unified State Examination). Ang sumusunod na dalawang seksyon sa paksang ito ay nakatuon sa talakayan ng mga pamamaraan para sa paglutas ng mga problema C2 (ang problema ng stereometry).

Saan magiging lohikal na simulan ang pagtalakay sa paraan ng coordinate? Marahil ay may konsepto ng isang coordinate system. Alalahanin mo noong una mo siyang nakilala. Tila sa akin na sa ika-7 baitang, nang malaman mo ang tungkol sa pagkakaroon linear function, Halimbawa. Hayaan mong ipaalala ko sa iyo na binuo mo ito sa bawat punto. naalala mo ba Pumili ka ng arbitrary na numero, pinalitan ito sa formula at nakalkula sa ganitong paraan. Halimbawa, kung, pagkatapos, kung, pagkatapos, atbp. Ano ang nakuha mo bilang isang resulta? At nakatanggap ka ng mga puntos na may mga coordinate: at. Pagkatapos ay gumuhit ka ng isang "krus" (coordinate system), pumili ng isang sukat dito (kung gaano karaming mga cell ang mayroon ka bilang isang solong segment) at minarkahan ang mga puntos na natanggap mo dito, na pagkatapos ay ikinonekta mo sa isang tuwid na linya, ang resultang linya ay ang graph ng function.

Mayroong ilang mga bagay na kailangang ipaliwanag sa iyo nang mas detalyado:

1. Pumili ka ng isang segment para sa mga kadahilanan ng kaginhawahan, upang ang lahat ay magkasya nang maayos at compact sa larawan

2. Ipinapalagay na ang axis ay napupunta mula kaliwa hanggang kanan, at ang axis ay mula sa ibaba hanggang sa itaas

3. Sila ay bumalandra sa isang tamang anggulo, at ang punto ng kanilang intersection ay tinatawag na pinagmulan. Ito ay minarkahan ng isang liham.

4. Sa talaan ng coordinate ng isang punto, halimbawa, sa kaliwa sa mga bracket ay ang coordinate ng punto kasama ang axis, at sa kanan, kasama ang axis. Sa partikular, nangangahulugan lamang na ang punto

5. Upang maitakda ang anumang punto sa coordinate axis, kailangan mong tukuyin ang mga coordinate nito (2 numero)

6. Para sa anumang puntong nakahiga sa axis,

7. Para sa anumang puntong nakahiga sa axis,

8. Ang axis ay tinatawag na x-axis

9. Ang axis ay tinatawag na y-axis

Ngayon gawin natin ang susunod na hakbang kasama mo: markahan ang dalawang puntos. Ikonekta ang dalawang puntong ito sa isang linya. At ilagay natin ang arrow na parang gumuguhit tayo ng isang segment mula sa punto hanggang punto: ibig sabihin, gagawin nating direksyon ang ating segment!

Tandaan kung ano ang isa pang pangalan para sa isang nakadirekta na segment? Tama, vector ang tawag dun!

Kaya, kung ikinonekta natin ang isang tuldok sa isang tuldok, at ang simula ay magiging punto A, at ang wakas ay magiging punto B, pagkatapos ay kumuha kami ng isang vector. Ginawa mo rin ang pagtatayo na ito noong ika-8 baitang, tandaan?

Lumalabas na ang mga vector, tulad ng mga puntos, ay maaaring tukuyin ng dalawang numero: ang mga numerong ito ay tinatawag na mga coordinate ng vector. Tanong: sa tingin mo ba ay sapat na para sa amin na malaman ang mga coordinate ng simula at katapusan ng vector upang mahanap ang mga coordinate nito? Oo nga pala! At napakadaling gawin:

Kaya, dahil sa vector ang punto ay ang simula, at ang wakas, ang vector ay may mga sumusunod na coordinate:

Halimbawa, kung, pagkatapos ay ang mga coordinate ng vector

Ngayon gawin natin ang kabaligtaran, hanapin ang mga coordinate ng vector. Ano ang kailangan nating baguhin para dito? Oo, kailangan mong palitan ang simula at wakas: ngayon ang simula ng vector ay nasa isang punto, at ang dulo sa isang punto. Pagkatapos:

Tingnang mabuti, ano ang pagkakaiba ng mga vector at? Ang kanilang pagkakaiba lamang ay ang mga palatandaan sa mga coordinate. Magkatapat sila. Ang katotohanang ito ay nakasulat tulad nito:

Minsan, kung hindi partikular na nakasaad kung aling punto ang simula ng vector, at kung alin ang wakas, kung gayon ang mga vector ay tinutukoy hindi ng dalawang malalaking titik, ngunit ng isang maliit na titik, halimbawa:, atbp.

Ngayon ng kaunti pagsasanay at hanapin ang mga coordinate ng mga sumusunod na vectors:

Pagsusuri:

Ngayon lutasin ang problema nang medyo mas mahirap:

Ang isang vector torus na may on-cha-scrap sa isang punto ay may co-or-di-on-yo. Find-di-te abs-cis-su points.

Ang lahat ng pareho ay medyo prosaic: Hayaan ang mga coordinate ng punto. Pagkatapos

Inipon ko ang system sa pamamagitan ng pagtukoy kung ano ang mga coordinate ng isang vector. Pagkatapos ang punto ay may mga coordinate. Interesado kami sa abscissa. Pagkatapos

Sagot:

Ano pa ang maaari mong gawin sa mga vectors? Oo, halos lahat ay pareho sa ordinaryong numero(maliban kung hindi mo maaaring hatiin, ngunit maaari kang magparami sa dalawang paraan, ang isa ay tatalakayin natin dito sa ibang pagkakataon)

1. Maaaring isalansan ang mga vector sa isa't isa
2. Ang mga vector ay maaaring ibawas sa bawat isa
3. Maaaring i-multiply (o hatiin) ang mga vector sa isang arbitrary na hindi zero na numero
4. Maaaring i-multiply ang mga vector sa bawat isa

Ang lahat ng mga operasyong ito ay may medyo visual na geometric na representasyon. Halimbawa, ang panuntunang tatsulok (o paralelogram) para sa pagdaragdag at pagbabawas:

Ang isang vector ay umuunat o lumiliit o nagbabago ng direksyon kapag pinarami o hinati sa isang numero:

Gayunpaman, dito kami ay magiging interesado sa tanong kung ano ang mangyayari sa mga coordinate.

1. Kapag nagdadagdag (nagbabawas) ng dalawang vector, idinaragdag namin (ibawas) ang kanilang mga coordinate na elemento sa pamamagitan ng elemento. I.e:

2. Kapag nagpaparami (naghahati) ng isang vector sa isang numero, ang lahat ng mga coordinate nito ay i-multiply (hinati) sa numerong ito:

Halimbawa:

· Hanapin-di-ang kabuuan ng ko-o-di-nat siglo-to-ra.

Hanapin muna natin ang mga coordinate ng bawat isa sa mga vectors. Pareho silang may iisang pinanggalingan - ang pinanggalingan. Magkaiba ang kanilang mga dulo. Pagkatapos, . Ngayon kinakalkula namin ang mga coordinate ng vector Pagkatapos ang kabuuan ng mga coordinate ng nagresultang vector ay katumbas ng.

Sagot:

Ngayon lutasin ang sumusunod na problema sa iyong sarili:

· Hanapin ang kabuuan ng mga coordinate ng vector

Sinusuri namin:

Isaalang-alang natin ngayon ang sumusunod na problema: mayroon tayong dalawang punto sa coordinate plane. Paano mahahanap ang distansya sa pagitan nila? Hayaang ang unang punto ay, at ang pangalawa. Tukuyin natin ang distansya sa pagitan nila bilang . Gawin natin ang sumusunod na pagguhit para sa kalinawan:

Ang aking nagawa? Nakipag-connect muna ako puntos at, a gumuhit din ng isang linya parallel sa axis mula sa punto, at gumuhit ng isang linya parallel sa axis mula sa punto. Nag-intersect ba sila sa isang punto, na bumubuo ng isang kahanga-hangang pigura? Bakit siya kahanga-hanga? Oo, ikaw at ako halos alam ang lahat kanang tatsulok. Well, ang Pythagorean theorem, sigurado. Ang nais na segment ay ang hypotenuse ng tatsulok na ito, at ang mga segment ay ang mga binti. Ano ang mga coordinate ng punto? Oo, ang mga ito ay madaling mahanap mula sa larawan: Dahil ang mga segment ay parallel sa mga axes at, ayon sa pagkakabanggit, ang kanilang mga haba ay madaling mahanap: kung tinutukoy namin ang mga haba ng mga segment, ayon sa pagkakabanggit, sa pamamagitan ng, pagkatapos

Ngayon ay gamitin natin ang Pythagorean theorem. Alam natin ang haba ng mga binti, makikita natin ang hypotenuse:

Kaya, ang distansya sa pagitan ng dalawang punto ay ang root sum ng mga squared differences mula sa mga coordinate. O - ang distansya sa pagitan ng dalawang punto ay ang haba ng segment na nagkokonekta sa kanila. Madaling makita na ang distansya sa pagitan ng mga punto ay hindi nakasalalay sa direksyon. Pagkatapos:

Mula dito gumuhit kami ng tatlong konklusyon:

Magsanay tayo nang kaunti sa pagkalkula ng distansya sa pagitan ng dalawang punto:

Halimbawa, kung, kung gayon ang distansya sa pagitan ng at ay

O mag-iba tayo: hanapin ang mga coordinate ng vector

At hanapin ang haba ng vector:

Tulad ng nakikita mo, ito ay pareho!

Ngayon magsanay ng kaunti sa iyong sarili:

Gawain: hanapin ang distansya sa pagitan ng mga ibinigay na puntos:

Sinusuri namin:

Narito ang ilang higit pang mga problema para sa parehong formula, kahit na medyo naiiba ang mga ito:

1. Find-di-te ang parisukat ng haba ng eyelid-to-ra.

2. Nai-di-te square ng eyelid length-to-ra

I'm guessing madali mo silang mahawakan? Sinusuri namin:

1. At ito ay para sa pagkaasikaso) Nahanap na namin ang mga coordinate ng mga vectors bago: . Pagkatapos ang vector ay may mga coordinate. Ang parisukat ng haba nito ay magiging:

2. Hanapin ang mga coordinate ng vector

Kung gayon ang parisukat ng haba nito ay

Walang kumplikado, tama? Simpleng arithmetic, wala nang iba pa.

Ang mga sumusunod na palaisipan ay hindi maaaring matukoy nang malinaw, ang mga ito ay para sa pangkalahatang karunungan at ang kakayahang gumuhit ng mga simpleng larawan.

1. Hanapin-di-yung mga sine ng anggulo sa-clo-on-mula sa-cut, ikonekta-one-n-th-th point, na may abscissa axis.

at

Paano natin gagawin dito? Kailangan mong hanapin ang sine ng anggulo sa pagitan at ng axis. At saan natin hahanapin ang sine? Tama, nasa tamang tatsulok. Kaya ano ang kailangan nating gawin? Buuin ang tatsulok na ito!

Dahil ang mga coordinate ng punto at, pagkatapos ay ang segment ay pantay, at ang segment. Kailangan nating hanapin ang sine ng anggulo. Hayaan akong ipaalala sa iyo na ang sine ay ang ratio ng kabaligtaran na binti sa hypotenuse, kung gayon

Ano ang natitira nating gawin? Hanapin ang hypotenuse. Magagawa mo ito sa dalawang paraan: gamit ang Pythagorean theorem (kilala ang mga binti!) o gamit ang formula para sa distansya sa pagitan ng dalawang puntos (aktwal na kapareho ng unang paraan!). Pupunta ako sa pangalawang paraan:

Sagot:

Ang susunod na gawain ay tila mas madali para sa iyo. Siya - sa mga coordinate ng punto.

Gawain 2. Mula sa punto, ang per-pen-di-ku-lar ay ibinababa sa abs-ciss axis. Nai-di-te abs-cis-su os-no-va-niya per-pen-di-ku-la-ra.

Gumawa tayo ng drawing:

Ang base ng perpendicular ay ang punto kung saan ito nag-intersect sa x-axis (axis) para sa akin ito ay isang punto. Ipinapakita ng figure na mayroon itong mga coordinate: . Kami ay interesado sa abscissa - iyon ay, ang "X" na bahagi. Siya ay pantay.

Sagot: .

Gawain 3. Sa ilalim ng mga kondisyon ng nakaraang problema, hanapin ang kabuuan ng mga distansya mula sa punto hanggang sa mga coordinate axes.

Ang gawain ay karaniwang elementarya kung alam mo kung ano ang distansya mula sa isang punto hanggang sa mga palakol. Alam mo? Umaasa ako, ngunit ipinaaalala ko pa rin sa iyo:

Kaya, sa aking pagguhit, na matatagpuan medyo mas mataas, nailarawan ko na ang isang tulad na patayo? Anong axis ito? sa axis. At ano ang haba nito? Siya ay pantay. Ngayon gumuhit ng patayo sa axis sa iyong sarili at hanapin ang haba nito. Magiging pantay, tama? Pagkatapos ang kanilang kabuuan ay pantay.

Sagot: .

Gawain 4. Sa mga kondisyon ng gawain 2, hanapin ang ordinate ng isang punto na simetriko sa isang punto tungkol sa x-axis.

Sa tingin ko intuitively mong nauunawaan kung ano ang simetrya? Napakaraming bagay ang mayroon nito: maraming gusali, mesa, eroplano, maraming geometric na hugis: isang bola, isang silindro, isang parisukat, isang rhombus, atbp. Sa madaling salita, ang simetrya ay maaaring maunawaan tulad ng sumusunod: ang isang pigura ay binubuo ng dalawa (o higit pa) magkaparehong kalahati. Ang simetrya na ito ay tinatawag na axial. Ano ang isang axis? Ito ang eksaktong linya kung saan ang pigura ay maaaring, medyo nagsasalita, ay "hiwain" sa magkatulad na mga kalahati (sa larawang ito, ang axis ng simetrya ay tuwid):

Ngayon ay bumalik tayo sa ating gawain. Alam namin na naghahanap kami ng isang punto na simetriko tungkol sa axis. Pagkatapos ang axis na ito ay ang axis ng simetrya. Kaya, kailangan nating markahan ang isang punto upang maputol ng axis ang segment sa dalawang pantay na bahagi. Subukang markahan ang gayong punto sa iyong sarili. Ngayon ihambing sa aking solusyon:

Ganoon din ba ang ginawa mo? Well! Sa nahanap na punto, kami ay interesado sa ordinate. Siya ay pantay

Sagot:

Ngayon sabihin sa akin, pagkatapos mag-isip ng isang segundo, ano ang magiging abscissa ng puntong simetriko sa point A tungkol sa y-axis? Ano ang iyong sagot? Tamang sagot: .

Sa pangkalahatan, ang panuntunan ay maaaring isulat tulad nito:

Ang isang puntong simetriko sa isang punto tungkol sa x-axis ay may mga coordinate:

Ang isang puntong simetriko sa isang punto tungkol sa y-axis ay may mga coordinate:

Well, ngayon ay talagang nakakatakot. gawain: Hanapin ang mga coordinate ng isang punto na simetriko sa isang punto, na nauugnay sa pinagmulan. Mag-isip ka muna para sa iyong sarili, at pagkatapos ay tingnan ang aking pagguhit!

Sagot:

Ngayon problema sa paralelogram:

Gawain 5: Ang mga puntos ay ver-shi-na-mi-pa-ral-le-lo-gram-ma. Find-dee-te o-dee-on-tu na mga puntos.

Maaari mong lutasin ang problemang ito sa dalawang paraan: lohika at paraan ng coordinate. Ilalapat ko muna ang paraan ng coordinate, at pagkatapos ay sasabihin ko sa iyo kung paano ka makakapagpasya kung hindi.

Ito ay lubos na malinaw na ang abscissa ng punto ay pantay. (ito ay namamalagi sa patayo na iginuhit mula sa punto hanggang sa x-axis). Kailangan nating hanapin ang ordinate. Samantalahin natin ang katotohanan na ang ating pigura ay isang paralelogram, na nangangahulugang iyon. Hanapin ang haba ng segment gamit ang formula para sa distansya sa pagitan ng dalawang puntos:

Ibinababa namin ang patayo na pagkonekta sa punto sa axis. Ang punto ng intersection ay tinutukoy ng isang titik.

Ang haba ng segment ay pantay. (hanapin ang problema sa iyong sarili, kung saan tinalakay natin ang sandaling ito), pagkatapos ay makikita natin ang haba ng segment gamit ang Pythagorean theorem:

Ang haba ng segment ay eksaktong kapareho ng ordinate nito.

Sagot: .

Isa pang solusyon (magbibigay lang ako ng isang larawan na naglalarawan nito)

Pag-unlad ng solusyon:

1. Gumastos

2. Maghanap ng mga coordinate ng punto at haba

3. Patunayan na.

Isa pa problema sa haba ng hiwa:

Ang mga puntos ay-la-yut-xia top-shi-on-mi tri-angle-no-ka. Hanapin ang haba ng kanyang midline, par-ral-lel-noy.

Naaalala mo ba kung ano ang gitnang linya ng isang tatsulok? Kung gayon para sa iyo ang gawaing ito ay elementarya. Kung hindi mo matandaan, pagkatapos ay ipapaalala ko sa iyo: ang gitnang linya ng isang tatsulok ay isang linya na nag-uugnay sa mga midpoint ng magkabilang panig. Ito ay kahanay sa base at katumbas ng kalahati nito.

Ang base ay isang segment. Kinailangan naming hanapin ang haba nito kanina, ito ay pantay. Pagkatapos ang haba ng midline ay kalahati ng haba at pantay.

Sagot: .

Komento: Ang problemang ito ay maaaring malutas sa ibang paraan, na tatalakayin natin sa ibang pagkakataon.

Pansamantala, narito ang ilang mga gawain para sa iyo, pagsasanay sa mga ito, ang mga ito ay medyo simple, ngunit nakakatulong ang mga ito na "ipasok ang iyong kamay" gamit ang paraan ng coordinate!

1. Lumilitaw ang mga puntos-la-yut-xia top-shi-on-mi tra-pe-tion. Hanapin ang haba ng midline nito.

2. Mga puntos at yav-la-yut-xia ver-shi-na-mi pa-ral-le-lo-gram-ma. Find-dee-te o-dee-on-tu na mga puntos.

3. Hanapin ang haba mula sa hiwa, ikonekta ang pangalawang punto at

4. Hanapin-di-te ang lugar para sa-the-red-shen-noy fi-gu-ry sa ko-or-di-nat-noy plane.

5. Ang isang bilog na nakasentro sa na-cha-le ko-or-di-nat ay dumadaan sa isang punto. Hanapin-de-te ang kanyang ra-di-bigote.

6. Nai-di-te ra-di-us circle-no-sti, describe-san-noy near the right-angle-no-ka, the tops-shi-ny of something-ro-go have co-or - di-na-you co-from-reply-pero

Mga solusyon:

1. Alam na ang midline ng isang trapezoid ay katumbas ng kalahati ng kabuuan ng mga base nito. Ang base ay pantay, ngunit ang base. Pagkatapos

Sagot:

2. Ang pinakamadaling paraan upang malutas ang problemang ito ay mapansin iyon (parallelogram rule). Kalkulahin ang mga coordinate ng mga vector at hindi mahirap: . Kapag nagdadagdag ng mga vector, idinaragdag ang mga coordinate. Pagkatapos ay may mga coordinate. Ang punto ay may parehong mga coordinate, dahil ang simula ng vector ay isang punto na may mga coordinate. Interesado kami sa ordinate. Siya ay pantay.

Sagot:

3. Agad kaming kumilos ayon sa formula para sa distansya sa pagitan ng dalawang punto:

Sagot:

4. Tingnan ang larawan at sabihin, sa pagitan ng dalawang pigura ay "pinipit" ang may kulay na lugar? Ito ay nasa pagitan ng dalawang parisukat. Kung gayon ang lugar ng nais na pigura ay katumbas ng lugar ng malaking parisukat minus ang lugar ng maliit. Ang gilid ng maliit na parisukat ay isang segment na nagkokonekta sa mga punto at ang haba nito ay

Pagkatapos ang lugar ng maliit na parisukat ay

Ginagawa namin ang parehong sa isang malaking parisukat: ang gilid nito ay isang segment na nagkokonekta sa mga punto at ang haba nito ay katumbas ng

Pagkatapos ang lugar ng malaking parisukat ay

Ang lugar ng nais na figure ay matatagpuan sa pamamagitan ng formula:

Sagot:

5. Kung ang bilog ay may pinanggalingan bilang sentro nito at dumaan sa isang punto, ang radius nito ay magiging eksaktong katumbas ng haba ng segment (gumawa ng drawing at mauunawaan mo kung bakit ito ay halata). Hanapin ang haba ng segment na ito:

Sagot:

6. Ito ay kilala na ang radius ng isang bilog na nakapaligid sa isang parihaba ay katumbas ng kalahati ng dayagonal nito. Hanapin natin ang haba ng alinman sa dalawang diagonal (pagkatapos ng lahat, sa isang parihaba sila ay pantay!)

Sagot:

Well, nakaya mo ba ang lahat? Hindi naman ganoon kahirap intindihin iyon, di ba? Mayroon lamang isang panuntunan dito - upang makagawa ng isang visual na larawan at simpleng "basahin" ang lahat ng data mula dito.

Kaunti na lang ang natitira sa amin. Mayroong literal na dalawa pang punto na nais kong talakayin.

Subukan nating lutasin ang simpleng problemang ito. Hayaan ang dalawang puntos at ibigay. Hanapin ang mga coordinate ng gitna ng segment. Ang solusyon sa problemang ito ay ang mga sumusunod: hayaang ang punto ay ang nais na gitna, pagkatapos ay mayroon itong mga coordinate:

I.e: coordinate ng gitna ng segment = arithmetic mean ng katumbas na coordinate ng mga dulo ng segment.

Ang panuntunang ito ay napakasimple at kadalasan ay hindi nagdudulot ng kahirapan sa mga mag-aaral. Tingnan natin kung anong mga problema at kung paano ito ginagamit:

1. Find-di-te or-di-na-tu se-re-di-us from-cut, connect-nya-yu-th-th point and

2. Ang mga puntos ay yav-la-yut-xia ver-shi-na-mi-che-you-reh-coal-no-ka. Find-di-te or-di-na-tu points of re-re-se-che-niya ng kanyang dia-go-on-lei.

3. Hanapin-di-te abs-cis-su ng gitna ng bilog, ilarawan-san-noy malapit sa parihaba-no-ka, ang mga tuktok-shi-mayroon tayong something-ro-go co-or-di- na-you co-from-vet-stvenno-but.

Mga solusyon:

1. Ang unang gawain ay isang klasiko lamang. Agad kaming kumilos sa pamamagitan ng pagtukoy sa midpoint ng segment. Siya ay may mga coordinate. Ang ordinate ay pantay.

Sagot:

2. Madaling makita na ang ibinigay na quadrilateral ay isang paralelogram (kahit isang rhombus!). Maaari mong patunayan ito sa iyong sarili sa pamamagitan ng pagkalkula ng mga haba ng mga gilid at paghahambing ng mga ito sa bawat isa. Ano ang alam ko tungkol sa paralelogram? Ang mga diagonal nito ay hinahati ng intersection point! Aha! Kaya ang punto ng intersection ng mga diagonal ay ano? Ito ang gitna ng alinman sa mga diagonal! Pipiliin ko, sa partikular, ang dayagonal. Pagkatapos ang punto ay may mga coordinate.Ang ordinate ng punto ay katumbas ng.

Sagot:

3. Ano ang gitna ng bilog na nakapaligid sa parihaba? Kasabay nito ang punto ng intersection ng mga diagonal nito. Ano ang alam mo tungkol sa mga dayagonal ng isang parihaba? Sila ay pantay at ang intersection point ay nahahati sa kalahati. Ang gawain ay nabawasan sa nauna. Kunin, halimbawa, ang dayagonal. At kung ang sentro ng circumscribed na bilog, kung gayon ang gitna. Naghahanap ako ng mga coordinate: Ang abscissa ay pantay.

Sagot:

Ngayon magsanay ng kaunti sa iyong sarili, ibibigay ko lamang ang mga sagot sa bawat problema upang masuri mo ang iyong sarili.

1. Nai-di-te ra-di-us circle-no-sti, describe-san-noy near the triangle-no-ka, the tops of someone-ro-go have ko-or-di -no misters

2. Hanapin-di-te o-di-na-tu ang gitna ng bilog, ilarawan ang san-noy malapit sa tatsulok-no-ka, ang tuktok-shi-mayroon tayong something-ro-go coordinates

3. Anong uri ng ra-di-y-sa ang dapat magkaroon ng isang bilog na may sentro sa isang punto upang mahawakan nito ang abs-ciss axis?

4. Find-di-te or-di-on-that point of re-re-se-che-ing of the axis and from-cut, connect-nya-yu-th-th point and

Mga sagot:

Nagtagumpay ba ang lahat? umaasa talaga ako! Ngayon - ang huling push. Ngayon mag-ingat lalo na. Ang materyal na ipapaliwanag ko ngayon ay direktang nauugnay hindi lamang sa mga simpleng gawain sa paraan ng coordinate mula sa bahagi B, ngunit nangyayari rin sa lahat ng dako sa problema C2.

Alin sa mga pangako ko ang hindi ko pa natutupad? Tandaan kung anong mga operasyon sa mga vector ang ipinangako kong ipakilala at alin ang ipinakilala ko sa kalaunan? Sigurado ba akong wala akong nakalimutan? Nakalimutan! Nakalimutan kong ipaliwanag kung ano ang ibig sabihin ng multiplication of vectors.

Mayroong dalawang paraan upang i-multiply ang isang vector sa isang vector. Depende sa napiling pamamaraan, makakakuha tayo ng mga bagay na may kakaibang kalikasan:

Ang produkto ng vector ay medyo nakakalito. Kung paano ito gagawin at kung bakit ito kinakailangan, tatalakayin namin sa iyo sa susunod na artikulo. At dito ay tututukan natin ang scalar product.

Mayroon nang dalawang paraan na nagpapahintulot sa amin na kalkulahin ito:

Tulad ng iyong nahulaan, ang resulta ay dapat na pareho! Kaya tingnan muna natin ang unang paraan:

Dot produkto sa pamamagitan ng mga coordinate

Hanapin: - karaniwang notasyon para sa tuldok na produkto

Ang formula para sa pagkalkula ay ang mga sumusunod:

Iyon ay, ang tuldok na produkto = ang kabuuan ng mga produkto ng mga coordinate ng mga vectors!

Halimbawa:

Hanapin-dee-te

Desisyon:

Hanapin ang mga coordinate ng bawat isa sa mga vectors:

Kinakalkula namin ang scalar product sa pamamagitan ng formula:

Sagot:

Tingnan mo, ganap na walang kumplikado!

Well, ngayon subukan ito sa iyong sarili:

Find-di-te scalar-noe pro-from-ve-de-nie century-to-ditch and

Inayos mo ba? Baka may napansin siyang maliit na pakulo? Suriin natin:

Vector coordinate, tulad ng sa nakaraang gawain! Sagot: .

Bilang karagdagan sa coordinate, mayroong isa pang paraan upang makalkula ang scalar na produkto, ibig sabihin, sa pamamagitan ng mga haba ng mga vector at ang cosine ng anggulo sa pagitan nila:

Nagsasaad ng anggulo sa pagitan ng mga vector at.

Iyon ay, ang scalar product ay katumbas ng produkto ng mga haba ng mga vectors at ang cosine ng anggulo sa pagitan nila.

Bakit kailangan natin ang pangalawang formula na ito, kung mayroon tayong una, na mas simple, hindi bababa sa walang mga cosine sa loob nito. At kailangan natin ito upang mula sa una at pangalawang mga formula maaari nating mahihinuha kung paano hanapin ang anggulo sa pagitan ng mga vector!

Hayaan Pagkatapos tandaan ang formula para sa haba ng isang vector!

Pagkatapos, kung isaksak ko ang data na ito sa formula ng produkto ng tuldok, makukuha ko ang:

Ngunit sa kabilang panig:

Kaya ano ang mayroon tayo? Mayroon na tayong formula para kalkulahin ang anggulo sa pagitan ng dalawang vectors! Minsan, para sa maikli, ito ay nakasulat din ng ganito:

Iyon ay, ang algorithm para sa pagkalkula ng anggulo sa pagitan ng mga vectors ay ang mga sumusunod:

1. Kinakalkula namin ang scalar product sa pamamagitan ng mga coordinate
2. Hanapin ang mga haba ng mga vector at i-multiply ang mga ito
3. Hatiin ang resulta ng punto 1 sa resulta ng punto 2

Magsanay tayo sa mga halimbawa:

1. Hanapin ang anggulo sa pagitan ng eyelids-to-ra-mi at. Ibigay ang iyong sagot sa antas.

2. Sa ilalim ng mga kondisyon ng nakaraang problema, hanapin ang cosine sa pagitan ng mga vectors

Gawin natin ito: Tutulungan kitang lutasin ang unang problema, at subukang gawin ang pangalawa sa iyong sarili! Sumasang-ayon ako? Pagkatapos ay magsimula tayo!

1. Ang mga vectors na ito ay ang mga dati nating kaibigan. Isinaalang-alang na namin ang kanilang scalar product at ito ay pantay. Ang kanilang mga coordinate ay: , . Pagkatapos ay makikita natin ang kanilang mga haba:

Pagkatapos ay hinahanap namin ang cosine sa pagitan ng mga vectors:

Ano ang cosine ng anggulo? Ito ang sulok.

Sagot:

Well, ngayon lutasin ang pangalawang problema sa iyong sarili, at pagkatapos ay ihambing! Magbibigay lang ako ng napakaikling solusyon:

2. may mga coordinate, may mga coordinate.

Hayaan ang anggulo sa pagitan ng mga vector at, pagkatapos

Sagot:

Dapat pansinin na ang mga gawain nang direkta sa mga vector at ang paraan ng mga coordinate sa bahagi B ng papel ng pagsusulit ay medyo bihira. Gayunpaman, ang karamihan sa mga problema sa C2 ay madaling malutas sa pamamagitan ng pagpapakilala ng isang coordinate system. Kaya't maaari mong isaalang-alang ang artikulong ito bilang isang pundasyon, batay sa kung saan gagawa kami ng medyo nakakalito na mga konstruksyon na kailangan naming lutasin mapaghamong mga gawain.

MGA COORDINATES AT MGA VECTOR. INTERMEDIATE LEVEL

Ikaw at ako ay patuloy na nag-aaral ng paraan ng mga coordinate. Sa huling bahagi, nag-deduce kami ng isang serye mahahalagang pormula, na nagpapahintulot sa:

1. Maghanap ng mga coordinate ng vector
2. Hanapin ang haba ng isang vector (alternatibo: ang distansya sa pagitan ng dalawang puntos)
3. Magdagdag, ibawas ang mga vector. I-multiply ang mga ito sa isang tunay na numero
4. Hanapin ang midpoint ng isang segment
5. Kalkulahin ang tuldok na produkto ng mga vector
6. Hanapin ang anggulo sa pagitan ng mga vector

Siyempre, ang buong paraan ng coordinate ay hindi magkasya sa 6 na puntos na ito. Pinagbabatayan nito ang gayong agham bilang analytical geometry, na makikilala mo sa unibersidad. Gusto ko lang bumuo ng isang pundasyon na magbibigay-daan sa iyo upang malutas ang mga problema sa isang estado. pagsusulit. Naisip namin ang mga gawain ng bahagi B sa Ngayon ay oras na upang lumipat sa isang husay na bagong antas! Ang artikulong ito ay ilalaan sa isang paraan para sa paglutas ng mga problemang C2 kung saan makatuwirang lumipat sa paraan ng coordinate. Ang pagiging makatwiran na ito ay tinutukoy ng kung ano ang kailangang matagpuan sa problema, at kung anong numero ang ibinigay. Kaya, gagamitin ko ang coordinate method kung ang mga tanong ay:

1. Hanapin ang anggulo sa pagitan ng dalawang eroplano
2. Hanapin ang anggulo sa pagitan ng isang linya at isang eroplano
3. Hanapin ang anggulo sa pagitan ng dalawang linya
4. Hanapin ang distansya mula sa isang punto patungo sa isang eroplano
5. Hanapin ang distansya mula sa isang punto hanggang sa isang linya
6. Hanapin ang distansya mula sa isang tuwid na linya hanggang sa isang eroplano
7. Hanapin ang distansya sa pagitan ng dalawang linya

Kung ang figure na ibinigay sa kondisyon ng problema ay isang katawan ng rebolusyon (bola, silindro, kono ...)

Ang mga angkop na numero para sa paraan ng coordinate ay:

1. kuboid
2. Pyramid (triangular, quadrangular, hexagonal)

Gayundin sa aking karanasan hindi angkop na gamitin ang coordinate method para sa:

1. Paghahanap ng mga lugar ng mga seksyon
2. Pagkalkula ng mga volume ng katawan

Gayunpaman, dapat na agad na tandaan na ang tatlong "hindi kanais-nais" na mga sitwasyon para sa paraan ng coordinate ay medyo bihira sa pagsasanay. Sa karamihan ng mga gawain, maaari itong maging iyong tagapagligtas, lalo na kung hindi ka masyadong malakas sa mga three-dimensional na konstruksyon (na kung minsan ay medyo masalimuot).

Ano ang lahat ng mga figure na nakalista ko sa itaas? Hindi na sila flat, tulad ng isang parisukat, tatsulok, bilog, ngunit napakalaki! Alinsunod dito, kailangan nating isaalang-alang hindi ang isang two-dimensional, ngunit isang three-dimensional na coordinate system. Madali itong binuo: bilang karagdagan sa abscissa at ordinates, ipakikilala namin ang isa pang axis, ang applicate axis. Ang figure ay schematically na nagpapakita ng kanilang relatibong posisyon:

Ang lahat ng mga ito ay mutually perpendicular, intersect sa isang punto, na kung saan ay tatawagin natin ang pinagmulan. Ang abscissa axis, tulad ng dati, ay ide-denote, ang ordinate axis - , at ang ipinakilala na applicate axis - .

Kung mas maaga ang bawat punto sa eroplano ay nailalarawan sa pamamagitan ng dalawang numero - ang abscissa at ang ordinate, kung gayon ang bawat punto sa espasyo ay inilarawan na ng tatlong numero - ang abscissa, ang ordinate, ang applicate. Halimbawa:

Alinsunod dito, ang abscissa ng punto ay pantay, ang ordinate ay , at ang applicate ay .

Minsan ang abscissa ng isang punto ay tinatawag ding projection ng punto papunta sa abscissa axis, ang ordinate ay ang projection ng punto papunta sa y-axis, at ang applicate ay ang projection ng punto papunta sa applicate axis. Alinsunod dito, kung ang isang punto ay ibinigay pagkatapos, isang punto na may mga coordinate:

tinatawag na projection ng isang punto sa isang eroplano

tinatawag na projection ng isang punto sa isang eroplano

Isang natural na tanong ang lumitaw: lahat ba ng mga formula na hinango para sa two-dimensional na kaso ay wasto sa kalawakan? Ang sagot ay oo, sila ay makatarungan at may parehong hitsura. Para sa isang maliit na detalye. Sa tingin ko nahulaan mo na kung alin. Sa lahat ng mga formula, kailangan nating magdagdag ng isa pang termino na responsable para sa applicate axis. Namely.

1. Kung ang dalawang puntos ay ibinigay: , kung gayon:

• Vector coordinate:
• Distansya sa pagitan ng dalawang puntos (o haba ng vector)
• May mga coordinate ang gitna ng segment

2. Kung ang dalawang vector ay ibinigay: at, pagkatapos:

• Ang kanilang tuldok na produkto ay:
• Ang cosine ng anggulo sa pagitan ng mga vectors ay:

Gayunpaman, ang espasyo ay hindi gaanong simple. Tulad ng naiintindihan mo, ang pagdaragdag ng isa pang coordinate ay nagpapakilala ng isang makabuluhang pagkakaiba-iba sa spectrum ng mga figure na "nabubuhay" sa espasyong ito. At para sa karagdagang pagsasalaysay, kailangan kong ipakilala ang ilan, sa halos pagsasalita, "paglalahat" ng tuwid na linya. Ang "generalization" na ito ay magiging isang eroplano. Ano ang alam mo tungkol sa eroplano? Subukan mong sagutin ang tanong, ano ang eroplano? Napakahirap sabihin. Gayunpaman, intuitive nating lahat na iniisip kung ano ang hitsura nito:

Sa halos pagsasalita, ito ay isang uri ng walang katapusang "dahon" na itinulak sa kalawakan. Ang "Infinity" ay dapat na maunawaan na ang eroplano ay umaabot sa lahat ng direksyon, iyon ay, ang lugar nito ay katumbas ng infinity. Gayunpaman, ang paliwanag na ito "sa mga daliri" ay hindi nagbibigay ng kaunting ideya tungkol sa istraktura ng eroplano. At magiging interesado kami dito.

Tandaan natin ang isa sa mga pangunahing axiom ng geometry:

• Ang isang tuwid na linya ay dumadaan sa dalawang magkaibang punto sa isang eroplano, bukod dito, isa lamang:

O ang analog nito sa espasyo:

Siyempre, naaalala mo kung paano makuha ang equation ng isang tuwid na linya mula sa dalawang ibinigay na mga punto, hindi ito mahirap: kung ang unang punto ay may mga coordinate: at ang pangalawa, kung gayon ang equation ng tuwid na linya ay ang mga sumusunod:

Naranasan mo ito noong ika-7 baitang. Sa espasyo, ang equation ng isang tuwid na linya ay ganito ang hitsura: magkaroon tayo ng dalawang puntos na may mga coordinate: , pagkatapos ay ang equation ng isang tuwid na linya na dumadaan sa kanila ay may anyo:

Halimbawa, ang isang linya ay dumadaan sa mga punto:

Paano ito dapat maunawaan? Dapat itong maunawaan bilang mga sumusunod: ang isang punto ay nasa isang linya kung ang mga coordinate nito ay nakakatugon sa sumusunod na sistema:

Hindi tayo magiging interesado sa equation ng isang tuwid na linya, ngunit kailangan nating bigyang pansin ang napakahalagang konsepto ng nagdidirekta na vector ng isang tuwid na linya. - anumang di-zero na vector na nakahiga sa isang naibigay na linya o kahanay nito.

Halimbawa, ang parehong mga vector ay mga vector ng direksyon ng isang tuwid na linya. Hayaan ang isang punto na nakahiga sa isang tuwid na linya, at maging ang nagdidirekta na vector. Pagkatapos ang equation ng isang tuwid na linya ay maaaring isulat sa sumusunod na anyo:

Muli, hindi ako magiging interesado sa equation ng isang tuwid na linya, ngunit kailangan ko talagang tandaan mo kung ano ang isang vector ng direksyon! muli: ito ay ANUMANG di-zero na vector na nakahiga sa isang linya, o kahanay nito.

Mag-withdraw three-point equation ng isang eroplano ay hindi na masyadong maliit, at kadalasan ay hindi sakop sa isang kurso sa high school. Ngunit walang kabuluhan! Ang pamamaraan na ito ay mahalaga kapag gumagamit tayo ng coordinate method upang malutas ang mga kumplikadong problema. Gayunpaman, ipinapalagay ko na puno ka ng pagnanais na matuto ng bago? Bukod dito, mapapahanga mo ang iyong guro sa unibersidad kapag lumabas na alam mo na kung paano gamitin ang teknik na karaniwang pinag-aaralan sa kurso ng analytic geometry. Kaya simulan na natin.

Ang equation ng isang eroplano ay hindi masyadong naiiba mula sa equation ng isang tuwid na linya sa isang eroplano, ibig sabihin, mayroon itong anyo:

ilang mga numero (hindi lahat ay katumbas ng zero), ngunit mga variable, halimbawa: atbp. Tulad ng nakikita mo, ang equation ng isang eroplano ay hindi masyadong naiiba mula sa equation ng isang tuwid na linya (linear function). Gayunpaman, tandaan kung ano ang pinagtatalunan namin sa iyo? Sinabi namin na kung mayroon kaming tatlong puntos na hindi nakahiga sa isang tuwid na linya, kung gayon ang equation ng eroplano ay kakaibang naibalik mula sa kanila. Pero paano? Susubukan kong ipaliwanag sa iyo.

Dahil ang equation ng eroplano ay:

At ang mga puntos ay nabibilang sa eroplanong ito, pagkatapos kapag pinapalitan ang mga coordinate ng bawat punto sa equation ng eroplano, dapat nating makuha ang tamang pagkakakilanlan:

Kaya, may pangangailangan na lutasin ang tatlong equation na may mga hindi alam! Dilemma! Gayunpaman, maaari nating palaging ipagpalagay na (para dito kailangan nating hatiin sa pamamagitan ng). Kaya, nakakakuha tayo ng tatlong equation na may tatlong hindi alam:

Gayunpaman, hindi namin malulutas ang gayong sistema, ngunit isulat ang misteryosong expression na sumusunod mula dito:

Equation ng isang eroplano na dumadaan sa tatlong ibinigay na puntos

\[\kaliwa| (\begin(array)(*(20)(c))(x - (x_0))&((x_1) - (x_0))&((x_2) - (x_0))\\(y - (y_0) )&((y_1) - (y_0))&((y_2) - (y_0))\\(z - (z_0))&((z_1) - (z_0))&((z_2) - (z_0)) \end(array)) \right| = 0\]

Tumigil ka! Ano pa ba ito? Ilang napaka hindi pangkaraniwang module! Gayunpaman, ang bagay na nakikita mo sa harap mo ay walang kinalaman sa modyul. Ang bagay na ito ay tinatawag na third-order determinant. Mula ngayon, kapag nakipag-usap ka sa paraan ng mga coordinate sa isang eroplano, madalas mong makikita ang parehong mga determinant na ito. Ano ang third order determinant? Kakatwa, ito ay isang numero lamang. Ito ay nananatiling maunawaan kung anong tiyak na numero ang ihahambing natin sa determinant.

Isulat muna natin ang third-order determinant sa higit pa pangkalahatang pananaw:

Nasaan ang ilang mga numero. Bukod dito, sa pamamagitan ng unang index ang ibig sabihin namin ay ang numero ng hilera, at sa pamamagitan ng index - ang numero ng hanay. Halimbawa, nangangahulugan ito na ang ibinigay na numero ay nasa intersection ng pangalawang row at ng ikatlong column. Ibigay natin ang sumusunod na tanong: paano natin eksaktong kalkulahin ang gayong determinant? Ibig sabihin, anong tiyak na numero ang ihahambing natin dito? Para sa tiyak na determinant ng ikatlong pagkakasunud-sunod, mayroong isang heuristic (visual) triangle na panuntunan, ganito ang hitsura:

1. Ang produkto ng mga elemento ng pangunahing dayagonal (mula sa kaliwa sa itaas hanggang sa ibabang kanan) ang produkto ng mga elemento na bumubuo sa unang tatsulok na "patayo" sa pangunahing dayagonal ang produkto ng mga elemento na bumubuo sa pangalawang tatsulok na "patayo" sa pangunahing dayagonal
2. Ang produkto ng mga elemento ng pangalawang dayagonal (mula sa kanang itaas hanggang sa kaliwang ibaba) ang produkto ng mga elemento na bumubuo sa unang tatsulok na "patayo" sa pangalawang dayagonal ang produkto ng mga elemento na bumubuo sa pangalawang tatsulok na "patayo" sa ang pangalawang dayagonal
3. Kung gayon ang determinant ay katumbas ng pagkakaiba sa pagitan ng mga halaga na nakuha sa hakbang at

Kung isusulat natin ang lahat ng ito sa mga numero, makukuha natin ang sumusunod na expression:

Gayunpaman, hindi mo kailangang kabisaduhin ang paraan ng pagkalkula sa form na ito, sapat na itago lamang ang mga tatsulok sa iyong ulo at ang mismong ideya ng kung ano ang idinagdag sa kung ano at kung ano ang ibawas mula sa kung ano).

Ilarawan natin ang pamamaraan ng tatsulok na may isang halimbawa:

1. Kalkulahin ang determinant:

Alamin natin kung ano ang idinaragdag at ibinabawas natin:

Mga tuntunin na may kasamang "plus":

Ito ang pangunahing dayagonal: ang produkto ng mga elemento ay

Ang unang tatsulok, "patayo sa pangunahing dayagonal: ang produkto ng mga elemento ay

Ang pangalawang tatsulok, "patayo sa pangunahing dayagonal: ang produkto ng mga elemento ay

Nagdagdag kami ng tatlong numero:

Mga tuntuning may kasamang "minus"

Ito ay isang side diagonal: ang produkto ng mga elemento ay

Ang unang tatsulok, "patayo sa pangalawang dayagonal: ang produkto ng mga elemento ay

Ang pangalawang tatsulok, "patayo sa pangalawang dayagonal: ang produkto ng mga elemento ay

Nagdagdag kami ng tatlong numero:

Ang kailangan lang gawin ay ibawas mula sa kabuuan ng mga plus terms ang kabuuan ng mga minus na termino:

kaya,

Tulad ng nakikita mo, walang kumplikado at supernatural sa pagkalkula ng mga determinant ng third-order. Mahalaga lamang na tandaan ang tungkol sa mga tatsulok at hindi gumawa ng mga pagkakamali sa aritmetika. Ngayon subukang kalkulahin ang iyong sarili:

Sinusuri namin:

1. Ang unang tatsulok na patayo sa pangunahing dayagonal:
2. Ang pangalawang tatsulok na patayo sa pangunahing dayagonal:
3. Ang kabuuan ng plus terms:
4. Unang tatsulok na patayo sa gilid na dayagonal:
5. Ang pangalawang tatsulok, patayo sa gilid na dayagonal:
6. Ang kabuuan ng mga termino na may minus:
7. Kabuuan ng mga plus na termino na binawasan ng kabuuan ng mga minus na termino:

Narito ang ilang higit pang mga determinant para sa iyo, kalkulahin ang kanilang mga halaga sa iyong sarili at ihambing sa mga sagot:

Mga sagot:

Buweno, tumugma ba ang lahat? Mahusay, pagkatapos ay maaari kang magpatuloy! Kung may mga paghihirap, kung gayon ang payo ko ay ito: sa Internet mayroong isang grupo ng mga programa para sa pagkalkula ng determinant online. Ang kailangan mo lang ay magkaroon ng sarili mong determinant, kalkulahin ito mismo, at pagkatapos ay ihambing ito sa kung ano ang kinakalkula ng programa. At iba pa hanggang sa magsimulang magtugma ang mga resulta. Sigurado akong hindi magtatagal ang sandaling ito!

Ngayon bumalik tayo sa determinant na isinulat ko noong pinag-usapan ko ang equation ng isang eroplano na dumadaan sa tatlong ibinigay na mga punto:

Ang kailangan mo lang gawin ay direktang kalkulahin ang halaga nito (gamit ang paraan ng tatsulok) at itakda ang resulta na katumbas ng zero. Naturally, dahil ang mga ito ay mga variable, makakakuha ka ng ilang expression na nakasalalay sa kanila. Ang expression na ito ang magiging equation ng isang eroplanong dumadaan sa tatlong ibinigay na mga punto na hindi nakahiga sa isang tuwid na linya!

Ilarawan natin ito sa isang simpleng halimbawa:

1. Buuin ang equation ng eroplanong dumadaan sa mga puntos

Bumubuo kami ng determinant para sa tatlong puntong ito:

Pinapasimple:

Ngayon ay direktang kinakalkula namin ito ayon sa panuntunan ng mga tatsulok:

\[(\left| (\begin(array)(*(20)(c))(x + 3)&2&6\\(y - 2)&0&1\\(z + 1)&5&0\end(array)) \ kanan| = \left((x + 3) \right) \cdot 0 \cdot 0 + 2 \cdot 1 \cdot \left((z + 1) \right) + \left((y - 2) \right) \cdot 5 \cdot 6 - )\]

Kaya, ang equation ng eroplano na dumadaan sa mga puntos ay:

Ngayon subukang lutasin ang isang problema sa iyong sarili, at pagkatapos ay tatalakayin natin ito:

2. Hanapin ang equation ng eroplanong dumadaan sa mga puntos

Well, pag-usapan natin ang solusyon ngayon:

Gumagawa kami ng determinant:

At kalkulahin ang halaga nito:

Pagkatapos ang equation ng eroplano ay may anyo:

O, pagbabawas ng, makukuha natin:

Ngayon dalawang gawain para sa pagpipigil sa sarili:

1. Buuin ang equation ng isang eroplanong dumadaan sa tatlong puntos:

Mga sagot:

Nagtugma ba ang lahat? Muli, kung may ilang mga paghihirap, kung gayon ang payo ko ay ito: kumuha ka ng tatlong puntos mula sa iyong ulo (na may mataas na antas ng posibilidad na hindi sila magsisinungaling sa isang tuwid na linya), bumuo ng isang eroplano sa kanila. At pagkatapos ay suriin ang iyong sarili online. Halimbawa, sa site:

Gayunpaman, sa tulong ng mga determinant, gagawin namin hindi lamang ang equation ng eroplano. Tandaan, sinabi ko sa iyo na para sa mga vector, hindi lamang ang produkto ng tuldok ang tinukoy. Mayroon ding isang vector, pati na rin ang isang halo-halong produkto. At kung ang scalar product ng dalawang vector ay magiging isang numero, kung gayon ang vector product ng dalawang vector ay magiging isang vector, at ang vector na ito ay magiging patayo sa mga ibinigay:

Bukod dito, ang modulus nito ay magiging katumbas ng lugar ng paralelogram na binuo sa mga vectors at. Kakailanganin natin ang vector na ito upang kalkulahin ang distansya mula sa isang punto hanggang sa isang linya. Paano natin makalkula ang cross product ng mga vectors at kung ang kanilang mga coordinate ay ibinigay? Ang determinant ng ikatlong order ay muling tumulong sa amin. Gayunpaman, bago ako lumipat sa algorithm para sa pagkalkula ng cross product, kailangan kong gumawa ng isang maliit na lyrical digression.

Ang paglihis na ito ay may kinalaman sa mga batayang vector.

Schematically ipinapakita ang mga ito sa figure:

Sa iyong palagay, bakit sila tinatawag na basic? Sa katotohanan ay :

O sa larawan:

Ang bisa ng formula na ito ay halata, dahil:

produkto ng vector

Ngayon ay maaari ko nang simulan ang pagpapakilala ng cross product:

Ang produkto ng vector ng dalawang vector ay isang vector na kinakalkula ayon sa sumusunod na panuntunan:

Ngayon magbigay tayo ng ilang halimbawa ng pagkalkula ng cross product:

Halimbawa 1: Hanapin ang cross product ng mga vectors:

Solusyon: Gumagawa ako ng determinant:

At kinakalkula ko ito:

Ngayon, mula sa pagsulat sa pamamagitan ng mga batayang vector, babalik ako sa karaniwang notasyon ng vector:

kaya:

Ngayon subukan.

handa na? Sinusuri namin:

At tradisyonal na dalawa mga gawain upang kontrolin:

1. Hanapin ang cross product ng mga sumusunod na vectors:
2. Hanapin ang cross product ng mga sumusunod na vectors:

Mga sagot:

Pinaghalong produkto ng tatlong vectors

Ang huling konstruksiyon na kailangan ko ay ang pinaghalong produkto ng tatlong vectors. Ito, tulad ng isang scalar, ay isang numero. Mayroong dalawang mga paraan upang makalkula ito. - sa pamamagitan ng determinant, - sa pamamagitan ng pinaghalong produkto.

Ibig sabihin, sabihin nating mayroon tayong tatlong vectors:

Pagkatapos ay ang pinaghalong produkto ng tatlong vectors, na tinutukoy ng ay maaaring kalkulahin bilang:

1. - ibig sabihin, ang pinaghalong produkto ay ang scalar product ng isang vector at ang vector product ng dalawang iba pang vectors

Halimbawa, ang pinaghalong produkto ng tatlong vectors ay:

Subukang kalkulahin ito sa iyong sarili gamit ang produkto ng vector at tiyaking tumutugma ang mga resulta!

Muli, dalawang halimbawa malayang desisyon:

Mga sagot:

Pagpili ng coordinate system

Well, ngayon mayroon na tayong lahat mahalagang pundasyon kaalaman upang malutas ang mga kumplikadong stereometric na problema sa geometry. Gayunpaman, bago magpatuloy nang direkta sa mga halimbawa at algorithm para sa paglutas ng mga ito, naniniwala ako na magiging kapaki-pakinabang na pag-isipan ang sumusunod na tanong: kung paano eksaktong pumili ng coordinate system para sa isang partikular na figure. Pagkatapos ng lahat, ito ang pagpipilian Kaugnay na posisyon Ang mga coordinate system at figure sa kalawakan ay sa huli ay matukoy kung gaano kahirap ang mga kalkulasyon.

Ipinaaalala ko sa iyo na sa seksyong ito ay isinasaalang-alang namin ang mga sumusunod na figure:

1. kuboid
2. Tuwid na prisma (tatsulok, heksagonal...)
3. Pyramid (triangular, quadrangular)
4. Tetrahedron (kapareho ng triangular pyramid)

Para sa isang cuboid o cube, inirerekomenda ko ang sumusunod na konstruksyon:

Iyon ay, ilalagay ko ang figure "sa sulok". Ang kubo at ang parallelepiped ay napaka magandang figures. Para sa kanila, madali mong mahahanap ang mga coordinate ng mga vertex nito. Halimbawa, kung (tulad ng ipinapakita sa larawan)

kung gayon ang mga coordinate ng vertex ay:

Siyempre, hindi mo kailangang tandaan ito, ngunit tandaan kung paano pinakamahusay na iposisyon ang kubo o kuboid- kanais-nais.

tuwid na prisma

Ang prism ay isang mas nakakapinsalang pigura. Maaari mo itong ayusin sa espasyo sa iba't ibang paraan. Gayunpaman, sa palagay ko ang sumusunod ay ang pinakamahusay na pagpipilian:

Triangular prism:

Iyon ay, inilalagay namin ang isa sa mga gilid ng tatsulok nang buo sa axis, at ang isa sa mga vertices ay tumutugma sa pinagmulan.

Hexagonal prism:

Iyon ay, ang isa sa mga vertices ay tumutugma sa pinagmulan, at ang isa sa mga gilid ay namamalagi sa axis.

Quadrangular at hexagonal pyramid:

Isang sitwasyon na katulad ng isang kubo: pinagsasama namin ang dalawang panig ng base na may mga coordinate axes, pinagsama namin ang isa sa mga vertices sa pinagmulan. Ang tanging maliit na kahirapan ay ang kalkulahin ang mga coordinate ng punto.

Para sa isang hexagonal pyramid - kapareho ng para sa isang hexagonal prism. Ang pangunahing gawain ay muli sa paghahanap ng mga coordinate ng vertex.

Tetrahedron (triangular pyramid)

Ang sitwasyon ay halos kapareho sa ibinigay ko para sa tatsulok na prisma: ang isang vertex ay nag-tutugma sa pinagmulan, ang isang panig ay namamalagi sa coordinate axis.

Well, ngayon ikaw at ako ay malapit nang magsimulang malutas ang mga problema. Mula sa sinabi ko sa pinakasimula ng artikulo, maaari mong gawin ang sumusunod na konklusyon: karamihan sa mga problema sa C2 ay nahahati sa 2 kategorya: mga problema para sa anggulo at mga problema para sa distansya. Una, isasaalang-alang namin ang mga problema para sa paghahanap ng isang anggulo. Sila naman, ay nahahati sa mga sumusunod na kategorya (habang tumataas ang pagiging kumplikado):

Mga problema sa paghahanap ng mga sulok

1. Paghahanap ng anggulo sa pagitan ng dalawang linya
2. Paghahanap ng anggulo sa pagitan ng dalawang eroplano

Isaalang-alang natin ang mga problemang ito nang sunud-sunod: magsimula tayo sa paghahanap ng anggulo sa pagitan ng dalawang tuwid na linya. Halika, tandaan, nalutas mo na ba namin ang mga katulad na halimbawa dati? Naaalala mo, dahil mayroon na kaming katulad ... Naghahanap kami ng isang anggulo sa pagitan ng dalawang vectors. Ipinaaalala ko sa iyo, kung ang dalawang vector ay ibinigay: at, pagkatapos ay ang anggulo sa pagitan ng mga ito ay matatagpuan mula sa kaugnayan:

Ngayon ay mayroon tayong layunin - ang paghahanap ng anggulo sa pagitan ng dalawang tuwid na linya. Lumiko tayo sa "flat na larawan":

Ilang anggulo ang makukuha natin kapag nagsalubong ang dalawang linya? Mga bagay na. Totoo, dalawa lamang sa kanila ang hindi pantay, habang ang iba ay patayo sa kanila (at samakatuwid ay nag-tutugma sa kanila). Kaya anong anggulo ang dapat nating isaalang-alang ang anggulo sa pagitan ng dalawang tuwid na linya: o? Narito ang panuntunan: ang anggulo sa pagitan ng dalawang tuwid na linya ay palaging hindi hihigit sa mga degree. Ibig sabihin, mula sa dalawang anggulo, lagi nating pipiliin ang anggulo na may pinakamaliit na sukat ng antas. Ibig sabihin, sa larawang ito, ang anggulo sa pagitan ng dalawang linya ay pantay. Upang hindi mag-abala sa paghahanap ng pinakamaliit sa dalawang anggulo sa bawat oras, iminungkahi ng mga tusong mathematician ang paggamit ng modyul. Kaya, ang anggulo sa pagitan ng dalawang tuwid na linya ay tinutukoy ng formula:

Ikaw, bilang isang matulungin na mambabasa, ay dapat may tanong: saan, sa katunayan, nakukuha natin ang mismong mga numerong ito na kailangan nating kalkulahin ang cosine ng isang anggulo? Sagot: kukunin namin sila mula sa mga vector ng direksyon ng mga linya! Kaya, ang algorithm para sa paghahanap ng anggulo sa pagitan ng dalawang linya ay ang mga sumusunod:

1. Inilapat namin ang formula 1.

O sa higit pang detalye:

1. Hinahanap namin ang mga coordinate ng vector ng direksyon ng unang tuwid na linya
2. Hinahanap namin ang mga coordinate ng vector ng direksyon ng pangalawang linya
3. Kalkulahin ang modulus ng kanilang scalar product
4. Hinahanap namin ang haba ng unang vector
5. Hinahanap namin ang haba ng pangalawang vector
6. I-multiply ang mga resulta ng point 4 sa mga resulta ng point 5
7. Hinahati namin ang resulta ng point 3 sa resulta ng point 6. Nakukuha namin ang cosine ng anggulo sa pagitan ng mga linya
8. Kung ang ibinigay na resulta ay nagbibigay-daan sa iyo upang tumpak na kalkulahin ang anggulo, hinahanap namin ito
9. Kung hindi, sumulat kami sa pamamagitan ng arccosine

Kaya, ngayon ay oras na upang magpatuloy sa mga gawain: Ipapakita ko ang solusyon ng unang dalawa nang detalyado, ipapakita ko ang solusyon ng isa pa sa buod, at para sa huling dalawang problema ay magbibigay lang ako ng mga sagot, dapat mong isagawa ang lahat ng mga kalkulasyon para sa kanila mismo.

Mga gawain:

1. Sa tamang tet-ra-ed-re, hanapin-di-te ang anggulo sa pagitan ng you-so-that tet-ra-ed-ra at ng me-di-a-noy bo-ko-how side.

2. Sa right-forward six-coal-pi-ra-mi-de, ang daang-ro-na-os-no-va-niya ay kahit papaano ay pantay, at ang mga gilid na tadyang ay pantay, hanapin ang anggulo sa pagitan ng tuwid mga linya at.

3. Ang haba ng lahat ng gilid ng kanang kamay na four-you-rech-coal-noy pi-ra-mi-dy ay pantay-pantay sa isa't isa. Hanapin ang anggulo sa pagitan ng mga tuwid na linya at kung from-re-zok - you-so-that given pi-ra-mi-dy, the point is se-re-di-on her bo-ko- th rib

4. Sa gilid ng kubo mula-me-che-sa isang punto upang Hanapin-di-te ang anggulo sa pagitan ng mga tuwid na linya at

5. Point - se-re-di-sa mga gilid ng kubo Nai-di-te ang anggulo sa pagitan ng mga tuwid na linya at.

Ito ay hindi nagkataon na inilagay ko ang mga gawain sa ganitong pagkakasunud-sunod. Habang wala ka pang oras upang simulan ang pag-navigate sa paraan ng coordinate, ako mismo ay susuriin ang pinaka "problemadong" figure, at iiwan kita upang harapin ang pinakasimpleng kubo! Unti-unti kailangan mong matutunan kung paano magtrabaho kasama ang lahat ng mga figure, dagdagan ko ang pagiging kumplikado ng mga gawain mula sa paksa hanggang sa paksa.

Simulan natin ang paglutas ng mga problema:

1. Gumuhit ng tetrahedron, ilagay ito sa coordinate system gaya ng iminungkahi ko kanina. Dahil ang tetrahedron ay regular, ang lahat ng mga mukha nito (kabilang ang base) ay regular na mga tatsulok. Dahil hindi kami binibigyan ng haba ng gilid, kaya ko itong pantay-pantay. Sa tingin ko naiintindihan mo na ang anggulo ay hindi talaga magdedepende kung gaano kalaki ang magiging "stretch" ng ating tetrahedron ?. Iguguhit ko rin ang taas at median sa tetrahedron. Sa daan, iguguhit ko ang base nito (magagamit din ito para sa atin).

Kailangan kong hanapin ang anggulo sa pagitan ng at. Ano ang alam natin? Coordinate of the point lang ang alam natin. Kaya, kailangan nating makahanap ng higit pang mga coordinate ng mga puntos. Ngayon ay iniisip natin: ang isang punto ay isang punto ng intersection ng mga taas (o mga bisector o median) ng isang tatsulok. Ang isang tuldok ay isang nakataas na punto. Ang punto ay ang midpoint ng segment. Pagkatapos ay sa wakas kailangan nating hanapin: ang mga coordinate ng mga puntos: .

Magsimula tayo sa pinakasimpleng: point coordinates. Tingnan ang figure: Ito ay malinaw na ang applicate ng isang punto ay katumbas ng zero (ang punto ay namamalagi sa isang eroplano). Ang ordinate nito ay pantay (dahil ito ang median). Mas mahirap hanapin ang abscissa nito. Gayunpaman, ito ay madaling gawin batay sa Pythagorean theorem: Isaalang-alang ang isang tatsulok. Ang hypotenuse nito ay pantay, at ang isa sa mga binti ay pantay Pagkatapos:

Sa wakas mayroon kaming:

Ngayon, hanapin natin ang mga coordinate ng punto. Ito ay malinaw na ang applicate nito ay muling katumbas ng zero, at ang ordinate nito ay kapareho ng sa isang punto, iyon ay. Hanapin natin ang abscissa nito. Ito ay ginagawa sa halip na walang kabuluhan kung ang isa ay naaalala iyon ang taas ng isang equilateral triangle ay hinati sa intersection point sa proporsyon pagbibilang mula sa itaas. Dahil:, kung gayon ang nais na abscissa ng punto, katumbas ng haba ng segment, ay katumbas ng:. Kaya, ang mga coordinate ng punto ay:

Hanapin natin ang mga coordinate ng punto. Malinaw na ang abscissa at ordinate nito ay kasabay ng abscissa at ordinate ng punto. At ang applique ay katumbas ng haba ng segment. - ito ay isa sa mga binti ng tatsulok. Ang hypotenuse ng isang tatsulok ay isang segment - isang binti. Hinahanap ito para sa mga dahilan na na-highlight ko nang naka-bold:

Ang punto ay ang midpoint ng segment. Pagkatapos ay kailangan nating tandaan ang formula para sa mga coordinate ng gitna ng segment:

Iyon lang, ngayon ay maaari nating hanapin ang mga coordinate ng mga vector ng direksyon:

Well, handa na ang lahat: pinapalitan namin ang lahat ng data sa formula:

kaya,

Sagot:

Hindi ka dapat matakot sa gayong "kakila-kilabot" na mga sagot: para sa mga problema C2 ito ay isang karaniwang kasanayan. Mas gugustuhin kong magulat sa "maganda" na sagot sa bahaging ito. Gayundin, tulad ng iyong nabanggit, halos hindi ako gumamit ng anumang bagay maliban sa Pythagorean theorem at ang pag-aari ng mga taas ng isang equilateral triangle. Iyon ay, upang malutas ang stereometric na problema, ginamit ko ang pinakamababang stereometry. Ang pakinabang dito ay bahagyang "napapatay" ng medyo masalimuot na mga kalkulasyon. Ngunit ang mga ito ay medyo algorithmic!

2. Gumuhit ng regular na hexagonal pyramid kasama ang coordinate system, pati na rin ang base nito:

Kailangan nating hanapin ang anggulo sa pagitan ng mga linya at. Kaya, ang aming gawain ay nabawasan sa paghahanap ng mga coordinate ng mga puntos: . Hahanapin natin ang mga coordinate ng huling tatlo mula sa maliit na guhit, at makikita natin ang coordinate ng vertex sa pamamagitan ng coordinate ng punto. Maraming trabaho, ngunit kailangan mong magsimula!

a) Coordinate: malinaw na ang applicate at ordinate nito ay zero. Hanapin natin ang abscissa. Upang gawin ito, isaalang-alang ang isang tamang tatsulok. Sa kasamaang palad, sa loob nito ay alam lamang natin ang hypotenuse, na katumbas ng. Susubukan naming hanapin ang binti (dahil malinaw na dalawang beses ang haba ng binti ay magbibigay sa amin ng abscissa ng punto). Paano natin siya hahanapin? Tandaan natin kung anong uri ng pigura ang mayroon tayo sa base ng pyramid? Ito ay isang regular na hexagon. Ano ang ibig sabihin nito? Nangangahulugan ito na ang lahat ng panig at lahat ng mga anggulo ay pantay. Kailangan nating makahanap ng isang ganoong sulok. Anumang mga ideya? Mayroong maraming mga ideya, ngunit mayroong isang formula:

Ang kabuuan ng mga anggulo ng isang regular na n-gon ay .

Kaya, ang kabuuan ng mga anggulo ng isang regular na hexagon ay mga degree. Pagkatapos ang bawat isa sa mga anggulo ay katumbas ng:

Tingnan natin muli ang larawan. Malinaw na ang segment ay ang bisector ng anggulo. Pagkatapos ang anggulo ay degrees. Pagkatapos:

Tapos saan.

Kaya mayroon itong mga coordinate

b) Ngayon ay madali nating mahahanap ang coordinate ng punto: .

c) Hanapin ang mga coordinate ng punto. Dahil ang abscissa nito ay tumutugma sa haba ng segment, ito ay pantay. Ang paghahanap ng ordinate ay hindi rin napakahirap: kung ikinonekta natin ang mga punto at at tukuyin ang punto ng intersection ng linya, sabihin para sa. (gawin mo ito sa iyong sarili simpleng konstruksiyon). Pagkatapos Kaya, ang ordinate ng point B ay katumbas ng kabuuan ng mga haba ng mga segment. Tingnan natin muli ang tatsulok. Pagkatapos

Then since Then may coordinate ang point

d) Ngayon hanapin ang mga coordinate ng punto. Isaalang-alang ang isang parihaba at patunayan na Kaya, ang mga coordinate ng punto ay:

e) Nananatili itong hanapin ang mga coordinate ng vertex. Malinaw na ang abscissa at ordinate nito ay kasabay ng abscissa at ordinate ng punto. Maghanap tayo ng app. Simula noon. Isaalang-alang ang isang tamang tatsulok. Sa pamamagitan ng kondisyon ng problema, ang lateral edge. Ito ang hypotenuse ng aking tatsulok. Pagkatapos ang taas ng pyramid ay ang binti.

Pagkatapos ang punto ay may mga coordinate:

Iyon lang, mayroon akong mga coordinate ng lahat ng mga punto ng interes sa akin. Naghahanap ako ng mga coordinate ng nagdidirekta ng mga vector ng mga tuwid na linya:

Hinahanap namin ang anggulo sa pagitan ng mga vector na ito:

Sagot:

Muli, kapag nilutas ang problemang ito, hindi ako gumamit ng anumang sopistikadong mga trick, maliban sa formula para sa kabuuan ng mga anggulo ng isang regular na n-gon, pati na rin ang kahulugan ng cosine at sine ng isang right triangle.

3. Dahil muli kaming hindi binibigyan ng mga haba ng mga gilid sa pyramid, ituturing ko silang katumbas ng isa. Kaya, dahil ang LAHAT ng mga gilid, at hindi lamang ang mga gilid, ay pantay-pantay sa bawat isa, pagkatapos ay sa base ng pyramid at ako ay namamalagi ng isang parisukat, at ang mga gilid na mukha ay regular na mga tatsulok. Ilarawan natin ang gayong pyramid, pati na rin ang base nito sa isang eroplano, na minarkahan ang lahat ng data na ibinigay sa teksto ng problema:

Hinahanap namin ang anggulo sa pagitan ng at. Gagawa ako ng napakaikling mga kalkulasyon kapag hinahanap ko ang mga coordinate ng mga puntos. Kakailanganin mong "i-decrypt" ang mga ito:

b) - ang gitna ng segment. Ang kanyang mga coordinate:

c) Hahanapin ko ang haba ng segment gamit ang Pythagorean theorem sa isang tatsulok. Hahanapin ko sa pamamagitan ng Pythagorean theorem sa isang tatsulok.

Mga Coordinate:

d) - ang gitna ng segment. Ang mga coordinate nito ay

e) Mga coordinate ng vector

f) Vector coordinate

g) Naghahanap ng anggulo:

Cube - pinakasimpleng pigura. Sigurado ako na maaari mong malaman ito sa iyong sarili. Ang mga sagot sa mga problema 4 at 5 ay ang mga sumusunod:

Paghahanap ng anggulo sa pagitan ng isang linya at isang eroplano

Well, ang oras para sa mga simpleng puzzle ay tapos na! Ngayon ang mga halimbawa ay magiging mas mahirap. Upang mahanap ang anggulo sa pagitan ng isang linya at isang eroplano, magpapatuloy kami bilang mga sumusunod:

1. Gamit ang tatlong puntos, binubuo namin ang equation ng eroplano
   ,
   gamit ang third order determinant.
2. Sa pamamagitan ng dalawang puntos hinahanap namin ang mga coordinate ng nagdidirekta na vector ng tuwid na linya:
3. Inilapat namin ang formula upang kalkulahin ang anggulo sa pagitan ng isang tuwid na linya at isang eroplano:

Tulad ng nakikita mo, ang formula na ito ay halos kapareho sa ginamit namin upang mahanap ang mga anggulo sa pagitan ng dalawang linya. Ang istraktura ng kanang bahagi ay pareho lamang, at sa kaliwa ay naghahanap kami ngayon ng isang sine, at hindi isang cosine, tulad ng dati. Well, isang pangit na aksyon ang idinagdag - ang paghahanap para sa equation ng eroplano.

Huwag tayong mag-shelve mga halimbawa ng paglutas:

1. Os-no-va-ni-em straight-my prize-we are-la-et-xia equal-but-poor-ren-ny triangle-nick you-with-na premyong-tayo ay pantay-pantay. Hanapin ang anggulo sa pagitan ng tuwid na linya at ng eroplano

2. Sa isang parihabang pa-ral-le-le-pi-pe-de mula sa Kanluran Nai-di-te ang anggulo sa pagitan ng tuwid na linya at ng eroplano

3. Sa kanang kamay na anim na coal prism, ang lahat ng mga gilid ay pantay. Hanapin ang anggulo sa pagitan ng tuwid na linya at ng eroplano.

4. Sa kanang tatsulok na pi-ra-mi-de na may os-but-va-ni-em mula sa kanluran ng rib Nai-di-te angle, ob-ra-zo-van -ny plane ng os -no-va-niya at straight-my, dumadaan sa se-re-di-na ng mga tadyang at

5. Ang mga haba ng lahat ng mga gilid ng kanang quadrangular pi-ra-mi-dy na may tuktok ay katumbas ng bawat isa. Hanapin ang anggulo sa pagitan ng tuwid na linya at ng eroplano, kung ang punto ay se-re-di-sa bo-ko-in-th na gilid ng pi-ra-mi-dy.

Muli, malulutas ko ang unang dalawang problema nang detalyado, ang pangatlo - sa madaling sabi, at iiwan ko ang huling dalawa para malutas mo nang mag-isa. Bilang karagdagan, kailangan mo nang harapin ang triangular at quadrangular pyramids, ngunit hindi pa sa prisms.

Mga solusyon:

1. Gumuhit ng isang prisma, pati na rin ang base nito. Pagsamahin natin ito sa coordinate system at markahan ang lahat ng data na ibinigay sa pahayag ng problema:

Humihingi ako ng paumanhin para sa ilang hindi pagsunod sa mga sukat, ngunit para sa paglutas ng problema na ito, sa katunayan, ay hindi napakahalaga. Ang eroplano lang" pader sa likod» ng aking prisma. Sapat na hulaan lamang na ang equation ng naturang eroplano ay may anyo:

Gayunpaman, maaari rin itong direktang ipakita:

Pinipili namin ang arbitrary na tatlong punto sa eroplanong ito: halimbawa, .

Gawin natin ang equation ng eroplano:

Mag-ehersisyo para sa iyo: kalkulahin ang determinant na ito sa iyong sarili. Nagtagumpay ka ba? Pagkatapos ang equation ng eroplano ay may anyo:

O kaya lang

kaya,

Upang malutas ang halimbawa, kailangan kong hanapin ang mga coordinate ng nagdidirekta na vector ng tuwid na linya. Dahil ang punto ay nag-tutugma sa pinanggalingan, ang mga coordinate ng vector ay mag-tutugma lamang sa mga coordinate ng punto. Upang gawin ito, hahanapin muna natin ang mga coordinate ng punto.

Upang gawin ito, isaalang-alang ang isang tatsulok. Gumuhit tayo ng taas (isa rin itong median at bisector) mula sa itaas. Dahil, kung gayon ang ordinate ng punto ay pantay. Upang mahanap ang abscissa ng puntong ito, kailangan nating kalkulahin ang haba ng segment. Sa pamamagitan ng Pythagorean theorem mayroon tayo:

Pagkatapos ang punto ay may mga coordinate:

Ang isang tuldok ay isang "itinaas" sa isang tuldok:

Pagkatapos ang mga coordinate ng vector:

Sagot:

Tulad ng nakikita mo, walang pangunahing mahirap sa paglutas ng mga naturang problema. Sa katunayan, ang "straightness" ng isang figure tulad ng isang prism ay nagpapadali sa proseso ng kaunti pa. Ngayon ay lumipat tayo sa susunod na halimbawa:

2. Gumuhit kami ng isang parallelepiped, gumuhit ng isang eroplano at isang tuwid na linya sa loob nito, at hiwalay din na gumuhit ng mas mababang base nito:

Una, nakita natin ang equation ng eroplano: Ang mga coordinate ng tatlong puntos na nakahiga dito:

(ang unang dalawang coordinate ay nakuha sa isang malinaw na paraan, at madali mong mahanap ang huling coordinate mula sa larawan mula sa punto). Pagkatapos ay binubuo namin ang equation ng eroplano:

Kinakalkula namin:

Hinahanap namin ang mga coordinate ng vector ng direksyon: Malinaw na ang mga coordinate nito ay nag-tutugma sa mga coordinate ng punto, hindi ba? Paano makahanap ng mga coordinate? Ito ang mga coordinate ng punto, na nakataas sa kahabaan ng applicate axis ng isa! . Pagkatapos ay hinahanap namin ang nais na anggulo:

Sagot:

3. Gumuhit ng isang regular na hexagonal pyramid, at pagkatapos ay gumuhit ng isang eroplano at isang tuwid na linya sa loob nito.

Narito ito ay kahit na may problema upang gumuhit ng isang eroplano, hindi sa banggitin ang solusyon ng problemang ito, ngunit ang coordinate na paraan ay walang pakialam! Nasa kagalingan nito ang pangunahing bentahe nito!

Ang eroplano ay dumaan sa tatlong punto: . Hinahanap namin ang kanilang mga coordinate:

isa). Ipakita ang mga coordinate para sa huling dalawang puntos sa iyong sarili. Kakailanganin mong lutasin ang problema sa isang hexagonal pyramid para dito!

2) Binubuo namin ang equation ng eroplano:

Hinahanap namin ang mga coordinate ng vector: . (Tingnan muli ang triangular pyramid problem!)

3) Naghahanap kami ng isang anggulo:

Sagot:

Gaya ng nakikita mo, walang supernatural na mahirap sa mga gawaing ito. Kailangan mo lamang na maging maingat sa mga ugat. Sa huling dalawang problema, ibibigay ko lamang ang mga sagot:

Tulad ng nakikita mo, ang pamamaraan para sa paglutas ng mga problema ay pareho sa lahat ng dako: ang pangunahing gawain ay upang mahanap ang mga coordinate ng mga vertex at palitan ang mga ito sa ilang mga formula. Nananatili para sa amin na isaalang-alang ang isa pang klase ng mga problema para sa pagkalkula ng mga anggulo, katulad:

Pagkalkula ng mga anggulo sa pagitan ng dalawang eroplano

Ang algorithm ng solusyon ay ang mga sumusunod:

1. Para sa tatlong puntos hinahanap namin ang equation ng unang eroplano:
2. Para sa iba pang tatlong punto, hinahanap namin ang equation ng pangalawang eroplano:
3. Inilapat namin ang formula:

Tulad ng nakikita mo, ang formula ay halos kapareho sa naunang dalawa, sa tulong kung saan kami ay naghahanap ng mga anggulo sa pagitan ng mga tuwid na linya at sa pagitan ng isang tuwid na linya at isang eroplano. Kaya't ang pag-alala sa isang ito ay hindi magiging mahirap para sa iyo. Pumunta tayo sa problema:

1. Ang isang daang-ro-sa batayan ng kanang tatsulok na prism ay pantay, at ang dia-go-nal ng gilid na mukha ay pantay. Hanapin ang anggulo sa pagitan ng eroplano at ng eroplano ng base ng premyo.

2. Sa right-forward four-you-re-coal-noy pi-ra-mi-de, lahat ng mga gilid ng isang tao ay pantay, hanapin ang sine ng anggulo sa pagitan ng eroplano at ng eroplanong Ko-Stu, na dumadaan ang punto ng per-pen-di-ku-lyar-but straight-my.

3. Sa isang regular na four-coal prism, ang mga gilid ng os-no-va-nia ay pantay, at ang mga gilid ng gilid ay pantay. Sa gilid from-me-che-to the point so that. Hanapin ang anggulo sa pagitan ng mga eroplano at

4. Sa kanang quadrangular prism, ang mga gilid ng mga base ay pantay, at ang mga gilid na gilid ay pantay. Sa gilid mula-me-che-sa isang punto upang Hanapin ang anggulo sa pagitan ng mga eroplano at.

5. Sa kubo, hanapin ang co-si-nus ng anggulo sa pagitan ng mga eroplano at

Mga solusyon sa problema:

1. Gumuhit ako ng isang regular (sa base - isang equilateral triangle) na tatsulok na prisma at minarkahan dito ang mga eroplano na lumilitaw sa kondisyon ng problema:

Kailangan nating hanapin ang mga equation ng dalawang eroplano: Ang base equation ay nakuha nang walang kabuluhan: maaari mong gawin ang katumbas na determinant para sa tatlong puntos, ngunit gagawin ko kaagad ang equation:

Ngayon hanapin natin ang equation Point ay may mga coordinate Point - Dahil - ang median at ang taas ng tatsulok, ito ay madaling mahanap sa pamamagitan ng Pythagorean theorem sa isang tatsulok. Pagkatapos ang punto ay may mga coordinate: Hanapin ang applicate ng punto Upang gawin ito, isaalang-alang ang isang tamang tatsulok

Pagkatapos ay nakuha namin ang mga sumusunod na coordinate: Binubuo namin ang equation ng eroplano.

Kinakalkula namin ang anggulo sa pagitan ng mga eroplano:

Sagot:

2. Paggawa ng drawing:

Ang pinakamahirap na bagay ay upang maunawaan kung anong uri ng misteryosong eroplano ito, na dumadaan sa isang punto nang patayo. Well, ang pangunahing bagay ay kung ano ito? Ang pangunahing bagay ay pagkaasikaso! Sa katunayan, ang linya ay patayo. Ang linya ay patayo din. Pagkatapos ang eroplanong dumadaan sa dalawang linyang ito ay magiging patayo sa linya, at, sa pamamagitan ng paraan, ay dadaan sa punto. Ang eroplanong ito ay dumadaan din sa tuktok ng pyramid. Pagkatapos ay ang nais na eroplano - At ang eroplano ay ibinigay na sa amin. Naghahanap kami ng mga coordinate ng mga puntos.

Nahanap namin ang coordinate ng punto sa pamamagitan ng punto. Mula sa maliit na guhit madaling mahihinuha na ang mga coordinate ng punto ay ang mga sumusunod: Ano ngayon ang natitira upang mahanap upang mahanap ang mga coordinate ng tuktok ng pyramid? Kailangan pa ring kalkulahin ang taas nito. Ginagawa ito gamit ang parehong Pythagorean theorem: una, patunayan iyon (trivially mula sa maliliit na triangles na bumubuo ng isang parisukat sa base). Dahil ayon sa kondisyon, mayroon kaming:

Ngayon handa na ang lahat: vertex coordinates:

Binubuo namin ang equation ng eroplano:

Dalubhasa ka na sa pagkalkula ng mga determinant. Madaling matatanggap mo ang:

O kung hindi man (kung i-multiply natin ang parehong bahagi sa ugat ng dalawa)

Ngayon hanapin natin ang equation ng eroplano:

(Hindi mo nakalimutan kung paano natin nakuha ang equation ng eroplano, di ba? Kung hindi mo naiintindihan kung saan nanggaling ang minus one na ito, pagkatapos ay bumalik sa kahulugan ng equation ng eroplano! Laging lumalabas bago iyon. na ang aking eroplano ay kabilang sa pinanggalingan!)

Kinakalkula namin ang determinant:

(Maaari mong mapansin na ang equation ng eroplano ay tumutugma sa equation ng tuwid na linya na dumadaan sa mga punto at! Isipin kung bakit!)

Ngayon kinakalkula namin ang anggulo:

Kailangan nating hanapin ang sine:

Sagot:

3. Isang nakakalito na tanong: ano ang isang parihabang prisma, ano sa palagay mo? Isa lang itong kilalang parallelepiped sa iyo! Drawing agad! Maaari mo ring hindi hiwalay na ilarawan ang base, mayroong maliit na paggamit dito:

Ang eroplano, tulad ng nabanggit namin kanina, ay nakasulat bilang isang equation:

Ngayon gumawa kami ng eroplano

Agad naming binubuo ang equation ng eroplano:

Naghahanap ng anggulo

Ngayon ang mga sagot sa huling dalawang problema:

Kaya, ngayon na ang oras para magpahinga, dahil ikaw at ako ay mahusay at nakagawa ng isang mahusay na trabaho!

Mga coordinate at vector. Advanced na antas

Sa artikulong ito, tatalakayin namin sa iyo ang isa pang klase ng mga problema na maaaring malutas gamit ang coordinate method: mga problema sa distansya. Namely, isasaalang-alang natin mga sumusunod na kaso:

1. Kinakalkula ang distansya sa pagitan ng mga skew na linya.

Iniutos ko ang mga ibinigay na gawain habang lumalaki ang kanilang pagiging kumplikado. Ang pinakamadaling hanapin ituro ang distansya ng eroplano at ang pinakamahirap na bahagi ay ang paghahanap distansya sa pagitan ng mga interseksyon na linya. Bagaman, siyempre, walang imposible! Huwag nating ipagpaliban at agad na magpatuloy sa pagsasaalang-alang sa unang klase ng mga problema:

Pagkalkula ng distansya mula sa isang punto patungo sa isang eroplano

Ano ang kailangan natin upang malutas ang problemang ito?

1. Point coordinates

Kaya, sa sandaling makuha namin ang lahat ng kinakailangang data, inilalapat namin ang formula:

Dapat alam mo na kung paano namin binuo ang equation ng eroplano mula sa mga nakaraang problema na sinuri ko sa huling bahagi. Bumaba na tayo sa negosyo kaagad. Ang scheme ay ang mga sumusunod: 1, 2 - Tinutulungan kitang magpasya, at sa ilang mga detalye, 3, 4 - ang sagot lamang, ikaw mismo ang gumawa ng desisyon at ihambing. Nagsimula na!

Mga gawain:

1. Binigyan ng kubo. Ang haba ng gilid ng kubo ay Hanapin-di-te ang distansya mula sa se-re-di-ny mula sa hiwa hanggang sa patag

2. Given the right-vil-naya four-you-rekh-coal-naya pi-ra-mi-da Bo-ko-voe edge hundred-ro-on ang os-no-va-nia ay pantay. Hanapin-di-mga distansya mula sa isang punto patungo sa isang eroplano kung saan - se-re-di-sa mga gilid.

3. Sa kanang tatsulok na pi-ra-mi-de na may os-but-va-ni-em, ang kabilang gilid ay pantay, at isang daang-ro-on os-no-va- niya ay katumbas. Hanapin-di-mga distansya mula sa itaas hanggang sa eroplano.

4. Sa kanang kamay na anim na coal prism, lahat ng mga gilid ay pantay. Hanapin-di-mga distansya mula sa isang punto patungo sa isang eroplano.

Mga solusyon:

1. Gumuhit ng isang kubo na may mga solong gilid, bumuo ng isang segment at isang eroplano, ipahiwatig ang gitna ng segment sa pamamagitan ng titik

.

Una, magsimula tayo sa isang madaling: hanapin ang mga coordinate ng isang punto. Simula noon (tandaan ang mga coordinate ng gitna ng segment!)

Ngayon binubuo namin ang equation ng eroplano sa tatlong puntos

\[\kaliwa| (\begin(array)(*(20)(c))x&0&1\\y&1&0\\z&1&1\end(array)) \right| = 0\]

Ngayon ay maaari kong simulan ang paghahanap ng distansya:

2. Nagsisimula kaming muli sa isang pagguhit, kung saan minarkahan namin ang lahat ng data!

Para sa isang pyramid, magiging kapaki-pakinabang na iguhit ang base nito nang hiwalay.

Kahit na ang pagguhit ko na parang paa ng manok ay hindi makahahadlang sa amin na madaling malutas ang problemang ito!

Ngayon ay madali nang mahanap ang mga coordinate ng isang punto

Dahil ang mga coordinate ng punto

2. Dahil ang mga coordinate ng point a ay ang gitna ng segment, kung gayon

Madali nating mahahanap ang mga coordinate ng dalawa pang punto sa eroplano. Binubuo natin ang equation ng eroplano at pinasimple ito:

\[\kaliwa| (\kaliwa| (\begin(array)(*(20)(c))x&1&(\frac(3)(2))\\y&0&(\frac(3)(2))\\z&0&(\frac( (\sqrt 3 ))(2))\end(array)) \right|) \right| = 0\]

Dahil ang punto ay may mga coordinate: , pagkatapos ay kinakalkula namin ang distansya:

Sagot (napakabihirang!):

Well, naintindihan mo ba? Para sa akin, ang lahat ng bagay dito ay kasing teknikal tulad ng sa mga halimbawa na itinuring namin sa iyo sa nakaraang bahagi. Kaya sigurado ako na kung napag-aralan mo na ang materyal na iyon, hindi magiging mahirap para sa iyo na lutasin ang natitirang dalawang problema. Ibibigay ko lang sa iyo ang mga sagot:

Pagkalkula ng Distansya mula sa isang Linya patungo sa isang Eroplano

Sa totoo lang, wala namang bago dito. Paano matatagpuan ang isang linya at isang eroplano na may kaugnayan sa bawat isa? Nasa kanila ang lahat ng posibilidad: mag-intersect, o ang isang tuwid na linya ay kahanay sa eroplano. Ano sa palagay mo ang distansya mula sa linya hanggang sa eroplano kung saan nagsa-intersect ang ibinigay na linya? Tila sa akin ay malinaw na ang gayong distansya ay katumbas ng zero. Hindi kawili-wiling kaso.

Ang pangalawang kaso ay mas nakakalito: dito ang distansya ay hindi zero. Gayunpaman, dahil ang linya ay parallel sa eroplano, ang bawat punto ng linya ay katumbas ng layo mula sa eroplanong ito:

kaya:

At nangangahulugan ito na ang aking gawain ay nabawasan sa nauna: hinahanap namin ang mga coordinate ng anumang punto sa linya, hinahanap namin ang equation ng eroplano, kinakalkula namin ang distansya mula sa punto hanggang sa eroplano. Sa katunayan, ang mga ganitong gawain sa pagsusulit ay napakabihirang. Nakahanap lang ako ng isang problema, at ang data sa loob nito ay hindi masyadong naaangkop dito ang paraan ng coordinate!

Ngayon lumipat tayo sa isa pa, higit pa mahalagang klase mga gawain:

Pagkalkula ng Distansya ng isang Punto sa isang Linya

Ano ang kakailanganin natin?

1. Ang mga coordinate ng punto kung saan namin hinahanap ang distansya:

2. Coordinates ng anumang punto na nakahiga sa isang tuwid na linya

3. Direction vector coordinates ng tuwid na linya

Anong formula ang ginagamit natin?

Ano ang ibig sabihin sa iyo ng denominator ng fraction na ito at kaya dapat itong maging malinaw: ito ang haba ng nagdidirekta na vector ng tuwid na linya. Narito ang isang napaka nakakalito na numerator! Ang expression ay nangangahulugan ng module (haba) ng vector product ng mga vectors at Paano makalkula ang vector product, pinag-aralan namin sa nakaraang bahagi ng trabaho. I-refresh ang iyong kaalaman, ito ay magiging lubhang kapaki-pakinabang sa amin ngayon!

Kaya, ang algorithm para sa paglutas ng mga problema ay ang mga sumusunod:

1. Hinahanap namin ang mga coordinate ng punto kung saan hinahanap namin ang distansya:

2. Hinahanap namin ang mga coordinate ng anumang punto sa linya kung saan hinahanap namin ang distansya:

3. Pagbuo ng isang vector

4. Binubuo namin ang vector ng direksyon ng tuwid na linya

5. Kalkulahin ang cross product

6. Hinahanap namin ang haba ng resultang vector:

7. Kalkulahin ang distansya:

Marami kaming trabaho, at ang mga halimbawa ay magiging kumplikado! Kaya ngayon ituon ang lahat ng iyong pansin!

1. Ang Dana ay isang kanang kamay na tatsulok na pi-ra-mi-da na may vertex. Isang daang-ro-on ang os-no-va-niya pi-ra-mi-dy ay pantay, you-so-ta ay pantay. Hanapin-di-yaong mga distansya mula sa se-re-di-ny ng bo-ko-th na gilid hanggang sa tuwid na linya, kung saan ang mga punto at ang se-re-di-ny ng ribs at co-from- vet -stven-pero.

2. Ang mga haba ng ribs at ang right-angle-no-para-ral-le-le-pi-pe-da ay pantay, ayon sa pagkakabanggit, at Find-di-te distance mula sa top-shi-ny hanggang straight-my

3. Sa kanang anim na coal prism, ang lahat ng mga gilid ng isang kuyog ay pantay na find-di-mga distansya mula sa isang punto hanggang sa isang tuwid na linya

Mga solusyon:

1. Gumagawa kami ng maayos na pagguhit, kung saan minarkahan namin ang lahat ng data:

Marami kaming trabaho para sa iyo! Gusto ko munang ilarawan sa mga salita kung ano ang hahanapin natin at sa anong pagkakasunud-sunod:

1. Coordinates ng mga puntos at

2. Point coordinates

3. Coordinates ng mga puntos at

4. Coordinates ng mga vectors at

5. Ang kanilang cross product

6. Haba ng vector

7. Ang haba ng produkto ng vector

8. Distansya mula sa

Well, marami tayong gagawin! I-roll up natin ang ating manggas!

1. Upang mahanap ang mga coordinate ng taas ng pyramid, kailangan nating malaman ang mga coordinate ng punto.Ang applicate nito ay zero, at ang ordinate ay katumbas ng abscissa nito. Sa wakas, nakuha namin ang mga coordinate:

Point coordinates

2. - gitna ng segment

3. - gitna ng segment

gitnang punto

4. Coordinates

Vector coordinate

5. Kalkulahin ang produkto ng vector:

6. Ang haba ng vector: ang pinakamadaling paraan ay palitan na ang segment ay ang gitnang linya ng tatsulok, na nangangahulugang ito ay katumbas ng kalahati ng base. Kaya yun.

7. Isinasaalang-alang namin ang haba ng produkto ng vector:

8. Panghuli, hanapin ang distansya:

Phew, yun lang! Sasabihin ko sa iyo nang tapat: ang solusyon sa problemang ito tradisyonal na pamamaraan(sa pamamagitan ng mga build) ay magiging mas mabilis. Pero dito ko binawasan ang lahat tapos na algorithm! Sa tingin ko ay malinaw sa iyo ang algorithm ng solusyon? Samakatuwid, hihilingin ko sa iyo na lutasin ang natitirang dalawang problema sa iyong sarili. Ihambing ang mga sagot?

Muli, inuulit ko: mas madali (mas mabilis) na lutasin ang mga problemang ito sa pamamagitan ng mga konstruksyon, sa halip na gumamit paraan ng coordinate. Ipinakita ko ang ganitong paraan ng paglutas lamang upang ipakita sa iyo ang isang unibersal na pamamaraan na nagpapahintulot sa iyo na "huwag tapusin ang anuman".

Panghuli, isaalang-alang ang huling klase ng mga problema:

Kinakalkula ang distansya sa pagitan ng mga skew na linya

Narito ang algorithm para sa paglutas ng mga problema ay magiging katulad ng nauna. Kung anong meron tayo:

3. Anumang vector na nagkokonekta sa mga punto ng una at pangalawang linya:

Paano natin mahahanap ang distansya sa pagitan ng mga linya?

Ang formula ay:

Ang numerator ay ang module ng halo-halong produkto (ipinakilala namin ito sa nakaraang bahagi), at ang denominator - tulad ng sa nakaraang formula (ang module ng produkto ng vector ng mga nagdidirekta na mga vector ng mga linya, ang distansya sa pagitan ng kung saan kami ay naghahanap para sa).

Ipapaalala ko sayo yan

pagkatapos ang formula ng distansya ay maaaring muling isulat bilang:

Hatiin ang determinant na ito sa determinant! Bagaman, sa totoo lang, wala ako sa mood para sa mga biro dito! Ang formula na ito, sa katunayan, ay napakahirap at humahantong sa medyo kumplikadong mga kalkulasyon. Kung ako sa iyo, gagamitin ko lang ito bilang isang huling paraan!

Subukan nating lutasin ang ilang mga problema gamit ang pamamaraan sa itaas:

1. Sa kanang tatsulok na prism, ang lahat ng mga gilid ay kahit papaano ay pantay, hanapin ang distansya sa pagitan ng mga tuwid na linya at.

2. Dahil sa isang kanang-harap na hugis tatsulok na prisma, ang lahat ng mga gilid ng os-no-va-niya ng isang tao ay katumbas ng Se-che-tion, na dumadaan sa kabilang tadyang at se-re-di-nu ribs ay yav-la-et-sya square-ra-tom. Find-di-te dis-sto-I-nie between straight-we-mi and

Ako ang magpapasya sa una, at batay dito, ikaw ang magpapasya sa pangalawa!

1. Gumuhit ako ng prisma at minarkahan ang mga linya at

Point C coordinate: pagkatapos

Point coordinates

Vector coordinate

Point coordinates

Vector coordinate

Vector coordinate

\[\left((B,\overrightarrow (A(A_1))) \overrightarrow (B(C_1)) ) \right) = \left| (\begin(array)(*(20)(l))(\begin(array)(*(20)(c))0&1&0\end(array))\\(\begin(array)(*(20) (c))0&0&1\end(array))\\(\begin(array)(*(20)(c))(\frac((\sqrt 3 ))(2))&( - \frac(1) (2))&1\end(array))\end(array)) \right| = \frac((\sqrt 3 ))(2)\]

Isinasaalang-alang namin ang cross product sa pagitan ng mga vectors at

\[\overrightarrow (A(A_1)) \cdot \overrightarrow (B(C_1)) = \left| \begin(array)(l)\begin(array)(*(20)(c))(\overrightarrow i )&(\overrightarrow j )&(\overrightarrow k )\end(array)\\\begin(array )(*(20)(c))0&0&1\end(array)\\\begin(array)(*(20)(c))(\frac((\sqrt 3 ))(2))&( - \ frac(1)(2))&1\end(array)\end(array) \right| - \frac((\sqrt 3 ))(2)\overrightarrow k + \frac(1)(2)\overrightarrow i \]

Ngayon ay isinasaalang-alang namin ang haba nito:

Sagot:

Ngayon subukang maingat na kumpletuhin ang pangalawang gawain. Ang sagot dito ay:.

Mga coordinate at vector. Maikling paglalarawan at mga pangunahing formula

Ang vector ay isang nakadirekta na segment. - ang simula ng vector, - ang dulo ng vector.
Ang vector ay tinutukoy ng o.

Ganap na halaga vector - ang haba ng segment na kumakatawan sa vector. Itinalaga bilang.

Vector coordinate:

,
nasaan ang mga dulo ng vector \displaystyle a .

Kabuuan ng mga vector: .

Ang produkto ng mga vectors:

tuldok na produkto ng mga vector:

Maaaring itakda iba't ibang paraan(isang punto at isang vector, dalawang puntos at isang vector, tatlong puntos, atbp.). Ito ay nasa isip na ang equation ng eroplano ay maaaring magkaroon iba't ibang uri. Gayundin, sa ilalim ng ilang mga kundisyon, ang mga eroplano ay maaaring magkatulad, patayo, intersecting, atbp. Pag-uusapan natin ito sa artikulong ito. Matututunan natin kung paano isulat ang pangkalahatang equation ng eroplano at hindi lamang.

Normal na anyo ng equation

Sabihin nating mayroong puwang R 3 na mayroong isang parihabang coordinate system na XYZ. Itakda natin ang vector α, na ilalabas mula sa inisyal na punto O. Sa dulo ng vector α iguguhit natin ang eroplanong P, na magiging patayo dito.

Tukuyin ng P ang isang arbitraryong punto Q=(x, y, z). Pipirmahan natin ang radius vector ng puntong Q na may letrang p. Ang haba ng vector α ay p=IαI at Ʋ=(cosα,cosβ,cosγ).

Ito ay isang unit vector na nakaturo patagilid, tulad ng vector α. Ang α, β at γ ay ang mga anggulo na nabubuo sa pagitan ng vector Ʋ at ang mga positibong direksyon ng space axes x, y, z, ayon sa pagkakabanggit. Ang projection ng ilang point QϵП papunta sa vector Ʋ ay isang pare-parehong halaga na katumbas ng р: (р,Ʋ) = р(р≥0).

Makatuwiran ang equation na ito kapag p=0. Ang tanging bagay ay ang eroplano P sa kasong ito ay magsa-intersect sa puntong O (α=0), na siyang pinagmulan, at ang unit vector Ʋ, na inilabas mula sa puntong O, ay magiging patayo sa P, anuman ang direksyon nito, na nangangahulugan na ang vector Ʋ ay tinutukoy mula sa sign-accurate. Ang nakaraang equation ay ang equation ng aming P plane, na ipinahayag sa vector form. Ngunit sa mga coordinate ito ay magiging ganito:

Ang P dito ay mas malaki sa o katumbas ng 0. Nahanap namin ang equation ng isang eroplano sa espasyo sa normal nitong anyo.

Pangkalahatang Equation

Kung i-multiply natin ang equation sa mga coordinate sa anumang numero na hindi katumbas ng zero, makakakuha tayo ng equation na katumbas ng ibinigay, na tumutukoy sa parehong eroplano. Magiging ganito ang hitsura:

Narito ang A, B, C ay mga numero na magkasabay na naiiba sa zero. Ang equation na ito ay tinutukoy bilang ang general plane equation.

Mga equation ng eroplano. Mga espesyal na kaso

Ang equation sa pangkalahatang anyo ay maaaring mabago sa pagkakaroon ng mga karagdagang kundisyon. Isaalang-alang natin ang ilan sa mga ito.

Ipagpalagay na ang coefficient A ay 0. Nangangahulugan ito na ang ibinigay na eroplano ay parallel sa ibinigay na axis Ox. Sa kasong ito, magbabago ang anyo ng equation: Ву+Cz+D=0.

Katulad nito, magbabago ang anyo ng equation sa ilalim ng mga sumusunod na kondisyon:

• Una, kung B = 0, ang equation ay magbabago sa Ax + Cz + D = 0, na magsasaad ng parallelism sa Oy axis.
• Pangalawa, kung С=0, ang equation ay binago sa Ах+Ву+D=0, na magsasaad ng parallelism sa ibinigay na axis Oz.
• Pangatlo, kung D=0, ang equation ay magmumukhang Ax+By+Cz=0, na nangangahulugan na ang eroplano ay nag-intersect sa O (ang pinanggalingan).
• Pang-apat, kung A=B=0, ang equation ay magbabago sa Cz+D=0, na magpapatunay na parallel sa Oxy.
• Ikalima, kung B=C=0, ang equation ay magiging Ax+D=0, na nangangahulugan na ang eroplano sa Oyz ay parallel.
• Pang-anim, kung A=C=0, ang equation ay kukuha ng form na Ву+D=0, iyon ay, mag-uulat ito ng parallelism sa Oxz.

Uri ng equation sa mga segment

Kung ang mga numerong A, B, C, D ay hindi zero, ang anyo ng equation (0) ay maaaring ang mga sumusunod:

x/a + y/b + z/c = 1,

kung saan ang isang \u003d -D / A, b \u003d -D / B, c \u003d -D / C.

Nakukuha namin bilang isang resulta Dapat tandaan na ang eroplanong ito ay magsa-intersect sa Ox axis sa isang punto na may mga coordinate (a,0,0), Oy - (0,b,0), at Oz - (0,0,c) .

Isinasaalang-alang ang equation na x/a + y/b + z/c = 1, madaling makitang kinakatawan ang pagkakalagay ng eroplano na nauugnay sa isang ibinigay na sistema ng coordinate.

Normal na mga coordinate ng vector

Ang normal na vector n sa eroplanong P ay may mga coefficient na mga coefficient ng pangkalahatang equation ng ibinigay na eroplano, iyon ay, n (A, B, C).

Upang matukoy ang mga coordinate ng normal na n, sapat na malaman ang pangkalahatang equation ng isang naibigay na eroplano.

Kapag ginagamit ang equation sa mga segment, na may anyong x/a + y/b + z/c = 1, gayundin kapag ginagamit ang pangkalahatang equation, maaaring isulat ng isa ang mga coordinate ng anumang normal na vector ng isang naibigay na eroplano: (1 /a + 1/b + 1/ kasama).

Dapat tandaan na ang normal na vector ay nakakatulong upang malutas ang iba't ibang mga problema. Ang pinakakaraniwan ay mga gawain na binubuo sa pagpapatunay ng perpendicularity o parallelism ng mga eroplano, mga problema sa paghahanap ng mga anggulo sa pagitan ng mga eroplano o mga anggulo sa pagitan ng mga eroplano at linya.

Tingnan ang equation ng eroplano ayon sa mga coordinate ng punto at ang normal na vector

Ang isang non-zero vector n patayo sa isang partikular na eroplano ay tinatawag na normal (normal) para sa isang partikular na eroplano.

Ipagpalagay na sa coordinate space (rectangular coordinate system) ang Oxyz ay ibinibigay:

• punto Mₒ na may mga coordinate (xₒ,yₒ,zₒ);
• zero vector n=A*i+B*j+C*k.

Kinakailangang bumuo ng isang equation para sa isang eroplano na dadaan sa puntong Mₒ patayo sa normal na n.

Sa espasyo, pipili tayo ng anumang di-makatwirang punto at tinutukoy ito ng M (x y, z). Hayaang ang radius vector ng anumang punto M (x, y, z) ay r=x*i+y*j+z*k, at ang radius vector ng point Mₒ (xₒ,yₒ,zₒ) - rₒ=xₒ* i+yₒ *j+zₒ*k. Ang puntong M ay mapapabilang sa ibinigay na eroplano kung ang vector MₒM ay patayo sa vector n. Sinusulat namin ang kondisyon ng orthogonality gamit ang scalar product:

[MₒM, n] = 0.

Dahil MₒM \u003d r-rₒ, ang vector equation ng eroplano ay magiging ganito:

Ang equation na ito ay maaaring kumuha ng ibang anyo. Upang gawin ito, ang mga katangian ng scalar na produkto ay ginagamit, at ang kaliwang bahagi ng equation ay binago. = - . Kung tinukoy bilang c, kung gayon ang sumusunod na equation ay makukuha: - c \u003d 0 o \u003d c, na nagpapahayag ng pare-pareho ng mga projection sa normal na vector ng radius vectors ng mga ibinigay na punto na kabilang sa eroplano.

Ngayon ay maaari mong makuha ang coordinate form ng pagsulat ng vector equation ng ating eroplano = 0. Dahil r-rₒ = (x-xₒ)*i + (y-yₒ)*j + (z-zₒ)*k, at n = A*i+B *j+C*k, mayroon kaming:

Lumalabas na mayroon tayong equation para sa isang eroplanong dumadaan sa isang puntong patayo sa normal na n:

A*(x-xₒ)+B*(y-yₒ)C*(z-zₒ)=0.

Tingnan ang equation ng eroplano ayon sa mga coordinate ng dalawang puntos at isang vector collinear sa eroplano

Tinutukoy namin ang dalawang arbitraryong puntos na M′ (x′,y′,z′) at M″ (x″,y″,z″), pati na rin ang vector a (a′,a″,a‴).

Ngayon ay maaari na tayong bumuo ng isang equation para sa isang naibigay na eroplano, na dadaan sa magagamit na mga puntos na M′ at M″, pati na rin ang anumang punto M na may mga coordinate (x, y, z) na kahanay sa ibinigay na vector a.

Sa kasong ito, ang mga vectors na M′M=(x-x′;y-y′;z-z′) at M″M=(x″-x′;y″-y′;z″-z′) ay dapat magkatugma sa vector a=(a′,a″,a‴), na nangangahulugang (M′M, M″M, a)=0.

Kaya, ang aming equation ng isang eroplano sa kalawakan ay magiging ganito:

Uri ng equation ng isang eroplano na nagsasalubong sa tatlong puntos

Ipagpalagay na mayroon tayong tatlong puntos: (x′, y′, z′), (x″,y″,z″), (x‴,y‴,z‴), na hindi kabilang sa parehong tuwid na linya. Kinakailangang isulat ang equation ng eroplano na dumadaan sa ibinigay na tatlong puntos. Sinasabi ng teorya ng geometry na ang ganitong uri ng eroplano ay talagang umiiral, tanging ito lamang ang isa at walang katulad. Dahil ang eroplanong ito ay nag-intersect sa punto (x′, y′, z′), ang anyo ng equation nito ay magiging ganito:

Dito ang A, B, C ay iba sa zero sa parehong oras. Gayundin, ang ibinigay na eroplano ay nag-intersect sa dalawa pang punto: (x″,y″,z″) at (x‴,y‴,z‴). Kaugnay nito, ang mga sumusunod na kondisyon ay dapat matugunan:

Ngayon ay maaari na tayong bumuo ng isang homogenous na sistema na may mga hindi kilalang u, v, w:

Sa aming kaso x,y o ang z ay isang di-makatwirang punto na nakakatugon sa equation (1). Dahil sa equation (1) at sa sistema ng mga equation (2) at (3), ang sistema ng mga equation na ipinahiwatig sa figure sa itaas ay nakakatugon sa vector N (A, B, C), na hindi mahalaga. Iyon ang dahilan kung bakit ang determinant ng sistemang ito ay katumbas ng zero.

Ang equation (1), na aming nakuha, ay ang equation ng eroplano. Ito ay eksaktong pumasa sa 3 puntos, at ito ay madaling suriin. Para magawa ito, kailangan nating palawakin ang ating determinant sa mga elemento sa unang hilera. Ito ay sumusunod mula sa mga umiiral na katangian ng determinant na ang ating eroplano ay sabay-sabay na nag-intersect sa tatlong unang ibinigay na puntos (x′, y′, z′), (x″,y″,z″), (x‴,y‴,z‴) . Ibig sabihin, nalutas na natin ang gawaing itinakda sa harap natin.

Dihedral anggulo sa pagitan ng mga eroplano

Ang dihedral na anggulo ay isang spatial geometric na pigura, na nabuo ng dalawang kalahating eroplano na nagmumula sa isang tuwid na linya. Sa madaling salita, ito ang bahagi ng espasyo na nililimitahan ng mga kalahating eroplanong ito.

Sabihin nating mayroon tayong dalawang eroplano na may mga sumusunod na equation:

Alam namin na ang mga vectors N=(A,B,C) at N¹=(A¹,B¹,C¹) ay patayo ayon sa ibinigay na mga eroplano. Kaugnay nito, ang anggulo φ sa pagitan ng mga vectors N at N¹ ay katumbas ng anggulo (dihedral), na nasa pagitan ng mga eroplanong ito. Ang scalar product ay may anyo:

NN¹=|N||N¹|cos φ,

tiyak dahil

cosφ= NN¹/|N||N¹|=(AA¹+BB¹+CC¹)/((√(A²+B²+C²))*(√(A¹)²+(B¹)²+(C¹)²)).

Ito ay sapat na upang isaalang-alang na 0≤φ≤π.

Sa katunayan, ang dalawang eroplano na nagsalubong ay bumubuo ng dalawang (dihedral) na anggulo: φ 1 at φ 2 . Ang kanilang kabuuan ay katumbas ng π (φ 1 + φ 2 = π). Tulad ng para sa kanilang mga cosine, ang kanilang mga ganap na halaga ay pantay, ngunit naiiba sila sa mga palatandaan, iyon ay, cos φ 1 =-cos φ 2. Kung sa equation (0) papalitan natin ang A, B at C ng mga numero -A, -B at -C, ayon sa pagkakabanggit, ang equation na makukuha natin ay tutukoy sa parehong eroplano, ang tanging anggulo φ sa equation cos φ= NN 1 // N||N 1 | ay papalitan ng π-φ.

Perpendicular plane equation

Ang mga eroplano ay tinatawag na patayo kung ang anggulo sa pagitan ng mga ito ay 90 degrees. Gamit ang materyal na nakabalangkas sa itaas, mahahanap natin ang equation ng isang eroplanong patayo sa isa pa. Sabihin nating mayroon tayong dalawang eroplano: Ax+By+Cz+D=0 at A¹x+B¹y+C¹z+D=0. Maaari nating sabihin na sila ay magiging patayo kung cosφ=0. Nangangahulugan ito na NN¹=AA¹+BB¹+CC¹=0.

Parallel plane equation

Parallel ay dalawang eroplano na hindi naglalaman ng mga karaniwang punto.

Ang kundisyon (ang kanilang mga equation ay kapareho ng sa nakaraang talata) ay ang mga vectors N at N¹, na patayo sa kanila, ay collinear. Nangangahulugan ito na ang mga sumusunod na kondisyon ng proporsyonalidad ay natutugunan:

A/A¹=B/B¹=C/C¹.

Kung ang mga kondisyon ng proporsyonalidad ay pinalawig - A/A¹=B/B¹=C/C¹=DD¹,

ito ay nagpapahiwatig na ang mga eroplanong ito ay magkasabay. Nangangahulugan ito na ang mga equation na Ax+By+Cz+D=0 at A¹x+B¹y+C¹z+D¹=0 ay naglalarawan ng isang eroplano.

Distansya sa eroplano mula sa punto

Sabihin nating mayroon tayong eroplanong P, na ibinibigay ng equation (0). Kinakailangang hanapin ang distansya dito mula sa puntong may mga coordinate (xₒ,yₒ,zₒ)=Qₒ. Upang gawin ito, kailangan mong dalhin ang equation ng eroplano P sa normal na anyo:

(ρ,v)=p (p≥0).

AT kasong itoρ (x, y, z) ay ang radius vector ng aming punto Q, na matatagpuan sa P, p ay ang haba ng patayo P, na inilabas mula sa zero point, v ay ang unit vector na matatagpuan sa isang direksyon.

Ang pagkakaiba ρ-ρº ng radius vector ng ilang punto Q=(x,y,z) na kabilang sa P, pati na rin ang radius vector ng isang naibigay na punto Q 0 =(xₒ,yₒ,zₒ) ay tulad ng isang vector, ganap na halaga na ang projection sa v ay katumbas ng distansya d, na dapat matagpuan mula Q 0 \u003d (xₒ, yₒ, zₒ) hanggang P:

D=|(ρ-ρ 0 ,v)|, ngunit

(ρ-ρ 0 ,v)= (ρ,v)-(ρ 0 ,v) =р-(ρ 0 ,v).

Kaya pala

d=|(ρ 0 ,v)-p|.

Sa gayon ay mahahanap natin ganap na halaga ang resultang expression, iyon ay, ang kinakailangan d.

Gamit ang wika ng mga parameter, nakukuha namin ang halata:

d=|Axₒ+Vuₒ+Czₒ|/√(A²+B²+C²).

Kung ang ibinigay na punto Ang Q 0 ay nasa kabilang panig ng P plane, gayundin ang pinanggalingan, pagkatapos ay sa pagitan ng vector ρ-ρ 0 at v ay:

d=-(ρ-ρ 0 ,v)=(ρ 0 ,v)-p>0.

Sa kaso kapag ang punto Q 0, kasama ang pinagmulan, ay matatagpuan sa parehong bahagi ng P, kung gayon ang anggulo na nilikha ay talamak, iyon ay:

d \u003d (ρ-ρ 0, v) \u003d p - (ρ 0, v)>0.

Bilang resulta, lumalabas na sa unang kaso (ρ 0 ,v)> р, sa pangalawa (ρ 0 ,v)<р.

Tangent plane at ang equation nito

Ang tangent plane sa ibabaw sa tangent point Mº ay ang eroplanong naglalaman ng lahat ng posibleng tangents sa mga curve na iginuhit sa puntong ito sa surface.

Sa form na ito ng surface equation F (x, y, z) \u003d 0, ang equation ng tangent plane sa tangent point Mº (xº, yº, zº) ay magiging ganito:

F x (xº, yº, zº)(x- xº)+ F x (xº, yº, zº)(y-yº)+ F x (xº, yº, zº)(z-zº)=0.

Kung tinukoy mo ang ibabaw sa tahasang anyo z=f (x, y), ang tangent plane ay ilalarawan ng equation:

z-zº = f(xº, yº)(x- xº)+f(xº, yº)(y-yº).

Intersection ng dalawang eroplano

Sa coordinate system (parihaba) Oxyz ay matatagpuan, dalawang eroplano П′ at П″ ay ibinigay, na bumalandra at hindi nag-tutugma. Dahil ang anumang eroplano na matatagpuan sa isang rectangular coordinate system ay tinutukoy ng isang pangkalahatang equation, ipagpalagay natin na ang P′ at P″ ay ibinibigay ng mga equation na A′x+B′y+C′z+D′=0 at A″x +B″y+ С″z+D″=0. Sa kasong ito, mayroon tayong normal na n′ (A′, B′, C′) ng P′ plane at ang normal na n″ (A″, B″, C″) ng P″ plane. Dahil ang aming mga eroplano ay hindi parallel at hindi nagtutugma, ang mga vectors na ito ay hindi collinear. Gamit ang wika ng matematika, maaari nating isulat ang kundisyong ito tulad ng sumusunod: n′≠ n″ ↔ (A′, B′, C′) ≠ (λ*A″,λ*B″,λ*C″), λϵR. Hayaang ang linya na nasa intersection ng P′ at P″ ay ipahiwatig ng titik a, sa kasong ito a = P′ ∩ P″.

a ay isang tuwid na linya na binubuo ng hanay ng lahat ng mga punto ng (karaniwang) eroplano П′ at П″. Nangangahulugan ito na ang mga coordinate ng anumang punto na kabilang sa linya a ay dapat magkasabay na matugunan ang mga equation na A′x+B′y+C′z+D′=0 at A″x+B″y+C″z+D″= 0. Nangangahulugan ito na ang mga coordinate ng punto ay magiging isang partikular na solusyon ng sumusunod na sistema ng mga equation:

Bilang resulta, lumalabas na ang (pangkalahatang) solusyon ng sistemang ito ng mga equation ay tutukoy sa mga coordinate ng bawat isa sa mga punto ng tuwid na linya, na magsisilbing intersection point ng П′ at П″, at matukoy ang tuwid linya a sa coordinate system na Oxyz (parihaba) sa espasyo.