Pagbubuo ng kahulugan ng anggulo sa pagitan ng isang tuwid na linya at isang eroplano. Anggulo sa pagitan ng isang tuwid na linya at isang eroplano: kahulugan, mga halimbawa ng paghahanap

Ang pagpapanatili ng iyong privacy ay mahalaga sa amin. Para sa kadahilanang ito, bumuo kami ng Patakaran sa Privacy na naglalarawan kung paano namin ginagamit at iniimbak ang iyong impormasyon. Pakisuri ang aming mga kasanayan sa privacy at ipaalam sa amin kung mayroon kang anumang mga tanong.

Pagkolekta at paggamit ng personal na impormasyon

Ang personal na impormasyon ay tumutukoy sa data na maaaring magamit upang makilala o makipag-ugnayan sa isang partikular na tao.

Maaaring hilingin sa iyo na ibigay ang iyong personal na impormasyon anumang oras kapag nakipag-ugnayan ka sa amin.

Nasa ibaba ang ilang halimbawa ng mga uri ng personal na impormasyon na maaari naming kolektahin at kung paano namin magagamit ang naturang impormasyon.

Anong personal na impormasyon ang aming kinokolekta:

• Kapag nagsumite ka ng kahilingan sa site, maaari kaming mangolekta ng iba't ibang impormasyon, kabilang ang iyong pangalan, numero ng telepono, address email atbp.

Paano namin ginagamit ang iyong personal na impormasyon:

• Kinokolekta namin personal na impormasyon nagbibigay-daan sa amin na makipag-ugnayan sa iyo at ipaalam sa iyo ang tungkol sa mga natatanging alok, promosyon at iba pang mga kaganapan at paparating na mga kaganapan.
• Paminsan-minsan, maaari naming gamitin ang iyong personal na impormasyon upang magpadala ng mahahalagang paunawa at komunikasyon.
• Maaari rin kaming gumamit ng personal na impormasyon para sa mga panloob na layunin tulad ng pag-audit, pagsusuri ng data at iba't ibang pag-aaral upang mapagbuti ang mga serbisyong ibinibigay namin at mabigyan ka ng mga rekomendasyon tungkol sa aming mga serbisyo.
• Kung lalahok ka sa isang premyo na draw, paligsahan o katulad na promosyon, maaari naming gamitin ang impormasyong ibibigay mo upang pangasiwaan ang mga naturang programa.

Pagbubunyag ng impormasyon sa mga ikatlong partido

Hindi namin ibinubunyag ang impormasyong natanggap mula sa iyo sa mga ikatlong partido.

Mga pagbubukod:

• Kung kinakailangan, alinsunod sa batas, hudisyal na pamamaraan, V pagsubok, at/o batay sa mga pampublikong kahilingan o kahilingan mula sa mga ahensya ng gobyerno sa teritoryo ng Russian Federation - ibunyag ang iyong personal na impormasyon. Maaari rin kaming magbunyag ng impormasyon tungkol sa iyo kung matukoy namin na ang naturang pagsisiwalat ay kinakailangan o naaangkop para sa seguridad, pagpapatupad ng batas, o iba pang layunin ng pampublikong kalusugan. mahahalagang kaso.
• Kung sakaling magkaroon ng muling pagsasaayos, pagsasanib, o pagbebenta, maaari naming ilipat ang personal na impormasyong kinokolekta namin sa naaangkop na third party na kahalili.

Proteksyon ng personal na impormasyon

Gumagawa kami ng mga pag-iingat - kabilang ang administratibo, teknikal at pisikal - upang protektahan ang iyong personal na impormasyon mula sa pagkawala, pagnanakaw, at maling paggamit, pati na rin ang hindi awtorisadong pag-access, pagsisiwalat, pagbabago at pagkasira.

Igalang ang iyong privacy sa antas ng kumpanya

Upang matiyak na ligtas ang iyong personal na impormasyon, ipinapaalam namin ang mga pamantayan sa privacy at seguridad sa aming mga empleyado at mahigpit na ipinapatupad ang mga kasanayan sa privacy.

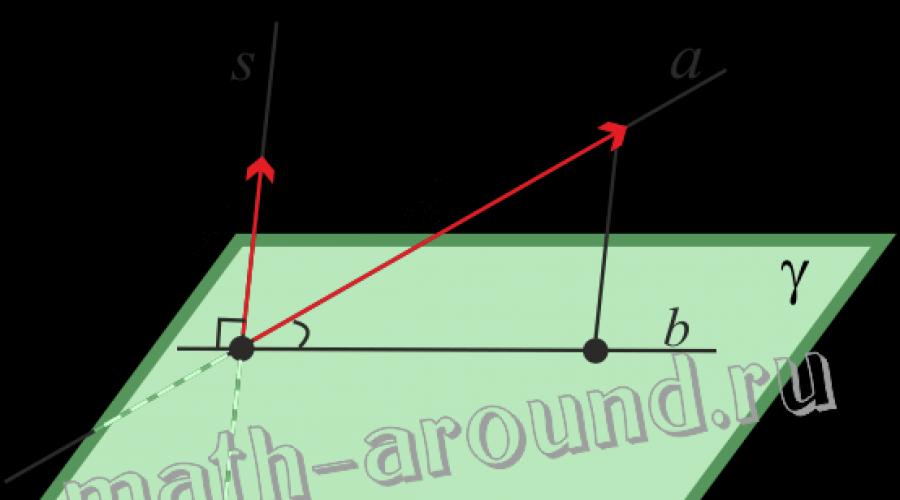
Ulitin natin ang kahulugan ng anggulo sa pagitan ng isang tuwid na linya at isang eroplano.

Kahulugan. Ang anggulo sa pagitan ng isang tuwid na linya at isang eroplano na nagsasalubong sa tuwid na linya na ito at hindi patayo dito, ay ang anggulo sa pagitan ng isang tuwid na linya at ang projection nito sa isang eroplano.

Hayaang magbigay ng isang eroplanong γ at isang linyang a, na nag-intersect sa eroplanong ito at hindi patayo dito.

Buuin natin ang anggulo sa pagitan ng tuwid na linya a at eroplano γ:

1. Mula sa anumang punto sa tuwid na linya a na maginhawa para sa amin, binababa namin ang isang patayo sa eroplano γ;
2. Sa pamamagitan ng mga punto ng mga base ng hilig at patayo gumuhit kami ng isang tuwid na linya b. Ang linya b ay ang projection ng linya a papunta sa eroplanong γ;
3. Ang matinding anggulo sa pagitan ng mga tuwid na linya a at b ay ang anggulo sa pagitan ng tuwid na linya a at eroplano γ, i.e. ∠(a;b)= ∠(a;γ) , kung saan ang ∠(a;b) ay ang anggulo sa pagitan ng mga linyang a at b; ∠(a;γ) - anggulo sa pagitan ng tuwid na linya a at eroplanong γ.

Upang malutas ang mga problema gamit ang coordinate method, kailangan nating tandaan ang mga sumusunod:

3. Kung ang mga coordinate ng vector ng direksyon ( a 1 ; b 1 ; c 1 ) at ang normal na vector ay kilala
(a; b; c), pagkatapos ay ang anggulo sa pagitan ng tuwid na linya a at eroplano γ ay kinakalkula gamit ang formula na makukuha natin ngayon.

Alam namin ang formula para sa paghahanap ng anggulo sa pagitan ng mga tuwid na linya:

; (1)
∠(s; a) = 90°-∠(a; b), pagkatapos cos∠(s;a)=cos (90°-∠(a;b))=sin ∠(a;b) ; (2)
Mula sa (1) at (2) => ; (3)
, saan ang anggulo sa pagitan ng mga vectors m at n; (4)
Pinapalitan namin ang (4) sa (3), atbp. ∠(a;b)= ∠(a;γ), pagkatapos ay makukuha natin:

4. Kung ang mga coordinate ng normal na vector ay hindi alam, kailangan nating malaman ang equation ng eroplano.

Anumang eroplano sa isang rectangular coordinate system ay maaaring ibigay ng equation

ax + by + cz + d = 0,

kung saan ang hindi bababa sa isa sa mga coefficient a, b, c ay iba sa zero. Ang mga coefficient na ito ay magiging mga coordinate ng normal na vector, i.e. (a; b; c).

Algorithm para sa paglutas ng mga problema sa paghahanap ng anggulo sa pagitan ng isang tuwid na linya at isang eroplano gamit ang coordinate method:

1. Gumagawa kami ng isang guhit kung saan minarkahan namin ang isang tuwid na linya at isang eroplano;
2. Ipinakilala namin ang isang rectangular coordinate system;
3. Nahanap namin ang mga coordinate ng vector ng direksyon mula sa mga coordinate ng simula at pagtatapos nito;
4. Hanapin ang mga coordinate ng normal na vector sa eroplano;
5. Pinapalitan namin ang nakuhang data sa formula para sa sine ng anggulo sa pagitan ng isang tuwid na linya at isang eroplano;
6. Hanapin ang halaga ng anggulo mismo.

Isaalang-alang natin ang problema:
1. Sa cube ABCDA 1 B 1 C 1 D 1, hanapin ang padaplis ng anggulo sa pagitan ng tuwid na linya AC 1 at eroplano BDD 1.
Solusyon:

1. Ipakilala natin ang isang rectangular coordinate system na may pinanggalingan sa punto D.
2. Hanapin ang mga coordinate ng direction vector AC 1. Upang gawin ito, tukuyin muna ang mga coordinate ng mga puntos A at C 1:
A(0; 1; 0);
C 1 (1; 0; 1).
{1; -1; 1}.
3. Hanapin ang mga coordinate ng normal na vector sa eroplano BB 1 D 1 . Upang gawin ito, nakita namin ang mga coordinate ng tatlong punto ng eroplano na hindi nakahiga sa parehong linya, at gumuhit ng isang equation ng eroplano:
D(0; 0; 0);
D 1 (0; 0; 1);
B(1; 1; 0);
D: a⋅0+b⋅0+c⋅0+d=0;
D 1: a⋅0+b⋅0+c⋅1+d=0;
B: a⋅1+b⋅1+c⋅0+d=0.

I-substitute natin ang equation: a⋅x+(-a)⋅y+0⋅z+0 = 0;
a⋅x-a⋅y = 0; |:a
x-y = 0.
Kaya, ang normal na vector sa eroplano BDD 1 ay may mga coordinate:
{1;-1; 0}.
4. Hanapin natin ang sine sa pagitan ng tuwid na linya AC 1 at eroplano BDD 1:

5. Gamitin natin ang pangunahing trigonometric identity at hanapin ang cosine ng anggulo sa pagitan ng tuwid na linya AC 1 at plane BDD 1:

6. Hanapin ang tangent ng anggulo sa pagitan ng tuwid na linya AC 1 at eroplano BDD 1:

Sagot: .

2. Sa isang regular na quadrilateral pyramid SABCD, lahat ng mga gilid ay katumbas ng 1, hanapin ang sine ng anggulo sa pagitan ng linyang BD at eroplanong SBC.

Solusyon:

1. Ipakilala natin ang isang rectangular coordinate system na may pinanggalingan sa punto B.
2. Hanapin ang mga coordinate ng direction vector BD. Upang gawin ito, tukuyin muna ang mga coordinate ng mga puntos B at D:

3. Hanapin ang mga coordinate ng normal na vector sa SBC plane. Upang gawin ito, nakita namin ang mga coordinate ng tatlong punto ng eroplano na hindi nakahiga sa parehong tuwid na linya, at binubuo ang equation ng SBC plane:

Paano mo nakuha ang mga coordinate ng point S?

Mula sa punto S isang patayo ay ibinababa sa base plane ABC. Ang intersection point ay itinalagang O. Ang Point O ay ang projection ng point S papunta sa ABC plane. Ang x at y coordinate nito ang magiging unang dalawang coordinate ng point S.

Nang malaman ang taas ng pyramid, natagpuan namin ang ikatlong coordinate ng punto S (sa kahabaan ng z axis)

Ang Triangle SOB ay hugis-parihaba, samakatuwid, ayon sa Pythagorean theorem:

Ang equation ng eroplano ay ax+by+cz+d=0. Palitan natin ang mga coordinate ng mga puntos sa equation na ito:

Nakuha namin ang isang sistema ng tatlong equation:

Ipalit natin sa equation:

Kaya, ang normal na vector sa eroplano ng SBD ay may mga coordinate:

.
4. Hanapin ang sine sa pagitan ng tuwid na linyang BD at ang eroplanong SBD.

Ang konsepto ng projection ng isang figure papunta sa isang eroplano

Upang ipakilala ang konsepto ng isang anggulo sa pagitan ng isang linya at isang eroplano, kailangan mo munang maunawaan ang isang konsepto tulad ng projection ng isang arbitrary figure sa isang eroplano.

Kahulugan 1

Bigyan tayo ng di-makatwirang punto $A$. Ang puntong $A_1$ ay tinatawag na projection ng puntong $A$ papunta sa eroplanong $\alpha $ kung ito ang base ng isang patayo na iginuhit mula sa puntong $A$ patungo sa eroplanong $\alpha $ (Fig. 1).

Figure 1. Projection ng isang punto papunta sa isang eroplano

Kahulugan 2

Bigyan tayo ng arbitrary figure na $F$. Ang figure na $F_1$ ay tinatawag na projection ng figure na $F$ papunta sa plane $\alpha $, na binubuo ng mga projection ng lahat ng point ng figure na $F$ papunta sa plane $\alpha $ (Fig. 2).

Figure 2. Projection ng isang figure papunta sa isang eroplano

Teorama 1

Ang isang projection na hindi patayo sa eroplano ng isang tuwid na linya ay isang tuwid na linya.

Patunay.

Bigyan tayo ng isang eroplanong $\alpha $ at isang tuwid na linya na $d$ na nagsasalubong dito, hindi patayo dito. Pumili tayo ng puntong $M$ sa linyang $d$ at iguhit ang projection nito na $H$ papunta sa eroplanong $\alpha $. Sa pamamagitan ng tuwid na linya $(MH)$ iginuhit namin ang eroplano $\beta $. Malinaw, ang eroplanong ito ay magiging patayo sa $\alpha $ na eroplano. Hayaang mag-intersect sila sa tuwid na linya $m$. Isaalang-alang natin ang isang di-makatwirang punto $M_1$ ng linyang $d$ at gumuhit ng linyang $(M_1H_1$) sa pamamagitan nito na kahanay sa linyang $(MH)$ (Fig. 3).

Larawan 3.

Dahil ang eroplanong $\beta $ ay patayo sa eroplanong $\alpha $, kung gayon ang $M_1H_1$ ay patayo sa linyang $m$, iyon ay, ang puntong $H_1$ ay ang projection ng puntong $M_1$ papunta sa eroplano $\alpha $. Dahil sa arbitrariness ng pagpili ng puntong $M_1$, lahat ng mga punto ng linyang $d$ ay inaasahang papunta sa linyang $m$.

Nangangatuwiran sa katulad na paraan. Sa reverse order, makukuha natin na ang bawat punto sa linyang $m$ ay projection ng anumang punto sa linyang $d$.

Nangangahulugan ito na ang linyang $d$ ay inaasahang papunta sa linyang $m$.

Ang teorama ay napatunayan.

Ang konsepto ng anggulo sa pagitan ng isang tuwid na linya at isang eroplano

Kahulugan 3

Ang anggulo sa pagitan ng isang tuwid na linya na nagsasalubong sa isang eroplano at ang projection nito sa eroplanong ito ay tinatawag na anggulo sa pagitan ng tuwid na linya at ng eroplano (Larawan 4).

Figure 4. Anggulo sa pagitan ng isang tuwid na linya at isang eroplano

Gumawa tayo ng ilang mga tala dito.

Tandaan 1

Kung ang linya ay patayo sa eroplano. Pagkatapos ang anggulo sa pagitan ng tuwid na linya at ng eroplano ay $90^\circ$.

Tandaan 2

Kung ang linya ay parallel o nasa isang eroplano. Pagkatapos ang anggulo sa pagitan ng tuwid na linya at ng eroplano ay $0^\circ$.

Mga halimbawa ng problema

Halimbawa 1

Bigyan tayo ng paralelogram na $ABCD$ at isang puntong $M$ na hindi nasa eroplano ng paralelogram. Patunayan na ang mga tatsulok na $AMB$ at $MBC$ ay right-angled kung ang point $B$ ay ang projection ng point $M$ papunta sa parallelogram plane.

Patunay.

Ilarawan natin ang kondisyon ng problema sa figure (Larawan 5).

Larawan 5.

Dahil ang point $B$ ay ang projection ng point $M$ papunta sa plane $(ABC)$, kung gayon ang straight line na $(MB)$ ay patayo sa plane $(ABC)$. Sa pamamagitan ng Puna 1, nakita namin na ang anggulo sa pagitan ng tuwid na linya na $(MB)$ at ang eroplanong $(ABC)$ ay katumbas ng $90^\circ$. Kaya naman

\[\angle MBC=MBA=(90)^0\]

Nangangahulugan ito na ang mga tatsulok na $AMB$ at $MBC$ ay mga tamang tatsulok.

Halimbawa 2

Binigyan ng eroplano $\alpha $. Ang isang segment ay iginuhit sa isang anggulo na $\varphi $ sa eroplanong ito, ang simula nito ay nasa eroplanong ito. Ang projection ng segment na ito ay kalahati ng laki ng segment mismo. Hanapin ang halaga ng $\varphi$.

Solusyon.

Isaalang-alang ang Larawan 6.

Larawan 6.

Sa kondisyon, mayroon tayo

Dahil ang tatsulok na $BCD$ ay right-angled, kung gayon, sa pamamagitan ng kahulugan ng cosine

\ \[\varphi =arccos\frac(1)(2)=(60)^0\]

Kasama sa kursong video na "Kumuha ng A" ang lahat ng mga paksang kinakailangan para sa matagumpay pagpasa sa Unified State Exam sa matematika para sa 60-65 puntos. Ganap ang lahat ng mga gawain 1-13 ng Profile Unified State Exam sa matematika. Angkop din para sa pagpasa sa Basic Unified State Examination sa matematika. Kung gusto mong makapasa sa Unified State Exam na may 90-100 points, kailangan mong lutasin ang part 1 sa loob ng 30 minuto at walang pagkakamali!

Kurso sa paghahanda para sa Unified State Exam para sa grade 10-11, gayundin para sa mga guro. Lahat ng kailangan mo para malutas ang Part 1 ng Unified State Exam sa matematika (ang unang 12 problema) at Problema 13 (trigonometry). At ito ay higit sa 70 puntos sa Unified State Exam, at hindi magagawa ng isang 100-point na mag-aaral o ng isang mag-aaral sa humanities kung wala sila.

Lahat ng kinakailangang teorya. Mabilis na paraan mga solusyon, mga pitfalls at mga lihim ng Unified State Exam. Ang lahat ng kasalukuyang gawain ng bahagi 1 mula sa FIPI Task Bank ay nasuri. Ang kurso ay ganap na sumusunod sa mga kinakailangan ng Unified State Exam 2018.

Ang kurso ay naglalaman ng 5 malalaking paksa, 2.5 oras bawat isa. Ang bawat paksa ay ibinigay mula sa simula, simple at malinaw.

Daan-daang mga gawain ng Pinag-isang State Exam. Mga problema sa salita at teorya ng posibilidad. Simple at madaling matandaan ang mga algorithm para sa paglutas ng mga problema. Geometry. Teorya, sangguniang materyal, pagsusuri ng lahat ng uri ng mga gawain sa Pinag-isang Estado ng Pagsusuri. Stereometry. Mga Tricky Trick mga solusyon, kapaki-pakinabang na cheat sheet, pagbuo ng spatial na imahinasyon. Trigonometry mula sa simula hanggang sa problema 13. Pag-unawa sa halip na pag-cramming. Malinaw na pagpapaliwanag ng mga kumplikadong konsepto. Algebra. Mga ugat, kapangyarihan at logarithms, function at derivative. Batayan para sa solusyon kumplikadong mga gawain 2 bahagi ng Unified State Exam.

Ang artikulo ay nagsisimula sa kahulugan ng anggulo sa pagitan ng isang tuwid na linya at isang eroplano. Ipapakita sa iyo ng artikulong ito kung paano hanapin ang anggulo sa pagitan ng isang tuwid na linya at isang eroplano gamit ang coordinate method. Ang mga solusyon sa mga halimbawa at problema ay tatalakayin nang detalyado.

Yandex.RTB R-A-339285-1

Una, kinakailangang ulitin ang konsepto ng isang tuwid na linya sa kalawakan at ang konsepto ng isang eroplano. Upang matukoy ang anggulo sa pagitan ng isang tuwid na linya at isang eroplano, kailangan ang ilang mga pantulong na kahulugan. Tingnan natin ang mga kahulugang ito nang detalyado.

Kahulugan 1

Isang tuwid na linya at isang eroplano ay nagsalubong sa kaso kapag mayroon sila karaniwang punto, iyon ay, ito ay ang intersection point ng isang tuwid na linya at isang eroplano.

Ang isang tuwid na linya na bumabagtas sa isang eroplano ay maaaring patayo sa eroplano.

Kahulugan 2

Ang isang tuwid na linya ay patayo sa isang eroplano kapag ito ay patayo sa anumang linya na matatagpuan sa eroplanong ito.

Kahulugan 3

Projection ng point M sa isang eroplano Ang γ ay ang punto mismo kung ito ay nasa binigay na eroplano, o ang punto ng intersection ng eroplano na may linyang patayo sa eroplanong γ na dumadaan sa puntong M, sa kondisyon na hindi ito kabilang sa eroplanong γ.

Kahulugan 4

Projection ng linya a papunta sa isang eroplano Ang γ ay ang hanay ng mga projection ng lahat ng mga punto ng isang naibigay na linya papunta sa eroplano.

Mula dito nakuha namin na ang projection ng isang tuwid na linya patayo sa eroplano γ ay may intersection point. Nalaman namin na ang projection ng linya a ay isang linya na kabilang sa eroplano γ at dumadaan sa intersection point ng linya a at ng eroplano. Tingnan natin ang figure sa ibaba.

Naka-on sa ngayon mayroon kaming lahat ng kinakailangang impormasyon at data upang mabuo ang kahulugan ng anggulo sa pagitan ng isang tuwid na linya at isang eroplano

Kahulugan 5

Ang anggulo sa pagitan ng isang tuwid na linya at isang eroplano ang anggulo sa pagitan ng tuwid na linyang ito at ang projection nito sa eroplanong ito ay tinatawag, at ang tuwid na linya ay hindi patayo dito.

Ang kahulugan ng anggulo na ibinigay sa itaas ay nakakatulong na magkaroon ng konklusyon na ang anggulo sa pagitan ng isang linya at isang eroplano ay ang anggulo sa pagitan ng dalawang intersecting na linya, iyon ay, isang ibinigay na linya kasama ang projection nito papunta sa eroplano. Nangangahulugan ito na ang anggulo sa pagitan nila ay palaging magiging talamak. Tingnan natin ang larawan sa ibaba.

Ang anggulo na matatagpuan sa pagitan ng isang tuwid na linya at isang eroplano ay itinuturing na tama, iyon ay, katumbas ng 90 degrees, ngunit ang anggulo na matatagpuan sa pagitan ng parallel straight lines ay hindi tinukoy. May mga kaso kapag ang halaga nito ay kinuha katumbas ng zero.

Ang mga problema kung saan kinakailangan upang mahanap ang anggulo sa pagitan ng isang tuwid na linya at isang eroplano ay may maraming mga pagkakaiba-iba sa solusyon. Ang kurso ng solusyon mismo ay nakasalalay sa magagamit na data sa kondisyon. Ang mga madalas na kasama sa solusyon ay mga palatandaan ng pagkakatulad o pagkakapantay-pantay ng mga numero, cosine, sine, tangent ng mga anggulo. Ang paghahanap ng anggulo ay posible gamit ang coordinate method. Tingnan natin ito nang mas detalyado.

Kung ang isang hugis-parihaba na sistema ng coordinate O x y z ay ipinakilala sa tatlong-dimensional na espasyo, kung gayon ang isang tuwid na linya a ay tinukoy sa loob nito, na intersecting ang eroplano γ sa punto M, at hindi ito patayo sa eroplano. Ito ay kinakailangan upang mahanap ang anggulo α na matatagpuan sa pagitan ng isang ibinigay na tuwid na linya at ang eroplano.

Una kailangan mong ilapat ang kahulugan ng anggulo sa pagitan ng isang tuwid na linya at isang eroplano gamit ang paraan ng coordinate. Pagkatapos ay makuha namin ang sumusunod.

Sa sistema ng coordinate O x y z, tinukoy ang isang tuwid na linya a, na tumutugma sa mga equation ng tuwid na linya sa kalawakan at ang nagdidirekta na vector ng tuwid na linya sa espasyo para sa eroplanong γ ay tumutugma sa equation ng eroplano at ang normal vector ng eroplano. Pagkatapos a → = (a x , a y , a z) ay ang vector ng direksyon ng ibinigay na linya a, at n → (n x , n y, n z) ay ang normal na vector para sa eroplanong γ. Kung iniisip natin na mayroon tayong mga coordinate ng vector ng direksyon ng tuwid na linya a at ang normal na vector ng eroplano γ, kung gayon ang kanilang mga equation ay kilala, iyon ay, tinukoy sila ng kondisyon, kung gayon posible na matukoy ang mga vectors a → at n → batay sa equation.

Upang kalkulahin ang anggulo, kinakailangang ibahin ang anyo ng formula upang makuha ang halaga ng anggulong ito gamit ang umiiral na mga coordinate ng nagdidirekta na vector ng tuwid na linya at ang normal na vector.

Kinakailangang i-plot ang mga vectors a → at n →, simula sa punto ng intersection ng tuwid na linya a sa eroplano γ. Mayroong 4 na opsyon para sa lokasyon ng mga vector na ito na may kaugnayan sa mga ibinigay na linya at eroplano. Tingnan ang larawan sa ibaba, na nagpapakita ng lahat ng 4 na variation.

Mula dito nakuha namin na ang anggulo sa pagitan ng mga vectors a → at n → ay itinalagang isang → , n → ^ at talamak, pagkatapos ay ang nais na anggulo α na matatagpuan sa pagitan ng tuwid na linya at ang eroplano ay kinumpleto, iyon ay, nakakakuha tayo ng isang expression ng anyong a → , n → ^ = 90 ° - α. Kapag, ayon sa kondisyon, a →, n → ^ > 90 °, pagkatapos ay mayroon tayong →, n → ^ = 90 ° + α.

Mula dito mayroon tayong mga cosine pantay na anggulo ay pantay, pagkatapos ay ang huling pagkakapantay-pantay ay nakasulat sa anyo ng isang sistema

cos a → , n → ^ = cos 90 ° - α , a → , n → ^< 90 ° cos a → , n → ^ = cos 90 ° + α , a → , n → ^ >90°

Dapat kang gumamit ng mga formula ng pagbabawas upang pasimplehin ang mga expression. Pagkatapos ay makakakuha tayo ng mga pagkakapantay-pantay ng anyo na cos a → , n → ^ = sin α , a → , n → ^< 90 ° cos a → , n → ^ = - s i n α , a → , n → ^ >90°

Pagkatapos isagawa ang mga pagbabagong-anyo, ang sistema ay nasa anyo na sin α = cos a → , n → ^ , a → , n → ^< 90 ° sin α = - cos a → , n → ^ , a → , n → ^ >90 ° ⇔ sin α = cos a → , n → ^ , a → , n → ^ > 0 sin α = - cos a → , n → ^ , a → , n → ^< 0 ⇔ ⇔ sin α = cos a → , n → ^

Mula dito nakuha namin na ang sine ng anggulo sa pagitan ng tuwid na linya at ng eroplano ay katumbas ng modulus ng cosine ng anggulo sa pagitan ng nagdidirekta na vector ng tuwid na linya at ng normal na vector ng ibinigay na eroplano.

Ang seksyon sa paghahanap ng anggulo na nabuo ng dalawang vectors ay nagsiwalat na ang anggulong ito ay tumatagal ng halaga ng scalar product ng mga vectors at ang produkto ng mga haba na ito. Ang proseso ng pagkalkula ng sine ng anggulo na nakuha ng intersection ng isang tuwid na linya at isang eroplano ay isinasagawa ayon sa formula

sin α = cos a → , n → ^ = a → , n → ^ a → n → = a x n x + a y n y + a z n z a x 2 + a y 2 + a z 2 n x 2 + n y 2 + n z 2

Nangangahulugan ito na ang formula para sa pagkalkula ng anggulo sa pagitan ng isang tuwid na linya at isang eroplano na may mga coordinate ng nagdidirekta na vector ng tuwid na linya at ang normal na vector ng eroplano pagkatapos ng pagbabago ay nasa anyo.

α = a r c sin a → , n → ^ a → n → = a r c sin a x n x + a y n y + a z n z a x 2 + a y 2 + a z 2 n x 2 + n y 2 + n z 2

Ang paghahanap ng cosine na may kilalang sine ay pinahihintulutan sa pamamagitan ng paglalapat ng basic trigonometriko pagkakakilanlan. Ang intersection ng isang tuwid na linya at isang eroplano ay bumubuo matinding anggulo. Iminumungkahi nito na ang halaga nito ay magiging isang positibong numero, at ang pagkalkula nito ay ginawa mula sa formula na cos α = 1 - sin α.

Lutasin natin ang ilang katulad na halimbawa upang pagsama-samahin ang materyal.

Halimbawa 1

Hanapin ang anggulo, sine, cosine ng anggulo na nabuo ng tuwid na linya x 3 = y + 1 - 2 = z - 11 6 at ang eroplanong 2 x + z - 1 = 0.

Solusyon

Upang makuha ang mga coordinate ng vector ng direksyon, kinakailangang isaalang-alang ang mga canonical equation ng isang tuwid na linya sa espasyo. Pagkatapos ay makukuha natin na ang a → = (3, - 2, 6) ay ang vector ng direksyon ng tuwid na linya x 3 = y + 1 - 2 = z - 11 6.

Upang mahanap ang mga coordinate ng isang normal na vector, kinakailangang isaalang-alang ang pangkalahatang equation ng eroplano, dahil ang kanilang presensya ay tinutukoy ng mga coefficient na magagamit sa harap ng mga variable ng equation. Pagkatapos ay nakita namin na para sa eroplano 2 x + z - 1 = 0 ang normal na vector ay may anyo n → = (2, 0, 1).

Kinakailangang magpatuloy sa pagkalkula ng sine ng anggulo sa pagitan ng tuwid na linya at ng eroplano. Upang gawin ito, kinakailangan na palitan ang mga coordinate ng mga vectors a → at b → sa ibinigay na formula. Nakakakuha kami ng expression ng form

sin α = cos a → , n → ^ = a → , n → ^ a → n → = a x n x + a y n y + a z n z a x 2 + a y 2 + a z 2 n x 2 + n y 2 + n z 2 = = 3 2 + (- 2 ) 0 + 6 1 3 2 + (- 2) 2 + 6 2 2 2 + 0 2 + 1 2 = 12 7 5

Mula dito makikita natin ang halaga ng cosine at ang halaga ng mismong anggulo. Nakukuha namin:

cos α = 1 - sin α = 1 - 12 7 5 2 = 101 7 5

Sagot: sin α = 12 7 5, cos α = 101 7 5, α = a r c cos 101 7 5 = a r c sin 12 7 5.

Halimbawa 2

Mayroong isang pyramid na binuo gamit ang mga halaga ng mga vectors A B → = 1, 0, 2, A C → = (- 1, 3, 0), A D → = 4, 1, 1. Hanapin ang anggulo sa pagitan ng tuwid na linya A D at eroplano A B C.

Solusyon

Upang makalkula ang nais na anggulo, kinakailangan na magkaroon ng mga coordinate ng nagdidirekta na vector ng tuwid na linya at ang normal na vector ng eroplano. para sa isang tuwid na linya A D ang vector ng direksyon ay may mga coordinate A D → = 4, 1, 1.

Ang normal na vector n → na kabilang sa eroplano A B C ay patayo sa vector A B → at A C →. Ito ay nagpapahiwatig na ang normal na vector ng eroplanong A B C ay maaaring isaalang-alang produkto ng vector mga vector A B → at A C → . Kinakalkula namin ito gamit ang formula at makuha ang:

n → = A B → × A C → = i → j → k → 1 0 2 - 1 3 0 = - 6 · i → - 2 · j → + 3 · k → ⇔ n → = (- 6 , - 2 , 3 )

Kinakailangan na palitan ang mga coordinate ng mga vectors upang makalkula ang nais na anggulo na nabuo sa pamamagitan ng intersection ng isang tuwid na linya at isang eroplano. nakakakuha kami ng expression ng form:

α = a r c sin A D → , n → ^ A D → · n → = a r c sin 4 · - 6 + 1 · - 2 + 1 · 3 4 2 + 1 2 + 1 2 · - 6 2 + - 2 2 + 3 2 = a r c sin 23 21 2

Sagot: a r c sin 23 21 2 .

Kung may napansin kang error sa text, paki-highlight ito at pindutin ang Ctrl+Enter