Qual é a fórmula do cosseno alfa. Fórmulas de duplo ângulo e adição de argumentos. Gráfico da função cotangente, y = ctg x
Leia também
Centrado no ponto A.
α é o ângulo expresso em radianos.
Tangente ( tgα) é uma função trigonométrica que depende do ângulo α entre a hipotenusa e o cateto triângulo retângulo, igual à razão o comprimento da perna oposta |BC| ao comprimento da perna adjacente |AB| .
Cotangente ( ctgα) é uma função trigonométrica que depende do ângulo α entre a hipotenusa e o cateto de um triângulo retângulo, igual à razão do comprimento do cateto adjacente |AB| ao comprimento da perna oposta |BC| .
Tangente
Onde n- inteira.
Na literatura ocidental, a tangente é denotada da seguinte forma:
.
;
;
.
Gráfico da função tangente, y = tg x
Co-tangente
Onde n- inteira.
Na literatura ocidental, a cotangente é denotada da seguinte forma:
.
A seguinte notação também foi adotada:
;
;
.
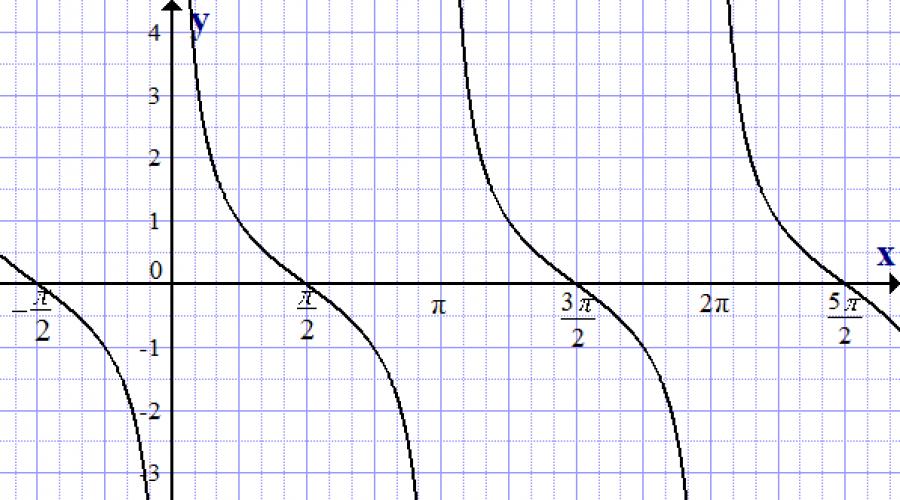
Gráfico da função cotangente, y = ctg x

Propriedades da tangente e cotangente
Periodicidade
Funções y= tg x e y= ctg x são periódicas com período π.
Paridade
As funções tangente e cotangente são ímpares.
Domínios de definição e valores, ascendentes, descendentes
As funções tangente e cotangente são contínuas em seu domínio de definição (veja a prova de continuidade). As principais propriedades da tangente e da cotangente são apresentadas na tabela ( n- inteiro).
| y= tg x | y= ctg x | |
| Escopo e continuidade | ||
| Faixa de valores | -∞ < y < +∞ | -∞ < y < +∞ |
| Ascendente | - | |
| descendente | - | |
| Extremos | - | - |
| Zeros, y = 0 | ||
| Pontos de interseção com o eixo y, x = 0 | y= 0 | - |
Fórmulas
Expressões em termos de seno e cosseno
;
;
;
;
;
Fórmulas para tangente e cotangente de soma e diferença
O resto das fórmulas são fáceis de obter, por exemplo
Produto de tangentes
A fórmula da soma e diferença de tangentes
Esta tabela mostra os valores de tangentes e cotangentes para alguns valores do argumento. 
Expressões em termos de números complexos
Expressões em termos de funções hiperbólicas
;
;
Derivativos
; .
.
Derivada da enésima ordem em relação à variável x da função:
.
Derivação de fórmulas para tangente > > > ; para cotangente > > >
Integrais
Expansões em série
Para obter a expansão da tangente em potências de x, você precisa tomar vários termos da expansão em série de potência para funções pecado x e cos x e divida esses polinômios entre si , . Isso resulta nas seguintes fórmulas.
No .
no .
Onde B n- Números de Bernoulli. Eles são determinados a partir da relação de recorrência:
;
;
Onde .
Ou de acordo com a fórmula de Laplace: 
Funções inversas
As funções inversas de tangente e cotangente são arcotangente e arcotangente, respectivamente.
Arctangente, arctg
, Onde n- inteira.
Arco tangente, arcctg
, Onde n- inteira.
Referências:
DENTRO. Bronstein, K. A. Semendyaev, Manual de Matemática para Engenheiros e Estudantes de Instituições de Ensino Superior, Lan, 2009.
G. Korn, Manual de Matemática para cientistas e engenheiros, 2012.
- 2. Faixa de valores: [-1;1]
- 3. Função ímpar.
- 7. Intervalos em que a função é positiva: (2*pi*n; pi+2*pi*n)
- 8. Intervalos em que a função é negativa: (-pi + 2*pi*n; 2*pi*n)
- 9. Aumente os intervalos: [-pi/2 +2*pi*n; pi/2 +2*pi*n]
- 10. Intervalos descendentes:
- 11. Pontos baixos: -pi/2 +2*pi*n
- 12. Função mínima: -1
- 13. Pontos altos: pi/2 +2*pi*n
- 14. Função máxima: 1
Propriedades do cosseno
.jpg)
- 1. Domínio de definição: todo o eixo numérico
- 2. Faixa de valores: [-1;1]
- 3. Função uniforme.
- 4. O menor período positivo: 2*pi
- 5. Coordenadas dos pontos de intersecção do gráfico da função com o eixo Ox: (pi / 2 + pi * n; 0)
- 6. Coordenadas dos pontos de intersecção do gráfico da função com o eixo Oy: (0;1)
- 7. Intervalos em que a função é positiva: (-pi/2 +2*pi*n; pi/2 +2*pi*n)
- 8. Intervalos em que a função é negativa: (pi/2 +2*pi*n; 3*pi/2 +2*pi*n)
- 9. Aumente os intervalos: [-pi + 2*pi*n; 2*pi*n]
- 10. Intervalos descendentes:
- 11. Pontos baixos: pi+2*pi*n
- 12. Função mínima: -1
- 13. Pontos altos: 2*pi*n
- 14. Função máxima: 1
Propriedades Tangentes
.jpg)
- 1. Domínio de definição: (-pi/2 +pi*n; pi/2 +pi*n)
- 3. Função ímpar.
- 5. Coordenadas dos pontos de intersecção do gráfico da função com o eixo Ox: (pi * n; 0)
- 6. Coordenadas dos pontos de intersecção do gráfico da função com o eixo Oy: (0; 0)
- 9. A função aumenta em intervalos (-pi/2 + pi*n; pi/2 + pi*n)
Propriedades Cotangentes
.jpg)
- 1. Domínio de definição: (pi*n; pi +pi*n)
- 2. Faixa de valores: todo o eixo numérico
- 3. Função ímpar.
- 4. O menor período positivo: pi
- 5. Coordenadas dos pontos de intersecção do gráfico da função com o eixo Ox: (pi / 2 + pi * n; 0)
- 6. Coordenadas dos pontos de intersecção do gráfico da função com o eixo Oy: não
- 7. Intervalos em que a função é positiva: (pi*n; pi/2 + pi*n)
- 8. Intervalos em que a função é negativa: (-pi/2 + pi*n; pi*n)
- 9. A função diminui em intervalos (pi*n; pi + pi*n)
- 10. Não há pontos máximos e mínimos.
A figura abaixo mostra vários círculos unitários, nos quais os sinais de seno, cosseno, tangente e cotangente são indicados em vários quartos de coordenadas.
Inicialmente, seno e cosseno surgiram devido à necessidade de calcular quantidades em triângulos retângulos. Percebeu-se que se o valor da medida em grau dos ângulos em um triângulo retângulo não for alterado, então a razão de aspecto, não importa o quanto esses lados mudem de comprimento, permanece sempre a mesma.
Foi assim que os conceitos de seno e cosseno foram introduzidos. O seno de um ângulo agudo em um triângulo retângulo é a razão entre o cateto oposto e a hipotenusa, e o cosseno é a razão entre o cateto adjacente e a hipotenusa.
Teoremas de cossenos e senos
Mas cossenos e senos podem ser usados não apenas em triângulos retângulos. Para encontrar o valor de um ângulo obtuso ou agudo, o lado de qualquer triângulo, basta aplicar o teorema do cosseno e do seno.
O teorema do cosseno é bastante simples: "O quadrado de um lado de um triângulo é igual à soma dos quadrados dos outros dois lados menos duas vezes o produto desses lados pelo cosseno do ângulo entre eles".
Existem duas interpretações do teorema do seno: pequena e estendida. De acordo com o pequeno: "Em um triângulo, os ângulos são proporcionais aos lados opostos." Este teorema é muitas vezes estendido devido à propriedade do círculo circunscrito em torno de um triângulo: "Em um triângulo, os ângulos são proporcionais aos lados opostos e sua razão é igual ao diâmetro do círculo circunscrito".
Derivativos
Uma derivada é uma ferramenta matemática que mostra a rapidez com que uma função muda em relação a uma mudança em seu argumento. As derivadas são usadas em geometria e em várias disciplinas técnicas.
Ao resolver problemas, você precisa saber valores da tabela derivados funções trigonométricas: seno e cosseno. A derivada do seno é o cosseno, e a derivada do cosseno é o seno, mas com sinal negativo.
Aplicação em matemática
Especialmente frequentemente, senos e cossenos são usados para resolver triângulos retângulos e problemas relacionados a eles.
A conveniência de senos e cossenos também se reflete na tecnologia. Ângulos e lados eram fáceis de avaliar usando os teoremas do cosseno e do seno, quebrando formas e objetos complexos em triângulos "simples". Engenheiros e, muitas vezes lidando com cálculos de proporção e medidas de grau, gastaram muito tempo e esforço calculando cossenos e senos de ângulos que não são de mesa.
Então as tabelas Bradis vieram em socorro, contendo milhares de valoresde senos, cossenos, tangentes e cotangentes ângulos diferentes. Nos tempos soviéticos, alguns professores forçavam seus alunos a memorizar as páginas das tabelas Bradis.
Radiano - magnitude angular arcos, longitudinalmente igual ao raio ou 57,295779513 graus.
Grau (em geometria) - 1/360 de um círculo ou 1/90 de um ângulo reto.
π = 3,141592653589793238462… (valor aproximado de pi).
Tabela de cossenos para ângulos: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Ângulo x (em graus) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ângulo x (em radianos) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3xπ/4 | 5xπ/6 | π | 7xπ/6 | 5xπ/4 | 4xπ/3 | 3xπ/2 | 5xπ/3 | 7xπ/4 | 11xπ/6 | 2xπ |
| cos x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |
Anotações importantes!
1. Se em vez de fórmulas você vir abracadabra, limpe o cache. Como fazer isso no seu navegador está escrito aqui:
2. Antes de começar a ler o artigo, preste atenção ao nosso navegador para os mais recurso útil para
Seno, cosseno, tangente, cotangente
Os conceitos de seno (), cosseno (), tangente (), cotangente () estão inextricavelmente ligados ao conceito de ângulo. Para entender bem esses conceitos, à primeira vista, complexos (que causam um estado de horror em muitos escolares), e ter certeza de que “o diabo não é tão assustador quanto é pintado”, vamos começar do início e entender o conceito de ângulo.
O conceito de ângulo: radiano, grau
Vamos olhar para a imagem. O vetor "virou" em relação ao ponto por uma certa quantidade. Então a medida dessa rotação em relação à posição inicial será injeção.
O que mais você precisa saber sobre o conceito de ângulo? Bem, unidades de ângulo, é claro!
O ângulo, tanto em geometria quanto em trigonometria, pode ser medido em graus e radianos.
Um ângulo de (um grau) é chamado canto central em um círculo, com base em um arco circular igual a uma parte do círculo. Assim, todo o círculo consiste em "pedaços" de arcos circulares, ou seja, o ângulo descrito pelo círculo é igual.

Ou seja, a figura acima mostra um ângulo que é igual, ou seja, esse ângulo é baseado em um arco circular com o tamanho da circunferência.
Um ângulo em radianos é um ângulo central em um círculo, baseado em um arco circular, cujo comprimento é igual ao raio do círculo. Bem, você entendeu? Se não, então vamos olhar para a imagem.

Assim, a figura mostra um ângulo igual a um radiano, ou seja, esse ângulo é baseado em um arco circular, cujo comprimento é igual ao raio do círculo (o comprimento é igual ao comprimento ou raio igual ao comprimento arcos). Assim, o comprimento do arco é calculado pela fórmula:
Onde é o ângulo central em radianos.
Bem, sabendo disso, você pode responder quantos radianos contém um ângulo descrito por um círculo? Sim, para isso você precisa se lembrar da fórmula da circunferência de um círculo. Aqui está ela:
Bem, agora vamos correlacionar essas duas fórmulas e fazer com que o ângulo descrito pelo círculo seja igual. Ou seja, correlacionando o valor em graus e radianos, obtemos isso. Respectivamente, . Como você pode ver, ao contrário de "graus", a palavra "radiano" é omitida, pois a unidade de medida geralmente é clara no contexto.
Quantos radianos são? Está certo!
Entendi? Em seguida, aperte para a frente:
Alguma dificuldade? Então veja respostas:
Triângulo retângulo: seno, cosseno, tangente, cotangente de um ângulo
Então, com o conceito de ângulo descoberto. Mas o que é o seno, cosseno, tangente, cotangente de um ângulo? Vamos descobrir. Para isso, um triângulo retângulo nos ajudará.

Como se chamam os lados de um triângulo retângulo? Isso mesmo, a hipotenusa e os catetos: a hipotenusa é o lado oposto ao ângulo reto (no nosso exemplo, este é o lado); as pernas são os dois lados restantes e (aqueles adjacentes ângulo certo), além disso, se considerarmos as pernas em relação ao ângulo, então a perna é a perna adjacente e a perna é a oposta. Então, agora vamos responder a pergunta: quais são o seno, cosseno, tangente e cotangente de um ângulo?
Seno de um ânguloé a razão da perna oposta (distante) para a hipotenusa.
em nosso triângulo.
Cosseno de um ângulo- esta é a razão da perna adjacente (próxima) para a hipotenusa.
em nosso triângulo.
Ângulo tangente- esta é a proporção da perna oposta (distante) para a adjacente (perto).
em nosso triângulo.
Cotangente de um ângulo- esta é a proporção da perna adjacente (próxima) para a oposta (distante).
em nosso triângulo.
Essas definições são necessárias lembrar! Para tornar mais fácil lembrar qual perna dividir por qual, você precisa entender claramente que em tangente e co-tangente apenas as pernas ficam sentadas, e a hipotenusa aparece apenas em seio e cosseno. E então você pode criar uma cadeia de associações. Por exemplo, este:
cosseno→toque→toque→adjacente;
Cotangente→toque→toque→adjacente.
Antes de tudo, é necessário lembrar que o seno, cosseno, tangente e cotangente como razões dos lados de um triângulo não dependem dos comprimentos desses lados (em um ângulo). Não acredite? Então certifique-se olhando para a imagem:

Considere, por exemplo, o cosseno de um ângulo. Por definição, a partir de um triângulo: , mas podemos calcular o cosseno de um ângulo a partir de um triângulo: . Você vê, os comprimentos dos lados são diferentes, mas o valor do cosseno de um ângulo é o mesmo. Assim, os valores de seno, cosseno, tangente e cotangente dependem apenas da magnitude do ângulo.
Se você entende as definições, vá em frente e corrija-as!
Para o triângulo mostrado na figura abaixo, encontramos.

Bem, você conseguiu? Então tente você mesmo: calcule o mesmo para o canto.
Círculo unitário (trigonométrico)
Entendendo os conceitos de graus e radianos, consideramos um círculo com um raio igual a. Tal círculo é chamado solteiro. É muito útil no estudo da trigonometria. Portanto, nos debruçamos sobre isso com um pouco mais de detalhes.

Como você pode ver, este círculo é construído no sistema de coordenadas cartesianas. O raio do círculo é igual a um, enquanto o centro do círculo está na origem, a posição inicial do vetor de raio é fixada ao longo da direção positiva do eixo (no nosso exemplo, este é o raio).
Cada ponto do círculo corresponde a dois números: a coordenada ao longo do eixo e a coordenada ao longo do eixo. Quais são esses números de coordenadas? E, em geral, o que eles têm a ver com o tema em questão? Para fazer isso, lembre-se do triângulo retângulo considerado. Na figura acima, você pode ver dois triângulos retângulos inteiros. Considere um triângulo. É retangular porque é perpendicular ao eixo.
O que é igual a de um triângulo? Está certo. Além disso, sabemos que é o raio do círculo unitário e, portanto, . Substitua esse valor em nossa fórmula de cosseno. Aqui está o que acontece:
E o que é igual a de um triângulo? Bem, claro, ! Substitua o valor do raio nesta fórmula e obtenha:
Então, você pode dizer quais coordenadas um ponto tem, pertencente ao círculo? Bem, de jeito nenhum? E se você perceber isso e são apenas números? A que coordenada corresponde? Bem, é claro, a coordenada! A que coordenada corresponde? Isso mesmo, coordenar! Assim, o ponto.

E o que então são iguais e? Isso mesmo, vamos usar as definições apropriadas de tangente e cotangente e obter isso, a.
E se o ângulo for maior? Aqui, por exemplo, como nesta imagem:

O que mudou neste exemplo? Vamos descobrir. Para fazer isso, voltamos novamente para um triângulo retângulo. Considere um triângulo retângulo: um ângulo (como adjacente a um ângulo). Qual é o valor do seno, cosseno, tangente e cotangente de um ângulo? Isso mesmo, aderimos às definições correspondentes das funções trigonométricas:
Bem, como você pode ver, o valor do seno do ângulo ainda corresponde à coordenada; o valor do cosseno do ângulo - a coordenada; e os valores de tangente e cotangente às razões correspondentes. Assim, essas relações são aplicáveis a quaisquer rotações do vetor raio.
Já foi mencionado que a posição inicial do vetor raio é ao longo da direção positiva do eixo. Até agora, giramos esse vetor no sentido anti-horário, mas o que acontece se o girarmos no sentido horário? Nada de extraordinário, você também obterá um ângulo de um determinado tamanho, mas apenas negativo. Assim, ao girar o vetor raio no sentido anti-horário, obtemos ângulos positivos, e ao girar no sentido horário - negativo.
Então, sabemos que toda uma revolução do vetor raio ao redor do círculo é ou. É possível girar o vetor raio por ou por? Bem, claro que você pode! No primeiro caso, portanto, o vetor raio fará uma revolução completa e parará na posição ou.
No segundo caso, ou seja, o raio vetor fará três voltas completas e parará na posição ou.
Assim, a partir dos exemplos acima, podemos concluir que os ângulos que diferem por ou (onde é qualquer número inteiro) correspondem à mesma posição do vetor raio.
A figura abaixo mostra um ângulo. A mesma imagem corresponde ao canto, e assim por diante. Esta lista pode ser continuada indefinidamente. Todos esses ângulos podem ser escritos com a fórmula geral ou (onde é qualquer número inteiro)

Agora, conhecendo as definições das funções trigonométricas básicas e usando o círculo unitário, tente responder a quais valores são iguais:
Aqui está um círculo unitário para ajudá-lo:

Alguma dificuldade? Então vamos descobrir. Então sabemos que:
A partir daqui, determinamos as coordenadas dos pontos correspondentes a certas medidas do ângulo. Bem, vamos começar pela ordem: o canto em corresponde a um ponto com coordenadas, portanto:
Não existe;
Além disso, seguindo a mesma lógica, descobrimos que os cantos em correspondem a pontos com coordenadas, respectivamente. Sabendo disso, é fácil determinar os valores das funções trigonométricas nos pontos correspondentes. Tente você mesmo primeiro, depois verifique as respostas.
Respostas:
Assim, podemos fazer a seguinte tabela:

Não há necessidade de lembrar todos esses valores. Basta lembrar a correspondência entre as coordenadas dos pontos no círculo unitário e os valores das funções trigonométricas:
Mas os valores das funções trigonométricas dos ângulos e, dados na tabela abaixo, deve ser lembrado:

Não tenha medo, agora vamos mostrar um dos exemplos memorização bastante simples dos valores correspondentes:
Para usar este método, é vital lembrar os valores do seno para todas as três medidas do ângulo (), bem como o valor da tangente do ângulo em. Conhecendo esses valores, é bastante fácil restaurar toda a tabela - os valores de cosseno são transferidos de acordo com as setas, ou seja:
Sabendo disso, você pode restaurar os valores para. O numerador " " corresponderá e o denominador " " corresponderá. Os valores cotangentes são transferidos de acordo com as setas mostradas na figura. Se você entender isso e se lembrar do diagrama com setas, será suficiente lembrar o valor inteiro da tabela.
Coordenadas de um ponto em um círculo
É possível encontrar um ponto (suas coordenadas) em um círculo, conhecendo as coordenadas do centro do círculo, seu raio e ângulo de rotação?
Bem, claro que você pode! Vamos trazer para fora Fórmula geral encontrar as coordenadas de um ponto.
Aqui, por exemplo, temos esse círculo:

Nos é dado que o ponto é o centro do círculo. O raio do círculo é igual. É necessário encontrar as coordenadas do ponto obtidas girando o ponto em graus.
Como pode ser visto na figura, a coordenada do ponto corresponde ao comprimento do segmento. O comprimento do segmento corresponde à coordenada do centro do círculo, ou seja, é igual a. O comprimento de um segmento pode ser expresso usando a definição de cosseno:
Então temos que para o ponto a coordenada.
Pela mesma lógica, encontramos o valor da coordenada y para o ponto. Por isso,
Então em visão geral as coordenadas do ponto são determinadas pelas fórmulas:
Coordenadas do centro do círculo,
raio do círculo,
Ângulo de rotação do vetor raio.
Como você pode ver, para o círculo unitário que estamos considerando, essas fórmulas são significativamente reduzidas, pois as coordenadas do centro são zero e o raio é igual a um:
Bem, vamos tentar essas fórmulas para dar um gostinho, praticando encontrar pontos em um círculo?
1. Encontre as coordenadas de um ponto em um círculo unitário obtido girando um ponto.
2. Encontre as coordenadas de um ponto em um círculo unitário obtido pela rotação de um ponto.
3. Encontre as coordenadas de um ponto em um círculo unitário obtido girando um ponto.
4. Ponto - o centro do círculo. O raio do círculo é igual. É necessário encontrar as coordenadas do ponto obtidas pela rotação do vetor raio inicial por.
5. Ponto - o centro do círculo. O raio do círculo é igual. É necessário encontrar as coordenadas do ponto obtidas pela rotação do vetor raio inicial por.
Tendo problemas para encontrar as coordenadas de um ponto em um círculo?
Resolva esses cinco exemplos (ou entenda bem a solução) e você aprenderá como encontrá-los!
RESUMO E FÓRMULA BÁSICA
O seno de um ângulo é a razão entre o cateto oposto (distante) e a hipotenusa.
O cosseno de um ângulo é a razão entre o cateto adjacente (próximo) e a hipotenusa.
A tangente de um ângulo é a razão entre a perna oposta (distante) e a adjacente (próxima).
A cotangente de um ângulo é a razão entre a perna adjacente (próxima) e a oposta (distante).
Bom, o assunto acabou. Se você está lendo essas linhas, então você é muito legal.
Porque apenas 5% das pessoas são capazes de dominar algo por conta própria. E se você leu até o final, então você está nos 5%!
Agora o mais importante.
Você descobriu a teoria sobre este tópico. E, repito, é... é simplesmente super! Você já é melhor do que a grande maioria de seus pares.
O problema é que isso pode não ser suficiente...
Para que?
Por entrega bem sucedida Exame Estadual Unificado, para admissão ao instituto no orçamento e, MAIS IMPORTANTE, para a vida.
Não vou te convencer de nada, só vou dizer uma coisa...
Pessoas que receberam uma boa educação, ganham muito mais do que quem não recebeu. Isso é estatística.
Mas isso não é o principal.
O principal é que eles são MAIS FELIZES (existem esses estudos). Talvez porque muito se abre diante deles. mais possibilidades e a vida se torna mais brilhante? Não sei...
Mas pense por si mesmo...
O que é preciso para ter certeza de ser melhor do que os outros no exame e ser finalmente... mais feliz?
ENCHE A MÃO, RESOLVENDO PROBLEMAS NESSE ASSUNTO.
No exame, você não será perguntado teoria.
Você vai precisar resolver problemas na hora.
E, se você não os resolveu (MUITO!), você definitivamente cometerá um erro estúpido em algum lugar ou simplesmente não o fará a tempo.
É como nos esportes - você precisa repetir muitas vezes para ganhar com certeza.
Encontre uma coleção onde quiser necessariamente com soluções análise detalhada e decidir, decidir, decidir!
Você pode usar nossas tarefas (não necessárias) e certamente as recomendamos.
Para obter ajuda com a ajuda de nossas tarefas, você precisa ajudar a prolongar a vida útil do livro YouClever que está lendo no momento.
Como? Existem duas opções:
- Desbloqueie o acesso a todas as tarefas ocultas neste artigo -
- Desbloqueie o acesso a todas as tarefas ocultas em todos os 99 artigos do tutorial - Compre um livro - 499 rublos
Sim, temos 99 desses artigos no livro didático e acesso a todas as tarefas e todos os textos ocultos neles podem ser abertos imediatamente.
O acesso a todas as tarefas ocultas é fornecido durante toda a vida útil do site.
Em conclusão...
Se você não gosta de nossas tarefas, encontre outras. Só não pare com a teoria.
“Entendido” e “eu sei resolver” são habilidades completamente diferentes. Você precisa de ambos.
Encontre problemas e resolva!
A trigonometria, como ciência, originou-se no Oriente Antigo. Primeiro relações trigonométricas foram criados por astrônomos para criar um calendário preciso e orientação pelas estrelas. Esses cálculos estavam relacionados à trigonometria esférica, enquanto que em curso escolar estude a razão entre os lados e o ângulo de um triângulo plano.
A trigonometria é um ramo da matemática que trata das propriedades das funções trigonométricas e da relação entre os lados e os ângulos dos triângulos.
Durante o apogeu da cultura e da ciência do 1º milênio d.C., o conhecimento se espalhou de oriente antigo para a Grécia. Mas as principais descobertas da trigonometria são mérito dos homens do califado árabe. Em particular, o cientista turcomeno al-Marazvi introduziu funções como tangente e cotangente, compilou as primeiras tabelas de valores para senos, tangentes e cotangentes. O conceito de seno e cosseno foi introduzido por cientistas indianos. Muita atenção é dedicada à trigonometria nas obras de grandes figuras da antiguidade como Euclides, Arquimedes e Eratóstenes.
Quantidades básicas de trigonometria
Funções trigonométricas básicas argumento numérico são seno, cosseno, tangente e cotangente. Cada um deles tem seu próprio gráfico: seno, cosseno, tangente e cotangente.
As fórmulas para calcular os valores dessas quantidades são baseadas no teorema de Pitágoras. É mais conhecido pelos escolares na formulação: “Calças pitagóricas, iguais em todas as direções”, pois a prova é dada no exemplo de um triângulo retângulo isósceles.
Seno, cosseno e outras dependências estabelecem uma relação entre cantos afiados e lados de qualquer triângulo retângulo. Damos fórmulas para calcular essas quantidades para o ângulo A e traçamos a relação das funções trigonométricas:

Como você pode ver, tg e ctg são funções inversas. Se representarmos o cateto a como o produto de sen A e a hipotenusa c, e o cateto b como cos A * c, obtemos as seguintes fórmulas para a tangente e a cotangente:

círculo trigonométrico
Graficamente, a razão das quantidades mencionadas pode ser representada da seguinte forma:

círculo, em este caso, representa todos os valores possíveis do ângulo α — de 0° a 360°. Como pode ser visto na figura, cada função assume um valor negativo ou positivo dependendo do ângulo. Por exemplo, sen α estará com sinal “+” se α pertencer aos quartos I e II do círculo, ou seja, estiver na faixa de 0 ° a 180 °. Com α de 180° a 360° (quartos III e IV), sen α só pode ser um valor negativo.
Vamos tentar construir tabelas trigonométricas para ângulos específicos e descubra o significado das quantidades.

Os valores de α iguais a 30°, 45°, 60°, 90°, 180° e assim por diante são chamados de casos especiais. Os valores das funções trigonométricas para eles são calculados e apresentados na forma de tabelas especiais.

Esses ângulos não foram escolhidos por acaso. A designação π nas tabelas é para radianos. Rad é o ângulo no qual o comprimento de um arco circular corresponde ao seu raio. Este valor foi introduzido para estabelecer uma relação universal; ao calcular em radianos, o comprimento real do raio em cm não importa.

Os ângulos nas tabelas para funções trigonométricas correspondem a valores radianos:

Portanto, não é difícil adivinhar que 2π é um círculo completo ou 360°.
Propriedades das funções trigonométricas: seno e cosseno
Para considerar e comparar as propriedades básicas de seno e cosseno, tangente e cotangente, é necessário desenhar suas funções. Isso pode ser feito na forma de uma curva localizada em um sistema de coordenadas bidimensional.
Considerar Tabela de comparação propriedades para onda senoidal e cosseno:

| sinusóide | onda cosseno |
|---|---|
| y = sen x | y = cos x |
| ODZ [-1; 1] | ODZ [-1; 1] |
| sen x = 0, para x = πk, onde k ϵ Z | cos x = 0, para x = π/2 + πk, onde k ϵ Z |
| sen x = 1, para x = π/2 + 2πk, onde k ϵ Z | cos x = 1, para x = 2πk, onde k ϵ Z |
| sen x = - 1, em x = 3π/2 + 2πk, onde k ϵ Z | cos x = - 1, para x = π + 2πk, onde k ϵ Z |
| sin (-x) = - sin x, ou seja, função ímpar | cos (-x) = cos x, ou seja, a função é par |
| a função é periódica, o menor período é 2π | |
| sen x › 0, com x pertencente aos quartos I e II ou de 0° a 180° (2πk, π + 2πk) | cos x › 0, com x pertencente aos quartos I e IV ou de 270° a 90° (- π/2 + 2πk, π/2 + 2πk) |
| sen x ‹ 0, com x pertencente aos quartos III e IV ou de 180° a 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, com x pertencente aos quartos II e III ou de 90° a 270° (π/2 + 2πk, 3π/2 + 2πk) |
| aumenta no intervalo [- π/2 + 2πk, π/2 + 2πk] | aumenta no intervalo [-π + 2πk, 2πk] |
| diminui nos intervalos [π/2 + 2πk, 3π/2 + 2πk] | diminui nos intervalos |
| derivada (sen x)' = cos x | derivada (cos x)' = - sin x |
Determinar se uma função é par ou não é muito simples. Basta imaginar um círculo trigonométrico com sinais de grandezas trigonométricas e “dobrar” mentalmente o gráfico em relação ao eixo OX. Se os sinais são iguais, a função é par; caso contrário, é ímpar.

A introdução dos radianos e a enumeração das principais propriedades da onda senoidal e cosseno permitem trazer o seguinte padrão:

É muito fácil verificar a exatidão da fórmula. Por exemplo, para x = π/2, o seno é igual a 1, assim como o cosseno de x = 0. A verificação pode ser feita olhando tabelas ou traçando curvas de função para valores dados.
Propriedades de tangentóide e cotangentóide
Os gráficos das funções tangente e cotangente diferem significativamente da onda senoidal e cosseno. Os valores tg e ctg são inversos entre si.


- Y = tgx.
- A tangente tende para os valores de y em x = π/2 + πk, mas nunca os atinge.
- O menor período positivo da tangenteide é π.
- Tg (- x) \u003d - tg x, ou seja, a função é ímpar.
- Tg x = 0, para x = πk.
- A função está aumentando.
- Tg x › 0, para x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, para x ϵ (— π/2 + πk, πk).
- Derivada (tg x)' = 1/cos 2 x .
Considerar imagem gráfica cotangentóides abaixo.

As principais propriedades do cotangentoide:
- Y = ctgx.
- Ao contrário das funções seno e cosseno, na tangente Y pode assumir os valores do conjunto de todos os números reais.
- O cotangentoide tende aos valores de y em x = πk, mas nunca os atinge.
- O menor período positivo do cotangentóide é π.
- Ctg (- x) \u003d - ctg x, ou seja, a função é ímpar.
- Ctg x = 0, para x = π/2 + πk.
- A função está diminuindo.
- Ctg x › 0, para x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, para x ϵ (π/2 + πk, πk).
- Derivado (ctg x)' = - 1/sen 2 x Fixo