Wielkie twierdzenie Fermata: dowód Wilesa i Perelmana, wzory, zasady obliczeń i pełny dowód twierdzenia. Dowód twierdzenia Fermata jest elementarny, prosty, zrozumiały Twierdzenie, którego nie da się udowodnić

Tak więc ostatnie twierdzenie Fermata (często nazywane ostatnim twierdzeniem Fermata), sformułowane w 1637 r. przez genialnego francuskiego matematyka Pierre'a Fermata, jest bardzo proste w swojej istocie i zrozumiałe dla każdej osoby z wykształceniem średnim. Mówi, że wzór a do potęgi n + b do potęgi n \u003d c do potęgi n nie ma naturalnych (czyli nieułamkowych) rozwiązań dla n> 2. Wszystko wydaje się proste i jasne , ale najlepsi matematycy i zwykli amatorzy walczyli o znalezienie rozwiązania przez ponad trzy i pół wieku.

Grigorij Perelman. Odmowa

Wasilij Maksimow

W sierpniu 2006 roku ogłoszono nazwiska najlepszych matematyków świata, którzy otrzymali najbardziej prestiżowy Medal Fieldsa - swego rodzaju odpowiednik Nagrody Nobla, której matematycy, z kaprysu Alfreda Nobla, zostali pozbawieni. Medal Fieldsa – oprócz odznaki honorowej laureaci otrzymują czek na piętnaście tysięcy dolarów kanadyjskich – przyznawany jest przez Międzynarodowy Kongres Matematyków co cztery lata. Został ustanowiony przez kanadyjskiego naukowca Johna Charlesa Fieldsa i po raz pierwszy został nagrodzony w 1936 roku. Od 1950 r. Medal Fieldsa jest regularnie osobiście przyznawany przez króla Hiszpanii za wkład w rozwój nauk matematycznych. Laureatami nagrody może zostać od jednego do czterech naukowców w wieku poniżej czterdziestu lat. Nagrodę otrzymało już czterdziestu czterech matematyków, w tym ośmiu Rosjan.

Grigorij Perelman. Henryka Poincarego.

W 2006 roku laureatami zostali Francuz Wendelin Werner, Australijczyk Terence Tao oraz dwóch Rosjan, pracujący w USA Andriej Okounkow i Grigorij Perelman, naukowiec z Petersburga. Jednak w ostatniej chwili okazało się, że Perelman odmówił przyjęcia tej prestiżowej nagrody – jak ogłosili organizatorzy, „z powodów zasadniczych”.

Tak ekstrawagancki wyczyn rosyjskiego matematyka nie był zaskoczeniem dla ludzi, którzy go znali. To nie pierwszy raz, kiedy odmawia przyznania nagród matematycznych, tłumacząc swoją decyzję tym, że nie lubi uroczystych imprez i nadmiernego szumu wokół swojego imienia. Dziesięć lat temu, w 1996 roku, Perelman odmówił przyjęcia nagrody Europejskiego Kongresu Matematycznego, powołując się na fakt, że nie ukończył prac nad zgłoszonym do nagrody problemem naukowym, a to nie był ostatni przypadek. Wydaje się, że rosyjski matematyk postawił sobie za cel życiowy zaskakiwanie ludzi, wbrew opinii publicznej i społeczności naukowej.

Grigorij Jakowlewicz Perelman urodził się 13 czerwca 1966 roku w Leningradzie. Od najmłodszych lat lubił nauki ścisłe, znakomicie ukończył słynne 239. liceum z dogłębną nauką matematyki, wygrał liczne konkursy matematyczne: na przykład w 1982 r. brał udział w Międzynarodowej Olimpiadzie Matematycznej, która odbyła się w Budapeszcie. Perelman bez egzaminów został zapisany na wydział mechaniki i matematyki Uniwersytetu Leningradzkiego, gdzie studiował „doskonale”, nadal wygrywając w konkursach matematycznych na wszystkich poziomach. Po ukończeniu uniwersytetu z wyróżnieniem wstąpił do szkoły podyplomowej na wydziale petersburskim Instytutu Matematycznego im. Stekłowa. Jego przełożonym był słynny matematyk akademik Aleksandrow. Po obronie pracy doktorskiej Grigorij Perelman pozostał w instytucie, w laboratorium geometrii i topologii. Znany ze swojej pracy nad teorią przestrzeni Aleksandrowa, był w stanie znaleźć dowody na szereg ważnych hipotez. Mimo licznych ofert czołowych zachodnich uczelni Perelman woli pracować w Rosji.

Jego najbardziej znanym sukcesem było rozwiązanie w 2002 r. słynnej hipotezy Poincarego, opublikowanej w 1904 r. i od tamtej pory nie udowodnionej. Perelman pracował nad nim przez osiem lat. Hipotezę Poincarégo uważano za jedną z największych zagadek matematycznych, a jej rozwiązanie za najważniejsze osiągnięcie nauk matematycznych: natychmiast posunęłoby naprzód badania nad fizycznymi i matematycznymi podstawami wszechświata. Najjaśniejsze umysły na planecie przewidziały jego rozwiązanie dopiero za kilka dekad, a Clay Institute of Mathematics w Cambridge w stanie Massachusetts uczynił problem Poincarego jednym z siedmiu najciekawszych nierozwiązanych problemów matematycznych tysiąclecia, z których każdy obiecano milionom nagroda dolara (Problemy nagrody milenijnej) .

Hipoteza (czasami nazywana problemem) francuskiego matematyka Henri Poincaré (1854–1912) jest sformułowana w następujący sposób: każda zamknięta, po prostu spójna trójwymiarowa przestrzeń jest homeomorficzna z trójwymiarową kulą. Dla wyjaśnienia posłużono się dobrym przykładem: jeśli owiniesz jabłko gumką, to w zasadzie, ciągnąc taśmę, możesz ścisnąć jabłko w punkt. Jeśli owiniesz pączka tą samą taśmą, nie możesz go ścisnąć w punkt bez rozerwania pączka lub gumy. W tym kontekście jabłko nazywane jest figurą „pojedynczo połączoną”, ale pączek nie jest po prostu połączony. Prawie sto lat temu Poincaré ustalił, że sfera dwuwymiarowa jest po prostu spójna i zasugerował, że sfera trójwymiarowa jest również po prostu spójna. Najlepsi matematycy na świecie nie potrafili udowodnić tego przypuszczenia.

Aby zakwalifikować się do nagrody Clay Institute, Perelman musiał tylko opublikować swoje rozwiązanie w jednym z czasopism naukowych, a jeśli w ciągu dwóch lat nikt nie znajdzie błędu w jego obliczeniach, rozwiązanie zostanie uznane za prawidłowe. Jednak Perelman od samego początku odbiegał od zasad, publikując swoje rozwiązanie na stronie preprint Los Alamos Science Laboratory. Być może bał się, że do jego obliczeń wkradł się błąd – podobna historia wydarzyła się już w matematyce. W 1994 roku angielski matematyk Andrew Wiles zaproponował rozwiązanie słynnego twierdzenia Fermata, a kilka miesięcy później okazało się, że do jego obliczeń wkradł się błąd (choć później został poprawiony, a sensacja nadal występowała). Nadal nie ma oficjalnej publikacji dowodu hipotezy Poincarego - ale istnieje autorytatywna opinia najlepszych matematyków na planecie, potwierdzająca poprawność obliczeń Perelmana.

Medal Fieldsa został przyznany Grigorijowi Perelmanowi właśnie za rozwiązanie problemu Poincarégo. Ale rosyjski naukowiec odmówił nagrody, na którą niewątpliwie zasługuje. „Grigory powiedział mi, że czuje się odizolowany od międzynarodowej społeczności matematycznej, poza tą społecznością, i dlatego nie chce otrzymać nagrody” – powiedział John Ball, prezes Światowej Unii Matematyków (WCM), na konferencji prasowej w Madryt.

Krążą pogłoski, że Grigorij Perelman zamierza całkowicie porzucić naukę: sześć miesięcy temu odszedł z rodzinnego Instytutu Matematycznego Stiekłowa i mówi się, że nie będzie już zajmował się matematyką. Być może rosyjski naukowiec uważa, że ​​udowadniając słynną hipotezę, zrobił dla nauki wszystko, co mógł. Ale kto podejmie się mówić o toku myślenia tak błyskotliwego naukowca i niezwykłej osoby?… Perelman odmawia jakichkolwiek komentarzy i powiedział gazecie The Daily Telegraph: „Nic, co mogę powiedzieć, nie ma najmniejszego znaczenia dla opinii publicznej”. Czołowe publikacje naukowe były jednak zgodne w swoich ocenach, gdy donosiły, że „Grigorij Perelman, rozwiązawszy twierdzenie Poincarego, stał na równi z największymi geniuszami przeszłości i teraźniejszości”.

Miesięcznik i wydawnictwo literacko-dziennikarskie.

W XVII wieku we Francji mieszkał prawnik i matematyk na pół etatu Pierre Fermat, który poświęcał swojemu hobby długie godziny wolnego czasu. Pewnego zimowego wieczoru, siedząc przy kominku, wygłosił jedno z najciekawszych stwierdzeń z dziedziny teorii liczb - nazwano je później Wielkim lub Wielkim Twierdzeniem Fermata. Być może w kręgach matematycznych emocje nie byłyby tak duże, gdyby nie wydarzyło się jedno wydarzenie. Matematyk często spędzał wieczory studiując ulubioną księgę Diofantusa z Aleksandrii „Arytmetyka” (III w.), jednocześnie zapisując ważne myśli na jej marginesach – ta rzadkość została pieczołowicie zachowana dla potomności przez jego syna. Tak więc na szerokich marginesach tej książki ręka Fermata pozostawiła ten napis: „Mam dość uderzający dowód, ale jest za duży, aby umieścić go na marginesach”. To właśnie ten wpis wywołał ogromne poruszenie wokół twierdzenia. Wśród matematyków nie było wątpliwości, że wielki uczony oświadczył, że udowodnił swoje własne twierdzenie. Zastanawiacie się zapewne: „Czy rzeczywiście to udowodnił, czy to było banalne kłamstwo, a może są inne wersje, dlaczego ten wpis, który nie dawał spać spokojnie matematykom kolejnych pokoleń, znalazł się na marginesie książka?".

Istota Wielkiego Twierdzenia

Dość dobrze znane twierdzenie Fermata jest w swej istocie proste i polega na tym, że pod warunkiem, że n jest większe niż dwa, liczba dodatnia, równanie X n + Y n \u003d Z n nie będzie miało rozwiązań typu zerowego w obrębie ramy liczb naturalnych. Niewiarygodna złożoność była maskowana w tej pozornie prostej formule, a udowodnienie tego zajęło trzy stulecia. Jest jedna osobliwość - twierdzenie spóźniło się z narodzinami, ponieważ jego szczególny przypadek dla n = 2 pojawił się 2200 lat temu - to nie mniej znane twierdzenie Pitagorasa.

Warto zaznaczyć, że opowieść o znanym twierdzeniu Fermata jest bardzo pouczająca i zabawna nie tylko dla matematyków. Co najciekawsze, nauka nie była dla naukowca pracą, a zwykłym hobby, które z kolei sprawiało Farmerowi ogromną przyjemność. Utrzymywał również stały kontakt z matematykiem, aw niepełnym wymiarze godzin, także przyjacielem, dzielił się pomysłami, ale, co dziwne, nie dążył do opublikowania własnej pracy.

Postępowanie matematyka Rolnika

Jeśli chodzi o prace samego Farmera, znaleziono je właśnie w formie zwykłych listów. W niektórych miejscach nie zachowały się całe strony, zachowały się jedynie fragmenty korespondencji. Bardziej interesujący jest fakt, że przez trzy stulecia naukowcy poszukiwali twierdzenia odkrytego w pismach Fermera.

Ale kto nie odważył się tego udowodnić, próby zostały zredukowane do „zera”. Słynny matematyk Kartezjusz zarzucił nawet naukowcowi przechwałki, ale wszystko sprowadzało się do najzwyklejszej zazdrości. Oprócz tworzenia Farmer udowodnił także swoje własne twierdzenie. To prawda, że ​​rozwiązanie zostało znalezione dla przypadku, gdy n=4. Jeśli chodzi o przypadek dla n=3, zidentyfikował go matematyk Euler.

Jak próbowali udowodnić twierdzenie Fermera

Na samym początku XIX wieku twierdzenie to nadal istniało. Matematycy znaleźli wiele dowodów twierdzeń, które ograniczały się do liczb naturalnych w granicach dwustu.

A w 1909 roku postawiono na szali dość dużą kwotę, równą stu tysiącom marek pochodzenia niemieckiego - a wszystko to tylko po to, by rozwiązać problem związany z tym twierdzeniem. Fundusz samej kategorii nagród pozostawił zamożny miłośnik matematyki Paul Wolfskell, pochodzący zresztą z Niemiec, to on chciał „położyć na siebie ręce”, ale dzięki takiemu zaangażowaniu w twierdzenie Fermera chciał relacja na żywo. Wynikające z tego podniecenie dało początek tonom „dowodów”, które zalały niemieckie uniwersytety, aw kręgu matematyków narodził się przydomek „fermista”, którym na wpół pogardliwie nazywano każdego ambitnego nowicjusza, który nie przedstawił jasnych dowodów.

Hipoteza japońskiego matematyka Yutaki Taniyamy

Aż do połowy XX wieku nie było żadnych zmian w historii Wielkiego Twierdzenia, ale wydarzyło się jedno interesujące wydarzenie. W 1955 roku japoński matematyk Yutaka Taniyama, który miał 28 lat, ujawnił światu stwierdzenie z zupełnie innej dziedziny matematyki – jego hipoteza, w przeciwieństwie do Fermata, wyprzedzała swoje czasy. Mówi: „Dla każdej krzywej eliptycznej istnieje odpowiednia forma modułowa”. Wydaje się to absurdem dla każdego matematyka, jak to, że drzewo składa się z pewnego metalu! Hipoteza paradoksalna, podobnie jak większość innych oszałamiających i pomysłowych odkryć, nie została zaakceptowana, ponieważ po prostu jeszcze do niej nie dojrzeli. A Yutaka Taniyama popełnił samobójstwo trzy lata później - niewytłumaczalny czyn, ale prawdopodobnie honor prawdziwego geniusza samuraja był przede wszystkim.

Przez całą dekadę o hipotezie nie pamiętano, ale w latach siedemdziesiątych osiągnęła ona szczyt popularności – potwierdzali ją wszyscy, którzy mogli ją zrozumieć, ale podobnie jak twierdzenie Fermata pozostała nieudowodniona.

Jak hipoteza Taniyamy i twierdzenie Fermata są powiązane

Piętnaście lat później w matematyce miało miejsce kluczowe wydarzenie, które połączyło słynną japońską hipotezę i twierdzenie Fermata. Gerhard Gray stwierdził, że kiedy hipoteza Taniyamy zostanie udowodniona, zostaną znalezione dowody twierdzenia Fermata. Oznacza to, że ta ostatnia jest konsekwencją hipotezy Taniyamy, a półtora roku później twierdzenie Fermata zostało udowodnione przez profesora Uniwersytetu Kalifornijskiego, Kennetha Ribeta.

Czas mijał, regres ustąpił miejsca postępowi, a nauka szybko posuwała się do przodu, zwłaszcza w dziedzinie techniki komputerowej. W ten sposób wartość n zaczęła coraz bardziej rosnąć.

Pod koniec XX wieku najpotężniejsze komputery znajdowały się w laboratoriach wojskowych, prowadzono programowanie w celu uzyskania rozwiązania znanego problemu Fermata. W wyniku wszystkich prób okazało się, że twierdzenie to jest poprawne dla wielu wartości n, x, y. Ale niestety nie stało się to ostatecznym dowodem, ponieważ nie było żadnych szczegółów jako takich.

John Wiles udowodnił Wielkie Twierdzenie Fermata

I wreszcie, dopiero pod koniec 1994 roku matematyk z Anglii, John Wiles, znalazł i zademonstrował dokładny dowód kontrowersyjnego twierdzenia Fermera. Następnie, po wielu ulepszeniach, dyskusje na ten temat doszły do ​​logicznego wniosku.

Obalenie zostało opublikowane na ponad stu stronach jednego magazynu! Co więcej, twierdzenie zostało udowodnione na nowocześniejszym aparacie matematyki wyższej. I o dziwo, w czasach, gdy Rolnik pisał swoje dzieło, taki aparat nie istniał w przyrodzie. Jednym słowem człowiek został uznany za geniusza w tej dziedzinie, z czym nikt nie mógł się spierać. Pomimo wszystkiego, co się wydarzyło, dziś możesz być pewien, że przedstawione twierdzenie wielkiego naukowca Farmera jest uzasadnione i udowodnione, a żaden matematyk ze zdrowym rozsądkiem nie rozpocznie sporów na ten temat, z czym zgadzają się nawet najbardziej zagorzali sceptycy całej ludzkości.

Pełne imię i nazwisko osoby, od której imienia zostało nazwane prezentowane twierdzenie, brzmiało Pierre de Fermer. Wniósł wkład w wiele różnych dziedzin matematyki. Ale niestety większość jego prac została opublikowana dopiero po jego śmierci.

Nie ma zbyt wielu ludzi na świecie, którzy nigdy nie słyszeli o Wielkim Twierdzeniu Fermata - być może jest to jedyny problem matematyczny, który stał się tak powszechnie znany i stał się prawdziwą legendą. Wspomina się o nim w wielu książkach i filmach, a głównym kontekstem prawie wszystkich wzmianek jest niemożność udowodnienia twierdzenia.

Tak, to twierdzenie jest bardzo znane iw pewnym sensie stało się „bożkiem” czczonym przez matematyków amatorów i zawodowych, ale niewiele osób wie, że jego dowód został znaleziony, a stało się to w 1995 roku. Ale najpierw najważniejsze.

Tak więc ostatnie twierdzenie Fermata (często nazywane ostatnim twierdzeniem Fermata), sformułowane w 1637 r. przez genialnego francuskiego matematyka Pierre'a Fermata, ma bardzo prosty charakter i jest zrozumiałe dla każdej osoby z wykształceniem średnim. Mówi, że wzór a do potęgi n + b do potęgi n \u003d c do potęgi n nie ma naturalnych (czyli nieułamkowych) rozwiązań dla n> 2. Wszystko wydaje się proste i jasne , ale najlepsi matematycy i zwykli amatorzy walczyli o znalezienie rozwiązania przez ponad trzy i pół wieku.

Dlaczego jest tak sławna? Teraz dowiedzmy się...

Czy istnieje niewiele udowodnionych, nieudowodnionych, a jednak nieudowodnionych twierdzeń? Rzecz w tym, że ostatnie twierdzenie Fermata jest największym kontrastem między prostotą sformułowania a złożonością dowodu. Wielkie twierdzenie Fermata to niezwykle trudne zadanie, a jednak jego sformułowanie może zrozumieć każdy, kto ma 5 klas szkoły średniej, ale dowód jest daleki nawet od każdego zawodowego matematyka. Ani w fizyce, ani w chemii, ani w biologii, ani w tej samej matematyce nie ma ani jednego problemu, który zostałby sformułowany w tak prosty sposób, ale pozostawał nierozwiązany przez tak długi czas. 2. Z czego się składa?

Zacznijmy od pitagorejskich spodni Sformułowanie jest naprawdę proste - na pierwszy rzut oka. Jak wiemy z dzieciństwa, „spodnie pitagorejskie są równe ze wszystkich stron”. Zadanie wydaje się takie proste, ponieważ opiera się na znanym wszystkim matematycznym stwierdzeniu - twierdzeniu Pitagorasa: w dowolnym trójkącie prostokątnym kwadrat zbudowany na przeciwprostokątnej jest równy sumie kwadratów zbudowanych na nogach.

W V wieku pne. Pitagoras założył bractwo pitagorejskie. Pitagorejczycy badali między innymi trójki całkowite spełniające równanie x²+y²=z². Udowodnili, że trójek pitagorejskich jest nieskończenie wiele i uzyskali ogólne wzory ich znajdowania. Prawdopodobnie próbowali szukać trójek i wyższych stopni. Przekonani, że to nie zadziałało, pitagorejczycy porzucili daremne próby. Członkowie bractwa byli bardziej filozofami i estetami niż matematykami.

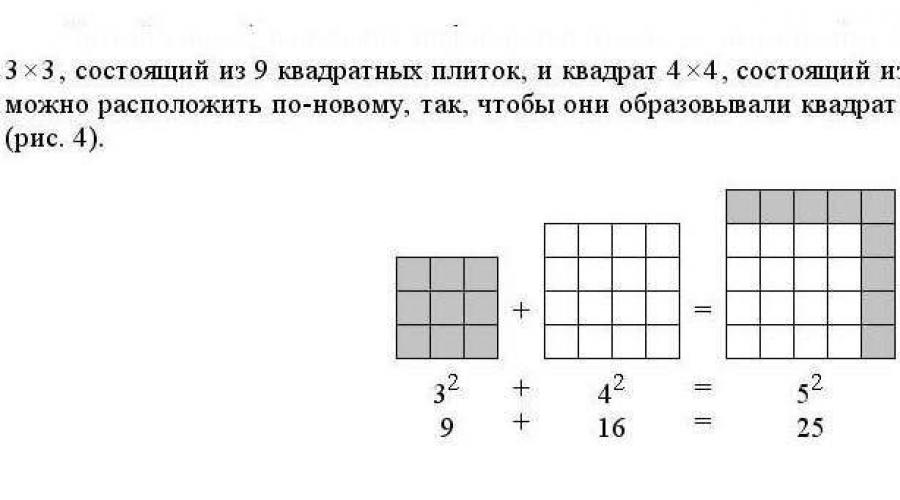
Oznacza to, że łatwo jest wybrać zbiór liczb, które doskonale spełniają równość x² + y² = z²

Począwszy od 3, 4, 5 - rzeczywiście uczeń podstawówki rozumie, że 9 + 16 = 25.

Lub 5, 12, 13: 25 + 144 = 169. Świetnie.

Cóż, okazuje się, że nie. Tu zaczyna się sztuczka. Prostota jest pozorna, ponieważ trudno jest udowodnić nie obecność czegoś, ale wręcz przeciwnie, nieobecność. Gdy trzeba udowodnić, że rozwiązanie istnieje, można i należy po prostu to rozwiązanie przedstawić.

Trudniej jest udowodnić brak: na przykład ktoś mówi: takie a takie równanie nie ma rozwiązań. Wsadzić go do kałuży? proste: bam - i oto jest rozwiązanie! (podaj rozwiązanie). I to wszystko, przeciwnik zostaje pokonany. Jak udowodnić nieobecność?

Powiedzieć: „nie znalazłem takich rozwiązań”? A może źle szukałeś? A co jeśli są, tylko bardzo duże, cóż, takie, że nawet supermocny komputer nie ma jeszcze wystarczającej siły? To właśnie jest trudne.

Wizualnie można to pokazać w następujący sposób: jeśli weźmiemy dwa kwadraty o odpowiednich rozmiarach i rozłożymy je na kwadraty jednostkowe, to z tej wiązki kwadratów jednostkowych otrzymamy trzeci kwadrat (ryc. 2):


I zróbmy to samo z trzecim wymiarem (ryc. 3) – to nie działa. Nie ma wystarczającej liczby kostek lub pozostają dodatkowe:

Ale XVII-wieczny matematyk, Francuz Pierre de Fermat, entuzjastycznie studiował równanie ogólne x n + y n \u003d z n. I na koniec doszedł do wniosku, że dla n>2 rozwiązań całkowitoliczbowych nie istnieją. Dowód Fermata jest bezpowrotnie utracony. Rękopisy płoną! Pozostaje tylko jego uwaga w Arytmetyce Diofantusa: „Znalazłem naprawdę zdumiewający dowód tego twierdzenia, ale marginesy tutaj są zbyt wąskie, aby go pomieścić”.

W rzeczywistości twierdzenie bez dowodu nazywa się hipotezą. Ale Fermat słynie z tego, że nigdy się nie myli. Nawet jeśli nie zostawił dowodu na żadne oświadczenie, zostało ono później potwierdzone. Ponadto Fermat udowodnił swoją tezę dla n=4. Tak więc hipoteza francuskiego matematyka przeszła do historii jako Wielkie Twierdzenie Fermata.

Po Fermacie nad poszukiwaniem dowodu pracowały tak wielkie umysły jak Leonhard Euler (w 1770 r. zaproponował rozwiązanie dla n = 3),

Adrien Legendre i Johann Dirichlet (ci naukowcy wspólnie znaleźli dowód na n = 5 w 1825 r.), Gabriel Lame (który znalazł dowód na n = 7) i wielu innych. W połowie lat 80. ubiegłego wieku stało się jasne, że świat naukowy jest na drodze do ostatecznego rozwiązania Wielkiego Twierdzenia Fermata, ale dopiero w 1993 roku matematycy dostrzegli i uwierzyli, że trwająca trzy stulecia saga znalezienia dowodu Ostatnie twierdzenie Fermata prawie się skończyło.

Łatwo pokazać, że wystarczy udowodnić twierdzenie Fermata tylko dla liczb pierwszych n: 3, 5, 7, 11, 13, 17, … Dla złożonego n dowód pozostaje ważny. Ale liczb pierwszych jest nieskończenie wiele...

W 1825 roku, stosując metodę Sophie Germain, matematyczki Dirichlet i Legendre niezależnie udowodniły twierdzenie dla n=5. W 1839 roku Francuz Gabriel Lame wykazał prawdziwość twierdzenia dla n=7 używając tej samej metody. Stopniowo twierdzenie zostało udowodnione dla prawie wszystkich n mniejszych niż sto.

Wreszcie niemiecki matematyk Ernst Kummer wykazał w błyskotliwym badaniu, że XIX-wieczne metody matematyczne nie mogą dowieść twierdzenia w ogólnej formie. Nagroda Francuskiej Akademii Nauk, ustanowiona w 1847 r. za dowód twierdzenia Fermata, pozostała nieprzydzielona.

W 1907 roku zamożny niemiecki przemysłowiec Paul Wolfskel postanowił odebrać sobie życie z powodu nieodwzajemnionej miłości. Jak prawdziwy Niemiec wyznaczył datę i godzinę samobójstwa: dokładnie o północy. Ostatniego dnia sporządził testament i napisał listy do przyjaciół i krewnych. Biznes zakończył się przed północą. Muszę powiedzieć, że Paul interesował się matematyką. Nie mając nic do roboty, poszedł do biblioteki i zaczął czytać słynny artykuł Kummera. Nagle wydało mu się, że Kummer popełnił błąd w rozumowaniu. Wolfskehl z ołówkiem w dłoni zaczął analizować tę część artykułu. Minęła północ, nadszedł ranek. Luka w dowodzie została wypełniona. A sam powód samobójstwa wyglądał teraz zupełnie śmiesznie. Paul podarł listy pożegnalne i przepisał testament.

Wkrótce zmarł z przyczyn naturalnych. Spadkobiercy byli dość zaskoczeni: 100 000 marek (ponad 1 000 000 obecnych funtów szterlingów) wpłynęło na konto Królewskiego Towarzystwa Naukowego w Getyndze, które w tym samym roku ogłosiło konkurs o Nagrodę Wolfskela. 100 000 marek opierało się na dowodzie twierdzenia Fermata. Ani fenig nie miał być zapłacony za obalenie twierdzenia ...

Większość zawodowych matematyków uważała poszukiwanie dowodu Wielkiego Twierdzenia Fermata za sprawę przegraną i zdecydowanie odmawiała marnowania czasu na tak daremne zadanie. Ale amatorzy igrają dla chwały. Kilka tygodni po ogłoszeniu na Uniwersytet w Getyndze spadła lawina „dowodów”. Profesor E. M. Landau, którego obowiązkiem była analiza przesłanych dowodów, rozdał swoim uczniom karty:

Szanowni Państwo. . . . . . . .

Dziękuję za przesłany manuskrypt z dowodem ostatniego twierdzenia Fermata. Pierwszy błąd znajduje się na stronie ... w wierszu ... . Z tego powodu cały dowód traci ważność.
Profesor EM Landau

W 1963 roku Paul Cohen, opierając się na ustaleniach Gödla, udowodnił nierozwiązywalność jednego z dwudziestu trzech problemów Hilberta, hipotezy kontinuum. Co jeśli ostatnie twierdzenie Fermata jest również nierozwiązywalne?! Ale prawdziwi fanatycy Wielkiego Twierdzenia wcale nie zawiedli. Pojawienie się komputerów nieoczekiwanie dało matematykom nową metodę dowodzenia. Po II wojnie światowej grupy programistów i matematyków udowodniły Wielkie Twierdzenie Fermata dla wszystkich wartości n do 500, następnie do 1000, a później do 10 000.

W latach 80. Samuel Wagstaff podniósł granicę do 25 000, a w latach 90. matematycy twierdzili, że Wielkie Twierdzenie Fermata jest prawdziwe dla wszystkich wartości n do 4 milionów. Ale jeśli nawet bilion bilionów zostanie odjęty od nieskończoności, nie zmniejszy się. Matematyków nie przekonują statystyki. Udowodnienie Wielkiego Twierdzenia oznaczało udowodnienie go dla WSZYSTKICH n dążących do nieskończoności.

W 1954 roku dwóch przyjaciół japońskich matematyków podjęło badanie form modułowych. Formy te generują serie liczb, z których każda jest własną serią. Przypadkowo Taniyama porównał te serie z szeregami generowanymi przez równania eliptyczne. Pasowali! Ale formy modułowe są obiektami geometrycznymi, podczas gdy równania eliptyczne są algebraiczne. Pomiędzy tak różnymi obiektami nigdy nie znaleziono połączenia.

Niemniej jednak, po dokładnych testach, przyjaciele wysunęli hipotezę: każde równanie eliptyczne ma bliźniaka - formę modułową i odwrotnie. To właśnie ta hipoteza stała się podstawą całego nurtu w matematyce, ale dopóki hipoteza Taniyamy-Shimury nie została udowodniona, cały budynek mógł w każdej chwili się zawalić.

W 1984 roku Gerhard Frey wykazał, że rozwiązanie równania Fermata, jeśli istnieje, może być zawarte w pewnym równaniu eliptycznym. Dwa lata później profesor Ken Ribet udowodnił, że to hipotetyczne równanie nie może mieć odpowiednika w świecie modułowym. Odtąd ostatnie twierdzenie Fermata było nierozerwalnie związane z hipotezą Taniyamy-Shimury. Udowodniwszy, że dowolna krzywa eliptyczna jest modułowa, dochodzimy do wniosku, że nie istnieje równanie eliptyczne z rozwiązaniem równania Fermata, a ostatnie twierdzenie Fermata zostałoby natychmiast udowodnione. Ale przez trzydzieści lat nie można było udowodnić hipotezy Taniyamy-Shimury, a nadzieje na sukces były coraz mniejsze.

W 1963 roku, gdy miał zaledwie dziesięć lat, Andrew Wiles był już zafascynowany matematyką. Kiedy dowiedział się o Wielkim Twierdzeniu, zdał sobie sprawę, że nie może od niego odejść. Jako uczeń, student, doktorant przygotowywał się do tego zadania.

Dowiedziawszy się o odkryciach Kena Ribeta, Wiles rzucił się w wir udowodnienia hipotezy Taniyamy-Shimury. Postanowił pracować w całkowitej izolacji i tajemnicy. „Zrozumiałem, że wszystko, co ma coś wspólnego z Wielkim Twierdzeniem Fermata, jest zbyt interesujące… Zbyt wielu widzów celowo przeszkadza w osiągnięciu celu”. Siedem lat ciężkiej pracy opłaciło się, Wiles w końcu ukończył dowód hipotezy Taniyamy-Shimury.

W 1993 roku angielski matematyk Andrew Wiles przedstawił światu swój dowód Wielkiego Twierdzenia Fermata (Wiles przeczytał swój sensacyjny raport na konferencji w Instytucie Sir Isaaca Newtona w Cambridge), nad którym prace trwały ponad siedem lat.

Podczas gdy szum w prasie trwał, rozpoczęto poważne prace nad weryfikacją dowodów. Każdy dowód musi zostać dokładnie zbadany, zanim będzie można go uznać za rygorystyczny i dokładny. Wiles spędził gorączkowe lato, czekając na opinie recenzentów, mając nadzieję, że uda mu się zdobyć ich aprobatę. Pod koniec sierpnia biegli stwierdzili niewystarczająco uzasadniony wyrok.

Okazało się, że decyzja ta zawiera rażący błąd, choć generalnie jest to prawda. Wiles nie poddał się, zwrócił się o pomoc do znanego specjalisty od teorii liczb Richarda Taylora i już w 1994 roku opublikowali poprawiony i uzupełniony dowód twierdzenia. Najbardziej zdumiewające jest to, że praca ta zajęła aż 130 (!) stron w czasopiśmie matematycznym Annals of Mathematics. Ale i na tym historia się nie skończyła – ostatnia uwaga została podjęta dopiero w następnym roku, 1995, kiedy opublikowano ostateczną i „idealną” z matematycznego punktu widzenia wersję dowodu.

„...pół minuty po rozpoczęciu uroczystej kolacji z okazji jej urodzin wręczyłem Nadii rękopis kompletnego dowodu” (Andrew Wales). Czy wspominałem, że matematycy to dziwni ludzie?

Tym razem nie było wątpliwości co do dowodu. Najbardziej wnikliwej analizie poddano dwa artykuły, które w maju 1995 r. zostały opublikowane w Annals of Mathematics.

Od tego momentu minęło sporo czasu, ale w społeczeństwie nadal panuje opinia o nierozwiązywalności Wielkiego Twierdzenia Fermata. Ale nawet ci, którzy wiedzą o znalezionym dowodzie, nadal pracują w tym kierunku - niewiele osób jest zadowolonych z faktu, że Wielkie Twierdzenie wymaga rozwiązania na 130 stronach!

Dlatego teraz siły tak wielu matematyków (głównie amatorów, a nie profesjonalnych naukowców) są rzucane w poszukiwaniu prostego i zwięzłego dowodu, ale ta ścieżka najprawdopodobniej nigdzie nie doprowadzi ...

źródło

Plik FERMA-KDVar © N. M. Koziy, 2008

Certyfikat Ukrainy nr 27312

KRÓTKI DOWÓD WIELKIEGO TWIERDZENIA FERMATA

Wielkie twierdzenie Fermata jest sformułowane w następujący sposób: Równanie diofantyczne (http://soluvel.okis.ru/evrika.html):

ALE n + W n = C n * /1/

gdzie n- dodatnia liczba całkowita większa od dwóch nie ma rozwiązania w dodatnich liczbach całkowitych A , B , Z .

DOWÓD

Ze sformułowania Wielkiego Twierdzenia Fermata wynika: jeśli n jest dodatnią liczbą całkowitą większą niż dwa, a następnie, pod warunkiem, że dwie z trzech liczb ALE , W lub Z są dodatnimi liczbami całkowitymi, jedna z tych liczb nie jest dodatnią liczbą całkowitą.

Dowód budujemy w oparciu o fundamentalne twierdzenie arytmetyki, które nazywa się „twierdzeniem o jednoznaczności rozkładu na czynniki” lub „twierdzeniem o jednoznaczności rozkładu liczb całkowitych złożonych na czynniki pierwsze”. Możliwe wykładniki parzyste i nieparzyste n . Rozpatrzmy oba przypadki.

1. Przypadek pierwszy: wykładnik n - liczba nieparzysta.

W tym przypadku wyrażenie /1/ jest konwertowane według znanych wzorów w następujący sposób:

ALE n + W n = Z n /2/

Wierzymy, że A oraz B są dodatnimi liczbami całkowitymi.

Liczby ALE , W oraz Z muszą być liczbami względnie pierwszymi.

Z równania /2/ wynika, że ​​dla danych wartości liczb A oraz B czynnik ( A + B ) n , Z.

Powiedzmy liczbę Z - dodatnia liczba całkowita. Biorąc pod uwagę przyjęte warunki i podstawowe twierdzenie arytmetyki, warunek :

Z n = ZA n + B n =(A+B) n ∙ re n , / 3/

gdzie jest mnożnik D n D

Z równania /3/ wynika:

Z równania /3/ wynika również, że liczba [ C n = Jakiś + B n ] pod warunkiem, że numer Z ( A + B ) n. Wiadomo jednak, że:

Jakiś + B n < ( A + B ) n /5/

W konsekwencji:

jest liczbą ułamkową mniejszą od jeden. /6/

Liczba ułamkowa.

n

Dla nieparzystych wykładników n >2 numer:

< 1- дробное число, не являющееся рациональной дробью.

Z analizy równania /2/ wynika, że ​​z nieparzystym wykładnikiem n numer:

Z n = ALE n + W n = (A+B)

składa się z dwóch określonych czynników algebraicznych i dla dowolnej wartości wykładnika n czynnik algebraiczny pozostaje niezmieniony ( A + B ).

Zatem ostatnie twierdzenie Fermata nie ma rozwiązania w dodatnich liczbach całkowitych dla nieparzystego wykładnika n >2.

2. Przypadek drugi: wykładnik n - Liczba parzysta .

Istota ostatniego twierdzenia Fermata nie ulegnie zmianie, jeśli równanie /1/ zapiszemy następująco:

Jakiś = C n - B n /7/

W tym przypadku równanie /7/ przekształca się w następujący sposób:

ZA n = C n - B n = ( Z +B)∙(C n-1 + C n-2 B+ C n-3 ∙ B 2 +…+ C ∙ B n -2 + B n -1 ). /8/

Akceptujemy to Z oraz W- wszystkie liczby.

Z równania /8/ wynika, że ​​dla danych wartości liczb B oraz C czynnik (C+ B ) ma taką samą wartość dla dowolnej wartości wykładnika n , stąd jest dzielnikiem liczby A .

Powiedzmy liczbę ALE jest liczbą całkowitą. Biorąc pod uwagę przyjęte warunki i podstawowe twierdzenie arytmetyki, warunek :

ALE n = C n - B n =(C+ B ) n ∙ D n , / 9/

gdzie jest mnożnik D n musi być liczbą całkowitą, a zatem liczbą D musi być również liczbą całkowitą.

Z równania /9/ wynika:

/10/

Z równania /9/ wynika również, że liczba [ ALE n = Z n - B n ] pod warunkiem, że numer ALE- liczba całkowita, musi być podzielna przez liczbę (C+ B ) n. Wiadomo jednak, że:

Z n - B n < (С+ B ) n /11/

W konsekwencji:

jest liczbą ułamkową mniejszą od jeden. /12/

Liczba ułamkowa.

Wynika z tego, że dla nieparzystej wartości wykładnika n równanie /1/ ostatniego twierdzenia Fermata nie ma rozwiązania w dodatnich liczbach całkowitych.

Z parzystymi wykładnikami n >2 numer:

< 1- дробное число, не являющееся рациональной дробью.

Zatem ostatnie twierdzenie Fermata nie ma rozwiązania w dodatnich liczbach całkowitych i dla parzystego wykładnika n >2.

Z powyższego wynika ogólny wniosek: równanie /1/ ostatniego twierdzenia Fermata nie ma rozwiązania w dodatnich liczbach całkowitych A, B oraz Z pod warunkiem, że wykładnik n>2.

DODATKOWE PRZYCZYNY

W przypadku wykładnika n – liczba parzysta, wyrażenie algebraiczne ( C n - B n ) rozkłada się na czynniki algebraiczne:

C 2 - B 2 \u003d(C-B) ∙ (C+B); /13/

C 4 – B 4 = ( C-B) ∙ (C+B) (C 2 + B 2);/14/

do 6 - b 6 =(C-B) ∙ (C + B) (C 2 -CB + B 2) ∙ (C 2 + CB + B 2) ; /15/

C 8 - B 8= (C-B) ∙ (C+B) ∙ (C 2 + B 2) ∙ (C 4 + B 4)./16/

Podajmy przykłady w liczbach.

PRZYKŁAD 1: B=11; C=35.

C 2 – B 2 = (2 2 ∙ 3) ∙ (2 23) = 2 4 3 23;

C 4 – B 4 = (2 2 ∙ 3) ∙ (2 23) (2 673) = 2 4 3 23 673;

C 6 – B 6 = (2 2 ∙ 3) ∙ (2 23) (31 2) (3 577) =2 ∙ 3 ​​​​∙ 23 ∙ 31 2 ∙ 577;

C 8 – B 8 = (2 2 ∙ 3) ∙ (2 23) (2 673) ∙ (2 75633) = 2 5 ∙ 3 ∙ 23 ∙673 ∙ 75633 .

PRZYKŁAD 2: B=16; C=25.

C 2 – B 2 = (3 2) ∙ (41) = 3 2 ∙ 41;

C 4 – B 4 = (3 2) ∙ (41) (881) =3 2 ∙ 41 881;

C 6 – B 6 = (3 2) ∙ (41) ∙ (2 2 ∙ 3) ∙ (13 37) (3 ∙ 7 61) = 3 3 7 ∙ 13 37 ∙ 41 ∙ 61;

C 8 – B 8 = (3 2) ∙ (41) ∙ (881) ∙ (17 26833) = 3 2 ∙ 41 ∙ 881 ∙ 17 26833.

Z analizy równań /13/, /14/, /15/ i /16/ oraz odpowiadających im przykładów liczbowych wynika:

Dla danego wykładnika n , jeśli jest to liczba parzysta, liczba ALE n = C n - B n rozkłada się na dobrze określoną liczbę dobrze zdefiniowanych czynników algebraicznych;

Na dowolny stopień n , jeśli jest to liczba parzysta, w wyrażeniu algebraicznym ( C n - B n ) zawsze są mnożniki ( C - B ) oraz ( C + B ) ;

Każdy czynnik algebraiczny odpowiada dobrze zdefiniowanemu czynnikowi liczbowemu;

Dla podanych wartości liczb W oraz Z czynniki liczbowe mogą być liczbami pierwszymi lub złożonymi czynnikami liczbowymi;

Każdy złożony czynnik liczbowy jest iloczynem liczb pierwszych, które są częściowo lub całkowicie nieobecne w innych złożonych czynnikach liczbowych;

Wartość liczb pierwszych w składzie złożonych czynników liczbowych rośnie wraz ze wzrostem tych czynników;

Skład największego złożonego czynnika liczbowego odpowiadającego największemu czynnikowi algebraicznemu zawiera największą liczbę pierwszą do potęgi mniejszej niż wykładnik n(najczęściej w pierwszym stopniu).

WNIOSKI: dodatkowe uzasadnienia przemawiają za wnioskiem, że Wielkie Twierdzenie Fermata nie ma rozwiązania w dodatnich liczbach całkowitych.

inżynier mechanik