Metoda koordinata za određivanje kuta između ravnih linija. Metoda koordinata u prostoru: formule i komentari mentora

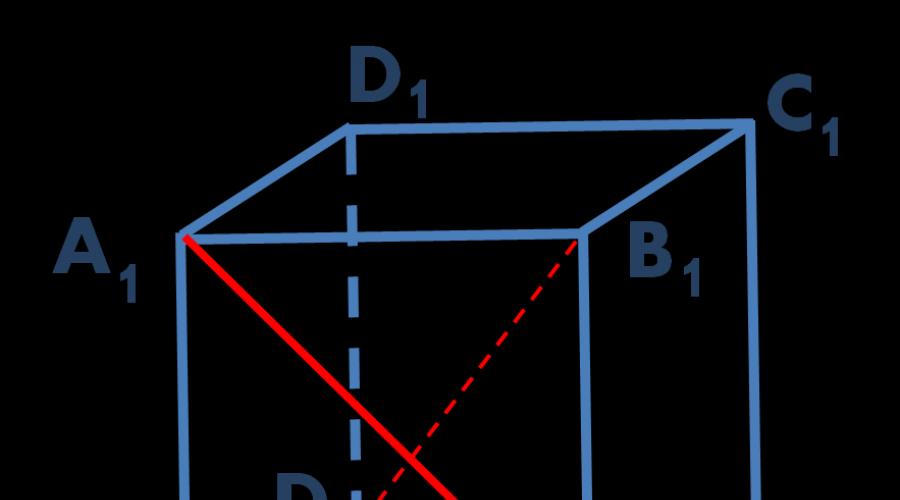
Metoda koordinata za određivanje kuta između ravnih linija. Metoda koordinata u prostoru: formule i komentari mentora
Metoda koordinata za određivanje kuta između ravnih linija. Metoda koordinata u prostoru: formule i komentari mentora
22.09.2019

U ovom članku, na primjeru rješavanja problema C2 iz Jedinstvenog državnog ispita, analizira se metoda pronalaženja pomoću koordinatne metode. Podsjetimo se da su ravne linije nagnute ako ne leže u istoj ravnini. Konkretno, ako jedan pravac leži u ravnini, a drugi pravac siječe tu ravninu u točki koja ne leži na prvom pravcu, tada se takvi pravci sijeku (vidi sliku).

Pronaći udaljenosti između križnih linija potrebno:

  1. Nacrtaj ravninu kroz jednu od presječnih pravaca koja je paralelna s drugom sjecicom.
  2. Spustite okomicu iz bilo koje točke druge crte na rezultirajuću ravninu. Duljina ove okomice bit će traženi razmak između linija.

Analizirajmo ovaj algoritam detaljnije koristeći primjer rješavanja problema C2 iz Jedinstvenog državnog ispita iz matematike.

Udaljenost između linija u prostoru

Zadatak. U jediničnoj kocki ABCDA 1 B 1 C 1 D 1 pronaći udaljenost između linija B.A. 1 i D.B. 1 .

Riža. 1. Crtež za zadatak

Riješenje. Kroz sredinu dijagonale kocke D.B. 1 (točka O) nacrtati pravac paralelan s pravcem A 1 B. Točke sjecišta ove linije s rubovima prije Krista I A 1 D 1 je označeno u skladu s tim N I M. Ravno MN leži u ravnini MNB 1 i paralelna s pravcem A 1 B, koji ne leži u ovoj ravnini. To znači da ravna crta A 1 B paralelno s ravninom MNB 1 na temelju paralelnosti pravca i ravnine (slika 2).

Riža. 2. Potrebna udaljenost između križnih linija jednaka je udaljenosti od bilo koje točke odabrane linije do prikazane ravnine

Sada tražimo udaljenost od neke točke na liniji A 1 B Gornja traka MNB 1 . Ova će udaljenost, prema definiciji, biti potrebna udaljenost između križnih linija.

Za pronalaženje ove udaljenosti koristit ćemo koordinatnu metodu. Uvedimo pravokutni Kartezijev koordinatni sustav tako da se njegovo ishodište podudara s točkom B, osi x bio usmjeren uz rub B.A., os Y- uz rub prije Krista, os Z- uz rub BB 1 (slika 3).

Riža. 3. Odaberemo pravokutni Kartezijev koordinatni sustav kao što je prikazano na slici

Nalaženje jednadžbe ravnine MNB 1 u ovom koordinatnom sustavu. Da bismo to učinili, prvo odredimo koordinate točaka M, N I B 1: Dobivene koordinate zamijenimo u opću jednadžbu ravne linije i dobijemo sljedeći sustav jednadžbi:

Iz druge jednadžbe sustava dobivamo iz treće dobivamo nakon čega iz prve dobivamo Dobivene vrijednosti zamijenimo u opću jednadžbu ravne linije:

Napominjemo da inače avion MNB 1 bi prošao kroz ishodište. Podijelimo obje strane ove jednadžbe s i dobit ćemo:

Udaljenost od točke do ravnine određena je formulom.

Primjena koordinatne metode pri računanju kuta

između ravnina

Najviše opća metoda pronalaženje kutaizmeđu ravnina - koordinatna metoda (ponekad pomoću vektora). Može se koristiti kada su svi ostali isprobani. Ali postoje situacije u kojima metodu koordinata ima smisla primijeniti odmah, naime kada je koordinatni sustav prirodno povezan s poliedrom navedenim u izjavi problema, tj. Jasno su vidljive tri u paru okomite linije na kojima se mogu odrediti koordinatne osi. Takvi poliedri su kuboidan a pravilna četverokutna piramida. U prvom slučaju, koordinatni sustav može se odrediti bridovima koji se protežu iz jednog vrha (slika 1), u drugom - visinom i dijagonalama baze (slika 2)

Primjena koordinatne metode je sljedeća.

Uvodi se pravokutni koordinatni sustav u prostoru. Preporučljivo ga je uvesti na "prirodan" način - "povezati" ga s triom upareno okomitih linija koje imaju zajedničku točku.

Za svaku od ravnina, kut između kojih se traži, sastavljena je jednadžba. Najlakši način za sastavljanje takve jednadžbe je poznavanje koordinata tri točke na ravnini koje ne leže na istoj liniji.

Jednadžba ravnine u opći pogled izgleda kao Ax + By + Cz + D = 0.

Koeficijenti A, B, Cs u ovoj jednadžbi su koordinate normalnog vektora ravnine (vektora okomitog na ravninu). Zatim se određuju duljine i skalarni umnožak normalnih vektora na ravnine među kojima se traži kut. Ako koordinate tih vektora(A 1, B 1; C 1) i (A 2; B 2; C 2 ), zatim željeni kutizračunati po formuli

Komentar. Treba imati na umu da kut između vektora (za razliku od kuta između ravnina) može biti tup, a kako bi se izbjegle moguće nesigurnosti, brojnik na desnoj strani formule sadrži modul.

Riješite ovaj zadatak metodom koordinata.

Zadatak 1. Dana je kocka ABCDA 1 B 1 C 1 D 1 . Točka K je sredina ruba AD, točka L je sredina ruba CD. Koliki je kut između ravnina A? 1 KL i A 1 AD?

Riješenje . Neka je ishodište koordinatnog sustava u točki A, a koordinatne osi idu duž zraka AD, AB, AA 1 (slika 3). Uzmimo da je rub kocke jednak 2 (zgodno ga je podijeliti na pola). Zatim koordinate točaka A1, K, L su sljedeći: A1 (0; 0; 2), K(1; 0; 0), L(2; 1; 0).

Riža. 3

Zapišimo jednadžbu ravnine A 1 K L općenito. Zatim u nju zamijenimo koordinate odabranih točaka ove ravnine. Dobivamo sustav od tri jednadžbe s četiri nepoznanice:

Izrazimo koeficijente A, B, C do D i dolazimo do jednadžbe

Podijelivši oba dijela na D (zašto D = 0?) i zatim množenjem s -2, dobivamo jednadžbu ravnine A 1 KL: 2x - 2 y + z - 2 = 0. Tada vektor normale na tu ravninu ima koordinate (2: -2; 1). Jednadžba ravnine 1 AD je: y=0, i koordinate vektora normale na njega, na primjer, (0; 2: 0). Prema gornjoj formuli za kosinus kuta između ravnina dobivamo:

U zadatku C2 iz matematike najčešće treba riješiti zadatak u kojem treba odrediti:

  1. Udaljenost između dvije točke
  2. Udaljenost od točke do linije
  3. Udaljenost od točke do ravnine
  4. Udaljenost između križnih linija
  5. Kut između dviju ravnih linija
  6. Kut između pravca i ravnine
  7. Kut između ravnina
Zadaci su elementarni ako slijedite algoritam rješavanja C2 i zapamtite osnove trigonometrijska svojstva, kao što su svojstva dijagonala ili površina poliedra. Osnovni zadaci pomoći će vam da zapamtite ova osnovna svojstva.

Sada prijeđimo izravno na algoritme.

1. Za određivanje udaljenosti između dviju točaka A i B koristimo jednu od dvije metode:

  • Uvrstimo AB u neki trokut i nađemo njegovu duljinu kao stranicu trokuta
  • Prema formuli

Štoviše, koordinatna metoda je, po mom mišljenju, najjednostavnija; samo trebate pažljivo odrediti koordinate svake točke.

2. Za određivanje udaljenosti od točke do pravca izračunaj

  • kao duljina okomitog segmenta, ako je moguće taj segment uključiti u neki trokut kao jednu od visina
koordinatnom metodom pomoću formula za izračunavanje površine, u kojoj će tražena udaljenost biti visina i

3. Udaljenost od točke do ravnine je

  • duljina okomice spuštene iz ove točke na ravninu. Da bismo to učinili, pažljivo konstruiramo presjek koji je okomit na ravninu i prolazi kroz nju dana točka. Potrebna udaljenost bit će jednaka visini rezultirajućeg novog poliedra.
  • Metodom koordinata

Jednadžba se nalazi zamjenom koordinata tri točke koje pripadaju ovoj ravnini

  • Korištenje vektorske metode
Da bismo to učinili, moramo zapamtiti pravila za zbrajanje i oduzimanje vektora, da je umnožak okomitih vektora jednak nuli.
  • Metodom volumena, ako postoji piramida ABCM, tada se udaljenost od točke M do ravnine koja sadrži trokut ABC izračunava po formuli
  • Korištenje metode referentnih problema, koji se mogu pogledati
4. Udaljenost između križnih linija može se riješiti pomoću

4.1. Metoda izračunavanja korak po korak:

  • konstruirati zajedničku okomicu dvaju pravaca koji se sijeku i pronaći njezinu duljinu;
  • konstruirajte ravninu koja sadrži jedan od pravaca i paralelna je s drugom. Tada će tražena udaljenost biti jednaka udaljenosti od točke do pravca konstruiranog u ravnini;
  • priložite podatke izravno paralelne ravnine, prolazeći kroz ove križne linije, pronađite udaljenost između tih ravnina
  • konstruirajte ravninu okomitu na jedan od ovih pravaca i konstruirajte ortogonalnu projekciju drugog pravca

4.2. Metoda vektorskih koordinata

  • Odredite koordinate krajeva odsječka koji je zajednička okomica na dva pravca koji se sijeku
  • Određivanje udaljenosti između dviju točaka
4.3. Vektorska metoda
Problem svodimo na određivanje duljine vektora koji pripada okomici koja je zajednička okomica dviju kosih pravaca

6. Kut između pravca i ravnine određeno uključivanjem u pravokutni trokut kao jedan od oštri kutovi, ili metodom vektorske koordinacije

U sljedećoj lekciji ćemo vidjeti kako se određuje kut između ravnina. Ovi algoritmi za rješavanje C2 doprinose sveobuhvatnom razumijevanju metode rješavanja problema. "Časopis za školarce i njihove roditelje za pomoć školarcima." Pročitajte više: http://education-club.ru/#ixzz2IXf5GOJU

7. Kut između ravnina(geometrijska metoda)

  • 1. Nađi pravac po kojem se sijeku ravnine.
  • 2. Odaberite točku na ovoj liniji i povucite na nju dvije okomice koje leže u tim ravninama. Ili nacrtajte ravninu okomitu na crtu presjeka ravnina.
  • 3. Odredite trigonometrijsku funkciju kuta što ga čine okomice na sjecište ravnina. U pravilu to radimo kroz trokut koji uključuje željeni kut.
  • 4. Zapišite vrijednost kuta u svoj odgovor, odn trigonometrijska funkcija kutak.

Kut između ravnina. Metoda koordinata. Zadatak C2

Dvije ravnine koje se sijeku tvore dva para jednakih diedarskih kutova:

Veličina diedralnog kuta mjeri se veličinom odgovarajućeg linearnog kuta.

Da biste konstruirali linearni kut diedralnog kuta, trebate uzeti proizvoljnu točku na liniji presjeka ravnina iu svakoj ravnini nacrtati zraku do ove točke okomito na liniju presjeka ravnina. Kut koji čine ove zrake linearni je kut diedralnog kuta:

Veličina kuta između ravnina je veličina kuta manjeg od diedra.

Neka su naše ravnine definirane jednadžbama:

Kosinus kuta između ravnina nalazi se sljedećom formulom:

U odgovoru pišemo , budući da je vrijednost kuta između ravnina vrijednost manjeg diedarskog kuta.

U desnoj četverokutna prizma s osnovnom stranom 12 i visinom 21, na rubu se uzima točka M tako da je . Točka K je uzeta na rubu tako da je . Nađi kut između ravnine i ravnine.

Napravimo crtež. Budući da ćemo koristiti koordinatni metod, odmah ćemo uvesti koordinatni sustav: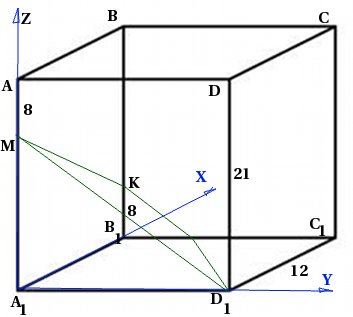

Sada se suočavamo sa zadatkom da napišemo jednadžbe ravnine i ravnine.

Opisao sam detaljan algoritam za pronalaženje jednadžbe ravnine pomoću tri točke.

Nakon što pronađemo koeficijente u ravnini i jednadžbama ravnine, zamijenimo ih u formulu da pronađemo kosinus kuta između ravnina i pronađemo kut.

Predlažem da pogledate detaljno video rješenje ovog problema:


Još jedan zadatak Inne Vladimirovne Feldman


Video lekcije "Metoda koordinata za rješavanje problema s-2"

Lekcija 2 http://youtu.be/dKQWG8OZRGo
Lekcija 3 http://youtu.be/ddgr0PnbFno
Lekcija 4 http://youtu.be/n6yx2pQC0Lo
Lekcija 5 http://youtu.be/JkWbxAw1YLI
Lekcija 6 http://youtu.be/gybIqCMKBiI
lekcija 7 http://youtu.be/_LpARpYxp5g
Lekcija 8 http://youtu.be/XJhyZQoofD8

Metoda koordinata je vrlo učinkovita i univerzalna metoda pronalaženje bilo kakvih kutova ili udaljenosti između stereometrijskih objekata u prostoru. Ako je vaš učitelj matematike visoko kvalificiran, onda bi to trebao znati. U suprotnom, savjetovao bih promjenu mentora za “C” dio. Moja priprema za Jedinstveni državni ispit iz matematike C1-C6 obično uključuje analizu osnovnih algoritama i formula opisanih u nastavku.

Kut između pravaca a i b

Kut između pravaca u prostoru je kut između bilo kojih pravaca koji se sijeku paralelnih s njima. Ovaj kut jednak kutu između vektora smjera ovih ravnih linija (ili ga nadopunjuje do 180 stupnjeva).

Koji algoritam učitelj matematike koristi za pronalaženje kuta?

1) Odaberite bilo koji vektor a ima pravce ravnih pravaca a i b (s njima paralelnih).
2) Koordinate vektora određujemo pomoću odgovarajućih koordinata njihovih početaka i krajeva (koordinate početka potrebno je oduzeti od koordinata kraja vektora).
3) Zamijenite pronađene koordinate u formulu:
. Da biste pronašli sam kut, morate pronaći arc kosinus rezultata.

Normalno za ravninu

Normala na ravninu je svaki vektor okomit na tu ravninu.
Kako pronaći normalno? Da bismo pronašli koordinate normale, dovoljno je znati koordinate bilo koje tri točke M, N i K koje leže u datoj ravnini. Pomoću ovih koordinata nalazimo koordinate vektora i i zahtijevamo da su ispunjeni uvjeti i . Izjednačavanjem skalarnog umnoška vektora s nulom stvaramo sustav jednadžbi s tri varijable iz kojih možemo pronaći koordinate normale.

Bilješka profesora matematike : Uopće nije potrebno riješiti sustav u potpunosti, jer je dovoljno odabrati barem jednu normalu. Da biste to učinili, možete zamijeniti bilo koji broj (na primjer, jedan) umjesto bilo koje njegove nepoznate koordinate i riješiti sustav dviju jednadžbi s preostale dvije nepoznanice. Ako nema rješenja, to znači da u obitelji normala ne postoji nijedna čija je vrijednost jedan u odabranoj varijabli. Zatim zamijenite jednu drugom varijablom (drugom koordinatom) i riješite novi sustav. Ako opet promašite, tada će vaša normala imati jednu na posljednjoj koordinati, a sama će se pokazati paralelnom s nekom koordinatnom ravninom (u ovom slučaju je lako pronaći bez sustava).

Pretpostavimo da su nam zadane pravac i ravnina s koordinatama vektora pravca i normale
Kut između pravca i ravnine izračunava se pomoću sljedeće formule:

Neka i budu bilo koje dvije normale na ove ravnine. Tada je kosinus kuta između ravnina jednak modulu kosinusa kuta između normala:

Jednadžba ravnine u prostoru

Točke koje zadovoljavaju jednakost tvore ravninu s normalom. Koeficijent je odgovoran za količinu odstupanja (paralelni pomak) između dvije ravnine s istom zadanom normalom. Da biste napisali jednadžbu ravnine, prvo morate pronaći njenu normalu (kao što je gore opisano), a zatim zamijeniti koordinate bilo koje točke na ravnini zajedno s koordinatama pronađene normale u jednadžbu i pronaći koeficijent.

MOU prosjek sveobuhvatna škola №13

Metoda koordinata


2008
Plan:


  1. Uvod


  3. Bit koordinatne metode

  4. Sustavi koordinatnih metoda

  5. Osnovne formule koordinatne metode

  6. Problemi različitih razina složenosti na temu "Metoda koordinata"
(s detaljnim rješenjima)

  1. Zaključak

  2. Bibliografija

Uvod

Koristi se u geometriji razne metode rješavanje problema je sintetička (čisto geometrijska) metoda, metoda transformacije, vektorska metoda, koordinatna metoda i druge. Zauzimaju različite položaje u školi. Glavna metoda se smatra sintetičkom, a od ostalih, koordinatna metoda zauzima najviše mjesto jer je usko povezana s algebrom. Elegancija sintetičke metode postiže se uz pomoć intuicije, nagađanja i dodatnih konstrukcija. Metoda koordinata to ne zahtijeva: rješavanje problema je većim dijelom algoritamsko, što u većini slučajeva pojednostavljuje traženje i rješavanje samog problema.

Metoda koordinata- način određivanja položaja točke ili tijela pomoću brojeva ili drugih simbola.

Koordinatni sustav- skup definicija koji implementira metodu koordinata, tj. način određivanja položaja točke ili tijela pomoću brojeva ili drugih simbola.

Dajući geometrijskim studijama algebarski karakter, koordinatna metoda najviše prenosi važna značajka algebra – jednoobraznost načina rješavanja problema. Ako se u aritmetici i elementarnoj geometriji u pravilu za svaki problem traži poseban put rješenja, onda se u algebri i analitičkoj geometriji rješenja provode prema planu zajedničkom za sve probleme, lako prilagodljivom svakom problemu. Prijenos metoda za rješavanje problema koji su karakteristični za algebru i stoga imaju veliku općenitost u geometriji glavna je vrijednost koordinatne metode. Još jedna prednost koordinatne metode je ta što njezina uporaba eliminira potrebu za vizualnim prikazom složenih prostornih slika.

Ciljevi proučavanja koordinatne metode

Možemo istaknuti sljedeće ciljeve proučavanja koordinatne metode u školskom tečaju geometrije:


  • dati učenicima učinkovita metoda rješavanje problema i dokazivanje niza teorema;

  • pokazati, na temelju ove metode, usku povezanost algebre i geometrije;

  • doprinose razvoju računalne i grafičke kulture učenika.

Bit koordinatne metode

Bit koordinatne metode kao metode rješavanja zadataka je da se zadavanjem likova jednadžbama i izražavanjem različitih geometrijskih odnosa u koordinatama, algebrom riješi geometrijski problem. Obrnuto, korištenjem koordinata moguće je geometrijski tumačiti algebarske i analitičke odnose i činjenice i tako primijeniti geometriju na rješavanje algebarskih problema.

Metoda koordinata je univerzalna metoda.

U vezi školski tečaj U geometriji možemo reći da u nekim slučajevima koordinatna metoda omogućuje konstruiranje dokaza i rješavanje mnogih problema racionalnije i ljepše nego čisto geometrijskim metodama. Metoda koordinata povezana je, međutim, s jednom geometrijskom složenošću. Isti problem dobiva različit analitički prikaz ovisno o određenom izboru koordinatnog sustava. I samo dovoljno iskustva omogućuje vam odabir najprikladnijeg koordinatnog sustava.


Koordinatni sustavi:
1. Pravokutni (kartezijanski) koordinatni sustav (Descartes Rene (1596.-1650.))

Rođen u Torinu u imućnoj plemićkoj obitelji. Nekoliko dana kasnije, njegova majka je umrla od konzumiranja; njegova medicinska sestra je izašla i spasila mu život. U dobi od 8 godina, Rene je dobio punu skrb u jednom od najboljih isusovačkih koledža. Descartes je od djetinjstva volio rješavati probleme i sve svoje slobodno vrijeme posvetio proučavanju matematike. Descartes je studirao filozofiju, matematiku, fiziku, astronomiju i filologiju. Descartes je prvi pokazao kako se matematika može koristiti za vizualizaciju i matematička analiza za široku lepezu prirodnih i društvenih pojava.

U njegovim se djelima prvi put pojavljuju:


  1. varijable

  2. strogi zakoni geometrije prevedeni su na algebarski jezik

  3. predloženo je prikazati veze među prirodnim pojavama zakrivljenim linijama i zapisati ih u algebarskim izrazima

  4. latinična slova konstanti i varijable, kao i oznake stupnja
2.Kosi koordinatni sustav razlikuje se od pravokutnog po tome što mu osi nisu okomite. Koordinate točke određuju se kao u pravokutnom koordinatnom sustavu duž ravnih paralelnih osi.

3. Polarni koordinatni sustav . Polarne koordinate točke određuju se na sljedeći način: na ravnini je određena numerička zraka OX. Početak zrake, točka O, naziva se pol, a os OX naziva se polarna os. Da biste odredili položaj točke M u polarnom koordinatnom sustavu, označite udaljenost od pola do te točke i smjer u kojem se nalazi. Udaljenost od točke do pola naziva se polarni radijus točke i označava se slovom (izgovara se "roh").

Smjer se određuje kutom rotacije od grede OX do grede OM

Metoda koordinata

formule

Duljina vektora na temelju njegovih koordinata

Formula za pronalaženje koordinata sredine segmenta

Udaljenost između dvije točke

Jednadžba kruga,(krug središte
, polumjer r)

Jednadžba pravca
, s obzirom na to
(jednadžba pravca u pravokutnom koordinatnom sustavu je jednadžba prvog stupnja)

Svaka ravna linija dana je jednadžbom. pri čemu brojevi a,b,c određuju se za svaku ravnu liniju jedinstveno do proporcionalnosti (ako ih pomnožite s istim brojem
, zatim rezultirajuća jednadžba
definirat će istu liniju).

Udaljenost od točke
na ravnu liniju m
,jednako

Udaljenost od točke
Gornja traka
, jednako

Izvođenje formule
.

Spustimo se s teme
okomita AB na ravninu , dano jednadžbom
.Neka
- sjecište ove okomice s ravninom . Zatim
- udaljenost od točke
Gornja traka .Budući da je vektor okomit na ravninu , kolinearan je vektoru
.To znači da
,Ako
, ili
,Ako
, to je
.Prepišimo ovu jednakost u koordinatama: .Ali točka
, Zato
I
=
.
(Stewartov teorem)

Ako je dan trokut ABC a na temelju njega točka D , koja leži između točaka B i C, tada vrijedi jednakost:

Dokaz:

Odaberimo koordinatni sustav kao što je prikazano na slici.

U odabranom koordinatnom sustavu vrhovi trokuta ABC imat će sljedeće koordinate:

Sjekira 1 ;y 1 ), B(x 2 ;0), C(0;0) i točka D(x 3 ;0) .

Izračunajmo sve veličine uključene u jednakost:

Zamijenimo sve ove vrijednosti u lijeva strana jednakost:

Q.E.D.

Zadatak 1. Odredite udaljenost od točke A(-1,3,0) do ravnine , zadan jednadžbom x -3y -2z +5=0.

Riješenje. Prema formuli
dobivamo:

.

Odgovor:
.


Problem 2. Vektori I međusobno okomiti, a vektor sa svakom od njih zaklapa kut od 60˚. Znajući da
, izračunajte skalarni produkt

Riješenje. Koristeći svojstvo skalarnog produkta, otvorimo zagrade:

=

Iz definicije skalarnog produkta dobivamo:
(jer I okomito);

Zamjena ovih vrijednosti u izraz
=, nalazimo skalarni produkt:
=0 – 50+9 12 -120=-62

Odgovor:
=0 – 50+9 12 -120=-62
Problem 3.Dat je kvadrat ABCD sa strane A . Odredite udaljenost između sredine segmenta AM , Gdje M – sredina Sunce , i točka N na strani CD , podijelivši ga tako da CN:ND=3:1 .

Riješenje:


Odaberimo koordinatni sustav kao što je prikazano na slici.

Zatim bodovi M I N , prema stanju, imat će koordinate:

odnosno.

Jer E – sredina AM , tada će njegove koordinate biti sljedeće:

Sredstva, E .

Nađimo udaljenost između točaka E I N :

Odgovor: EN =


Problem 4 Dana je kocka ABCDA1B1C1D1 s bridovima duljine 1. Na njezinom bočnom rubu AA 1 uzeta je točka E tako da je
.Na rubu BC uzeta je točka F tako da
Kroz središte kocke i točke E i F povučena je ravnina .Naći udaljenost vrha B od ravnine .

Riješenje.

Uvedimo koordinatni sustav sa središtem u vrhu B. Tada
Nađimo jednadžbu ravnine . Neka ova jednadžba bude . primijeti da ne prolazi kroz ishodište, dakle
a jednadžba se može podijeliti s D; dobivamo sljedeću jednadžbu:
ili sjekira + by + cz +1=0

Da bismo odredili nepoznate koeficijente a, b i c, zamijenimo u jednadžbu ax + by + cz +1=0 koordinate tri točke E, F i O koje zadovoljavaju ovu jednadžbu (budući da te točke leže u ravnini ).Dobijamo sustav jednadžbi:
Transformirajmo sustav množenjem prve jednadžbe s 3, druge s 4, a treće s -6 i zbrajanjem prve jednadžbe s trećom dobivamo
, b=-4,
.Dakle jednadžba ravnine ima oblik:

5x + 8y - 9z – 2 =0. Sada nalazimo udaljenost od točke B1(0,0,1) do ravnine
.

Odgovor:
.


Problem 5.Baza trokutasta piramida SABC je jednakostranični trokut ABC čija je stranica jednaka 4. Također je poznato da je AS = BS =
, i CS=3. Odredite površinu sfere opisane oko ove piramide.