Le dernier théorème de Fermat : preuve de Wiles et Perelman, formules, règles de calcul et preuve complète du théorème. La preuve du théorème de Fermat est élémentaire, simple, compréhensible. Un théorème qui ne peut être prouvé.
Lire aussi
Ainsi, le dernier théorème de Fermat (souvent appelé dernier théorème de Fermat), formulé en 1637 par le brillant mathématicien français Pierre Fermat, est de nature très simple et compréhensible pour toute personne ayant une éducation secondaire. Il dit que la formule a à la puissance n + b à la puissance n = c à la puissance n n'a pas de solutions naturelles (c'est-à-dire non fractionnaires) pour n > 2. Tout semble simple et clair, mais le Les meilleurs mathématiciens et les amateurs ordinaires ont lutté pour trouver une solution pendant plus de trois siècles et demi.
Pourquoi est-elle si célèbre ? Maintenant, nous allons le découvrir...
Existe-t-il de nombreux théorèmes prouvés, non prouvés et encore non prouvés ? Le point ici est que le dernier théorème de Fermat représente le plus grand contraste entre la simplicité de la formulation et la complexité de la preuve. Le dernier théorème de Fermat est un problème incroyablement difficile, et pourtant sa formulation peut être comprise par toute personne ayant atteint la 5e année du lycée, mais même tous les mathématiciens professionnels ne peuvent pas comprendre la preuve. Ni en physique, ni en chimie, ni en biologie, ni en mathématiques, il n'y a pas un seul problème qui puisse être formulé aussi simplement, mais qui soit resté aussi longtemps sans solution. 2. De quoi s’agit-il ?
Commençons par le pantalon pythagoricien. Le libellé est très simple – à première vue. Comme nous le savons depuis l’enfance, « les pantalons pythagoriciens sont égaux de tous côtés ». Le problème semble si simple car il repose sur un énoncé mathématique que tout le monde connaît - le théorème de Pythagore : dans tout triangle rectangle, le carré construit sur l'hypoténuse est égal à la somme des carrés construits sur les jambes.
Au 5ème siècle avant JC. Pythagore a fondé la confrérie pythagoricienne. Les Pythagoriciens, entre autres, étudiaient les triplets entiers satisfaisant l'égalité x²+y²=z². Ils ont prouvé qu’il existe une infinité de triplets pythagoriciens et ont obtenu des formules générales pour les trouver. Ils ont probablement essayé de rechercher des diplômes C et supérieurs. Convaincus que cela ne marchait pas, les Pythagoriciens abandonnèrent leurs tentatives inutiles. Les membres de la confrérie étaient plus des philosophes et des esthètes que des mathématiciens.
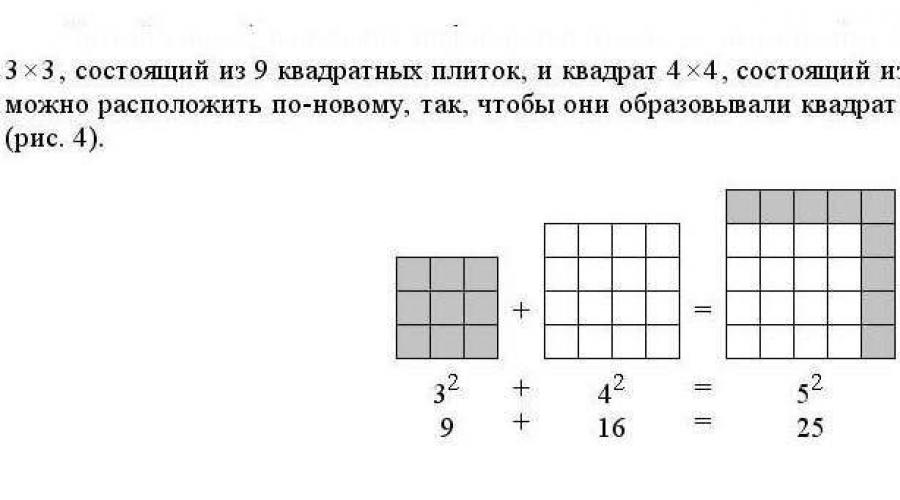
Autrement dit, il est facile de sélectionner un ensemble de nombres qui satisfont parfaitement à l'égalité x²+y²=z²
En partant de 3, 4, 5 - en effet, un étudiant junior comprend que 9 + 16 = 25.
Ou 5, 12, 13 : 25 + 144 = 169. Génial.
Et ainsi de suite. Et si nous prenions une équation similaire x³+y³=z³ ? Peut-être qu'il existe aussi de tels chiffres ?
Et ainsi de suite (Fig. 1).
Il s’avère donc qu’ils ne le sont PAS. C'est là que le truc commence. La simplicité apparaît, car il est difficile de prouver non pas la présence de quelque chose, mais au contraire son absence. Lorsque vous devez prouver qu’il existe une solution, vous pouvez et devez simplement présenter cette solution.
Prouver l'absence est plus difficile : par exemple, quelqu'un dit : telle ou telle équation n'a pas de solution. Le mettre dans une flaque d'eau ? facile : bam - et la voici, la solution ! (donner la solution). Et voilà, l’adversaire est vaincu. Comment prouver son absence ?
Dire : « Je n’ai pas trouvé de telles solutions » ? Ou peut-être que vous n'aviez pas l'air bien ? Et s’ils existaient, seulement très grands, très grands, de telle sorte que même un ordinateur super puissant n’ait toujours pas assez de puissance ? C’est ça qui est difficile.
Cela peut être représenté visuellement comme ceci : si vous prenez deux carrés de tailles appropriées et les démontez en carrés unitaires, alors à partir de cette pile de carrés unitaires, vous obtenez un troisième carré (Fig. 2) :

Mais faisons la même chose avec la troisième dimension (Fig. 3) – ça ne marche pas. Il n'y a pas assez de cubes, ou il en reste des supplémentaires :

Mais le mathématicien français du XVIIe siècle Pierre de Fermat a étudié avec enthousiasme l'équation générale x n + y n = z n . Et enfin, j'ai conclu : pour n>2 il n'y a pas de solutions entières. La preuve de Fermat est irrémédiablement perdue. Les manuscrits brûlent ! Il ne reste que sa remarque dans l’Arithmétique de Diophante : « J’ai trouvé une preuve vraiment étonnante de cette proposition, mais les marges ici sont trop étroites pour la contenir. »
En fait, un théorème sans preuve s’appelle une hypothèse. Mais Fermat a la réputation de ne jamais commettre d’erreur. Même s'il n'a laissé aucune preuve de sa déclaration, celle-ci a été confirmée par la suite. De plus, Fermat a prouvé sa thèse pour n=4. Ainsi, l’hypothèse du mathématicien français est entrée dans l’histoire sous le nom du dernier théorème de Fermat.
Après Fermat, de grands esprits comme Léonhard Euler travaillèrent à la recherche d'une preuve (en 1770 il proposa une solution pour n = 3),
Adrien Legendre et Johann Dirichlet (ces scientifiques ont trouvé conjointement la preuve de n = 5 en 1825), Gabriel Lamé (qui a trouvé la preuve de n = 7) et bien d'autres. Au milieu des années 80 du siècle dernier, il est devenu clair que le monde scientifique était sur le point de trouver la solution finale au dernier théorème de Fermat, mais ce n'est qu'en 1993 que les mathématiciens ont vu et cru que l'épopée de trois siècles de recherche d'une preuve du dernier théorème de Fermat était pratiquement terminé.
On montre facilement qu’il suffit de prouver le théorème de Fermat uniquement pour n simple : 3, 5, 7, 11, 13, 17, ... Pour n composé, la preuve reste valable. Mais il existe une infinité de nombres premiers...
En 1825, en utilisant la méthode de Sophie Germain, les mathématiciennes Dirichlet et Legendre démontrèrent indépendamment le théorème pour n=5. En 1839, en utilisant la même méthode, le Français Gabriel Lame montra la vérité du théorème pour n=7. Peu à peu, le théorème a été prouvé pour presque tous les n inférieurs à cent.
Enfin, le mathématicien allemand Ernst Kummer, dans une brillante étude, a montré que le théorème en général ne peut être prouvé en utilisant les méthodes mathématiques du XIXe siècle. Le Prix de l'Académie française des sciences, créé en 1847 pour la preuve du théorème de Fermat, n'a pas été décerné.
En 1907, le riche industriel allemand Paul Wolfskehl décide de se suicider à cause d'un amour non partagé. En vrai Allemand, il a fixé la date et l’heure du suicide : exactement à minuit. Le dernier jour, il a rédigé un testament et écrit des lettres à ses amis et à ses proches. Les choses se sont terminées avant minuit. Il faut dire que Paul s'intéressait aux mathématiques. N’ayant rien d’autre à faire, il se rendit à la bibliothèque et commença à lire le célèbre article de Kummer. Soudain, il lui sembla que Kummer s'était trompé dans son raisonnement. Wolfskel a commencé à analyser cette partie de l'article avec un crayon à la main. Minuit est passé, le matin est venu. La lacune dans la preuve a été comblée. Et la raison même du suicide paraissait désormais complètement ridicule. Paul a déchiré ses lettres d'adieu et réécrit son testament.
Il mourut bientôt de causes naturelles. Les héritiers furent assez surpris : 100 000 marks (plus de 1 000 000 de livres sterling actuelles) furent transférés sur le compte de la Société scientifique royale de Göttingen, qui annonça la même année un concours pour le prix Wolfskehl. 100 000 points ont été attribués à celui qui a prouvé le théorème de Fermat. Pas un pfennig n'a été attribué pour réfuter le théorème...
La plupart des mathématiciens professionnels considéraient la recherche d'une preuve du dernier théorème de Fermat comme une tâche désespérée et refusaient résolument de perdre du temps dans un exercice aussi inutile. Mais les amateurs se sont éclatés. Quelques semaines après l’annonce, une avalanche de « preuves » s’est abattue sur l’université de Göttingen. Le professeur E.M. Landau, dont la responsabilité était d'analyser les preuves envoyées, a distribué des cartes à ses étudiants :
Cher. . . . . . . .
Merci de m'avoir envoyé le manuscrit avec la preuve du dernier théorème de Fermat. La première erreur est à la page... en ligne... . De ce fait, toute la preuve perd sa validité.
Professeur E.M. Landau


En 1963, Paul Cohen, s'appuyant sur les découvertes de Gödel, prouva l'insolvabilité de l'un des vingt-trois problèmes de Hilbert : l'hypothèse du continuum. Et si le dernier théorème de Fermat était également indécidable ?! Mais les vrais fanatiques du Grand Théorème n’ont pas été déçus du tout. L’avènement des ordinateurs a soudainement offert aux mathématiciens une nouvelle méthode de preuve. Après la Seconde Guerre mondiale, des équipes de programmeurs et de mathématiciens ont prouvé le dernier théorème de Fermat pour toutes les valeurs de n jusqu'à 500, puis jusqu'à 1 000, et plus tard jusqu'à 10 000.
Dans les années 1980, Samuel Wagstaff a élevé la limite à 25 000, et dans les années 1990, les mathématiciens ont déclaré que le dernier théorème de Fermat était vrai pour toutes les valeurs de n jusqu'à 4 millions. Mais si vous soustrayez ne serait-ce qu’un billion de milliards à l’infini, il ne deviendra pas plus petit. Les mathématiciens ne sont pas convaincus par les statistiques. Démontrer le Grand Théorème signifiait le prouver pour TOUT n allant vers l’infini.

En 1954, deux jeunes amis mathématiciens japonais se lancent dans des recherches sur les formes modulaires. Ces formes génèrent des séries de nombres, chacun avec sa propre série. Par hasard, Taniyama a comparé ces séries avec des séries générées par des équations elliptiques. Ils correspondaient ! Mais les formes modulaires sont des objets géométriques et les équations elliptiques sont algébriques. Aucun lien n'a jamais été trouvé entre des objets aussi différents.
Cependant, après des tests minutieux, des amis ont avancé une hypothèse : chaque équation elliptique a une jumelle - une forme modulaire, et vice versa. C'est cette hypothèse qui est devenue la base de toute une direction des mathématiques, mais jusqu'à ce que l'hypothèse de Taniyama-Shimura soit prouvée, le bâtiment entier pourrait s'effondrer à tout moment.
En 1984, Gerhard Frey a montré qu'une solution de l'équation de Fermat, si elle existe, peut être incluse dans une équation elliptique. Deux ans plus tard, le professeur Ken Ribet démontrait que cette équation hypothétique ne pouvait avoir d'équivalent dans le monde modulaire. Désormais, le dernier théorème de Fermat était inextricablement lié à la conjecture de Taniyama-Shimura. Après avoir prouvé que toute courbe elliptique est modulaire, nous concluons qu'il n'existe pas d'équation elliptique avec une solution à l'équation de Fermat, et le dernier théorème de Fermat serait immédiatement prouvé. Mais pendant trente ans, il n'a pas été possible de prouver l'hypothèse de Taniyama-Shimura, et il y avait de moins en moins d'espoir de succès.
En 1963, alors qu’il n’a que dix ans, Andrew Wiles est déjà fasciné par les mathématiques. Lorsqu’il a entendu parler du Grand Théorème, il s’est rendu compte qu’il ne pouvait pas y renoncer. En tant qu'écolier, étudiant et étudiant diplômé, il s'est préparé à cette tâche.
Ayant pris connaissance des découvertes de Ken Ribet, Wiles se lança tête baissée dans la preuve de la conjecture de Taniyama-Shimura. Il a décidé de travailler dans l'isolement et le secret complets. "Je me suis rendu compte que tout ce qui avait à voir avec le dernier théorème de Fermat suscitait trop d'intérêt... Trop de spectateurs interféraient évidemment avec la réalisation de l'objectif." Sept années de travail acharné ont porté leurs fruits ; Wiles a finalement achevé la preuve de la conjecture de Taniyama-Shimura.
En 1993, le mathématicien anglais Andrew Wiles a présenté au monde sa preuve du dernier théorème de Fermat (Wiles a lu son article sensationnel lors d'une conférence à l'Institut Sir Isaac Newton de Cambridge.), dont les travaux ont duré plus de sept ans.

Alors que le battage médiatique se poursuivait dans la presse, un travail sérieux a commencé pour vérifier les preuves. Chaque élément de preuve doit être soigneusement examiné avant de pouvoir être considéré comme rigoureux et exact. Wiles a passé un été agité à attendre les commentaires des critiques, espérant qu'il serait en mesure de gagner leur approbation. Fin août, les experts ont jugé le jugement insuffisamment motivé.
Il s'est avéré que cette décision contient une erreur grossière, même si en général elle est correcte. Wiles n'a pas abandonné, a fait appel au célèbre spécialiste de la théorie des nombres Richard Taylor, et déjà en 1994, ils ont publié une preuve corrigée et développée du théorème. Le plus étonnant est que ce travail a occupé jusqu'à 130 (!) pages dans la revue mathématique Annals of Mathematics. Mais l'histoire ne s'est pas arrêtée là non plus - le point final n'a été atteint que l'année suivante, 1995, lorsque la version finale et « idéale », d'un point de vue mathématique, de la preuve a été publiée.
«... une demi-minute après le début du dîner de fête à l'occasion de son anniversaire, j'ai présenté à Nadya le manuscrit de la preuve complète» (Andrew Wales). N'ai-je pas encore dit que les mathématiciens sont des gens étranges ?

Cette fois, il n’y avait aucun doute sur les preuves. Deux articles ont fait l'objet d'une analyse minutieuse et ont été publiés en mai 1995 dans les Annals of Mathematics.
Beaucoup de temps s'est écoulé depuis ce moment, mais il existe toujours dans la société une opinion selon laquelle le dernier théorème de Fermat est insoluble. Mais même ceux qui connaissent la preuve trouvée continuent de travailler dans cette direction - peu sont convaincus que le Grand Théorème nécessite une solution de 130 pages !
Par conséquent, maintenant les efforts de nombreux mathématiciens (pour la plupart des amateurs et non des scientifiques professionnels) sont consacrés à la recherche d'une preuve simple et concise, mais ce chemin, très probablement, ne mènera nulle part...
Grigori Perelman. refusnik
Vassili Maksimov
En août 2006, les noms des meilleurs mathématiciens de la planète ont été annoncés, qui ont reçu la prestigieuse médaille Fields - une sorte d'analogue du prix Nobel, dont les mathématiciens, au gré d'Alfred Nobel, ont été privés. La Médaille Fields - en plus d'un insigne d'honneur, les gagnants reçoivent un chèque de quinze mille dollars canadiens - est décernée par le Congrès international des mathématiciens tous les quatre ans. Il a été créé par le scientifique canadien John Charles Fields et a été décerné pour la première fois en 1936. Depuis 1950, la médaille Fields est régulièrement décernée personnellement par le roi d'Espagne pour sa contribution au développement de la science mathématique. Les lauréats peuvent être de un à quatre scientifiques âgés de moins de quarante ans. Quarante-quatre mathématiciens, dont huit Russes, ont déjà reçu ce prix.

Grigori Perelman. Henri Poincaré.
En 2006, les lauréats étaient le Français Wendelin Werner, l'Australien Terence Tao et deux Russes - Andrey Okunkov travaillant aux États-Unis et Grigory Perelman, un scientifique de Saint-Pétersbourg. Cependant, au dernier moment, on a appris que Perelman avait refusé cette prestigieuse récompense - comme l'ont annoncé les organisateurs, "pour des raisons de principe".
Un acte aussi extravagant de la part du mathématicien russe n’a pas surpris ceux qui le connaissaient. Ce n'est pas la première fois qu'il refuse des récompenses mathématiques, expliquant sa décision en disant qu'il n'aime pas les cérémonies et le battage médiatique inutile autour de son nom. Il y a dix ans, en 1996, Perelman a refusé le prix du Congrès mathématique européen, invoquant le fait qu'il n'avait pas terminé les travaux sur le problème scientifique nominé pour le prix, et ce n'était pas le dernier cas. Le mathématicien russe semblait avoir pour objectif de surprendre les gens, à contre-courant de l’opinion publique et de la communauté scientifique.
Grigori Yakovlevich Perelman est né le 13 juin 1966 à Léningrad. Dès son plus jeune âge, il est passionné de sciences exactes, brillamment diplômé de la célèbre 239e école secondaire avec une étude approfondie des mathématiques, remporte de nombreuses Olympiades de mathématiques : par exemple, en 1982, au sein d'une équipe d'écoliers soviétiques, il participe à l'Olympiade internationale de mathématiques, organisée à Budapest. Sans examens, Perelman a été inscrit à la Faculté de mécanique et de mathématiques de l'Université de Léningrad, où il a étudié avec d'excellentes notes, continuant à remporter des concours de mathématiques à tous les niveaux. Après avoir obtenu son diplôme universitaire avec mention, il est entré aux études supérieures à la branche de Saint-Pétersbourg de l'Institut mathématique Steklov. Son directeur scientifique était le célèbre mathématicien académicien Alexandrov. Après avoir soutenu sa thèse de doctorat, Grigory Perelman est resté à l'institut, dans le laboratoire de géométrie et de topologie. Ses travaux sur la théorie des espaces d'Alexandrov sont connus ; il a pu trouver des preuves d'un certain nombre de conjectures importantes. Malgré les nombreuses offres des grandes universités occidentales, Perelman préfère travailler en Russie.
Son succès le plus notable fut la solution en 2002 de la célèbre conjecture de Poincaré, publiée en 1904 et restée non prouvée depuis. Perelman y a travaillé pendant huit ans. La conjecture de Poincaré était considérée comme l'un des plus grands mystères mathématiques, et sa solution était considérée comme la réalisation la plus importante de la science mathématique : elle ferait immédiatement progresser la recherche sur les problèmes des fondements physiques et mathématiques de l'univers. Les esprits les plus éminents de la planète n'ont prédit sa solution que dans quelques décennies, et le Clay Institute of Mathematics de Cambridge, Massachusetts, a inclus le problème de Poincaré parmi les sept problèmes mathématiques non résolus les plus intéressants du millénaire, pour la solution de chacun desquels un prix d'un million de dollars a été promis (Millennium Prize Problems).
La conjecture (parfois appelée le problème) du mathématicien français Henri Poincaré (1854-1912) est formulée comme suit : tout espace tridimensionnel fermé simplement connecté est homéomorphe à une sphère tridimensionnelle. Pour clarifier, utilisez un exemple clair : si vous enveloppez une pomme avec un élastique, alors, en principe, en serrant le ruban, vous pouvez comprimer la pomme en une pointe. Si vous enveloppez un beignet avec le même ruban adhésif, vous ne pouvez pas le comprimer jusqu'à un certain point sans déchirer ni le beignet ni le caoutchouc. Dans ce contexte, une pomme est appelée une figure « simplement connectée », mais un beignet n’est pas simplement connecté. Il y a près de cent ans, Poincaré établissait qu’une sphère bidimensionnelle est simplement connectée et suggérait qu’une sphère tridimensionnelle était également simplement connectée. Les meilleurs mathématiciens du monde n’ont pas pu prouver cette hypothèse.
Pour se qualifier pour le Clay Institute Prize, Perelman n'avait qu'à publier sa solution dans l'une des revues scientifiques, et si dans deux ans personne ne trouvait d'erreur dans ses calculs, alors la solution serait considérée comme correcte. Cependant, Perelman s'est écarté des règles dès le début en publiant sa décision sur le site Web de prépublication du laboratoire scientifique de Los Alamos. Peut-être avait-il peur qu'une erreur se soit glissée dans ses calculs - une histoire similaire s'était déjà produite en mathématiques. En 1994, le mathématicien anglais Andrew Wiles a proposé une solution au célèbre théorème de Fermat, et quelques mois plus tard, il s'est avéré qu'une erreur s'était glissée dans ses calculs (cependant, elle a été corrigée plus tard et la sensation a toujours eu lieu). Il n’existe pas encore de publication officielle de la preuve de la conjecture de Poincaré, mais il existe une opinion faisant autorité des meilleurs mathématiciens de la planète confirmant l’exactitude des calculs de Perelman.
La médaille Fields a été décernée à Grigory Perelman précisément pour avoir résolu le problème Poincaré. Mais le scientifique russe a refusé le prix qu’il mérite sans aucun doute. "Gregory m'a dit qu'il se sent isolé de la communauté mathématique internationale, en dehors de cette communauté, et qu'il ne veut donc pas recevoir ce prix", a déclaré l'Anglais John Ball, président de l'Union mondiale des mathématiciens (WUM), lors d'une conférence de presse à Londres. Madrid.
Il y a des rumeurs selon lesquelles Grigori Perelman serait sur le point d'abandonner complètement la science : il y a six mois, il a démissionné de son institut mathématique Steklov natal, et on dit qu'il n'étudiera plus les mathématiques. Peut-être que le scientifique russe pense qu'en prouvant la célèbre hypothèse, il a fait tout ce qu'il pouvait pour la science. Mais qui entreprendra de discuter de la pensée d’un scientifique aussi brillant et d’une personne aussi extraordinaire ? Perelman refuse tout commentaire et a déclaré au journal The Daily Telegraph : « Rien de ce que je peux dire n’est du moindre intérêt public. » Cependant, les principales publications scientifiques ont été unanimes dans leurs évaluations lorsqu'elles ont rapporté que "Grigori Perelman, après avoir résolu le théorème de Poincaré, était à égalité avec les plus grands génies du passé et du présent".
Magazine et maison d'édition mensuel littéraire et journalistique.
Au XVIIe siècle, vivait en France un avocat et mathématicien à temps partiel Pierre Fermat, qui consacrait de longues heures de loisirs à son passe-temps. Un soir d'hiver, assis près de la cheminée, il a avancé une déclaration des plus curieuses dans le domaine de la théorie des nombres : c'est celle-ci qui fut plus tard appelée le Grand Théorème de Fermat. Peut-être que l’excitation n’aurait pas été aussi importante dans les cercles mathématiques si un événement ne s’était pas produit. Le mathématicien passait souvent ses soirées à étudier son livre préféré « Arithmétique » de Diophante d'Alexandrie (IIIe siècle), tout en notant dans ses marges des pensées importantes - cette rareté était soigneusement préservée pour la postérité par son fils. Ainsi, sur les larges marges de ce livre, la main de Fermat a laissé l’inscription suivante : « J’ai une preuve assez frappante, mais elle est trop grande pour être placée en marge. » C'est cet enregistrement qui a provoqué l'enthousiasme stupéfiant autour du théorème. Les mathématiciens n'avaient aucun doute sur le fait que le grand scientifique déclarait avoir prouvé son propre théorème. Vous vous posez probablement la question : « L'a-t-il vraiment prouvé, ou était-ce un mensonge banal, ou peut-être existe-t-il d'autres versions expliquant pourquoi cette note, qui n'a pas permis aux mathématiciens des générations suivantes de dormir paisiblement, s'est retrouvée en marge de le livre?"
L'essence du Grand Théorème
Le théorème assez connu de Fermat est simple dans son essence et réside dans le fait que, à condition que n soit supérieur à deux, nombre positif, l'équation X n + Y n = Z n n'aura pas de solutions de type zéro dans le cadre des nombres naturels. Cette formule apparemment simple masquait une incroyable complexité, et sa preuve a été disputée pendant trois siècles. Il y a une chose étrange - le théorème est né tardivement, puisque son cas particulier avec n = 2 est apparu il y a 2200 ans - c'est le non moins célèbre théorème de Pythagore.
Il convient de noter que l’histoire du théorème bien connu de Fermat est très instructive et divertissante, et pas seulement pour les mathématiciens. Ce qui est le plus intéressant, c'est que la science n'était pas un travail de scientifique, mais un simple passe-temps, qui à son tour procurait un grand plaisir à l'agriculteur. Il restait également constamment en contact avec un mathématicien, mais aussi un ami, et partageait des idées, mais curieusement, il ne s'efforçait pas de publier ses propres travaux.
Œuvres du mathématicien Farmer
Quant aux œuvres du Fermier elles-mêmes, elles ont été découvertes précisément sous la forme de lettres ordinaires. À certains endroits, des pages entières manquaient et seuls des fragments de correspondance ont survécu. Plus intéressant est le fait que depuis trois siècles, les scientifiques recherchent le théorème découvert dans les travaux de Farmer.
Mais peu importe qui osait le prouver, les tentatives étaient réduites à « zéro ». Le célèbre mathématicien Descartes a même accusé le scientifique de se vanter, mais tout cela se résumait à l'envie la plus courante. En plus de le créer, le Fermier a également prouvé son propre théorème. Certes, la solution a été trouvée pour le cas où n=4. Quant au cas n=3, il a été découvert par le mathématicien Euler.
Comment ils ont essayé de prouver le théorème de Farmer
Au tout début du XIXe siècle, ce théorème perdurait. Les mathématiciens ont trouvé de nombreuses preuves de théorèmes limités aux nombres naturels inférieurs à deux cents.
Et en 1909, une somme assez importante fut mise en jeu, égale à cent mille marks d'origine allemande - et tout cela juste pour résoudre le problème lié à ce théorème. Le fonds du prix lui-même a été laissé par un riche amateur de mathématiques, Paul Wolfskehl, originaire d'Allemagne ; d'ailleurs, c'était lui qui voulait « se suicider », mais grâce à une telle implication dans le théorème de Fermer, il voulait vivre. L’enthousiasme qui en a résulté a donné lieu à des tonnes de « preuves » qui ont inondé les universités allemandes, et parmi les mathématiciens est né le surnom de « fermier », utilisé avec un certain mépris pour décrire tout parvenu ambitieux incapable de fournir des preuves claires.
Conjecture du mathématicien japonais Yutaka Taniyama
Les changements dans l’histoire du Grand Théorème n’ont été observés qu’au milieu du XXe siècle, mais un événement intéressant s’est produit. En 1955, le mathématicien japonais Yutaka Taniyama, âgé de 28 ans, a montré au monde une affirmation issue d'un domaine mathématique complètement différent : son hypothèse, contrairement à celle de Fermat, était en avance sur son temps. Il dit : « Chaque courbe elliptique correspond à une forme modulaire spécifique. » Cela semble absurde pour tout mathématicien, comme l'idée qu'un arbre soit constitué d'un certain métal ! L’hypothèse paradoxale, comme la plupart des autres découvertes étonnantes et ingénieuses, n’a pas été acceptée, car ils n’y étaient tout simplement pas encore parvenus. Et Yutaka Taniyama s'est suicidé trois ans plus tard - un acte inexplicable, mais probablement l'honneur pour un véritable génie samouraï était avant tout.
L'hypothèse n'est pas restée dans les mémoires pendant une décennie entière, mais dans les années 70, elle a atteint son apogée - elle a été confirmée par tous ceux qui pouvaient la comprendre, mais, comme le théorème de Fermat, elle n'a pas été prouvée.
Quel est le lien entre la conjecture de Taniyama et le théorème de Fermat ?
15 ans plus tard, un événement clé s’est produit en mathématiques, et il a réuni l’hypothèse du célèbre théorème japonais et de Fermat. Gerhard Gray a déclaré que lorsque la conjecture de Taniyama sera prouvée, il y aura alors des preuves du théorème de Fermat. Autrement dit, cette dernière est une conséquence de la conjecture de Taniyama et, en un an et demi, le théorème de Fermat a été prouvé par le professeur Kenneth Ribet de l’Université de Californie.
Au fil du temps, la régression a été remplacée par le progrès et la science a rapidement progressé, notamment dans le domaine de la technologie informatique. Ainsi, la valeur de n a commencé à augmenter de plus en plus.

À la toute fin du XXe siècle, les ordinateurs les plus puissants se trouvaient dans les laboratoires militaires ; la programmation était réalisée pour trouver une solution au célèbre problème de Fermat. À la suite de toutes les tentatives, il a été révélé que ce théorème est correct pour de nombreuses valeurs de n, x, y. Mais malheureusement, cela n'est pas devenu une preuve définitive, car il n'y avait aucun détail en tant que tel.
John Wiles a prouvé le grand théorème de Fermat
Et finalement, ce n’est qu’à la fin de 1994 qu’un mathématicien anglais, John Wiles, a trouvé et démontré une preuve précise du théorème controversé de Fermer. Puis, après de nombreuses modifications, les discussions sur cette question ont abouti à leur conclusion logique.
La réfutation a été publiée sur plus d'une centaine de pages d'un seul magazine ! De plus, le théorème a été prouvé à l'aide d'un appareil plus moderne de mathématiques supérieures. Et ce qui est surprenant, c'est qu'à l'époque où le Fermier écrivait son ouvrage, un tel dispositif n'existait pas dans la nature. En un mot, l'homme était reconnu comme un génie dans ce domaine, avec lequel personne ne pouvait contester. Malgré tout ce qui s'est passé, vous pouvez aujourd'hui être sûr que le théorème présenté par le grand scientifique Farmer est justifié et prouvé, et pas un seul mathématicien doté de bon sens ne lancera un débat sur ce sujet, ce que même les sceptiques les plus invétérés de toute l'humanité sont d'accord. avec.
Le nom complet de la personne après laquelle le théorème a été présenté s'appelait Pierre de Fermer. Il a apporté des contributions à une grande variété de domaines des mathématiques. Mais malheureusement, la plupart de ses œuvres n’ont été publiées qu’après sa mort.
Il n'y a pas beaucoup de gens dans le monde qui n'ont jamais entendu parler du dernier théorème de Fermat - c'est peut-être le seul problème mathématique qui soit devenu aussi largement connu et est devenu une véritable légende. Il est mentionné dans de nombreux livres et films, et le contexte principal de presque toutes les mentions est l'impossibilité de prouver le théorème.
Oui, ce théorème est très connu et, dans un sens, est devenu une « idole » vénérée par les mathématiciens amateurs et professionnels, mais peu de gens savent que sa preuve a été trouvée, et cela s'est produit en 1995. Mais tout d’abord.
Ainsi, le dernier théorème de Fermat (souvent appelé dernier théorème de Fermat), formulé en 1637 par le brillant mathématicien français Pierre Fermat, est très simple dans son essence et compréhensible pour toute personne ayant une éducation secondaire. Il dit que la formule a à la puissance n + b à la puissance n = c à la puissance n n'a pas de solutions naturelles (c'est-à-dire non fractionnaires) pour n > 2. Tout semble simple et clair, mais le Les meilleurs mathématiciens et les amateurs ordinaires ont lutté pour trouver une solution pendant plus de trois siècles et demi.
Pourquoi est-elle si célèbre ? Maintenant, nous allons le découvrir...
Existe-t-il de nombreux théorèmes prouvés, non prouvés et encore non prouvés ? Le point ici est que le dernier théorème de Fermat représente le plus grand contraste entre la simplicité de la formulation et la complexité de la preuve. Le dernier théorème de Fermat est une tâche incroyablement difficile, et pourtant sa formulation peut être comprise par toute personne ayant atteint la 5e année du lycée, mais même tous les mathématiciens professionnels ne peuvent pas comprendre la preuve. Ni en physique, ni en chimie, ni en biologie, ni en mathématiques, il n'y a pas un seul problème qui puisse être formulé aussi simplement, mais qui soit resté aussi longtemps sans solution. 2. De quoi s’agit-il ?
Commençons par le pantalon pythagoricien. Le libellé est très simple – à première vue. Comme nous le savons depuis l’enfance, « les pantalons pythagoriciens sont égaux de tous côtés ». Le problème semble si simple car il repose sur un énoncé mathématique que tout le monde connaît - le théorème de Pythagore : dans tout triangle rectangle, le carré construit sur l'hypoténuse est égal à la somme des carrés construits sur les jambes.
Au 5ème siècle avant JC. Pythagore a fondé la confrérie pythagoricienne. Les Pythagoriciens, entre autres, étudiaient les triplets entiers satisfaisant l'égalité x²+y²=z². Ils ont prouvé qu’il existe une infinité de triplets pythagoriciens et ont obtenu des formules générales pour les trouver. Ils ont probablement essayé de rechercher des diplômes C et supérieurs. Convaincus que cela ne marchait pas, les Pythagoriciens abandonnèrent leurs tentatives inutiles. Les membres de la confrérie étaient plus des philosophes et des esthètes que des mathématiciens.

Autrement dit, il est facile de sélectionner un ensemble de nombres qui satisfont parfaitement à l'égalité x²+y²=z²
En partant de 3, 4, 5 - en effet, un étudiant junior comprend que 9 + 16 = 25.
Ou 5, 12, 13 : 25 + 144 = 169. Génial.
Il s’avère donc qu’ils ne le sont PAS. C'est là que le truc commence. La simplicité apparaît, car il est difficile de prouver non pas la présence de quelque chose, mais au contraire son absence. Lorsque vous devez prouver qu’il existe une solution, vous pouvez et devez simplement présenter cette solution.
Prouver l'absence est plus difficile : par exemple, quelqu'un dit : telle ou telle équation n'a pas de solution. Le mettre dans une flaque d'eau ? facile : bam - et la voici, la solution ! (donner la solution). Et voilà, l’adversaire est vaincu. Comment prouver son absence ?
Dire : « Je n’ai pas trouvé de telles solutions » ? Ou peut-être que vous n'aviez pas l'air bien ? Et s’ils existaient, seulement très grands, très grands, de telle sorte que même un ordinateur super puissant n’ait toujours pas assez de puissance ? C’est ça qui est difficile.
Cela peut être représenté visuellement comme ceci : si vous prenez deux carrés de tailles appropriées et les démontez en carrés unitaires, alors à partir de cette pile de carrés unitaires, vous obtenez un troisième carré (Fig. 2) : 
Mais faisons la même chose avec la troisième dimension (Fig. 3) : ça ne marche pas. Il n'y a pas assez de cubes, ou il en reste des supplémentaires :

Mais le mathématicien français du XVIIe siècle Pierre de Fermat a étudié avec enthousiasme l'équation générale x n + y n = z n. Et enfin, j'ai conclu : pour n>2 il n'y a pas de solutions entières. La preuve de Fermat est irrémédiablement perdue. Les manuscrits brûlent ! Il ne reste que sa remarque dans l’Arithmétique de Diophante : « J’ai trouvé une preuve vraiment étonnante de cette proposition, mais les marges ici sont trop étroites pour la contenir. »
En fait, un théorème sans preuve s’appelle une hypothèse. Mais Fermat a la réputation de ne jamais commettre d’erreur. Même s'il n'a laissé aucune preuve de sa déclaration, celle-ci a été confirmée par la suite. De plus, Fermat a prouvé sa thèse pour n=4. Ainsi, l’hypothèse du mathématicien français est entrée dans l’histoire sous le nom du dernier théorème de Fermat.

Après Fermat, de grands esprits comme Léonhard Euler travaillèrent à la recherche d'une preuve (en 1770 il proposa une solution pour n = 3),

Adrien Legendre et Johann Dirichlet (ces scientifiques ont trouvé conjointement la preuve de n = 5 en 1825), Gabriel Lamé (qui a trouvé la preuve de n = 7) et bien d'autres. Au milieu des années 80 du siècle dernier, il est devenu clair que le monde scientifique était sur le point de trouver la solution finale au dernier théorème de Fermat, mais ce n'est qu'en 1993 que les mathématiciens ont vu et cru que l'épopée de trois siècles de recherche d'une preuve de Le dernier théorème de Fermat était pratiquement terminé.
On montre facilement qu’il suffit de prouver le théorème de Fermat uniquement pour n simple : 3, 5, 7, 11, 13, 17, ... Pour n composé, la preuve reste valable. Mais il existe une infinité de nombres premiers...
En 1825, en utilisant la méthode de Sophie Germain, les mathématiciennes Dirichlet et Legendre démontrèrent indépendamment le théorème pour n=5. En 1839, en utilisant la même méthode, le Français Gabriel Lame montra la vérité du théorème pour n=7. Peu à peu, le théorème a été prouvé pour presque tous les n inférieurs à cent.

Enfin, le mathématicien allemand Ernst Kummer, dans une brillante étude, a montré que le théorème en général ne peut être prouvé en utilisant les méthodes mathématiques du XIXe siècle. Le Prix de l'Académie française des sciences, créé en 1847 pour la preuve du théorème de Fermat, n'a pas été décerné.

En 1907, le riche industriel allemand Paul Wolfskehl décide de se suicider à cause d'un amour non partagé. En vrai Allemand, il a fixé la date et l’heure du suicide : exactement à minuit. Le dernier jour, il a rédigé un testament et écrit des lettres à ses amis et à ses proches. Les choses se sont terminées avant minuit. Il faut dire que Paul s'intéressait aux mathématiques. N’ayant rien d’autre à faire, il se rendit à la bibliothèque et commença à lire le célèbre article de Kummer. Soudain, il lui sembla que Kummer s'était trompé dans son raisonnement. Wolfskel a commencé à analyser cette partie de l'article avec un crayon à la main. Minuit est passé, le matin est venu. La lacune dans la preuve a été comblée. Et la raison même du suicide paraissait désormais complètement ridicule. Paul a déchiré ses lettres d'adieu et réécrit son testament.
Il mourut bientôt de causes naturelles. Les héritiers furent assez surpris : 100 000 marks (plus de 1 000 000 de livres sterling actuelles) furent transférés sur le compte de la Société scientifique royale de Göttingen, qui annonça la même année un concours pour le prix Wolfskehl. 100 000 points ont été attribués à celui qui a prouvé le théorème de Fermat. Pas un pfennig n'a été attribué pour réfuter le théorème...
La plupart des mathématiciens professionnels considéraient la recherche d'une preuve du dernier théorème de Fermat comme une tâche désespérée et refusaient résolument de perdre du temps dans un exercice aussi inutile. Mais les amateurs se sont éclatés. Quelques semaines après l’annonce, une avalanche de « preuves » s’est abattue sur l’université de Göttingen. Le professeur E.M. Landau, dont la responsabilité était d'analyser les preuves envoyées, a distribué des cartes à ses étudiants :
Cher. . . . . . . .
Merci de m'avoir envoyé le manuscrit avec la preuve du dernier théorème de Fermat. La première erreur est à la page... en ligne... . De ce fait, toute la preuve perd sa validité.
Professeur E.M. Landau


En 1963, Paul Cohen, s'appuyant sur les découvertes de Gödel, prouva l'insolvabilité de l'un des vingt-trois problèmes de Hilbert : l'hypothèse du continuum. Et si le dernier théorème de Fermat était également indécidable ?! Mais les vrais fanatiques du Grand Théorème n’ont pas été déçus du tout. L’avènement des ordinateurs a soudainement offert aux mathématiciens une nouvelle méthode de preuve. Après la Seconde Guerre mondiale, des équipes de programmeurs et de mathématiciens ont prouvé le dernier théorème de Fermat pour toutes les valeurs de n jusqu'à 500, puis jusqu'à 1 000, et plus tard jusqu'à 10 000.
Dans les années 1980, Samuel Wagstaff a élevé la limite à 25 000, et dans les années 1990, les mathématiciens ont déclaré que le dernier théorème de Fermat était vrai pour toutes les valeurs de n jusqu'à 4 millions. Mais si vous soustrayez ne serait-ce qu’un billion de milliards à l’infini, il ne deviendra pas plus petit. Les mathématiciens ne sont pas convaincus par les statistiques. Démontrer le Grand Théorème signifiait le prouver pour TOUT n allant vers l’infini.

En 1954, deux jeunes amis mathématiciens japonais se lancent dans des recherches sur les formes modulaires. Ces formes génèrent des séries de nombres, chacun avec sa propre série. Par hasard, Taniyama a comparé ces séries avec des séries générées par des équations elliptiques. Ils correspondaient ! Mais les formes modulaires sont des objets géométriques et les équations elliptiques sont algébriques. Aucun lien n'a jamais été trouvé entre des objets aussi différents.
Cependant, après des tests minutieux, des amis ont avancé une hypothèse : chaque équation elliptique a une jumelle - une forme modulaire, et vice versa. C'est cette hypothèse qui est devenue la base de toute une direction des mathématiques, mais jusqu'à ce que l'hypothèse de Taniyama-Shimura soit prouvée, le bâtiment entier pourrait s'effondrer à tout moment.
En 1984, Gerhard Frey a montré qu'une solution de l'équation de Fermat, si elle existe, peut être incluse dans une équation elliptique. Deux ans plus tard, le professeur Ken Ribet démontrait que cette équation hypothétique ne pouvait avoir d'équivalent dans le monde modulaire. Désormais, le dernier théorème de Fermat était inextricablement lié à la conjecture de Taniyama-Shimura. Après avoir prouvé que toute courbe elliptique est modulaire, nous concluons qu'il n'existe pas d'équation elliptique avec une solution à l'équation de Fermat, et le dernier théorème de Fermat serait immédiatement prouvé. Mais pendant trente ans, il n'a pas été possible de prouver l'hypothèse de Taniyama-Shimura, et il y avait de moins en moins d'espoir de succès.
En 1963, alors qu’il n’a que dix ans, Andrew Wiles est déjà fasciné par les mathématiques. Lorsqu’il a entendu parler du Grand Théorème, il s’est rendu compte qu’il ne pouvait pas y renoncer. En tant qu'écolier, étudiant et étudiant diplômé, il s'est préparé à cette tâche.
Ayant pris connaissance des découvertes de Ken Ribet, Wiles s'est plongé tête baissée dans la preuve de l'hypothèse de Taniyama-Shimura. Il a décidé de travailler dans l'isolement et le secret complets. "Je me suis rendu compte que tout ce qui avait à voir avec le dernier théorème de Fermat suscitait trop d'intérêt... Trop de spectateurs interféraient évidemment avec la réalisation de l'objectif." Sept années de travail acharné ont porté leurs fruits, Wiles a finalement achevé la preuve de la conjecture de Taniyama-Shimura.
En 1993, le mathématicien anglais Andrew Wiles a présenté au monde sa preuve du dernier théorème de Fermat (Wiles a lu son article sensationnel lors d'une conférence à l'Institut Sir Isaac Newton de Cambridge.), dont les travaux ont duré plus de sept ans.
Alors que le battage médiatique se poursuivait dans la presse, un travail sérieux a commencé pour vérifier les preuves. Chaque élément de preuve doit être soigneusement examiné avant de pouvoir être considéré comme rigoureux et exact. Wiles a passé un été agité à attendre les commentaires des critiques, espérant qu'il serait en mesure de gagner leur approbation. Fin août, les experts ont jugé le jugement insuffisamment motivé.
Il s'est avéré que cette décision contient une erreur grossière, même si en général elle est correcte. Wiles n'a pas abandonné, a fait appel au célèbre spécialiste de la théorie des nombres Richard Taylor, et déjà en 1994, ils ont publié une preuve corrigée et développée du théorème. Le plus étonnant est que ce travail a occupé jusqu'à 130 (!) pages dans la revue mathématique Annals of Mathematics. Mais l'histoire ne s'est pas arrêtée là non plus - le point final n'a été atteint que l'année suivante, 1995, lorsque la version finale et « idéale », d'un point de vue mathématique, de la preuve a été publiée.
«... une demi-minute après le début du dîner de fête à l'occasion de son anniversaire, j'ai présenté à Nadya le manuscrit de la preuve complète» (Andrew Wales). N'ai-je pas encore dit que les mathématiciens sont des gens étranges ?

Cette fois, il n’y avait aucun doute sur les preuves. Deux articles ont fait l'objet d'une analyse minutieuse et ont été publiés en mai 1995 dans les Annals of Mathematics.
Beaucoup de temps s'est écoulé depuis ce moment, mais il existe toujours dans la société une opinion selon laquelle le dernier théorème de Fermat est insoluble. Mais même ceux qui connaissent la preuve trouvée continuent de travailler dans cette direction - peu sont convaincus que le Grand Théorème nécessite une solution de 130 pages !
Par conséquent, maintenant les efforts de nombreux mathématiciens (pour la plupart des amateurs et non des scientifiques professionnels) sont consacrés à la recherche d'une preuve simple et concise, mais ce chemin, très probablement, ne mènera nulle part...
source
Déposer FERMA-KDVar © N.M. Koziy, 2008
Certificat de l'Ukraine n° 27312
BRÈVE PREUVE DU Dernier Théorème de FERmat
Le dernier théorème de Fermat est formulé comme suit : Équation diophantienne (http://soluvel.okis.ru/evrika.html) :
UN n +B n =C n * /1/
Où n- un entier positif supérieur à deux n'a pas de solution en entiers positifs UN , B , AVEC .
PREUVE
De la formulation du dernier théorème de Fermat il résulte : si n est un entier positif supérieur à deux, alors à condition que deux des trois nombres UN , DANS ou AVEC- des entiers positifs, un de ces nombres n'est pas un entier positif.
Nous construisons la preuve sur la base du théorème fondamental de l’arithmétique, appelé « théorème d’unicité de factorisation » ou « théorème d’unicité de factorisation d’entiers composés ». Les exposants impairs et pairs sont possibles n . Considérons les deux cas.
1. Premier cas : exposant n - nombre impair.
Dans ce cas, l'expression /1/ est transformée selon les formules connues comme suit :
UN n + DANS n = AVEC n /2/
Nous croyons cela UN Et B– des entiers positifs.
Nombres UN , DANS Et AVEC doivent être des nombres premiers entre eux.
De l'équation /2/ il s'ensuit que pour des valeurs données de nombres UN Et B facteur ( UN + B ) n , AVEC.
Supposons que le nombre AVEC - entier positif. Compte tenu des conditions acceptées et du théorème fondamental de l'arithmétique, la condition doit être satisfaite :
AVEC n = UNE n + B n =(A+B) n ∙ D n , / 3/
où est le facteur Dn D
De l’équation /3/ il résulte :
De l'équation /3/, il s'ensuit également que le nombre [ CN = Un + Bn ] à condition que le numéro AVEC ( UN + B ) n. Or, on sait que :
Un + Bn < ( UN + B ) n /5/
Ainsi:
![]() - un nombre fractionnaire inférieur à un. /6/
- un nombre fractionnaire inférieur à un. /6/
Un nombre fractionnaire.
n
Pour les exposants impairs n >2 nombre:
 < 1- дробное число, не являющееся рациональной дробью.
< 1- дробное число, не являющееся рациональной дробью.
De l’analyse de l’équation /2/ il résulte que pour un exposant impair n nombre:
AVEC n = UN n + DANS n = (A+B)
se compose de deux facteurs algébriques spécifiques, et pour toute valeur de l'exposant n le facteur algébrique reste inchangé ( UN + B ).
Ainsi, le dernier théorème de Fermat n'a pas de solution en entiers positifs pour les exposants impairs n >2.
2. Deuxième cas : exposant n - nombre pair .
L'essence du dernier théorème de Fermat ne changera pas si l'on réécrit l'équation /1/ comme suit :
Un = CN - Bn /7/
Dans ce cas, l'équation /7/ est transformée comme suit :
UNE n = C n - B n = ( AVEC +B)∙(C n-1 + C n-2 · B+ C n-3 ∙ B 2 +…+ C ∙ Bn -2 + Bn -1 ). /8/
Nous acceptons que AVEC Et DANS- des nombres entiers.
De l'équation /8/ il s'ensuit que pour des valeurs données de nombres B Et C facteur (C+ B ) a la même valeur pour n'importe quelle valeur de l'exposant n , c'est donc un diviseur du nombre UN .
Supposons que le nombre UN- un nombre entier. Compte tenu des conditions acceptées et du théorème fondamental de l'arithmétique, la condition doit être satisfaite :
UN n =C n - Bn =(C+ B ) n ∙ Dn , / 9/
où est le facteur Dn doit être un entier et donc le nombre D doit également être un entier.
De l’équation /9/ il résulte :
![]() /10/
/10/
De l'équation /9/, il s'ensuit également que le nombre [ UN n = AVEC n - Bn ] à condition que le numéro UN– un nombre entier, doit être divisible par un nombre (C+ B ) n. Or, on sait que :
AVEC n - Bn < (С+ B ) n /11/
Ainsi:
![]() - un nombre fractionnaire inférieur à un. /12/
- un nombre fractionnaire inférieur à un. /12/
Un nombre fractionnaire.
Il s’ensuit que pour une valeur impaire de l’exposant n l'équation /1/ du dernier théorème de Fermat n'a pas de solution en entiers positifs.
Pour les exposants pairs n >2 nombre:
 < 1- дробное число, не являющееся рациональной дробью.
< 1- дробное число, не являющееся рациональной дробью.
Ainsi, le dernier théorème de Fermat n'a pas de solution dans les entiers positifs et pour les exposants pairs n >2.
La conclusion générale découle de ce qui précède : l’équation /1/ du dernier théorème de Fermat n’a pas de solution en entiers positifs UN B Et AVECà condition que l'exposant n >2.
JUSTIFICATION SUPPLÉMENTAIRE
Dans le cas où l'exposant n – nombre pair, expression algébrique ( CN - Bn ) se décompose en facteurs algébriques :
C2 – B2 =(C-B) ∙ (C+B); /13/
C4 – B4 = ( C-B) ∙ (C+B) (C 2 + B 2);/14/
C6 – B6 =(C-B) ∙ (C+B) · (C 2 –CB + B 2) ∙ (C 2 +CB+ B 2) ; /15/
C8 – B8= (C-B) ∙ (C+B) ∙ (C 2 + B 2) ∙ (C 4 + B 4)./16/
Donnons des exemples chiffrés.
EXEMPLE 1 : B=11 ; C=35.
C 2 – B 2 = (2 2 ∙ 3) ∙ (2 23) = 2 4 3 23 ;
C 4 – B 4 = (2 2 ∙ 3) ∙ (2 23) (2 673) = 2 4 3 23 673 ;
C 6 – B 6 = (2 2 ∙ 3) ∙ (2 · 23) · (31 2) · (3 · 577) =2 ∙ 3 ∙ 23 ∙ 31 2 ∙ 577 ;
C 8 – B 8 = (2 2 ∙ 3) ∙ (2 23) (2 673) ∙ (2 75633) = 2 5 ∙ 3 ∙ 23 ∙673 ∙ 75633 .
EXEMPLE 2 : B = 16 ; C=25.
C 2 – B 2 = (3 2) ∙ (41) = 3 2 ∙ 41;
C 4 – B 4 = (3 2) ∙ (41) · (881) =3 2 ∙ 41 · 881;
C 6 – B 6 = (3 2) ∙ (41) ∙ (2 2 ∙ 3) ∙ (13 37) (3 ∙ 7 61) = 3 3 7 ∙ 13 37 ∙ 41 ∙ 61 ;
C 8 – B 8 = (3 2) ∙ (41) ∙ (881) ∙ (17 26833) = 3 2 ∙ 41 ∙ 881 ∙ 17 26833.
De l’analyse des équations /13/, /14/, /15/ et /16/ et des exemples numériques correspondants, il résulte :
Pour un exposant donné n , si c'est un nombre pair, le nombre UN n =C n - Bn se décompose en un nombre bien défini de facteurs algébriques bien définis ;
Pour tout exposant n , si c'est un nombre pair, dans l'expression algébrique ( CN - Bn ) il y a toujours des multiplicateurs ( C - B ) Et ( C + B ) ;
À chaque facteur algébrique correspond un facteur numérique bien défini ;
Pour des nombres donnés DANS Et AVEC les facteurs numériques peuvent être des nombres premiers ou des facteurs numériques composés ;
Chaque facteur numérique composite est un produit de nombres premiers partiellement ou totalement absents des autres facteurs numériques composites ;
La taille des nombres premiers dans la composition des facteurs numériques composites augmente avec l'augmentation de ces facteurs ;
Le plus grand facteur numérique composite correspondant au plus grand facteur algébrique inclut le plus grand nombre premier à une puissance inférieure à l'exposant n(le plus souvent au premier degré).
CONCLUSIONS : Des preuves supplémentaires soutiennent la conclusion selon laquelle le dernier théorème de Fermat n'a pas de solution dans les entiers positifs.
ingénieur mécanique