En électrotechnique, ce sont les séries de Fourier et les composantes harmoniques (spectre de fréquence) qui sont utilisées. Théoriquement, la fonction peut être décomposée en d'autres composants en utilisant d'autres séries. Que se passe-t-il si le processus est perturbé par une fonction discontinue ? L'homme et la transformation
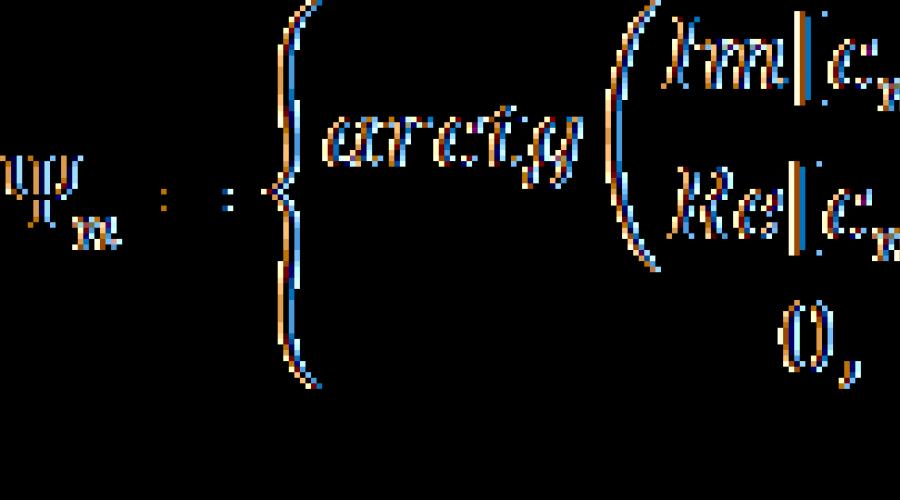
Lire aussi
La possibilité d'approcher des séries de Fourier dans le cas d'un signal linéaire peut être nécessaire pour construire des fonctions dans le cas de signaux discontinus. éléments périodiques. Possibilité d'utilisation cette méthode les construire et les décomposer en utilisant montants finaux Série de Fourier utilisée pour résoudre de nombreux problèmes de diverses sciences, telles que la physique, la sismologie, etc. Les processus des marées océaniques et de l'activité solaire sont considérés par la méthode de décomposition des processus oscillatoires et des fonctions décrites par ces transformations. Avec développement la technologie informatique Les séries de Fourier ont commencé à être utilisées de plus en plus tâches complexes, et aussi grâce à cela, il est devenu possible d'utiliser ces transformations dans des sciences indirectes, comme la médecine et la chimie. La transformée de Fourier est décrite à la fois en réel et en forme complexe, la deuxième distribution a permis de faire une percée dans la recherche Cosmos. Le résultat de ce travail est l'application des séries de Fourier à la linéarisation d'une fonction discontinue et la sélection du nombre de coefficients de la série pour une imposition plus précise de la série sur la fonction. De plus, lors de l'utilisation du développement en série de Fourier, cette fonction cesse d'être discontinue et déjà à des valeurs suffisamment petites, une bonne approximation de la fonction utilisée est obtenue.
série de Fourier
Transformée de Fourier
spectre de phases.
1. Alasheyeva E.A., Rogova N.V. Méthode numérique pour résoudre le problème de l'électrodynamique dans l'approximation du fil mince. Science et paix. International Revue scientifique, n° 8(12), 2014. Volume 1. Volgograd. P.17-19.
2. Vorobyov N.N. Théorie des séries. Éd. Science, Rédaction principale de littérature physique et mathématique, M., 1979, -408 S.
3. Kalinina V.N., Pankin V.F. Statistiques mathématiques. - M. : lycée, 2001.
4. Série R. Edwards Fourier dans une présentation moderne. Éd. Monde. En 2 tomes. Tome 1. 1985. 362 p.
5. V.P. Sigorski Appareil mathématique d'ingénieur. Éd. 2ème stéréotype. "Techniques", 1997. – 768 p.
La représentation d'une fonction arbitraire avec une période spécifique sous la forme d'une série est appelée série de Fourier. Un développement dans une base orthogonale s’appelle cette décision V vue générale. L'expansion des fonctions de la série de Fourier est un outil assez puissant pour résoudre une variété de problèmes. Parce que Les propriétés de cette transformation lors de l'intégration, de la différenciation, ainsi que du déplacement d'une expression par argument et convolution sont bien connues et étudiées. Une personne qui ne connaît pas mathématiques supérieures, ainsi qu'avec les travaux du scientifique français Fourier, ne comprendront probablement pas ce que sont ces «séries» et à quoi elles servent. Cette transformée de Fourier fait désormais partie intégrante de nos vies. Il est utilisé non seulement par les mathématiciens, mais aussi par les physiciens, les chimistes, les médecins, les astronomes, les sismologues, les océanographes et bien d'autres.
Les séries de Fourier sont utilisées pour résoudre de nombreux problèmes appliqués. La transformée de Fourier peut être réalisée à l'aide de méthodes analytiques, numériques et autres. Des processus tels que les marées océaniques et les ondes lumineuses Les cycles d'activité solaire font référence à la méthode numérique de décomposition de tout processus oscillatoire en une série de Fourier. À l’aide de ces techniques mathématiques, vous pouvez analyser des fonctions, représentant tout processus oscillatoire comme une série de composants sinusoïdaux qui se déplacent du minimum au maximum et inversement. La transformée de Fourier est une fonction qui décrit la phase et l'amplitude des sinusoïdes correspondant à une fréquence spécifique. Cette transformation est utilisée pour résoudre très équations complexes, qui décrivent des processus dynamiques survenant sous l'influence de la chaleur, de la lumière ou énergie électrique. Aussi, les séries de Fourier permettent d'isoler des composantes constantes dans des signaux oscillatoires complexes, permettant d'interpréter correctement les observations expérimentales obtenues en médecine, chimie et astronomie.
Avec le développement de la technologie, c'est-à-dire l'avènement et le développement de l'ordinateur ont amené la transformée de Fourier à nouveau niveau. Cette technique solidement implanté dans presque tous les domaines de la science et de la technologie. Un exemple est l’audio et la vidéo numériques. Ce qui est devenu une claire concrétisation de la croissance processus scientifique et applications des séries de Fourier. Ainsi, la série de Fourier sous une forme complexe a permis de faire une percée dans l'étude de l'espace. De plus, cela a influencé l'étude de la physique matériaux semi-conducteurs et plasma, acoustique micro-ondes, océanographie, radar, sismologie.
Considérons le spectre de phase d'un signal périodique déterminé à partir de l'expression suivante :

où les symboles et désignent respectivement les parties imaginaire et réelle de la quantité entre crochets.
Si on le multiplie par une valeur constante réelle K, alors le développement en série de Fourier a la forme suivante :

De l'expression (1), il résulte que le spectre de Fourier de phase a les propriétés suivantes :
1) est fonction de , c'est-à-dire que contrairement au spectre de puissance, qui ne dépend pas de , il change à mesure que le signal se déplace le long de l'axe du temps ;
2) ne dépend pas de K, c'est-à-dire qu'il est invariant à l'amplification ou à l'atténuation du signal, alors que le spectre de puissance est fonction de K.
3) ![]() c'est-à-dire que c'est une fonction impaire de n.
c'est-à-dire que c'est une fonction impaire de n.
Note. Compte tenu de l’interprétation géométrique des considérations ci-dessus, il peut être exprimé en termes de spectre de puissance et de spectre de phase comme suit :
Parce que le

puis de (2) et (3) il s'ensuit qu'il peut être reconstruit sans ambiguïté si les spectres d'amplitude (ou de puissance) et de phase sont connus.
Regardons un exemple. On nous a donné une fonction ![]() entre
entre
Vue générale de la série de Fourier :


Remplaçons nos valeurs et obtenons :

Remplaçons nos valeurs et obtenons.
Ce qui est déjà assez ennuyeux. Et je pense que le moment est venu où il est temps d’extraire de nouvelles conserves des réserves stratégiques de la théorie. Est-il possible d'étendre la fonction en série d'une autre manière ? Par exemple, exprimer un segment de droite en termes de sinus et de cosinus ? Cela semble incroyable, mais des fonctions aussi lointaines peuvent être
"réunification". En plus des diplômes théoriques et pratiques habituels, il existe d’autres approches pour étendre une fonction en série.
Dans cette leçon, nous ferons connaissance avec série trigonométrique Fourier, nous aborderons la question de sa convergence et de sa somme et, bien sûr, nous analyserons de nombreux exemples d'expansion de fonctions dans une série de Fourier. Je voulais sincèrement appeler cet article « Série de Fourier pour les nuls », mais ce serait fallacieux, car la résolution des problèmes nécessiterait la connaissance d’autres branches de l’analyse mathématique et une certaine expérience pratique. Le préambule ressemblera donc à un entraînement d'astronaute =)
Tout d'abord, vous devez aborder l'étude des documents de page sous une excellente forme. Somnolent, reposé et sobre. Sans émotions fortes à propos de la jambe cassée d'un hamster et sans pensées obsessionnelles sur les difficultés de la vie poissons d'aquarium. La série de Fourier n'est pas difficile à comprendre, mais les tâches pratiques nécessitent simplement une concentration accrue de l'attention. Idéalement, vous devriez vous détacher complètement des stimuli externes. La situation est aggravée par le fait qu’il n’existe pas de moyen simple de vérifier la solution et la réponse. Ainsi, si votre santé est inférieure à la moyenne, il vaut mieux faire quelque chose de plus simple. Est-ce vrai.
Deuxièmement, avant de voler dans l'espace, vous devez étudier le tableau de bord vaisseau spatial. Commençons par les valeurs des fonctions sur lesquelles il faut cliquer sur la machine :
Pour toute valeur naturelle :
1) . En effet, la sinusoïde « coud » l’axe des x à travers chaque « pi » :
. Dans le cas de valeurs négatives de l'argument, le résultat sera bien entendu le même : .
2) . Mais tout le monde ne le savait pas. Le cosinus « pi » est l'équivalent d'un « clignotant » :
Un argument négatif ne change rien : ![]() .
.
C'est peut-être suffisant.
Et troisièmement, chers corps de cosmonautes, vous devez être capables de... intégrer.
En particulier, en toute confiance subsumer la fonction sous le signe différentiel, intégrer au coup par coup et sois en paix avec Formule de Newton-Leibniz. Commençons les exercices importants avant le vol. Je déconseille catégoriquement de le sauter, pour ne pas s'écraser en apesanteur plus tard :
Exemple 1
Calculer des intégrales définies

où prend les valeurs naturelles.
Solution: l'intégration s'effectue sur la variable « x » et sur à ce stade la variable discrète "en" est considérée comme une constante. Dans toutes les intégrales mettre la fonction sous le signe différentiel:
Une version courte de la solution qu’il serait bon de cibler ressemble à ceci :
Habituons-nous à cela :
Les quatre points restants dépendent de vous. Essayez d'aborder la tâche consciencieusement et de compléter les intégrales le chemin court. Exemples de solutions à la fin de la leçon.
Après Performance de qualité exercices, enfiler des combinaisons spatiales
et on se prépare à commencer !
Développement d'une fonction en série de Fourier sur l'intervalle
Considérons une fonction qui déterminé au moins pendant un certain temps (et éventuellement pendant une période plus longue). Si cette fonction est intégrable sur l'intervalle, alors elle peut être étendue en trigonométrique série de Fourier:![]() , où sont les soi-disant Coefficients de Fourier.
, où sont les soi-disant Coefficients de Fourier.
Dans ce cas, le numéro est appelé période de décomposition, et le numéro est demi-vie de décomposition.
Il est évident que dans le cas général la série de Fourier est constituée de sinus et de cosinus : ![]()
En effet, écrivons-le en détail :
Le terme zéro de la série s'écrit généralement sous la forme .
Les coefficients de Fourier sont calculés à l'aide des formules suivantes : 
Je comprends parfaitement que ceux qui commencent à étudier le sujet ne comprennent toujours pas les nouveaux termes : période de décomposition, demi-cycle, Coefficients de Fourier etc. Pas de panique, ce n’est pas comparable à l’excitation avant de sortir espace ouvert. Voyons tout cela dans l'exemple suivant, avant de l'exécuter, il est logique de se poser quelques questions vitales : questions pratiques:
Que devez-vous faire dans les tâches suivantes ?
Développez la fonction en une série de Fourier. De plus, il est souvent nécessaire de représenter un graphique d'une fonction, un graphique de la somme d'une série, une somme partielle, et dans le cas de fantasmes professeurs sophistiqués, de faire autre chose.
Comment étendre une fonction en série de Fourier ?
En gros, il faut trouver Coefficients de Fourier, c'est-à-dire composer et calculer trois Intégrale définie.
Veuillez copier la forme générale de la série de Fourier et les trois formules de travail dans votre cahier. Je suis très heureux que certains visiteurs du site réalisent sous mes yeux leur rêve d'enfant de devenir astronaute =)
Exemple 2
Développez la fonction en une série de Fourier sur l'intervalle. Construire un graphique, un graphique de la somme des séries et de la somme partielle.
Solution: La première partie de la tâche consiste à étendre la fonction en une série de Fourier.
Le début est standard, assurez-vous de noter que :
Dans ce problème, la période d’expansion est une demi-période.
Développons la fonction en une série de Fourier sur l'intervalle : ![]()
En utilisant les formules appropriées, on trouve Coefficients de Fourier. Nous devons maintenant composer et calculer trois Intégrale définie. Pour plus de commodité, je numéroterai les points :
1) La première intégrale est la plus simple, cependant, elle nécessite également des globes oculaires : 
2) Utilisez la deuxième formule :
Cette intégrale est bien connue et il le prend morceau par morceau: 
Utilisé une fois trouvé méthode pour subsumer une fonction sous le signe différentiel.
Dans la tâche considérée, il est plus pratique d'utiliser immédiatement formule d'intégration par parties dans une intégrale définie  :
:

Quelques notes techniques. Tout d'abord, après avoir appliqué la formule l'expression entière doit être placée entre grandes parenthèses, puisqu'il y a une constante avant l'intégrale d'origine. Ne la perdons pas! Les parenthèses peuvent être développées à toute étape ultérieure ; je l'ai fait en dernier recours. Dans le premier "morceau" ![]() Nous apportons un soin extrême à la substitution ; comme vous pouvez le constater, la constante n'est pas utilisée et les limites d'intégration sont substituées dans le produit. Cette action est mise en évidence entre crochets. Eh bien, vous connaissez l'intégrale du deuxième « morceau » de la formule de la tâche de formation ;-)
Nous apportons un soin extrême à la substitution ; comme vous pouvez le constater, la constante n'est pas utilisée et les limites d'intégration sont substituées dans le produit. Cette action est mise en évidence entre crochets. Eh bien, vous connaissez l'intégrale du deuxième « morceau » de la formule de la tâche de formation ;-)
Et surtout, une concentration maximale !
3) On recherche le troisième coefficient de Fourier :
On obtient un relatif de l’intégrale précédente, qui est également intègre au coup par coup:
Cette instance est un peu plus compliquée, je vais commenter les étapes suivantes étape par étape : 
(1) L'expression est entièrement entourée de grandes parenthèses. Je ne voulais pas paraître ennuyeux, ils perdent trop souvent la constante.
(2)V dans ce cas J'ai immédiatement ouvert ces grandes parenthèses. Attention particulière
Nous nous consacrons au premier « morceau » : le constant fume en marge et ne participe pas à la substitution des limites d'intégration ( et ) dans le produit. En raison de l'encombrement de l'enregistrement, il est à nouveau conseillé de mettre en évidence cette action entre crochets. Avec le deuxième "morceau" ![]() tout est plus simple : ici la fraction est apparue après avoir ouvert les grandes parenthèses, et la constante - suite à l'intégration de l'intégrale familière ;-)
tout est plus simple : ici la fraction est apparue après avoir ouvert les grandes parenthèses, et la constante - suite à l'intégration de l'intégrale familière ;-)
(3) On effectue les transformations entre crochets, et dans l'intégrale de droite on substitue les limites d'intégration.
(4) Nous supprimons le « feu clignotant » des crochets : , puis ouvrons les crochets intérieurs : .
(5) Nous annulons 1 et –1 entre parenthèses et effectuons de dernières simplifications.
Finalement, les trois coefficients de Fourier sont trouvés : ![]()
Remplaçons-les dans la formule ![]() :
:
En même temps, n'oubliez pas de diviser en deux. A la dernière étape, la constante (« moins deux »), qui ne dépend pas de « en », est prise en dehors de la somme.
Ainsi, nous avons obtenu le développement de la fonction en une série de Fourier sur l'intervalle : ![]()
Étudions la question de la convergence de la série de Fourier. J'expliquerai la théorie, en particulier Théorème de Dirichlet, littéralement « sur les doigts », donc si vous avez besoin de formulations strictes, veuillez vous référer au manuel sur analyse mathematique (par exemple, le 2ème tome de Bohan ; ou le 3ème tome de Fichtenholtz, mais c'est plus difficile).
La deuxième partie du problème nécessite de tracer un graphique, un graphique de la somme d'une série et un graphique d'une somme partielle.
Le graphique de la fonction est le habituel ligne droite dans un avion, qui est dessiné avec une ligne pointillée noire : 
Calculons la somme de la série. Comme vous le savez, les séries de fonctions convergent vers les fonctions. Dans notre cas, la série de Fourier construite ![]() pour toute valeur de "x" convergera vers la fonction, qui est affichée en rouge. Cette fonction perdure ruptures du 1er type aux points, mais est également défini en eux (points rouges dans le dessin)
pour toute valeur de "x" convergera vers la fonction, qui est affichée en rouge. Cette fonction perdure ruptures du 1er type aux points, mais est également défini en eux (points rouges dans le dessin)
Ainsi: ![]() . Il est facile de voir qu'elle est sensiblement différente de la fonction d'origine, c'est pourquoi dans l'entrée
. Il est facile de voir qu'elle est sensiblement différente de la fonction d'origine, c'est pourquoi dans l'entrée ![]() Un tilde est utilisé à la place du signe égal.
Un tilde est utilisé à la place du signe égal.
Étudions un algorithme pratique pour construire la somme d'une série.
Sur l'intervalle central, la série de Fourier converge vers la fonction elle-même (le segment central rouge coïncide avec la ligne pointillée noire de la fonction linéaire).
Parlons maintenant un peu de la nature du développement trigonométrique considéré. série de Fourier ![]() comprend uniquement les fonctions périodiques (constante, sinus et cosinus), donc la somme de la série
comprend uniquement les fonctions périodiques (constante, sinus et cosinus), donc la somme de la série ![]() représente également fonction périodique
.
représente également fonction périodique
.
Qu'est-ce que cela signifie dans notre exemple spécifique? Et cela signifie que la somme de la série ![]() –certainement périodique et le segment rouge de l'intervalle doit être répété à l'infini à gauche et à droite.
–certainement périodique et le segment rouge de l'intervalle doit être répété à l'infini à gauche et à droite.
Je pense que le sens de l’expression « période de décomposition » est enfin devenu clair. Pour faire simple, à chaque fois, la situation se répète encore et encore.
En pratique, il suffit généralement de représenter trois périodes de décomposition, comme cela est fait dans le dessin. Eh bien, et aussi des « souches » de périodes voisines - pour qu'il soit clair que le graphique continue.
Sont particulièrement intéressants points de discontinuité du 1er type. En de tels points, la série de Fourier converge vers des valeurs isolées, situées exactement au milieu du « saut » de la discontinuité (points rouges sur le dessin). Comment connaître l'ordonnée de ces points ? Tout d'abord, trouvons l'ordonnée " dernier étage" : pour ce faire, on calcule la valeur de la fonction au point le plus à droite de la période centrale du développement : . Pour calculer l'ordonnée " Rez-de-chaussée"Il est plus facile de prendre l'extrême valeur gauche de la même période : ![]() . L'ordonnée de la moyenne est la moyenne somme arithmétique"haut et bas": . Un fait agréable est que lors de la construction d'un dessin, vous verrez immédiatement si le milieu est calculé correctement ou incorrectement.
. L'ordonnée de la moyenne est la moyenne somme arithmétique"haut et bas": . Un fait agréable est que lors de la construction d'un dessin, vous verrez immédiatement si le milieu est calculé correctement ou incorrectement.
Construisons une somme partielle de la série et répétons en même temps le sens du terme « convergence ». Le motif est également connu grâce à la leçon sur somme d'une série de nombres. Décrivons notre richesse en détail :
Pour composer une somme partielle, vous devez écrire zéro + deux termes supplémentaires de la série. C'est,
Le dessin montre le graphique de la fonction vert, et, comme vous pouvez le voir, il « enveloppe » le montant total assez étroitement. Si nous considérons une somme partielle de cinq termes de la série, alors le graphique de cette fonction se rapprochera encore plus précisément des lignes rouges s'il y a cent termes, alors le « serpent vert » fusionnera en fait complètement avec les segments rouges ; etc. Ainsi, la série de Fourier converge vers sa somme.
Il est intéressant de noter que tout montant partiel est fonction continue, cependant, la somme totale de la série est encore discontinue.
En pratique, il n’est pas si rare de construire un graphe somme partielle. Comment faire? Dans notre cas, il faut considérer la fonction sur le segment, calculer ses valeurs aux extrémités du segment et aux points intermédiaires (plus vous considérez de points, plus le graphique sera précis). Ensuite, vous devez marquer ces points sur le dessin et dessiner soigneusement un graphique sur la période, puis le « reproduire » dans des intervalles adjacents. Sinon comment? Après tout, l'approximation est aussi une fonction périodique... ...à certains égards, son graphique me rappelle un rythme cardiaque régulier sur l'écran d'un appareil médical.
Bien entendu, réaliser la construction n'est pas très pratique, car il faut être extrêmement prudent, en maintenant une précision d'au moins un demi-millimètre. Cependant, je ferai plaisir aux lecteurs qui ne sont pas à l'aise avec le dessin - dans un problème « réel » il n'est pas toujours nécessaire de réaliser un dessin dans environ 50 % des cas il faut étendre la fonction dans une série de Fourier et c'est tout ; .
Après avoir terminé le dessin, nous terminons la tâche :
Répondre: ![]()
Dans de nombreuses tâches, la fonction souffre rupture du 1er type juste pendant la période de décomposition :
Exemple 3
Développez la fonction donnée sur l'intervalle en une série de Fourier. Dessinez un graphique de la fonction et de la somme totale de la série.
![]()
La fonction proposée est spécifiée par morceaux (et, attention, uniquement sur le segment) et perdure rupture du 1er type au point . Est-il possible de calculer des coefficients de Fourier ? Aucun problème. Les côtés gauche et droit de la fonction sont intégrables sur leurs intervalles, donc les intégrales dans chacun des trois formules doit être présenté comme la somme de deux intégrales. Voyons par exemple comment cela se fait pour un coefficient nul :
La deuxième intégrale s'est avérée égale à zéro, ce qui a réduit le travail, mais ce n'est pas toujours le cas.
Les deux autres coefficients de Fourier sont décrits de la même manière.
Comment afficher la somme d'une série ? Sur l'intervalle de gauche, nous dessinons un segment de droite et sur l'intervalle - un segment de droite (nous mettons en évidence la section de l'axe en gras et en gras). C'est-à-dire que sur l'intervalle d'expansion, la somme de la série coïncide avec la fonction partout sauf pour trois « mauvais » points. Au point de discontinuité de la fonction, la série de Fourier convergera vers une valeur isolée, qui se situe exactement au milieu du « saut » de la discontinuité. Il n'est pas difficile de le voir oralement : limite gauche : , limite droite : ![]() et, évidemment, l’ordonnée du point médian est 0,5.
et, évidemment, l’ordonnée du point médian est 0,5.
En raison de la périodicité de la somme, l'image doit être « multipliée » en périodes adjacentes, en particulier, la même chose doit être représentée sur les intervalles et . Dans le même temps, en certains points, la série de Fourier convergera vers les valeurs médianes.
En fait, il n’y a rien de nouveau ici.
Essayez de faire face à cette tâche vous-même. Échantillon approximatif conception finale et dessin à la fin de la leçon.
Développement d'une fonction en série de Fourier sur une période arbitraire
Pour une période d'expansion arbitraire, où « el » est un nombre positif, les formules de la série de Fourier et des coefficients de Fourier se distinguent par un argument légèrement plus compliqué pour le sinus et le cosinus :

Si , alors nous obtenons les formules d’intervalle avec lesquelles nous avons commencé.
L'algorithme et les principes de résolution du problème sont entièrement conservés, mais la complexité technique des calculs augmente :
Exemple 4
Développez la fonction en une série de Fourier et tracez la somme. ![]()
Solution: en fait un analogue de l'exemple n°3 avec discontinuité de 1ère sorte au point . Dans ce problème, la période d’expansion est une demi-période. La fonction est définie uniquement sur le demi-intervalle, mais cela ne change rien : il est important que les deux éléments de la fonction soient intégrables.
Développons la fonction en une série de Fourier :
La fonction étant discontinue à l'origine, chaque coefficient de Fourier doit évidemment s'écrire comme la somme de deux intégrales :
1) J'écrirai la première intégrale de la manière la plus détaillée possible :
2) On regarde attentivement la surface de la Lune :
Deuxième intégrale prends-le morceau par morceau:

À quoi devons-nous prêter une attention particulière après avoir ouvert la suite de la solution par un astérisque ?
Premièrement, on ne perd pas la première intégrale  , où nous exécutons immédiatement souscrire au signe différentiel. Deuxièmement, n'oubliez pas la constante malheureuse avant les grandes parenthèses et ne vous laissez pas dérouter par les signes lors de l'utilisation d'une formule
, où nous exécutons immédiatement souscrire au signe différentiel. Deuxièmement, n'oubliez pas la constante malheureuse avant les grandes parenthèses et ne vous laissez pas dérouter par les signes lors de l'utilisation d'une formule  . Les grands supports sont encore plus pratiques à ouvrir immédiatement à l'étape suivante.
. Les grands supports sont encore plus pratiques à ouvrir immédiatement à l'étape suivante.
Le reste est une question de technique ; les difficultés ne peuvent être causées que par une expérience insuffisante dans la résolution des intégrales.
Oui, ce n'est pas pour rien que les éminents collègues du mathématicien français Fourier se sont indignés : comment a-t-il osé disposer les fonctions en séries trigonométriques ?! =) À propos, tout le monde s'intéresse probablement au sens pratique de la tâche en question. Fourier lui-même a travaillé sur un modèle mathématique de conductivité thermique et, par la suite, la série qui porte son nom a commencé à être utilisée pour étudier de nombreux processus périodiques, visibles et invisibles dans le monde environnant. Au fait, je me suis surpris à penser que ce n'était pas un hasard si j'avais comparé le graphique du deuxième exemple avec le rythme périodique du cœur. Les personnes intéressées peuvent se familiariser avec l'application pratique Transformée de Fourier dans des sources tierces. ...Même s'il vaut mieux ne pas le faire - on s'en souviendra comme du Premier Amour =)
3) Compte tenu des maillons faibles évoqués à plusieurs reprises, regardons le troisième coefficient :
Intégrons par parties : 

Remplaçons les coefficients de Fourier trouvés dans la formule ![]() , sans oublier de diviser le coefficient zéro par deux :
, sans oublier de diviser le coefficient zéro par deux :
Traçons la somme de la série. Répétons brièvement la procédure : on construit une droite sur un intervalle, et une droite sur un intervalle. Si la valeur « x » est nulle, nous plaçons un point au milieu du « saut » de l'écart et « répliquons » le graphique pour les périodes adjacentes : 
Aux « jonctions » des périodes, la somme sera également égale aux milieux du « saut » de l’écart.
Prêt. Permettez-moi de vous rappeler que la fonction elle-même est définie par condition uniquement sur un demi-intervalle et, évidemment, coïncide avec la somme des séries sur les intervalles
Répondre:
Parfois, une fonction donnée par morceaux est continue pendant la période d’expansion. L'exemple le plus simple: ![]() . Solution (voir Bohan tome 2) la même chose que dans les deux exemples précédents : malgré continuité de fonction au point , chaque coefficient de Fourier est exprimé comme la somme de deux intégrales.
. Solution (voir Bohan tome 2) la même chose que dans les deux exemples précédents : malgré continuité de fonction au point , chaque coefficient de Fourier est exprimé comme la somme de deux intégrales.
Sur l'intervalle de décomposition points de discontinuité du 1er type et/ou il peut y avoir plus de points de « jonction » sur le graphique (deux, trois et généralement n'importe quel final quantité). Si une fonction est intégrable sur chaque partie, alors elle est également extensible dans une série de Fourier. Mais de expérience pratique Je ne me souviens pas d'une telle cruauté. Cependant, il existe des tâches plus difficiles que celles qui viennent d'être envisagées, et à la fin de l'article il y a des liens vers des séries de Fourier d'une complexité accrue pour tout le monde.
En attendant, détendons-nous, adossons-nous à nos chaises et contemplons les étendues infinies d’étoiles :
Exemple 5
Développez la fonction en une série de Fourier sur l'intervalle et tracez la somme de la série.
Dans ce problème, la fonction continu sur le demi-intervalle de dilatation, ce qui simplifie la solution. Tout est très similaire à l'exemple n°2. Il n'y a pas d'échappatoire au vaisseau spatial - vous devrez décider =) Un exemple de conception approximatif à la fin de la leçon, un planning est joint.
Expansion en série de Fourier des fonctions paires et impaires
Avec même et fonctions impaires le processus de résolution du problème est sensiblement simplifié. Et c'est pourquoi. Revenons au développement d'une fonction dans une série de Fourier de période « deux pi » ![]() et période arbitraire "deux el"
et période arbitraire "deux el" ![]() .
.
Supposons que notre fonction soit paire. Le terme général de la série, comme vous pouvez le constater, contient des cosinus pairs et des sinus impairs. Et si nous développons une fonction PAIRE, alors pourquoi avons-nous besoin de sinus impairs ?! Réinitialisons le coefficient inutile : .
Ainsi, une fonction paire ne peut être développée dans une série de Fourier qu'en cosinus:
Parce que le intégrales de fonctions paires le long d'un segment d'intégration symétrique par rapport à zéro peut être doublé, alors les coefficients de Fourier restants sont simplifiés.
Pour l'écart : 
Pour un intervalle arbitraire : 
Les exemples de manuels, que l'on peut trouver dans presque tous les manuels d'analyse mathématique, incluent des extensions même les fonctions ![]() . De plus, ils ont été rencontrés à plusieurs reprises dans ma pratique personnelle :
. De plus, ils ont été rencontrés à plusieurs reprises dans ma pratique personnelle :
Exemple 6
La fonction est donnée. Requis:
1) développer la fonction en une série de Fourier de période , où est un nombre positif arbitraire ;
2) notez le développement sur l'intervalle, construisez une fonction et représentez graphiquement la somme totale de la série.
Solution: dans le premier paragraphe il est proposé de résoudre le problème sous forme générale, et c'est très pratique ! Si le besoin s’en fait sentir, remplacez simplement votre valeur.
1) Dans ce problème, la période d’expansion est une demi-période. Pendant actions supplémentaires, notamment lors de l'intégration, "el" est considéré comme une constante
La fonction est paire, ce qui signifie qu'elle peut être développée en une série de Fourier uniquement en cosinus : ![]() .
.
On recherche les coefficients de Fourier à l'aide des formules  . Faites attention à leurs avantages inconditionnels. Premièrement, l'intégration s'effectue sur le segment positif de l'expansion, ce qui signifie que nous nous débarrassons du module en toute sécurité.
. Faites attention à leurs avantages inconditionnels. Premièrement, l'intégration s'effectue sur le segment positif de l'expansion, ce qui signifie que nous nous débarrassons du module en toute sécurité. ![]() , en considérant uniquement le « X » des deux pièces. Et deuxièmement, l’intégration est sensiblement simplifiée.
, en considérant uniquement le « X » des deux pièces. Et deuxièmement, l’intégration est sensiblement simplifiée.
Deux: 
Intégrons par parties :


Ainsi:
, tandis que la constante , qui ne dépend pas de « en », est prise en dehors de la somme.
Répondre: 
2) Écrivons le développement sur l'intervalle, à cet effet dans formule générale remplaçant Valeur souhaitée demi-cycle :
On voit plus haut que l'expansion des fonctions en séries entières permet de calculer des valeurs approximatives de ces fonctions avec la précision requise. Mais de nombreuses fonctions ne peuvent pas être étendues aux séries de puissance (séries Taylor ou Maclaurin), car les exigences relatives aux fonctions sont assez strictes (la fonction doit être infiniment différentiable, etc.). Par conséquent, d'autres types de séries fonctionnelles sont également utilisés, dans lesquels les conditions d'expansion sont moins lourdes. Ces lignes comprennent série trigonométrique.
Définition: Série trigonométrique série fonctionnelle de la forme :, (1)
où il y a des nombres constants appelés :
Coefficients des séries trigonométriques.
Tous les membres de la série (1) sont fonctionnels non périodiques et ont une période minimale commune de 2p. Il s'ensuit : si la fonction f(x) est développée en une série trigonométrique (1), c'est-à-dire c'est la somme de cette série, alors cette fonction elle-même doit être la somme des séries (1) seulement dans un certain intervalle de longueur 2p.
Les propriétés fondamentales de la série trigonométrique découlent des propriétés fondamentales du système de fonctions trigonométriques. J'ai trouvé une définition.
Définition:
Système infini de fonctions j1(x),j2(x),...,j3(x)...  défini sur un segment est appelé orthogonal sur ce segment, si les conditions suivantes sont remplies :
défini sur un segment est appelé orthogonal sur ce segment, si les conditions suivantes sont remplies :  pour m¹n ;
pour m¹n ;
 pour tout n.
pour tout n.
Théorème: Système fonctions trigonométriques est orthogonal sur l'intervalle [-p,p].
Preuve: Il faut vérifier les conditions 1) et 2) de la définition précédente.
1) Considérons les intégrales :
Appliquons des formules trigonométriques :
Évidemment, avec leur aide, toutes les intégrales précédentes se réduisent à des intégrales de la forme :  Et
Et 
Calculons-les.
;
Ainsi, la première exigence d’orthogonalité sera satisfaite.
2)
 ;
;
 et la deuxième condition est remplie, etc.
et la deuxième condition est remplie, etc.
Série de Fourier trigonométrique.
Soit la fonction périodique f(x) de période 2p soit représentée comme la somme d'une série trigonométrique  (1).
(1).
pour tout x à partir d’un intervalle de longueur 2p. Mais la somme de la série S(x) est une fonction périodique de période 2p. Par conséquent, les valeurs de f(x) et S(x) coïncident sur toute la droite numérique (-¥, +¥). Par conséquent, il suffit d’étudier l’égalité (1) sur un intervalle de longueur 2p, généralement [-p,p] .
Soit donc f(x) la somme des séries (1) sur [-p,p] et, en plus, supposons qu'elle puisse être intégrée terme par terme donc à l'intervalle. Ceci est par exemple possible si la série numérique des coefficients de la série (1) converge de manière absolue, c'est-à-dire la série converge
 (2).
(2).
Dans ce cas, les termes de la série fonctionnelle (1) en valeur absolue ne dépassent pas les termes correspondants de la série (2), ce qui implique la convergence uniforme de la série (1), et donc la possibilité de sa non-convergence. -intégration de termes sur [-p,p].
Nous l'utilisons pour calculer le coefficient a 0 . Intégrons les deux côtés de l'inégalité (1) terme à terme sur [-p,p] :
Toutes les intégrales de droite, selon la propriété d'orthogonalité des fonctions trigonométriques, sont égales à zéro sauf la première. C'est pourquoi:  , où
, où 
 (3).
(3).
Pour calculer a k /k¹0/ nous multiplions les deux côtés de (1) par coskx. La série résultante convergera également uniformément vers [-p,p], car ½coskx½£1 et il peut être intégré terme par terme sur [-p,p].
Par la même propriété d'orthogonalité, toutes les intégrales de droite sont égales à zéro sauf celle contenant un k.
Alors  . Où
. Où
 (4).
(4).
En multipliant les deux côtés de (1) par sin kx et en intégrant l'égalité résultante par , on obtient  . Où
. Où
 (5).
(5).
Les coefficients calculés à l'aide des formules (3) à (5) sont appelés
Coefficients de Fourier pour la fonction f(x), et la série trigonométrique (1) avec ces coefficients est Série de Fourier de la fonction (x).
Il est à noter qu'il n'est pas toujours possible d'intégrer la série (1) terme par terme. Par conséquent, il est formellement possible de calculer les coefficients de Fourier et d'établir la série de Fourier (1), mais il ne peut pas être garanti que cette série converge ; et si elle converge, alors sa somme est une fonction f(x). Dans de tels cas, au lieu de l’égalité (1), nous nous sommes mis d’accord sur la « correspondance » :

Pour vérifier si le programme fonctionne correctement, nous formerons un tableau d'échantillons comme la somme de deux sinusoïdes sin(10*2*pi*x)+0,5*sin(5*2*pi*x) et le glisserons dans le programme. . Le programme a dessiné les éléments suivants :
Fig.1 Graphique de la fonction temps du signal

Fig.2 Graphique du spectre du signal
Sur le graphique du spectre il y a deux bâtons (harmoniques) 5 Hz avec une amplitude de 0,5 V et 10 Hz avec une amplitude de 1 V, tout est comme dans la formule du signal d'origine. Tout va bien, bravo programmeur ! Le programme fonctionne correctement.
Cela signifie que si nous appliquons un signal réel provenant d'un mélange de deux sinusoïdes à l'entrée du CAN, nous obtiendrons un spectre similaire composé de deux harmoniques.
Au total, notre réel signal mesuré, dure 5 secondes, numérisé par l'ADC, c'est-à-dire représenté discret compte, a discret non périodique gamme.
D’un point de vue mathématique, combien d’erreurs y a-t-il dans cette phrase ?
Maintenant que les autorités ont décidé, nous avons décidé que 5 secondes, c'est trop long, mesurons le signal en 0,5 seconde.

Fig.3 Graphique de la fonction sin(10*2*pi*x)+0,5*sin(5*2*pi*x) pour une période de mesure de 0,5 sec

Fig.4 Spectre de fonctions
Quelque chose ne semble pas normal ! L'harmonique de 10 Hz est dessinée normalement, mais à la place du bâton de 5 Hz, plusieurs harmoniques étranges apparaissent. Nous regardons sur Internet ce qui se passe...
Eh bien, ils disent que vous devez ajouter des zéros à la fin de l'échantillon et le spectre sera dessiné normalement.

Fig.5 Ajout de zéros jusqu'à 5 secondes

Fig.6 Spectre reçu
Ce n'est toujours pas la même chose qu'à 5 secondes. Nous devrons traiter de la théorie. Allons à Wikipédia- source de connaissances.
2. Fonction continue et sa représentation en série de Fourier
Mathématiquement, notre signal d'une durée de T secondes est une certaine fonction f(x) spécifiée sur l'intervalle (0, T) (X dans ce cas est le temps). Une telle fonction peut toujours être représentée comme une somme de fonctions harmoniques (sinus ou cosinus) de la forme : (1), où :
(1), où :
K - numéro de fonction trigonométrique (numéro de composant harmonique, numéro harmonique)
T - segment où la fonction est définie (durée du signal)
Ak est l'amplitude de la k-ième composante harmonique,
θk- phase initiale de la k-ème composante harmonique
Que signifie « représenter une fonction comme la somme d’une série » ? Cela signifie qu'en additionnant les valeurs des composantes harmoniques de la série de Fourier en chaque point, nous obtenons la valeur de notre fonction en ce point.
(Plus strictement, l'écart quadratique moyen de la série par rapport à la fonction f(x) tendra vers zéro, mais malgré la convergence quadratique moyenne, la série de Fourier d'une fonction, d'une manière générale, n'est pas obligée de y convergent ponctuellement. Voir https://ru.wikipedia.org/wiki/Fourier_Series.)
Cette série peut également s’écrire :
 (2),
(2),
Où , k-ème complexe amplitude.
La relation entre les coefficients (1) et (3) est exprimée par les formules suivantes :
![]()

Notez que ces trois représentations de la série de Fourier sont complètement équivalentes. Parfois, lorsque l'on travaille avec des séries de Fourier, il est plus pratique d'utiliser les exposants de l'argument imaginaire au lieu des sinus et des cosinus, c'est-à-dire d'utiliser la transformée de Fourier sous une forme complexe. Mais il nous convient d'utiliser la formule (1), où la série de Fourier est présentée comme une somme d'ondes cosinusoïdales avec les amplitudes et phases correspondantes. Quoi qu’il en soit, il est inexact de dire que la transformée de Fourier d’un signal réel aboutira à des amplitudes harmoniques complexes. Comme Wiki l'indique à juste titre, « La transformée de Fourier (ℱ) est une opération qui associe une fonction d'une variable réelle à une autre fonction, également une variable réelle. »
Total:
La base mathématique de l'analyse spectrale des signaux est la transformée de Fourier.
La transformée de Fourier permet de représenter une fonction continue f(x) (signal), définie sur le segment (0, T) comme la somme d'un nombre infini (série infinie) de fonctions trigonométriques (sinus et/ou cosinus) avec certaines amplitudes et phases, également considérées sur le segment (0, T). Une telle série est appelée série de Fourier.
Notons encore quelques points dont la compréhension est nécessaire pour application correcte Transformées de Fourier pour l'analyse du signal. Si l'on considère la série de Fourier (la somme des sinusoïdes) sur tout l'axe X, on voit qu'en dehors du segment (0, T) la fonction représentée par la série de Fourier répétera périodiquement notre fonction.
Par exemple, dans le graphique de la figure 7, la fonction d'origine est définie sur le segment (-T\2, +T\2), et la série de Fourier représente une fonction périodique définie sur tout l'axe des x.
Cela se produit parce que les sinusoïdes elles-mêmes sont des fonctions périodiques et que, par conséquent, leur somme sera une fonction périodique.

Fig.7 Représentation d'une fonction originale non périodique par une série de Fourier
Ainsi:
Notre fonction originale est continue, non périodique, définie sur un certain segment de longueur T.
Le spectre de cette fonction est discret, c'est-à-dire qu'il se présente sous la forme d'une série infinie de composantes harmoniques - la série de Fourier.
En fait, la série de Fourier définit une certaine fonction périodique qui coïncide avec la nôtre sur le segment (0, T), mais pour nous cette périodicité n'est pas significative.
Les périodes des composantes harmoniques sont des multiples de la valeur du segment (0, T) sur lequel la fonction originale f(x) est définie. Autrement dit, les périodes harmoniques sont des multiples de la durée de la mesure du signal. Par exemple, la période de la première harmonique de la série de Fourier est égale à l'intervalle T sur lequel est définie la fonction f(x). La période de la deuxième harmonique de la série de Fourier est égale à l'intervalle T/2. Et ainsi de suite (voir Fig. 8).

Fig.8 Périodes (fréquences) des composantes harmoniques de la série de Fourier (ici T = 2π)
En conséquence, les fréquences des composantes harmoniques sont des multiples de 1/T. Autrement dit, les fréquences des composantes harmoniques Fk sont égales à Fk= k\T, où k va de 0 à ∞, par exemple k=0 F0=0 ; k=1 F1=1\T; k=2 F2=2\T; k=3 F3=3\T;… Fk= k\T (à fréquence nulle - composante constante).
Soit notre fonction originale un signal enregistré pendant T=1 sec. Alors la période de la première harmonique sera égale à la durée de notre signal T1=T=1 sec et la fréquence harmonique sera de 1 Hz. La période de la deuxième harmonique sera égale à la durée du signal divisée par 2 (T2=T/2=0,5 sec) et la fréquence sera de 2 Hz. Pour la troisième harmonique T3=T/3 sec et la fréquence est de 3 Hz. Et ainsi de suite.
Le pas entre les harmoniques dans ce cas est de 1 Hz.
Ainsi, un signal d'une durée de 1 seconde peut être décomposé en composantes harmoniques (obtention d'un spectre) avec une résolution en fréquence de 1 Hz.
Pour augmenter la résolution de 2 fois à 0,5 Hz, vous devez augmenter la durée de mesure de 2 fois - jusqu'à 2 secondes. Un signal d'une durée de 10 secondes peut être décomposé en composantes harmoniques (pour obtenir un spectre) avec une résolution en fréquence de 0,1 Hz. Il n’existe aucun autre moyen d’augmenter la résolution en fréquence.
Il existe un moyen d'augmenter artificiellement la durée d'un signal en ajoutant des zéros au tableau d'échantillons. Mais cela n’augmente pas la résolution en fréquence réelle.
3. Signaux discrets et transformée de Fourier discrète
Avec développement technologie digitale Les méthodes de stockage des données de mesure (signaux) ont également changé. Si auparavant un signal pouvait être enregistré sur un magnétophone et stocké sur bande sous forme analogique, les signaux sont désormais numérisés et stockés dans des fichiers dans la mémoire de l'ordinateur sous la forme d'un ensemble de nombres (échantillons).Le schéma habituel pour mesurer et numériser un signal est le suivant.

Fig.9 Schéma du canal de mesure
Le signal du transducteur de mesure arrive à l'ADC pendant un temps T. Les échantillons de signal (échantillonnage) obtenus pendant le temps T sont transmis à l'ordinateur et stockés en mémoire.

Fig. 10 Signal numérisé - N échantillons reçus pendant le temps T
Quelles sont les exigences relatives aux paramètres de numérisation du signal ? Un appareil qui convertit l'entrée Signal analogique au code discret ( signal numérique) est appelé convertisseur analogique-numérique (ADC, anglais Analog-to-digital converter, ADC) (Wiki).
L'un des principaux paramètres de l'ADC est la fréquence d'échantillonnage maximale (ou taux d'échantillonnage, taux d'échantillonnage anglais) - le taux d'échantillonnage d'un signal continu dans le temps lors de son échantillonnage. Elle se mesure en hertz. ((Wiki))
Selon le théorème de Kotelnikov, si un signal continu a un spectre limité par la fréquence Fmax, alors il peut être reconstruit complètement et de manière unique à partir de ses échantillons discrets prélevés à intervalles de temps.  , c'est à dire. avec une fréquence Fd ≥ 2*Fmax, où Fd est la fréquence d'échantillonnage ; Fmax - fréquence maximale du spectre du signal. Autrement dit, la fréquence de numérisation du signal (fréquence d'échantillonnage ADC) doit être au moins 2 fois supérieure à la fréquence maximale du signal que l'on souhaite mesurer.
, c'est à dire. avec une fréquence Fd ≥ 2*Fmax, où Fd est la fréquence d'échantillonnage ; Fmax - fréquence maximale du spectre du signal. Autrement dit, la fréquence de numérisation du signal (fréquence d'échantillonnage ADC) doit être au moins 2 fois supérieure à la fréquence maximale du signal que l'on souhaite mesurer.
Que se passera-t-il si nous prélevons des échantillons avec une fréquence inférieure à celle requise par le théorème de Kotelnikov ?
Dans ce cas, il se produit l'effet « aliasing » (également connu sous le nom d'effet stroboscopique, effet moiré), dans lequel un signal haute fréquence, après numérisation, se transforme en un signal basse fréquence, qui n'existe pas en réalité. En figue. L'onde sinusoïdale haute fréquence 11 rouge est un signal réel. Une sinusoïde bleue d'une fréquence inférieure est un signal fictif qui apparaît du fait que pendant la période d'échantillonnage, plus d'une demi-période du signal haute fréquence a le temps de passer.

Riz. 11. L'apparition d'un faux signal basse fréquence à une fréquence d'échantillonnage insuffisamment élevée
Pour éviter l'effet de crénelage, un filtre anti-crénelage spécial est placé devant l'ADC - un filtre passe-bas (LPF), qui laisse passer les fréquences inférieures à la moitié de la fréquence d'échantillonnage de l'ADC et coupe les fréquences plus élevées.
Afin de calculer le spectre d'un signal à partir de ses échantillons discrets, la transformée de Fourier discrète (TFD) est utilisée. Notons encore une fois que le spectre d'un signal discret « par définition » est limité par la fréquence Fmax, qui est inférieure à la moitié de la fréquence d'échantillonnage Fd. Par conséquent, le spectre d'un signal discret peut être représenté par la somme d'un nombre fini d'harmoniques, contrairement à la somme infinie pour la série de Fourier d'un signal continu, dont le spectre peut être illimité. Selon le théorème de Kotelnikov, la fréquence maximale d'une harmonique doit être telle qu'elle représente au moins deux échantillons, donc le nombre d'harmoniques est égal à la moitié du nombre d'échantillons d'un signal discret. Autrement dit, s’il y a N échantillons dans l’échantillon, alors le nombre d’harmoniques dans le spectre sera égal à N/2.
Considérons maintenant la transformée de Fourier discrète (TFD).

Comparaison avec la série de Fourier

Nous voyons qu'ils coïncident, sauf que le temps dans la DFT est de nature discrète et que le nombre d'harmoniques est limité par N/2 - la moitié du nombre d'échantillons.
Les formules DFT sont écrites en variables entières sans dimension k, s, où k sont le nombre d'échantillons de signal, s est le nombre de composantes spectrales.
La valeur s indique le nombre d'oscillations harmoniques complètes sur la période T (durée de mesure du signal). La transformée de Fourier discrète est utilisée pour trouver les amplitudes et les phases des harmoniques à l'aide d'une méthode numérique, c'est-à-dire "sur l'ordinateur"
Revenons aux résultats obtenus au début. Comme mentionné ci-dessus, lors de l'expansion d'une fonction non périodique (notre signal) en une série de Fourier, la série de Fourier résultante correspond en fait à une fonction périodique de période T (Fig. 12).

Fig. 12 Fonction périodique f(x) avec période T0, avec période de mesure T>T0
Comme on peut le voir sur la figure 12, la fonction f(x) est périodique de période T0. Cependant, du fait que la durée de l'échantillon de mesure T ne coïncide pas avec la période de la fonction T0, la fonction obtenue sous forme de série de Fourier présente une discontinuité au point T. De ce fait, le spectre de cette fonction contiendra un grand nombre d'harmoniques haute fréquence. Si la durée de l'échantillon de mesure T coïncidait avec la période de la fonction T0, alors le spectre obtenu après transformée de Fourier ne contiendrait que la première harmonique (sinusoïde de période égale à la durée d'échantillonnage), puisque la fonction f(x) est une sinusoïde.
En d'autres termes, le programme DFT "ne sait pas" que notre signal est un "morceau de sinusoïde", mais essaie de représenter une fonction périodique sous la forme d'une série, qui présente une discontinuité due à l'incohérence des morceaux individuels de la sinusoïde.
De ce fait, des harmoniques apparaissent dans le spectre, qui doivent résumer la forme de la fonction, y compris cette discontinuité.
Ainsi, pour obtenir le spectre « correct » d’un signal qui est la somme de plusieurs sinusoïdes de différentes périodes, il faut que la période de mesure du signal contienne un nombre entier de périodes de chaque sinusoïde. En pratique, cette condition peut être remplie pour une durée de mesure du signal suffisamment longue.

Fig. 13 Exemple de fonction et de spectre du signal d'erreur cinématique de la boîte de vitesses
Avec une durée plus courte, l'image sera « pire » :

Fig. 14 Exemple de fonction et de spectre d'un signal de vibration du rotor
En pratique, il peut être difficile de comprendre où sont les « composantes réelles » et où sont les « artefacts » provoqués par les périodes non multiples des composantes et la durée d’échantillonnage du signal ou les « sauts et ruptures » dans la forme du signal. . Bien sûr, les mots « composants réels » et « artefacts » sont mis entre guillemets pour une raison. La présence de nombreuses harmoniques sur le graphique du spectre ne signifie pas que notre signal en est réellement « constitué ». Cela revient à penser que le nombre 7 « se compose » des nombres 3 et 4. Le nombre 7 peut être représenté comme la somme des nombres 3 et 4 – c’est exact.
Donc notre signal... ou plutôt même pas « notre signal », mais une fonction périodique composée de la répétition de notre signal (échantillonnage) peut être représentée comme une somme d'harmoniques (ondes sinusoïdales) avec certaines amplitudes et phases. Mais dans de nombreux cas importants pour la pratique (voir les figures ci-dessus), il est effectivement possible de relier les harmoniques obtenues dans le spectre à processus réels, qui sont de nature cyclique et apportent une contribution significative à la forme du signal.
Quelques résultats
1. Un signal réel mesuré d'une durée de T secondes, numérisé par un CAN, c'est-à-dire représenté par un ensemble d'échantillons discrets (N pièces), possède un spectre discret non périodique, représenté par un ensemble d'harmoniques (N/ 2 pièces).2. Le signal est représenté par un ensemble de valeurs réelles et son spectre est représenté par un ensemble de valeurs réelles. Les fréquences harmoniques sont positives. Le fait qu’il soit plus pratique pour les mathématiciens de représenter le spectre sous une forme complexe en utilisant des fréquences négatives ne signifie pas que « c’est correct » et que « cela devrait toujours être fait ».
3. Un signal mesuré sur un intervalle de temps T est déterminé uniquement sur un intervalle de temps T. Ce qui s'est passé avant que nous commencions à mesurer le signal, et ce qui se passera après cela, est inconnu de la science. Et dans notre cas, ce n’est pas intéressant. La TFD d'un signal limité dans le temps donne son « vrai » spectre, dans le sens où, sous certaines conditions, elle permet de calculer l'amplitude et la fréquence de ses composantes.
Matériaux utilisés et autres matériaux utiles.
Dans de nombreux cas, la tâche consistant à obtenir (calculer) le spectre d'un signal ressemble à ceci. Il existe un CAN qui, avec une fréquence d'échantillonnage Fd, convertit un signal continu arrivant à son entrée pendant le temps T en échantillons numériques - N morceaux. Ensuite, le tableau d'échantillons est introduit dans un certain programme qui produit N/2 de certaines valeurs numériques (le programmeur qui volé sur Internet a écrit un programme, assure qu'il fait la transformée de Fourier).Pour vérifier si le programme fonctionne correctement, nous formerons un tableau d'échantillons comme la somme de deux sinusoïdes sin(10*2*pi*x)+0,5*sin(5*2*pi*x) et le glisserons dans le programme. . Le programme a dessiné les éléments suivants :
Fig.1 Graphique de la fonction temps du signal

Fig.2 Graphique du spectre du signal
Sur le graphique du spectre il y a deux bâtons (harmoniques) 5 Hz avec une amplitude de 0,5 V et 10 Hz avec une amplitude de 1 V, tout est comme dans la formule du signal d'origine. Tout va bien, bravo programmeur ! Le programme fonctionne correctement.
Cela signifie que si nous appliquons un signal réel provenant d'un mélange de deux sinusoïdes à l'entrée du CAN, nous obtiendrons un spectre similaire composé de deux harmoniques.
Au total, notre réel signal mesuré, dure 5 secondes, numérisé par l'ADC, c'est-à-dire représenté discret compte, a discret non périodique gamme.
D’un point de vue mathématique, combien d’erreurs y a-t-il dans cette phrase ?
Maintenant que les autorités ont décidé, nous avons décidé que 5 secondes, c'est trop long, mesurons le signal en 0,5 seconde.

Fig.3 Graphique de la fonction sin(10*2*pi*x)+0,5*sin(5*2*pi*x) pour une période de mesure de 0,5 sec

Fig.4 Spectre de fonctions
Quelque chose ne semble pas normal ! L'harmonique de 10 Hz est dessinée normalement, mais à la place du bâton de 5 Hz, plusieurs harmoniques étranges apparaissent. Nous regardons sur Internet ce qui se passe...
Eh bien, ils disent que vous devez ajouter des zéros à la fin de l'échantillon et le spectre sera dessiné normalement.

Fig.5 Ajout de zéros jusqu'à 5 secondes

Fig.6 Spectre reçu
Ce n'est toujours pas la même chose qu'à 5 secondes. Nous devrons traiter de la théorie. Allons à Wikipédia- source de connaissances.
2. Fonction continue et sa représentation en série de Fourier
Mathématiquement, notre signal d'une durée de T secondes est une certaine fonction f(x) spécifiée sur l'intervalle (0, T) (X dans ce cas est le temps). Une telle fonction peut toujours être représentée comme une somme de fonctions harmoniques (sinus ou cosinus) de la forme : (1), où :
(1), où :
K - numéro de fonction trigonométrique (numéro de composant harmonique, numéro harmonique)
T - segment où la fonction est définie (durée du signal)
Ak est l'amplitude de la k-ième composante harmonique,
θk- phase initiale de la k-ème composante harmonique
Que signifie « représenter une fonction comme la somme d’une série » ? Cela signifie qu'en additionnant les valeurs des composantes harmoniques de la série de Fourier en chaque point, nous obtenons la valeur de notre fonction en ce point.
(Plus strictement, l'écart quadratique moyen de la série par rapport à la fonction f(x) tendra vers zéro, mais malgré la convergence quadratique moyenne, la série de Fourier d'une fonction, d'une manière générale, n'est pas obligée de y convergent ponctuellement. Voir https://ru.wikipedia.org/wiki/Fourier_Series.)
Cette série peut également s’écrire :
 (2),
(2),
où , k-ème amplitude complexe.
La relation entre les coefficients (1) et (3) est exprimée par les formules suivantes :
![]()

Notez que ces trois représentations de la série de Fourier sont complètement équivalentes. Parfois, lorsque l'on travaille avec des séries de Fourier, il est plus pratique d'utiliser les exposants de l'argument imaginaire au lieu des sinus et des cosinus, c'est-à-dire d'utiliser la transformée de Fourier sous une forme complexe. Mais il nous convient d'utiliser la formule (1), où la série de Fourier est présentée comme une somme d'ondes cosinusoïdales avec les amplitudes et phases correspondantes. Quoi qu’il en soit, il est inexact de dire que la transformée de Fourier d’un signal réel aboutira à des amplitudes harmoniques complexes. Comme Wiki l'indique à juste titre, « La transformée de Fourier (ℱ) est une opération qui associe une fonction d'une variable réelle à une autre fonction, également une variable réelle. »
Total:
La base mathématique de l'analyse spectrale des signaux est la transformée de Fourier.
La transformée de Fourier permet de représenter une fonction continue f(x) (signal), définie sur le segment (0, T) comme la somme d'un nombre infini (série infinie) de fonctions trigonométriques (sinus et/ou cosinus) avec certaines amplitudes et phases, également considérées sur le segment (0, T). Une telle série est appelée série de Fourier.
Notons encore quelques points dont la compréhension est nécessaire à l'application correcte de la transformée de Fourier à l'analyse du signal. Si l'on considère la série de Fourier (la somme des sinusoïdes) sur tout l'axe X, on voit qu'en dehors du segment (0, T) la fonction représentée par la série de Fourier répétera périodiquement notre fonction.
Par exemple, dans le graphique de la figure 7, la fonction d'origine est définie sur le segment (-T\2, +T\2), et la série de Fourier représente une fonction périodique définie sur tout l'axe des x.
Cela se produit parce que les sinusoïdes elles-mêmes sont des fonctions périodiques et que, par conséquent, leur somme sera une fonction périodique.

Fig.7 Représentation d'une fonction originale non périodique par une série de Fourier
Ainsi:
Notre fonction originale est continue, non périodique, définie sur un certain segment de longueur T.
Le spectre de cette fonction est discret, c'est-à-dire qu'il se présente sous la forme d'une série infinie de composantes harmoniques - la série de Fourier.
En fait, la série de Fourier définit une certaine fonction périodique qui coïncide avec la nôtre sur le segment (0, T), mais pour nous cette périodicité n'est pas significative.
Les périodes des composantes harmoniques sont des multiples de la valeur du segment (0, T) sur lequel la fonction originale f(x) est définie. Autrement dit, les périodes harmoniques sont des multiples de la durée de la mesure du signal. Par exemple, la période de la première harmonique de la série de Fourier est égale à l'intervalle T sur lequel est définie la fonction f(x). La période de la deuxième harmonique de la série de Fourier est égale à l'intervalle T/2. Et ainsi de suite (voir Fig. 8).

Fig.8 Périodes (fréquences) des composantes harmoniques de la série de Fourier (ici T = 2π)
En conséquence, les fréquences des composantes harmoniques sont des multiples de 1/T. Autrement dit, les fréquences des composantes harmoniques Fk sont égales à Fk= k\T, où k va de 0 à ∞, par exemple k=0 F0=0 ; k=1 F1=1\T; k=2 F2=2\T; k=3 F3=3\T;… Fk= k\T (à fréquence nulle - composante constante).
Soit notre fonction originale un signal enregistré pendant T=1 sec. Alors la période de la première harmonique sera égale à la durée de notre signal T1=T=1 sec et la fréquence harmonique sera de 1 Hz. La période de la deuxième harmonique sera égale à la durée du signal divisée par 2 (T2=T/2=0,5 sec) et la fréquence sera de 2 Hz. Pour la troisième harmonique T3=T/3 sec et la fréquence est de 3 Hz. Et ainsi de suite.
Le pas entre les harmoniques dans ce cas est de 1 Hz.
Ainsi, un signal d'une durée de 1 seconde peut être décomposé en composantes harmoniques (obtention d'un spectre) avec une résolution en fréquence de 1 Hz.
Pour augmenter la résolution de 2 fois à 0,5 Hz, vous devez augmenter la durée de mesure de 2 fois - jusqu'à 2 secondes. Un signal d'une durée de 10 secondes peut être décomposé en composantes harmoniques (pour obtenir un spectre) avec une résolution en fréquence de 0,1 Hz. Il n’existe aucun autre moyen d’augmenter la résolution en fréquence.
Il existe un moyen d'augmenter artificiellement la durée d'un signal en ajoutant des zéros au tableau d'échantillons. Mais cela n’augmente pas la résolution en fréquence réelle.
3. Signaux discrets et transformée de Fourier discrète
Avec le développement de la technologie numérique, les méthodes de stockage des données de mesure (signaux) ont également changé. Si auparavant un signal pouvait être enregistré sur un magnétophone et stocké sur bande sous forme analogique, les signaux sont désormais numérisés et stockés dans des fichiers dans la mémoire de l'ordinateur sous la forme d'un ensemble de nombres (échantillons).Le schéma habituel pour mesurer et numériser un signal est le suivant.

Fig.9 Schéma du canal de mesure
Le signal du transducteur de mesure arrive à l'ADC pendant un temps T. Les échantillons de signal (échantillonnage) obtenus pendant le temps T sont transmis à l'ordinateur et stockés en mémoire.

Fig. 10 Signal numérisé - N échantillons reçus pendant le temps T
Quelles sont les exigences relatives aux paramètres de numérisation du signal ? Un appareil qui convertit un signal analogique d'entrée en un code discret (signal numérique) est appelé convertisseur analogique-numérique (ADC) (Wiki).
L'un des principaux paramètres de l'ADC est la fréquence d'échantillonnage maximale (ou taux d'échantillonnage, taux d'échantillonnage anglais) - le taux d'échantillonnage d'un signal continu dans le temps lors de son échantillonnage. Elle se mesure en hertz. ((Wiki))
Selon le théorème de Kotelnikov, si un signal continu a un spectre limité par la fréquence Fmax, alors il peut être reconstruit complètement et de manière unique à partir de ses échantillons discrets prélevés à intervalles de temps.  , c'est à dire. avec une fréquence Fd ≥ 2*Fmax, où Fd est la fréquence d'échantillonnage ; Fmax - fréquence maximale du spectre du signal. Autrement dit, la fréquence de numérisation du signal (fréquence d'échantillonnage ADC) doit être au moins 2 fois supérieure à la fréquence maximale du signal que l'on souhaite mesurer.
, c'est à dire. avec une fréquence Fd ≥ 2*Fmax, où Fd est la fréquence d'échantillonnage ; Fmax - fréquence maximale du spectre du signal. Autrement dit, la fréquence de numérisation du signal (fréquence d'échantillonnage ADC) doit être au moins 2 fois supérieure à la fréquence maximale du signal que l'on souhaite mesurer.
Que se passera-t-il si nous prélevons des échantillons avec une fréquence inférieure à celle requise par le théorème de Kotelnikov ?
Dans ce cas, il se produit l'effet « aliasing » (également connu sous le nom d'effet stroboscopique, effet moiré), dans lequel un signal haute fréquence, après numérisation, se transforme en un signal basse fréquence, qui n'existe pas en réalité. En figue. L'onde sinusoïdale haute fréquence 11 rouge est un signal réel. Une sinusoïde bleue d'une fréquence inférieure est un signal fictif qui apparaît du fait que pendant la période d'échantillonnage, plus d'une demi-période du signal haute fréquence a le temps de passer.

Riz. 11. L'apparition d'un faux signal basse fréquence à une fréquence d'échantillonnage insuffisamment élevée
Pour éviter l'effet de crénelage, un filtre anti-crénelage spécial est placé devant l'ADC - un filtre passe-bas (LPF), qui laisse passer les fréquences inférieures à la moitié de la fréquence d'échantillonnage de l'ADC et coupe les fréquences plus élevées.
Afin de calculer le spectre d'un signal à partir de ses échantillons discrets, la transformée de Fourier discrète (TFD) est utilisée. Notons encore une fois que le spectre d'un signal discret « par définition » est limité par la fréquence Fmax, qui est inférieure à la moitié de la fréquence d'échantillonnage Fd. Par conséquent, le spectre d'un signal discret peut être représenté par la somme d'un nombre fini d'harmoniques, contrairement à la somme infinie pour la série de Fourier d'un signal continu, dont le spectre peut être illimité. Selon le théorème de Kotelnikov, la fréquence maximale d'une harmonique doit être telle qu'elle représente au moins deux échantillons, donc le nombre d'harmoniques est égal à la moitié du nombre d'échantillons d'un signal discret. Autrement dit, s’il y a N échantillons dans l’échantillon, alors le nombre d’harmoniques dans le spectre sera égal à N/2.
Considérons maintenant la transformée de Fourier discrète (TFD).

Comparaison avec la série de Fourier

Nous voyons qu'ils coïncident, sauf que le temps dans la DFT est de nature discrète et que le nombre d'harmoniques est limité par N/2 - la moitié du nombre d'échantillons.
Les formules DFT sont écrites en variables entières sans dimension k, s, où k sont le nombre d'échantillons de signal, s est le nombre de composantes spectrales.
La valeur s indique le nombre d'oscillations harmoniques complètes sur la période T (durée de mesure du signal). La transformée de Fourier discrète est utilisée pour trouver les amplitudes et les phases des harmoniques à l'aide d'une méthode numérique, c'est-à-dire "sur l'ordinateur"
Revenons aux résultats obtenus au début. Comme mentionné ci-dessus, lors de l'expansion d'une fonction non périodique (notre signal) en une série de Fourier, la série de Fourier résultante correspond en fait à une fonction périodique de période T (Fig. 12).

Fig. 12 Fonction périodique f(x) avec période T0, avec période de mesure T>T0
Comme on peut le voir sur la figure 12, la fonction f(x) est périodique de période T0. Cependant, du fait que la durée de l'échantillon de mesure T ne coïncide pas avec la période de la fonction T0, la fonction obtenue sous forme de série de Fourier présente une discontinuité au point T. De ce fait, le spectre de cette fonction contiendra un grand nombre d'harmoniques haute fréquence. Si la durée de l'échantillon de mesure T coïncidait avec la période de la fonction T0, alors le spectre obtenu après transformée de Fourier ne contiendrait que la première harmonique (sinusoïde de période égale à la durée d'échantillonnage), puisque la fonction f(x) est une sinusoïde.
En d'autres termes, le programme DFT "ne sait pas" que notre signal est un "morceau de sinusoïde", mais essaie de représenter une fonction périodique sous la forme d'une série, qui présente une discontinuité due à l'incohérence des morceaux individuels de la sinusoïde.
De ce fait, des harmoniques apparaissent dans le spectre, qui doivent résumer la forme de la fonction, y compris cette discontinuité.
Ainsi, afin d'obtenir le spectre « correct » d'un signal, qui est la somme de plusieurs sinusoïdes de périodes différentes, il est nécessaire qu'un nombre entier de périodes de chaque sinusoïde rentre dans la période de mesure du signal. En pratique, cette condition peut être remplie pour une durée de mesure du signal suffisamment longue.

Fig. 13 Exemple de fonction et de spectre du signal d'erreur cinématique de la boîte de vitesses
Avec une durée plus courte, l'image sera « pire » :

Fig. 14 Exemple de fonction et de spectre d'un signal de vibration du rotor
En pratique, il peut être difficile de comprendre où sont les « composantes réelles » et où sont les « artefacts » provoqués par les périodes non multiples des composantes et la durée d’échantillonnage du signal ou les « sauts et ruptures » dans la forme du signal. . Bien sûr, les mots « composants réels » et « artefacts » sont mis entre guillemets pour une raison. La présence de nombreuses harmoniques sur le graphique du spectre ne signifie pas que notre signal en est réellement « constitué ». Cela revient à penser que le nombre 7 « se compose » des nombres 3 et 4. Le nombre 7 peut être représenté comme la somme des nombres 3 et 4 – c’est exact.
Donc notre signal... ou plutôt même pas « notre signal », mais une fonction périodique composée de la répétition de notre signal (échantillonnage) peut être représentée comme une somme d'harmoniques (ondes sinusoïdales) avec certaines amplitudes et phases. Mais dans de nombreux cas importants pour la pratique (voir les figures ci-dessus), il est en effet possible d'associer les harmoniques obtenues dans le spectre à des processus réels, de nature cyclique et apportant une contribution significative à la forme du signal.
Quelques résultats
1. Un signal réel mesuré d'une durée de T secondes, numérisé par un CAN, c'est-à-dire représenté par un ensemble d'échantillons discrets (N pièces), possède un spectre discret non périodique, représenté par un ensemble d'harmoniques (N/ 2 pièces).2. Le signal est représenté par un ensemble de valeurs réelles et son spectre est représenté par un ensemble de valeurs réelles. Les fréquences harmoniques sont positives. Le fait qu’il soit plus pratique pour les mathématiciens de représenter le spectre sous une forme complexe en utilisant des fréquences négatives ne signifie pas que « c’est correct » et que « cela devrait toujours être fait ».
3. Un signal mesuré sur un intervalle de temps T est déterminé uniquement sur un intervalle de temps T. Ce qui s'est passé avant que nous commencions à mesurer le signal, et ce qui se passera après cela, est inconnu de la science. Et dans notre cas, ce n’est pas intéressant. La TFD d'un signal limité dans le temps donne son « vrai » spectre, dans le sens où, sous certaines conditions, elle permet de calculer l'amplitude et la fréquence de ses composantes.
Matériaux utilisés et autres matériaux utiles.