Fonctions trigonométriques de la leçon d'argument angulaire. Fonctions trigonométriques d'argument numérique et angulaire. Lignes de sinus, cosinus, tangentes et cotangentes

24.11.2019

Lignes de sinus, cosinus, tangentes et cotangentes

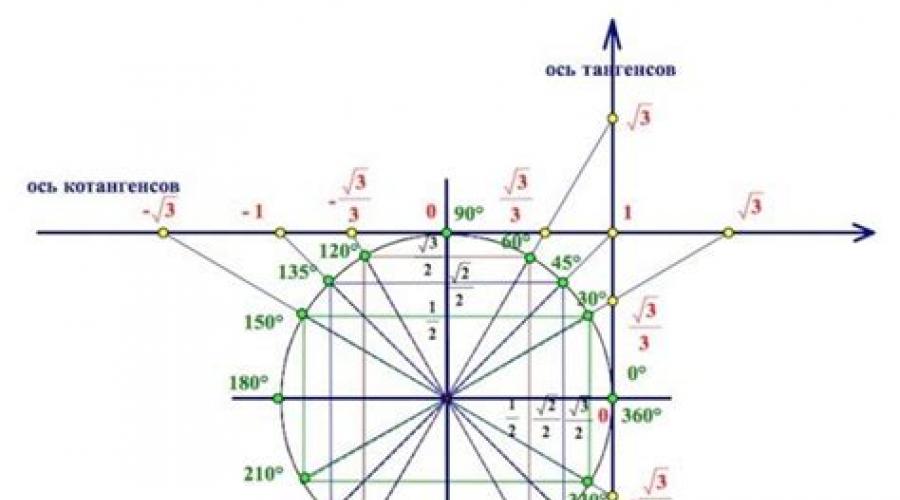
N'oublie jamais cela L'axe Y est la ligne des sinus, L'axe X est une ligne de cosinus! Les points obtenus du cercle sont marqués sur ces axes.

UN les lignes de tangentes et cotangentes leur sont parallèles et passent par les points (1 ; 0) et (0 ; 1) respectivement.

Quel que soit le nombre réel t pris, il peut être associé à un nombre sin t défini de manière unique. Certes, la règle de correspondance est assez complexe comme nous l’avons vu ci-dessus, elle est la suivante.

Pour trouver par numéro t valeur du péché t, il te faut :

1) positionner le cercle numérique dans le plan de coordonnées de manière à ce que le centre du cercle coïncide avec l'origine des coordonnées et que le point de départ A du cercle tombe au point (1 ; 0) ;

2) trouver un point sur le cercle correspondant au nombre t ;

3) trouver l'ordonnée de ce point.

Cette ordonnée est sin t.

En fait nous parlons deà propos de la fonction u = sin t, où t est n'importe quel nombre réel.

Toutes ces fonctions sont appelées fonctions trigonométriques de l'argument numérique t.

Manger ligne entière relations reliant les valeurs de diverses fonctions trigonométriques, nous avons déjà obtenu certaines de ces relations :

péché 2 t+cos 2 t = 1

A partir des deux dernières formules, il est facile d'obtenir une relation reliant tg t et ctg t :

Toutes ces formules sont utilisées dans les cas où, connaissant la valeur d'une fonction trigonométrique, il est nécessaire de calculer les valeurs d'autres fonctions trigonométriques.

Les termes « sinus », « cosinus », « tangente » et « cotangente » étaient en réalité familiers, mais ils étaient encore utilisés dans une interprétation légèrement différente : en géométrie et en physique, ils considéraient le sinus, le cosinus, la tangente et la cotangente. à la tête(mais non

chiffres, comme c'était le cas dans les paragraphes précédents).

De la géométrie, on sait que le sinus (cosinus) angle aigu est le rapport d'une branche d'un triangle rectangle à son hypoténuse, et la tangente (cotangente) d'un angle est le rapport des branches d'un triangle rectangle. Une approche différente des notions de sinus, cosinus, tangente et cotangente a été développée dans les paragraphes précédents. En fait, ces approches sont interdépendantes.

Prenons un angle de degré b o et plaçons-le dans le modèle « cercle numérique dans un système de coordonnées rectangulaires », comme le montre la Fig. 14

le sommet de l'angle est compatible avec le centre

des cercles (avec l'origine du système de coordonnées),

et un côté de l'angle est compatible avec

le rayon positif de l’axe des x. Arrêt complet

intersection du deuxième côté de l'angle avec

désigner par le cercle la lettre M. Ordina-

14 b o, et l'abscisse de ce point est le cosinus de l'angle b o.

Pour trouver le sinus ou le cosinus d'un angle b o il n'est pas du tout nécessaire de faire à chaque fois ces constructions très complexes.

Il suffit de noter que l'arc AM constitue la même partie de la longueur du cercle numérique que l'angle b o fait à partir du coin de 360°. Si la longueur de l'arc AM est notée par la lettre t, on obtient :

Ainsi,

Par exemple,

On pense que 30° est une mesure en degrés d’un angle et une mesure en radians du même angle : 30° = rad. Du tout:

En particulier, je suis heureux d’où, à notre tour, nous le tirons.

Alors, qu'est-ce que 1 radian ? Manger diverses mesures longueurs des segments : centimètres, mètres, yards, etc. Il existe également diverses mesures pour indiquer l'ampleur des angles. On considère les angles au centre du cercle unité. Un angle de 1° est angle central, reposant sur un arc faisant partie d'un cercle. Un angle de 1 radian est l'angle au centre sous-tendu par un arc de longueur 1, c'est-à-dire sur un arc dont la longueur est égale au rayon du cercle. D'après la formule, nous trouvons que 1 rad = 57,3°.

Lorsqu'on considère la fonction u = sin t (ou toute autre fonction trigonométrique), on peut considérer la variable indépendante t comme un argument numérique, comme c'était le cas dans les paragraphes précédents, mais on peut aussi considérer cette variable comme une mesure de l'angle, c'est-à-dire argument de coin. Par conséquent, lorsqu’on parle d’une fonction trigonométrique, dans un certain sens, cela ne fait aucune différence de la considérer comme une fonction d’un argument numérique ou angulaire.

La leçon vidéo "Fonctions trigonométriques de l'argument angulaire" présente matériel visuel donner un cours de mathématiques sur un sujet pertinent. La vidéo est conçue de manière à ce que le matériel étudié soit présenté aussi facilement que possible pour que les étudiants puissent comprendre, soit facile à retenir et révèle bien le lien entre les informations disponibles sur les fonctions trigonométriques de la section sur l'étude des triangles et leur définition à l'aide de l'unité. cercle. Cela peut devenir partie indépendante leçon, car elle couvre entièrement ce sujet, complétée par des commentaires importants lors du voicing.

Pour démontrer clairement le lien différentes définitions des fonctions trigonométriques, des effets d'animation sont utilisés. La mise en évidence du texte avec une police de couleur, des constructions claires et compréhensibles et l'ajout de commentaires vous aident à maîtriser et à mémoriser rapidement le matériel et à atteindre rapidement les objectifs de la leçon. Les liens entre les définitions des fonctions trigonométriques sont clairement démontrés par des effets d'animation et des surlignages de couleurs, favorisant la compréhension et la mémorisation du matériel. Le manuel vise à accroître l'efficacité de la formation.

La leçon commence par l'introduction du sujet. Puis sont rappelées les définitions du sinus, du cosinus, de la tangente et de la cotangente d'un angle aigu d'un triangle rectangle. La définition mise en évidence dans le cadre nous rappelle que le sinus et le cosinus se forment comme le rapport de la jambe à l'hypoténuse, la tangente et la cotangente sont formées par le rapport des jambes. On rappelle également aux élèves le matériel récemment appris selon lequel, lorsqu'on considère un point sur le cercle unité, l'abscisse du point est le cosinus et l'ordonnée est le sinus du nombre correspondant à ce point. Le lien entre ces concepts est démontré à l’aide de la construction. L'écran affiche un cercle unité placé de manière à ce que son centre coïncide avec l'origine. A partir de l'origine des coordonnées, on construit un rayon qui fait un angle α avec l'axe des demi-abscisses positives. Ce rayon coupe le cercle unité au point O. À partir de ce point, les perpendiculaires descendent vers l'axe des abscisses et des ordonnées, démontrant que les coordonnées de ce point déterminent le cosinus et le sinus de l'angle α. Il est à noter que la longueur de l'arc AO depuis le point d'intersection du cercle unité avec la direction positive de l'axe des abscisses jusqu'au point O est la même partie de l'arc entier que l'angle α de 360°. Cela permet de créer la proportion α/360=t/2π, qui s'affiche immédiatement et est surlignée en rouge pour la mémorisation. De cette proportion est dérivée la valeur t = πα/180°. En tenant compte de cela, la relation entre les définitions du sinus et du cosinus est déterminée : sinα°= sint= sinπα/180, cosα°=cost=cosπα/180. Par exemple, trouver sin60° est donné. En substituant la mesure en degrés de l'angle dans la formule, nous obtenons sin π·60°/180°. En réduisant la fraction de 60, on obtient sin π/3, qui est égal à √3/2. Il est à noter que si 60° est une mesure en degrés d’un angle, alors π/3 est appelé une mesure en radians d’un angle. Il existe deux notations possibles pour le rapport entre la mesure en degrés d'un angle et la mesure en radian : 60°=π/3 et 60°=π/3 rad.

La notion d'angle d'un degré est définie comme l'angle au centre sous-tendu par un arc dont la longueur 1/360 représente une partie de la circonférence. La définition suivante révèle le concept d'angle d'un radian - l'angle au centre basé sur un arc de longueur un, ou égal au rayon du cercle. Les définitions sont marquées comme importantes et mises en évidence pour qu'il soit important de les retenir.

Pour convertir une mesure en degré d'un angle en mesure en radian et vice versa, utilisez la formule α°=πα/180 rad. Cette formule est mise en évidence dans un cadre à l'écran. De cette formule il résulte que 1° = π/180 rad. Dans ce cas, un radian correspond à un angle de 180°/π≈57,3°. Il est à noter que lors de la recherche des valeurs des fonctions trigonométriques de la variable indépendante t, celle-ci peut être considérée à la fois comme un argument numérique et angulaire.

Ce qui suit montre des exemples d’utilisation des connaissances acquises pour résoudre des problèmes mathématiques. Dans l'exemple 1, vous devez convertir les valeurs de degrés en radians 135° et 905°. Sur le côté droit de l’écran se trouve une formule montrant la relation entre les degrés et les radians. Après avoir substitué la valeur dans la formule, nous obtenons (π/180)·135. Après avoir réduit cette fraction de 45, on obtient la valeur 135° = 3π/4. Pour convertir un angle de 905° en mesure en radian, la même formule est utilisée. Après y avoir substitué la valeur, il s'avère que (π/180)·905=181π/36 rad.

Dans le deuxième exemple, le problème inverse est résolu : la mesure en degrés des angles exprimée en radians π/12, -21π/20, 2,4π est trouvée. Sur le côté droit de l'écran, on rappelle la formule étudiée pour le lien entre la mesure en degré et en radian de l'angle 1 rad = 180°/π. Chaque exemple est résolu en remplaçant la mesure du radian dans la formule. En remplaçant π/12, nous obtenons (180°/π)·(π/12)=15°. Les valeurs des angles restants se retrouvent de la même manière -21π/20=-189° et 2,4π=432°.

La leçon vidéo « Fonctions trigonométriques de l'argument angulaire » est recommandée pour une utilisation dans les cours de mathématiques traditionnels afin d'augmenter l'efficacité de l'apprentissage. Le matériel contribuera à assurer la visibilité de l'apprentissage lors de l'enseignement à distance sur ce sujet. Une explication détaillée et compréhensible du sujet et des solutions aux problèmes qui s'y rapportent peuvent aider l'étudiant à maîtriser le matériel de manière indépendante.

DÉCODAGE DE TEXTE :

"Fonctions trigonométriques de l'argument angulaire."

Nous savons déjà grâce à la géométrie que le sinus (cosinus) d'un angle aigu d'un triangle rectangle est le rapport de la jambe à l'hypoténuse, et la tangente (cotangente) est le rapport des jambes. Et en algèbre, on appelle l'abscisse d'un point du cercle unité un cosinus, et l'ordonnée de ce point un sinus. Assurons-nous que tout cela est étroitement lié.

Plaçons un angle de degré α° (degrés alpha), comme le montre la figure 1 : le sommet de l'angle est compatible avec le centre du cercle unité (avec l'origine du système de coordonnées), et un côté de l'angle est compatible avec le rayon positif de l’axe des abscisses. Le deuxième côté de l'angle coupe le cercle au point O. L'ordonnée du point O est le sinus de l'angle alpha, et l'abscisse de ce point est le cosinus de alpha.

Notez que l’arc AO est la même partie de la longueur du cercle unité que l’angle alpha de l’angle de trois cent soixante degrés. Notons la longueur de l'arc AO par t(te), alors nous composerons la proportion =

(alpha est à soixante confiances comme te est à deux pi. De là, nous trouvons te : t = = (te est égal à pi alpha divisé par cent quatre-vingts).

Ainsi, pour trouver le sinus ou le cosinus de l'angle alpha degrés, vous pouvez utiliser la formule :

sin α° = sint = sin (sinus alpha degrés égal au sinus te et est égal au sinus du pi partiel alpha à cent quatre-vingts),

cosα° = coût = cos (le cosinus des degrés alpha est égal au cosinus de te et est égal au cosinus du pi alpha partiel à cent quatre-vingts).

Par exemple, sin 60° = sin = sin = (le sinus de soixante degrés est égal au sinus de pi par trois, selon le tableau des valeurs de base des sinus, égal à la racine de trois par deux).

On pense que 60° est une mesure en degrés d'un angle et que (pi par trois) est une mesure en radians du même angle, c'est-à-dire 60° = content(Soixante degrés équivaut à pi fois trois radians). Par souci de concision, nous nous sommes mis d'accord sur la désignation content omettre, c'est-à-dire que l'entrée suivante est acceptable : 60°= (afficher les abréviations radian mesure = rad.)

Un angle d'un degré est un angle central qui sous-tend un arc qui fait (trois cent soixantième) partie de l'arc. Un angle d'un radian est l'angle au centre qui repose sur un arc de longueur un, c'est-à-dire sur un arc dont la longueur est égale au rayon du cercle (on considère les angles au centre d'un cercle unité pour montrer un angle en pi radians sur un cercle).

Souvenons-nous formule importante convertir des degrés en radians :

α° = content. (alpha est égal à pi alpha divisé par cent quatre-vingts radians) Plus précisément, 1° = content(un degré est égal à pi divisé par cent quatre-vingts radians).

De là, nous pouvons trouver qu'un radian égal au rapport cent quatre-vingts degrés en pi et est approximativement égal à cinquante-sept virgule trois degrés : 1 content= ≈ 57,3°.

D'après ce qui précède : lorsque nous parlons de n'importe quelle fonction trigonométrique, par exemple de la fonction s = sint (es est égal au sinus te), la variable indépendante t(te) peut être considérée à la fois comme un argument numérique et un argument angulaire.

Regardons des exemples.

EXEMPLE 1. Convertir des degrés en radians : a) 135° ; b) 905°.

Solution. Utilisons la formule pour convertir les degrés en radians :

a) 135° = 1° ∙ 135 = content ∙ 135 = content

(Cent trente-cinq degrés est égal à pi fois cent quatre-vingts radians multiplié par cent trente-cinq, et après réduction est égal à trois pi fois quatre radians)

b) De même, en utilisant la formule de conversion d'une mesure en degré en mesure en radian, on obtient

905° = content ∙ 905 = content.

(neuf cent cinq degrés égale cent quatre-vingt-un pi fois trente-six radians).

EXEMPLE 2. Exprimer en degrés : a) ; b) - ; c) 2,4π

(pi sur douze ; moins vingt et un pi sur vingt ; deux virgule quatre pi).

Solution. a) Exprimons pi par douze en degrés, utilisons la formule pour convertir la mesure radian d'un angle en degré en 1 content=, on obtient

content = 1 content∙ = ∙ = 15° (pi fois douze radians est égal au produit d'un radian et pi fois douze. En substituant cent quatre-vingts à pi au lieu d'un radian et en réduisant, nous obtenons quinze degrés)

Similaire à b) - = 1 content∙ (-) = ∙ (-)= - 189° (moins vingt et un pi fois vingt égale moins cent quatre-vingt-neuf degrés),

c) 2,4π = 1 content∙ 2,4π = ∙ 2,4π = 432° (deux virgule quatre pi équivaut à quatre cent trente-deux degrés).

Leçon et présentation sur le thème : "Fonction trigonométrique de l'argument angulaire, mesure en degré de l'angle et des radians"

Matériaux additionnels
Chers utilisateurs, n'oubliez pas de laisser vos commentaires, avis, souhaits. Tous les documents ont été vérifiés par un programme antivirus.

Manuels et simulateurs dans la boutique en ligne Integral pour la 10e année à partir de 1C
Nous résolvons des problèmes de géométrie. Tâches de construction interactives
Nous résolvons des problèmes de géométrie. Tâches interactives pour construire dans l'espace

Ce que nous étudierons :
1. Rappelons-nous la géométrie.
2. Définition de l'argument angulaire.
3. Mesure en degrés de l'angle.
4. Mesure radian de l'angle.
5. Qu'est-ce qu'un radian ?
6. Exemples et tâches pour une solution indépendante.

Répétition de la géométrie

Les gars, dans nos fonctions :

y= sin(t), y= cos(t), y= tg(t), y= ctg(t)

La variable t peut non seulement prendre des valeurs numériques, c'est-à-dire être un argument numérique, mais elle peut également être considérée comme une mesure d'angle - un argument angulaire.

Souvenons-nous de la géométrie !
Comment y avons-nous défini sinus, cosinus, tangente, cotangente ?

Sinus d'un angle - le rapport du côté opposé à l'hypoténuse

Cosinus de l'angle - le rapport de la jambe adjacente à l'hypoténuse

La tangente d'un angle est le rapport du côté opposé au côté adjacent.

La cotangente d'un angle est le rapport du côté adjacent au côté opposé.

Définition de la fonction trigonométrique de l'argument d'angle

Définissons les fonctions trigonométriques comme fonctions de l'argument angulaire sur le cercle numérique :
En utilisant le cercle numérique et le système de coordonnées, nous pouvons toujours trouver facilement le sinus, le cosinus, la tangente et la cotangente d'un angle :

Plaçons le sommet de notre angle α au centre du cercle, c'est-à-dire au centre de l'axe des coordonnées, et positionner l'un des côtés de manière à ce qu'il coïncide avec la direction positive de l'axe des abscisses (OA)
Ensuite, le deuxième côté coupe le cercle numérique au point M.

Ordonnée point M : sinus de l'angle α
Abscisse point M : cosinus de l'angle α

Notez que la longueur de l'arc AM est la même partie du cercle unité que notre angle α de 360 degrés : où t est la longueur de l’arc AM.

Mesure en degrés de l'angle

1) Les gars, nous avons une formule pour déterminer la mesure en degrés d'un angle passant par la longueur de l'arc d'un cercle numérique, regardons-la de plus près :

Ensuite on écrit des fonctions trigonométriques sous la forme :

Par exemple:

Mesure radian des angles

Lorsque vous calculez la mesure en degrés ou en radians d’un angle, n’oubliez pas ! :
Par exemple:

D'ailleurs! Désignation rad. tu peux le baisser !

Qu'est-ce qu'un radian ?

Chers amis, nous sommes confrontés à un nouveau concept - Radian. Alors c'est quoi?

Il existe différentes mesures de longueur, de temps, de poids, par exemple : mètre, kilomètre, seconde, heure, gramme, kilogramme et autres. Le Radian est donc l’une des mesures d’angle. Il convient de considérer les angles centraux, c'est-à-dire ceux situés au centre du cercle numérique.
Un angle de 1 degré est l'angle au centre sous-tendu par un arc égal à 1/360 de la circonférence.

Un angle de 1 radian est l'angle au centre sous-tendu par un arc égal à 1 dans un cercle unité, et dans un cercle arbitraire par un arc égal au rayon cercles.

Exemples: