Le sujet de la leçon est "Division avec reste. Trouver le dividende du quotient incomplet et du reste de la division". Division avec reste
Lire aussi
Lisez le sujet de la leçon : « Division avec reste ». Que savez-vous déjà sur ce sujet ?
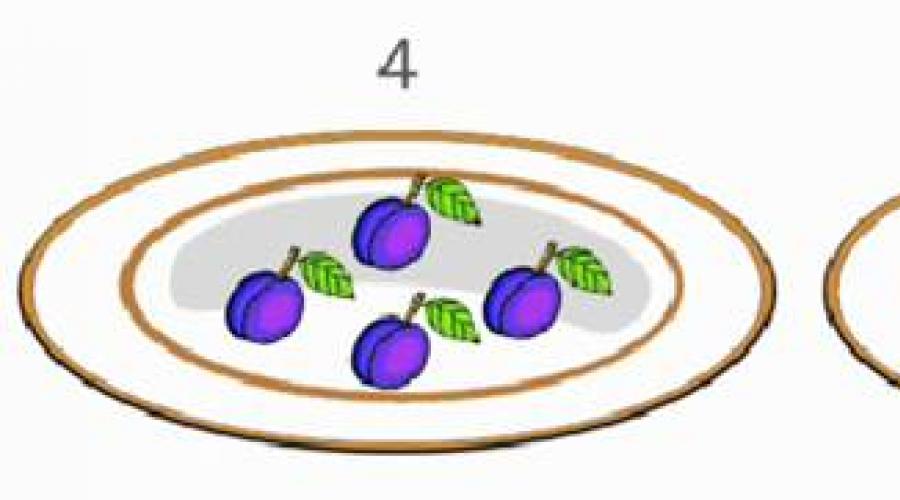
Pouvez-vous répartir 8 prunes à parts égales sur deux assiettes (Fig. 1) ?
Riz. 1. Illustration par exemple
Vous pouvez mettre 4 prunes dans chaque assiette (Fig. 2).

Riz. 2. Illustration par exemple
L’action que nous avons effectuée peut s’écrire ainsi.
8: 2 = 4
Pensez-vous qu'il soit possible de répartir 8 prunes à parts égales sur 3 assiettes (Fig. 3) ?

Riz. 3. Illustration par exemple
Agissons ainsi. Mettez d’abord une prune dans chaque assiette, puis une deuxième prune. Il nous restera 2 prunes, mais 3 assiettes. Cela signifie que nous ne pouvons pas les répartir davantage de manière égale. Nous avons mis 2 prunes dans chaque assiette, et il nous restait 2 prunes (Fig. 4).

Riz. 4. Illustration par exemple
Continuons à observer.
Lisez les chiffres. Parmi les nombres donnés, trouvez ceux qui sont divisibles par 3.
11, 12, 13, 14, 15, 16, 17, 18, 19
Testez-vous.
Les nombres restants (11, 13, 14, 16, 17, 19) ne sont pas divisibles par 3, ou on dit "partagé avec le reste."
Trouvons la valeur du quotient.
Voyons combien de fois 3 est contenu dans le nombre 17 (Fig. 5).

Riz. 5. Illustration par exemple
On voit que 3 ovales s'adaptent 5 fois et qu'il reste 2 ovales.
L'action terminée peut être écrite comme ceci.
17 : 3 = 5 (2 restants)
Vous pouvez également l'écrire dans une colonne (Fig. 6)

Riz. 6. Illustration par exemple
Regarde les photos. Expliquez les légendes de ces figures (Fig. 7).

Riz. 7. Illustration par exemple
Regardons la première image (Fig. 8).

Riz. 8. Illustration par exemple
On voit que 15 ovales ont été divisés en 2. 2 ont été répétés 7 fois, le reste étant 1 ovale.
Regardons la deuxième image (Fig. 9).

Riz. 9. Illustration par exemple
Dans cette figure, 15 carrés ont été divisés en 4. 4 ont été répétés 3 fois, le reste étant constitué de 3 carrés.
Regardons la troisième image (Fig. 10).

Riz. 10. Illustration par exemple
On peut dire que 15 ovales ont été divisés en 3. 3 ont été répétés 5 fois également. Dans de tels cas, le reste est dit égal à 0.
Faisons la division.
Nous divisons sept carrés en trois. Nous obtenons deux groupes et il reste un carré. Écrivons la solution (Fig. 11).

Riz. 11. Illustration par exemple
Faisons la division.
Voyons combien de fois quatre sont contenues dans le nombre 10. On voit que le nombre 10 contient quatre fois 2 fois et qu'il reste 2 carrés. Écrivons la solution (Fig. 12).

Riz. 12. Illustration par exemple
Faisons la division.
Voyons combien de fois deux sont contenus dans le nombre 11. Nous voyons que dans le nombre 11 deux sont contenus 5 fois et il reste 1 carré. Écrivons la solution (Fig. 13).

Riz. 13. Illustration par exemple
Tirons une conclusion. Diviser par un reste, c'est savoir combien de fois le diviseur est contenu dans le dividende et combien d'unités il reste.
La division avec un reste peut également être effectuée sur la droite numérique.
Sur la droite numérique, nous marquons les segments de 3 divisions et voyons qu'il y a trois divisions trois fois et qu'il reste une division (Fig. 14).
Riz. 14. Illustration par exemple
Écrivons la solution.
10 : 3 = 3 (1 restant)
Faisons la division.
Sur la droite numérique, nous marquons les segments de 3 divisions et voyons qu'il y a trois divisions trois fois et qu'il reste deux divisions (Fig. 15).
Riz. 15. Illustration par exemple
Écrivons la solution.
11 : 3 = 3 (2 restants)
Faisons la division.
Sur la droite numérique, nous marquons les segments de 3 divisions et voyons que nous avons obtenu exactement 4 fois, il n'y a pas de reste (Fig. 16).
Riz. 16. Illustration par exemple
Écrivons la solution.
12: 3 = 4
Aujourd'hui, dans la leçon, nous nous sommes familiarisés avec la division avec un reste, avons appris à effectuer l'action nommée à l'aide d'un dessin et d'une droite numérique et avons pratiqué la résolution d'exemples sur le sujet de la leçon.
Bibliographie
- MI. Moreau, M.A. Bantova et autres : Mathématiques. 3e année : en 2 parties, partie 1. - M. : « Lumières », 2012.
- MI. Moreau, M.A. Bantova et autres : Mathématiques. 3e année : en 2 parties, partie 2. - M. : « Lumières », 2012.
- MI. Moro. Cours de mathématiques : Des lignes directrices pour le professeur. 3ème année. - M. : Éducation, 2012.
- Document réglementaire. Suivi et évaluation des acquis d’apprentissage. - M. : « Lumières », 2011.
- "École de Russie": programmes pour école primaire. - M. : « Lumières », 2011.
- SI. Volkova. Mathématiques: Travail d'essai. 3ème année. - M. : Éducation, 2012.
- V.N. Rudnitskaïa. Essais. - M. : « Examen », 2012.
- Nsportal.ru ().
- Prosv.ru ().
- Do.gendocs.ru ().
Devoirs
1. Notez les nombres divisibles par 2 sans reste.
2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19
2. Effectuez une division avec un reste à l'aide d'une image.
3. Effectuez une division avec un reste en utilisant la droite numérique.
4. Créez un devoir pour vos amis sur le sujet de la leçon.
Dans cet article, nous examinerons division d'entiers avec reste. Commençons avec principe général division des entiers avec reste, nous formulerons et prouverons le théorème sur la divisibilité des entiers avec reste, nous tracerons les liens entre le dividende, le diviseur, le quotient incomplet et le reste. Ensuite, nous décrirons les règles selon lesquelles les nombres entiers sont divisés par un reste et considérerons l'application de ces règles lors de la résolution d'exemples. Après cela, nous apprendrons comment vérifier le résultat de la division d’entiers avec un reste.
Navigation dans les pages.
Compréhension générale de la division d'entiers avec un reste
Nous considérerons la division d'entiers avec reste comme une généralisation de la division avec reste d'entiers naturels. Cela est dû au fait que les nombres naturels sont partie intégrante entiers.
Commençons par les termes et désignations utilisés dans la description.
Semblable à la division nombres naturels avec reste nous supposerons que le résultat de la division avec reste de deux entiers a et b (b n'est pas égal à zéro) est deux entiers c et d. Les nombres a et b sont appelés divisible Et diviseur par conséquent, le nombre d – le reste en divisant a par b, et l'entier c est appelé privé incomplet(ou simplement privé, si le reste est nul).
Acceptons de supposer que le reste est un entier non négatif et que sa valeur ne dépasse pas b, c'est-à-dire (nous avons rencontré des chaînes d'inégalités similaires lorsque nous avons parlé de comparer trois entiers ou plus).
Si le nombre c est un quotient incomplet et que le nombre d est le reste de la division de l'entier a par l'entier b, alors nous écrirons brièvement ce fait comme une égalité de la forme a:b=c (reste d).
Notez que lorsque l’on divise un entier a par un entier b, le reste peut être nul. Dans ce cas on dit que a est divisible par b sans laisser de trace(ou complètement). Ainsi, la division d'entiers sans reste est un cas particulier de division d'entiers avec reste.
Il convient également de dire que lors de la division de zéro par un nombre entier, nous avons toujours affaire à une division sans reste, puisque dans ce cas le quotient sera égal à zéro (voir la section théorique sur la division de zéro par un nombre entier), et le reste sera également égal à zéro.
Nous avons décidé de la terminologie et de la notation, comprenons maintenant la signification de diviser des nombres entiers par un reste.
Diviser un entier négatif a par un entier positif b peut également avoir un sens. Pour ce faire, considérez un entier négatif comme une dette. Imaginons cette situation. La dette qui constitue les objets doit être remboursée par b personnes en apportant une contribution égale. Valeur absolue le quotient incomplet c dans ce cas déterminera le montant de la dette de chacune de ces personnes, et le reste d montrera combien d'éléments resteront après avoir remboursé la dette. Donnons un exemple. Disons que 2 personnes doivent 7 pommes. Si nous supposons que chacun d’eux doit 4 pommes, alors après avoir payé la dette, il lui restera 1 pomme. Cette situation correspond à l'égalité (−7) :2=−4 (restant 1).
Division avec un reste d'un entier arbitraire a par un entier un nombre négatif nous n'attacherons aucune signification, mais nous nous réserverons le droit d'exister.
Théorème sur la divisibilité des entiers avec reste
Lorsque nous avons parlé de diviser des nombres naturels par un reste, nous avons découvert que le dividende a, le diviseur b, le quotient partiel c et le reste d sont liés par l'égalité a=b·c+d. Les entiers a, b, c et d ont la même relation. Cette connexion est confirmée comme suit théorème de divisibilité avec reste.
Théorème.
Tout entier a peut être représenté de manière unique par un nombre entier et non nul b sous la forme a=b·q+r, où q et r sont des entiers, et .
Preuve.
Premièrement, nous prouvons la possibilité de représenter a=b·q+r.
Si les entiers a et b sont tels que a est divisible par b, alors par définition il existe un entier q tel que a=b·q. Dans ce cas, l'égalité a=b·q+r à r=0 est vraie.
Supposons maintenant que b est un entier positif. Choisissons un entier q pour que le produit b·q ne dépasse pas le nombre a, et que le produit b·(q+1) soit déjà supérieur à a. Autrement dit, nous prenons q tel que les inégalités b q Il reste à prouver la possibilité de représenter a=b·q+r pour b négatif . Puisque le module du nombre b dans ce cas est un nombre positif, alors il existe une représentation où q 1 est un nombre entier et r est un nombre entier qui satisfait aux conditions. Ensuite, en prenant q=−q 1, nous obtenons la représentation dont nous avons besoin a=b·q+r pour b négatif. Passons à la preuve d'unicité. Supposons qu'en plus de la représentation a=b·q+r, q et r soient des entiers et , il existe une autre représentation a=b·q 1 +r 1, où q 1 et r 1 sont des entiers, et q 1 ≠ q et . Après avoir soustrait respectivement les côtés gauche et droit de la deuxième égalité des côtés gauche et droit de la première égalité, nous obtenons 0=b·(q−q 1)+r−r 1, ce qui équivaut à l'égalité r− r 1 =b·(q 1 −q) . Alors une égalité de la forme D’après les conditions, nous pouvons conclure cela. Puisque q et q 1 sont des entiers et q≠q 1, alors nous concluons que L'égalité a=b·c+d permet de trouver le dividende inconnu a si le diviseur b, le quotient partiel c et le reste d sont connus. Regardons un exemple. Exemple. Quelle est la valeur du dividende si, divisé par l’entier −21, le résultat est un quotient incomplet de 5 et un reste de 12 ? Solution. Il faut calculer le dividende a lorsque le diviseur b=−21, le quotient partiel c=5 et le reste d=12 sont connus. En passant à l'égalité a=b·c+d, on obtient a=(−21)·5+12. En observant, on multiplie d'abord les entiers −21 et 5 selon la règle de multiplication des entiers de signes différents, après quoi on effectue l'addition des entiers de signes différents : (−21)·5+12=−105+12=−93 . Répondre: −93
.
Les relations entre le dividende, le diviseur, le quotient partiel et le reste sont également exprimées par des égalités de la forme b=(a−d):c, c=(a−d):b et d=a−b·c. Ces égalités vous permettent de calculer respectivement le diviseur, le quotient partiel et le reste. On devra souvent trouver le reste en divisant un entier a par un entier b lorsque le dividende, le diviseur et le quotient partiel sont connus, en utilisant la formule d=a−b·c. Pour éviter toute autre question, regardons un exemple de calcul du reste. Exemple. Trouvez le reste en divisant l'entier −19 par l'entier 3 si vous savez que le quotient partiel est égal à −7. Solution. Pour calculer le reste de la division, nous utilisons une formule de la forme d=a−b·c. À partir de la condition, nous avons toutes les données nécessaires a=−19, b=3, c=−7. On obtient d=a−b·c=−19−3·(−7)= −19−(−21)=−19+21=2 (nous avons calculé la différence −19−(−21) en utilisant la règle de en soustrayant un entier négatif). Répondre: Comme nous l’avons noté à plusieurs reprises, les entiers positifs sont des nombres naturels. Par conséquent, la division avec un reste d'entiers positifs s'effectue selon toutes les règles de la division avec un reste d'entiers naturels. Il est très important de pouvoir effectuer facilement une division avec un reste d'entiers naturels, car c'est précisément cela qui sous-tend non seulement la division d'entiers positifs, mais aussi la base de toutes les règles de division avec un reste d'entiers arbitraires. De notre point de vue, il est plus pratique d'effectuer une division en colonnes ; cette méthode permet d'obtenir à la fois un quotient incomplet (ou simplement un quotient) et un reste. Regardons un exemple de division avec un reste d'entiers positifs. Exemple. Divisez avec le reste 14 671 par 54. Solution. Divisons ces entiers positifs par une colonne : Le quotient partiel s'est avéré être égal à 271 et le reste est égal à 37. Répondre: 14 671:54=271 (reste 37) . Formulons une règle qui nous permet d'effectuer une division avec un reste d'un entier positif par un entier négatif. Le quotient partiel de la division d'un entier positif a par un entier négatif b est l'opposé du quotient partiel de la division de a par le module de b, et le reste de la division de a par b est égal au reste de la division par. De cette règle, il s'ensuit que le quotient partiel de la division d'un entier positif par un entier négatif est un entier non positif. Transformons la règle énoncée en un algorithme permettant de diviser avec un reste un entier positif par un entier négatif : Donnons un exemple d'utilisation de l'algorithme de division d'un entier positif par un entier négatif. Exemple. Divisez avec un reste de l'entier positif 17 par l'entier négatif −5. Solution. Utilisons l'algorithme pour diviser avec un reste un entier positif par un entier négatif. En divisant Le nombre opposé à 3 est −3. Ainsi, le quotient partiel requis pour diviser 17 par −5 est −3 et le reste est 2. Répondre: 17 :(−5)=−3 (restant 2). Exemple. Diviser 45 par −15. Solution. Les modules du dividende et du diviseur sont respectivement 45 et 15. Le nombre 45 est divisible par 15 sans reste et le quotient est 3. Par conséquent, l'entier positif 45 est divisé par l'entier négatif −15 sans reste, et le quotient est égal au nombre opposé à 3, soit −3. En effet, d'après la règle de division des entiers de signes différents, on a . Répondre: 45:(−15)=−3
.
Donnons la formulation de la règle pour diviser un entier négatif avec un reste par un entier positif. Pour obtenir un quotient incomplet c en divisant un entier négatif a par un entier positif b, vous devez prendre le nombre opposé au quotient incomplet en divisant les modules des nombres d'origine et en soustraire un, après quoi le reste d est calculé en utilisant la formule d=a−b·c. De cette règle de division avec reste il résulte que le quotient partiel de la division d'un entier négatif par un entier positif est un entier négatif. De la règle énoncée découle un algorithme pour diviser avec un reste un entier négatif a par un entier positif b : Analysons la solution de l'exemple dans lequel nous utilisons l'algorithme de division écrite avec un reste. Exemple. Trouvez le quotient partiel et le reste en divisant l'entier négatif −17 par l'entier positif 5. Solution. Le module du dividende −17 est égal à 17, et le module du diviseur 5 est égal à 5. En divisant 17 par 5, on obtient le quotient partiel 3 et le reste 2. L’opposé de 3 est −3. Soustrayez un de −3 : −3−1=−4. Ainsi, le quotient partiel requis est égal à −4. Il ne reste plus qu'à calculer le reste. Dans notre exemple a=−17 , b=5 , c=−4 , alors d=a−b·c=−17−5·(−4)= −17−(−20)=−17+20=3 . Ainsi, le quotient partiel de la division de l'entier négatif −17 par l'entier positif 5 est −4 et le reste est 3. Répondre: (−17) :5=−4 (3 restants) . Exemple. Divisez l'entier négatif −1 404 par l'entier positif 26. Solution. Le module du dividende est 1404, le module du diviseur est 26. Divisez 1 404 par 26 à l’aide d’une colonne : Puisque le module du dividende est divisé par le module du diviseur sans reste, les entiers initiaux sont divisés sans reste et le quotient souhaité est égal au nombre opposé à 54, soit −54. Répondre: (−1 404):26=−54
.
Formulons la règle de division avec un reste d'entiers négatifs. Pour obtenir un quotient incomplet c en divisant un entier négatif a par un entier négatif b, vous devez calculer le quotient incomplet en divisant les modules des nombres d'origine et y ajouter un, après quoi le reste d est calculé à l'aide de la formule d = a−b·c. De cette règle, il s'ensuit que le quotient partiel de la division des entiers négatifs est un entier positif. Réécrivons la règle énoncée sous la forme d'un algorithme de division d'entiers négatifs : Considérons l'utilisation de l'algorithme de division d'entiers négatifs lors de la résolution d'un exemple. Exemple. Trouvez le quotient partiel et le reste en divisant un entier négatif −17 par un entier négatif −5. Solution. Utilisons l'algorithme de division approprié avec un reste. Le module du dividende est 17, le module du diviseur est 5. Division 17 sur 5 donne le quotient partiel 3 et le reste 2. Au quotient incomplet 3 on ajoute un : 3+1=4. Par conséquent, le quotient partiel requis pour diviser −17 par −5 est égal à 4. Il ne reste plus qu'à calculer le reste. Dans cet exemple a=−17 , b=−5 , c=4 , alors d=a−b·c=−17−(−5)·4= −17−(−20)=−17+20=3 . Ainsi, le quotient partiel de la division d'un entier négatif −17 par un entier négatif −5 est 4 et le reste est 3. Répondre: (−17):(−5)=4 (3 restants) . Après avoir divisé des nombres entiers par un reste, il est utile de vérifier le résultat. La vérification s'effectue en deux étapes. Dans un premier temps, on vérifie si le reste d est un nombre non négatif, et on vérifie également si la condition est remplie. Si toutes les conditions de la première étape de vérification sont remplies, vous pouvez alors passer à la deuxième étape de vérification, sinon on peut affirmer qu'une erreur a été commise quelque part lors de la division avec un reste. Dans un deuxième temps, la validité de l'égalité a=b·c+d est vérifiée. Si cette égalité est vraie, alors la division avec un reste a été effectuée correctement, sinon une erreur a été commise quelque part. Examinons des solutions à des exemples dans lesquels le résultat de la division d'entiers avec un reste est vérifié. Exemple. En divisant le nombre −521 par −12, le quotient partiel était de 44 et le reste était de 7, vérifiez le résultat. Solution. −2 pour b=−3, c=7, d=1. Nous avons b·c+d=−3·7+1=−21+1=−20. Ainsi, l'égalité a=b·c+d est incorrecte (dans notre exemple a=−19). Par conséquent, la division avec reste n’a pas été effectuée correctement. Cible: Formation d'aptitudes et de compétences en division avec reste, recherche du dividende par quotient incomplet et reste de division, application des connaissances lors de la résolution de problèmes. Tâches: Type de cours : Leçon sur la consolidation des connaissances acquises à l'aide des TIC. Méthode d'enseignement : Méthode d'acquisition de connaissances basée sur une activité cognitive à caractère reproductif. Structure de la leçon : Pendant les cours 1. Rassemblez des cahiers avec des devoirs. Rassemblez des projets prêts à l'emploi « Méthodes anciennes de multiplication et de division ». 2. Afficher la présentation. Un message sur le sujet, le but de la leçon, les objectifs de la leçon, la devise de la leçon. La devise de la leçon : « La division nous sert dans la pratique ; 3. Travail oral. Calcul mental – développement des compétences informatiques chez les étudiants (Annexe 1). Présentation tirée du site « Pocket for a Mathematician » L'image assemblée est la clé du succès des calculs. Travail oral pour revoir les aspects théoriques du thème « Division avec reste » Quels sont les restes possibles en divisant avec un reste par 8 ? Qu'est-ce que cela signifie si le reste est supérieur au diviseur ? Qu'est-ce que cela signifie si le reste d'une division est nul ? 4. Motivation et mise à jour du nouveau matériel. Tâche. 4 petits-enfants sont venus rendre visite à leur grand-mère. La grand-mère a décidé d'offrir des friandises à ses petits-enfants. Il y a 23 bonbons dans un bol. Combien de bonbons chaque petit-enfant recevra-t-il si grand-mère propose de partager les bonbons à parts égales ? Solution : 23:4=5 (3 restants) Questions pour les étudiants : Dividende -> quotient partiel -> diviseur -> reste 5. Consolidation primaire et résolution de problèmes. Effectuer la division avec reste et vérifier : 882:40 Travailler avec le manuel : n° 536 oralement ; n° 537 oralement ; n° 538 oralement ; N° 518 6. Vérification de la maîtrise du matériel – carte perforée. Vérifiez l'achèvement des tâches de cartes perforées. Définir des repères : Moins de 4 tâches correctement complétées – « 2 » Attirez l'attention des enfants sur l'analyse des erreurs commises. 7. Devoirs : N° 540, 541, travaux sur le projet, règle. 8. Résumer la leçon construire en répondant aux questions suivantes : Par exemple 40:6=6 (4) Dans cet exemple dividende -40, le nombre avant le signe de division, 6-diviseur, le nombre après le signe de division ou par lequel on divise le dividende. 6-partiel, ce qui résulte de la division 4-reste, le nombre restant après la division Dans l'exemple : 20 est le dividende (ce qui est divisé), 10 est un diviseur (ce qui divise), 2 est un quotient (celui qui, multiplié par un diviseur, forme le dividende). Prenons un autre exemple : 17 : 3 = 5 (2), où 17 - dividende, 3 - diviseur, 5 - quotient incomplet, 2 est le reste. Il est intéressant de noter que le reste est toujours inférieur au quotient partiel. Afin de ne pas se tromper dans la détermination des quantités avec lesquelles il faut traiter dans le processus de division, les gens ont depuis longtemps trouvé des noms appropriés pour elles. Tout d’abord, le numéro lui-même. qu'ils divisent a commencé à être appelé Divisible, car ce nombre est divisible en parties, il est littéralement divisible. Par exemple, la récolte des fruits. Un nombre qui montre en combien de parties nous allons diviser. Le dividende a commencé à être appelé le diviseur. Sa tâche est de diviser le nombre en plusieurs groupes afin que chacun en ait assez. Le résultat de la division s'appelait Partielle - ce nombre indique combien d'unités se trouvent dans chaque groupe, une grappe de fruits, une fois la totalité de la récolte divisée. Enfin, le reste est ce nombre entier de fruits qui ne peuvent être répartis également entre tous. Vous avez collecté 51 pommes. Ceci est divisible. Nous avons décidé de le partager à parts égales entre papa, maman, fille et fils, soit quatre. C'est un diviseur. Ils l'ont divisé et ont obtenu que tout le monde avait droit à 12 pommes - c'est un quotient. Mais trois pommes ne peuvent pas être divisées en quatre et c'est le reste. 51:4=12 (reste 3). Le dividende est le nombre que nous diviserons. Le diviseur est le nombre sur que nous diviserons Un quotient est un nombre qui se forme lorsqu'il est divisé Le reste est le nombre qui reste une fois divisé (dans ce cas le quotient sera incomplet) Par exemple Ici 30 est le dividende, 4 est le diviseur, 7 est le quotient, 2 est le reste Il est en fait plus facile d’expliquer ce qu’est un dividende, un diviseur, un quotient et un reste à l’aide de divers exemples. Voici l'option la plus simple, ici tout est divisé sans laisser de trace. Ou voici un autre exemple. Comme on le voit, il n’y a rien de compliqué ; les enfants apprennent tout cela à l’école primaire dans les cours de mathématiques. Donnons immédiatement un exemple (même plusieurs exemples sont possibles) : 2). 21 : 5 = 4,2 ou 4 et 1 comme reste. Le dividende est le nombre que nous divisons (dans nos exemples, les dividendes sont 18 et 21). Le diviseur est le nombre par lequel on divise le dividende (les diviseurs dans nos exemples sont 9 et 5). Le quotient est le résultat d'une division (le quotient dans le premier exemple est 2 et dans le deuxième exemple 4,2). Dans le premier cas, le dividende est divisé sans reste, et dans le second nous avons un reste - 1. Les notions de dividende, de diviseur, de quotient et de reste commencent à étudier la division au lycée. C’est donc un incontournable lorsqu’on étudie les mathématiques. Et donc le divisible est le nombre qui est divisé. Le diviseur est le nombre par lequel on divise, et par conséquent le quotient est le résultat de la division. Mais c’est ce qui arrive lorsque le nombre divisé n’est pas divisible par un tout. Il s'agit du nombre formé lors du processus de division qui est inférieur au diviseur et qui ne peut pas être divisé complètement et est appelé le reste. Un exemple peut être donné comme suit. Par exemple. 34 : 5 = 6 (reste 4) Dans ce cas, 34 est le dividende. 5 est un diviseur. 6 - départements privés 4 est le reste. reste du quotient du diviseur de dividende Tout cela fait partie d'une opération mathématique - Divisions. Je vais essayer dans des langages simples, comme on me l'a expliqué.. il y a une trentaine d'années..) Dividende- c'est le nombre à gauche du signe de division que l'on divise (fraction) Diviseur- c'est le nombre à droite du signe de division, le nombre par lequel on divise le dividende (par quelles parties on divise, fraction) Privé- c'est le nombre après le signe égal, résultat de la division (l'expression numérique du nombre de parties entières - diviseurs dans le dividende) Quotient partiel- c'est le nombre après le signe égal, résultat d'une division qui a laissé un nombre supplémentaire inférieur au diviseur. Un quotient incomplet est uniquement le nombre de parties entières. Toujours écrit avec le numéro Reste. Reste- c'est le nombre restant indivisible, qui est inférieur au Diviseur. Et maintenant pour des exemples - 10: 5 = 2
Dans cet exemple, 10 est le dividende, 5 est le diviseur et 2 est le quotient. 13: 5 = 2 (3)
Dans cet exemple, 13 est le dividende, 5 est le diviseur, 2 est le quotient incomplet, 3 est le reste (généralement écrit entre parenthèses à côté du quotient incomplet). Ces concepts arithmétiques sont plus faciles à comprendre avec un exemple. Exemple : 17 : 8 = 2 (reste - 1). Dans cet exemple, 17 est le dividende (le nombre qui est divisé), 8 est le diviseur (ce par quoi nous divisons), 2 est le reste (ce que nous obtenons en divisant), 1 est le reste. Tous les concepts évoqués dans la question sont directement liés à la division en mathématiques. Commençons donc par le dividende - nous entendons par là le nombre qui sera divisé ; Le diviseur implique déjà le nombre par lequel le dividende existant sera divisé. Le quotient représente le résultat obtenu par division. Le reste est le nombre restant lors de la division, nous aurons donc un quotient incomplet. Voici un exemple : Enseigner la division longue à votre enfant est facile. Il est nécessaire d'expliquer l'algorithme de cette action et de consolider la matière abordée. Important : Pour qu'un enfant comprenne la division des nombres, il doit bien connaître la table de multiplication. Si votre enfant ne connaît pas bien la multiplication, il ne comprendra pas la division. Lors des activités périscolaires à la maison, vous pouvez utiliser des aide-mémoire, mais l'enfant doit apprendre la table de multiplication avant de commencer le sujet « Division ». Alors, comment expliquer à un enfant division par colonne: La division est toujours un peu plus difficile pour les enfants que la multiplication. Mais des études supplémentaires assidues à la maison aideront l'enfant à comprendre l'algorithme de cette action et à suivre ses pairs à l'école. Commencez par quelque chose de simple : divisez par un nombre à un chiffre : Important : Calculez mentalement pour que la division ressorte sans reste, sinon l'enfant risque de se perdre. Par exemple, 256 divisé par 4 : Lorsque l'enfant maîtrise la division par un nombre à un chiffre, vous pouvez passer à autre chose. La division écrite par un nombre à deux chiffres est un peu plus difficile, mais si l'enfant comprend comment cette action est effectuée, il ne lui sera pas difficile de résoudre de tels exemples. Important : Encore une fois, commencez à expliquer par des étapes simples. L'enfant apprendra à sélectionner correctement les nombres et il lui sera facile de diviser des nombres complexes. Faites cette action simple ensemble : 184:23 - comment expliquer : Important : Pour que votre enfant comprenne, essayez de prendre 9 au lieu de 8, laissez-le multiplier 9 par 23, il s'avère que 207 est plus que ce que nous avons dans le diviseur. Le chiffre 9 ne nous convient pas. Ainsi petit à petit le bébé comprendra la division, et il lui sera facile de diviser des nombres plus complexes : Si l'enfant a appris à diviser par un nombre à deux chiffres, il est alors nécessaire de passer au sujet suivant. L'algorithme de division par un nombre à trois chiffres est le même que l'algorithme de division par un nombre à deux chiffres. Par exemple: Important : Pour vérifier l'exactitude de la division, multipliez avec votre enfant dans une colonne - 204x716 = 146064. La division est effectuée correctement. Le moment est venu d'expliquer à l'enfant que la division peut être non seulement entière, mais aussi avec un reste. Le reste est toujours inférieur ou égal au diviseur. La division avec un reste doit être expliquée à l'aide d'un exemple simple : 35:8=4 (reste 3) : Après cela, l'enfant doit apprendre que la division peut être continuée en ajoutant 0 au chiffre 3 : Conseil : Si votre enfant ne comprend pas quelque chose, ne vous fâchez pas. Laissez passer quelques jours et réessayez d’expliquer le contenu. Les cours de mathématiques à l'école renforceront également les connaissances. Le temps passera et l'enfant résoudra rapidement et facilement tous les problèmes de division. L'algorithme de division des nombres est le suivant : Selon cet algorithme, la division est effectuée à la fois par des nombres à un chiffre et par tout nombre à plusieurs chiffres (à deux chiffres, à trois chiffres, à quatre chiffres, etc.). Lorsque vous travaillez avec votre enfant, donnez-lui souvent des exemples sur la façon de réaliser l'estimation. Il doit rapidement calculer la réponse dans sa tête. Par exemple: Pour consolider le résultat, vous pouvez utiliser les jeux de division suivants : Condition pour l'enfant : Parmi plusieurs exemples, un seul a été résolu correctement. Trouvez-le dans une minute. ![]() , et en raison des propriétés du module des nombres, l'égalité
, et en raison des propriétés du module des nombres, l'égalité ![]() .
.
![]() . A partir des inégalités obtenues et
. A partir des inégalités obtenues et ![]() il s'ensuit qu'une égalité de la forme
il s'ensuit qu'une égalité de la forme ![]() impossible selon notre hypothèse. Par conséquent, il n’existe pas d’autre représentation du nombre a autre que a=b·q+r.
impossible selon notre hypothèse. Par conséquent, il n’existe pas d’autre représentation du nombre a autre que a=b·q+r.Relations entre dividende, diviseur, quotient partiel et reste
Division avec reste d'entiers positifs, exemples

La règle pour diviser avec un reste un entier positif par un entier négatif, exemples
Division avec reste d'un entier négatif par un entier positif, exemples

Règle de division avec reste pour les entiers négatifs, exemples
Vérifier le résultat de la division d'entiers avec un reste
2*17+33
5+5*12
3500:100+400
48-12:3
200-20*5
13*8-34:2
6*15-15*5
6*4-4:2
68:17+17*2
Exercice
Réponse à la question
Quel est le reste de 57:8 ?
10
1
3
Quel est le reste de 90:8 ?
2
11
1
Entrez le reste 1213:12
101
12
1
Précisez le quotient incomplet 1213:12
101
11
1
Choisissez un reste possible lorsqu'il est divisé par 6
5
7
10
Choisissez un reste possible lorsqu'il est divisé par 3
3
2
5
Diviseur 8, quotient partiel 11, reste 3. A quoi est égal le dividende ?
35
41
91
Diviseur 7, quotient partiel 9, reste 6. A quoi est égal le dividende ?
69
61
51









Division écrite par deux chiffres










Vidéo : Jeu arithmétique pour enfants addition, soustraction, division, multiplication
Vidéo : Dessin animé pédagogique Mathématiques Apprendre par cœur les tables de multiplication et de division par 2