Tableaux des valeurs du péché. Fonctions trigonométriques
Lire aussi
Les notions de sinus (), cosinus (), tangente (), cotangente () sont inextricablement liées à la notion d'angle. Afin de bien comprendre ces concepts, à première vue complexes (qui provoquent un état d'horreur chez de nombreux écoliers), et pour s'assurer que « le diable n'est pas aussi terrible qu'on le peint », commençons par le tout début et comprendre le concept d’angle.
Notion d'angle : radian, degré
Regardons la photo. Le vecteur a « tourné » par rapport au point d’un certain montant. Donc la mesure de cette rotation par rapport à la position initiale sera coin.
Que devez-vous savoir d’autre sur le concept d’angle ? Et bien sûr, les unités d'angle !
L'angle, tant en géométrie qu'en trigonométrie, peut être mesuré en degrés et en radians.
L'angle (un degré) est l'angle au centre d'un cercle sous-tendu par un arc de cercle égal à une partie du cercle. Ainsi, le cercle entier est constitué de « morceaux » d'arcs de cercle, ou l'angle décrit par le cercle est égal.

Autrement dit, la figure ci-dessus montre un angle égal à, c'est-à-dire que cet angle repose sur un arc de cercle de la taille de la circonférence.
Un angle en radians est l'angle au centre d'un cercle sous-tendu par un arc de cercle dont la longueur est égale au rayon du cercle. Eh bien, avez-vous compris ? Sinon, comprenons-le à partir du dessin.

Ainsi, la figure montre un angle égal à un radian, c'est-à-dire que cet angle repose sur un arc de cercle dont la longueur est égale au rayon du cercle (la longueur est égale à la longueur ou le rayon est égal au longueur de l'arc). Ainsi, la longueur de l'arc est calculée par la formule :
Où est l’angle central en radians.
Eh bien, sachant cela, pouvez-vous répondre combien de radians sont contenus dans l’angle décrit par le cercle ? Oui, pour cela, vous devez vous rappeler la formule de la circonférence. Elle est là:
Eh bien, corrélons maintenant ces deux formules et constatons que l’angle décrit par le cercle est égal. Autrement dit, en corrélant la valeur en degrés et en radians, nous obtenons cela. Respectivement, . Comme vous pouvez le constater, contrairement à « degrés », le mot « radian » est omis, car l'unité de mesure ressort généralement clairement du contexte.
Combien y a-t-il de radians ? C'est exact!
J'ai compris? Alors allez-y et corrigez-le :
Vous rencontrez des difficultés ? Alors regarde réponses:
Triangle rectangle : sinus, cosinus, tangente, cotangente d'un angle
Nous avons donc compris le concept d'angle. Mais qu’est-ce que le sinus, le cosinus, la tangente et la cotangente d’un angle ? Voyons cela. Pour ce faire, un triangle rectangle nous aidera.

Comment s’appellent les côtés d’un triangle rectangle ? C'est vrai, l'hypoténuse et les jambes : l'hypoténuse est le côté qui se trouve à l'opposé de l'angle droit (dans notre exemple c'est le côté) ; les jambes sont les deux côtés restants et (ceux adjacents à l'angle droit), et si l'on considère les jambes par rapport à l'angle, alors la jambe est la jambe adjacente et la jambe est l'opposée. Alors maintenant, répondons à la question : que sont le sinus, le cosinus, la tangente et la cotangente d’un angle ?
Sinus d'angle- c'est le rapport de la jambe opposée (éloignée) à l'hypoténuse.
Dans notre triangle.
Cosinus de l'angle- c'est le rapport entre la jambe adjacente (fermée) et l'hypoténuse.
Dans notre triangle.
Tangente de l'angle- c'est le rapport du côté opposé (éloigné) au côté adjacent (proche).
Dans notre triangle.
Cotangente d'angle- c'est le rapport entre la jambe adjacente (proche) et la jambe opposée (éloignée).
Dans notre triangle.
Ces définitions sont nécessaires souviens-toi! Pour qu'il soit plus facile de se rappeler quelle jambe diviser en quoi, vous devez clairement comprendre que dans tangente Et cotangente seules les jambes sont assises et l'hypoténuse n'apparaît que dans sinus Et cosinus. Et puis vous pouvez créer une chaîne d’associations. Par exemple, celui-ci :
Cosinus → toucher → toucher → adjacent ;
Cotangente → toucher → toucher → adjacent.
Tout d'abord, vous devez vous rappeler que le sinus, le cosinus, la tangente et la cotangente, comme les rapports des côtés d'un triangle, ne dépendent pas des longueurs de ces côtés (au même angle). Ne crois pas? Assurez-vous ensuite en regardant la photo :

Prenons par exemple le cosinus d’un angle. Par définition, à partir d'un triangle : , mais on peut calculer le cosinus d'un angle à partir d'un triangle : . Vous voyez, les longueurs des côtés sont différentes, mais la valeur du cosinus d'un angle est la même. Ainsi, les valeurs du sinus, du cosinus, de la tangente et de la cotangente dépendent uniquement de la grandeur de l'angle.
Si vous comprenez les définitions, alors allez-y et consolidez-les !
Pour le triangle représenté dans la figure ci-dessous, nous trouvons.

Eh bien, tu l'as eu ? Alors essayez-le vous-même : calculez la même chose pour l’angle.
Cercle unitaire (trigonométrique)
Comprenant les notions de degré et de radian, nous avons considéré un cercle de rayon égal à. Un tel cercle s'appelle célibataire. Ce sera très utile lors de l’étude de la trigonométrie. Par conséquent, regardons-le un peu plus en détail.

Comme vous pouvez le voir, ce cercle est construit dans le système de coordonnées cartésiennes. Le rayon du cercle est égal à un, tandis que le centre du cercle se trouve à l'origine des coordonnées, la position initiale du vecteur rayon est fixée le long de la direction positive de l'axe (dans notre exemple, il s'agit du rayon).
Chaque point du cercle correspond à deux nombres : la coordonnée de l'axe et la coordonnée de l'axe. Quels sont ces numéros de coordonnées ? Et de manière générale, qu’ont-ils à voir avec le sujet abordé ? Pour ce faire, nous devons nous souvenir du triangle rectangle considéré. Dans la figure ci-dessus, vous pouvez voir deux triangles rectangles entiers. Considérons un triangle. Il est rectangulaire car perpendiculaire à l’axe.
A quoi est égal le triangle ? C'est exact. De plus, nous savons qu’il s’agit du rayon du cercle unité, ce qui signifie . Remplaçons cette valeur dans notre formule du cosinus. Voici ce qui se passe :
A quoi est égal le triangle ? Oui bien sur, ! Remplacez la valeur du rayon dans cette formule et obtenez :
Alors, pouvez-vous dire quelles sont les coordonnées d’un point appartenant à un cercle ? Eh bien, pas question ? Et si vous vous rendiez compte de cela et que vous n’étiez que des chiffres ? A quelle coordonnée correspond-il ? Et bien sûr, les coordonnées ! Et à quelle coordonnée correspond-elle ? C'est vrai, les coordonnées ! Donc point final.

À quoi valent donc et sont égaux ? C'est vrai, utilisons les définitions correspondantes de tangente et de cotangente et obtenons cela, a.
Et si l'angle est plus grand ? Par exemple, comme sur cette photo :

Qu'est-ce qui a changé dans cet exemple ? Voyons cela. Pour ce faire, revenons à un triangle rectangle. Considérons un triangle rectangle : angle (comme adjacent à un angle). Quelles sont les valeurs du sinus, du cosinus, de la tangente et de la cotangente pour un angle ? C'est vrai, nous adhérons aux définitions correspondantes des fonctions trigonométriques :
Eh bien, comme vous pouvez le constater, la valeur du sinus de l'angle correspond toujours à la coordonnée ; la valeur du cosinus de l'angle - la coordonnée ; et les valeurs de tangente et de cotangente aux rapports correspondants. Ainsi, ces relations s’appliquent à toute rotation du rayon vecteur.
Il a déjà été mentionné que la position initiale du rayon vecteur se situe dans la direction positive de l’axe. Jusqu’à présent, nous avons fait pivoter ce vecteur dans le sens inverse des aiguilles d’une montre, mais que se passe-t-il si nous le faisons pivoter dans le sens des aiguilles d’une montre ? Rien d'extraordinaire, vous obtiendrez aussi un angle d'une certaine valeur, mais seulement il sera négatif. Ainsi, en faisant tourner le rayon vecteur dans le sens inverse des aiguilles d'une montre, nous obtenons angles positifs, et en tournant dans le sens des aiguilles d'une montre - négatif.
Ainsi, nous savons qu’une révolution entière du rayon vecteur autour d’un cercle est ou. Est-il possible de faire pivoter le rayon vecteur vers ou vers ? Bien sûr que tu peux! Dans le premier cas, le rayon vecteur fera donc un tour complet et s'arrêtera en position ou.
Dans le deuxième cas, c'est-à-dire que le rayon vecteur fera trois tours complets et s'arrêtera en position ou.
Ainsi, à partir des exemples ci-dessus, nous pouvons conclure que les angles qui diffèrent par ou (où est un nombre entier) correspondent à la même position du rayon vecteur.
La figure ci-dessous montre un angle. La même image correspond au coin, etc. Cette liste peut être poursuivie indéfiniment. Tous ces angles peuvent être écrits par la formule générale ou (où est un nombre entier)

Maintenant, connaissant les définitions des fonctions trigonométriques de base et en utilisant le cercle unité, essayez de répondre quelles sont les valeurs :
Voici un cercle unitaire pour vous aider :

Vous rencontrez des difficultés ? Alors découvrons-le. Nous savons donc que :
A partir de là, on détermine les coordonnées des points correspondant à certaines mesures d'angle. Bon, commençons dans l'ordre : l'angle à correspond à un point avec des coordonnées, donc :
N'existe pas;
De plus, en adhérant à la même logique, nous découvrons que les coins correspondent respectivement à des points avec des coordonnées. Sachant cela, il est facile de déterminer les valeurs des fonctions trigonométriques aux points correspondants. Essayez-le vous-même d'abord, puis vérifiez les réponses.
Réponses:
N'existe pas
N'existe pas
N'existe pas
N'existe pas
Ainsi, nous pouvons faire le tableau suivant :

Il n’est pas nécessaire de mémoriser toutes ces valeurs. Il suffit de rappeler la correspondance entre les coordonnées des points sur le cercle unité et les valeurs des fonctions trigonométriques :
Mais les valeurs des fonctions trigonométriques des angles dans et, données dans le tableau ci-dessous, il faut se souvenir:

N'ayez pas peur, nous allons maintenant vous montrer un exemple assez simple pour retenir les valeurs correspondantes:
Pour utiliser cette méthode, il est essentiel de mémoriser les valeurs du sinus pour les trois mesures d'angle (), ainsi que la valeur de la tangente de l'angle. Connaissant ces valeurs, il est assez simple de restituer l'intégralité du tableau - les valeurs du cosinus sont transférées conformément aux flèches, soit :
Sachant cela, vous pouvez restaurer les valeurs de. Le numérateur " " correspondra et le dénominateur " " correspondra. Les valeurs cotangentes sont transférées conformément aux flèches indiquées sur la figure. Si vous comprenez cela et que vous vous souvenez du diagramme avec les flèches, il suffira alors de mémoriser toutes les valeurs du tableau.
Coordonnées d'un point sur un cercle
Est-il possible de trouver un point (ses coordonnées) sur un cercle, connaître les coordonnées du centre du cercle, son rayon et son angle de rotation?
Bien sûr que tu peux! Sortons-le formule générale pour trouver les coordonnées d'un point.
Par exemple, voici un cercle devant nous :

On nous dit que le point est le centre du cercle. Le rayon du cercle est égal. Il faut trouver les coordonnées d'un point obtenues en faisant pivoter le point de degrés.
Comme le montre la figure, la coordonnée du point correspond à la longueur du segment. La longueur du segment correspond à la coordonnée du centre du cercle, c'est-à-dire qu'elle est égale. La longueur d'un segment peut être exprimée en utilisant la définition du cosinus :
Ensuite, nous avons cela pour la coordonnée du point.
En utilisant la même logique, nous trouvons la valeur de coordonnée y du point. Ainsi,
Ainsi, en général, les coordonnées des points sont déterminées par les formules :
Coordonnées du centre du cercle,
Rayon du cercle,
L'angle de rotation du rayon vectoriel.
Comme vous pouvez le constater, pour le cercle unité que nous considérons, ces formules sont considérablement réduites, puisque les coordonnées du centre sont égales à zéro et le rayon est égal à un :
Eh bien, essayons ces formules en nous entraînant à trouver des points sur un cercle ?
1. Trouvez les coordonnées d'un point sur le cercle unité obtenu en faisant pivoter le point.
2. Trouvez les coordonnées d'un point sur le cercle unité obtenu en faisant pivoter le point.
3. Trouvez les coordonnées d'un point sur le cercle unité obtenu en faisant pivoter le point.
4. Le point est le centre du cercle. Le rayon du cercle est égal. Il faut retrouver les coordonnées du point obtenu en faisant tourner le rayon vecteur initial de.
5. Le point est le centre du cercle. Le rayon du cercle est égal. Il faut retrouver les coordonnées du point obtenu en faisant tourner le rayon vecteur initial de.
Vous avez du mal à trouver les coordonnées d'un point sur un cercle ?
Résolvez ces cinq exemples (ou apprenez à les résoudre) et vous apprendrez à les trouver !
1.
Vous pouvez le remarquer. Mais on sait ce qui correspond à une révolution complète du point de départ. Ainsi, le point souhaité sera dans la même position que lors du virage. Sachant cela, on trouve les coordonnées recherchées du point :
2. Le cercle unité est centré en un point, ce qui signifie que nous pouvons utiliser des formules simplifiées :
Vous pouvez le remarquer. On sait ce qui correspond à deux tours complets du point de départ. Ainsi, le point souhaité sera dans la même position que lors du virage. Sachant cela, on trouve les coordonnées recherchées du point :
Le sinus et le cosinus sont des valeurs de tableau. Nous rappelons leurs significations et obtenons :
Ainsi, le point souhaité possède des coordonnées.
3. Le cercle unité est centré en un point, ce qui signifie que nous pouvons utiliser des formules simplifiées :
Vous pouvez le remarquer. Représentons l'exemple en question dans la figure :

Le rayon fait des angles égaux à et avec l'axe. Sachant que les valeurs du tableau du cosinus et du sinus sont égales, et ayant déterminé que le cosinus prend ici une valeur négative et que le sinus prend une valeur positive, nous avons :
De tels exemples sont discutés plus en détail lors de l'étude des formules de réduction des fonctions trigonométriques dans le sujet.
Ainsi, le point souhaité possède des coordonnées.
4.
Angle de rotation du rayon du vecteur (par condition)
Pour déterminer les signes correspondants du sinus et du cosinus, nous construisons un cercle et un angle unitaires :

Comme vous pouvez le voir, la valeur est positive et la valeur est négative. Connaissant les valeurs tabulaires des fonctions trigonométriques correspondantes, on obtient que :
Remplaçons les valeurs obtenues dans notre formule et trouvons les coordonnées :
Ainsi, le point souhaité possède des coordonnées.
5. Pour résoudre ce problème, nous utilisons des formules sous forme générale, où
Coordonnées du centre du cercle (dans notre exemple,
Rayon du cercle (par condition)
Angle de rotation du rayon du vecteur (par condition).
Remplaçons toutes les valeurs dans la formule et obtenons :
et - les valeurs du tableau. Rappelons-les et substituons-les dans la formule :
Ainsi, le point souhaité possède des coordonnées.
RÉSUMÉ ET FORMULES DE BASE
Le sinus d'un angle est le rapport entre la jambe opposée (lointaine) et l'hypoténuse.
Le cosinus d'un angle est le rapport entre la jambe adjacente (fermée) et l'hypoténuse.
La tangente d'un angle est le rapport entre le côté opposé (éloigné) et le côté adjacent (proche).
La cotangente d'un angle est le rapport entre le côté adjacent (proche) et le côté opposé (éloigné).
Cet article contient tables de sinus, cosinus, tangentes et cotangentes. Tout d'abord, nous fournirons un tableau des valeurs de base des fonctions trigonométriques, c'est-à-dire un tableau des sinus, cosinus, tangentes et cotangentes des angles de 0, 30, 45, 60, 90, ..., 360 degrés ( 0, π/6, π/4, π/3, π/2, …, 2π radian). Après cela, nous donnerons un tableau des sinus et des cosinus, ainsi qu'un tableau des tangentes et cotangentes de V. M. Bradis, et montrerons comment utiliser ces tableaux pour trouver les valeurs des fonctions trigonométriques.
Navigation dans les pages.
Tableau des sinus, cosinus, tangentes et cotangentes pour des angles de 0, 30, 45, 60, 90, ... degrés
Bibliographie.
- Algèbre: Cahier de texte pour la 9ème année. moy. école/Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova ; Éd. S. A. Telyakovsky - M. : Éducation, 1990. - 272 pp. : ill. - ISBN 5-09-002727-7.
- Bashmakov M.I. Algèbre et débuts de l'analyse : Manuel. pour les classes 10-11. moy. école - 3e éd. - M. : Éducation, 1993. - 351 p. : ill. - ISBN5-09-004617-4.
- Algèbre et le début de l'analyse : Proc. pour les classes 10-11. enseignement général institutions / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn et autres ; Éd. A. N. Kolmogorov - 14e éd. - M. : Éducation, 2004. - 384 pp. : ill.
- Gusev V.A., Mordkovitch A.G. Mathématiques (un manuel pour ceux qui entrent dans les écoles techniques) : Proc. allocation.- M.; Plus haut école, 1984.-351 p., ill.
- Bradis V. M. Tableaux mathématiques à quatre chiffres : Pour l'enseignement général. cahier de texte établissements. - 2e éd. - M. : Outarde, 1999.- 96 p. : ill. ISBN5-7107-2667-2
Dans l'article, nous comprendrons parfaitement à quoi cela ressemble tableau des valeurs trigonométriques, sinus, cosinus, tangente et cotangente. Considérons la signification fondamentale des fonctions trigonométriques, sous un angle de 0,30,45,60,90,...,360 degrés. Et voyons comment utiliser ces tableaux pour calculer les valeurs des fonctions trigonométriques.
Regardons d'abord table de cosinus, sinus, tangente et cotangente sous un angle de 0, 30, 45, 60, 90,... degrés. La définition de ces grandeurs permet de déterminer la valeur des fonctions des angles de 0 et 90 degrés :
sin 0 0 =0, cos 0 0 = 1. tg 00 = 0, la cotangente de 00 sera indéfinie
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0, la tangente à partir de 90 0 sera incertaine
Si vous prenez des triangles rectangles dont les angles vont de 30 à 90 degrés. On a:
sin 30 0 = 1/2, cos 30 0 = √3/2, tan 30 0 = √3/3, cos 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tan 45 0 = 1, cos 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3, lit bébé 60 0 = √3/3
Représentons toutes les valeurs obtenues sous la forme table trigonométrique:
Tableau des sinus, cosinus, tangentes et cotangentes !
Si nous utilisons la formule de réduction, notre tableau augmentera en ajoutant des valeurs pour des angles jusqu'à 360 degrés. Cela ressemblera à :

De plus, en fonction des propriétés de périodicité, le tableau peut être augmenté si nous remplaçons les angles par 0 0 +360 0 *z .... 330 0 +360 0 *z, dans lequel z est un nombre entier. Dans ce tableau, il est possible de calculer la valeur de tous les angles correspondant aux points d'un même cercle.

Voyons comment utiliser le tableau dans une solution.
Tout est très simple. Puisque la valeur dont nous avons besoin se situe au point d’intersection des cellules dont nous avons besoin. Par exemple, prenons le cosinus d'un angle de 60 degrés, dans le tableau cela ressemblera à :

Dans le tableau final des principales valeurs des fonctions trigonométriques, on procède de la même manière. Mais dans ce tableau, il est possible de savoir quelle est la tangente d'un angle de 1020 degrés, elle = -√3 Vérifions 1020 0 = 300 0 +360 0 *2. Trouvons-le à l'aide du tableau.

Table Bradis. Pour sinus, cosinus, tangente et cotangente.
Les tables de Bradis sont divisées en plusieurs parties, constituées de tables de cosinus et de sinus, de tangente et de cotangente - qui sont divisées en deux parties (tg des angles jusqu'à 90 degrés et ctg des petits angles).
Sinus et cosinus


tg d'angle commençant par 00 se terminant par 760, ctg d'angle commençant par 140 se terminant par 900.


tg jusqu'à 900 et ctg des petits angles.
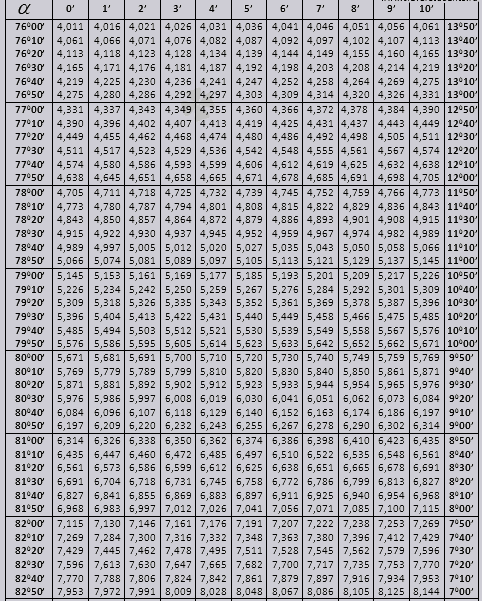

Voyons comment utiliser les tables de Bradis pour résoudre des problèmes.
Trouvons la désignation sin (désignation dans la colonne du bord gauche) 42 minutes (la désignation est sur la ligne du haut). Par intersection on cherche la désignation, elle = 0,3040.
Les valeurs des minutes sont indiquées avec un intervalle de six minutes, que faire si la valeur dont nous avons besoin se situe exactement dans cet intervalle. Prenons 44 minutes, mais il n'y en a que 42 dans le tableau. On prend 42 comme base et on utilise les colonnes supplémentaires du côté droit, on prend le 2ème amendement et on ajoute à 0,3040 + 0,0006 on obtient 0,3046.
Avec sin 47 minutes, on prend 48 minutes comme base et on en soustrait 1 correction, soit 0,3057 - 0,0003 = 0,3054
Lors du calcul du cos, nous travaillons de la même manière que le péché, sauf que nous prenons comme base la ligne du bas du tableau. Par exemple cos 20 0 = 0,9397
Les valeurs de l'angle tg jusqu'à 90 0 et du cot d'un petit angle sont correctes et ne contiennent aucune correction. Par exemple, trouvez tg 78 0 37min = 4,967 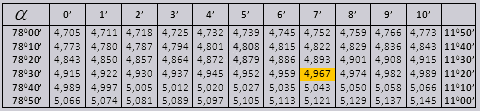
et ctg 20 0 13min = 25,83 
Eh bien, nous avons examiné les tables trigonométriques de base. Nous espérons que ces informations vous ont été extrêmement utiles. Si vous avez des questions sur les tableaux, n'hésitez pas à les écrire dans les commentaires !
Remarque : Les pare-chocs muraux sont des panneaux pare-chocs destinés à protéger les murs. Suivez le lien sur les pare-chocs muraux sans cadre (http://www.spi-polymer.ru/otboyniki/) et découvrez-en plus.
1. Fonctions trigonométriques sont des fonctions élémentaires dont l'argument est coin. Les fonctions trigonométriques décrivent les relations entre les côtés et les angles aigus d'un triangle rectangle. Les domaines d'application des fonctions trigonométriques sont extrêmement divers. Par exemple, tout processus périodique peut être représenté comme une somme de fonctions trigonométriques (série de Fourier). Ces fonctions apparaissent souvent lors de la résolution d'équations différentielles et fonctionnelles.
2. Les fonctions trigonométriques comprennent les 6 fonctions suivantes : sinus, cosinus, tangente,cotangente, sécante Et cosécante. Pour chacune de ces fonctions il existe une fonction trigonométrique inverse.
3. Il est pratique d'introduire la définition géométrique des fonctions trigonométriques en utilisant cercle unitaire. La figure ci-dessous montre un cercle de rayon r=1. Le point M(x,y) est marqué sur le cercle. L'angle entre le rayon vecteur OM et la direction positive de l'axe Ox est égal à α.
4. Sinus l'angle α est le rapport de l'ordonnée y du point M(x,y) au rayon r :
sinα = y/r.
Puisque r=1, alors le sinus est égal à l'ordonnée du point M(x,y).
5. Cosinus l'angle α est le rapport de l'abscisse x du point M(x,y) au rayon r :
cosα=x/r
6. Tangente l'angle α est le rapport de l'ordonnée y d'un point M(x,y) à son abscisse x :
tanα=y/x,x≠0
7. Cotangente l'angle α est le rapport de l'abscisse x d'un point M(x,y) à son ordonnée y :
cotα=x/y,y≠0
8. Sécante l'angle α est le rapport du rayon r à l'abscisse x du point M(x,y) :
secα=r/x=1/x,x≠0
9. Cosécante l'angle α est le rapport du rayon r à l'ordonnée y du point M(x,y) :
cscα=r/y=1/y,y≠0
10. Dans le cercle unité, les projections x, y, les points M(x,y) et le rayon r forment un triangle rectangle, dans lequel x,y sont les jambes et r est l'hypoténuse. Par conséquent, les définitions ci-dessus des fonctions trigonométriques appliquées à un triangle rectangle sont formulées comme suit :
Sinus l'angle α est le rapport du côté opposé à l'hypoténuse.
Cosinus l'angle α est le rapport entre la jambe adjacente et l'hypoténuse.
Tangente L'angle α est appelé la branche opposée à celle adjacente.
Cotangente L'angle α est appelé le côté adjacent au côté opposé.
Sécante l'angle α est le rapport de l'hypoténuse à la jambe adjacente.
Cosécante l'angle α est le rapport de l'hypoténuse à la jambe opposée.
11. Graphique de la fonction sinus
y=sinx, domaine de définition : x∈R, plage de valeurs : −1≤sinx≤1
12. Graphique de la fonction cosinus
y=cosx, domaine : x∈R, plage : −1≤cosx≤1
13. Graphique de la fonction tangente 14. Graphique de la fonction cotangente 15. Graphique de la fonction sécante
y=tanx, domaine : x∈R,x≠(2k+1)π/2, intervalle : −∞ 
y=cotx, domaine : x∈R,x≠kπ, intervalle : −∞ 
y=secx, domaine : x∈R,x≠(2k+1)π/2, plage : secx∈(−∞,−1]∪∪)