Table de réduction trigonométrique. Identité trigonométrique fondamentale
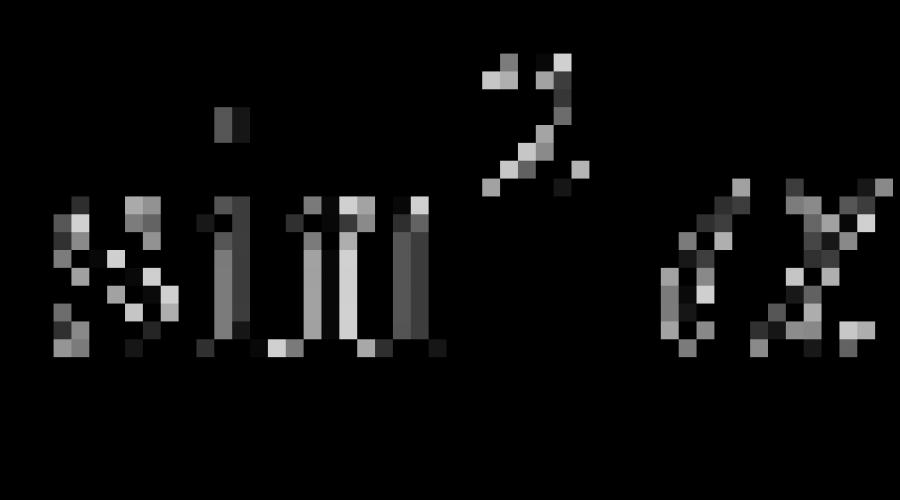
Dans cet article, nous allons jeter un regard complet. Les identités trigonométriques de base sont des égalités qui établissent une connexion entre le sinus, le cosinus, la tangente et la cotangente d'un angle, et permettent de trouver l'une de ces fonctions trigonométriques à travers un autre connu.
Listons immédiatement les principales identités trigonométriques que nous analyserons dans cet article. Écrivons-les dans un tableau, et ci-dessous nous donnerons le résultat de ces formules et fournirons les explications nécessaires.
Navigation dans les pages.
Relation entre le sinus et le cosinus d'un angle
Parfois, ils ne parlent pas des principales identités trigonométriques énumérées dans le tableau ci-dessus, mais d'une seule. identité trigonométrique de base gentil ![]() . L'explication de ce fait est assez simple : les égalités sont obtenues à partir de la formule de base identité trigonométrique après avoir divisé ses deux parties par et respectivement, et l'égalité
. L'explication de ce fait est assez simple : les égalités sont obtenues à partir de la formule de base identité trigonométrique après avoir divisé ses deux parties par et respectivement, et l'égalité  Et
Et ![]() découlent des définitions du sinus, du cosinus, de la tangente et de la cotangente. Nous en parlerons plus en détail dans les paragraphes suivants.
découlent des définitions du sinus, du cosinus, de la tangente et de la cotangente. Nous en parlerons plus en détail dans les paragraphes suivants.
C'est-à-dire que c'est l'égalité qui présente un intérêt particulier, à laquelle on a donné le nom d'identité trigonométrique principale.
Avant de prouver l'identité trigonométrique principale, donnons sa formulation : la somme des carrés du sinus et du cosinus d'un angle est identiquement égale à un. Maintenant, prouvons-le.
L'identité trigonométrique de base est très souvent utilisée lorsque conversion d'expressions trigonométriques. Il permet de remplacer la somme des carrés du sinus et du cosinus d'un angle par un. Non moins souvent, l'identité trigonométrique de base est utilisée dans l'ordre inverse : l'unité est remplacée par la somme des carrés du sinus et du cosinus de n'importe quel angle.
Tangente et cotangente par sinus et cosinus
Identités reliant la tangente et la cotangente au sinus et au cosinus d'un angle de vue et ![]() découlent immédiatement des définitions du sinus, du cosinus, de la tangente et de la cotangente. En effet, par définition, le sinus est l'ordonnée de y, le cosinus est l'abscisse de x, la tangente est le rapport de l'ordonnée à l'abscisse, soit
découlent immédiatement des définitions du sinus, du cosinus, de la tangente et de la cotangente. En effet, par définition, le sinus est l'ordonnée de y, le cosinus est l'abscisse de x, la tangente est le rapport de l'ordonnée à l'abscisse, soit ![]() , et la cotangente est le rapport de l'abscisse à l'ordonnée, c'est-à-dire
, et la cotangente est le rapport de l'abscisse à l'ordonnée, c'est-à-dire ![]() .
.
Grâce à une telle évidence des identités et ![]() La tangente et la cotangente sont souvent définies non pas par le rapport de l'abscisse et de l'ordonnée, mais par le rapport du sinus et du cosinus. Ainsi, la tangente d'un angle est le rapport du sinus au cosinus de cet angle, et la cotangente est le rapport du cosinus au sinus.
La tangente et la cotangente sont souvent définies non pas par le rapport de l'abscisse et de l'ordonnée, mais par le rapport du sinus et du cosinus. Ainsi, la tangente d'un angle est le rapport du sinus au cosinus de cet angle, et la cotangente est le rapport du cosinus au sinus.
En conclusion de ce point, il convient de noter que les identités et ![]() avoir lieu pour tous les angles sous lesquels les fonctions trigonométriques qu'ils contiennent ont un sens. Donc la formule est valable pour tout autre que (sinon le dénominateur aura zéro, et nous n'avons pas défini la division par zéro), et la formule
avoir lieu pour tous les angles sous lesquels les fonctions trigonométriques qu'ils contiennent ont un sens. Donc la formule est valable pour tout autre que (sinon le dénominateur aura zéro, et nous n'avons pas défini la division par zéro), et la formule ![]() - pour tout , différent de , où z est quelconque .
- pour tout , différent de , où z est quelconque .
Relation entre tangente et cotangente
Une identité trigonométrique encore plus évidente que les deux précédentes est l'identité reliant la tangente et la cotangente d'un angle de la forme ![]() . Il est clair que cela est valable pour tout angle autre que , sinon la tangente ou la cotangente ne sont pas définies.
. Il est clair que cela est valable pour tout angle autre que , sinon la tangente ou la cotangente ne sont pas définies.
Preuve de la formule ![]() très simple. Par définition et d'où
très simple. Par définition et d'où  . La preuve aurait pu être réalisée un peu différemment. Depuis
. La preuve aurait pu être réalisée un peu différemment. Depuis ![]() , Que
, Que  .
.
Ainsi, la tangente et la cotangente du même angle sous lequel elles ont un sens sont .
C'est le dernier et le plus leçon principale, nécessaire pour résoudre les problèmes B11. Nous savons déjà comment convertir des angles d'une mesure en radian en mesure en degré (voir la leçon « Mesure en radian et degré d'un angle »), et nous savons également déterminer le signe d'une fonction trigonométrique, en nous concentrant sur les quarts de coordonnées ( voir la leçon « Signes des fonctions trigonométriques »).
Il ne reste plus qu'à calculer la valeur de la fonction elle-même - le nombre même qui est écrit dans la réponse. C’est là que l’identité trigonométrique de base vient à la rescousse.
Identité trigonométrique de base. Pour tout angle α, l’énoncé suivant est vrai :
péché 2 α + cos 2 α = 1.
Cette formule relie le sinus et le cosinus d'un angle. Maintenant, connaissant le sinus, nous pouvons facilement trouver le cosinus - et vice versa. Il suffit de prendre la racine carrée :
Notez le signe "±" devant les racines. Le fait est qu'à partir de l'identité trigonométrique de base, il n'est pas clair ce qu'étaient le sinus et le cosinus d'origine : positifs ou négatifs. Après tout, la quadrature - même fonction, qui « brûle » tous les inconvénients (s'il y en avait).
C'est pourquoi dans tous les problèmes B11, que l'on retrouve dans l'examen d'État unifié de mathématiques, il existe nécessairement des conditions supplémentaires qui aident à éliminer l'incertitude avec les signes. Il s'agit généralement d'une indication du quartier de coordonnées, par lequel le signe peut être déterminé.
Un lecteur attentif demandera probablement : « Qu’en est-il de la tangente et de la cotangente ? Il est impossible de calculer directement ces fonctions à partir des formules ci-dessus. Cependant, il existe conséquences importantes de l'identité trigonométrique de base, qui contient déjà des tangentes et des cotangentes. À savoir:
Un corollaire important : pour tout angle α, l'identité trigonométrique de base peut être réécrite comme suit :
Ces équations se déduisent facilement de l'identité principale - il suffit de diviser les deux côtés par cos 2 α (pour obtenir la tangente) ou par sin 2 α (pour obtenir la cotangente).
Regardons tout cela à exemples spécifiques. Vous trouverez ci-dessous les vrais problèmes du B11, tirés des problèmes fictifs. Options d'examen d'État unifié en mathématiques 2012.
Nous connaissons le cosinus, mais nous ne connaissons pas le sinus. L'identité trigonométrique principale (sous sa forme « pure ») relie uniquement ces fonctions, nous allons donc travailler avec elle. Nous avons:
sin 2 α + cos 2 α = 1 ⇒ sin 2 α + 99/100 = 1 ⇒ sin 2 α = 1/100 ⇒ sin α = ±1/10 = ±0,1.
Pour résoudre le problème, il reste à trouver le signe du sinus. Puisque l'angle α ∈ (π /2; π ), alors en degré il s'écrit comme suit : α ∈ (90°; 180°).
Par conséquent, l'angle α se situe dans le deuxième quart de coordonnées - tous les sinus y sont positifs. Donc sin α = 0,1.
Donc, nous connaissons le sinus, mais nous devons trouver le cosinus. Ces deux fonctions appartiennent à l’identité trigonométrique de base. Remplaçons :
sin 2 α + cos 2 α = 1 ⇒ 3/4 + cos 2 α = 1 ⇒ cos 2 α = 1/4 ⇒ cos α = ±1/2 = ±0,5.
Reste à traiter le signe devant la fraction. Que choisir : plus ou moins ? Par condition, l'angle α appartient à l'intervalle (π 3π /2). Convertissons les angles des mesures en radians en degrés - nous obtenons : α ∈ (180° ; 270°).
Évidemment, il s’agit du quartier de coordonnées III, où tous les cosinus sont négatifs. Donc cos α = −0,5.
Tâche. Trouvez tan α si les éléments suivants sont connus :
La tangente et le cosinus sont liés par l'équation découlant de l'identité trigonométrique de base :
On obtient : tan α = ±3. Le signe de la tangente est déterminé par l'angle α. On sait que α ∈ (3π /2; 2π ). Convertissons les angles des mesures en radians en degrés - nous obtenons α ∈ (270° ; 360°).
Évidemment, il s’agit du quartier de coordonnées IV, où toutes les tangentes sont négatives. Donc tan α = −3.
Tâche. Trouvez cos α si les éléments suivants sont connus :
Encore une fois, le sinus est connu et le cosinus est inconnu. Écrivons la principale identité trigonométrique :
sin 2 α + cos 2 α = 1 ⇒ 0,64 + cos 2 α = 1 ⇒ cos 2 α = 0,36 ⇒ cos α = ±0,6.
Le signe est déterminé par l'angle. On a : α ∈ (3π /2 ; 2π ). Convertissons les angles de degrés en radians : α ∈ (270° ; 360°) est le quart de coordonnée IV, les cosinus y sont positifs. Donc cos α = 0,6.
Tâche. Trouvez sin α si les éléments suivants sont connus :
Écrivons une formule qui découle de l'identité trigonométrique de base et relie directement sinus et cotangente :
De là, nous obtenons que sin 2 α = 1/25, c'est-à-dire péché α = ±1/5 = ±0,2. On sait que l'angle α ∈ (0; π /2). En degré, cela s'écrit comme suit : α ∈ (0°; 90°) - Je coordonne le quart.
Ainsi, l'angle est dans le quadrant des coordonnées I - toutes les fonctions trigonométriques y sont positives, donc sin α = 0,2.
Définition. Les formules de réduction sont des formules qui permettent de passer des fonctions trigonométriques de la forme aux fonctions d'argument. Avec leur aide, le sinus, le cosinus, la tangente et la cotangente d'un angle arbitraire peuvent être réduits au sinus, au cosinus, à la tangente et à la cotangente d'un angle compris dans l'intervalle de 0 à 90 degrés (de 0 à radians). Ainsi, les formules de réduction permettent de passer au travail avec des angles inférieurs à 90 degrés, ce qui est sans doute très pratique.
Formules de réduction :

Il existe deux règles d'utilisation des formules de réduction.
1. Si l'angle peut être représenté par (π/2 ±a) ou (3*π/2 ±a), alors changement de nom de fonction péché en cos, cos en péché, tg en ctg, ctg en tg. Si l'angle peut être représenté sous la forme (π ±a) ou (2*π ±a), alors Le nom de la fonction reste inchangé.
Regardez l'image ci-dessous, elle montre schématiquement quand changer le signe et quand ne pas le faire

2. Signe de la fonction réduite reste le même. Si la fonction d'origine avait un signe plus, alors la fonction réduite a également un signe plus. Si la fonction originale avait un signe moins, alors la fonction réduite a également un signe moins.
La figure ci-dessous montre les signes des fonctions trigonométriques de base en fonction du quartier.

Exemple:
Calculer
Utilisons les formules de réduction :
Sin(150˚) est dans le deuxième quartier ; d'après la figure, nous voyons que le signe sin dans ce quartier est égal à « + ». Cela signifie que la fonction donnée aura également un signe « + ». Nous avons appliqué la deuxième règle.
Maintenant 150˚ = 90˚ +60˚. 90˚ est π/2. Autrement dit, nous avons affaire au cas π/2+60, donc, selon la première règle, nous changeons la fonction de sin en cos. En conséquence, nous obtenons Sin(150˚) = cos(60˚) = ½.
Les formules de réduction sont des relations qui permettent de passer du sinus, du cosinus, de la tangente et de la cotangente avec les angles `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi) 2 \pm \alpha`, `2\pi \pm \alpha` aux mêmes fonctions de l'angle `\alpha`, qui est situé dans le premier quart du cercle unité. Ainsi, les formules de réduction nous « amènent » à travailler avec des angles compris entre 0 et 90 degrés, ce qui est très pratique.
Au total, il existe 32 formules de réduction. Ils seront sans aucun doute utiles lors de l'examen d'État unifié, des examens et des tests. Mais prévenons-nous tout de suite : inutile de les mémoriser ! Vous devez passer un peu de temps et comprendre l'algorithme de leur application, alors il ne vous sera pas difficile de bon moment en tirer l’égalité nécessaire.
Tout d'abord, notons toutes les formules de réduction :
Pour l'angle (`\frac (\pi)2 \pm \alpha`) ou (`90^\circ \pm \alpha`) :
`sin(\frac (\pi)2 - \alpha)=cos \ \alpha;` ` sin(\frac (\pi)2 + \alpha)=cos \ \alpha`
`cos(\frac (\pi)2 - \alpha)=sin \ \alpha;` ` cos(\frac (\pi)2 + \alpha)=-sin \ \alpha`
`tg(\frac (\pi)2 — \alpha)=ctg \ \alpha;` ` tg(\frac (\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (\pi)2 — \alpha)=tg \ \alpha;` ` ctg(\frac (\pi)2 + \alpha)=-tg \ \alpha`
Pour l'angle (`\pi \pm \alpha`) ou (`180^\circ \pm \alpha`) :
`sin(\pi - \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi - \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi - \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi - \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
Pour l'angle (`\frac (3\pi)2 \pm \alpha`) ou (`270^\circ \pm \alpha`) :
`sin(\frac (3\pi)2 — \alpha)=-cos \ \alpha;` ` sin(\frac (3\pi)2 + \alpha)=-cos \ \alpha`
`cos(\frac (3\pi)2 — \alpha)=-sin \ \alpha;` ` cos(\frac (3\pi)2 + \alpha)=sin \ \alpha`
`tg(\frac (3\pi)2 — \alpha)=ctg \ \alpha;` ` tg(\frac (3\pi)2 + \alpha)=-ctg \ \alpha`
`ctg(\frac (3\pi)2 — \alpha)=tg \ \alpha;` ` ctg(\frac (3\pi)2 + \alpha)=-tg \ \alpha`
Pour l'angle (`2\pi \pm \alpha`) ou (`360^\circ \pm \alpha`) :
`sin(2\pi - \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi - \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi - \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi - \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
On trouve souvent des formules de réduction sous forme de tableau où les angles sont écrits en radians :
Pour l'utiliser, nous devons sélectionner la ligne avec la fonction dont nous avons besoin et la colonne avec l'argument souhaité. Par exemple, pour savoir à l'aide d'un tableau à quoi sera égal ` sin(\pi + \alpha)`, il suffit de trouver la réponse à l'intersection de la ligne ` sin \beta` et de la colonne ` \pi + \alpha`. Nous obtenons ` sin(\pi + \alpha)=-sin \ \alpha`.
Et le deuxième tableau similaire, où les angles sont écrits en degrés :

Règle mnémonique des formules de réduction ou comment les mémoriser
Comme nous l’avons déjà mentionné, il n’est pas nécessaire de mémoriser toutes les relations ci-dessus. Si vous les avez regardés attentivement, vous avez probablement remarqué certaines tendances. Ils nous permettent de formuler une règle mnémonique (mnémonique - rappelez-vous), à l'aide de laquelle nous pouvons facilement obtenir n'importe quelle formule de réduction.
Notons tout de suite que pour appliquer cette règle, il faut savoir identifier (ou mémoriser) les signes des fonctions trigonométriques dans les différents quarts du cercle unité.  Le vaccin lui-même contient 3 étapes :
Le vaccin lui-même contient 3 étapes :
- L'argument de la fonction doit être représenté par `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi)2 \pm \alpha`, `2\pi \ pm \alpha`, et `\alpha` est requis angle vif(de 0 à 90 degrés).
- Pour les arguments `\frac (\pi)2 \pm \alpha`, `\frac (3\pi)2 \pm \alpha` fonction trigonométrique l'expression convertie se transforme en cofonction, c'est-à-dire l'opposé (sinus en cosinus, tangente à cotangente et vice versa). Pour les arguments `\pi \pm \alpha`, `2\pi \pm \alpha` la fonction ne change pas.
- Le signe de la fonction d'origine est déterminé. La fonction résultante sur le côté droit aura le même signe.
Pour voir comment cette règle peut être appliquée en pratique, transformons plusieurs expressions :
1. `cos(\pi + \alpha)`.
La fonction n'est pas inversée. L'angle `\pi + \alpha` est dans le troisième quart, le cosinus dans ce quart a un signe « - », donc la fonction transformée aura également un signe « - ».
Réponse : ` cos(\pi + \alpha)= - cos \alpha`
2. `sin(\frac (3\pi)2 - \alpha)`.
Selon la règle mnémonique, la fonction sera inversée. L'angle `\frac (3\pi)2 - \alpha` est dans le troisième quart, le sinus a ici un signe « - », donc le résultat aura également un signe « - ».
Réponse : `sin(\frac (3\pi)2 - \alpha)= - cos \alpha`
3. `cos(\frac (7\pi)2 - \alpha)`.
`cos(\frac (7\pi)2 - \alpha)=cos(\frac (6\pi)2+\frac (\pi)2-\alpha)=cos (3\pi+(\frac(\pi )2-\alpha))`. Représentons `3\pi` par `2\pi+\pi`. `2\pi` est la période de la fonction.
Important : Les fonctions `cos \alpha` et `sin \alpha` ont une période de `2\pi` ou `360^\circ`, leurs valeurs ne changeront pas si l'argument est augmenté ou diminué de ces valeurs.
Sur cette base, notre expression peut s'écrire comme suit : `cos (\pi+(\frac(\pi)2-\alpha)`. En appliquant deux fois la règle mnémonique, nous obtenons : `cos (\pi+(\frac(\ pi) 2-\alpha)= - cos (\frac(\pi)2-\alpha)= - sin \alpha`.
Réponse : `cos(\frac (7\pi)2 - \alpha)=- sin \alpha`.
Règle du cheval
Le deuxième point de la règle mnémotechnique décrite ci-dessus est également appelé règle du cheval des formules de réduction. Je me demande pourquoi les chevaux ?
Nous avons donc des fonctions avec les arguments `\frac (\pi)2 \pm \alpha`, `\pi \pm \alpha`, `\frac (3\pi)2 \pm \alpha`, `2\pi \ pm \alpha`, les points `\frac (\pi)2`, `\pi`, `\frac (3\pi)2`, `2\pi` sont clés, ils sont situés sur les axes de coordonnées. `\pi` et `2\pi` sont sur l'axe des x horizontal, et `\frac (\pi)2` et `\frac (3\pi)2` sont sur axe vertical ordonnée
On se pose la question : « Une fonction se transforme-t-elle en cofonction ? Pour répondre à cette question, vous devez déplacer votre tête le long de l'axe sur lequel se trouve le point clé.
C'est-à-dire que pour les arguments dont les points clés sont situés sur l'axe horizontal, nous répondons « non » en secouant la tête sur les côtés. Et pour les virages avec des points clés situés sur l'axe vertical, on répond « oui » en hochant la tête de haut en bas, comme un cheval :)
Nous vous recommandons de regarder un didacticiel vidéo dans lequel l'auteur explique en détail comment mémoriser les formules de réduction sans les mémoriser.
Exemples pratiques d'utilisation de formules de réduction
L'utilisation des formules de réduction commence en 9e et 10e années. De nombreux problèmes d'utilisation ont été soumis à l'examen d'État unifié. Voici quelques-uns des problèmes auxquels vous devrez appliquer ces formules :
- problèmes pour résoudre un triangle rectangle ;
- transformation d'expressions trigonométriques numériques et alphabétiques, calcul de leurs valeurs ;
- tâches stéréométriques.
Exemple 1. Calculer à l'aide des formules de réduction a) `sin 600^\circ`, b) `tg 480^\circ`, c) `cos 330^\circ`, d) `sin 240^\circ`.
Solution : a) `sin 600^\circ=sin (2 \cdot 270^\circ+60^\circ)=-cos 60^\circ=-\frac 1 2` ;
b) `tg 480^\circ=tg (2 \cdot 270^\circ-60^\circ)=ctg 60^\circ=\frac(\sqrt 3)3` ;
c) `cos 330^\circ=cos (360^\circ-30^\circ)=cos 30^\circ=\frac(\sqrt 3)2` ;
d) `sin 240^\circ=sin (270^\circ-30^\circ)=-cos 30^\circ=-\frac(\sqrt 3)2`.
Exemple 2. Après avoir exprimé le cosinus par le sinus à l'aide de formules de réduction, comparez les nombres : 1) `sin \frac (9\pi)8` et `cos \frac (9\pi)8` ; 2) `sin \frac (\pi)8` et `cos \frac (3\pi)10`.
Solution : 1)`sin \frac (9\pi)8=sin (\pi+\frac (\pi)8)=-sin \frac (\pi)8`
`cos \frac (9\pi)8=cos (\pi+\frac (\pi)8)=-cos \frac (\pi)8=-sin \frac (3\pi)8`
`-sin \frac (\pi)8> -sin \frac (3\pi)8`
`sin \frac (9\pi)8>cos \frac (9\pi)8`.
2) `cos \frac (3\pi)10=cos (\frac (\pi)2-\frac (\pi)5)=sin \frac (\pi)5`
`sin \frac (\pi)8 `sin \frac (\pi)8 Démontrons d'abord deux formules pour le sinus et le cosinus de l'argument `\frac (\pi)2 + \alpha` : ` sin(\frac (\pi)2 + \alpha)=cos \ \alpha` et ` cos (\frac (\ pi)2 + \alpha)=-sin \ \alpha`. Le reste en dérive. Prenons un cercle unité et pointons A dessus avec les coordonnées (1,0). Laissons après s'être tourné vers En venant de la définition de la tangente et de la cotangente, on obtient ` tan(\frac (\pi)2 + \alpha)=\frac (sin(\frac (\pi)2 + \alpha))(cos(\frac (\ pi)2 + \alpha))=\frac (cos \alpha)(-sin \alpha)=-ctg \alpha` et ` сtg(\frac (\pi)2 + \alpha)=\frac (cos(\ frac (\ pi)2 + \alpha))(sin(\frac (\pi)2 + \alpha))=\frac (-sin \alpha)(cos \alpha)=-tg \alpha`, ce qui prouve le formules de réduction pour la tangente et la cotangente de l'angle `\frac (\pi)2 + \alpha`. Pour prouver des formules avec l'argument `\frac (\pi)2 - \alpha`, il suffit de le représenter comme `\frac (\pi)2 + (-\alpha)` et de suivre le même chemin que ci-dessus. Par exemple, `cos(\frac (\pi)2 - \alpha)=cos(\frac (\pi)2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`. Les angles `\pi + \alpha` et `\pi - \alpha` peuvent être représentés par `\frac (\pi)2 +(\frac (\pi)2+\alpha)` et `\frac (\pi ) 2 +(\frac (\pi)2-\alpha)` respectivement. Et `\frac (3\pi)2 + \alpha` et `\frac (3\pi)2 - \alpha` comme `\pi +(\frac (\pi)2+\alpha)` et `\pi +(\frac (\pi)2-\alpha)`. angle `\alpha` il ira au point `A_1(x, y)`, et après avoir tourné d'angle `\frac (\pi)2 + \alpha` au point `A_2(-y, x)`. En faisant tomber les perpendiculaires de ces points sur la droite OX, nous voyons que les triangles `OA_1H_1` et `OA_2H_2` sont égaux, puisque leurs hypoténuses et angles adjacents sont égaux. Ensuite, sur la base des définitions du sinus et du cosinus, nous pouvons écrire `sin\alpha=y`, `cos\alpha=x`, `sin(\frac (\pi)2 + \alpha)=x`, `cos (\frac (\ pi)2 + \alpha)=-y`. Où peut-on écrire que ` sin(\frac (\pi)2 + \alpha)=cos \alpha` et ` cos(\frac (\pi)2 + \alpha)=-sin \alpha`, ce qui prouve la réduction formules pour les angles sinus et cosinus `\frac (\pi)2 + \alpha`.
angle `\alpha` il ira au point `A_1(x, y)`, et après avoir tourné d'angle `\frac (\pi)2 + \alpha` au point `A_2(-y, x)`. En faisant tomber les perpendiculaires de ces points sur la droite OX, nous voyons que les triangles `OA_1H_1` et `OA_2H_2` sont égaux, puisque leurs hypoténuses et angles adjacents sont égaux. Ensuite, sur la base des définitions du sinus et du cosinus, nous pouvons écrire `sin\alpha=y`, `cos\alpha=x`, `sin(\frac (\pi)2 + \alpha)=x`, `cos (\frac (\ pi)2 + \alpha)=-y`. Où peut-on écrire que ` sin(\frac (\pi)2 + \alpha)=cos \alpha` et ` cos(\frac (\pi)2 + \alpha)=-sin \alpha`, ce qui prouve la réduction formules pour les angles sinus et cosinus `\frac (\pi)2 + \alpha`.