Sinus, cosinus, tangente et cotangente : définitions en trigonométrie, exemples, formules. Sinus, cosinus, tangente, cotangente d'un angle aigu. Fonctions trigonométriques
La trigonométrie est une branche de la science mathématique qui étudie les fonctions trigonométriques et leur utilisation en géométrie. Le développement de la trigonométrie a commencé à l'époque la Grèce ancienne. Au Moyen Âge, les scientifiques du Moyen-Orient et de l’Inde ont apporté d’importantes contributions au développement de cette science.
Cet article est dédié à concepts de base et définitions de la trigonométrie. Il discute des définitions des fonctions trigonométriques de base : sinus, cosinus, tangente et cotangente. Leur signification est expliquée et illustrée dans le contexte de la géométrie.
Yandex.RTB R-A-339285-1
Initialement, les définitions des fonctions trigonométriques dont l'argument est un angle étaient exprimées en termes de rapport des côtés d'un triangle rectangle.
Définitions des fonctions trigonométriques
Le sinus d'un angle (sin α) est le rapport de la jambe opposée à cet angle à l'hypoténuse.
Cosinus de l'angle (cos α) - le rapport de la jambe adjacente à l'hypoténuse.
Angle tangent (t g α) - le rapport du côté opposé au côté adjacent.
Angle cotangent (c t g α) - le rapport du côté adjacent au côté opposé.
Ces définitions sont données pour angle aigu triangle rectangle!
Donnons une illustration.
Dans le triangle ABC d'angle droit C, le sinus de l'angle A est égal au rapport jambe BC à l’hypoténuse AB.
Les définitions du sinus, du cosinus, de la tangente et de la cotangente permettent de calculer les valeurs de ces fonctions à partir des longueurs connues des côtés du triangle.
Important à retenir !
La plage de valeurs du sinus et du cosinus est de -1 à 1. En d'autres termes, le sinus et le cosinus prennent des valeurs de -1 à 1. La plage de valeurs de la tangente et de la cotangente est la droite numérique entière, c'est-à-dire que ces fonctions peuvent prendre n'importe quelle valeur.
Les définitions données ci-dessus s'appliquent aux angles aigus. En trigonométrie, on introduit la notion d'angle de rotation dont la valeur, contrairement à un angle aigu, n'est pas limitée à 0 à 90 degrés. L'angle de rotation en degrés ou en radians est exprimé par tout nombre réel compris entre - ∞ et + ∞. .
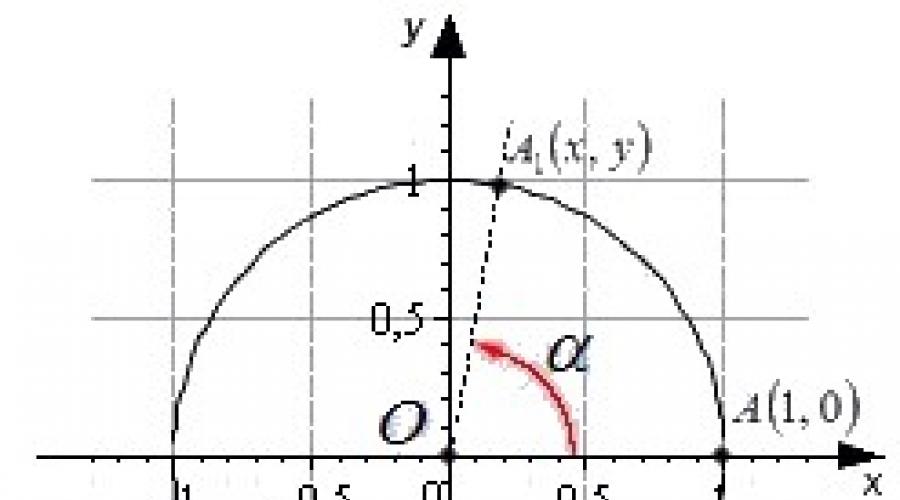
Dans ce contexte, on peut définir le sinus, le cosinus, la tangente et la cotangente d'un angle de grandeur arbitraire. Imaginons un cercle unité dont le centre est à l'origine du repère cartésien.

Le point initial A de coordonnées (1, 0) tourne autour du centre du cercle unité d'un certain angle α et va au point A 1. La définition est donnée en fonction des coordonnées du point A 1 (x, y).
Sinus (sin) de l'angle de rotation
Le sinus de l'angle de rotation α est l'ordonnée du point A 1 (x, y). péché α = y
Cosinus (cos) de l'angle de rotation
Le cosinus de l'angle de rotation α est l'abscisse du point A 1 (x, y). cos α = x
Tangente (tg) de l'angle de rotation
La tangente de l'angle de rotation α est le rapport de l'ordonnée du point A 1 (x, y) à son abscisse. t g α = y x
Cotangente (ctg) de l'angle de rotation
La cotangente de l'angle de rotation α est le rapport de l'abscisse du point A 1 (x, y) à son ordonnée. c t g α = x y
Le sinus et le cosinus sont définis pour n'importe quel angle de rotation. C'est logique, car l'abscisse et l'ordonnée d'un point après rotation peuvent être déterminées sous n'importe quel angle. La situation est différente avec la tangente et la cotangente. La tangente est indéfinie lorsqu'un point après rotation va à un point d'abscisse nulle (0, 1) et (0, - 1). Dans de tels cas, l'expression de la tangente t g α = y x n'a tout simplement pas de sens, puisqu'elle contient une division par zéro. La situation est similaire avec la cotangente. La différence est que la cotangente n'est pas définie dans les cas où l'ordonnée d'un point tend vers zéro.
Important à retenir !
Le sinus et le cosinus sont définis pour tout angle α.
La tangente est définie pour tous les angles sauf α = 90° + 180° k, k ∈ Z (α = π 2 + π k, k ∈ Z)
La cotangente est définie pour tous les angles sauf α = 180° k, k ∈ Z (α = π k, k ∈ Z)
Au moment de décider exemples pratiques ne dites pas "sinus de l'angle de rotation α". Les mots « angle de rotation » sont simplement omis, ce qui implique que le contexte montre déjà clairement de quoi il s’agit.
Nombres
Qu’en est-il de la détermination du sinus, du cosinus, de la tangente et de la cotangente d’un nombre, plutôt que de l’angle de rotation ?
Sinus, cosinus, tangente, cotangente d'un nombre
Sinus, cosinus, tangente et cotangente d'un nombre t est un nombre respectivement égal au sinus, au cosinus, à la tangente et à la cotangente dans t radian.
Par exemple, le sinus du nombre 10 π égal au sinus angle de rotation de 10 π rad.
Il existe une autre approche pour déterminer le sinus, le cosinus, la tangente et la cotangente d'un nombre. Regardons-le de plus près.
N'importe quel nombre réel t un point du cercle unité est associé au centre à l'origine du repère cartésien rectangulaire. Le sinus, le cosinus, la tangente et la cotangente sont déterminés grâce aux coordonnées de ce point.
Le point de départ du cercle est le point A de coordonnées (1, 0).
Nombre positif t
Nombre négatif t correspond au point auquel ira le point de départ s'il se déplace autour du cercle dans le sens inverse des aiguilles d'une montre et je suivrai le chemin t.
Maintenant que le lien entre un nombre et un point sur un cercle est établi, passons à la définition du sinus, du cosinus, de la tangente et de la cotangente.
Sinus (péché) de t
Sinus d'un nombre t- ordonnée d'un point sur le cercle unité correspondant au nombre t. péché t = y
Cosinus (cos) de t
Cosinus d'un nombre t- abscisse du point du cercle unité correspondant au nombre t. cos t = x
Tangente (tg) de t
Tangente d'un nombre t- le rapport de l'ordonnée à l'abscisse d'un point du cercle unité correspondant au nombre t. t g t = y x = sin t cos t
Les dernières définitions sont conformes et ne contredisent pas la définition donnée au début de ce paragraphe. Point sur le cercle correspondant au numéro t, coïncide avec le point auquel va le point de départ après avoir tourné d'un angle t radian.
Fonctions trigonométriques d'argument angulaire et numérique
Chaque valeur de l'angle α correspond à une certaine valeur du sinus et du cosinus de cet angle. Tout comme tous les angles α autres que α = 90° + 180° k, k ∈ Z (α = π 2 + π k, k ∈ Z) correspondent à une certaine valeur tangente. La cotangente, comme indiqué ci-dessus, est définie pour tout α sauf α = 180° k, k ∈ Z (α = π k, k ∈ Z).
On peut dire que sin α, cos α, t g α, c t g α sont des fonctions de l'angle alpha, ou des fonctions de l'argument angulaire.
De même, on peut parler de sinus, cosinus, tangente et cotangente en fonctions d'un argument numérique. Chaque nombre réel t correspond à une certaine valeur du sinus ou du cosinus d'un nombre t. Tous les nombres autres que π 2 + π · k, k ∈ Z, correspondent à une valeur tangente. De même, la cotangente est définie pour tous les nombres sauf π · k, k ∈ Z.
Fonctions de base de la trigonométrie
Le sinus, le cosinus, la tangente et la cotangente sont les fonctions trigonométriques de base.
Il ressort généralement clairement du contexte quel argument de la fonction trigonométrique ( argument d'angle ou un argument numérique) auquel nous avons affaire.
Revenons aux définitions données au tout début et à l'angle alpha, qui est compris entre 0 et 90 degrés. Définitions trigonométriques le sinus, le cosinus, la tangente et la cotangente sont tout à fait cohérents avec définitions géométriques, donné en utilisant les proportions d'un triangle rectangle. Montrons-le.

Prenons un cercle unité avec un centre dans un système de coordonnées cartésiennes rectangulaires. Faisons pivoter le point de départ A (1, 0) d'un angle allant jusqu'à 90 degrés et traçons une perpendiculaire à l'abscisse à partir du point résultant A 1 (x, y). Dans le triangle rectangle résultant, l'angle A 1 O H égal à l'angle tour α, la longueur de la jambe O H est égale à l'abscisse du point A 1 (x, y). La longueur de la jambe opposée à l'angle est égale à l'ordonnée du point A 1 (x, y), et la longueur de l'hypoténuse est égale à un, puisqu'il s'agit du rayon du cercle unité.
Conformément à la définition de la géométrie, le sinus de l'angle α est égal au rapport du côté opposé à l'hypoténuse.
péché α = A 1 H O A 1 = y 1 = y
Cela signifie que déterminer le sinus d'un angle aigu dans un triangle rectangle à travers le rapport d'aspect équivaut à déterminer le sinus de l'angle de rotation α, alpha étant compris entre 0 et 90 degrés.
De même, la correspondance des définitions peut être montrée pour le cosinus, la tangente et la cotangente.

Si vous remarquez une erreur dans le texte, veuillez la surligner et appuyer sur Ctrl+Entrée
Instructions
La première option est classique, utilisant du papier, un rapporteur et un crayon (ou stylo). Par définition, sinusoïdale. angleégal au côté opposé à l’hypoténuse d’un triangle rectangle. Autrement dit, pour calculer la valeur, vous devez utiliser un rapporteur pour construire un triangle rectangle dont l'un des angles est égal à celui dont le sinus vous intéresse. Mesurez ensuite la longueur de l'hypoténuse et de la jambe opposée et divisez la seconde par la première avec la précision requise.
La deuxième option est l'école. De l'école tout le monde se souvient des « tables de Bradis » contenant des milliers de valeurs trigonométriques de différents angles. Vous pouvez rechercher à la fois l'édition papier et son homologue électronique au format pdf - elles sont disponibles sur Internet. Après avoir trouvé les tables, trouvez la valeur sinus nécessaire angle ne sera pas difficile.
La troisième option est optimale. Si vous y avez accès, vous pouvez utiliser la calculatrice standard du système d'exploitation Windows. Il devrait être basculé en mode avancé. Pour ce faire, dans la section « Affichage » du menu, sélectionnez « Ingénierie ». L'apparence de la calculatrice changera - en particulier, des boutons pour calculer les fonctions trigonométriques apparaîtront maintenant. angle, dont vous devez calculer le sinus. Vous pouvez le faire soit à partir du clavier, soit en cliquant sur les touches souhaitées de la calculatrice avec le curseur de la souris. Ou vous pouvez simplement insérer la valeur dont vous avez besoin (CTRL + C et CTRL + V). Après cela, sélectionnez les unités dans lesquelles il doit être calculé - pour les fonctions trigonométriques, cela peut être des radians, des degrés ou des rads. Cela se fait en sélectionnant l'une des trois valeurs de commutateur situées sous le champ de saisie de la valeur calculée. Maintenant, en cliquant sur le bouton intitulé « péché », vous obtiendrez la réponse à votre question.
La quatrième option est la plus moderne. À l’ère d’Internet, il existe des solutions en ligne qui répondent à presque tous les problèmes qui se posent. Calculatrices en ligne de fonctions trigonométriques avec une interface conviviale, plus avancée Fonctionnalité je ne le trouve pas du tout. Les meilleurs d'entre eux proposent de calculer non seulement les valeurs d'une fonction individuelle, mais aussi tout à fait expressions complexesà partir de plusieurs fonctions.
Les fonctions sinus et Cie sinus appartiennent au domaine des mathématiques appelé trigonométrie, c'est pourquoi les fonctions elles-mêmes sont appelées trigonométriques. Selon la définition la plus ancienne, ils expriment la grandeur d'un angle aigu dans un triangle rectangle par le rapport des longueurs de ses côtés. Calcul des valeurs sinus et au niveau actuel de développement Technologie éléctronique- assez tâche simple.
Tu auras besoin de
- Calculatrice Windows.
Instructions
Utiliser pour calculer sinus et angle - le calcul des fonctions trigonométriques est fourni dans la plupart d'entre eux. Compte tenu de la présence d'une calculatrice dans de nombreux téléphones portables, certains poignets et autres gadgets mobiles, sans parler des ordinateurs, c'est peut-être manière abordable calculs sinus UN. Si vous décidez d'utiliser une calculatrice logicielle, recherchez un lien pour la lancer dans le menu principal du système d'exploitation. S'il s'agit de Windows, appuyez sur le bouton Win, sélectionnez « Tous les programmes » dans le menu, allez dans la sous-section « Standard » et cliquez sur la ligne « Calculatrice ». Pour ouvrir l'accès aux commandes de calcul des fonctions trigonométriques dans l'application lancée, appuyez sur la combinaison de touches Alt + 2.
Si la valeur initiale de l'angle est sinus que vous souhaitez calculer est indiqué, assurez-vous qu'à côté de l'inscription " " dans l'interface de la calculatrice
Le sinus est l'une des fonctions trigonométriques de base, dont l'utilisation ne se limite pas à la seule géométrie. Les tableaux de calcul des fonctions trigonométriques, comme les calculatrices d'ingénierie, ne sont pas toujours à portée de main, et le calcul du sinus est parfois nécessaire pour résoudre diverses tâches. En général, le calcul du sinus aidera à consolider les compétences en dessin et la connaissance des identités trigonométriques.
Jeux avec règle et crayon
Une tâche simple : comment trouver le sinus d'un angle dessiné sur papier ? Pour résoudre, vous aurez besoin d'une règle ordinaire, d'un triangle (ou d'un compas) et d'un crayon. La façon la plus simple de calculer le sinus d'un angle consiste à diviser la branche éloignée d'un triangle à angle droit par le côté long - l'hypoténuse. Ainsi, vous devez d'abord compléter l'angle aigu jusqu'à la forme d'un triangle rectangle en traçant une ligne perpendiculaire à l'un des rayons à une distance arbitraire du sommet de l'angle. Nous devrons maintenir un angle d’exactement 90°, pour lequel nous avons besoin d’un triangle clérical.
L'utilisation d'une boussole est un peu plus précise, mais prendra plus de temps. Sur l'un des rayons, vous devez marquer 2 points à une certaine distance, définir un rayon sur la boussole approximativement égal à la distance entre les points et tracer des demi-cercles avec des centres en ces points jusqu'à ce que les intersections de ces lignes soient obtenues. En reliant les points d'intersection de nos cercles entre eux, nous obtenons une stricte perpendiculaire au rayon de notre angle ; il ne reste plus qu'à prolonger la ligne jusqu'à ce qu'elle croise un autre rayon ;
Dans le triangle obtenu, vous devez utiliser une règle pour mesurer le côté opposé au coin et le côté long de l'un des rayons. Le rapport de la première dimension à la seconde sera la valeur souhaitée du sinus de l'angle aigu.
Trouver le sinus pour un angle supérieur à 90°
Pour un angle obtus, la tâche n’est pas beaucoup plus difficile. Nous devons tracer un rayon partant du sommet dans la direction opposée à l'aide d'une règle pour former une ligne droite avec l'un des rayons de l'angle qui nous intéresse. L'angle aigu résultant doit être traité comme décrit ci-dessus ; les sinus des angles adjacents qui forment ensemble un angle inversé de 180° sont égaux.

Calcul du sinus à l'aide d'autres fonctions trigonométriques
De plus, le calcul du sinus est possible si les valeurs d'autres fonctions trigonométriques de l'angle ou au moins les longueurs des côtés du triangle sont connues. Ils nous aideront avec ça identités trigonométriques. Regardons des exemples courants.
Comment trouver le sinus avec un cosinus connu d'un angle ? La première identité trigonométrique, basée sur le théorème de Pythagore, stipule que la somme des carrés du sinus et du cosinus du même angle est égale à un.

Comment trouver le sinus avec une tangente connue à un angle ? La tangente est obtenue en divisant le côté éloigné par le côté proche ou en divisant le sinus par le cosinus. Ainsi, le sinus sera le produit du cosinus et de la tangente, et le carré du sinus sera le carré de ce produit. Nous remplaçons le cosinus carré par la différence entre l'unité et le sinus carré selon la première identité trigonométrique et, par de simples manipulations, nous réduisons l'équation au calcul du sinus carré par la tangente en conséquence, pour calculer le sinus, vous obtiendrez ; il faut extraire la racine du résultat obtenu.

Comment trouver le sinus avec une cotangente connue d’un angle ? La valeur de la cotangente peut être calculée en divisant la longueur de la jambe la plus proche de l'angle par la longueur de la jambe la plus éloignée, ainsi qu'en divisant le cosinus par le sinus, c'est-à-dire que la cotangente est une fonction inverse de la tangente relative au nombre 1. Pour calculer le sinus, vous pouvez calculer la tangente en utilisant la formule tg α = 1 / ctg α et utiliser la formule de la deuxième option. Vous pouvez également dériver une formule directe par analogie avec la tangente, qui ressemblera à ceci.

Comment trouver le sinus de trois côtés d'un triangle
Il existe une formule pour trouver la longueur du côté inconnu d'un triangle, pas seulement d'un rectangle, à partir de deux fêtes connues en utilisant la fonction trigonométrique du cosinus de l'angle opposé. Elle ressemble à ça.

Nous commencerons notre étude de la trigonométrie par le triangle rectangle. Définissons ce que sont le sinus et le cosinus, ainsi que la tangente et la cotangente d'un angle aigu. Ce sont les bases de la trigonométrie.
Rappelons que angle droit est un angle égal à 90 degrés. En d’autres termes, un demi-angle tourné.
Angle vif- moins de 90 degrés.
Angle obtus- supérieur à 90 degrés. Appliqué sous un tel angle, « obtus » n'est pas une insulte, mais un terme mathématique :-)
Traçons un triangle rectangle. Un angle droit est généralement noté . Veuillez noter que le côté opposé au coin est indiqué par la même lettre, seulement en petite. Ainsi, le côté opposé à l'angle A est désigné .
L'angle est désigné par la lettre grecque correspondante.

Hypoténuse d'un triangle rectangle est le côté opposé à l'angle droit.
Jambes- les côtés opposés aux angles aigus.
La jambe située à l'opposé de l'angle s'appelle opposé(par rapport à l'angle). L'autre jambe, qui se trouve sur l'un des côtés de l'angle, s'appelle adjacent.
Sinus L'angle aigu dans un triangle rectangle est le rapport du côté opposé à l'hypoténuse :
Cosinus angle aigu dans un triangle rectangle - le rapport de la jambe adjacente à l'hypoténuse :
Tangente angle aigu dans un triangle rectangle - le rapport du côté opposé au côté adjacent :
Autre définition (équivalente) : la tangente d'un angle aigu est le rapport du sinus de l'angle à son cosinus :
Cotangente angle aigu dans un triangle rectangle - le rapport du côté adjacent au côté opposé (ou, ce qui revient au même, le rapport du cosinus au sinus) :
Notez les relations de base pour le sinus, le cosinus, la tangente et la cotangente ci-dessous. Ils nous seront utiles pour résoudre des problèmes.

Prouvons-en quelques-uns.
D'accord, nous avons donné des définitions et des formules écrites. Mais pourquoi avons-nous encore besoin de sinus, cosinus, tangente et cotangente ?
Nous savons que la somme des angles de tout triangle est égale à.
Nous connaissons la relation entre des soirées triangle rectangle. C'est le théorème de Pythagore : .
Il s'avère qu'en connaissant deux angles dans un triangle, vous pouvez trouver le troisième. Connaissant les deux côtés d’un triangle rectangle, vous pouvez trouver le troisième. Cela signifie que les angles ont leur propre rapport et que les côtés ont le leur. Mais que faire si dans un triangle rectangle vous connaissez un angle (sauf l'angle droit) et un côté, mais que vous devez trouver les autres côtés ?

C’est ce que les gens rencontraient autrefois lorsqu’ils dressaient des cartes de la région et du ciel étoilé. Après tout, il n’est pas toujours possible de mesurer directement tous les côtés d’un triangle.
Sinus, cosinus et tangente - on les appelle aussi fonctions d'angle trigonométrique- donner des relations entre des soirées Et coins Triangle. Connaissant l'angle, vous pouvez retrouver toutes ses fonctions trigonométriques à l'aide de tableaux spéciaux. Et connaissant les sinus, cosinus et tangentes des angles d’un triangle et d’un de ses côtés, vous pouvez trouver le reste.
Nous dresserons également un tableau des valeurs du sinus, du cosinus, de la tangente et de la cotangente pour les « bons » angles de à.
Veuillez noter les deux tirets rouges dans le tableau. Aux valeurs d'angle appropriées, la tangente et la cotangente n'existent pas.
Examinons plusieurs problèmes de trigonométrie de la banque de tâches FIPI.
1. Dans un triangle, l’angle est , . Trouver .
Le problème est résolu en quatre secondes.
Parce que le , .
2. Dans un triangle, l'angle est , , . Trouver .

Trouvons-le en utilisant le théorème de Pythagore.
Le problème est résolu.
Souvent, dans les problèmes, il y a des triangles avec des angles et ou avec des angles et. Retenez par cœur les ratios de base pour eux !

Pour un triangle avec des angles et la branche opposée à l'angle en est égale à la moitié de l'hypoténuse.
Un triangle avec des angles et est isocèle. Dans celui-ci, l'hypoténuse est plusieurs fois plus grande que la jambe.
Nous avons examiné des problèmes pour résoudre des triangles rectangles, c'est-à-dire trouver des côtés ou des angles inconnus. Mais ce n'est pas tout! DANS Options d'examen d'État unifié en mathématiques, il existe de nombreux problèmes dans lesquels apparaît le sinus, le cosinus, la tangente ou la cotangente de l'angle externe d'un triangle. Plus d’informations à ce sujet dans le prochain article.
Comment trouver le sinus ?



L'étude de la géométrie aide à développer la réflexion. Cette matière est obligatoirement incluse dans la formation scolaire. Dans la vie de tous les jours, la connaissance de ce sujet peut être utile, par exemple lors de la planification d'un appartement.
De l'histoire
Le cours de géométrie comprend également la trigonométrie, qui étudie les fonctions trigonométriques. En trigonométrie, nous étudions les sinus, les cosinus, les tangentes et les cotangentes des angles.
Mais sur ce moment Commençons par la chose la plus simple : le sinus. Examinons de plus près le tout premier concept : le sinus d'un angle en géométrie. Qu'est-ce que le sinus et comment le trouver ?
Le concept d'« angle sinusoïdal » et de sinusoïdes
Le sinus d'un angle est le rapport des valeurs du côté opposé et de l'hypoténuse d'un triangle rectangle. Il s'agit d'une fonction trigonométrique directe, qui s'écrit « sin (x) », où (x) est l'angle du triangle.
Sur le graphique, le sinus d’un angle est indiqué par une onde sinusoïdale ayant ses propres caractéristiques. Une onde sinusoïdale ressemble à une ligne ondulée continue située dans certaines limites du plan de coordonnées. La fonction est impaire, donc elle est symétrique par rapport à 0 sur le plan des coordonnées (elle sort de l'origine des coordonnées).
Le domaine de définition de cette fonction est compris entre -1 et +1 sur le repère cartésien. La période de la fonction angle sinusoïdal est de 2 Pi. Cela signifie que tous les 2 Pi, le motif se répète et l'onde sinusoïdale traverse un cycle complet.
Équation d'onde sinusoïdale
- péché x = a/c
- où a est la branche opposée à l'angle du triangle
- c - hypoténuse d'un triangle rectangle
Propriétés du sinus d'un angle
- péché(x) = - péché(x). Cette fonctionnalité démontre que la fonction est symétrique et si les valeurs x et (-x) sont tracées sur le système de coordonnées dans les deux sens, alors les ordonnées de ces points seront opposées. Ils seront à égale distance les uns des autres.
- Une autre particularité de cette fonction est que le graphique de la fonction augmente sur le segment [- P/2 + 2 Pn] ; [P/2 + 2Pn], où n est n'importe quel nombre entier. Une diminution du graphique du sinus de l'angle sera observée sur le segment : [P/2 + 2Pn] ; [3P/2 + 2Pn].
- sin(x) > 0 lorsque x est dans la plage (2Пn, П + 2Пn)
- (X)< 0, когда х находится в диапазоне (-П+2Пn, 2Пn)
Les valeurs des sinus de l'angle sont déterminées à l'aide de tableaux spéciaux. De tels tableaux ont été créés pour faciliter le processus de comptage formules complexes et les équations. Il est facile à utiliser et contient des significations non seulement fonctions péché(x), mais aussi les valeurs d'autres fonctions.
De plus, un tableau de valeurs standards pour ces fonctions est inclus avec le étude obligatoire pour la mémoire, comme une table de multiplication. Cela est particulièrement vrai pour les cours à tendance physique et mathématique. Dans le tableau vous pouvez voir les valeurs des principaux angles utilisés en trigonométrie : 0, 15, 30, 45, 60, 75, 90, 120, 135, 150, 180, 270 et 360 degrés.
Il existe également un tableau définissant les valeurs des fonctions trigonométriques des angles non standards. Prendre l'avantage différents tableaux, vous pouvez facilement calculer le sinus, le cosinus, la tangente et la cotangente de certains angles.
Les équations sont faites avec des fonctions trigonométriques. La résolution de ces équations est facile si vous connaissez les identités trigonométriques simples et les réductions de fonctions, par exemple telles que sin (P/2 + x) = cos (x) et autres. Un tableau distinct a également été établi pour ces réductions.
Comment trouver le sinus d'un angle
Lorsque la tâche consiste à trouver le sinus d'un angle et que, selon la condition, nous n'avons que le cosinus, la tangente ou la cotangente de l'angle, nous pouvons facilement calculer ce dont nous avons besoin en utilisant les identités trigonométriques.
- péché 2 x + cos 2 x = 1
À partir de cette équation, nous pouvons trouver à la fois le sinus et le cosinus, selon la valeur inconnue. On peut le faire équation trigonométrique avec une inconnue :
- péché 2 x = 1 - cos 2 x
- péché x = ± √ 1 - cos 2 x
- lit bébé 2 x + 1 = 1 / péché 2 x
A partir de cette équation, vous pouvez trouver la valeur du sinus, connaissant la valeur de la cotangente de l'angle. Pour simplifier, remplacez sin 2 x = y et vous obtenez une équation simple. Par exemple, la valeur de la cotangente est 1, alors :
- 1 + 1 = 1/an
- 2 = 1/an
- 2у = 1
- y = 1/2
Nous effectuons maintenant le remplacement inverse du lecteur :
- péché 2 x = ½
- péché x = 1 / √2
Puisque nous avons pris la valeur cotangente pour l'angle standard (45 0), les valeurs obtenues peuvent être vérifiées dans le tableau.
Si vous avez une valeur tangente et que vous devez trouver le sinus, une autre identité trigonométrique vous aidera :
- tg x * ctg x = 1
Il s'ensuit que :
- lit bébé x = 1 / tg x
Afin de trouver le sinus d'un angle non standard, par exemple 240 0, vous devez utiliser des formules de réduction d'angle. On sait que π correspond à 180 0. Ainsi, nous exprimons notre égalité en utilisant des angles standards par expansion.
- 240 0 = 180 0 + 60 0
Nous devons trouver ce qui suit : sin (180 0 + 60 0). En trigonométrie, il existe des formules de réduction qui dans ce cas sera utile. Voici la formule :
- péché (π + x) = - péché (x)
Ainsi, le sinus d’un angle de 240 degrés est égal à :
- péché (180 0 + 60 0) = - péché (60 0) = - √3/2
Dans notre cas, x = 60 et P, respectivement, 180 degrés. Nous avons trouvé la valeur (-√3/2) dans le tableau des valeurs des fonctions d'angles standards.
De cette façon, nous pouvons décomposer angles non standards, par exemple : 210 = 180 + 30.