Résoudre les inégalités avec des logarithmes en ligne. Tout sur les inégalités logarithmiques. Analyse d'exemples
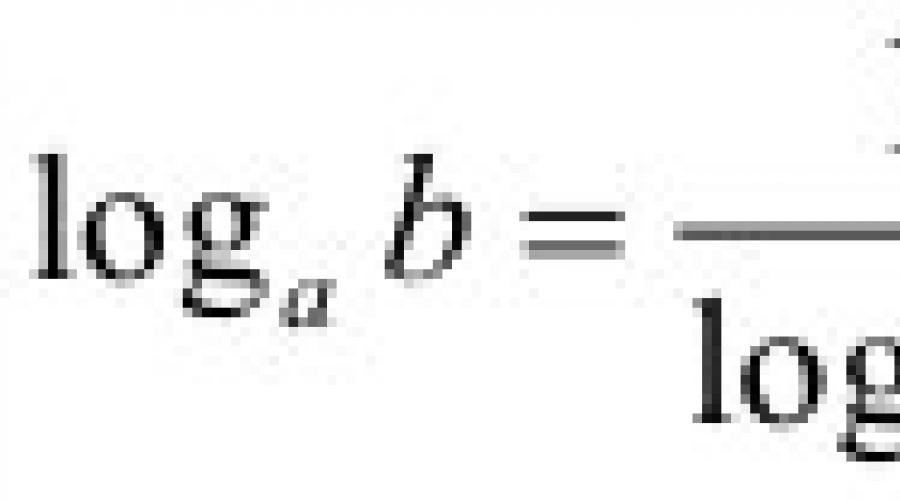
Lire aussi
Le maintien de votre vie privée est important pour nous. Pour cette raison, nous avons développé une politique de confidentialité qui décrit la manière dont nous utilisons et stockons vos informations. Veuillez consulter nos pratiques de confidentialité et faites-nous savoir si vous avez des questions.
Collecte et utilisation des informations personnelles
Les informations personnelles font référence aux données qui peuvent être utilisées pour identifier ou contacter une personne spécifique.
Il peut vous être demandé de fournir vos informations personnelles à tout moment lorsque vous nous contactez.
Vous trouverez ci-dessous quelques exemples des types d'informations personnelles que nous pouvons collecter et de la manière dont nous pouvons utiliser ces informations.
Quelles informations personnelles collectons-nous :
- Lorsque vous soumettez une demande sur le site, nous pouvons collecter diverses informations, notamment votre nom, numéro de téléphone, adresse e-mail etc.
Comment nous utilisons vos informations personnelles :
- Collecté par nos soins informations personnelles nous permet de vous contacter et de vous informer des offres uniques, des promotions et d'autres événements et événements à venir.
- De temps en temps, nous pouvons utiliser vos informations personnelles pour envoyer des notifications et des communications importantes.
- Nous pouvons également utiliser des informations personnelles à des fins internes telles que l'audit, l'analyse des données et diverses études afin d'améliorer les services que nous proposons et de vous fournir des recommandations concernant nos services.
- Si vous participez à un tirage au sort, un concours ou une promotion similaire, nous pouvons utiliser les informations que vous fournissez pour administrer ces programmes.
Divulgation d'informations à des tiers
Nous ne divulguons pas les informations reçues de votre part à des tiers.
Exceptions :
- Si nécessaire, conformément à la loi, procédure judiciaire, V procès, et/ou sur la base de demandes publiques ou de demandes de agences gouvernementales sur le territoire de la Fédération de Russie - divulguez vos informations personnelles. Nous pouvons également divulguer des informations vous concernant si nous déterminons qu'une telle divulgation est nécessaire ou appropriée à des fins de sécurité, d'application de la loi ou à d'autres fins de santé publique. cas importants.
- En cas de réorganisation, de fusion ou de vente, nous pouvons transférer les informations personnelles que nous collectons au tiers successeur concerné.
Protection des informations personnelles
Nous prenons des précautions - notamment administratives, techniques et physiques - pour protéger vos informations personnelles contre la perte, le vol et l'utilisation abusive, ainsi que contre l'accès, la divulgation, l'altération et la destruction non autorisés.
Respecter votre vie privée au niveau de l'entreprise
Pour garantir la sécurité de vos informations personnelles, nous communiquons les normes de confidentialité et de sécurité à nos employés et appliquons strictement les pratiques de confidentialité.
Définition du logarithme La façon la plus simple de l’écrire mathématiquement est :
La définition du logarithme peut s’écrire d’une autre manière :
Faites attention aux restrictions imposées sur la base du logarithme ( un) et à l'expression sublogarithmique ( x). À l'avenir, ces conditions se transformeront en restrictions importantes pour la DO, qui devront être prises en compte lors de la résolution de toute équation avec des logarithmes. Ainsi, désormais, en plus des conditions standards conduisant à des restrictions sur ODZ (positivité des expressions sous les racines de puissances paires, dénominateur non égal à zéro, etc.), les conditions suivantes doivent également être prises en compte :
- L'expression sublogarithmique ne peut être que positive.
- La base du logarithme ne peut être que positive et non égale à un.
Notez que ni la base du logarithme ni l'expression sous-logarithmique ne peuvent être égales à zéro. Veuillez également noter que la valeur du logarithme elle-même peut prendre toutes les valeurs possibles, c'est-à-dire Le logarithme peut être positif, négatif ou nul. Les logarithmes ont beaucoup diverses propriétés, qui découlent des propriétés des puissances et de la définition du logarithme. Listons-les. Ainsi, les propriétés des logarithmes :

Logarithme du produit :
Logarithme d'une fraction :

En sortant le degré du signe du logarithme :
Portez une attention particulière à celles des dernières propriétés répertoriées dans lesquelles le signe du module apparaît après l'obtention du diplôme. N'oubliez pas que lorsque vous placez une puissance paire en dehors du signe du logarithme, sous le logarithme ou à la base, vous devez laisser le signe du module.
Autre propriétés bénéfiques logarithmes :

![]()
Cette dernière propriété est très souvent utilisée dans les équations logarithmiques complexes et les inégalités. Il faut se souvenir de lui comme de tous les autres, même s'il est souvent oublié.
Le plus simple équations logarithmiques avoir la forme :
![]()
Et leur solution est donnée par une formule qui découle directement de la définition du logarithme :
D'autres équations logarithmiques simples sont celles qui, en utilisant transformations algébriques et les formules et propriétés des logarithmes ci-dessus peuvent être réduites à la forme :
La solution de telles équations prenant en compte l'ODZ est la suivante :

Quelques autres équations logarithmiques avec une variable à la base peut être réduit à la forme :
![]()
Dans de telles équations logarithmiques vue générale la solution découle également directement de la définition du logarithme. Ce n'est que dans ce cas qu'il existe des restrictions supplémentaires pour DZ qui doivent être prises en compte. En conséquence, pour résoudre une équation logarithmique avec une variable dans la base, vous devez résoudre le système suivant :

Lors de la résolution d'équations logarithmiques plus complexes qui ne peuvent être réduites à l'une des équations présentées ci-dessus, il est également activement utilisé méthode de remplacement des variables. Comme d'habitude, lorsque vous utilisez cette méthode, vous devez vous rappeler qu'après avoir introduit le remplacement, l'équation doit se simplifier et ne plus contenir l'ancienne inconnue. Vous devez également vous rappeler d'effectuer une substitution inverse des variables.
Parfois, lors de la résolution d'équations logarithmiques, vous devez également utiliser méthode graphique . Cette méthode consiste à construire des graphiques de fonctions qui se trouvent sur les côtés gauche et droit de l'équation aussi précisément que possible sur un plan de coordonnées, puis à trouver les coordonnées de leurs points d'intersection à partir du dessin. Les racines ainsi obtenues doivent être vérifiées par substitution dans l'équation d'origine.
Lors de la résolution d'équations logarithmiques, il est souvent également utile méthode de regroupement. Lors de l'utilisation de cette méthode, l'essentiel à retenir est que : pour que le produit de plusieurs facteurs soit égal à zéro, il faut qu'au moins l'un d'entre eux soit égal à zéro, et le reste existait. Lorsque les facteurs sont des logarithmes ou des parenthèses avec des logarithmes, et pas seulement des parenthèses avec des variables comme dans équations rationnelles, alors de nombreuses erreurs peuvent survenir. Étant donné que les logarithmes ont de nombreuses restrictions quant à la région où ils existent.
Au moment de décider systèmes d'équations logarithmiques le plus souvent, vous devez utiliser soit la méthode de substitution, soit la méthode de remplacement de variable. S'il existe une telle possibilité, alors lors de la résolution de systèmes d'équations logarithmiques, il faut s'efforcer de faire en sorte que chacune des équations du système soit amenée individuellement à une forme dans laquelle il sera possible de passer d'une équation logarithmique à une rationnel.
Les inégalités logarithmiques les plus simples sont résolues à peu près de la même manière que des équations similaires. Premièrement, en utilisant des transformations algébriques et les propriétés des logarithmes, nous devons essayer de les amener à une forme où les logarithmes des côtés gauche et droit de l'inégalité auront les mêmes bases, c'est-à-dire obtenir une inégalité de la forme :
Ensuite, vous devez aller à inégalité rationnelle, en tenant compte du fait que cette transition doit être effectuée comme suit : si la base du logarithme est supérieure à un, alors le signe de l'inégalité n'a pas besoin d'être changé, et si la base du logarithme est inférieure à un, alors l'inégalité le signe doit être remplacé par le signe opposé (cela signifie changer « moins » en « plus » ou vice versa). Dans ce cas, il n'est pas nécessaire de remplacer les signes moins par des plus, en contournant les règles précédemment apprises. Écrivons mathématiquement ce que nous obtenons en effectuant une telle transition. Si la base est supérieure à un, on obtient :

Si la base du logarithme est inférieure à un, on change le signe de l'inégalité et on obtient le système suivant :
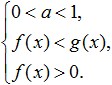
Comme on le voit, lors de la résolution des inégalités logarithmiques, comme d'habitude, l'ODZ est également pris en compte (c'est la troisième condition dans les systèmes ci-dessus). De plus, dans ce cas, il est possible de ne pas exiger la positivité des deux expressions sublogarithmiques, mais plutôt d’exiger uniquement la positivité de la plus petite d’entre elles.
Au moment de décider inégalités logarithmiques avec une variable à la base logarithme, il est nécessaire de considérer indépendamment les deux options (lorsque la base est inférieure à un et supérieure à un) et de combiner les solutions de ces cas dans un ensemble. En même temps, il ne faut pas oublier DL, c'est-à-dire sur le fait que la base et toutes les expressions sublogarithmiques doivent être positives. Ainsi, lors de la résolution d’une inégalité de la forme :
On obtient l’ensemble de systèmes suivant :

Des inégalités logarithmiques plus complexes peuvent également être résolues en utilisant des changements de variables. Certaines autres inégalités logarithmiques (ainsi que les équations logarithmiques) nécessitent la procédure consistant à prendre le logarithme des deux côtés de l'inégalité ou de l'équation à résoudre. même base. Ainsi, lorsqu'on effectue une telle procédure avec des inégalités logarithmiques, il y a une subtilité. Veuillez noter que lorsque vous prenez des logarithmes à une base supérieure à un, le signe d'inégalité ne change pas, mais si la base est inférieure à un, alors le signe d'inégalité est inversé.
Si une inégalité logarithmique ne peut être réduite à une inégalité rationnelle ou résolue par substitution, alors dans ce cas il faut utiliser méthode d'intervalle généralisée, qui est le suivant :
- Définir DL ;
- Transformez l'inégalité pour qu'il y ait un zéro du côté droit (du côté gauche, si possible, réduisez à dénominateur commun, factoriser, etc.);
- Trouvez toutes les racines du numérateur et du dénominateur et tracez-les sur l'axe des nombres, et si l'inégalité n'est pas stricte, peignez les racines du numérateur, mais dans tous les cas laissez les racines du dénominateur en pointillés ;
- Trouvez le signe de l'expression entière sur chacun des intervalles en substituant un nombre d'un intervalle donné dans l'inégalité transformée. Dans ce cas, il n'est plus possible d'alterner les panneaux lors du passage par des points sur l'axe. Il faut déterminer le signe d'une expression sur chaque intervalle en substituant la valeur de l'intervalle dans cette expression, et ainsi de suite pour chaque intervalle. Il n'y a pas d'autre moyen (c'est de ça qu'il s'agit, en gros, la différence entre la méthode des intervalles généralisés et la méthode habituelle) ;
- Trouvez l'intersection de l'ODZ et des intervalles qui satisfont l'inégalité, mais ne perdez pas les points individuels qui satisfont l'inégalité (les racines du numérateur dans les inégalités non strictes), et n'oubliez pas d'exclure de la réponse toutes les racines du dénominateur de toutes les inégalités.
- Dos
- Avant
Comment réussir sa préparation au CT en physique et mathématiques ?
Afin de réussir la préparation au CT en physique et en mathématiques, entre autres, il est nécessaire de remplir trois conditions les plus importantes :
- Étudiez tous les sujets et complétez tous les tests et devoirs donnés dans le matériel pédagogique de ce site. Pour ce faire, vous n'avez besoin de rien du tout, à savoir : consacrer trois à quatre heures chaque jour à préparer le CT en physique et mathématiques, à étudier la théorie et à résoudre des problèmes. Le fait est que CT est un examen où il ne suffit pas de connaître la physique ou les mathématiques, il faut aussi être capable de résoudre rapidement et sans échec. grand nombre tâches pour différents sujets Et de complexité variable. Cette dernière ne peut être apprise qu’en résolvant des milliers de problèmes.
- Apprenez toutes les formules et lois de la physique, ainsi que les formules et méthodes des mathématiques. En fait, c'est aussi très simple à faire, formules nécessaires en physique, il n'y en a qu'environ 200, et en mathématiques encore un peu moins. Chacun de ces sujets dispose d'une douzaine de méthodes standards pour résoudre des problèmes. niveau de base des difficultés qui peuvent également être apprises, et donc résolues de manière entièrement automatique et sans difficulté bon moment la plupart des DH. Après cela, vous n’aurez plus qu’à penser aux tâches les plus difficiles.
- Assistez aux trois étapes des tests de répétition en physique et en mathématiques. Chaque RT peut être visité deux fois pour décider des deux options. Encore une fois, sur le CT, en plus de la capacité à résoudre rapidement et efficacement des problèmes et de la connaissance des formules et des méthodes, vous devez également être capable de bien planifier le temps, de répartir les forces et, surtout, de remplir correctement le formulaire de réponse, sans confondre les nombres de réponses et de problèmes, ou votre propre nom de famille. De plus, pendant la RT, il est important de s'habituer au style de pose de questions dans les problèmes, qui peut sembler très inhabituel à une personne non préparée au DT.
La mise en œuvre réussie, assidue et responsable de ces trois points vous permettra de vous présenter au CT excellent résultat, le maximum de ce dont vous êtes capable.
Vous avez trouvé une erreur ?
Si vous pensez avoir trouvé une erreur dans matériel pédagogique, alors écrivez-nous par e-mail. Vous pouvez également signaler un bug à réseau social(). Dans la lettre, indiquez le sujet (physique ou mathématique), le nom ou le numéro du sujet ou du test, le numéro du problème, ou l'endroit dans le texte (page) où, à votre avis, il y a une erreur. Décrivez également quelle est l'erreur suspectée. Votre lettre ne passera pas inaperçue, soit l'erreur sera corrigée, soit on vous expliquera pourquoi ce n'est pas une erreur.
Une inégalité est dite logarithmique si elle contient une fonction logarithmique.
Les méthodes de résolution des inégalités logarithmiques ne diffèrent pas de celles-ci, à l'exception de deux choses.
Premièrement, lors du passage de inégalité logarithmique aux inégalités sous fonctions logarithmiques devrait suivre le signe de l'inégalité résultante. Il obéit à la règle suivante.
Si la base de la fonction logarithmique est supérieure à 1$, alors lors du passage de l'inégalité logarithmique à l'inégalité des fonctions sous-logarithmiques, le signe de l'inégalité est conservé, mais s'il est inférieur à 1$, alors il change à l'opposé .
Deuxièmement, la solution de toute inégalité est un intervalle, et, par conséquent, à la fin de la résolution de l'inégalité des fonctions sous-logarithmiques, il est nécessaire de créer un système de deux inégalités : la première inégalité de ce système sera l'inégalité des fonctions sous-logarithmiques, et le second sera l'intervalle du domaine de définition des fonctions logarithmiques incluses dans l'inégalité logarithmique.
Pratique.
Résolvons les inégalités :
1. $\log_(2)((x+3)) \geq 3.$
$D(y) : \x+3>0.$
$x \in (-3;+\infty)$
La base du logarithme est $2>1$, donc le signe ne change pas. En utilisant la définition du logarithme, on obtient :
$x+3 \geq 2^(3),$
$x \in )