Types simples de résistance. courbure plate. Courbe droite Courbe transversale plate Courbe droite et transversale

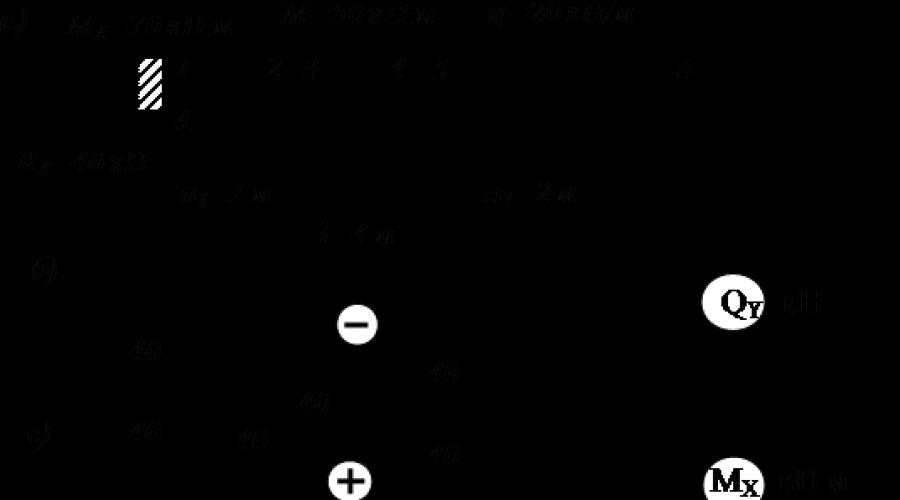
Courbe droite. Plat flexion transversale Construction de diagrammes de facteurs de force internes pour les poutres Construction de diagrammes de Q et M à l'aide d'équations Construction de diagrammes de Q et M à l'aide de sections caractéristiques (points) Calculs de résistance pour la flexion directe des poutres Contraintes principales lors de la flexion. Un contrôle complet de la résistance des poutres. La notion de centre de flexion. Détermination des déplacements des poutres lors de la flexion. Concepts de déformation des poutres et conditions de leur rigidité Équation différentielle axe courbe d'une poutre Méthode d'intégration directe Exemples de détermination des déplacements dans des poutres par la méthode d'intégration directe Signification physique des constantes d'intégration Méthode des paramètres initiaux (équation universelle de l'axe courbe d'une poutre). Exemples de détermination de déplacements dans une poutre par la méthode des paramètres initiaux Détermination des déplacements par la méthode de Mohr. Règle A.K. Vereshchagin. Calcul de l'intégrale de Mohr selon la règle d'A.K. Vereshchagina Exemples de détermination des déplacements à l'aide de l'intégrale de Mohr Bibliographie Flexion directe. Courbe transversale plate. 1.1. Construire des diagrammes de facteurs de force internes pour les poutres La flexion directe est un type de déformation dans lequel deux facteurs de force internes apparaissent dans les sections transversales de la tige : un moment de flexion et une force transversale. Dans un cas particulier, l'effort tranchant peut être nul, alors la flexion est dite pure. En flexion transversale plate, toutes les forces sont situées dans l'un des principaux plans d'inertie de la tige et perpendiculairement à son axe longitudinal, et les moments sont situés dans le même plan (Fig. 1.1, a, b). Riz. 1.1 La force transversale dans une section transversale arbitraire d'une poutre est numériquement égale à la somme algébrique des projections sur la normale à l'axe de la poutre de tous forces extérieures les poutres (Fig. 1.2, a) sont considérées comme positives si la résultante des forces externes à gauche de la section est dirigée vers le haut, et vers la droite - vers le bas, et négative - dans le cas contraire (Fig. 1.2, b). Riz. 1.2 Lors du calcul de la force transversale dans une section donnée, les forces extérieures situées à gauche de la section sont prises avec un signe plus si elles sont dirigées vers le haut, et avec un signe moins si elles sont dirigées vers le bas. Pour le côté droit de la poutre - vice versa. 5 Le moment de flexion dans une section transversale arbitraire d'une poutre est numériquement égal à la somme algébrique des moments autour de l'axe central z de la section de toutes les forces externes agissant sur un côté de la section considérée. Moment de flexion en section (Fig. 1.3, a) est considéré comme positif si le moment résultant des forces externes à gauche de la section est dirigé dans le sens des aiguilles d'une montre et vers la droite - dans le sens inverse des aiguilles d'une montre et négatif - dans le cas contraire (Fig. 1.3, b). Riz. 1.3 Lors du calcul du moment fléchissant dans une section donnée, les moments des forces extérieures situées à gauche de la section sont considérés comme positifs s'ils sont dirigés dans le sens des aiguilles d'une montre. Pour le côté droit de la poutre - vice versa. Il convient de déterminer le signe du moment fléchissant par la nature de la déformation de la poutre. Le moment de flexion est considéré comme positif si, dans la section considérée, la partie coupée de la poutre se courbe de manière convexe vers le bas, c'est-à-dire que les fibres inférieures sont étirées. Dans le cas contraire, le moment fléchissant dans la section est négatif. Il existe des relations différentielles entre le moment de flexion M, la force de cisaillement Q et l'intensité de la charge q. 1. La dérivée première de l'effort tranchant le long de l'abscisse de la section est égale à l'intensité de la charge répartie, c'est-à-dire Sur la base de l'analyse des diagrammes M et Q, les sections dangereuses du faisceau sont déterminées. Les ordonnées positives du diagramme Q sont tracées vers le haut et les ordonnées négatives sont tracées à partir de la ligne de base tracée parallèlement à l'axe longitudinal de la poutre. Les ordonnées positives du diagramme M sont tracées et les ordonnées négatives sont tracées vers le haut, c'est-à-dire que le diagramme M est construit du côté des fibres étirées. La construction des diagrammes Q et M pour les poutres doit commencer par la détermination des réactions d'appui. Pour une poutre avec une extrémité serrée et l'autre extrémité libre, la construction des diagrammes Q et M peut être démarrée à partir de l'extrémité libre, sans déterminer les réactions dans l'encastrement. 1.2. La construction des diagrammes Q et M à l'aide des équations de poutre est divisée en sections dans lesquelles les fonctions du moment de flexion et de la force de cisaillement restent constantes (ne présentent pas de discontinuités). Les limites des sections sont les points d'application des forces concentrées, des couples de forces et des lieux de changement de l'intensité de la charge répartie. À chaque section, une section arbitraire est prise à une distance x de l'origine des coordonnées, et pour cette section, des équations pour Q et M sont établies à l'aide de ces équations, des diagrammes de Q et M sont construits. Exemple 1.1 Construire des diagrammes transversaux. forces Q et moments fléchissants M pour une poutre donnée (Fig. 1.4,a). Solution : 1. Détermination des réactions de support. On compose des équations d'équilibre : à partir desquelles on obtient Les réactions des supports sont déterminées correctement. La poutre comporte quatre sections Fig. 1.4 charges : CA, AD, DB, BE. 2. Construire un diagramme Q. Section CA. Dans la section CA 1, nous dessinons une section arbitraire 1-1 à une distance x1 de l'extrémité gauche de la poutre. Nous définissons Q comme la somme algébrique de toutes les forces externes agissant à gauche de la section 1-1 : Le signe moins est pris car la force agissant à gauche de la section est dirigée vers le bas. L'expression de Q ne dépend pas de la variable x1. Le diagramme Q dans cette section sera représenté comme une ligne droite parallèle à l’axe des abscisses. Section AD. Sur la section, nous dessinons une section arbitraire 2-2 à une distance x2 de l'extrémité gauche de la poutre. On définit Q2 comme la somme algébrique de toutes les forces extérieures agissant à gauche de la section 2-2 : 8 La valeur de Q est constante dans la section (ne dépend pas de la variable x2). Le tracé Q sur la section est une droite parallèle à l’axe des abscisses. Tracer la base de données. Sur le site, nous dessinons une section arbitraire 3-3 à une distance x3 de l'extrémité droite de la poutre. Nous définissons Q3 comme la somme algébrique de toutes les forces extérieures agissant à droite de la section 3-3 : L'expression résultante est l'équation d'une droite inclinée. Section BE. Sur le chantier on dessine une section 4-4 à une distance x4 de l'extrémité droite de la poutre. Nous définissons Q comme la somme algébrique de toutes les forces externes agissant à droite de la section 4-4 : 4 Ici, le signe plus est pris car la charge résultante à droite de la section 4-4 est dirigée vers le bas. Sur la base des valeurs obtenues, nous construisons des diagrammes Q (Fig. 1.4, b). 3. Construction du schéma M. Section m1. Nous définissons le moment fléchissant dans la section 1-1 comme la somme algébrique des moments de forces agissant à gauche de la section 1-1. 1.5, ch. 1.3. Construire des diagrammes de Q et M à partir de sections caractéristiques (points) En utilisant les dépendances différentielles entre M, Q, q et les conclusions qui en découlent, il convient de construire des diagrammes de Q et M à partir de sections caractéristiques (sans établir d'équations). Grâce à cette méthode, les valeurs de Q et M sont calculées en sections caractéristiques. Les sections caractéristiques sont les sections limites des sections, ainsi que les sections dans lesquelles un facteur de force interne donné a une valeur extrême. Dans les limites entre les sections caractéristiques, le tracé 12 du diagramme est établi à partir des dépendances différentielles entre M, Q, q et des conclusions qui en découlent. Exemple 1.3 Construire les diagrammes Q et M pour la poutre illustrée à la Fig. 1.6, une. Riz. 1.6. Solution : Nous commençons à construire les diagrammes Q et M à partir de l'extrémité libre de la poutre, alors que les réactions dans l'encastrement n'ont pas besoin d'être déterminées. La poutre comporte trois sections de chargement : AB, BC, CD. Il n'y a pas de charge répartie dans les sections AB et BC. Les forces de cisaillement sont constantes. Le diagramme Q est limité aux lignes droites parallèles à l’axe des x. Les moments de flexion varient linéairement. Le diagramme M est limité par des droites inclinées vers l'axe des abscisses. Il y a une charge uniformément répartie sur la section CD. Les forces transversales changent selon une loi linéaire et les moments de flexion - selon la loi d'une parabole carrée à convexité dans la direction de la charge répartie. A la limite des sections AB et BC, la force transversale change brusquement. A la limite des sections BC et CD, le moment fléchissant change brusquement. 1. Construction du diagramme Q. Nous calculons les valeurs des forces transversales Q dans les sections limites des sections : Sur la base des résultats du calcul, nous construisons le diagramme Q pour la poutre (Fig. 1, b). Du diagramme Q il résulte que l'effort transversal sur la section CD est égal à zéro dans la section située à une distance qa a q du début de cette section. Dans cette section, le moment fléchissant a une valeur maximale. 2. Construction du diagramme M. Nous calculons les valeurs des moments fléchissants dans les sections limites des sections : Au moment maximum dans la section Sur la base des résultats du calcul, nous construisons le diagramme M (Fig. 5.6, c). Exemple 1.4 À l'aide d'un diagramme donné de moments fléchissants (Fig. 1.7, a) pour une poutre (Fig. 1.7, b), déterminer m-n poutres charges efficaces et construisons un diagramme Q. Le cercle indique le sommet d’une parabole carrée. Solution : Déterminons les charges agissant sur la poutre. La section AC est chargée d'une charge uniformément répartie, puisque le diagramme M dans cette section est une parabole carrée. Dans la section de référence B, un moment concentré est appliqué à la poutre, agissant dans le sens des aiguilles d'une montre, puisque dans le diagramme M nous avons un saut vers le haut de l'amplitude du moment. Dans la section NE, la poutre n'est pas chargée, puisque le diagramme M dans cette section est limité par une droite inclinée. La réaction du support B est déterminée à partir de la condition selon laquelle le moment de flexion dans la section C est égal à zéro, c'est-à-dire Pour déterminer l'intensité de la charge répartie, nous créons une expression pour le moment de flexion dans la section A comme la somme des moments de forces à droite et équivalons à zéro. Déterminons maintenant la réaction du support A. Pour cela, créons une expression pour les moments de flexion dans la section comme la somme des moments de forces à gauche Le diagramme de conception de la poutre avec. une charge est représentée sur la Fig. 1.7, ch. En partant de l'extrémité gauche de la poutre, on calcule les valeurs des efforts transversaux dans les sections limites des sections : le diagramme Q est représenté sur la Fig. 1.7, d. Le problème considéré peut être résolu en élaborant pour M, Q sur chaque site. Choisissons l'origine des coordonnées à l'extrémité gauche de la poutre. Dans la section AC, le diagramme M est exprimé par une parabole carrée dont l'équation a la forme Les constantes a, b, c sont trouvées à partir de la condition que la parabole passe par trois points de coordonnées connues : Remplacement des coordonnées des points dans l'équation de la parabole, nous obtenons : L'expression du moment fléchissant sera En différenciant la fonction M1 , nous obtenons la dépendance pour la force transversale. Après avoir différencié la fonction Q, nous obtenons une expression pour l'intensité de la charge répartie. Dans la section NE, l'expression du moment fléchissant est présentée sous la forme d'une fonction linéaire. Pour déterminer les constantes a et b, nous utilisons les conditions selon lesquelles cette droite passe par deux points dont les coordonnées sont connues. obtenir deux équations : ,b à partir desquelles nous obtenons un 20. L'équation du moment fléchissant dans la section NE sera Après double différenciation de M2, nous trouverons En utilisant les valeurs trouvées de M et Q, nous construisons des diagrammes de. moments de flexion et efforts tranchants de la poutre. En plus de la charge répartie, des forces concentrées sont appliquées à la poutre dans trois sections, où se trouvent des sauts sur le diagramme Q et des moments concentrés dans la section où il y a un saut sur le diagramme M. Exemple 1.5 Pour une poutre (Fig. 1.8, a), déterminer la position rationnelle de la charnière C, à laquelle le moment de flexion le plus important dans la travée est égal au moment de flexion dans l'encastrement (en valeur absolue). Construire des diagrammes de Q et M. Solution Détermination des réactions de support. Même si nombre total liens de support est égal à quatre, la poutre est statiquement déterminée. Le moment de flexion dans la charnière C est égal à zéro, ce qui permet de créer une équation supplémentaire : la somme des moments autour de la charnière de toutes les forces extérieures agissant d'un côté de cette charnière est égale à zéro. Compilons la somme des moments de toutes les forces à droite de la charnière C. Le diagramme Q de la poutre est limité par une droite inclinée, puisque q = const. On détermine les valeurs des efforts transversaux dans les sections limites de la poutre : L'abscisse xK de la section, où Q = 0, est déterminée à partir de l'équation à partir de laquelle le diagramme M de la poutre est limité par une parabole carrée. Les expressions pour les moments fléchissants dans les sections, où Q = 0, et dans l'encastrement s'écrivent respectivement comme suit : De la condition d'égalité des moments on obtient équation quadratique par rapport au paramètre x souhaité : Valeur réelle x2x 1,029 m. valeurs numériques efforts transversaux et moments fléchissants dans les sections caractéristiques de la poutre. La figure 1.8, b montre le diagramme Q, et sur la Fig. 1.8, c – schéma M. Le problème considéré pourrait être résolu en divisant la poutre articulée en ses éléments constitutifs, comme le montre la Fig. 1.8, d. Au début, les réactions des supports VC et VB sont déterminées. Des diagrammes de Q et M sont construits pour la poutre suspendue SV à partir de l'action de la charge qui lui est appliquée. Ensuite, ils se déplacent vers la poutre principale AC, en la chargeant d'une force supplémentaire VC, qui est la force de pression de la poutre CB sur la poutre AC. Ensuite, les diagrammes Q et M sont construits pour le faisceau AC. 1.4. Calculs de résistance pour la flexion directe des poutres Calculs de résistance basés sur les contraintes normales et de cisaillement. Lorsqu'une poutre se plie directement dans ses sections transversales, des contraintes normales et tangentielles apparaissent (Fig. 1.9). 18 Fig. 1.9 Les contraintes normales sont associées au moment de flexion, les contraintes tangentielles sont associées à la force de cisaillement. En flexion droite pure, les contraintes de cisaillement sont nulles. Contraintes normales en un point arbitraire coupe transversale les poutres sont déterminées par la formule (1.4) où M est le moment de flexion dans une section donnée ; Iz – moment d'inertie de la section par rapport à l'axe neutre z ; y est la distance entre le point où la tension normale est déterminée et l'axe z neutre. Les contraintes normales le long de la hauteur de la section changent selon une loi linéaire et atteignent leur plus grande valeur aux points les plus éloignés de l'axe neutre. Si la section est symétrique par rapport à l'axe neutre (Fig. 1.11), alors la Fig. 1.11 les contraintes de traction et de compression les plus élevées sont les mêmes et sont déterminées par la formule,  est le moment de résistance axial de la section pendant la flexion. Pour une section rectangulaire de largeur b et de hauteur h : (1.7) Pour anneaux. Pour les poutres en matières plastiques, les plus rationnelles sont les formes symétriques à 20 sections (poutre en I, en caisson, annulaire). Pour les poutres constituées de matériaux fragiles qui ne résistent pas également à la traction et à la compression, les sections asymétriques par rapport à l'axe z neutre (poutre en T, poutre en U, poutre en I asymétrique) sont rationnelles. Pour les poutres de section constante en matériaux plastiques avec des formes de section symétriques, la condition de résistance s'écrit comme suit : (1.10) où Mmax est le moment de flexion maximal en module ; – contrainte admissible pour le matériau. Pour les poutres de section constante en matériaux plastiques présentant des formes de section asymétriques, la condition de résistance s'écrit sous la forme suivante : (1.11) Pour les poutres en matériaux fragiles dont les sections sont asymétriques par rapport à l'axe neutre, si le diagramme M est sans ambiguïté (Fig. 1.12), vous devez écrire deux conditions de résistance - les distances de l'axe neutre aux points les plus éloignés des zones étirées et comprimées de la section dangereuse, respectivement ; P – contraintes admissibles pour la traction et la compression, respectivement. Figure 1.12. 17) où Szo,тmсax est le moment statique de la demi-section par rapport à l'axe neutre ; d – épaisseur de paroi de la poutre en I. Généralement, les dimensions de la section transversale d'une poutre sont déterminées à partir des conditions de résistance sous contraintes normales. Le contrôle de la résistance des poutres par contraintes tangentielles est obligatoire pour les poutres courtes et les poutres de toute longueur s'il existe des forces concentrées de grande ampleur à proximité des supports, ainsi que pour les poutres en bois, rivetées et soudées. Exemple 1.6 Vérifier la résistance d'une poutre en caisson (Fig. 1.14) en utilisant les contraintes normales et de cisaillement, si MPa. Construire des diagrammes dans la section dangereuse du faisceau. Riz. 1.14 Solution 23 1. Construire des diagrammes de Q et M à l'aide de sections caractéristiques. En considérant le côté gauche de la poutre, on obtient Le diagramme des forces transversales est présenté sur la Fig. 1.14, ch. Le diagramme des moments fléchissants est présenté sur la Fig. 5.14, g.2. section ronde section transversale 3. Les contraintes normales les plus élevées dans la section C, où Mmax agit (modulo) : MPa. Les contraintes normales maximales dans la poutre sont presque égales à celles admissibles. 4. Les contraintes tangentielles les plus élevées dans la section C (ou A), où max Q agit (modulo) : Voici le moment statique de l'aire de la demi-section par rapport à l'axe neutre ; b2 cm – largeur de section au niveau de l'axe neutre. 5. Contraintes tangentielles en un point (dans le mur) de la coupe C : Fig. 1.15 Ici Szomc 834,5 108 cm3 est le moment statique de l'aire de la section située au dessus de la ligne passant par le point K1 ; b2 cm – épaisseur de paroi au niveau du point K1. Les diagrammes  et  pour la section C de la poutre sont présentés sur la Fig. 1.15. Exemple 1.7 Pour la poutre illustrée à la Fig. 1.16, a, requis : 1. Construire des diagrammes des efforts transversaux et des moments fléchissants le long de sections caractéristiques (points). 2. Déterminez les dimensions de la section transversale sous la forme d'un cercle, d'un rectangle et d'une poutre en I à partir de l'état de résistance sous contraintes normales, comparez les surfaces de la section transversale. 3. Vérifiez les dimensions sélectionnées des sections de poutre en fonction de la contrainte tangentielle. Donné : Solution : 1. Déterminer les réactions des supports de poutre. Vérifier : 2. Construction des diagrammes Q et M. Valeurs des efforts transversaux dans les sections caractéristiques de la poutre 25 Fig. 1.16 Dans les sections CA et AD, intensité de charge q = const. Par conséquent, dans ces zones, le diagramme Q se limite à des droites inclinées par rapport à l'axe. Dans la section DB, l'intensité de la charge répartie est q = 0, donc dans cette section, le diagramme Q est limité à une droite parallèle à l'axe des x. Le diagramme Q du faisceau est présenté sur la Fig. 1.16, b. Valeurs des moments fléchissants dans les sections caractéristiques de la poutre : Dans la deuxième section, on détermine l'abscisse x2 de la section dans laquelle Q = 0 : Moment maximum dans la deuxième section Le diagramme M de la poutre est représenté sur la Fig. 1.16, ch. 2. Nous créons une condition de résistance basée sur les contraintes normales à partir de laquelle nous déterminons le moment de résistance axial requis de la section à partir de l'expression déterminée par le diamètre requis d d'une poutre de section circulaire Aire de section circulaire Pour une poutre de section rectangulaire Hauteur requise de la section Aire de section rectangulaire Déterminer le nombre requis poutre en I. En utilisant les tableaux de GOST 8239-89, nous trouvons le plus proche valeur plus élevée moment résistant axial 597 cm3, ce qui correspond à la poutre en I n°33 avec les caractéristiques : A z 9840 cm4. Contrôle de tolérance : (sous-charge de 1 % des 5 % admissibles) la poutre en I n° 30 la plus proche (W 2 cm3) entraîne une surcharge importante (plus de 5 %). Nous acceptons finalement la poutre en I n°33. Nous comparons les surfaces des sections rondes et rectangulaires avec la plus petite surface A de la poutre en I : Parmi les trois sections considérées, la plus économique est la section en I. 3. Nous calculons les contraintes normales les plus élevées dans la section dangereuse 27 de la poutre en I (Fig. 1.17, a) : Contraintes normales dans le mur près de la semelle de la section de la poutre en I. Le diagramme des contraintes normales dans la section dangereuse de le faisceau est montré sur la Fig. 1.17, b. 5. Déterminez les contraintes de cisaillement les plus élevées pour les sections sélectionnées de la poutre. UN) section rectangulaire poutres : b) section ronde de la poutre : c) section de poutre en I : Contraintes tangentielles dans le mur à proximité de l'aile de la poutre en I en section dangereuse A (à droite) (au point 2) : Le diagramme des contraintes tangentielles en section dangereuse Les sections de la poutre en I sont illustrées à la Fig. 1.17, ch. Les contraintes tangentielles maximales dans la poutre ne dépassent pas les contraintes admissibles. Exemple 1.8 Déterminer la charge admissible sur la poutre (Fig. 1.18, a), si 60 MPa, les dimensions de la section transversale sont données (Fig. 1.19, a). Construisez un diagramme des contraintes normales dans une section dangereuse d’une poutre à une charge admissible.

Figure 1.18 1. Détermination des réactions des supports de poutre. En raison de la symétrie du système 2. Construction des diagrammes Q et M à partir de sections caractéristiques. Efforts transversaux dans les sections caractéristiques d'une poutre : le diagramme Q pour une poutre est présenté sur la Fig. 5.18, b.- il s'agit d'un type de déformation dans lequel deux facteurs de force internes apparaissent dans les sections transversales de la tige : le moment de flexion et la force transversale.

Courbe propre- Ce cas particulier flexion directe, dans laquelle seul un moment de flexion se produit dans les sections transversales de la tige et la force transversale est nulle.

Exemple flexion pure- parcelle CD sur la tige AB. Moment de flexion est la quantité Pennsylvanie une paire de forces externes provoquant une flexion. De l'équilibre de la partie de la tige à gauche de la section transversale minute il s'ensuit que les efforts internes répartis sur cette section sont statiquement équivalents au moment M., égal et opposé au moment de flexion Pennsylvanie.

Pour connaître la répartition de ces efforts internes sur la section, il faut considérer la déformation de la tige.

Dans le cas le plus simple, la tige présente un plan de symétrie longitudinal et est soumise à l'action de couples de forces de flexion externes situés dans ce plan. Ensuite, la flexion se fera dans le même plan.

Axe de tige nn 1 est une ligne passant par les centres de gravité de ses sections transversales.

Soit la section transversale de la tige un rectangle. Traçons deux lignes verticales sur ses bords mm Et pp. Lors du pliage, ces lignes restent droites et tournent de manière à rester perpendiculaires aux fibres longitudinales de la tige.

Une autre théorie de la flexion est basée sur l'hypothèse que non seulement les lignes mm Et pp, mais toute la section transversale plate de la tige reste, après pliage, plate et normale aux fibres longitudinales de la tige. Ainsi, lors du pliage, les sections transversales mm Et pp tourner les uns par rapport aux autres autour d'axes perpendiculaires au plan de pliage (plan de dessin). Dans ce cas, les fibres longitudinales du côté convexe subissent une tension et les fibres du côté concave subissent une compression.

Surface neutre- Il s'agit d'une surface qui ne subit pas de déformation lors de la flexion. (Maintenant il est situé perpendiculairement au dessin, l'axe déformé de la tige nn 1 appartient à cette surface).

Axe neutre de section- il s'agit de l'intersection d'une surface neutre avec n'importe quelle section transversale (désormais également située perpendiculairement au dessin).

Soit une fibre arbitraire à distance ouià partir d'une surface neutre. ρ – rayon de courbure de l'axe courbe. Point Ô– centre de courbure. Traçons une ligne n 1 s 1 parallèle mm.article 1– allongement absolu des fibres.

Élongation εx fibres

Il en résulte que déformation des fibres longitudinales proportionnel à la distance oui de la surface neutre et inversement proportionnel au rayon de courbure ρ .

L'allongement longitudinal des fibres du côté convexe de la tige s'accompagne de rétrécissement latéral, et le raccourcissement longitudinal du côté concave est expansion latérale, comme dans le cas d’un simple étirement et compression. De ce fait, l'apparence de toutes les coupes change, les côtés verticaux du rectangle deviennent inclinés. Déformation latérale z:

μ – Coefficient de Poisson.

En raison de cette distorsion, toutes les lignes droites de section parallèles à l'axe z, sont courbés de manière à rester normaux aux côtés latéraux de la section. Le rayon de courbure de cette courbe R. sera plus que ρ au même titre que ε x en valeur absolue est supérieur à ε z et on obtient

Ces déformations des fibres longitudinales correspondent à des contraintes

La tension dans n'importe quelle fibre est proportionnelle à sa distance par rapport à l'axe neutre n 1 n 2. Position de l'axe neutre et rayon de courbure ρ – deux inconnues dans l'équation de σ x – peut être déterminé à partir de la condition selon laquelle les forces réparties sur n'importe quelle section transversale forment une paire de forces qui équilibre le moment externe M..

Tout ce qui précède est également vrai si la tige ne possède pas de plan de symétrie longitudinal dans lequel agit le moment de flexion, à condition que le moment de flexion agisse dans le plan axial qui contient l'un des deux axes principaux coupe transversale. Ces avions sont appelés plans de pliage principaux.

Lorsqu'il existe un plan de symétrie et que le moment fléchissant agit dans ce plan, la déflexion se produit précisément dans celui-ci. Moments d'efforts internes par rapport à l'axe zéquilibrer le moment extérieur M.. Moments d'effort autour de l'axe oui sont mutuellement détruits.

Pour une poutre en porte-à-faux chargée avec une charge répartie d'intensité kN/m et un moment concentré de kN m (Fig. 3.12), il faut : construire des diagrammes d'efforts tranchants et de moments fléchissants, sélectionner une poutre de section circulaire avec une contrainte normale admissible kN/cm2 et vérifier la résistance de la poutre en fonction des contraintes tangentielles avec une contrainte tangentielle admissible kN/cm2. Dimensions de la poutre m ; m; m.

Schéma de calcul pour le problème de flexion transversale directe

Riz. 3.12

Solution du problème « flexion transversale droite »

Déterminer les réactions de soutien

La réaction horizontale dans l'encastrement est nulle, puisque les charges externes dans la direction de l'axe z n'agissent pas sur la poutre.

Nous choisissons les directions des forces de réaction restantes apparaissant dans l’encastrement : nous dirigerons la réaction verticale, par exemple vers le bas, et le moment – ​​​​dans le sens des aiguilles d’une montre. Leurs valeurs sont déterminées à partir des équations statiques :

Lors de la composition de ces équations, nous considérons que le moment est positif lors d'une rotation dans le sens inverse des aiguilles d'une montre, et la projection de la force est positive si sa direction coïncide avec la direction positive de l'axe y.

A partir de la première équation on trouve le moment au joint :

De la deuxième équation - réaction verticale :

Les valeurs positives que nous avons obtenues pour l'instant et la réaction verticale dans l'encastrement indiquent que nous avons deviné leurs directions.

Conformément à la nature de la fixation et du chargement de la poutre, nous divisons sa longueur en deux sections. Le long des limites de chacune de ces sections, nous délimiterons quatre sections transversales (voir Fig. 3.12), dans lesquelles nous utiliserons la méthode des sections (ROZU) pour calculer les valeurs des efforts tranchants et des moments fléchissants.

Section 1. Rejetons mentalement le côté droit de la poutre. Remplaçons son action par celle restante côté gauche force de cisaillement et moment de flexion. Pour faciliter le calcul de leurs valeurs, recouvrons le côté droit de la poutre avec un morceau de papier, en alignant le bord gauche de la feuille avec la section considérée.

Rappelons que la force de cisaillement apparaissant dans toute section transversale doit équilibrer toutes les forces externes (actives et réactives) qui agissent sur la partie de la poutre considérée (c'est-à-dire visible) par nous. Par conséquent, la force de cisaillement doit être égale à la somme algébrique de toutes les forces que nous observons.

Présentons également la règle des signes de l'effort tranchant : une force extérieure agissant sur la partie de la poutre considérée et tendant à « faire tourner » cette partie par rapport à la section dans le sens des aiguilles d'une montre provoque une force de cisaillement positive dans la section. Une telle force externe est incluse dans la somme algébrique pour la définition avec un signe plus.

Dans notre cas, nous ne voyons que la réaction du support, qui fait tourner la partie du faisceau qui nous est visible par rapport à la première section (par rapport au bord de la feuille de papier) dans le sens inverse des aiguilles d'une montre. C'est pourquoi

kN.

Le moment de flexion dans n'importe quelle section doit équilibrer le moment créé par les forces externes visibles par rapport à la section en question. Par conséquent, il est égal à la somme algébrique des moments de toutes les forces qui agissent sur la partie de la poutre considérée, par rapport à la section considérée (c'est-à-dire par rapport au bord de la feuille de papier). Dans ce cas, la charge externe, courbant la partie de la poutre considérée avec sa convexité vers le bas, provoque un moment de flexion positif dans la section. Et le moment créé par une telle charge est inclus dans la somme algébrique pour détermination avec un signe « plus ».

Nous voyons deux efforts : la réaction et le moment de clôture. Cependant, l'effet de levier de la force par rapport à la section 1 est nul. C'est pourquoi

kNm.

Nous avons pris le signe « plus » car le moment réactif plie la partie du faisceau que nous voyons avec une convexité vers le bas.

Section 2. Comme précédemment, nous couvrirons tout le côté droit de la poutre avec un morceau de papier. Or, contrairement à la première section, la force a un épaulement : m.

kN ; kNm.

Section 3. En fermant le côté droit de la poutre, on trouve

kN ;

Section 4. Couvrir le côté gauche de la poutre avec une feuille. Alors

kNm.

kNm.

.

En utilisant les valeurs trouvées, nous construisons des diagrammes des forces de cisaillement (Fig. 3.12, b) et des moments de flexion (Fig. 3.12, c).

Sous les zones non chargées, le diagramme des forces de cisaillement est parallèle à l'axe de la poutre et sous une charge répartie q - le long d'une ligne droite inclinée vers le haut. Sous la réaction de support dans le diagramme, il y a un saut de la valeur de cette réaction, c'est-à-dire de 40 kN.

Dans le diagramme des moments fléchissants, nous voyons une rupture sous la réaction d'appui. L'angle de courbure est dirigé vers la réaction d'appui. Sous charge distribuée q, le diagramme change en fonction de parabole quadratique, dont la convexité est dirigée vers la charge. Dans la section 6 du diagramme, il y a un extremum, puisque le diagramme de la force de cisaillement à cet endroit passe par la valeur zéro.

Déterminer le diamètre de section transversale requis de la poutre

La condition normale de résistance à la contrainte a la forme :

,

où est le moment résistant de la poutre lors de la flexion. Pour une poutre de section circulaire, elle est égale à :

.

Le plus grand par valeur absolue le moment de flexion se produit dans la troisième section de la poutre : kN cm

Ensuite, le diamètre de faisceau requis est déterminé par la formule

cm.

Nous acceptons mm. Alors

kN/cm2 kN/cm2.

La « surtension » est

,

ce qui est permis.

Nous vérifions la résistance de la poutre par les contraintes de cisaillement les plus élevées

Les plus grandes contraintes de cisaillement apparaissant dans la section transversale d'une poutre de section circulaire sont calculées par la formule

,

où est la surface de la section transversale.

D'après le diagramme, la plus grande valeur algébrique de la force de cisaillement est égale à kN. Alors

kN/cm2 kN/cm2,

c'est-à-dire que la condition de résistance pour les contraintes tangentielles est également satisfaite, et avec une large marge.

Un exemple de résolution du problème « flexion transversale droite » n°2

Condition d'un exemple de problème en flexion transversale droite

Pour une poutre simplement appuyée chargée d'une charge répartie d'intensité kN/m, de force concentrée kN et de moment concentré kN m (Fig. 3.13), il est nécessaire de construire des diagrammes d'efforts tranchants et de moments fléchissants et de sélectionner une poutre de poutre en I. section transversale avec une contrainte normale admissible kN/cm2 et une contrainte tangentielle admissible kN/cm2. Portée du faisceau m.

Un exemple de problème de flexion droite - schéma de conception

Riz. 3.13

Solution d'un exemple de problème de pliage droit

Déterminer les réactions de soutien

Pour une poutre simplement appuyée donnée, il est nécessaire de trouver trois réactions d'appui : , et . Puisque seules les charges verticales perpendiculaires à son axe agissent sur la poutre, la réaction horizontale du support fixe articulé A est nulle : .

Les directions des réactions verticales sont choisies arbitrairement. Dirigons, par exemple, les deux réactions verticales vers le haut. Pour calculer leurs valeurs, créons deux équations statiques :

Rappelons que la résultante d'une charge linéaire , uniformément répartie sur une section de longueur l, est égale à , c'est-à-dire égale à l'aire du diagramme de cette charge et elle est appliquée au centre de gravité de cette diagramme, c'est-à-dire au milieu de la longueur.

;

kN.

Vérifions : .

Rappelons que les forces dont la direction coïncide avec la direction positive de l'axe y sont projetées (projetées) sur cet axe avec un signe plus :

c'est vrai.

Nous construisons des diagrammes d'efforts tranchants et de moments fléchissants

Nous divisons la longueur de la poutre en sections distinctes. Les limites de ces sections sont les points d'application des forces concentrées (actives et/ou réactives), ainsi que les points correspondant au début et à la fin de la charge répartie. Il y a trois sections de ce type dans notre problème. Le long des limites de ces sections, nous délimiterons six sections transversales dans lesquelles nous calculerons les valeurs des efforts tranchants et des moments fléchissants (Fig. 3.13, a).

Section 1. Rejetons mentalement le côté droit de la poutre. Pour faciliter le calcul de la force de cisaillement et du moment de flexion apparaissant dans cette section, nous couvrirons la partie de la poutre que nous avons jetée avec un morceau de papier, en alignant le bord gauche de la feuille de papier avec la section elle-même.

La force de cisaillement dans la section de poutre est égale à la somme algébrique de toutes les forces externes (actives et réactives) que nous observons. DANS dans ce cas nous voyons la réaction d'appui et la charge linéaire q réparties sur une longueur infinitésimale. La charge linéaire résultante est nulle. C'est pourquoi

kN.

Le signe plus est pris car la force fait tourner la partie du faisceau que nous voyons par rapport à la première section (le bord d'un morceau de papier) dans le sens des aiguilles d'une montre.

Le moment de flexion dans la section de poutre est égal à la somme algébrique des moments de toutes les forces que l'on voit par rapport à la section considérée (c'est-à-dire par rapport au bord de la feuille de papier). Nous voyons la réaction d'appui et la charge linéaire q réparties sur une longueur infinitésimale. Cependant, la force a un effet de levier nul. La charge linéaire résultante est également nulle. C'est pourquoi

Section 2. Comme précédemment, nous couvrirons tout le côté droit de la poutre avec un morceau de papier. Nous voyons maintenant la réaction et la charge q agissant sur une section de longueur . La charge linéaire résultante est égale à . Il est fixé au milieu d'un tronçon de longueur. C'est pourquoi

Rappelons que lors de la détermination du signe du moment fléchissant, nous libérons mentalement la partie de la poutre qui nous est visible de toutes les fixations de support réelles et l'imaginons comme pincée dans la section considérée (c'est-à-dire que nous imaginons mentalement le bord gauche d'un morceau de papier comme encastrement rigide).

Section 3. Fermons le côté droit. Nous obtenons

Section 4. Couvrir le côté droit de la poutre avec une feuille. Alors

Maintenant, pour vérifier l’exactitude des calculs, recouvrons le côté gauche de la poutre avec un morceau de papier. On voit la force concentrée P, la réaction de l'appui droit et la charge linéaire q répartie sur une longueur infinitésimale. La charge linéaire résultante est nulle. C'est pourquoi

kNm.

Autrement dit, tout est correct.

Section 5. Comme précédemment, fermez le côté gauche de la poutre. Nous aurons

kN ;

kNm.

Section 6. Fermons à nouveau le côté gauche de la poutre. Nous obtenons

kN ;

En utilisant les valeurs trouvées, nous construisons des diagrammes des forces de cisaillement (Fig. 3.13, b) et des moments de flexion (Fig. 3.13, c).

Nous veillons à ce que sous la zone non chargée, le diagramme des forces de cisaillement soit parallèle à l'axe de la poutre, et sous une charge répartie q - le long d'une ligne droite inclinée vers le bas. Il y a trois sauts dans le diagramme : sous la réaction - en hausse de 37,5 kN, sous la réaction - en hausse de 132,5 kN et sous la force P - en baisse de 50 kN.

Dans le diagramme des moments fléchissants, nous voyons des ruptures sous la force concentrée P et sous les réactions d'appui. Les angles de fracture sont dirigés vers ces forces. Sous une charge distribuée d'intensité q, le diagramme évolue le long d'une parabole quadratique dont la convexité est dirigée vers la charge. Sous le moment concentré, il y a un saut de 60 kN·m, c'est-à-dire de la valeur du moment lui-même. Dans la section 7 du diagramme, il y a un extremum, puisque le diagramme de la force de cisaillement pour cette section passe par la valeur zéro (). Déterminons la distance de la section 7 au support gauche.

Nous commencerons par le cas le plus simple, celui que l’on appelle le virage pur.

La flexion pure est un cas particulier de flexion dans lequel l'effort transversal dans les sections de la poutre est nul. La flexion pure ne peut se produire que lorsque le poids propre de la poutre est si faible que son influence peut être négligée. Pour les poutres sur deux appuis, exemples de charges provoquant des

flexion, illustrée à la Fig. 88. Dans les sections de ces poutres, où Q = 0 et, par conséquent, M = const ; une flexion pure a lieu.

Les forces dans n'importe quelle section de la poutre lors de la flexion pure sont réduites à une paire de forces dont le plan d'action passe par l'axe de la poutre et le moment est constant.

Les tensions peuvent être déterminées sur la base des considérations suivantes.

1. Les composantes tangentielles des forces le long des zones élémentaires de la section transversale d'une poutre ne peuvent être réduites à un couple de forces dont le plan d'action est perpendiculaire au plan de section. Il s'ensuit que l'effort de flexion dans la section est le résultat d'une action le long des zones élémentaires

uniquement les forces normales, et donc en flexion pure, les contraintes sont réduites uniquement à la normale.

2. Pour que les efforts sur les sites élémentaires soient réduits à seulement quelques forces, parmi elles il faut qu'il y ait à la fois du positif et du négatif. Par conséquent, les fibres de tension et de compression de la poutre doivent exister.

3. Du fait que les forces dans différentes sections sont les mêmes, les contraintes aux points correspondants des sections sont les mêmes.

Considérons un élément proche de la surface (Fig. 89, a). Puisqu’aucune force n’est appliquée le long de son bord inférieur, qui coïncide avec la surface de la poutre, aucune contrainte n’est exercée sur celle-ci. Il n'y a donc aucune contrainte sur le bord supérieur de l'élément, car sinon l'élément ne serait pas en équilibre. En considérant l'élément qui lui est adjacent en hauteur (Fig. 89, b), on arrive à.

La même conclusion, etc. Il s'ensuit qu'il n'y a aucune contrainte le long des bords horizontaux d'un élément. En considérant les éléments qui composent la couche horizontale, en commençant par l'élément proche de la surface de la poutre (Fig. 90), nous arrivons à la conclusion qu'il n'y a aucune contrainte le long des bords verticaux latéraux d'aucun élément. Ainsi, l'état de contrainte de tout élément (Fig. 91, a), et dans la limite de la fibre, doit être représenté comme le montre la Fig. 91,b, c'est-à-dire qu'il peut s'agir soit d'une traction axiale, soit d'une compression axiale.

4. En raison de la symétrie de l'application des forces externes, la section au milieu de la longueur de la poutre après déformation doit rester plate et normale à l'axe de la poutre (Fig. 92, a). Pour la même raison, les sections en quarts de longueur de la poutre restent également plates et normales à l'axe de la poutre (Fig. 92, b), à moins que les sections extrêmes de la poutre lors de la déformation restent plates et normales à l'axe de le faisceau. Une conclusion similaire est valable pour les sections en huitièmes de la longueur de la poutre (Fig. 92, c), etc. Par conséquent, si pendant la flexion les sections extérieures de la poutre restent plates, alors pour toute section, il reste

Il est juste de dire qu'après déformation, elle reste plate et normale à l'axe de la poutre incurvée. Mais dans ce cas, il est évident que le changement d'allongement des fibres de la poutre le long de sa hauteur doit se produire non seulement de manière continue, mais également de manière monotone. Si l'on appelle couche un ensemble de fibres ayant les mêmes allongements, alors il résulte de ce qui a été dit que les fibres étirées et comprimées de la poutre doivent être situées le long différents côtés de la couche dans laquelle les allongements des fibres sont nuls. On appellera neutres les fibres dont les allongements sont nuls ; une couche constituée de fibres neutres est une couche neutre ; la ligne d'intersection de la couche neutre avec le plan de section transversale du faisceau - la ligne neutre de cette section. Ensuite, sur la base du raisonnement précédent, on peut affirmer qu'avec la flexion pure d'une poutre, dans chaque section il y a une ligne neutre qui divise cette section en deux parties (zones) : une zone de fibres étirées (zone étirée) et une zone de fibres compressées (zone compressée). En conséquence, aux points de la zone étirée de la section, des contraintes de traction normales doivent agir, aux points de la zone comprimée - des contraintes de compression, et aux points de la ligne neutre les contraintes sont égales à zéro.

Ainsi, en flexion pure d'une poutre de section constante :

1) seules les contraintes normales agissent par sections ;

2) la section entière peut être divisée en deux parties (zones) - étirées et comprimées ; la limite des zones est la ligne de section neutre, aux points de laquelle les contraintes normales sont égales à zéro ;

3) tout élément longitudinal de la poutre (dans la limite, toute fibre) est soumis à tension axiale ou compression, de sorte que les fibres adjacentes n'interagissent pas les unes avec les autres ;

4) si les sections extrêmes de la poutre lors de la déformation restent plates et normales à l'axe, alors toutes ses sections transversales restent plates et normales à l'axe de la poutre courbe.

Etat de contrainte d'une poutre en flexion pure

Considérons un élément d'une poutre soumis à une flexion pure, en concluant situé entre les sections m-m et n-n, qui sont espacées les unes des autres d'une distance infinitésimale dx (Fig. 93). En raison de la position (4) du paragraphe précédent, les sections m- m et n - n, qui étaient parallèles avant déformation, restant plates après pliage, formeront un angle dQ et se couperont selon une droite passant par le point C, qui est le centre de courbure de la fibre neutre NN. Alors la partie AB de la fibre enfermée entre elles, située à une distance z de la fibre neutre (la direction positive de l'axe z est prise vers la convexité de la poutre lors de la flexion), se transformera après déformation en un arc AB. morceau de fibre neutre O1O2, s'étant transformé en arc, O1O2 ne changera pas de longueur, tandis que la fibre AB recevra un allongement :

avant déformation

après déformation

où p est le rayon de courbure de la fibre neutre.

L’allongement absolu du segment AB est donc égal à

et allongement relatif

Puisque, selon la position (3), la fibre AB est soumise à une tension axiale, alors lors de la déformation élastique

Cela montre que les contraintes normales le long de la hauteur de la poutre sont réparties selon une loi linéaire (Fig. 94). Puisque la force égale de toutes les forces sur toutes les sections élémentaires de la section doit être égale à zéro, alors

d'où, en substituant la valeur de (5.8), on trouve

Mais la dernière intégrale est un moment statique autour de l'axe Oy, perpendiculaire au plan d'action des forces de flexion.

Du fait de son égalité à zéro, cet axe doit passer par le centre de gravité O de la section. Ainsi, la ligne de section neutre de la poutre est une droite y, perpendiculaire au plan d'action des forces de flexion. C'est ce qu'on appelle l'axe neutre de la section de la poutre. Il résulte ensuite de (5.8) que les contraintes en des points situés à la même distance de l'axe neutre sont les mêmes.

Le cas de flexion pure, dans lequel les forces de flexion agissent dans un seul plan, provoquant une flexion uniquement dans ce plan, est une flexion pure plane. Si ledit plan passe par l'axe Oz, alors le moment des forces élémentaires par rapport à cet axe doit être égal à zéro, c'est-à-dire

En substituant ici la valeur de σ de (5.8), nous trouvons

L'intégrale du côté gauche de cette égalité, comme on le sait, est le moment d'inertie centrifuge de la section par rapport aux axes y et z, donc

Les axes autour desquels le moment d'inertie centrifuge de la section est nul sont appelés axes principaux d'inertie de cette section. S'ils traversent en outre le centre de gravité de la section, ils peuvent alors être appelés les principaux axes centraux d'inertie de la section. Ainsi, en flexion pure à plat, la direction du plan d'action des efforts de flexion et l'axe neutre de la section sont les principaux axes centraux d'inertie de cette dernière. En d'autres termes, pour obtenir une courbure plate et pure d'une poutre, la charge ne peut lui être appliquée arbitrairement : elle doit être réduite aux forces agissant dans le plan passant par l'un des principaux axes centraux inertie des sections de poutres ; dans ce cas, l'autre axe central principal d'inertie sera l'axe neutre de la section.

Comme on le sait, dans le cas d'une section symétrique par rapport à un axe quelconque, l'axe de symétrie est l'un de ses principaux axes centraux d'inertie. Par conséquent, dans ce cas particulier on obtiendra certainement une flexion pure en appliquant des charges appropriées dans un plan passant par l'axe longitudinal de la poutre et l'axe de symétrie de sa section. Une droite perpendiculaire à l'axe de symétrie et passant par le centre de gravité de la section est l'axe neutre de cette section.

Après avoir établi la position de l'axe neutre, il n'est pas difficile de trouver l'ampleur de la contrainte en tout point de la section. En effet, puisque la somme des moments des forces élémentaires par rapport à l'axe neutre yy doit être égale au moment fléchissant, alors

d'où, en substituant la valeur de σ de (5.8), nous trouvons

Puisque l'intégrale est. moment d'inertie de la section par rapport à l'axe yy, alors

et de l’expression (5.8) on obtient

Le produit EI Y est appelé rigidité en flexion de la poutre.

Les contraintes de traction et de compression les plus importantes en valeur absolue agissent aux points de la section pour lesquels valeur absolue z est le plus grand, c'est-à-dire aux points les plus éloignés de l'axe neutre. Avec la notation Fig. 95 nous avons

La valeur Jy/h1 est appelée moment de résistance de la section à la traction et est notée Wyr ; de même, Jy/h2 est appelé moment résistant de la section à la compression

et désignent Wyc, donc

et donc

Si l'axe neutre est l'axe de symétrie de la section, alors h1 = h2 = h/2 et donc Wyp = Wyc, il n'y a donc pas besoin de les distinguer, et ils utilisent la même notation :

appelant W y simplement le moment résistant de la section. Par conséquent, dans le cas d'une section symétrique par rapport à l'axe neutre,

Toutes les conclusions ci-dessus ont été obtenues sur la base de l'hypothèse selon laquelle les sections transversales de la poutre, lorsqu'elle est courbée, restent plates et normales à son axe (hypothèse des sections plates). Comme cela a été démontré, cette hypothèse n'est valable que dans le cas où les sections extrêmes (d'extrémité) de la poutre restent plates pendant la flexion. En revanche, de l'hypothèse des sections planes, il résulte que les forces élémentaires dans de telles sections doivent être réparties selon une loi linéaire. Par conséquent, pour la validité de la théorie résultante de flexion pure à plat, il est nécessaire que les moments de flexion aux extrémités de la poutre soient appliqués sous la forme d'efforts élémentaires répartis sur la hauteur de la section selon une loi linéaire (Fig. 96), coïncidant avec la loi de répartition des contraintes sur la hauteur des poutres profilées. Cependant, sur la base du principe de Saint-Venant, on peut affirmer que changer la méthode d'application des moments fléchissants aux extrémités de la poutre n'entraînera que des déformations locales dont l'effet n'affectera qu'une certaine distance de ces extrémités (approximativement égale à la hauteur de la section). Les sections situées sur le reste de la longueur de la poutre resteront plates. Par conséquent, la théorie énoncée de la flexion pure à plat pour toute méthode d'application des moments de flexion n'est valable que dans la partie médiane de la longueur de la poutre, située à partir de ses extrémités à des distances approximativement égales à la hauteur de la section. Il est donc clair que cette théorie est évidemment inapplicable si la hauteur de la section dépasse la moitié de la longueur ou de l'envergure de la poutre.

Classification des types de pliage de tiges

Plier Ce type de déformation est appelé dans lequel des moments de flexion se produisent dans les sections transversales de la tige. Une tige qui se plie est généralement appelée faisceau. Si les moments de flexion sont les seuls facteurs de force internes dans les sections transversales, alors la tige subit virage propre. Si les moments de flexion se produisent en même temps que les forces transversales, cette flexion est alors appelée transversal.

Les poutres, les essieux, les arbres et autres pièces structurelles fonctionnent pour le pliage.

Introduisons quelques concepts. Le plan passant par l'un des axes centraux principaux de la section et l'axe géométrique de la tige est appelé plan principal. Le plan dans lequel les charges externes agissent, provoquant la flexion de la poutre, est appelé plan de force. La ligne d'intersection du plan de force avec le plan de section transversale de la tige est appelée ligne électrique. Selon position relative La force et les plans principaux de la poutre se distinguent par une flexion directe ou oblique. Si le plan de force coïncide avec l'un des plans principaux, alors la tige subit virage droit(Fig. 5.1, UN), si cela ne correspond pas - oblique(Fig. 5.1, b).

Riz. 5.1. Courbure de la tige : UN- droit; b- oblique

D'un point de vue géométrique, la flexion de la tige s'accompagne d'une modification de la courbure de l'axe de la tige. L'axe initialement droit de la tige devient courbé lorsqu'elle est courbée. En cas de flexion directe, l'axe courbe de la tige se trouve dans le plan de force ; en cas de flexion oblique, il se trouve dans un plan différent du plan de force.

En observant la flexion d'une tige en caoutchouc, vous remarquerez qu'une partie de ses fibres longitudinales est étirée et l'autre partie est comprimée. Évidemment, entre les fibres étirées et comprimées de la tige se trouve une couche de fibres qui ne subissent ni tension ni compression - ce qu'on appelle couche neutre. La ligne d'intersection de la couche neutre de la tige avec le plan de sa section transversale est appelée ligne de section neutre.

En règle générale, les charges agissant sur une poutre peuvent être classées en trois types : forces concentrées R, moments concentrés M. charges distribuées intensité ts(Fig. 5.2). La partie I de la poutre située entre les supports est appelée en vol, partie II de la poutre située d'un côté du support - console.