Réduire une forme quadratique à une forme canonique en ligne. Formes bilinéaires et quadratiques. Réduction d'une forme quadratique à une forme canonique. Méthode de Lagrange
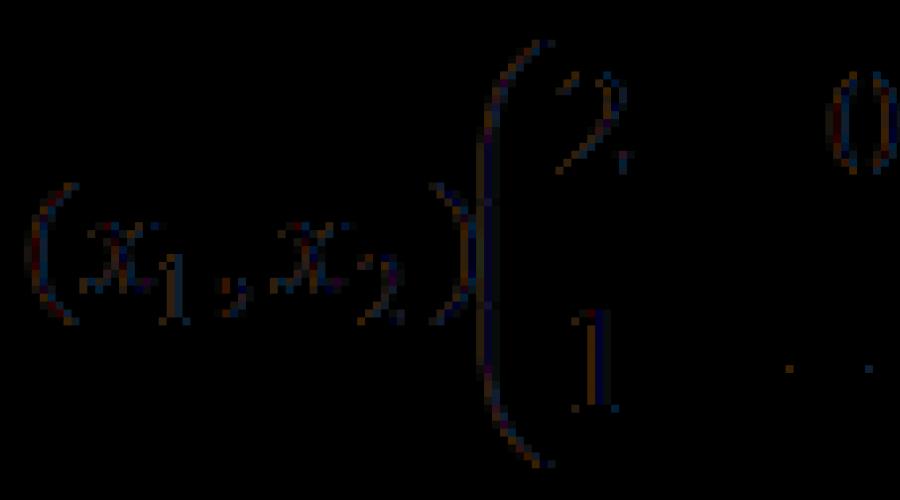
Lire aussi
220400 Algèbre et géométrie Tolstikov A.V.
Conférences 16. Formes bilinéaires et quadratiques.
Plan
1. Forme bilinéaire et ses propriétés.
2. Forme quadratique. Matrice de forme quadratique. Coordonner la transformation.
3. Réduction de la forme quadratique à la forme canonique. Méthode de Lagrange.
4. La loi d'inertie des formes quadratiques.
5. Réduction d'une forme quadratique à une forme canonique en utilisant la méthode des valeurs propres.
6. Critère de Silverst pour la définition positive d'une forme quadratique.
1. Cours de géométrie analytique et d'algèbre linéaire. Moscou : Nauka, 1984.
2. Bugrov Ya.S., Nikolsky S.M. Eléments d'algèbre linéaire et de géométrie analytique. 1997.
3. Voevodin V.V. Algèbre linéaire M. : Nauka 1980.
4. Collection de tâches pour les collèges techniques. Algèbre linéaire et principes fondamentaux de l'analyse mathématique. Éd. Efimov A.V., Demidovich B.P.. M.: Nauka, 1981.
5. Butuzov V.F., Krutitskaya N.Ch., Shishkin A.A. Algèbre linéaire en questions et problèmes. Moscou : Fizmatlit, 2001.
, , , ,
1. Forme bilinéaire et ses propriétés. Laisser V - n-espace vectoriel dimensionnel sur le champ P
Définition 1.forme bilinéaire défini sur V, un tel affichage est appelé g: V2® P, qui à chaque paire ordonnée ( X , y ) vecteurs X , y de mises en V faire correspondre le numéro du champ P, noté g(X , y ), et linéaire dans chacune des variables X , y , c'est à dire. ayant des propriétés :
1) ("X , y , z Î V)g(X + y , z ) = g(X , z ) + g(y , z );
2) ("X , y Î V) ("un О P)g(un X , y ) = un g(X , y );
3) ("X , y , z Î V)g(X , y + z ) = g(X , y ) + g(X , z );
4) ("X , y Î V) ("un О P)g(X , un y ) = un g(X , y ).
Exemple 1. Tout produit scalaire défini sur un espace vectoriel V est une forme bilinéaire.
2 . Une fonction h(X , y ) = 2X 1 y 1 - X 2 y 2 +X 2 y 1 , où X = (X 1 ,X 2), y = (y 1 ,y 2) О R 2, forme bilinéaire sur R 2 .
Définition 2. Laisser v = (v 1 , v 2 ,…, v n v.Matrice de forme bilinéaireg(X , y ) par rapport à la basev appelée matrice B=(b ij)n ´ n, dont les éléments sont calculés par la formule b ij = g(v je, v j):
Exemple 3. Forme bilinéaire matricielle h(X , y ) (voir exemple 2) par rapport à la base e 1 = (1,0), e 2 = (0,1) est égal à .
Théorème 1. LaisserColonnes de coordonnées X, Y respectivement de vecteursX , y en basev, B - matrice de forme bilinéaireg(X , y ) par rapport à la basev. Alors la forme bilinéaire peut s'écrire
g(X , y )=X t PAR. (1)
Preuve. Par les propriétés de la forme bilinéaire, on obtient
Exemple 3. forme bilinéaire h(X
,
y
) (voir exemple 2) peut s'écrire h(X
, y
)= .
.
Théorème 2. Laisser v = (v 1 , v 2 ,…, v n), tu = (tu 1 , tu 2 ,…, tu n) - deux bases spatiales vectoriellesV, T - matrice de transition à partir de la basev à la basetu. Laisser B= (b ij)n ´ n et À PARTIR DE=(avec ij)n ´ n - matrices de forme bilinéaireg(X , y ) respectivement par rapport aux basesv ettu. Puis
À PARTIR DE=T BT.(2)
Preuve. Par définition de la matrice de transition et de la matrice de la forme bilinéaire, on trouve :

Définition 2. Forme bilinéaire g(X , y ) est appelé symétrique, si g(X , y ) = g(y , X ) pour toute X , y Î v.
Théorème 3. Forme bilinéaireg(X , y )- symétrique si et seulement si la matrice de la forme bilinéaire est symétrique par rapport à toute base.
Preuve. Laisser v = (v 1 , v 2 ,…, v n) - base d'espace vectoriel V, B= (b ij)n ´ n- matrices de forme bilinéaire g(X , y ) par rapport à la base v. Soit la forme bilinéaire g(X , y ) est symétrique. Alors par définition 2 pour tout je, j = 1, 2,…, n Nous avons b ij = g(v je, v j) = g(v j, v je) = bji. Ensuite la matrice B- symétrique.
Inversement, laissez la matrice B- symétrique. Puis BT= B et pour tous les vecteurs X = X 1 v 1 + …+ x n v n =vx, y = y 1 v 1 + y 2 v 2 +…+ oui n v n =vY Î V, d'après la formule (1), on obtient (on tient compte du fait que le nombre est une matrice d'ordre 1, et ne change pas lors de la transposition)
g(X , y ) =g(X , y )t = (X t PAR)t = Y t B t X = g(y , X ).
2. Forme quadratique. Matrice de forme quadratique. Coordonner la transformation.
Définition 1.forme quadratique déterminé sur V, s'appelle la cartographie F:V® P, qui pour tout vecteur X à partir de V est défini par l'égalité F(X ) = g(X , X ), où g(X , y ) est une forme bilinéaire symétrique définie sur V .
Propriété 1.Par une forme quadratique donnéeF(X )la forme bilinéaire peut être trouvée uniquement par la formule
g(X , y ) = 1/2(F(X + y ) - F(X )-F(y )). (1)
Preuve. Pour tous les vecteurs X , y Î V on obtient par les propriétés de la forme bilinéaire
F(X + y ) = g(X + y , X + y ) = g(X , X + y ) + g(y , X + y ) = g(X , X ) + g(X , y ) + g(y , X ) + g(y , y ) = F(X ) + 2g(X , y ) + F(y ).
La formule (1) découle d'ici.
Définition 2.Matrice de forme quadratiqueF(X ) par rapport à la basev = (v 1 , v 2 ,…, v n) est la matrice de la forme bilinéaire symétrique correspondante g(X , y ) par rapport à la base v.
Théorème 1. LaisserX= (X 1 ,X 2 ,…, xn)t- colonne de coordonnées vectoriellesX en basev, B - matrice de forme quadratiqueF(X ) par rapport à la basev. Alors la forme quadratiqueF(X )
Définition 10.4.Vue canonique forme quadratique (10.1) est appelée la forme suivante : . (10.4)
Montrons que dans la base des vecteurs propres la forme quadratique (10.1) prend la forme canonique. Laisser
 - vecteurs propres normalisés correspondant aux valeurs propres λ 1 ,λ 2 ,λ 3 matrices (10.3) dans la base orthonormée . Alors la matrice de transition de l'ancienne base à la nouvelle sera la matrice
- vecteurs propres normalisés correspondant aux valeurs propres λ 1 ,λ 2 ,λ 3 matrices (10.3) dans la base orthonormée . Alors la matrice de transition de l'ancienne base à la nouvelle sera la matrice
 . Dans la nouvelle base, la matrice ET prend la forme diagonale (9.7) (par la propriété des vecteurs propres). Ainsi, en transformant les coordonnées selon les formules :
. Dans la nouvelle base, la matrice ET prend la forme diagonale (9.7) (par la propriété des vecteurs propres). Ainsi, en transformant les coordonnées selon les formules :
 ,
,
on obtient dans la nouvelle base la forme canonique d'une forme quadratique à coefficients égaux aux valeurs propres λ 1 , λ 2 , λ 3:
Remarque 1. D'un point de vue géométrique, la transformation de coordonnées considérée est une rotation du système de coordonnées, qui combine les anciens axes de coordonnées avec les nouveaux.
Remarque 2. Si l'une quelconque des valeurs propres de la matrice (10.3) coïncide, on peut ajouter un vecteur unitaire orthogonal à chacune d'elles aux vecteurs propres orthonormés correspondants et ainsi construire une base dans laquelle la forme quadratique prend la forme canonique.
Ramenons à la forme canonique la forme quadratique
X² + 5 y² + z² + 2 xy + 6xz + 2yz.
Sa matrice a la forme Dans l'exemple considéré au cours 9, on trouve les valeurs propres et les vecteurs propres orthonormés de cette matrice :
![]()
![]() Composons la matrice de transition à la base de ces vecteurs :
Composons la matrice de transition à la base de ces vecteurs :
 (l'ordre des vecteurs est modifié pour qu'ils forment un triplet droit). Transformons les coordonnées selon les formules :
(l'ordre des vecteurs est modifié pour qu'ils forment un triplet droit). Transformons les coordonnées selon les formules :
 .
.

Ainsi, la forme quadratique est réduite à la forme canonique avec des coefficients égaux aux valeurs propres de la matrice de la forme quadratique.
Conférence 11
Courbes du second ordre. Ellipse, hyperbole et parabole, leurs propriétés et équations canoniques. Réduction de l'équation du second ordre à la forme canonique.
Définition 11.1.Courbes du second ordre sur un plan sont appelées les lignes d'intersection d'un cône circulaire avec des plans qui ne passent pas par son sommet.
Si un tel plan coupe tous les générateurs d'une cavité du cône, alors dans la section il s'avère ellipse, à l'intersection des génératrices des deux cavités - hyperbole, et si le plan de coupe est parallèle à une génératrice quelconque, alors la section du cône est parabole.
Commenter. Toutes les courbes du second ordre sont données par des équations du second degré à deux variables.
Ellipse.
Définition 11.2.Ellipse est l'ensemble des points du plan dont la somme des distances à deux points fixes F 1 et F des trucs, est une valeur constante.
Commenter. Quand les points correspondent F 1 et F 2 l'ellipse se transforme en cercle.
On déduit l'équation de l'ellipse en choisissant le système cartésien
y M(x, y) coordonnées de sorte que l'axe Oh coïncidait avec la ligne F 1 F 2, commencer
r 1 r 2 coordonnées - avec le milieu du segment F 1 F 2. Laissez la longueur de ce
segment est 2 Avec, puis dans le repère choisi
F 1 O F 2 x F 1 (-c, 0), F 2 (c, 0). Laissez le point M(x, y) repose sur une ellipse, et
la somme des distances de celui-ci à F 1 et F 2 égale 2 un.
Puis r 1 + r 2 = 2un, mais ,
Par conséquent, en introduisant la notation b² = un²- c² et après de simples transformations algébriques, on obtient équation canonique d'une ellipse: (11.1)
Définition 11.3.excentricité l'ellipse est appelée la quantité e=c/a (11.2)
Définition 11.4.Directrice D je ellipse correspondant au foyer Fi Fi autour de l'axe UO perpendiculaire à l'axe Ohà distance un/e depuis l'origine.
Commenter. Avec un choix différent du système de coordonnées, l'ellipse peut être donnée non pas par l'équation canonique (11.1), mais par une équation du second degré d'un type différent.
Propriétés de l'ellipse :
1) L'ellipse a deux axes de symétrie mutuellement perpendiculaires (les axes principaux de l'ellipse) et un centre de symétrie (le centre de l'ellipse). Si une ellipse est donnée par une équation canonique, alors ses axes principaux sont les axes de coordonnées et le centre est l'origine. Puisque les longueurs des segments formés par l'intersection de l'ellipse avec les axes principaux sont égales à 2 un et 2 b (2un>2b), alors l'axe principal passant par les foyers est appelé grand axe de l'ellipse, et le deuxième grand axe est appelé petit axe.
2) L'ellipse entière est contenue dans le rectangle
3) Excentricité d'ellipse e< 1.
Vraiment,
4) Les directrices de l'ellipse sont situées à l'extérieur de l'ellipse (puisque la distance du centre de l'ellipse à la directrice est un/e, un e<1, следовательно, a/e>a, et l'ellipse entière est dans un rectangle )
5) Rapport de distance r je du point de l'ellipse au foyer Fiéloigner d je de ce point à la directrice correspondant au foyer est égale à l'excentricité de l'ellipse.
Preuve.
Distances d'un point M(x, y) aux foyers de l'ellipse peut être représentée comme suit :
On compose les équations directrices :
(ré 1), (ré 2). Puis ![]() D'ici r je / ré je = e, ce qui devait être prouvé.
D'ici r je / ré je = e, ce qui devait être prouvé.
Hyperbole.
Définition 11.5.Hyperbole est l'ensemble des points du plan pour lesquels le module de la différence entre les distances à deux points fixes F 1 et F 2 de cet avion, appelé des trucs, est une valeur constante.
Nous dérivons l'équation canonique de l'hyperbole par analogie avec la dérivation de l'équation de l'ellipse, en utilisant la même notation.
|r 1 - r 2 | = 2un, d'où Si désigne b² = c² - un², à partir de là, vous pouvez obtenir
- équation canonique d'une hyperbole. (11.3)
Définition 11.6.excentricité l'hyperbole est appelée la quantité e = c / a.
Définition 11.7.Directrice D je hyperbole correspondant au foyer Fi, est appelée une droite située dans le même demi-plan avec Fi autour de l'axe UO perpendiculaire à l'axe Ohà distance un / e depuis l'origine.
Propriétés d'une hyperbole :
1) Une hyperbole a deux axes de symétrie (axes principaux de l'hyperbole) et un centre de symétrie (le centre de l'hyperbole). De plus, l'un de ces axes coupe l'hyperbole en deux points, appelés sommets de l'hyperbole. On l'appelle l'axe réel de l'hyperbole (axe Oh pour le choix canonique du système de coordonnées). L'autre axe n'a pas de point commun avec l'hyperbole et est appelé son axe imaginaire (en coordonnées canoniques, l'axe UO). De chaque côté se trouvent les branches droite et gauche de l'hyperbole. Les foyers d'une hyperbole sont situés sur son axe réel.
2) Les branches de l'hyperbole ont deux asymptotes définies par les équations
3) Parallèlement à l'hyperbole (11.3), on peut considérer l'hyperbole dite conjuguée définie par l'équation canonique
pour lequel les axes réel et imaginaire sont intervertis tout en conservant les mêmes asymptotes.
4) Excentricité de l'hyperbole e> 1.
5) Rapport de distance r je du point d'hyperbole au foyer Fiéloigner d je de ce point à la directrice correspondant au foyer est égale à l'excentricité de l'hyperbole.
La preuve peut être effectuée de la même manière que pour l'ellipse.
Parabole.
Définition 11.8.parabole est l'ensemble des points du plan dont la distance à un point fixe F ce plan est égal à la distance à une ligne droite fixe. Point F appelé se concentrer paraboles, et une ligne droite - son directrice.
У Pour dériver l'équation de la parabole, on choisit l'équation cartésienne
système de coordonnées de sorte que son origine soit le milieu
D M(x,y) perpendiculaire DF, abaissé de focus à directri-
r su, et les axes de coordonnées étaient parallèles et
perpendiculaire au directeur. Soit la longueur du segment DF
D O F x est R. Alors de l'égalité r=d s'ensuit que
![]() parce que le
parce que le
![]() Par des transformations algébriques, cette équation peut être réduite à la forme : y² = 2 pixels, (11.4)
Par des transformations algébriques, cette équation peut être réduite à la forme : y² = 2 pixels, (11.4)
appelé l'équation canonique de la parabole. Évaluer R appelé paramètre paraboles.
Propriétés de la parabole :
1) La parabole a un axe de symétrie (l'axe de la parabole). Le point d'intersection de la parabole avec l'axe est appelé sommet de la parabole. Si la parabole est donnée par l'équation canonique, alors son axe est l'axe Oh, et le sommet est l'origine des coordonnées.
2) Toute la parabole est située dans le demi-plan droit du plan Ohu.
Commenter. En utilisant les propriétés des directrices d'une ellipse et d'une hyperbole et la définition d'une parabole, nous pouvons prouver l'affirmation suivante :
L'ensemble des points plans dont le rapport e la distance à un point fixe à la distance à une ligne droite est une valeur constante, est une ellipse (avec e<1), гиперболу (при e>1) ou une parabole (quand e=1).
Informations similaires.
Réduction des formes quadratiques
Considérons la méthode la plus simple et la plus souvent utilisée dans la pratique pour réduire une forme quadratique à une forme canonique, appelée Méthode de Lagrange. Il est basé sur la sélection d'un carré complet sous forme quadratique.
Théorème 10.1(Théorème de Lagrange) Toute forme quadratique (10.1) :
utilisant une transformation linéaire non singulière (10.4) peut se réduire à la forme canonique (10.6) :
 ,
,
□ Démontrons le théorème de manière constructive, en utilisant la méthode de Lagrange de sélection des carrés parfaits. Le problème est de trouver une matrice non singulière telle que la transformation linéaire (10.4) aboutisse à la forme quadratique (10.6) de la forme canonique. Cette matrice sera obtenue progressivement comme produit d'un nombre fini de matrices d'un type particulier.
Point 1 (préparatoire).
1.1. On distingue parmi les variables celle qui entre sous la forme quadratique au carré et au premier degré simultanément (on l'appelle variable principale). Passons au point 2.
1.2. S'il n'y a pas de variables principales dans la forme quadratique (pour tous : ), alors nous choisissons une paire de variables dont le produit entre dans la forme avec un coefficient non nul et passons à l'étape 3.
1.3. S'il n'y a pas de produits de variables de noms opposés sous une forme quadratique, alors la forme quadratique donnée est déjà représentée sous la forme canonique (10.6). La preuve du théorème est complète.
Point 2 (surlignant le carré entier).
2.1. Sur la base de la variable principale, nous sélectionnons le carré complet. Sans perte de généralité, nous supposons que la variable dominante est la variable . En regroupant les termes contenant , on obtient
 .
.
En distinguant le carré complet sur la variable dans ![]() , on a
, on a
 .
.
Ainsi, à la suite de la sélection du carré complet pour une variable, nous obtenons la somme du carré de la forme linéaire
qui inclut la variable principale , et la forme quadratique ![]() à partir de variables , dans lesquelles la variable principale n'est plus incluse. Faisons un changement de variables (introduisons de nouvelles variables)
à partir de variables , dans lesquelles la variable principale n'est plus incluse. Faisons un changement de variables (introduisons de nouvelles variables)


on obtient la matrice

() transformation linéaire non singulière , à la suite de laquelle la forme quadratique (10.1) prend la forme suivante
Avec forme quadratique ![]() Faisons comme au point 1.
Faisons comme au point 1.
2.1. Si la variable principale est la variable , alors il y a deux façons de le faire : soit sélectionner le carré complet pour cette variable, soit exécuter renommer (renumérotation) variables :
avec une matrice de transformation non singulière :
 .
.
Point 3 (création d'une variable pilote). La paire de variables sélectionnée sera remplacée par la somme et la différence de deux nouvelles variables, et le reste des anciennes variables sera remplacé par les nouvelles variables correspondantes. Si, par exemple, au paragraphe 1, le terme
alors le changement de variables correspondant a la forme
et sous forme quadratique (10.1) la variable principale sera obtenue.
Par exemple, en cas de substitution de variable :
la matrice de cette transformation linéaire non singulière a la forme
 .
.
Par suite de l'algorithme ci-dessus (application successive des points 1, 2, 3), la forme quadratique (10.1) sera réduite à la forme canonique (10.6).
Notons qu'à la suite des transformations effectuées sur la forme quadratique (sélection du carré plein, renommage et création de la variable dominante), nous avons utilisé des matrices élémentaires non singulières de trois types (ce sont des matrices de transition de base à base). La matrice désirée d'une transformation linéaire non singulière (10.4), dans laquelle la forme (10.1) a la forme canonique (10.6), est obtenue en multipliant un nombre fini de matrices élémentaires non singulières de trois types. ■
Exemple 10.2. Apporter une forme quadratique
à la forme canonique par la méthode de Lagrange. Spécifiez la transformation linéaire non singulière correspondante. Exécutez une vérification.
Décision. Nous choisissons la variable dominante (coefficient ). En regroupant les termes contenant , et en sélectionnant un carré complet dessus, on obtient
où indiqué
Faisons un changement de variables (introduisons de nouvelles variables)

Exprimer les anciennes variables en fonction des nouvelles :

on obtient la matrice
