Construisez un rectangle de superficie égale au trapèze donné. Trapèze rectangulaire : toutes les formules et exemples de problèmes

Note. Cela fait partie d'une leçon avec des problèmes de géométrie (section d'un trapèze rectangulaire). Si vous avez besoin de résoudre un problème de géométrie qui n'est pas ici, écrivez-le sur le forum. Dans les problèmes, au lieu du symbole "racine carrée", la fonction sqrt() est utilisée, dans laquelle sqrt est le symbole de la racine carrée et l'expression du radicand est indiquée entre parenthèses. Pour les expressions radicales simples, le signe peut être utilisé "√"

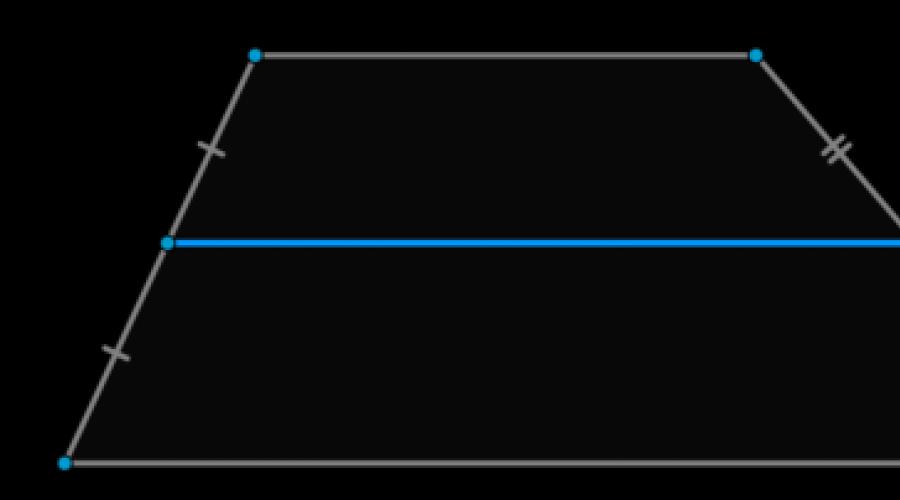
Propriétés d'un trapèze rectangulaire

• U trapèze rectangulaire et deux angles doivent être droits
• Les deux angles droits d'un trapèze rectangulaire appartiennent nécessairement à des sommets adjacents
• Les deux angles droits dans un trapèze rectangulaire ils sont nécessairement adjacents au même côté
• Diagonales d'un trapèze rectangulaire former un triangle rectangle d'un côté
• Longueur du côté d'un trapèze perpendiculaire aux bases est égal à sa hauteur
• À un trapèze rectangulaire les bases sont parallèles, un côté est perpendiculaire aux bases et le deuxième côté est incliné par rapport aux bases
• À un trapèze rectangulaire deux angles sont droits et les deux autres sont aigus et obtus

Tâche

DANS trapèze rectangulaire le plus grand côté est égal à la somme des bases, la hauteur est de 12 cm. Trouvez l'aire d'un rectangle dont les côtés sont égaux aux bases du trapèze.

Solution.
Notons le trapèze comme ABCD. Notons les longueurs des bases du trapèze par a (base plus grande AD) et b (base plus petite BC). Que ce soit un angle droit

∠UN.

L'aire d'un rectangle dont les côtés sont égaux aux bases du trapèze sera égale à
S = ab

Du sommet C de la base supérieure du trapèze ABCD on abaisse la hauteur CK jusqu'à la base inférieure. La hauteur du trapèze est connue à partir des conditions du problème. Alors, d'après le théorème de Pythagore
CK2 + KD

2 = CD 2

Puisque le plus grand côté latéral d’un trapèze est égal à la somme des bases, alors CD = a + b
Le trapèze étant rectangulaire, la hauteur tirée de la base supérieure du trapèze divise la base inférieure en deux segments.

AD = AK + KD. La valeur du premier segment est égale à la plus petite base du trapèze, puisque la hauteur formait un rectangle ABCK, c'est-à-dire BC = AK = b, donc KD sera égal à la différence des longueurs des bases du trapèze rectangulaire KD = a - b.
c'est
12 2 + (a - b) 2 = (a + b) 2
où
144 + une 2 - 2ab + b 2 = une 2 + 2ab + b 2
144 = 4ab

Puisque l'aire du rectangle est S = ab (voir ci-dessus), alors
144 = 4S
S = 144 / 4 = 36

Réponse : 36 cm

2 .

\[(\Large(\text(trapèze libre)))\]

Définitions

Un trapèze est un quadrilatère convexe dont deux côtés sont parallèles et les deux autres côtés ne sont pas parallèles.

Les côtés parallèles d’un trapèze sont appelés ses bases et les deux autres côtés sont appelés ses côtés latéraux.

La hauteur d'un trapèze est la perpendiculaire descendante d'un point quelconque d'une base à une autre base.

Théorèmes : propriétés d'un trapèze

1) La somme des angles sur le côté est \(180^\circ\) .

2) Les diagonales divisent le trapèze en quatre triangles, dont deux sont semblables et les deux autres sont de taille égale.

Preuve

1) Parce que \(AD\parallèle BC\), alors les angles \(\angle BAD\) et \(\angle ABC\) sont unilatéraux pour ces droites et la transversale \(AB\), donc, \(\angle MAUVAIS +\angle ABC=180^\circ\).

2) Parce que \(AD\parallel BC\) et \(BD\) sont sécants, alors \(\angle DBC=\angle BDA\) se trouvent transversalement.
Aussi \(\angle BOC=\angle AOD\) comme vertical.
Donc sous deux angles \(\triangle BOC \sim \triangle AOD\).

Prouvons que \(S_(\triangle AOB)=S_(\triangle COD)\). Soit \(h\) la hauteur du trapèze. Alors \(S_(\triangle ABD)=\frac12\cdot h\cdot AD=S_(\triangle ACD)\). Alors: \

Définition

La ligne médiane d'un trapèze est un segment reliant les milieux des côtés.

Théorème

La ligne médiane du trapèze est parallèle aux bases et égale à leur demi-somme.

Preuve*

1) Montrons le parallélisme.

Traçons par le point \(M\) la droite \(MN"\parallel AD\) (\(N"\in CD\) ). Alors, d’après le théorème de Thalès (puisque \(MN"\parallèle AD\parallèle BC, AM=MB\)) le point \(N"\) est le milieu du segment \(CD\). Cela signifie que les points \(N\) et \(N"\) coïncideront.

2) Démontrons la formule.

Faisons \(BB"\perp AD, CC"\perp AD\) . Laisser \(BB"\cap MN=M", CC"\cap MN=N"\).

Ensuite, d'après le théorème de Thales, \(M"\) et \(N"\) sont respectivement les milieux des segments \(BB"\) et \(CC"\). Cela signifie que \(MM"\) est la ligne médiane de \(\triangle ABB"\) , \(NN"\) est la ligne médiane de \(\triangle DCC"\) . C'est pourquoi: \

Parce que \(MN\AD parallèle\BC parallèle\) et \(BB", CC"\perp AD\) , alors \(B"M"N"C"\) et \(BM"N"C\) sont des rectangles. D'après le théorème de Thales, de \(MN\parallel AD\) et \(AM=MB\) il s'ensuit que \(B"M"=M"B\) . D'où \(B"M"N"C "\) et \(BM"N"C\) sont des rectangles égaux, donc \(M"N"=B"C"=BC\) .

Ainsi:

\ \[=\dfrac12 \left(AB"+B"C"+BC+C"D\right)=\dfrac12\left(AD+BC\right)\]

Théorème : propriété d'un trapèze arbitraire

Les milieux des bases, le point d'intersection des diagonales du trapèze et le point d'intersection des prolongements des côtés latéraux se trouvent sur une même droite.

Preuve*
Il est recommandé de vous familiariser avec la preuve après avoir étudié le thème « Similitude des triangles ».

1) Montrons que les points \(P\), \(N\) et \(M\) se trouvent sur la même droite.

Traçons une droite \(PN\) (\(P\) est le point d'intersection des extensions des côtés latéraux, \(N\) est le milieu de \(BC\)). Laissez-le couper le côté \(AD\) au point \(M\) . Montrons que \(M\) est le milieu de \(AD\) .

Considérez \(\triangle BPN\) et \(\triangle APM\) . Ils sont similaires à deux angles (\(\angle APM\) – général, \(\angle PAM=\angle PBN\) comme correspondant à \(AD\parallel BC\) et \(AB\) sécant). Moyens: \[\dfrac(BN)(AM)=\dfrac(PN)(PM)\]

Considérez \(\triangle CPN\) et \(\triangle DPM\) . Ils sont similaires à deux angles (\(\angle DPM\) – général, \(\angle PDM=\angle PCN\) comme correspondant à \(AD\parallel BC\) et \(CD\) sécant). Moyens: \[\dfrac(CN)(DM)=\dfrac(PN)(PM)\]

D'ici \(\dfrac(BN)(AM)=\dfrac(CN)(DM)\). Mais \(BN=NC\) donc \(AM=DM\) .

2) Montrons que les points \(N, O, M\) se trouvent sur la même droite.

Soit \(N\) le milieu de \(BC\) et \(O\) le point d'intersection des diagonales. Traçons une ligne droite \(NO\) , elle coupera le côté \(AD\) au point \(M\) . Montrons que \(M\) est le milieu de \(AD\) .

\(\triangle BNO\sim \triangle DMO\) le long de deux angles (\(\angle OBN=\angle ODM\) situés transversalement à \(BC\parallèle AD\) et \(BD\) sécants ; \(\angle BON=\angle DOM\) comme verticaux). Moyens: \[\dfrac(BN)(MD)=\dfrac(ON)(OM)\]

De même \(\triangle CON\sim \triangle AOM\). Moyens: \[\dfrac(CN)(MA)=\dfrac(ON)(OM)\]

D'ici \(\dfrac(BN)(MD)=\dfrac(CN)(MA)\). Mais \(BN=CN\) donc \(AM=MD\) .

\[(\Large(\text(Trapèze isocèle)))\]

Définitions

Un trapèze est dit rectangulaire si l’un de ses angles est droit.

Un trapèze est dit isocèle si ses côtés sont égaux.

Théorèmes : propriétés d'un trapèze isocèle

1) Un trapèze isocèle a des angles de base égaux.

2) Les diagonales d'un trapèze isocèle sont égales.

3) Deux triangles formés de diagonales et d'une base sont isocèles.

Preuve

1) Considérons le trapèze isocèle \(ABCD\) .

À partir des sommets \(B\) et \(C\), nous déposons respectivement les perpendiculaires \(BM\) et \(CN\) du côté \(AD\). Puisque \(BM\perp AD\) et \(CN\perp AD\) , alors \(BM\parallel CN\) ; \(AD\parallel BC\) , alors \(MBCN\) est un parallélogramme, donc \(BM = CN\) .

Considérons les triangles rectangles \(ABM\) et \(CDN\) . Puisque leurs hypoténuses sont égales et que la jambe \(BM\) est égale à la jambe \(CN\) , alors ces triangles sont égaux, donc \(\angle DAB = \angle CDA\) .

2)

Parce que \(AB=CD, \angle A=\angle D, AD\)– général, puis selon le premier signe. Par conséquent, \(AC=BD\) .

3) Parce que \(\triangle ABD=\triangle ACD\), puis \(\angle BDA=\angle CAD\) . Le triangle \(\triangle AOD\) est donc isocèle. De même, il est prouvé que \(\triangle BOC\) est isocèle.

Théorèmes : signes d'un trapèze isocèle

1) Si un trapèze a des angles de base égaux, alors il est isocèle.

2) Si un trapèze a des diagonales égales, alors il est isocèle.

Preuve

Considérons le trapèze \(ABCD\) tel que \(\angle A = \angle D\) .

Complétons le trapèze jusqu'au triangle \(AED\) comme indiqué sur la figure. Puisque \(\angle 1 = \angle 2\) , alors le triangle \(AED\) est isocèle et \(AE = ED\) . Les angles \(1\) et \(3\) sont égaux aux angles correspondants des lignes parallèles \(AD\) et \(BC\) et transversales \(AB\). De même, les angles \(2\) et \(4\) sont égaux, mais \(\angle 1 = \angle 2\), alors \(\angle 3 = \angle 1 = \angle 2 = \angle 4\), donc le triangle \(BEC\) est également isocèle et \(BE = EC\) .

Finalement \(AB = AE - BE = DE - CE = CD\), c'est-à-dire \(AB = CD\), ce qui devait être prouvé.

2) Soit \(AC=BD\) . Parce que \(\triangle AOD\sim \triangle BOC\), alors nous désignons leur coefficient de similarité par \(k\) . Alors si \(BO=x\) , alors \(OD=kx\) . Similaire à \(CO=y \Rightarrow AO=ky\) .

Parce que \(AC=BD\) , puis \(x+kx=y+ky \Rightarrow x=y\) . Cela signifie que \(\triangle AOD\) est isocèle et \(\angle OAD=\angle ODA\) .

Ainsi, d'après le premier signe \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\)- général). Alors, \(AB=CD\) , pourquoi.

Dans cet article, nous essaierons de refléter le plus complètement possible les propriétés d'un trapèze. Nous parlerons notamment de signes généraux et les propriétés d'un trapèze, ainsi que sur les propriétés d'un trapèze inscrit et sur un cercle inscrit dans un trapèze. Nous aborderons également les propriétés d'un trapèze isocèle et rectangulaire.

Un exemple de résolution d'un problème en utilisant les propriétés discutées vous aidera à le comprendre dans votre tête et à mieux mémoriser le matériel.

Trapèze et tout-tout-tout

Pour commencer, rappelons brièvement ce qu'est un trapèze et quels autres concepts lui sont associés.

Ainsi, un trapèze est une figure quadrilatère dont deux côtés sont parallèles entre eux (ce sont les bases). Et les deux ne sont pas parallèles : ce sont les côtés.

Dans un trapèze, la hauteur peut être abaissée - perpendiculairement aux bases. La ligne médiane et les diagonales sont tracées. Il est également possible de tracer une bissectrice sous n'importe quel angle du trapèze.

À propos diverses propriétés, associés à tous ces éléments et à leurs combinaisons, nous allons maintenant en parler.

Propriétés des diagonales trapézoïdales

Pour que ce soit plus clair, pendant que vous lisez, dessinez le trapèze ACME sur une feuille de papier et dessinez-y des diagonales.

1. Si vous trouvez les milieux de chacune des diagonales (appelons ces points X et T) et que vous les reliez, vous obtenez un segment. L'une des propriétés des diagonales d'un trapèze est que le segment HT se situe sur la ligne médiane. Et sa longueur peut être obtenue en divisant la différence des bases par deux : ХТ = (a – b)/2.
2. Devant nous se trouve le même trapèze ACME. Les diagonales se coupent au point O. Regardons les triangles AOE et MOK, formés par les segments des diagonales ainsi que les bases du trapèze. Ces triangles sont similaires. Le coefficient de similarité k des triangles s'exprime par le rapport des bases du trapèze : k = AE/KM.
   Le rapport des aires des triangles AOE et MOK est décrit par le coefficient k 2 .
3. Le même trapèze, les mêmes diagonales se coupant au point O. Seulement cette fois, nous considérerons les triangles que les segments des diagonales formaient avec les côtés du trapèze. Les aires des triangles AKO et EMO sont de taille égale - leurs aires sont les mêmes.
4. Une autre propriété d'un trapèze implique la construction de diagonales. Donc, si vous continuez les côtés de AK et ME en direction de la base la plus petite, tôt ou tard, ils se croiseront à un certain point. Ensuite, tracez une ligne droite passant par le milieu des bases du trapèze. Il coupe les bases aux points X et T.
   Si l'on prolonge maintenant la ligne XT, alors elle reliera entre eux le point d'intersection des diagonales du trapèze O, le point où se croisent les prolongements des côtés et le milieu des bases X et T.
5. Par le point d'intersection des diagonales, nous tracerons un segment qui reliera les bases du trapèze (T se trouve sur la plus petite base KM, X sur la plus grande AE). Le point d'intersection des diagonales divise ce segment dans le rapport suivant : TO/OX = KM/AE.
6. Maintenant, passant par le point d'intersection des diagonales, nous allons tracer un segment parallèle aux bases du trapèze (a et b). Le point d'intersection le divisera en deux parties égales. Vous pouvez trouver la longueur du segment en utilisant la formule 2ab/(a+b).

Propriétés de la ligne médiane d'un trapèze

Tracez la ligne médiane du trapèze parallèlement à ses bases.

1. La longueur de la ligne médiane d'un trapèze peut être calculée en additionnant les longueurs des bases et en les divisant par deux : m = (une + b)/2.
2. Si vous dessinez un segment (hauteur, par exemple) passant par les deux bases du trapèze, la ligne médiane le divisera en deux parties égales.

Propriété de la bissectrice du trapèze

Sélectionnez n’importe quel angle du trapèze et tracez une bissectrice. Prenons par exemple l'angle KAE de notre trapèze ACME. Après avoir terminé la construction vous-même, vous pouvez facilement vérifier que la bissectrice coupe de la base (ou de son prolongement en ligne droite à l'extérieur de la figure elle-même) un segment de même longueur que le côté.

Propriétés des angles trapézoïdaux

1. Quelle que soit la paire d'angles adjacents au côté que vous choisissez, la somme des angles de la paire est toujours de 180 0 : α + β = 180 0 et γ + δ = 180 0.
2. Relions les milieux des bases du trapèze avec un segment TX. Regardons maintenant les angles aux bases du trapèze. Si la somme des angles de l'un d'eux est de 90 0, la longueur du segment TX peut être facilement calculée en fonction de la différence des longueurs des bases, divisées en deux : TX = (AE – KM)/2.
3. Si des lignes parallèles sont tracées à travers les côtés d’un angle trapézoïdal, elles diviseront les côtés de l’angle en segments proportionnels.

Propriétés d'un trapèze isocèle (équilatéral)

1. Dans un trapèze isocèle, les angles à n’importe quelle base sont égaux.
2. Maintenant, construisez à nouveau un trapèze pour pouvoir imaginer plus facilement de quoi nous parlons. Regardez attentivement la base AE - le sommet de la base opposée M est projeté jusqu'à un certain point sur la ligne qui contient AE. La distance du sommet A au point de projection du sommet M et la ligne médiane d'un trapèze isocèle sont égales.
3. Quelques mots sur la propriété des diagonales d'un trapèze isocèle : leurs longueurs sont égales. Et aussi les angles d'inclinaison de ces diagonales par rapport à la base du trapèze sont les mêmes.
4. Ce n'est qu'autour d'un trapèze isocèle qu'un cercle peut être décrit, puisque la somme des angles opposés d'un quadrilatère est de 180 0 - une condition préalable pour cela.
5. La propriété d'un trapèze isocèle découle du paragraphe précédent - si un cercle peut être décrit à proximité du trapèze, il est isocèle.
6. Des caractéristiques d'un trapèze isocèle découle la propriété de la hauteur d'un trapèze : si ses diagonales se coupent à angle droit, alors la longueur de la hauteur est égale à la moitié de la somme des bases : h = (une + b)/2.
7. Encore une fois, tracez le segment TX passant par les milieux des bases du trapèze - dans un trapèze isocèle, il est perpendiculaire aux bases. Et en même temps TX est l’axe de symétrie d’un trapèze isocèle.
8. Cette fois, abaissez la hauteur du sommet opposé du trapèze sur la base la plus grande (appelons-la a). Vous obtiendrez deux segments. La longueur d'un peut être trouvée si les longueurs des bases sont additionnées et divisées en deux : (une + b)/2. Nous obtenons le deuxième lorsque nous soustrayons le plus petit de la plus grande base et divisons la différence résultante par deux : (a-b)/2.

Propriétés d'un trapèze inscrit dans un cercle

Puisque nous parlons déjà d'un trapèze inscrit dans un cercle, attardons-nous plus en détail sur cette question. En particulier, où se trouve le centre du cercle par rapport au trapèze. Ici aussi, il est recommandé de prendre le temps de prendre un crayon et de dessiner ce qui sera évoqué ci-dessous. De cette façon, vous comprendrez plus rapidement et vous mémoriserez mieux.

1. L'emplacement du centre du cercle est déterminé par l'angle d'inclinaison de la diagonale du trapèze par rapport à son côté. Par exemple, une diagonale peut s'étendre du haut d'un trapèze à angle droit par rapport au côté. Dans ce cas, la plus grande base coupe le centre du cercle circonscrit exactement au milieu (R = ½AE).
2. La diagonale et le côté peuvent également se rencontrer selon un angle aigu - le centre du cercle se trouve alors à l'intérieur du trapèze.
3. Le centre du cercle circonscrit peut être à l'extérieur du trapèze, au-delà de sa plus grande base, s'il est compris entre la diagonale du trapèze et le côté - angle obtus.
4. L'angle formé par la diagonale et la plus grande base du trapèze ACME (angle inscrit) est la moitié de celui angle central, ce qui lui correspond : MAE = ½MOE.
5. En bref, deux façons de trouver le rayon d'un cercle circonscrit. Première méthode : regardez attentivement votre dessin – que voyez-vous ? Vous remarquerez facilement que la diagonale divise le trapèze en deux triangles. Le rayon peut être trouvé par le rapport du côté du triangle au sinus de l'angle opposé, multiplié par deux. Par exemple, R = AE/2*sinAME. La formule peut être écrite de la même manière pour n’importe lequel des côtés des deux triangles.
6. Deuxième méthode : trouver le rayon du cercle circonscrit passant par l'aire du triangle formé par la diagonale, le côté et la base du trapèze : R = AM*ME*AE/4*S AME.

Propriétés d'un trapèze circonscrit à un cercle

Vous pouvez insérer un cercle dans un trapèze si une condition est remplie. En savoir plus ci-dessous. Et ensemble, cette combinaison de chiffres possède un certain nombre de propriétés intéressantes.

1. Si un cercle est inscrit dans un trapèze, la longueur de sa ligne médiane peut être facilement trouvée en additionnant les longueurs des côtés et en divisant la somme obtenue par deux : m = (c + d)/2.
2. Pour le trapèze ACME, décrit autour d'un cercle, la somme des longueurs des bases est égale à la somme des longueurs des côtés : AK + MOI = KM + AE.
3. De cette propriété des bases d'un trapèze découle l'énoncé inverse : un cercle peut être inscrit dans un trapèze dont la somme des bases est égale à la somme de ses côtés.
4. Le point tangent d'un cercle de rayon r inscrit dans un trapèze divise le côté en deux segments, appelons-les a et b. Le rayon d'un cercle peut être calculé à l'aide de la formule : r = √ab.
5. Et encore une propriété. Pour éviter toute confusion, dessinez également cet exemple vous-même. Nous avons le bon vieux trapèze ACME, décrit autour d'un cercle. Il contient des diagonales qui se coupent au point O. Les triangles AOK et EOM formés par les segments des diagonales et les côtés latéraux sont rectangulaires.
   Les hauteurs de ces triangles, abaissées jusqu'aux hypoténuses (c'est-à-dire les côtés latéraux du trapèze), coïncident avec les rayons du cercle inscrit. Et la hauteur du trapèze coïncide avec le diamètre du cercle inscrit.

Propriétés d'un trapèze rectangulaire

Un trapèze est dit rectangulaire si l’un de ses angles est droit. Et ses propriétés découlent de cette circonstance.

1. Un trapèze rectangulaire a un de ses côtés perpendiculaire à sa base.
2. Hauteur et côté latéral du trapèze adjacent à angle droit, sont égaux. Cela permet de calculer l'aire d'un trapèze rectangulaire ( formule générale S = (une + b) * h/2) non seulement par la hauteur, mais aussi par le côté adjacent à l'angle droit.
3. Pour un trapèze rectangulaire, les propriétés générales des diagonales d'un trapèze déjà décrites ci-dessus sont pertinentes.

Preuve de certaines propriétés du trapèze

Égalité des angles à la base d'un trapèze isocèle :

• Vous avez probablement déjà deviné qu'ici nous aurons à nouveau besoin du trapèze AKME - dessinez un trapèze isocèle. Tracez une ligne droite MT à partir du sommet M, parallèle au côté de AK (MT || AK).

Le quadrilatère AKMT résultant est un parallélogramme (AK || MT, KM || AT). Puisque ME = KA = MT, ∆ MTE est isocèle et MET = MTE.

AK || MT, donc MTE = KAE, MET = MTE = KAE.

D'où AKM = 180 0 - MET = 180 0 - KAE = KME.

Q.E.D.

Maintenant, en nous basant sur la propriété d'un trapèze isocèle (égalité des diagonales), nous prouvons que le trapèze ACME est isocèle:

• Tout d’abord, traçons une ligne droite MX – MX || KÉ. On obtient un parallélogramme KMHE (base – MX || KE et KM || EX).

∆AMX est isocèle, puisque AM = KE = MX et MAX = MEA.

MH || KE, KEA = MHE, donc MAE = MHE.

Il s’est avéré que les triangles AKE et EMA sont égaux, puisque AM = KE et AE sont le côté commun des deux triangles. Et aussi MAE = MXE. On peut conclure que AK = ME, et il en résulte que le trapèze AKME est isocèle.

Tâche de révision

Les bases du trapèze ACME mesurent 9 cm et 21 cm, le côté latéral KA, égal à 8 cm, forme un angle de 150 0 avec la plus petite base. Vous devez trouver l'aire du trapèze.

Solution : À partir du sommet K, nous abaissons la hauteur jusqu'à la plus grande base du trapèze. Et commençons par regarder les angles du trapèze.

Les angles AEM et KAN sont unilatéraux. Cela signifie qu'au total, ils donnent 180 0. Par conséquent, KAN = 30 0 (basé sur la propriété des angles trapézoïdaux).

Considérons maintenant le ∆ANC rectangulaire (je pense que ce point est évident pour les lecteurs sans preuve supplémentaire). À partir de là, nous trouverons la hauteur du trapèze KH - dans un triangle, c'est une jambe opposée à l'angle de 30 0. Donc KN = ½AB = 4 cm.

On trouve l'aire du trapèze à l'aide de la formule : S ACME = (KM + AE) * KN/2 = (9 + 21) * 4/2 = 60 cm 2.

Épilogue

Si vous avez étudié attentivement et attentivement cet article, n'avez pas été trop paresseux pour dessiner des trapèzes pour toutes les propriétés données avec un crayon dans vos mains et les analyser dans la pratique, vous devriez avoir bien maîtrisé le matériau.

Bien sûr, il y a ici beaucoup d'informations, variées et parfois même confuses : il n'est pas si difficile de confondre les propriétés du trapèze décrit avec les propriétés de celui inscrit. Mais vous avez constaté vous-même que la différence est énorme.

Vous avez maintenant un résumé détaillé de tous les propriétés générales trapèzes. Ainsi que les propriétés et caractéristiques spécifiques des trapèzes isocèles et rectangulaires. Il est très pratique à utiliser pour préparer les tests et examens. Essayez-le vous-même et partagez le lien avec vos amis !

blog.site, lors de la copie totale ou partielle du matériel, un lien vers la source originale est requis.

Au Ve siècle avant JC, l’ancien philosophe grec Zénon d’Élée formula ses célèbres apories, dont la plus célèbre est l’aporie « Achille et la tortue ». Voici à quoi cela ressemble :

Disons qu'Achille court dix fois plus vite que la tortue et se trouve mille pas derrière elle. Pendant le temps qu'il faudra à Achille pour parcourir cette distance, la tortue fera cent pas dans la même direction. Quand Achille fait cent pas, la tortue rampe encore dix pas, et ainsi de suite. Le processus se poursuivra à l'infini, Achille ne rattrapera jamais la tortue.

Ce raisonnement est devenu un choc logique pour toutes les générations suivantes. Aristote, Diogène, Kant, Hegel, Hilbert... Tous ont considéré, d'une manière ou d'une autre, l'aporie de Zénon. Le choc a été si fort que " ...les discussions se poursuivent à ce jour ; la communauté scientifique n'a pas encore réussi à se mettre d'accord sur l'essence des paradoxes...ont été impliqués dans l'étude de la question. analyse mathematique, théorie des ensembles, nouvelles approches physiques et philosophiques ; aucun d'entre eux n'est devenu une solution généralement acceptée au problème..."[Wikipédia, "L'aporie de Zeno". Tout le monde comprend qu'ils se font berner, mais personne ne comprend en quoi consiste la tromperie.

D'un point de vue mathématique, Zénon dans son aporie a clairement démontré le passage de la quantité à . Cette transition implique des applications plutôt que des applications permanentes. D’après ce que je comprends, l’appareil mathématique permettant d’utiliser des unités de mesure variables n’a pas encore été développé, ou bien il n’a pas été appliqué à l’aporie de Zénon. Appliquer notre logique habituelle nous conduit dans un piège. En raison de l'inertie de la pensée, nous appliquons des unités de temps constantes à la valeur réciproque. D'un point de vue physique, cela ressemble à un temps qui ralentit jusqu'à s'arrêter complètement au moment où Achille rattrape la tortue. Si le temps s'arrête, Achille ne peut plus distancer la tortue.

Si l’on renverse notre logique habituelle, tout se met en place. Achille court avec vitesse constante. Chaque segment suivant de son chemin est dix fois plus court que le précédent. Ainsi, le temps consacré à le surmonter est dix fois inférieur au précédent. Si nous appliquons le concept « d'infini » dans cette situation, alors il serait correct de dire « Achille rattrapera la tortue infiniment rapidement ».

Comment éviter ce piège logique ? Restez en unités de temps constantes et ne passez pas aux unités réciproques. Dans la langue de Zeno, cela ressemble à ceci :

Le temps qu'il faut à Achille pour faire mille pas, la tortue rampera cent pas dans la même direction. Au cours du prochain intervalle de temps égal au premier, Achille fera encore mille pas et la tortue rampera cent pas. Achille a désormais huit cents longueurs d'avance sur la tortue.

Cette approche décrit adéquatement la réalité sans aucun paradoxe logique. Mais cela ne constitue pas une solution complète au problème. La déclaration d’Einstein sur l’irrésistibilité de la vitesse de la lumière est très similaire à l’aporie de Zénon « Achille et la tortue ». Nous devons encore étudier, repenser et résoudre ce problème. Et la solution ne doit pas être recherchée en nombres infiniment grands, mais en unités de mesure.

Une autre aporie intéressante de Zénon parle d'une flèche volante :

Une flèche volante est immobile, puisqu'à tout instant elle est au repos, et puisqu'elle est au repos à tout instant, elle est toujours au repos.

Dans cette aporie, le paradoxe logique est surmonté très simplement - il suffit de préciser qu'à chaque instant une flèche volante est au repos en différents points de l'espace, ce qui, en fait, est un mouvement. Un autre point doit être souligné ici. À partir d'une photographie d'une voiture sur la route, il est impossible de déterminer ni le fait de son mouvement ni la distance qui la sépare. Pour déterminer si une voiture bouge, vous avez besoin de deux photographies prises du même point à des moments différents, mais vous ne pouvez pas déterminer la distance qui les sépare. Pour déterminer la distance jusqu'à une voiture, vous avez besoin de deux photographies prises à partir de différents points de l'espace à un moment donné, mais à partir d'elles, vous ne pouvez pas déterminer le fait du mouvement (bien sûr, vous avez toujours besoin de données supplémentaires pour les calculs, la trigonométrie vous aidera ). Ce que je veux souligner Attention particulière, c'est que deux points dans le temps et deux points dans l'espace sont des choses différentes qu'il ne faut pas confondre, car ils offrent des opportunités de recherche différentes.

mercredi 4 juillet 2018

Les différences entre set et multiset sont très bien décrites sur Wikipédia. Voyons.

Comme vous pouvez le voir, « il ne peut pas y avoir deux éléments identiques dans un ensemble », mais s'il y a des éléments identiques dans un ensemble, un tel ensemble est appelé « multiensemble ». Les êtres raisonnables ne comprendront jamais une logique aussi absurde. C'est le niveau des perroquets parlants et des singes dressés, qui n'ont aucune intelligence du mot « complètement ». Les mathématiciens agissent comme de simples formateurs, nous prêchant leurs idées absurdes.

Il était une fois, les ingénieurs qui ont construit le pont se trouvaient dans un bateau sous le pont pendant qu'ils testaient le pont. Si le pont s'effondrait, l'ingénieur médiocre mourait sous les décombres de sa création. Si le pont pouvait résister à la charge, le talentueux ingénieur construisait d'autres ponts.

Peu importe la manière dont les mathématiciens se cachent derrière l’expression « attention, je suis à la maison » ou plutôt « les mathématiques étudient les concepts abstraits », il existe un cordon ombilical qui les relie inextricablement à la réalité. Ce cordon ombilical, c'est de l'argent. En vigueur théorie mathématique aux mathématiciens eux-mêmes.

Nous avons très bien étudié les mathématiques et maintenant nous sommes assis à la caisse et distribuons les salaires. Alors un mathématicien vient nous voir pour son argent. Nous lui comptons le montant total et le disposons sur notre table en différentes piles, dans lesquelles nous mettons des billets de même valeur. Ensuite, nous prenons une facture de chaque pile et donnons au mathématicien son « salaire mathématique ». On explique au mathématicien qu'il ne recevra les factures restantes que lorsqu'il prouvera qu'un ensemble sans éléments identiques n'est pas égal à un ensemble avec éléments identiques. C'est là que le plaisir commence.

Tout d’abord, la logique des députés fonctionnera : « Cela peut s’appliquer aux autres, mais pas à moi ! Ensuite, ils commenceront à nous rassurer sur le fait que les billets de même valeur ont des numéros de billets différents, ce qui signifie qu'ils ne peuvent pas être considérés comme les mêmes éléments. D'accord, comptons les salaires en pièces - il n'y a pas de chiffres sur les pièces. Ici, le mathématicien commencera à se souvenir frénétiquement de la physique : différentes pièces de monnaie ont différentes quantités de saleté, la structure cristalline et la disposition des atomes sont uniques pour chaque pièce...

Et maintenant j'ai le plus intérêt Demander: où est la ligne au-delà de laquelle les éléments d'un multiset se transforment en éléments d'un ensemble et vice versa ? Une telle ligne n'existe pas - tout est décidé par les chamanes, la science n'est même pas près de mentir ici.

Regardez ici. Nous sélectionnons des stades de football ayant la même superficie de terrain. Les zones des champs sont les mêmes, ce qui signifie que nous avons un multiset. Mais si on regarde les noms de ces mêmes stades, on en trouve beaucoup, car les noms sont différents. Comme vous pouvez le constater, le même ensemble d’éléments est à la fois un ensemble et un multiensemble. Qui est correct? Et ici, le mathématicien-chaman-aiguiseur sort un as d'atout de sa manche et commence à nous parler soit d'un ensemble, soit d'un multiensemble. En tout cas, il nous convaincra qu’il a raison.

Pour comprendre comment les chamanes modernes opèrent avec la théorie des ensembles, en la liant à la réalité, il suffit de répondre à une question : en quoi les éléments d'un ensemble diffèrent-ils des éléments d'un autre ensemble ? Je vais vous le montrer, sans aucun « concevable comme un tout unique » ou « non concevable comme un tout unique ».

dimanche 18 mars 2018

La somme des chiffres d’un nombre est une danse de chamanes avec un tambourin, qui n’a rien à voir avec les mathématiques. Oui, dans les cours de mathématiques, on nous apprend à trouver la somme des chiffres d’un nombre et à l’utiliser, mais c’est pourquoi ils sont chamanes, pour enseigner à leurs descendants leurs compétences et leur sagesse, sinon les chamanes disparaîtront tout simplement.

Avez-vous besoin d'une preuve ? Ouvrez Wikipédia et essayez de trouver la page "Somme des chiffres d'un nombre". Elle n'existe pas. Il n’existe aucune formule mathématique permettant de calculer la somme des chiffres d’un nombre quelconque. Après tout, les nombres sont des symboles graphiques avec lesquels nous écrivons des nombres, et dans le langage mathématique, la tâche ressemble à ceci : « Trouvez la somme des symboles graphiques représentant n'importe quel nombre ». Les mathématiciens ne peuvent pas résoudre ce problème, mais les chamanes peuvent le faire facilement.

Voyons quoi et comment nous faisons pour trouver la somme des chiffres d'un nombre donné. Et donc, ayons le nombre 12345. Que faut-il faire pour trouver la somme des chiffres de ce nombre ? Considérons toutes les étapes dans l'ordre.

1. Notez le numéro sur une feuille de papier. Qu'avons-nous fait? Nous avons converti le nombre en un symbole numérique graphique. Ce n'est pas une opération mathématique.

2. Nous découpons une image résultante en plusieurs images contenant des numéros individuels. Découper une image n’est pas une opération mathématique.

3. Convertissez des symboles graphiques individuels en nombres. Ce n'est pas une opération mathématique.

4. Ajoutez les nombres résultants. Maintenant, ce sont des mathématiques.

La somme des chiffres du nombre 12345 est 15. Ce sont les « cours de coupe et de couture » dispensés par les chamanes et utilisés par les mathématiciens. Mais ce n'est pas tout.

D'un point de vue mathématique, peu importe dans quel système numérique nous écrivons un nombre. Alors, dans différents systèmes En calcul, la somme des chiffres d’un même nombre sera différente. En mathématiques, le système numérique est indiqué en indice à droite du nombre. Avec le grand nombre 12345, je ne veux pas me tromper, considérons le nombre 26 de l'article sur. Écrivons ce nombre dans les systèmes numériques binaires, octaux, décimaux et hexadécimaux. Nous n’examinerons pas chaque étape au microscope ; nous l’avons déjà fait. Regardons le résultat.

Comme vous pouvez le constater, dans différents systèmes numériques, la somme des chiffres d'un même nombre est différente. Ce résultat n'a rien à voir avec les mathématiques. C’est comme si vous déterminiez l’aire d’un rectangle en mètres et en centimètres, vous obtiendriez des résultats complètement différents.

Le zéro se ressemble dans tous les systèmes numériques et n’a pas de somme de chiffres. C'est un autre argument en faveur du fait que. Question pour les mathématiciens : comment désigne-t-on en mathématiques quelque chose qui n'est pas un nombre ? Quoi, pour les mathématiciens, rien n’existe à part les nombres ? Je peux autoriser cela pour les chamanes, mais pas pour les scientifiques. La réalité n’est pas qu’une question de chiffres.

Le résultat obtenu doit être considéré comme la preuve que les systèmes numériques sont des unités de mesure des nombres. Après tout, nous ne pouvons pas comparer des nombres avec des unités de mesure différentes. Si les mêmes actions avec différentes unités de mesure de la même quantité conduisent à résultats différents après les avoir comparés, cela signifie que cela n'a rien à voir avec les mathématiques.

Que sont les vraies mathématiques ? C'est alors que le résultat d'une opération mathématique ne dépend pas de la taille du nombre, de l'unité de mesure utilisée et de la personne qui effectue cette action.

Inscrivez-vous sur la porte Il ouvre la porte et dit :

Oh! Ce n'est pas les toilettes des femmes ?
- Jeune femme! Il s'agit d'un laboratoire pour l'étude de la sainteté indéphilique des âmes lors de leur ascension au ciel ! Halo en haut et flèche vers le haut. Quelles autres toilettes ?

Femelle... Le halo en haut et la flèche vers le bas sont masculins.

Si une telle œuvre d'art du design clignote devant vos yeux plusieurs fois par jour,

Il n’est alors pas surprenant que vous trouviez soudainement une étrange icône dans votre voiture :

Personnellement, je m'efforce de voir moins quatre degrés chez une personne qui fait caca (une image) (une composition de plusieurs images : un signe moins, le chiffre quatre, une désignation de degrés). Et je ne pense pas que cette fille soit stupide, non connaisseur en physique. Elle a juste un fort stéréotype de perception des images graphiques. Et les mathématiciens nous l’enseignent tout le temps. Voici un exemple.

1A n’est pas « moins quatre degrés » ou « un a ». Il s’agit de « l’homme qui fait caca » ou du nombre « vingt-six » en notation hexadécimale. Les personnes qui travaillent constamment dans ce système numérique perçoivent automatiquement un chiffre et une lettre comme un seul symbole graphique.

Les problèmes de trapèze ne semblent pas difficiles dans un certain nombre de formes étudiées précédemment. Comment cas particulier on considère un trapèze rectangulaire. Et lors de la recherche de son aire, il est parfois plus pratique de la diviser en deux déjà familières : un rectangle et un triangle. Il vous suffit de réfléchir un peu et vous trouverez certainement une solution.

Définition d'un trapèze rectangulaire et de ses propriétés

Un trapèze arbitraire a des bases parallèles et les côtés peuvent avoir des angles arbitraires. Si l'on considère un trapèze rectangulaire, alors l'un de ses côtés est toujours perpendiculaire aux bases. Autrement dit, deux angles seront égaux à 90 degrés. De plus, ils appartiennent toujours à des sommets adjacents ou, en d’autres termes, au même côté.

Les autres angles d'un trapèze rectangulaire sont toujours aigus et obtus. De plus, leur somme sera toujours égale à 180 degrés.

Chaque diagonale forme un triangle rectangle avec son plus petit côté. Et la hauteur, qui est tirée d'un sommet à angle obtus, divise la figure en deux. L’un d’eux est un rectangle et l’autre un triangle rectangle. D'ailleurs, ce côté est toujours égal à la hauteur du trapèze.

Quelles notations sont utilisées dans les formules présentées ?

Il convient de préciser immédiatement toutes les grandeurs utilisées dans les différentes expressions qui décrivent un trapèze et de les présenter dans un tableau :

Formules qui décrivent les éléments d'un trapèze rectangulaire

Le plus simple d'entre eux concerne la hauteur et le petit côté :

Quelques formules supplémentaires pour ce côté d'un trapèze rectangulaire :

с = d *sinα;

c = (a - b) * bronzage α ;

c = √ (d 2 - (a - b) 2).

Le premier découle d’un triangle rectangle. Et il est dit que la jambe jusqu'à l'hypoténuse donne le sinus de l'angle opposé.

Dans un même triangle, la deuxième jambe est égale à la différence des deux bases. Par conséquent, l’affirmation selon laquelle la tangente d’un angle est assimilée au rapport des jambes est vraie.

Du même triangle, une formule peut être dérivée basée sur la connaissance du théorème de Pythagore. C'est la troisième expression enregistrée.

Vous pouvez écrire des formules pour l’autre côté. Il y en a également trois :

d = (a - b) /cosα;

d = c / péché α ;

d = √ (c 2 + (a - b) 2).

Les deux premiers sont à nouveau obtenus à partir du rapport des côtés d’un même triangle rectangle, et le second est dérivé du théorème de Pythagore.

Quelle formule pouvez-vous utiliser pour calculer la superficie ?

Celui offert gratuitement en trapèze. Il faut juste tenir compte du fait que la hauteur est le côté perpendiculaire aux bases.

S = (une + b) * h / 2.

Ces quantités ne sont pas toujours données explicitement. Par conséquent, pour calculer l'aire d'un trapèze rectangulaire, vous devrez effectuer quelques calculs mathématiques.

Et si vous deviez calculer des diagonales ?

Dans ce cas, vous devez voir qu’ils forment deux triangles rectangles. Cela signifie que vous pouvez toujours utiliser le théorème de Pythagore. Alors la première diagonale s’exprimera comme suit :

d1 = √ (c 2 + b 2)

ou d'une autre manière, en remplaçant « c » par « h » :

d1 = √ (h 2 + b 2).

Les formules pour la deuxième diagonale sont obtenues de la même manière :

d2 = √ (c 2 + b 2) ou d 2 = √ (h 2 + une 2).

Tâche n°1

Condition. L'aire d'un trapèze rectangulaire est connue et égale à 120 dm 2. Sa hauteur a une longueur de 8 cm. Il est nécessaire de calculer tous les côtés du trapèze. Une condition supplémentaire est qu'une base soit 6 dm plus petite que l'autre.

Solution. Puisqu'on nous donne un trapèze rectangulaire dont la hauteur est connue, on peut immédiatement dire que l'un des côtés mesure 8 dm, c'est-à-dire le plus petit côté.

Maintenant vous pouvez compter l'autre : d = √ (c 2 + (a - b) 2). De plus, ici le côté c et la différence des bases sont donnés à la fois. Ce dernier est égal à 6 dm, cela est connu par la condition. Alors d sera égal à la racine carrée de (64 + 36), soit de 100. C'est ainsi que l'on trouve un autre côté, égal à 10 dm.

La somme des bases peut être trouvée à partir de la formule de l’aire. Elle sera égale au double de la surface divisée par la hauteur. Si vous comptez, vous obtenez 240/8. Cela signifie que la somme des bases est de 30 dm. En revanche, leur différence est de 6 dm. En combinant ces équations, vous pouvez compter les deux bases :

a + b = 30 et a - b = 6.

Vous pouvez exprimer a comme (b + 6), le remplacer par la première égalité. Ensuite, il s'avère que 2b sera égal à 24. Par conséquent, simplement b sera égal à 12 dm.

Alors le dernier côté a mesure 18 dm.

Répondre. Côtés d'un trapèze rectangulaire : a = 18 dm, b = 12 dm, c = 8 dm, d = 10 dm.

Tâche n°2

Condition.Étant donné un trapèze rectangulaire. Son grand côté est égal à la somme des bases. Sa hauteur est de 12 cm de long. Un rectangle est construit dont les côtés sont égaux aux bases du trapèze. Il faut calculer l'aire de ce rectangle.

Solution. Vous devez commencer par ce que vous recherchez. La surface requise est déterminée comme le produit de a et b. Ces deux quantités sont inconnues.

Il faudra utiliser des égalités supplémentaires. L'un d'eux est basé sur l'énoncé de la condition : d = a + b. Il faut utiliser la troisième formule pour ce côté, donnée ci-dessus. Il s'avère : d 2 = c 2 + (a - b) 2 ou (a + b) 2 = c 2 + (a - b) 2.

Il faut faire des transformations en substituant à la place c sa valeur de la condition - 12. Après avoir ouvert les parenthèses et ramené des termes similaires, il s'avère que 144 = 4 ab.

Au début de la solution, il était dit que a*b donnait la surface requise. Par conséquent, dans la dernière expression, vous pouvez remplacer ce produit par S. Un simple calcul donnera la valeur de l’aire. S = 36 cm2.

Répondre. La surface requise est de 36 cm 2.

Tâche n°3

Condition. L'aire d'un trapèze rectangulaire est de 150√3 cm². Angle vif est égal à 60 degrés. L’angle entre la petite base et la plus petite diagonale a la même signification. Nous devons calculer la plus petite diagonale.

Solution. D'après les propriétés des angles d'un trapèze, il s'avère que son angle obtus est de 120º. Ensuite, la diagonale le divise en parties égales, car une partie fait déjà 60 degrés. Alors l’angle entre cette diagonale et la deuxième base est également de 60 degrés. Autrement dit, un triangle formé d’une grande base, d’un côté incliné et d’une diagonale plus petite est équilatéral. Ainsi, la diagonale souhaitée sera égale à a, ainsi que le côté côté d = a.

Nous devons maintenant considérer un triangle rectangle. Le troisième angle est de 30 degrés. Cela signifie que la jambe opposée est égale à la moitié de l'hypoténuse. C'est-à-dire que la plus petite base du trapèze est égale à la moitié de la diagonale souhaitée : b = a/2. À partir de là, vous devez trouver la hauteur égale au côté perpendiculaire aux bases. Le côté avec la jambe ici. Du théorème de Pythagore :

c = (une/2) * √3.

Il ne reste plus qu'à substituer toutes les quantités dans la formule d'aire :

150√3 = (une + une/2) * (une/2 * √3) / 2.

La résolution de cette équation donne la racine 20

Répondre. La plus petite diagonale a une longueur de 20 cm.