Nok 34 et 2 solution. Comment trouver le plus petit commun multiple de deux nombres
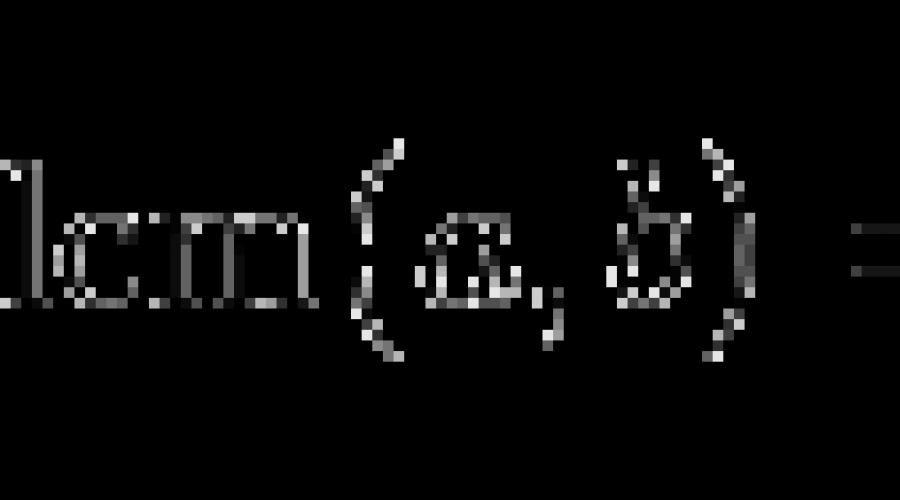
Lire aussi
Le plus grand commun diviseur et le plus petit commun multiple sont des concepts arithmétiques clés qui vous permettent d'opérer sans effort. fractions ordinaires. LCM et sont le plus souvent utilisés pour trouver le dénominateur commun de plusieurs fractions.
Concepts de base
Le diviseur d'un entier X est un autre entier Y par lequel X est divisé sans laisser de reste. Par exemple, le diviseur de 4 est 2 et 36 est 4, 6, 9. Un multiple d'un entier X est un nombre Y divisible par X sans reste. Par exemple, 3 est un multiple de 15 et 6 est un multiple de 12.
Pour toute paire de nombres, nous pouvons trouver leurs diviseurs et multiples communs. Par exemple, pour 6 et 9, le commun multiple est 18 et le commun diviseur est 3. Évidemment, les paires peuvent avoir plusieurs diviseurs et multiples, donc les calculs utilisent le plus grand diviseur GCD et le plus petit multiple LCM.
Le plus petit diviseur n’a aucun sens puisque pour tout nombre, il vaut toujours un. Le plus grand multiple n’a également aucun sens, puisque la séquence des multiples va vers l’infini.
Trouver pgcd
Il existe de nombreuses méthodes pour trouver le plus grand diviseur commun, dont les plus connues sont :
- énumération séquentielle des diviseurs, sélection des diviseurs communs pour une paire et recherche du plus grand d'entre eux ;
- décomposition des nombres en facteurs indivisibles ;
- Algorithme euclidien ;
- algorithme binaire.
Aujourd'hui à établissements d'enseignement les plus populaires sont les méthodes de décomposition en facteurs premiers et l'algorithme euclidien. Ce dernier, à son tour, est utilisé lors de la résolution d'équations diophantiennes : la recherche de GCD est nécessaire pour vérifier l'équation pour la possibilité de résolution en nombres entiers.
Trouver le CNO
Le multiple le plus petit commun est également déterminé par énumération séquentielle ou factorisation en facteurs indivisibles. De plus, il est facile de trouver le LCM si le plus grand diviseur a déjà été déterminé. Pour les nombres X et Y, le LCM et le GCD sont liés par la relation suivante :
LCD(X,Y) = X × Y / PGCD(X,Y).
Par exemple, si GCM(15,18) = 3, alors LCM(15,18) = 15 × 18 / 3 = 90. L'exemple le plus évident d'utilisation de LCM consiste à trouver le dénominateur commun, qui est le plus petit commun multiple de fractions données.
Nombres premiers entre eux
Si une paire de nombres n’a pas de diviseur commun, alors une telle paire est appelée premier entre eux. Le pgcd de ces paires est toujours égal à un, et sur la base de la relation entre les diviseurs et les multiples, le pgcd des paires premières entre elles est égal à leur produit. Par exemple, les nombres 25 et 28 sont relativement premiers, car ils n'ont pas de diviseur commun, et LCM(25, 28) = 700, ce qui correspond à leur produit. Deux nombres indivisibles seront toujours premiers relativement.
Diviseur commun et calculateur multiple
À l'aide de notre calculatrice, vous pouvez calculer GCD et LCM pour un nombre arbitraire de nombres parmi lesquels choisir. Les tâches de calcul des diviseurs communs et des multiples se trouvent en arithmétique de 5e et 6e années, mais GCD et LCM sont des concepts clés en mathématiques et sont utilisés en théorie des nombres, en planimétrie et en algèbre communicative.
Exemples concrets
Dénominateur commun des fractions
Le plus petit commun multiple est utilisé pour trouver le dénominateur commun de plusieurs fractions. Disons que dans un problème arithmétique, vous devez additionner 5 fractions :
1/8 + 1/9 + 1/12 + 1/15 + 1/18.
Pour additionner des fractions, l'expression doit être réduite à dénominateur commun, ce qui se réduit au problème de trouver le LCM. Pour ce faire, sélectionnez 5 nombres dans la calculatrice et saisissez les valeurs des dénominateurs dans les cellules appropriées. Le programme calculera le LCM (8, 9, 12, 15, 18) = 360. Vous devez maintenant calculer des facteurs supplémentaires pour chaque fraction, qui sont définis comme le rapport du LCM au dénominateur. Les multiplicateurs supplémentaires ressembleraient donc à :
- 360/8 = 45
- 360/9 = 40
- 360/12 = 30
- 360/15 = 24
- 360/18 = 20.
Après cela, nous multiplions toutes les fractions par le facteur supplémentaire correspondant et obtenons :
45/360 + 40/360 + 30/360 + 24/360 + 20/360.
Nous pouvons facilement additionner ces fractions et obtenir le résultat 159/360. Nous réduisons la fraction de 3 et voyons la réponse finale - 53/120.
Résolution d'équations diophantiennes linéaires
Les équations diophantiennes linéaires sont des expressions de la forme ax + by = d. Si le rapport d / pgcd(a, b) est un nombre entier, alors l'équation peut être résolue en nombres entiers. Vérifions quelques équations pour voir si elles ont une solution entière. Vérifions d'abord l'équation 150x + 8y = 37. À l'aide d'une calculatrice, nous trouvons PGCD (150,8) = 2. Divisons 37/2 = 18,5. Le nombre n’est pas un nombre entier, donc l’équation n’a pas de racines entières.
Vérifions l'équation 1320x + 1760y = 10120. Utilisez une calculatrice pour trouver PGCD(1320, 1760) = 440. Divisons 10120/440 = 23. En conséquence, nous obtenons un nombre entier, par conséquent, l'équation diophantienne peut être résolue en coefficients entiers. .
Conclusion
GCD et LCM jouent un rôle important dans la théorie des nombres, et les concepts eux-mêmes sont largement utilisés dans la plupart des domaines. différents domaines mathématiques. Utilisez notre calculatrice pour calculer les plus grands diviseurs et les plus petits multiples d'un nombre quelconque de nombres.
Mais de nombreux nombres naturels sont également divisibles par d’autres nombres naturels.
Par exemple:
Le nombre 12 est divisible par 1, par 2, par 3, par 4, par 6, par 12 ;
Le nombre 36 est divisible par 1, par 2, par 3, par 4, par 6, par 12, par 18, par 36.
Les nombres par lesquels le nombre est divisible par un tout (pour 12 ce sont 1, 2, 3, 4, 6 et 12) sont appelés diviseurs de nombres. Diviseur d'un nombre naturel un- est un nombre naturel qui divise un nombre donné un sans laisser de trace. Un nombre naturel qui a plus de deux diviseurs s'appelle composite .
Veuillez noter que les nombres 12 et 36 ont des facteurs communs. Ces nombres sont : 1, 2, 3, 4, 6, 12. Le plus grand diviseur de ces nombres est 12. Le diviseur commun de ces deux nombres un Et b- c'est le nombre par lequel les deux nombres donnés sont divisés sans reste un Et b.
Multiples communs plusieurs nombres est un nombre divisible par chacun de ces nombres. Par exemple, les nombres 9, 18 et 45 ont un multiple commun de 180. Mais 90 et 360 sont aussi leurs multiples communs. Parmi tous les multiples communs, il y en a toujours un plus petit, en dans ce cas c'est 90. Ce numéro s'appelle le plus petitcommun multiple (CMM).
Le LCM est toujours un nombre naturel qui doit être supérieur au plus grand des nombres pour lesquels il est défini.
Le plus petit commun multiple (LCM). Propriétés.
Commutativité:
Associativité :
![]()
En particulier, si et sont des nombres premiers entre eux, alors :
Plus petit commun multiple de deux entiers m Et n est un diviseur de tous les autres multiples communs m Et n. De plus, l’ensemble des multiples communs m, n coïncide avec l'ensemble des multiples de LCM ( m, n).
Les asymptotiques de peuvent être exprimées en termes de certaines fonctions de la théorie des nombres.
Donc, Fonction Chebyshev. Et aussi :
Cela découle de la définition et des propriétés de la fonction de Landau g(n).
Ce qui découle de la loi de distribution des nombres premiers.
Recherche du plus petit commun multiple (LCM).
CNP ( une, b) peut être calculé de plusieurs manières :
1. Si le plus grand diviseur commun est connu, vous pouvez utiliser sa connexion avec le LCM :
![]()
2. Connaître la décomposition canonique des deux nombres en facteurs premiers :
![]()
Où p 1 ,...,pk- divers nombres premiers, UN d 1 ,...,dk Et e 1 ,...,ek— des entiers non négatifs (ils peuvent être des zéros si le nombre premier correspondant n'est pas dans le développement).
Puis CNP ( un,b) est calculé par la formule :
En d'autres termes, la décomposition LCM contient tous les facteurs premiers inclus dans au moins une des décompositions de nombres une, b, et le plus grand des deux exposants de ce multiplicateur est pris.
Exemple:
Le calcul du plus petit commun multiple de plusieurs nombres peut se réduire à plusieurs calculs séquentiels du LCM de deux nombres :
Règle. Pour trouver le LCM d'une série de nombres, il vous faut :
- décomposer les nombres en facteurs premiers ;
- transférer la plus grande expansion (le produit des facteurs du produit souhaité) dans les facteurs du produit souhaité grand nombreà partir de ceux donnés), puis ajoutez des facteurs provenant de l'expansion d'autres nombres qui n'apparaissent pas dans le premier nombre ou qui y apparaissent moins de fois ;
— le produit résultant de facteurs premiers sera le LCM des nombres donnés.
Deux ou plus nombres naturels avoir leur propre CNO. Si les nombres ne sont pas des multiples les uns des autres ou n'ont pas les mêmes facteurs d'expansion, alors leur LCM est égal au produit de ces nombres.

Les facteurs premiers du nombre 28 (2, 2, 7) sont complétés par le facteur 3 (le nombre 21), le produit résultant (84) sera le plus petit nombre, qui est divisible par 21 et 28.

Les facteurs premiers du plus grand nombre 30 sont complétés par le facteur 5 du nombre 25, le produit résultant 150 est supérieur au plus grand nombre 30 et est divisible par tous les nombres donnés sans reste. Il s'agit du plus petit produit possible (150, 250, 300...) qui est un multiple de tous les nombres donnés.

Les nombres 2,3,11,37 sont des nombres premiers, donc leur LCM est égal au produit des nombres donnés.
Règle. Pour calculer le LCM des nombres premiers, vous devez multiplier tous ces nombres entre eux.
Autre possibilité :
Pour trouver le plus petit commun multiple (LCM) de plusieurs nombres dont vous avez besoin :
1) représenter chaque nombre comme un produit de ses facteurs premiers, par exemple :
504 = 2 2 2 3 3 7,
2) écrire les puissances de tous les facteurs premiers :
504 = 2 2 2 3 3 7 = 2 3 3 2 7 1,
3) noter tous les diviseurs premiers (multiplicateurs) de chacun de ces nombres ;
4) choisir le plus grand degré de chacun d'eux, trouvé dans tous les développements de ces nombres ;
5) multiplier ces pouvoirs.
Exemple. Trouvez le LCM des nombres : 168, 180 et 3024.
Solution. 168 = 2 2 2 3 7 = 2 3 3 1 7 1,
180 = 2 2 3 3 5 = 2 2 3 2 5 1,
3024 = 2 2 2 2 3 3 3 7 = 2 4 3 3 7 1.
Nous notons les plus grandes puissances de tous les diviseurs premiers et les multiplions :
CNP = 2 4 3 3 5 1 7 1 = 15 120.
Un multiple est un nombre divisible par un nombre donné sans reste. Le plus petit commun multiple (LCM) d'un groupe de nombres est le plus petit nombre divisible par chaque nombre du groupe sans laisser de reste. Pour trouver le plus petit commun multiple, vous devez trouver les facteurs premiers de nombres donnés. Le LCM peut également être calculé à l'aide d'un certain nombre d'autres méthodes qui s'appliquent à des groupes de deux nombres ou plus.
Mesures
Série de multiples
- Par exemple, trouvez le plus petit commun multiple de 5 et 8. Ce sont de petits nombres, vous pouvez donc utiliser cette méthode.
-
Un multiple est un nombre divisible par un nombre donné sans reste. Les multiples peuvent être trouvés dans la table de multiplication.
- Par exemple, les nombres multiples de 5 sont : 5, 10, 15, 20, 25, 30, 35, 40.
-
Écrivez une série de nombres multiples du premier nombre. Faites cela sous des multiples du premier nombre pour comparer deux ensembles de nombres.
- Par exemple, les nombres multiples de 8 sont : 8, 16, 24, 32, 40, 48, 56 et 64.
-
Trouvez le plus petit nombre présent dans les deux ensembles de multiples. Vous devrez peut-être écrire de longues séries de multiples pour trouver nombre total. Le plus petit nombre présent dans les deux ensembles de multiples est le plus petit commun multiple.
- Par exemple, le plus petit nombre qui apparaît dans la série des multiples de 5 et 8 est le nombre 40. Par conséquent, 40 est le plus petit commun multiple de 5 et 8.
Factorisation première
-
Regardez ces chiffres. La méthode décrite ici est mieux utilisée lorsqu’on lui donne deux nombres, chacun étant supérieur à 10. Si des nombres plus petits sont donnés, utilisez une méthode différente.
- Par exemple, trouvez le plus petit commun multiple des nombres 20 et 84. Chacun des nombres est supérieur à 10, vous pouvez donc utiliser cette méthode.
-
Factorisez le premier nombre en facteurs premiers. Autrement dit, vous devez trouver des nombres premiers qui, une fois multipliés, donneront un nombre donné. Une fois que vous avez trouvé les facteurs premiers, écrivez-les sous forme d’égalités.
- Par exemple, 2 × 10 = 20 (\displaystyle (\mathbf (2))\times 10=20) Et 2 × 5 = 10 (\displaystyle (\mathbf (2) )\times (\mathbf (5) )=10). Ainsi, les facteurs premiers du nombre 20 sont les nombres 2, 2 et 5. Écrivez-les sous forme d'expression : .
-
Factorisez le deuxième nombre en facteurs premiers. Faites cela de la même manière que vous avez factorisé le premier nombre, c'est-à-dire trouvez des nombres premiers qui, une fois multipliés, donneront le nombre donné.
- Par exemple, 2 × 42 = 84 (\displaystyle (\mathbf (2))\times 42=84), 7 × 6 = 42 (\displaystyle (\mathbf (7))\times 6=42) Et 3 × 2 = 6 (\displaystyle (\mathbf (3) )\times (\mathbf (2) )=6). Ainsi, les facteurs premiers du nombre 84 sont les nombres 2, 7, 3 et 2. Écrivez-les sous forme d'expression : .
-
Notez les facteurs communs aux deux nombres.Écrivez des facteurs tels qu’une opération de multiplication. Au fur et à mesure que vous écrivez chaque facteur, rayez-le dans les deux expressions (expressions qui décrivent les factorisations de nombres en facteurs premiers).
- Par exemple, les deux nombres ont un facteur commun de 2, alors écrivez 2 × (\displaystyle 2\times) et rayez le 2 dans les deux expressions.
- Ce que les deux nombres ont en commun est un autre facteur de 2, alors écrivez 2 × 2 (\displaystyle 2\times 2) et rayez le deuxième 2 dans les deux expressions.
-
Ajoutez les facteurs restants à l’opération de multiplication. Il s’agit de facteurs qui ne sont pas barrés dans les deux expressions, c’est-à-dire qui ne sont pas communs aux deux nombres.
- Par exemple, dans l'expression 20 = 2 × 2 × 5 (\displaystyle 20=2\times 2\times 5) Les deux deux (2) sont barrés car ce sont des facteurs communs. Le facteur 5 n'est pas barré, alors écrivez l'opération de multiplication comme ceci : 2 × 2 × 5 (\displaystyle 2\times 2\times 5)
- En expression 84 = 2 × 7 × 3 × 2 (\displaystyle 84=2\times 7\times 3\times 2) les deux deux (2) sont également barrés. Les facteurs 7 et 3 ne sont pas barrés, alors écrivez l'opération de multiplication comme ceci : 2 × 2 × 5 × 7 × 3 (\displaystyle 2\times 2\times 5\times 7\times 3).
-
Calculez le plus petit commun multiple. Pour ce faire, multipliez les nombres dans l'opération de multiplication écrite.
- Par exemple, 2 × 2 × 5 × 7 × 3 = 420 (\displaystyle 2\times 2\times 5\times 7\times 3=420). Le plus petit commun multiple de 20 et 84 est donc 420.
Trouver des facteurs communs
-
Dessinez une grille comme pour un jeu de tic-tac-toe. Une telle grille se compose de deux lignes parallèles qui se croisent (à angle droit) avec deux autres lignes parallèles. Cela vous donnera trois lignes et trois colonnes (la grille ressemble beaucoup à l'icône #). Écrivez le premier nombre dans la première ligne et la deuxième colonne. Écrivez le deuxième nombre dans la première ligne et la troisième colonne.
- Par exemple, trouvez le plus petit commun multiple des nombres 18 et 30. Écrivez le nombre 18 dans la première ligne et la deuxième colonne, et écrivez le nombre 30 dans la première ligne et la troisième colonne.
-
Trouvez le diviseur commun aux deux nombres. Notez-le dans la première ligne et la première colonne. Il est préférable de rechercher des facteurs premiers, mais ce n'est pas une obligation.
- Par exemple, 18 et 30 sont des nombres pairs, donc leur facteur commun est 2. Écrivez donc 2 dans la première ligne et la première colonne.
-
Divisez chaque nombre par le premier diviseur.Écrivez chaque quotient sous le numéro approprié. Un quotient est le résultat de la division de deux nombres.
- Par exemple, 18 ÷ 2 = 9 (\displaystyle 18\div 2=9), alors écrivez 9 sous 18 ans.
- 30 ÷ 2 = 15 (\displaystyle 30\div 2=15), alors notez 15 sous 30.
-
Trouvez le diviseur commun aux deux quotients. S'il n'existe pas de diviseur de ce type, ignorez les deux étapes suivantes. Sinon, écrivez le diviseur dans la deuxième ligne et la première colonne.
- Par exemple, 9 et 15 sont divisibles par 3, alors écrivez 3 dans la deuxième ligne et la première colonne.
-
Divisez chaque quotient par son deuxième diviseur.Écrivez chaque résultat de division sous le quotient correspondant.
- Par exemple, 9 ÷ 3 = 3 (\displaystyle 9\div 3=3), alors écrivez 3 sous 9.
- 15 ÷ 3 = 5 (\displaystyle 15\div 3=5), alors écrivez 5 sous 15.
-
Si nécessaire, ajoutez des cellules supplémentaires à la grille. Répétez les étapes décrites jusqu'à ce que les quotients aient un diviseur commun.
-
Encerclez les nombres dans la première colonne et la dernière ligne de la grille.Écrivez ensuite les nombres sélectionnés sous forme d’opération de multiplication.
- Par exemple, les nombres 2 et 3 sont dans la première colonne, et les nombres 3 et 5 sont dans la dernière ligne, alors écrivez l'opération de multiplication comme ceci : 2 × 3 × 3 × 5 (\displaystyle 2\times 3\times 3\times 5).
-
Trouvez le résultat de la multiplication de nombres. Cela calculera le plus petit commun multiple de deux nombres donnés.
- Par exemple, 2 × 3 × 3 × 5 = 90 (\displaystyle 2\times 3\times 3\times 5=90). Le plus petit commun multiple de 18 et 30 est donc 90.
L'algorithme d'Euclide
-
N'oubliez pas la terminologie associée à l'opération de division. Le dividende est le nombre qui est divisé. Le diviseur est le nombre par lequel on divise. Un quotient est le résultat de la division de deux nombres. Un reste est le nombre restant lorsque deux nombres sont divisés.
- Par exemple, dans l'expression 15 ÷ 6 = 2 (\displaystyle 15\div 6=2) ost. 3 :
15 est le dividende
6 est un diviseur
2 est le quotient
3 est le reste.
- Par exemple, dans l'expression 15 ÷ 6 = 2 (\displaystyle 15\div 6=2) ost. 3 :
Regardez ces chiffres. La méthode décrite ici est mieux utilisée lorsqu’on lui donne deux nombres, chacun étant inférieur à 10. Si des nombres plus grands sont donnés, utilisez une méthode différente.
Le matériel présenté ci-dessous est suite logique théories de l'article intitulé LCM - plus petit commun multiple, définition, exemples, lien entre LCM et GCD. Ici, nous parlerons de trouver le plus petit commun multiple (LCM), Et attention particulière Concentrons-nous sur la résolution d'exemples. Tout d’abord, nous montrerons comment le LCM de deux nombres est calculé à l’aide du PGCD de ces nombres. Ensuite, nous verrons comment trouver le plus petit commun multiple en factorisant les nombres en facteurs premiers. Après cela, nous nous concentrerons sur la recherche du LCM de trois et plus nombres, et faites également attention au calcul du LCM des nombres négatifs.
Navigation dans les pages.
Calcul du plus petit commun multiple (LCM) via GCD
Une façon de trouver le multiple le plus petit commun est basée sur la relation entre LCM et GCD. La connexion existante entre LCM et GCD nous permet de calculer le plus petit commun multiple de deux entiers positifs via un plus grand commun diviseur connu. La formule correspondante est LCM(a, b)=ab:PGCD(a, b) . Examinons des exemples de recherche du LCM à l'aide de la formule donnée.
Exemple.
Trouvez le plus petit commun multiple de deux nombres 126 et 70.
Solution.
Dans cet exemple a=126 , b=70 . Utilisons la connexion entre LCM et GCD, exprimée par la formule LCM(a, b)=ab:PGCD(a, b). Autrement dit, nous devons d’abord trouver le plus grand diviseur commun des nombres 70 et 126, après quoi nous pouvons calculer le LCM de ces nombres à l’aide de la formule écrite.
Trouvons GCD(126, 70) en utilisant l'algorithme euclidien : 126=70·1+56, 70=56·1+14, 56=14·4, donc, GCD(126, 70)=14.
Nous trouvons maintenant le plus petit commun multiple requis : PGCD(126, 70)=126·70 : PGCD(126, 70)= 126·70:14=630.
Répondre:
LCM(126, 70)=630 .
Exemple.
À quoi est égal LCM(68, 34) ?
Solution.
Parce que 68 est divisible par 34, alors PGCD(68, 34)=34. Calculons maintenant le plus petit commun multiple : PGCD(68, 34)=68·34:PGCD(68, 34)= 68·34:34=68.
Répondre:
LCM(68, 34)=68 .
Notez que l'exemple précédent correspond à la règle suivante pour trouver le LCM pour les entiers positifs a et b : si le nombre a est divisible par b, alors le plus petit commun multiple de ces nombres est a.
Trouver le LCM en factorisant les nombres en facteurs premiers
Une autre façon de trouver le plus petit commun multiple consiste à factoriser les nombres en facteurs premiers. Si vous composez un produit à partir de tous les facteurs premiers de nombres donnés, puis excluez de ce produit tous les facteurs premiers communs présents dans les décompositions de nombres donnés, alors le produit résultant sera égal au plus petit commun multiple des nombres donnés. .
La règle énoncée pour trouver le LCM découle de l'égalité LCM(a, b)=ab:PGCD(a, b). En effet, le produit des nombres a et b est égal au produit de tous les facteurs impliqués dans le développement des nombres a et b. À son tour, GCD(a, b) est égal au produit de tous les facteurs premiers simultanément présents dans les développements des nombres a et b (comme décrit dans la section sur la recherche de GCD en utilisant le développement des nombres en facteurs premiers).
Donnons un exemple. Sachons que 75=3·5·5 et 210=2·3·5·7. Composons le produit à partir de tous les facteurs de ces développements : 2·3·3·5·5·5·7 . Maintenant, de ce produit, nous excluons tous les facteurs présents à la fois dans le développement du nombre 75 et dans le développement du nombre 210 (ces facteurs sont 3 et 5), alors le produit prendra la forme 2·3·5·5·7. . La valeur de ce produit est égale au plus petit commun multiple de 75 et 210, soit CNP(75, 210)= 2·3·5·5·7=1 050.
Exemple.
Factorisez les nombres 441 et 700 en facteurs premiers et trouvez le plus petit commun multiple de ces nombres.
Solution.
Factorisons les nombres 441 et 700 en facteurs premiers :
On obtient 441=3·3·7·7 et 700=2·2·5·5·7.
Faisons maintenant un produit de tous les facteurs impliqués dans l'expansion de ces nombres : 2·2·3·3·5·5·7·7·7. Excluons de ce produit tous les facteurs qui sont simultanément présents dans les deux expansions (il n'y a qu'un seul de ces facteurs - c'est le nombre 7) : 2·2·3·3·5·5·7·7. Ainsi, LCM(441, 700)=2·2·3·3·5·5·7·7=44 100.
Répondre:
CNP(441, 700)= 44 100 .
La règle permettant de trouver le LCM en utilisant la factorisation des nombres en facteurs premiers peut être formulée un peu différemment. Si les facteurs manquants du développement du nombre b sont ajoutés aux facteurs du développement du nombre a, alors la valeur du produit résultant sera égale au plus petit commun multiple des nombres a et b..
Par exemple, prenons les mêmes nombres 75 et 210, leurs décompositions en facteurs premiers sont les suivantes : 75=3·5·5 et 210=2·3·5·7. Aux facteurs 3, 5 et 5 du développement du nombre 75 on ajoute les facteurs manquants 2 et 7 du développement du nombre 210, on obtient le produit 2·3·5·5·7 dont la valeur est égal à LCM(75, 210).
Exemple.
Trouvez le plus petit commun multiple de 84 et 648.
Solution.
On obtient d'abord les décompositions des nombres 84 et 648 en facteurs premiers. Ils ressemblent à 84=2·2·3·7 et 648=2·2·2·3·3·3·3. Aux facteurs 2, 2, 3 et 7 du développement du nombre 84 on ajoute les facteurs manquants 2, 3, 3 et 3 du développement du nombre 648, on obtient le produit 2 2 2 3 3 3 3 7, ce qui est égal à 4 536 . Ainsi, le plus petit commun multiple souhaité de 84 et 648 est 4 536.
Répondre:
LCM(84, 648)=4 536 .
Trouver le LCM de trois nombres ou plus
Le plus petit commun multiple de trois nombres ou plus peut être trouvé en trouvant séquentiellement le LCM de deux nombres. Rappelons le théorème correspondant, qui permet de trouver le LCM de trois nombres ou plus.
Théorème.
Soit des nombres entiers positifs a 1 , a 2 , …, a k, le plus petit commun multiple m k de ces nombres est trouvé en calculant séquentiellement m 2 = LCM(a 1 , a 2) , m 3 = LCM(m 2 , a 3) , … , m k = LCM(m k−1 , a k) .
Considérons l'application de ce théorème en utilisant l'exemple de la recherche du plus petit commun multiple de quatre nombres.
Exemple.
Trouvez le LCM de quatre nombres 140, 9, 54 et 250.
Solution.
Dans cet exemple, un 1 =140, un 2 =9, un 3 =54, un 4 =250.
On trouve d'abord m 2 = LOC(une 1 , une 2) = LOC(140, 9). Pour ce faire, en utilisant l'algorithme euclidien, on détermine PGCD(140, 9), on a 140=9·15+5, 9=5·1+4, 5=4·1+1, 4=1·4, donc, GCD(140, 9)=1 , d'où PGCD(140, 9)=140 9:PGCD(140, 9)= 140·9:1=1 260. C'est-à-dire m 2 =1 260.
Maintenant nous trouvons m 3 = LOC (m 2 , a 3) = LOC (1 260, 54). Calculons-le via PGCD(1 260, 54), que nous déterminons également à l'aide de l'algorithme euclidien : 1 260=54·23+18, 54=18·3. Alors pgcd(1,260, 54)=18, d'où pgcd(1,260, 54)= 1,260·54:gcd(1,260, 54)= 1,260·54:18=3,780. C'est-à-dire m 3 =3 780.
Il ne reste plus qu'à trouver m 4 = LOC(m 3, une 4) = LOC(3 780, 250). Pour ce faire, on trouve GCD(3,780, 250) en utilisant l'algorithme euclidien : 3,780=250·15+30, 250=30·8+10, 30=10·3. Par conséquent, GCM(3,780, 250)=10, d’où GCM(3,780, 250)= 3 780 250 : PGCD(3 780, 250)= 3 780·250:10=94 500. C'est-à-dire m 4 =94 500.
Ainsi, le plus petit commun multiple des quatre nombres originaux est 94 500.
Répondre:
LCM(140, 9, 54, 250)=94 500.
Dans de nombreux cas, il est pratique de trouver le plus petit commun multiple de trois nombres ou plus en utilisant des factorisations premières des nombres donnés. Dans ce cas, vous devez respecter la règle suivante. Le plus petit commun multiple de plusieurs nombres est égal au produit qui se compose comme suit : les facteurs manquants du développement du deuxième nombre s'ajoutent à tous les facteurs du développement du premier nombre, les facteurs manquants du développement du premier nombre le troisième nombre est ajouté aux facteurs résultants, et ainsi de suite.
Examinons un exemple de recherche du multiple le plus petit commun à l'aide de la factorisation première.
Exemple.
Trouvez le plus petit commun multiple des cinq nombres 84, 6, 48, 7, 143.
Solution.
Tout d'abord, on obtient des décompositions de ces nombres en facteurs premiers : 84=2·2·3·7, 6=2·3, 48=2·2·2·2·3, 7 (7 est un nombre premier, il coïncide avec sa décomposition en facteurs premiers) et 143=11·13.
Pour trouver le LCM de ces nombres, aux facteurs du premier nombre 84 (ils sont 2, 2, 3 et 7), il faut ajouter les facteurs manquants du développement du deuxième nombre 6. La décomposition du nombre 6 ne contient pas de facteurs manquants, puisque 2 et 3 sont déjà présents dans la décomposition du premier nombre 84. Ensuite, aux facteurs 2, 2, 3 et 7, nous ajoutons les facteurs manquants 2 et 2 issus du développement du troisième nombre 48, nous obtenons un ensemble de facteurs 2, 2, 2, 2, 3 et 7. Il ne sera pas nécessaire d’ajouter des multiplicateurs à cet ensemble à l’étape suivante, puisque 7 y est déjà contenu. Enfin, aux facteurs 2, 2, 2, 2, 3 et 7 on ajoute les facteurs manquants 11 et 13 issus du développement du nombre 143. On obtient le produit 2·2·2·2·3·7·11·13, qui est égal à 48,048.
Plus grand diviseur commun
Définition 2
Si un nombre naturel a est divisible par un nombre naturel $b$, alors $b$ est appelé un diviseur de $a$ et $a$ est appelé un multiple de $b$.
Soient $a$ et $b$ des nombres naturels. Le nombre $c$ est appelé le diviseur commun de $a$ et de $b$.
L'ensemble des diviseurs communs des nombres $a$ et $b$ est fini, puisqu'aucun de ces diviseurs ne peut être supérieur à $a$. Cela signifie que parmi ces diviseurs, il y en a un plus grand, qui est appelé le plus grand diviseur commun des nombres $a$ et $b$ et est noté par les notations suivantes :
$PGCD\(a;b)\ ou \D\(a;b)$
Pour trouver le plus grand diviseur commun de deux nombres, il vous faut :
- Trouvez le produit des nombres trouvés à l’étape 2. Le nombre obtenu sera le plus grand diviseur commun souhaité.
Exemple 1
Trouvez le pgcd des nombres $121$ et $132.$
242$=2\cdot 11\cdot 11$
$132=2\cdot 2\cdot 3\cdot 11$
Choisissez les nombres qui sont inclus dans l'expansion de ces nombres
242$=2\cdot 11\cdot 11$
$132=2\cdot 2\cdot 3\cdot 11$
Trouvez le produit des nombres trouvés à l’étape 2. Le nombre obtenu sera le plus grand diviseur commun souhaité.
$PGCD=2\cdot 11=22$
Exemple 2
Trouvez le pgcd des monômes $63$ et $81$.
Nous trouverons selon l'algorithme présenté. Pour ce faire :
Factorisons les nombres en facteurs premiers
63$=3\cdot 3\cdot 7$
$81=3\cdot 3\cdot 3\cdot 3$
Nous sélectionnons les nombres qui sont inclus dans l'expansion de ces nombres
63$=3\cdot 3\cdot 7$
$81=3\cdot 3\cdot 3\cdot 3$
Trouvons le produit des nombres trouvés à l'étape 2. Le nombre résultant sera le plus grand diviseur commun souhaité.
$PGCD=3\cdot 3=9$
Vous pouvez trouver le pgcd de deux nombres d’une autre manière, en utilisant un ensemble de diviseurs de nombres.
Exemple 3
Trouvez le pgcd des nombres 48$ et 60$.
Solution:
Trouvons l'ensemble des diviseurs du nombre $48$ : $\left\((\rm 1,2,3.4.6,8,12,16,24,48)\right\)$
Trouvons maintenant l'ensemble des diviseurs du nombre $60$:$\ \left\((\rm 1,2,3,4,5,6,10,12,15,20,30,60)\right\) $
Trouvons l'intersection de ces ensembles : $\left\((\rm 1,2,3,4,6,12)\right\)$ - cet ensemble déterminera l'ensemble des diviseurs communs des nombres $48$ et $60 $. Le plus grand élément dans ensemble donné le numéro sera de 12$. Cela signifie que le plus grand diviseur commun des nombres 48$ et 60$ est 12$.
Définition du NPL
Définition 3
Multiples communs de nombres naturels$a$ et $b$ sont un nombre naturel qui est un multiple de $a$ et $b$.
Les multiples communs de nombres sont des nombres divisibles par les nombres d'origine sans reste. Par exemple, pour les nombres 25$ et 50$, les multiples communs seront les nombres 50,100,150,200$, etc.
Le plus petit commun multiple sera appelé plus petit commun multiple et sera noté LCM$(a;b)$ ou K$(a;b).$
Pour trouver le LCM de deux nombres, vous devez :
- Factoriser les nombres en facteurs premiers
- Notez les facteurs qui font partie du premier nombre et ajoutez-y les facteurs qui font partie du second et ne font pas partie du premier.
Exemple 4
Trouvez le LCM des nombres 99$ et 77$.
Nous trouverons selon l'algorithme présenté. Pour ça
Factoriser les nombres en facteurs premiers
99$=3\cdot 3\cdot 11$
Notez les facteurs inclus dans le premier
ajoutez-y des multiplicateurs qui font partie du second et ne font pas partie du premier
Trouvez le produit des nombres trouvés à l'étape 2. Le nombre résultant sera le plus petit commun multiple souhaité
$NOK=3\cdot 3\cdot 11\cdot 7=693$
Compiler des listes de diviseurs de nombres est souvent une tâche très laborieuse. Il existe un moyen de trouver GCD appelé algorithme euclidien.
Énoncés sur lesquels est basé l'algorithme euclidien :
Si $a$ et $b$ sont des nombres naturels et $a\vdots b$, alors $D(a;b)=b$
Si $a$ et $b$ sont des nombres naturels tels que $b
En utilisant $D(a;b)= D(a-b;b)$, on peut réduire successivement les nombres considérés jusqu'à atteindre une paire de nombres telle que l'un d'eux soit divisible par l'autre. Ensuite, le plus petit de ces nombres sera le plus grand diviseur commun souhaité pour les nombres $a$ et $b$.
Propriétés de GCD et LCM
- Tout multiple commun de $a$ et $b$ est divisible par K$(a;b)$
- Si $a\vdots b$ , alors К$(a;b)=a$
Si K$(a;b)=k$ et $m$ est un nombre naturel, alors K$(am;bm)=km$
Si $d$ est un diviseur commun pour $a$ et $b$, alors K($\frac(a)(d);\frac(b)(d)$)=$\ \frac(k)(d )$
Si $a\vdots c$ et $b\vdots c$ , alors $\frac(ab)(c)$ est le multiple commun de $a$ et $b$
Pour tout nombre naturel $a$ et $b$, l'égalité est vraie
$D(a;b)\cdot К(a;b)=ab$
Tout diviseur commun des nombres $a$ et $b$ est un diviseur du nombre $D(a;b)$