Inégalités avec des exemples de logarithmes de l'examen d'État unifié. Inégalités logarithmiques – Hypermarché du savoir
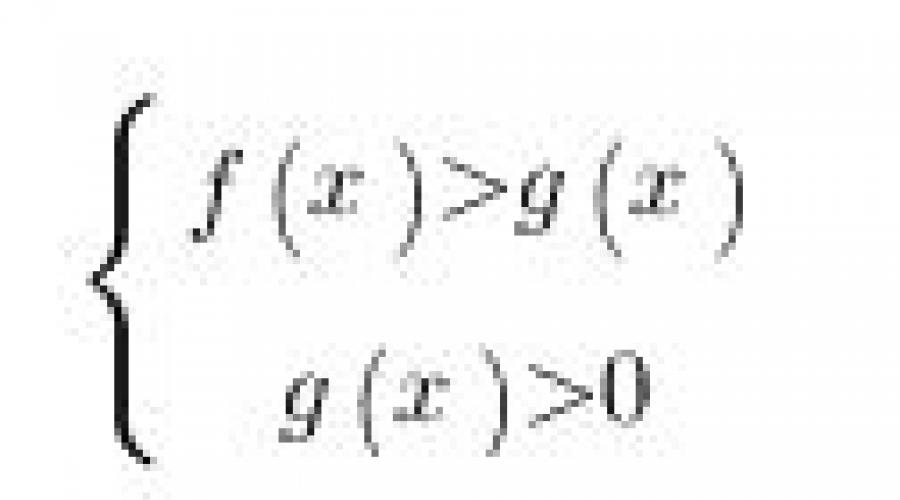
Lire aussi
Inégalités logarithmiques
Dans les leçons précédentes, nous nous sommes familiarisés avec les équations logarithmiques et maintenant nous savons ce qu'elles sont et comment les résoudre. La leçon d'aujourd'hui sera consacrée à l'étude des inégalités logarithmiques. Quelles sont ces inégalités et quelle est la différence entre résoudre une équation logarithmique et une inégalité ?
Les inégalités logarithmiques sont des inégalités dont une variable apparaît sous le signe du logarithme ou à sa base.
Ou bien, on peut aussi dire qu'une inégalité logarithmique est une inégalité dans laquelle sa valeur inconnue, comme dans une équation logarithmique, apparaîtra sous le signe du logarithme.
Protozoaires inégalités logarithmiques ressemble à ca:
où f(x) et g(x) sont des expressions qui dépendent de x.
Regardons cela en utilisant cet exemple : f(x)=1+2x+x2, g(x)=3x−1.
Résoudre les inégalités logarithmiques
Avant de résoudre les inégalités logarithmiques, il convient de noter qu’une fois résolues, elles sont similaires à inégalités exponentielles, à savoir :
Premièrement, lorsque nous passons des logarithmes aux expressions sous le signe du logarithme, nous devons également comparer la base du logarithme avec une seule ;
Deuxièmement, lors de la résolution d’une inégalité logarithmique à l’aide d’un changement de variables, nous devons résoudre les inégalités par rapport au changement jusqu’à obtenir l’inégalité la plus simple.
Mais vous et moi avons examiné des aspects similaires de la résolution des inégalités logarithmiques. Faisons maintenant attention à une différence assez significative. Vous et moi savons que la fonction logarithmique a zone limitée définitions, donc, en passant des logarithmes aux expressions sous le signe du logarithme, il faut prendre en compte l'aire valeurs acceptables(ODZ).
Autrement dit, il convient de garder à l'esprit que lors de la résolution d'une équation logarithmique, vous et moi pouvons d'abord trouver les racines de l'équation, puis vérifier cette solution. Mais résoudre une inégalité logarithmique ne fonctionnera pas de cette façon, puisque lorsqu'on passe des logarithmes aux expressions sous le signe du logarithme, il faudra écrire l'ODZ de l'inégalité.
De plus, il convient de rappeler que la théorie des inégalités se compose de nombres réels, positifs et nombres négatifs, ainsi que le chiffre 0.
Par exemple, lorsque le nombre « a » est positif, alors vous devez utiliser la notation suivante : a >0. Dans ce cas, la somme et le produit de ces nombres seront également positifs.
Le principe principal pour résoudre une inégalité est de la remplacer par une inégalité plus simple, mais l'essentiel est qu'elle soit équivalente à celle donnée. De plus, nous avons également obtenu une inégalité et l'avons à nouveau remplacée par une autre qui a une forme plus simple, etc.
Lorsque vous résolvez des inégalités avec une variable, vous devez trouver toutes ses solutions. Si deux inégalités ont la même variable x, alors ces inégalités sont équivalentes, à condition que leurs solutions coïncident.
Lorsque vous effectuez des tâches de résolution d'inégalités logarithmiques, vous devez vous rappeler que lorsque a > 1, alors la fonction logarithmique augmente et lorsque 0< a < 1, то такая функция имеет свойство убывать. Эти свойства вам будут необходимы при решении логарифмических неравенств, поэтому вы их должны хорошо знать и помнить.
Méthodes de résolution des inégalités logarithmiques
Examinons maintenant certaines des méthodes utilisées pour résoudre les inégalités logarithmiques. Pour une meilleure compréhension et assimilation, nous tenterons de les comprendre à l’aide d’exemples précis.
Nous savons tous que l’inégalité logarithmique la plus simple a la forme suivante :
Dans cette inégalité, V – est l’un des signes d’inégalité suivants :<,>, ≤ ou ≥.
Lorsque la base d'un logarithme donné est supérieure à un (a>1), faisant le passage des logarithmes aux expressions sous le signe du logarithme, alors dans cette version le signe de l'inégalité est conservé, et l'inégalité aura la forme suivante :
ce qui est équivalent à ce système :

Dans le cas où la base du logarithme est supérieure à zéro et inférieure à un (0 C'est équivalent à ce système : Examinons d'autres exemples de résolution des inégalités logarithmiques les plus simples présentées dans l'image ci-dessous : Exercice. Essayons de résoudre cette inégalité : Résoudre la plage de valeurs acceptables. Essayons maintenant de multiplier son côté droit par : Voyons ce que nous pouvons proposer : Passons maintenant à la conversion d'expressions sublogarithmiques. Étant donné que la base du logarithme est 0< 1/4 <1, то от сюда следует, что знак неравенства изменится на противоположный: 3x-8 > 16 ; Et il s'ensuit que l'intervalle que nous avons obtenu appartient entièrement à l'ODZ et est une solution à une telle inégalité. Voici la réponse que nous avons obtenue : Essayons maintenant d'analyser ce dont nous avons besoin pour réussir à résoudre les inégalités logarithmiques ? Tout d’abord, concentrez toute votre attention et essayez de ne pas commettre d’erreurs lorsque vous effectuez les transformations données dans cette inégalité. En outre, il convient de rappeler que lors de la résolution de telles inégalités, il est nécessaire d'éviter les expansions et les contractions de l'ODZ d'inégalité, qui peuvent conduire à la perte ou à l'acquisition de solutions superflues. Deuxièmement, lors de la résolution d'inégalités logarithmiques, vous devez apprendre à penser logiquement et à comprendre la différence entre des concepts tels qu'un système d'inégalités et un ensemble d'inégalités, afin de pouvoir facilement sélectionner des solutions à l'inégalité, tout en étant guidé par son DL. Troisièmement, pour réussir à résoudre de telles inégalités, chacun de vous doit parfaitement connaître toutes les propriétés fonctions élémentaires et comprendre clairement leur signification. De telles fonctions incluent non seulement les fonctions logarithmiques, mais aussi rationnelles, de puissance, trigonométriques, etc., en un mot, toutes celles que vous avez étudiées tout au long de scolarité algèbre. Comme vous pouvez le constater, après avoir étudié le sujet des inégalités logarithmiques, il n'y a rien de difficile à résoudre ces inégalités, à condition que vous soyez prudent et persévérant dans la réalisation de vos objectifs. Pour éviter tout problème lors de la résolution des inégalités, vous devez vous entraîner autant que possible, résoudre diverses tâches et en même temps vous rappeler les méthodes de base pour résoudre ces inégalités et leurs systèmes. Si vous ne parvenez pas à résoudre les inégalités logarithmiques, vous devez analyser soigneusement vos erreurs afin de ne plus y revenir à l'avenir. Pour mieux comprendre le sujet et consolider la matière abordée, résolvez les inégalités suivantes : Le maintien de votre vie privée est important pour nous. Pour cette raison, nous avons développé une politique de confidentialité qui décrit la manière dont nous utilisons et stockons vos informations. Veuillez consulter nos pratiques de confidentialité et faites-nous savoir si vous avez des questions. Les informations personnelles font référence aux données qui peuvent être utilisées pour identifier ou contacter une personne spécifique. Il peut vous être demandé de fournir vos informations personnelles à tout moment lorsque vous nous contactez. Vous trouverez ci-dessous quelques exemples des types d'informations personnelles que nous pouvons collecter et de la manière dont nous pouvons utiliser ces informations. Quelles informations personnelles collectons-nous : Comment utilisons-nous vos informations personnelles: Nous ne divulguons pas les informations reçues de votre part à des tiers. Des exceptions: Nous prenons des précautions - notamment administratives, techniques et physiques - pour protéger vos informations personnelles contre la perte, le vol et l'utilisation abusive, ainsi que contre l'accès, la divulgation, l'altération et la destruction non autorisés. Pour garantir la sécurité de vos informations personnelles, nous communiquons les normes de confidentialité et de sécurité à nos employés et appliquons strictement les pratiques de confidentialité. Une inégalité est dite logarithmique si elle contient une fonction logarithmique. Les méthodes de résolution des inégalités logarithmiques ne diffèrent pas de celles-ci, à l'exception de deux choses. Premièrement, lorsqu’on passe de l’inégalité logarithmique à l’inégalité sous fonctions logarithmiques devrait suivre le signe de l'inégalité résultante. Il obéit à la règle suivante. Si la base de la fonction logarithmique est supérieure à 1$, alors lors du passage de l'inégalité logarithmique à l'inégalité des fonctions sous-logarithmiques, le signe de l'inégalité est conservé, mais s'il est inférieur à 1$, alors il change à l'opposé . Deuxièmement, la solution de toute inégalité est un intervalle, et, par conséquent, à la fin de la résolution de l'inégalité des fonctions sous-logarithmiques, il est nécessaire de créer un système de deux inégalités : la première inégalité de ce système sera l'inégalité des fonctions sous-logarithmiques, et le second sera l'intervalle du domaine de définition des fonctions logarithmiques incluses dans l'inégalité logarithmique. Résolvons les inégalités : 1.
$\log_(2)((x+3)) \geq 3.$ $D(y) : \x+3>0.$ $x \in (-3;+\infty)$ La base du logarithme est $2>1$, donc le signe ne change pas. En utilisant la définition du logarithme, on obtient : $x+3 \geq 2^(3),$ $x\in\) Très important! Dans toute inégalité, le passage de la forme \(\log_a(f(x)) ˅ \log_a(g(x))\) à la comparaison d'expressions sous logarithmes ne peut se faire que si : Exemple
. Résoudre l'inégalité : \(\log\)\(≤-1\) Solution:
\(\enregistrer\) \(_(\frac(1)(3))(\frac(3x-2)(2x-3))\)\(≤-1\) Écrivons l'ODZ. ODZ : \(\frac(3x-2)(2x-3)\) \(>0\) \(\frac(3x-2-3(2x-3))(2x-3)\)\(≥\) \(0\) Nous ouvrons les supports et apportons . \(\frac(-3x+7)(2x-3)\) \(≥\) \(0\) On multiplie l'inégalité par \(-1\), sans oublier d'inverser le signe de comparaison. \(\frac(3x-7)(2x-3)\) \(≤\) \(0\) \(\frac(3(x-\frac(7)(3)))(2(x-\frac(3)(2)))\)\(≤\) \(0\) Construisons une droite numérique et marquons les points \(\frac(7)(3)\) et \(\frac(3)(2)\) dessus. Veuillez noter que le point du dénominateur est supprimé, malgré le fait que l'inégalité ne soit pas stricte. Le fait est que ce point ne sera pas une solution, puisque substitué à l’inégalité, il nous conduira à la division par zéro. Maintenant, nous traçons l'ODZ sur le même axe numérique et notons en réponse l'intervalle qui tombe dans l'ODZ. Nous écrivons la réponse finale. Exemple
. Résoudre l'inégalité : \(\log^2_3x-\log_3x-2>0\) Solution:
\(\log^2_3x-\log_3x-2>0\) Écrivons l'ODZ. ODZ : \(x>0\) Passons à la solution. Solution : \(\log^2_3x-\log_3x-2>0\) Nous avons ici une inégalité logarithmique carrée typique. Faisons-le. \(t=\log_3x\) \(D=1+8=9\) Nous devons maintenant revenir à la variable d'origine - x. Pour ce faire, allons à , qui a la même solution, et effectuons la substitution inverse. \(\left[ \begin(rassemblé) t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3x>2\\\log_3x<-1 \end{gathered} \right.\) Transformez \(2=\log_39\), \(-1=\log_3\frac(1)(3)\). \(\left[ \begin(rassemblé) \log_3x>\log_39 \\ \log_3x<\log_3\frac{1}{3} \end{gathered} \right.\) Passons à la comparaison des arguments. Les bases des logarithmes sont supérieures à \(1\), donc le signe des inégalités ne change pas. \(\left[ \begin(rassemblé) x>9 \\ x<\frac{1}{3} \end{gathered} \right.\) Combinons la solution de l'inégalité et de l'ODZ en une seule figure. Écrivons la réponse. Objectifs de la leçon: Didactique: Éducatif: développer la mémoire, l'attention, la pensée logique, les capacités de comparaison, être capable de généraliser et de tirer des conclusions Éducatif: cultiver la précision, la responsabilité de la tâche accomplie et l’entraide. Méthodes d'enseignement:
verbal ,
visuel ,
pratique ,
recherche partielle ,
autonomie gouvernementale ,
contrôle. Formes d'organisation activité cognitiveétudiants:
frontale ,
individuel ,
travailler en équipe de deux. Équipement:
un ensemble de tâches de test, des notes de référence, des feuilles vierges pour les solutions. Type de cours : apprendre du nouveau matériel. Pendant les cours 1. Moment organisationnel. Le sujet et les objectifs du cours, le plan du cours sont annoncés : chaque élève reçoit une fiche d'évaluation, qu'il remplit pendant le cours ; pour chaque paire d'étudiants - les documents imprimés avec les tâches doivent être complétés par paires ; des feuilles de solutions vierges ; fiches supports : définition du logarithme ; graphique d'une fonction logarithmique, ses propriétés ; propriétés des logarithmes ; algorithme de résolution des inégalités logarithmiques. Toutes les décisions après auto-évaluation sont soumises à l'enseignant. Feuille de notes de l'élève 2. Actualisation des connaissances. Consignes du professeur. Rappelez-vous la définition d'un logarithme, le graphique d'une fonction logarithmique et ses propriétés. Pour ce faire, lisez le texte aux pages 88-90, 98-101 du manuel « L'algèbre et les débuts de l'analyse 10-11 » édité par Sh.A Alimov, Yu.M Kolyagin et autres. Les étudiants reçoivent des fiches sur lesquelles sont inscrites : la définition d'un logarithme ; montre un graphique d'une fonction logarithmique et de ses propriétés ; propriétés des logarithmes ; algorithme de résolution d'inégalités logarithmiques, un exemple de résolution d'une inégalité logarithmique qui se réduit à une inégalité quadratique. 3. Étudier du nouveau matériel. La résolution des inégalités logarithmiques repose sur la monotonie de la fonction logarithmique. Algorithme de résolution des inégalités logarithmiques : A) Trouver le domaine de définition de l'inégalité (l'expression sublogarithmique est supérieure à zéro). Élément d'apprentissage n°1. Objectif : consolider la solution aux inégalités logarithmiques les plus simples Forme d'organisation de l'activité cognitive des élèves : travail individuel. Tâches pour travail indépendant pendant 10 minutes. Pour chaque inégalité, il y a plusieurs réponses possibles ; vous devez choisir la bonne et la vérifier à l'aide de la clé. Élément d'apprentissage n°2. Objectif : consolider la solution des inégalités logarithmiques en utilisant les propriétés des logarithmes. Consignes du professeur. Rappelez-vous les propriétés de base des logarithmes. Pour ce faire, lisez le texte du manuel aux pp. 92, 103-104. Tâches de travail indépendant pendant 10 minutes. CLÉ : 2113, nombre maximum de points – 8 points. Élément d'apprentissage n°3. Objectif : étudier la solution des inégalités logarithmiques par la méthode de réduction au quadratique. Consignes de l'enseignant : la méthode pour réduire une inégalité à une inégalité quadratique consiste à transformer l'inégalité sous une forme telle qu'une certaine fonction logarithmique soit désignée par une nouvelle variable, obtenant ainsi une inégalité quadratique par rapport à cette variable. Utilisons la méthode des intervalles. Vous avez réussi le premier niveau de maîtrise de la matière. Vous devez maintenant choisir votre propre méthode de solution équations logarithmiques en utilisant toutes vos connaissances et capacités. Élément d'apprentissage n°4. Objectif : consolider la solution aux inégalités logarithmiques en choisissant indépendamment une méthode de solution rationnelle. Tâches de travail indépendant pendant 10 minutes Élément d'apprentissage n°5. Consignes du professeur. Bien joué! Vous maîtrisez la résolution d’équations du deuxième niveau de complexité. L'objectif de vos travaux ultérieurs est d'appliquer vos connaissances et vos compétences dans des situations plus complexes et non standard. Tâches pour une solution indépendante : Consignes du professeur. C'est génial si vous avez terminé toute la tâche. Bien joué! La note pour l'ensemble de la leçon dépend du nombre de points marqués pour tous les éléments pédagogiques : Remettre les épreuves d'évaluation à l'enseignant. 5. Devoirs: si vous n'avez pas obtenu plus de 15 points, travaillez sur vos erreurs (les solutions peuvent être prises auprès du professeur), si vous avez obtenu plus de 15 points, réalisez une tâche créative sur le thème « Inégalités logarithmiques ».

Exemples de résolution
![]()



3x > 24 ;
x > 8. ![]()
Que faut-il pour résoudre les inégalités logarithmiques ?
Devoirs

Collecte et utilisation des informations personnelles
Divulgation d'informations à des tiers
Protection des informations personnelles
Respecter votre vie privée au niveau de l'entreprise
Pratique.
Répondre:
\(x∈(\)\(\frac(3)(2)\) \(;\)\(\frac(7)(3)]\)

\(x∈(\)\(\frac(3)(2)\) \(;\)\(\frac(7)(3)]\)

Répondre:
\((0; \frac(1)(3))∪(9;∞)\)
\(t^2-t-2>0\) Mise en page côté gauche inégalités sur .
\(t_1= \frac(1+3)(2)=2\)
\(t_2=\frac(1-3)(2)=-1\)
\((t+1)(t-2)>0\)

B) Représentez (si possible) les côtés gauche et droit de l’inégalité sous forme de logarithmes sur la même base.
C) Déterminer si la fonction logarithmique est croissante ou décroissante : si t>1, alors croissante ; si 0
D) Aller à plus inégalité simple(expressions sublogarithmiques), en tenant compte du fait que le signe d'inégalité restera si la fonction augmente, et changera si elle diminue.
CLÉ : 13321, nombre maximum de points – 6 points.



