Qu'est-ce qui est affecté par c dans une fonction quadratique. Tutoriels vidéo avec paraboles. Cas IV, "b" apparaît

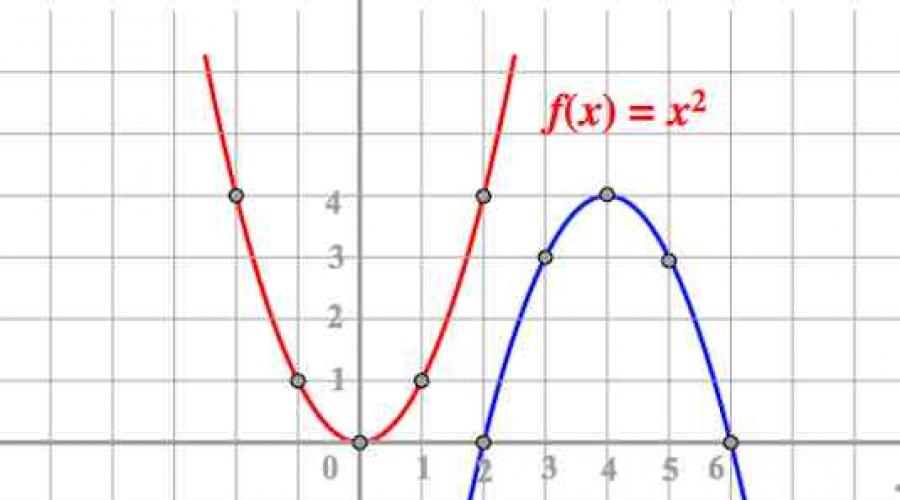
Une fonction de la forme où est appelée fonction quadratique.

Calendrier fonction quadratique – parabole.

Considérons les cas :

I CASE, PARABOLE CLASSIQUE

C'est , ,

Pour construire, remplissez le tableau en substituant les valeurs x dans la formule :

Marquez les points (0;0); (1;1); (-1;1), etc. sur le plan de coordonnées (plus le pas que nous prenons les valeurs x (en dans ce casétape 1), et plus on prend de valeurs x, plus la courbe sera lisse), on obtient une parabole :

Il est facile de voir que si l'on prend le cas , , , alors on obtient une parabole symétrique par rapport à l'axe (oh). Il est facile de le vérifier en remplissant un tableau similaire :

II CAS, « a » EST DIFFÉRENT DE L'UNITÉ

Que se passera-t-il si nous prenons , , ? Comment le comportement de la parabole va-t-il changer ? Avec title="(!LANG : Rendu par QuickLaTeX.com" height="20" width="55" style="vertical-align: -5px;"> парабола изменит форму, она “похудеет” по сравнению с параболой (не верите – заполните соответствующую таблицу – и убедитесь сами):!}

Sur la première image (voir ci-dessus) on voit clairement que les points du tableau de la parabole (1;1), (-1;1) ont été transformés en points (1;4), (1;-4), c'est-à-dire qu'avec les mêmes valeurs, l'ordonnée de chaque point est multipliée par 4. Cela arrivera à tous les points clés du tableau d'origine. Nous raisonnons de la même manière dans les cas des images 2 et 3.

Et quand la parabole « devient plus large » que la parabole :

Résumons :

1)Le signe du coefficient détermine la direction des branches. Avec title="(!LANG : Rendu par QuickLaTeX.com" height="14" width="47" style="vertical-align: 0px;"> ветви направлены вверх, при - вниз. !}

2) Valeur absolue Le coefficient (module) est responsable de la « dilatation » et de la « compression » de la parabole. Plus , plus la parabole est étroite ; plus |a| est petite, plus la parabole est large.

CAS III, « C » APPARAÎT

Introduisons maintenant dans le jeu (c'est-à-dire considérons le cas où), nous considérerons des paraboles de la forme . Il n'est pas difficile de deviner (vous pouvez toujours vous référer au tableau) que la parabole se déplacera vers le haut ou vers le bas le long de l'axe selon le signe :

CAS IV, « b » APPARAÎT

Quand la parabole va-t-elle « se détacher » de l'axe et finalement « marcher » le long de tout le plan de coordonnées ? Quand cessera-t-il d’être égal ?

Ici, pour construire une parabole, nous avons besoin formule de calcul du sommet : , .

Donc à ce stade (comme au point (0;0) nouveau système coordonnées), nous allons construire une parabole, ce que nous pouvons déjà faire. Si nous traitons du cas, alors à partir du sommet, nous plaçons un segment unitaire vers la droite, un vers le haut, - le point résultant est le nôtre (de même, un pas vers la gauche, un pas vers le haut est notre point) ; si nous avons affaire, par exemple, à partir du sommet, nous plaçons un segment unitaire vers la droite, deux vers le haut, etc.

Par exemple, le sommet d'une parabole :

Maintenant, la principale chose à comprendre est qu'à ce sommet, nous allons construire une parabole selon le modèle de parabole, car dans notre cas.

Lors de la construction d'une parabole après avoir trouvé les coordonnées du sommet trèsIl convient de considérer les points suivants :

1) parabole je passerai certainement par le point . En effet, en substituant x=0 dans la formule, nous obtenons que . C'est-à-dire que l'ordonnée du point d'intersection de la parabole avec l'axe (oy) est . Dans notre exemple (ci-dessus), la parabole coupe l'ordonnée au point , puisque .

2) axe de symétrie paraboles est une ligne droite, donc tous les points de la parabole seront symétriques par rapport à elle. Dans notre exemple, on prend immédiatement le point (0 ; -2) et on le construit symétriquement par rapport à l'axe de symétrie de la parabole, on obtient le point (4 ; -2) par lequel passera la parabole.

3) En égalant à , on retrouve les points d'intersection de la parabole avec l'axe (oh). Pour ce faire, nous résolvons l’équation. En fonction du discriminant, nous obtiendrons un (, ), deux ( title="Rendered by QuickLaTeX.com" height="14" width="54" style="vertical-align: 0px;">, ) или нИсколько () точек пересечения с осью (ох) !} . Dans l'exemple précédent, notre racine du discriminant n'est pas un entier ; lors de la construction, cela n'a pas beaucoup de sens pour nous de trouver les racines, mais on voit bien que nous aurons deux points d'intersection avec l'axe (oh) (depuis title="(!LANG : Rendu par QuickLaTeX.com" height="14" width="54" style="vertical-align: 0px;">), хотя, в общем, это видно и без дискриминанта.!}

Alors trouvons une solution

Algorithme de construction d'une parabole si elle est donnée sous la forme

1) déterminer la direction des branches (a>0 – vers le haut, a<0 – вниз)

2) on trouve les coordonnées du sommet de la parabole à l'aide de la formule , .

3) on trouve le point d'intersection de la parabole avec l'axe (oy) à l'aide du terme libre, on construit un point symétrique à ce point par rapport à l'axe de symétrie de la parabole (à noter qu'il arrive qu'il ne soit pas rentable de marquer ce point, par exemple, parce que la valeur est grande... on saute ce point...)

4) Au point trouvé - le sommet de la parabole (comme au point (0;0) du nouveau système de coordonnées), nous construisons une parabole. Si title="(!LANG : Rendu par QuickLaTeX.com" height="20" width="55" style="vertical-align: -5px;">, то парабола становится у’же по сравнению с , если , то парабола расширяется по сравнению с !}

5) On retrouve les points d'intersection de la parabole avec l'axe (oy) (s'ils n'ont pas encore « fait surface ») en résolvant l'équation

Exemple 1

Exemple 2

Note 1. Si la parabole nous est initialement donnée sous la forme , où sont des nombres (par exemple ), alors il sera encore plus facile de la construire, car on nous a déjà donné les coordonnées du sommet . Pourquoi?

Prenons trinôme quadratique et sélectionnez-y un carré complet : Regardez, nous avons ça , . Vous et moi appelions auparavant le sommet d'une parabole, c'est-à-dire maintenant .

Par exemple, . On marque le sommet de la parabole sur le plan, on comprend que les branches sont dirigées vers le bas, la parabole est élargie (par rapport à ). C'est-à-dire que nous réalisons les points 1 ; 3 ; 4 ; 5 de l'algorithme de construction d'une parabole (voir ci-dessus).

Note 2. Si la parabole est donnée sous une forme similaire à celle-ci (c'est-à-dire présentée comme le produit de deux facteurs linéaires), alors nous voyons immédiatement les points d'intersection de la parabole avec l'axe (bœuf). Dans ce cas – (0;0) et (4;0). Pour le reste, nous agissons selon l'algorithme en ouvrant les parenthèses.

Comment construire une parabole ? Il existe plusieurs façons de représenter graphiquement une fonction quadratique. Chacun d'eux a ses avantages et ses inconvénients. Considérons deux manières.

Commençons par tracer une fonction quadratique de la forme y=x²+bx+c et y= -x²+bx+c.

Exemple.

Représentez graphiquement la fonction y=x²+2x-3.

Solution:

y=x²+2x-3 est une fonction quadratique. Le graphique est une parabole avec des branches vers le haut. Coordonnées du sommet de la parabole

A partir du sommet (-1;-4) on construit un graphe de la parabole y=x² (à partir de l'origine des coordonnées. Au lieu de (0;0) - sommet (-1;-4). De (-1; -4) on va à droite d'1 unité et en haut d'1 unité, puis à gauche de 1 et en haut de 1 puis : 2 - à droite, 4 - en haut, 2 - à gauche, 3 - en haut, 3 - ; à gauche, 9 - en haut Si. ces 7 points ne suffisent pas, alors 4 à droite, 16 en haut, etc.).

Le graphique de la fonction quadratique y= -x²+bx+c est une parabole dont les branches sont dirigées vers le bas. Pour construire un graphique, on cherche les coordonnées du sommet et à partir de là on construit une parabole y= -x².

Exemple.

Représentez graphiquement la fonction y= -x²+2x+8.

Solution:

y= -x²+2x+8 est une fonction quadratique. Le graphique est une parabole avec des branches vers le bas. Coordonnées du sommet de la parabole

Du haut nous construisons une parabole y= -x² (1 - à droite, 1- en bas ; 1 - à gauche, 1 - en bas ; 2 - à droite, 4 - en bas ; 2 - à gauche, 4 - en bas, etc.) :

Cette méthode permet de construire une parabole rapidement et n'est pas difficile si vous savez représenter graphiquement les fonctions y=x² et y= -x². Inconvénient : si les coordonnées du sommet sont nombres fractionnaires, construire un graphique n’est pas très pratique. Si tu as besoin de savoir valeurs exactes points d'intersection du graphique avec l'axe Ox, vous devrez en plus résoudre l'équation x²+bx+c=0 (ou -x²+bx+c=0), même si ces points peuvent être directement déterminés à partir du dessin.

Une autre façon de construire une parabole est par points, c'est-à-dire que vous pouvez trouver plusieurs points sur le graphique et tracer une parabole à travers eux (en tenant compte du fait que la ligne x=xₒ est son axe de symétrie). Habituellement, pour cela, ils prennent le sommet de la parabole, les points d'intersection du graphique avec les axes de coordonnées et 1-2 points supplémentaires.

Tracez un graphique de la fonction y=x²+5x+4.

Solution:

y=x²+5x+4 est une fonction quadratique. Le graphique est une parabole avec des branches vers le haut. Coordonnées du sommet de la parabole

c'est-à-dire que le sommet de la parabole est le point (-2,5 ; -2,25).

Sont en train de chercher . Au point d'intersection avec l'axe Ox y=0 : x²+5x+4=0. Les racines de l'équation quadratique x1=-1, x2=-4, c'est-à-dire que nous avons deux points sur le graphique (-1 ; 0) et (-4 ; 0).

Au point d'intersection du graphique avec l'axe Oy x=0 : y=0²+5∙0+4=4. Nous avons marqué le point (0 ; 4).

Pour clarifier le graphique, vous pouvez trouver un point supplémentaire. Prenons x=1, alors y=1²+5∙1+4=10, c'est-à-dire qu'un autre point sur le graphique est (1 ; 10). Nous marquons ces points sur le plan de coordonnées. Compte tenu de la symétrie de la parabole par rapport à la droite passant par son sommet, on marque deux autres points : (-5 ; 6) et (-6 ; 10) et on trace une parabole à travers eux :

Représentez graphiquement la fonction y= -x²-3x.

Solution:

y= -x²-3x est une fonction quadratique. Le graphique est une parabole avec des branches vers le bas. Coordonnées du sommet de la parabole

Le sommet (-1,5 ; 2,25) est le premier point de la parabole.

Aux points d'intersection du graphique avec l'axe des abscisses y=0, c'est-à-dire que nous résolvons l'équation -x²-3x=0. Ses racines sont x=0 et x=-3, soit (0;0) et (-3;0) - deux points supplémentaires sur le graphique. Le point (o; 0) est aussi le point d'intersection de la parabole avec l'axe des ordonnées.

À x=1 y=-1²-3∙1=-4, c'est-à-dire (1; -4) est un point supplémentaire pour le tracé.

Construire une parabole à partir de points est une méthode plus laborieuse que la première. Si la parabole ne coupe pas l'axe Ox, davantage de points supplémentaires seront nécessaires.

Avant de continuer à construire des graphes de fonctions quadratiques de la forme y=ax²+bx+c, considérons la construction de graphes de fonctions utilisant des transformations géométriques. Il est également plus pratique de construire des graphiques de fonctions de la forme y=x²+c en utilisant l'une de ces transformations : la traduction parallèle.

Une fonction quadratique est une fonction de la forme :
y=a*(x^2)+b*x+c,
où a est le coefficient du plus haut degré d'inconnu x,
b - coefficient pour x inconnu,
et c est un membre gratuit.
Le graphique d’une fonction quadratique est une courbe appelée parabole. Forme générale La parabole est représentée dans la figure ci-dessous.

Fig.1 Vue générale de la parabole.

Il y a un peu de diverses façons tracer une fonction quadratique. Nous examinerons les principaux et les plus généraux d'entre eux.

Algorithme pour tracer une fonction quadratique y=a*(x^2)+b*x+c

1. Construisez un système de coordonnées, marquez un segment unitaire et une étiquette axes de coordonnées.

2. Déterminez la direction des branches de la parabole (vers le haut ou vers le bas).
Pour ce faire, il faut regarder le signe du coefficient a. S'il y a un plus, alors les branches sont dirigées vers le haut, s'il y a un moins, alors les branches sont dirigées vers le bas.

3. Déterminez la coordonnée x du sommet de la parabole.
Pour ce faire, vous devez utiliser la formule Xvertex = -b/2*a.

4. Déterminez la coordonnée au sommet de la parabole.
Pour ce faire, remplacez dans l'équation Uvershiny = a*(x^2)+b*x+c au lieu de x, la valeur de Xverhiny trouvée à l'étape précédente.

5. Tracez le point résultant sur le graphique et tracez un axe de symétrie qui le traverse, parallèle à l'axe de coordonnées Oy.

6. Trouvez les points d'intersection du graphique avec l'axe Ox.
Pour ce faire, vous devez résoudre équation quadratique a*(x^2)+b*x+c = 0 l'un des méthodes connues. Si l'équation n'a pas de racines réelles, alors le graphique de la fonction ne coupe pas l'axe Ox.

7. Trouvez les coordonnées du point d'intersection du graphique avec l'axe Oy.
Pour ce faire, nous substituons la valeur x=0 dans l’équation et calculons la valeur de y. Nous marquons ceci ainsi qu'un point symétrique sur le graphique.

8. Trouver les coordonnées d'un point arbitraire A(x,y)
Pour ce faire, choisissez une valeur arbitraire pour la coordonnée x et remplacez-la dans notre équation. Nous obtenons la valeur de y à ce stade. Tracez le point sur le graphique. Et marquez également un point sur le graphique qui est symétrique au point A(x,y).

9. Reliez les points obtenus sur le graphique avec une ligne lisse et continuez le graphique au-delà points extrêmes, jusqu'à la fin de l'axe des coordonnées. Étiquetez le graphique soit sur le repère, soit, si l'espace le permet, le long du graphique lui-même.

Exemple de tracé

A titre d'exemple, traçons une fonction quadratique donné par l'équation y=x^2+4*x-1
1. Dessinez des axes de coordonnées, étiquetez-les et marquez un segment unitaire.
2. Valeurs des coefficients a=1, b=4, c= -1. Puisque a=1, qui est supérieur à zéro, les branches de la parabole sont dirigées vers le haut.
3. Déterminez la coordonnée X du sommet de la parabole Xvertices = -b/2*a = -4/2*1 = -2.
4. Déterminer la coordonnée Y du sommet de la parabole
Sommets = a*(x^2)+b*x+c = 1*((-2)^2) + 4*(-2) - 1 = -5.
5. Marquez le sommet et dessinez l’axe de symétrie.
6. Trouvez les points d'intersection du graphique de la fonction quadratique avec l'axe Ox. Nous résolvons l'équation quadratique x^2+4*x-1=0.
x1=-2-√3 x2 = -2+√3. Nous marquons les valeurs obtenues sur le graphique.
7. Trouvez les points d'intersection du graphique avec l'axe Oy.
x=0 ; y=-1
8. Choisissez un point arbitraire B. Laissez-lui la coordonnée x=1.
Alors y=(1)^2 + 4*(1)-1= 4.
9. Reliez les points obtenus et signez le graphique.

Le maintien de votre vie privée est important pour nous. Pour cette raison, nous avons développé une politique de confidentialité qui décrit la manière dont nous utilisons et stockons vos informations. Veuillez consulter nos pratiques de confidentialité et faites-nous savoir si vous avez des questions.

Collecte et utilisation des informations personnelles

Les informations personnelles font référence aux données qui peuvent être utilisées pour identifier ou contacter une personne spécifique.

Il peut vous être demandé de fournir vos informations personnelles à tout moment lorsque vous nous contactez.

Vous trouverez ci-dessous quelques exemples des types d'informations personnelles que nous pouvons collecter et de la manière dont nous pouvons utiliser ces informations.

Quelles informations personnelles collectons-nous :

• Lorsque vous soumettez une demande sur le site, nous pouvons collecter diverses informations, notamment votre nom, numéro de téléphone, adresse E-mail etc.

Comment utilisons-nous vos informations personnelles:

• Collecté par nos soins informations personnelles nous permet de vous contacter et de vous informer des offres uniques, des promotions et d'autres événements et événements à venir.
• De temps en temps, nous pouvons utiliser vos informations personnelles pour envoyer des notifications et des communications importantes.
• Nous pouvons également utiliser des informations personnelles à des fins internes telles que l'audit, l'analyse des données et diverses études afin d'améliorer les services que nous proposons et de vous fournir des recommandations concernant nos services.
• Si vous participez à un tirage au sort, un concours ou une promotion similaire, nous pouvons utiliser les informations que vous fournissez pour administrer ces programmes.

Divulgation d'informations à des tiers

Nous ne divulguons pas les informations reçues de votre part à des tiers.

Des exceptions:

• Si nécessaire, conformément à la loi, procédure judiciaire, V procès, et/ou sur la base de demandes publiques ou de demandes de organismes gouvernementaux sur le territoire de la Fédération de Russie - divulguez vos informations personnelles. Nous pouvons également divulguer des informations vous concernant si nous déterminons qu'une telle divulgation est nécessaire ou appropriée à des fins de sécurité, d'application de la loi ou à d'autres fins d'importance publique.
• En cas de réorganisation, de fusion ou de vente, nous pouvons transférer les informations personnelles que nous collectons au tiers successeur concerné.

Protection des informations personnelles

Nous prenons des précautions - notamment administratives, techniques et physiques - pour protéger vos informations personnelles contre la perte, le vol et l'utilisation abusive, ainsi que contre l'accès, la divulgation, l'altération et la destruction non autorisés.

Respecter votre vie privée au niveau de l'entreprise

Pour garantir la sécurité de vos informations personnelles, nous communiquons les normes de confidentialité et de sécurité à nos employés et appliquons strictement les pratiques de confidentialité.