Espérance mathématique d'une variable aléatoire discrète en ligne. Fondements de la théorie des probabilités. Espérance mathématique de valeur
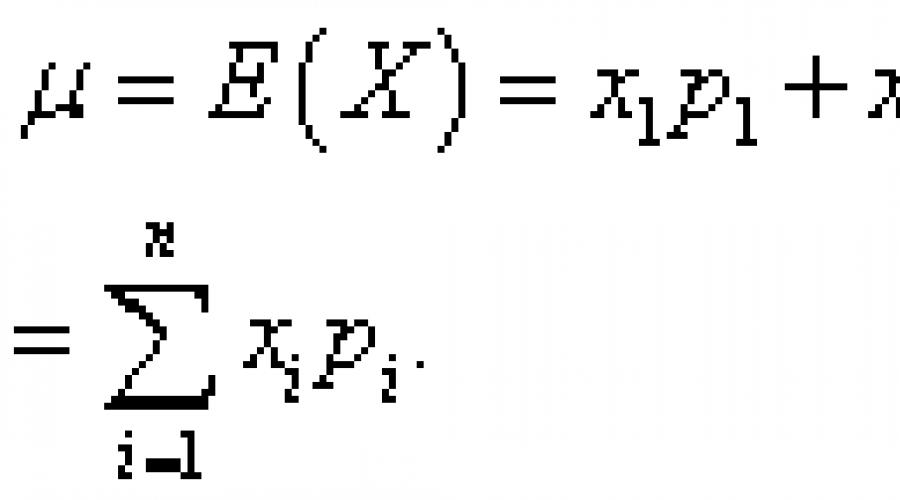
Lire aussi
Espérance mathématique (valeur moyenne) Variable aléatoire X donné sur un espace de probabilité discret est appelé le nombre m =M[X]=∑x i p i si la série converge absolument.
Objet de la prestation. Utiliser le service dans mode en ligne l'espérance mathématique, la variance et l'écart type sont calculés(voir exemple). De plus, un graphique de la fonction de distribution F(X) est tracé.
Propriétés de l'espérance mathématique d'une variable aléatoire
- L'espérance mathématique d'une valeur constante est égale à elle-même : M[C]=C, C – constante ;
- M=CM[X]
- L'espérance mathématique de la somme des variables aléatoires est égale à la somme de leurs espérances mathématiques : M=M[X]+M[Y]
- L'espérance mathématique du produit de variables aléatoires indépendantes est égale au produit de leurs espérances mathématiques : M=M[X] M[Y] , si X et Y sont indépendants.
Propriétés de dispersion
- La variance d'une valeur constante est nulle : D(c)=0.
- Le facteur constant peut être retiré sous le signe de dispersion en le mettant au carré : D(k*X)= k 2 D(X).
- Si les variables aléatoires X et Y sont indépendantes, alors la variance de la somme est égale à la somme des variances : D(X+Y)=D(X)+D(Y).
- Si les variables aléatoires X et Y sont dépendantes : D(X+Y)=DX+DY+2(X-M[X])(Y-M[Y])
- La formule de calcul suivante est valable pour la dispersion :
D(X)=M(X2)-(M(X))2
Exemple. Les attentes mathématiques et les variances de deux variables aléatoires indépendantes X et Y sont connues : M(x)=8, M(Y)=7, D(X)=9, D(Y)=6. Trouvez l'espérance mathématique et la variance de la variable aléatoire Z=9X-8Y+7.
Solution. Basé sur les propriétés de l'espérance mathématique : M(Z) = M(9X-8Y+7) = 9*M(X) - 8*M(Y) + M(7) = 9*8 - 8*7 + 7 = 23 .
Basé sur les propriétés de dispersion : D(Z) = D(9X-8Y+7) = D(9X) - D(8Y) + D(7) = 9^2D(X) - 8^2D(Y) + 0 = 81*9 - 64*6 = 345
Algorithme de calcul de l'espérance mathématique
Propriétés des variables aléatoires discrètes : toutes leurs valeurs peuvent être renumérotées nombres naturels; Attribuez à chaque valeur une probabilité non nulle.- On multiplie les paires une à une : x i par p i .
- Ajoutez le produit de chaque paire x i p i .
Par exemple, pour n = 4 : m = ∑x i p i = x 1 p 1 + x 2 p 2 + x 3 p 3 + x 4 p 4
Exemple n°1.
| x je | 1 | 3 | 4 | 7 | 9 |
| p je | 0.1 | 0.2 | 0.1 | 0.3 | 0.3 |
Nous trouvons l'espérance mathématique en utilisant la formule m = ∑x i p i .
Attente M[X].
M[x] = 1*0,1 + 3*0,2 + 4*0,1 + 7*0,3 + 9*0,3 = 5,9
Nous trouvons la variance en utilisant la formule d = ∑x 2 i p i - M[x] 2 .
Écart D[X].
D[X] = 1 2 *0,1 + 3 2 *0,2 + 4 2 *0,1 + 7 2 *0,3 + 9 2 *0,3 - 5,9 2 = 7,69
Écart type σ(x).
σ = carré(D[X]) = carré(7,69) = 2,78
Exemple n°2. Une variable aléatoire discrète a la série de distribution suivante :
| X | -10 | -5 | 0 | 5 | 10 |
| R. | UN | 0,32 | 2un | 0,41 | 0,03 |
Solution. La valeur de a se trouve à partir de la relation : Σp i = 1
Σp je = une + 0,32 + 2 une + 0,41 + 0,03 = 0,76 + 3 une = 1
0,76 + 3 a = 1 ou 0,24=3 a , d'où a = 0,08
Exemple n°3. Déterminer la loi de distribution d'une variable aléatoire discrète si sa variance est connue, et x 1
p1 = 0,3 ; p2 = 0,3 ; p3 = 0,1; p4 =0,3
d(x)=12,96
Solution.
Ici, vous devez créer une formule pour trouver la variance d(x) :
d(x) = x 1 2 p 1 +x 2 2 p 2 +x 3 2 p 3 +x 4 2 p 4 -m(x) 2
où l'espérance m(x)=x 1 p 1 +x 2 p 2 +x 3 p 3 +x 4 p 4
Pour nos données
m(x)=6*0,3+9*0,3+x 3 *0,1+15*0,3=9+0,1x 3
12,96 = 6 2 0,3+9 2 0,3+x 3 2 0,1+15 2 0,3-(9+0,1x 3) 2
ou -9/100 (x 2 -20x+96)=0
En conséquence, nous devons trouver les racines de l’équation, et il y en aura deux.
x3 =8, x3 =12
Choisissez celui qui satisfait à la condition x 1
Loi de distribution d'une variable aléatoire discrète
x1 =6 ; x2 =9 ; x3 =12 ; x4 =15
p1 = 0,3 ; p2 = 0,3 ; p3 = 0,1; p4 =0,3
L'espérance et la variance sont les caractéristiques numériques les plus couramment utilisées d'une variable aléatoire. Ils caractérisent les caractéristiques les plus importantes de la distribution : sa position et son degré de diffusion. Dans de nombreux problèmes pratiques, une caractéristique complète et exhaustive d'une variable aléatoire - la loi de distribution - soit ne peut pas être obtenue, soit n'est pas du tout nécessaire. Dans ces cas, on se limite à une description approximative d'une variable aléatoire à l'aide de caractéristiques numériques.
La valeur attendue est souvent appelée simplement la valeur moyenne d’une variable aléatoire. La dispersion d'une variable aléatoire est une caractéristique de la dispersion, la propagation d'une variable aléatoire autour de son espérance mathématique.
Attente d'une variable aléatoire discrète
Abordons le concept d'espérance mathématique, basé d'abord sur l'interprétation mécanique de la distribution d'une variable aléatoire discrète. Soit la masse unitaire soit répartie entre les points de l'axe des x X1 , X 2 , ..., X n, et chaque point matériel a une masse correspondante de p1 , p 2 , ..., p n. Il est nécessaire de sélectionner un point sur l'axe des abscisses, caractérisant la position de l'ensemble du système de points matériels, en tenant compte de leurs masses. Il est naturel de prendre le centre de masse du système de points matériels comme tel. Il s'agit de la moyenne pondérée de la variable aléatoire X, à laquelle l'abscisse de chaque point Xje entre avec un « poids » égal à la probabilité correspondante. La valeur moyenne de la variable aléatoire ainsi obtenue X s'appelle son espérance mathématique.
L'espérance mathématique d'une variable aléatoire discrète est la somme des produits de toutes ses valeurs possibles et des probabilités de ces valeurs :

Exemple 1. Une loterie gagnant-gagnant a été organisée. Il y a 1 000 gains, dont 400 valent 10 roubles. 300 à 20 roubles chacun. 200 à 100 roubles chacun. et 100 à 200 roubles chacun. Quel est le gain moyen pour quelqu’un qui achète un billet ?
Solution. Nous trouverons les gains moyens si nous divisons le montant total des gains, qui est 10*400 + 20*300 + 100*200 + 200*100 = 50 000 roubles, par 1 000 (montant total des gains). Ensuite, nous obtenons 50 000/1 000 = 50 roubles. Mais l'expression de calcul des gains moyens peut se présenter sous la forme suivante :

En revanche, dans ces conditions, le montant gagnant est une variable aléatoire, qui peut prendre des valeurs de 10, 20, 100 et 200 roubles. avec des probabilités égales à 0,4, respectivement ; 0,3 ; 0,2 ; 0,1. Par conséquent, le gain moyen attendu est égal à la somme des produits de la taille des gains et de la probabilité de les recevoir.
Exemple 2. L'éditeur a décidé de publier un nouveau livre. Il envisage de vendre le livre pour 280 roubles, dont il recevra lui-même 200, 50 pour la librairie et 30 pour l'auteur. Le tableau fournit des informations sur les coûts de publication d'un livre et la probabilité de vendre un certain nombre d'exemplaires du livre.
Trouvez le bénéfice attendu de l'éditeur.
Solution. La variable aléatoire « profit » est égale à la différence entre le revenu des ventes et le coût des coûts. Par exemple, si 500 exemplaires d'un livre sont vendus, le revenu de la vente est de 200 * 500 = 100 000 et le coût de publication est de 225 000 roubles. Ainsi, l'éditeur fait face à une perte de 125 000 roubles. Le tableau suivant résume les valeurs attendues de la variable aléatoire - profit :
| Nombre | Profit Xje | Probabilité pje | Xje p je |
| 500 | -125000 | 0,20 | -25000 |
| 1000 | -50000 | 0,40 | -20000 |
| 2000 | 100000 | 0,25 | 25000 |
| 3000 | 250000 | 0,10 | 25000 |
| 4000 | 400000 | 0,05 | 20000 |
| Total: | 1,00 | 25000 |
Ainsi, nous obtenons l’espérance mathématique du profit de l’éditeur :
![]() .
.
Exemple 3. Probabilité de toucher d'un seul coup p= 0,2. Déterminez la consommation de projectiles qui fournissent une espérance mathématique du nombre de coups égal à 5.
Solution. À partir de la même formule d’espérance mathématique que nous avons utilisée jusqu’à présent, nous exprimons X- consommation de coque :
![]() .
.
Exemple 4. Déterminer l'espérance mathématique d'une variable aléatoire X nombre de coups sûrs avec trois tirs, si la probabilité d'un coup sûr à chaque tir p = 0,4 .
Astuce : trouvez la probabilité de valeurs de variables aléatoires en La formule de Bernoulli .
Propriétés de l'espérance mathématique
Considérons les propriétés de l'espérance mathématique.
Propriété 1. L'espérance mathématique d'une valeur constante est égale à cette constante :
Propriété 2. Le facteur constant peut être retiré du signe d’espérance mathématique :
![]()
Propriété 3. L'espérance mathématique de la somme (différence) des variables aléatoires est égale à la somme (différence) de leurs espérances mathématiques :
Propriété 4. L'espérance mathématique d'un produit de variables aléatoires est égale au produit de leurs espérances mathématiques :
Propriété 5. Si toutes les valeurs d'une variable aléatoire X diminuer (augmenter) du même nombre AVEC, alors son espérance mathématique diminuera (augmentera) du même nombre :
![]()
Quand on ne peut pas se limiter aux attentes mathématiques
Dans la plupart des cas, seule l’espérance mathématique ne peut suffire à caractériser une variable aléatoire.
Laissez les variables aléatoires X Et Oui sont données par les lois de distribution suivantes :
| Signification X | Probabilité |
| -0,1 | 0,1 |
| -0,01 | 0,2 |
| 0 | 0,4 |
| 0,01 | 0,2 |
| 0,1 | 0,1 |
| Signification Oui | Probabilité |
| -20 | 0,3 |
| -10 | 0,1 |
| 0 | 0,2 |
| 10 | 0,1 |
| 20 | 0,3 |
Les attentes mathématiques de ces quantités sont les mêmes - égales à zéro :


Cependant, leurs modes de distribution sont différents. Valeur aléatoire X ne peut prendre que des valeurs qui diffèrent peu de l'espérance mathématique, et la variable aléatoire Oui peut prendre des valeurs qui s'écartent considérablement de l'attente mathématique. Un exemple similaire : le salaire moyen ne permet pas de juger de la part des travailleurs bien et mal payés. En d’autres termes, on ne peut pas juger à partir de l’espérance mathématique quels écarts par rapport à celle-ci, du moins en moyenne, sont possibles. Pour ce faire, vous devez trouver la variance de la variable aléatoire.
Variance d'une variable aléatoire discrète
Variance variable aléatoire discrète X s'appelle l'espérance mathématique du carré de son écart par rapport à l'espérance mathématique :

L'écart type d'une variable aléatoire X la valeur arithmétique de la racine carrée de sa variance s'appelle :
![]() .
.
Exemple 5. Calculer les variances et les écarts types de variables aléatoires X Et Oui, dont les lois de distribution sont données dans les tableaux ci-dessus.
Solution. Attentes mathématiques des variables aléatoires X Et Oui, comme indiqué ci-dessus, sont égaux à zéro. D'après la formule de dispersion à E(X)=E(oui)=0 on obtient :


Puis les écarts types des variables aléatoires X Et Oui se maquiller
![]() .
.
Ainsi, avec les mêmes attentes mathématiques, la variance de la variable aléatoire X très petit, mais une variable aléatoire Oui- significatif. Ceci est une conséquence des différences dans leur répartition.
Exemple 6. L'investisseur dispose de 4 projets d'investissement alternatifs. Le tableau résume le profit attendu dans ces projets avec la probabilité correspondante.
| Projet 1 | Projet 2 | Projet 3 | Projet 4 |
| 500, P.=1 | 1000, P.=0,5 | 500, P.=0,5 | 500, P.=0,5 |
| 0, P.=0,5 | 1000, P.=0,25 | 10500, P.=0,25 | |
| 0, P.=0,25 | 9500, P.=0,25 |
Trouvez l’espérance mathématique, la variance et l’écart type pour chaque alternative.
Solution. Montrons comment ces valeurs sont calculées pour la 3ème alternative :
Le tableau résume les valeurs trouvées pour toutes les alternatives.
Toutes les alternatives ont les mêmes attentes mathématiques. Cela signifie qu’à long terme, tout le monde dispose du même revenu. L'écart type peut être interprété comme une mesure du risque : plus il est élevé, plus le risque de l'investissement est grand. Un investisseur qui ne veut pas beaucoup de risque choisira le projet 1 car il présente le plus petit écart type (0). Si l'investisseur préfère le risque et des rendements élevés sur une courte période, il choisira alors le projet avec le plus grand écart type - le projet 4.
Propriétés de dispersion
Présentons les propriétés de dispersion.
Propriété 1. La variance d'une valeur constante est nulle :
Propriété 2. Le facteur constant peut être soustrait du signe de dispersion en le mettant au carré :
![]() .
.
Propriété 3. La variance d'une variable aléatoire est égale à l'espérance mathématique du carré de cette valeur, à laquelle est soustrait le carré de l'espérance mathématique de la valeur elle-même :
![]() ,
,
Où ![]() .
.
Propriété 4. La variance de la somme (différence) des variables aléatoires est égale à la somme (différence) de leurs variances :
Exemple 7. On sait qu'une variable aléatoire discrète X ne prend que deux valeurs : −3 et 7. De plus, l'espérance mathématique est connue : E(X) = 4 . Trouvez la variance d'une variable aléatoire discrète.
Solution. Notons par p la probabilité avec laquelle une variable aléatoire prend une valeur X1 = −3 . Alors la probabilité de la valeur X2 = 7 sera 1 - p. Dérivons l'équation de l'espérance mathématique :
E(X) = X 1 p + X 2 (1 − p) = −3p + 7(1 − p) = 4 ,
où l'on obtient les probabilités : p= 0,3 et 1 − p = 0,7 .
Loi de distribution d'une variable aléatoire :
| X | −3 | 7 |
| p | 0,3 | 0,7 |
On calcule la variance de cette variable aléatoire en utilisant la formule de la propriété 3 de dispersion :
D(X) = 2,7 + 34,3 − 16 = 21 .
Trouvez vous-même l'espérance mathématique d'une variable aléatoire, puis regardez la solution
Exemple 8. Variable aléatoire discrète X ne prend que deux valeurs. Il accepte la plus grande des valeurs 3 avec une probabilité de 0,4. De plus, la variance de la variable aléatoire est connue D(X) = 6 . Trouvez l'espérance mathématique d'une variable aléatoire.
Exemple 9. Il y a 6 boules blanches et 4 boules noires dans une urne. 3 boules sont tirées de l'urne. Le nombre de boules blanches parmi les boules tirées est une variable aléatoire discrète X. Trouvez l'espérance mathématique et la variance de cette variable aléatoire.
Solution. Valeur aléatoire X peut prendre les valeurs 0, 1, 2, 3. Les probabilités correspondantes peuvent être calculées à partir de règle de multiplication de probabilité. Loi de distribution d'une variable aléatoire :
| X | 0 | 1 | 2 | 3 |
| p | 1/30 | 3/10 | 1/2 | 1/6 |
D'où l'espérance mathématique de cette variable aléatoire :
M.(X) = 3/10 + 1 + 1/2 = 1,8 .
La variance d'une variable aléatoire donnée est :
D(X) = 0,3 + 2 + 1,5 − 3,24 = 0,56 .
Attente et variance d'une variable aléatoire continue
Pour une variable aléatoire continue, l'interprétation mécanique de l'espérance mathématique gardera le même sens : le centre de masse pour une unité de masse répartie continûment sur l'axe des x avec densité F(X). Contrairement à une variable aléatoire discrète, dont l'argument de fonction Xje change brusquement ; pour une variable aléatoire continue, l’argument change continuellement. Mais l’espérance mathématique d’une variable aléatoire continue est également liée à sa valeur moyenne.
Pour trouver l'espérance mathématique et la variance d'une variable aléatoire continue, vous devez trouver des intégrales définies . Si la fonction de densité d'une variable aléatoire continue est donnée, alors elle entre directement dans l'intégrande. Si une fonction de distribution de probabilité est donnée, alors en la différenciant, vous devez trouver la fonction de densité.
La moyenne arithmétique de toutes les valeurs possibles d'une variable aléatoire continue est appelée son espérance mathématique, noté ou .
– le nombre de garçons sur 10 nouveau-nés.
Il est tout à fait clair que ce nombre n'est pas connu à l'avance, et les dix prochains enfants nés pourraient inclure :
Ou des garçons - seul et l'unique parmi les options répertoriées.
Et, pour garder la forme, un peu d'éducation physique :
– distance de saut en longueur (dans certaines unités).
Même un maître du sport ne peut pas le prédire :)
Cependant, vos hypothèses ?
2) Variable aléatoire continue – accepte Tous valeurs numériques d'un intervalle fini ou infini.
Note : les abréviations DSV et NSV sont populaires dans la littérature pédagogique
Analysons d’abord la variable aléatoire discrète, puis - continu.
Loi de distribution d'une variable aléatoire discrète
- Ce correspondance entre les valeurs possibles de cette quantité et leurs probabilités. Le plus souvent, la loi est écrite dans un tableau : 
Le terme apparaît assez souvent rangée
distribution, mais dans certaines situations, cela semble ambigu, et je m'en tiendrai donc à la "loi".
Et maintenant point très important: puisque la variable aléatoire Nécessairement va accepter une des valeurs, puis les événements correspondants se forment groupe complet et la somme des probabilités de leur apparition est égale à un :
ou, s'il est écrit condensé :
Ainsi, par exemple, la loi de distribution de probabilité des points lancés sur un dé a la forme suivante : 
Sans commentaires.
Vous avez peut-être l’impression qu’une variable aléatoire discrète ne peut prendre que de « bonnes » valeurs entières. Dissipons l'illusion - ils peuvent être n'importe quoi :
Exemple 1
Certains jeux ont la loi de distribution gagnante suivante : 
...vous rêvez probablement de telles tâches depuis longtemps :) Je vais vous confier un secret - moi aussi. Surtout après avoir fini de travailler sur théorie des champs.
Solution: puisqu'une variable aléatoire ne peut prendre qu'une seule valeur parmi trois, les événements correspondants forment groupe complet, ce qui signifie que la somme de leurs probabilités est égale à un : ![]()
Dénoncer le « partisan » : ![]()
– ainsi, la probabilité de gagner des unités conventionnelles est de 0,4.
Contrôler : c’est de cela qu’il fallait s’assurer.
Répondre:
Il n'est pas rare que vous deviez rédiger vous-même une loi sur la distribution. Pour cela, ils utilisent définition classique de la probabilité, théorèmes de multiplication/addition pour les probabilités d'événements et autres chips tervera:
Exemple 2
La boîte contient 50 billets de loterie, parmi lesquels 12 sont gagnants, et 2 d'entre eux gagnent 1 000 roubles chacun, et le reste - 100 roubles chacun. Élaborez une loi pour la distribution d'une variable aléatoire - le montant des gains, si un ticket est tiré au hasard dans la boîte.
Solution: comme vous l'avez remarqué, les valeurs d'une variable aléatoire sont généralement placées dans Dans l'ordre croissant. Par conséquent, nous commençons par les plus petits gains, à savoir les roubles.
Il y a 50 billets de ce type au total - 12 = 38, et selon définition classique:
– la probabilité qu’un ticket tiré au sort soit perdant.
Dans d'autres cas, tout est simple. La probabilité de gagner des roubles est :
Vérifiez : – et c'est un moment particulièrement agréable de telles tâches !
Répondre: la loi souhaitée de répartition des gains : ![]()
La tâche suivante est à résoudre par vous-même :
Exemple 3
La probabilité que le tireur atteigne la cible est de . Établissez une loi de distribution pour une variable aléatoire - le nombre de coups après 2 tirs.
...Je savais qu'il te manquait :) Souvenons-nous théorèmes de multiplication et d'addition. La solution et la réponse se trouvent à la fin de la leçon.
La loi de distribution décrit complètement une variable aléatoire, mais en pratique il peut être utile (et parfois plus utile) de n'en connaître qu'une partie. caractéristiques numériques .
Attente d'une variable aléatoire discrète
En termes simples, c'est valeur moyenne attendue lorsque les tests sont répétés plusieurs fois. Laissez la variable aléatoire prendre des valeurs avec des probabilités ![]() respectivement. Alors l’espérance mathématique de cette variable aléatoire est égale à somme de produits toutes ses valeurs aux probabilités correspondantes :
respectivement. Alors l’espérance mathématique de cette variable aléatoire est égale à somme de produits toutes ses valeurs aux probabilités correspondantes :
ou effondré : ![]()
Calculons, par exemple, l'espérance mathématique d'une variable aléatoire - le nombre de points lancés sur un dé :
Rappelons maintenant notre jeu hypothétique : 
La question se pose : est-il rentable de jouer à ce jeu ? ...qui a des impressions ? On ne peut donc pas le dire « à la légère » ! Mais on peut facilement répondre à cette question en calculant l’espérance mathématique, essentiellement : moyenne pondérée par probabilité de gagner :
Ainsi, l'espérance mathématique de ce jeu perdant.
Ne vous fiez pas à vos impressions, faites confiance aux chiffres !
Oui, ici, vous pouvez gagner 10 et même 20 à 30 fois de suite, mais à long terme, nous serons confrontés à une ruine inévitable. Et je ne vous conseillerais pas de jouer à de tels jeux :) Eh bien, peut-être seulement pour s'amuser.
De tout ce qui précède, il s'ensuit que l'espérance mathématique n'est plus une valeur ALÉATOIRE.
Tâche créative pour une recherche indépendante :
Exemple 4
M. X joue à la roulette européenne selon le système suivant : il mise constamment 100 roubles sur le « rouge ». Élaborez une loi de distribution d'une variable aléatoire - ses gains. Calculez l'espérance mathématique des gains et arrondissez-la au kopeck le plus proche. Combien moyenne Le joueur perd-il pour chaque cent misé ?
Référence : La roulette européenne contient 18 secteurs rouges, 18 noirs et 1 secteur vert (« zéro »). Si un « rouge » apparaît, le joueur est payé le double de la mise, sinon cela va aux revenus du casino.
Il existe de nombreux autres systèmes de roulette pour lesquels vous pouvez créer vos propres tables de probabilités. Mais c’est le cas lorsque nous n’avons besoin d’aucune loi ou table de distribution, car il est établi avec certitude que l’espérance mathématique du joueur sera exactement la même. La seule chose qui change d'un système à l'autre est
Le concept d'espérance mathématique peut être envisagé à l'aide de l'exemple du lancement d'un dé. A chaque lancer, les points perdus sont enregistrés. Pour les exprimer, des valeurs naturelles comprises entre 1 et 6 sont utilisées.
Après un certain nombre de lancers, à l'aide de calculs simples, vous pouvez connaître la moyenne arithmétique des points obtenus.
Tout comme l'occurrence de l'une des valeurs de la plage, cette valeur sera aléatoire.
Et si vous augmentiez plusieurs fois le nombre de lancers ? Avec un grand nombre de lancers, la moyenne arithmétique des points se rapprochera d'un nombre spécifique, appelé en théorie des probabilités l'espérance mathématique.
Ainsi, par attente mathématique, nous entendons la valeur moyenne d’une variable aléatoire. Cet indicateur peut également être présenté comme une somme pondérée de valeurs probables.
Ce concept a plusieurs synonymes :
- valeur moyenne;
- valeur moyenne;
- indicateur de tendance centrale ;
- premier instant.
En d’autres termes, ce n’est rien de plus qu’un nombre autour duquel sont réparties les valeurs d’une variable aléatoire.
Dans différentes sphères de l'activité humaine, les approches pour comprendre les attentes mathématiques seront quelque peu différentes.
Il peut être considéré comme :
- le bénéfice moyen obtenu en prenant une décision, lorsqu'une telle décision est considérée du point de vue de la théorie des grands nombres ;
- le montant possible de gain ou de perte (théorie du jeu), calculé en moyenne pour chaque pari. En argot, ils sonnent comme « avantage du joueur » (positif pour le joueur) ou « avantage du casino » (négatif pour le joueur) ;
- pourcentage de profit reçu des gains.
L'attente n'est pas obligatoire pour absolument toutes les variables aléatoires. Il est absent pour ceux qui ont un écart dans la somme ou intégrale correspondante.
Propriétés de l'espérance mathématique
Comme tout paramètre statistique, l'espérance mathématique a les propriétés suivantes :

Formules de base pour l'espérance mathématique
Le calcul de l'espérance mathématique peut être effectué à la fois pour des variables aléatoires caractérisées à la fois par la continuité (formule A) et la discrétion (formule B) :
- M(X)=∑i=1nxi⋅pi, où xi sont les valeurs de la variable aléatoire, pi sont les probabilités :
- M(X)=∫+∞−∞f(x)⋅xdx, où f(x) est la densité de probabilité donnée.
Exemples de calcul d'espérance mathématique
Exemple A.
Est-il possible de connaître la taille moyenne des nains dans le conte de Blanche-Neige. On sait que chacun des 7 nains avait une certaine taille : 1,25 ; 0,98 ; 1,05 ; 0,71 ; 0,56 ; 0,95 et 0,81 m.
L'algorithme de calcul est assez simple :
- on retrouve la somme de toutes les valeurs de l'indicateur de croissance (variable aléatoire) :
1,25+0,98+1,05+0,71+0,56+0,95+ 0,81 = 6,31; - divisez le montant obtenu par le nombre de gnomes :
6,31:7=0,90.
Ainsi, la taille moyenne des gnomes dans un conte de fées est de 90 cm. En d'autres termes, c'est l'espérance mathématique de la croissance des gnomes.
Formule de travail - M(x)=4 0,2+6 0,3+10 0,5=6
Mise en œuvre pratique de l'espérance mathématique
Le calcul de l'indicateur statistique de l'espérance mathématique est utilisé dans divers domaines d'activité pratique. Tout d’abord, nous parlons de la sphère commerciale. Après tout, l’introduction par Huygens de cet indicateur est associée à la détermination des chances qui peuvent être favorables ou, au contraire, défavorables pour un événement.
 Ce paramètre est largement utilisé pour évaluer les risques, notamment lorsqu'il s'agit d'investissements financiers.
Ce paramètre est largement utilisé pour évaluer les risques, notamment lorsqu'il s'agit d'investissements financiers.
Ainsi, en entreprise, le calcul de l'espérance mathématique agit comme une méthode d'évaluation du risque lors du calcul des prix.
Cet indicateur peut également être utilisé pour calculer l'efficacité de certaines mesures, par exemple la protection du travail. Grâce à lui, vous pouvez calculer la probabilité qu'un événement se produise.
Un autre domaine d'application de ce paramètre est la gestion. Il peut également être calculé lors du contrôle qualité du produit. Par exemple, en utilisant un tapis. attentes, vous pouvez calculer le nombre possible de pièces défectueuses produites.
L'espérance mathématique s'avère également indispensable lors de la réalisation du traitement statistique des résultats obtenus lors de la recherche scientifique. Il permet de calculer la probabilité d'un résultat souhaité ou indésirable d'une expérience ou d'une étude en fonction du niveau d'atteinte de l'objectif. Après tout, sa réalisation peut être associée à un gain et à un bénéfice, et son échec peut être associé à une perte ou à une perte.
Utiliser les attentes mathématiques sur le Forex
L'application pratique de ce paramètre statistique est possible lors de la réalisation de transactions sur le marché des changes. Avec son aide, vous pouvez analyser le succès des transactions commerciales. De plus, une augmentation de la valeur attendue indique une augmentation de leur succès.
Il est également important de rappeler que l’espérance mathématique ne doit pas être considérée comme le seul paramètre statistique utilisé pour analyser la performance d’un trader. L'utilisation de plusieurs paramètres statistiques ainsi que de la valeur moyenne augmente considérablement la précision de l'analyse.
Ce paramètre a fait ses preuves dans le suivi des observations des comptes de trading. Grâce à lui, une évaluation rapide du travail effectué sur le compte de dépôt est réalisée. Dans les cas où l’activité du commerçant réussit et évite les pertes, il n’est pas recommandé d’utiliser exclusivement le calcul de l’espérance mathématique. Dans ces cas, les risques ne sont pas pris en compte, ce qui réduit l'efficacité de l'analyse.
Les études menées sur les tactiques des traders indiquent que :
- Les tactiques les plus efficaces sont celles basées sur l’entrée aléatoire ;
- Les moins efficaces sont les tactiques basées sur des apports structurés.
Pour obtenir des résultats positifs, il n’est pas moins important :
- tactiques de gestion financière ;
- stratégies de sortie.
En utilisant un indicateur tel que l'espérance mathématique, vous pouvez prédire quel sera le profit ou la perte en investissant 1 dollar. On sait que cet indicateur, calculé pour l’ensemble des jeux pratiqués dans le casino, est en faveur de l’établissement. C'est ce qui vous permet de gagner de l'argent. Dans le cas d'une longue série de jeux, la probabilité qu'un client perde de l'argent augmente considérablement.
Les jeux joués par des joueurs professionnels sont limités à de courtes périodes, ce qui augmente les chances de gagner et réduit le risque de perdre. Le même schéma est observé lors de la réalisation d’opérations d’investissement.
Un investisseur peut gagner une somme importante en ayant des attentes positives et en effectuant un grand nombre de transactions sur une courte période.
L'espérance peut être considérée comme la différence entre le pourcentage de profit (PW) multiplié par le profit moyen (AW) et la probabilité de perte (PL) multipliée par la perte moyenne (AL).
A titre d'exemple, nous pouvons considérer ce qui suit : position – 12,5 mille dollars, portefeuille – 100 mille dollars, risque de dépôt – 1%. La rentabilité des transactions est de 40% des cas avec un profit moyen de 20%. En cas de sinistre, la perte moyenne est de 5%. Le calcul de l'espérance mathématique de la transaction donne une valeur de 625 $.
La propriété la plus importante d'une variable aléatoire après l'espérance mathématique est sa dispersion, définie comme l'écart carré moyen par rapport à la moyenne :
Si elle est notée alors, la variance VX sera la valeur attendue. C'est une caractéristique de la « dispersion » de la distribution de X.
Comme exemple simple de calcul de l'écart, disons que nous venons de recevoir une offre que nous ne pouvons pas refuser : quelqu'un nous a donné deux certificats pour la même loterie. Les organisateurs de la loterie vendent 100 billets chaque semaine et participent à un tirage séparé. Le tirage au sort sélectionne l'un de ces billets selon un processus aléatoire uniforme - chaque billet a une chance égale d'être sélectionné - et le propriétaire de ce billet chanceux reçoit cent millions de dollars. Les 99 détenteurs de billets de loterie restants ne gagnent rien.
Nous pouvons utiliser le cadeau de deux manières : acheter soit deux billets pour une loterie, soit un pour chacun pour participer à deux loteries différentes. Quelle stratégie est la meilleure ? Essayons de l'analyser. Pour ce faire, désignons par variables aléatoires représentant la taille de nos gains sur le premier et le deuxième tickets. La valeur attendue en millions est
et il en va de même pour les valeurs attendues sont additives, donc notre gain total moyen sera
quelle que soit la stratégie adoptée.
Toutefois, les deux stratégies semblent différentes. Allons au-delà des valeurs attendues et étudions la distribution de probabilité complète

Si nous achetons deux billets à la même loterie, nos chances de ne rien gagner seront de 98 % et de 2 % - les chances de gagner 100 millions. Si nous achetons des billets pour différents tirages, les chiffres seront les suivants : 98,01 % - la chance de ne rien gagner, ce qui est légèrement plus élevé qu'avant ; 0,01 % - chance de gagner 200 millions, également un peu plus qu'avant ; et la chance de gagner 100 millions est désormais de 1,98 %. Ainsi, dans le deuxième cas, la distribution des amplitudes est un peu plus dispersée ; la valeur moyenne, 100 millions de dollars, est légèrement moins probable, tandis que les valeurs extrêmes sont plus probables.
C’est ce concept de propagation d’une variable aléatoire que la dispersion est censée refléter. Nous mesurons la propagation sur le carré de l'écart d'une variable aléatoire par rapport à son espérance mathématique. Ainsi, dans le cas 1, la variance sera
dans le cas 2, la variance est
Comme nous nous y attendions, cette dernière valeur est légèrement plus grande, puisque la distribution dans le cas 2 est un peu plus étalée.
Lorsque nous travaillons avec des variances, tout est au carré, le résultat peut donc être des nombres assez grands. (Le multiplicateur est de mille milliards, ça devrait être impressionnant
même les joueurs habitués aux paris importants.) Pour convertir les valeurs en une échelle originale plus significative, la racine carrée de la variance est souvent prise. Le nombre obtenu est appelé écart type et est généralement désigné par la lettre grecque a :
Les écarts types de grandeur pour nos deux stratégies de loterie sont . À certains égards, la deuxième option est environ 71 247 $ plus risquée.
Comment la variance aide-t-elle dans le choix d’une stratégie ? Ce n'est pas clair. Une stratégie avec une variance plus élevée est plus risquée ; mais qu'est-ce qui est mieux pour notre portefeuille : le risque ou le jeu en toute sécurité ? Ayons la possibilité d'acheter non pas deux billets, mais cent. Nous pourrions alors garantir de gagner à une loterie (et la variance serait nulle) ; ou vous pourriez jouer à une centaine de tirages différents, sans rien obtenir avec une probabilité, mais avec une chance non nulle de gagner jusqu'à 100 dollars. Choisir l’une de ces alternatives dépasse le cadre de ce livre ; tout ce que nous pouvons faire ici, c'est expliquer comment faire les calculs.
En fait, il existe une manière plus simple de calculer la variance que d’utiliser directement la définition (8.13). (Il y a toutes les raisons de soupçonner ici une sorte de mathématiques cachées ; sinon, pourquoi la variance dans les exemples de loterie se révélerait-elle être un multiple entier ? Nous avons
depuis - constant ; ainsi,
"La variance est la moyenne du carré moins le carré de la moyenne."
Par exemple, dans le problème de la loterie, la valeur moyenne s'avère être ou La soustraction (le carré de la moyenne) donne des résultats que nous avons déjà obtenus plus tôt de manière plus difficile.
Il existe cependant une formule encore plus simple qui s’applique lorsque nous calculons pour X et Y indépendants. Nous avons

puisque, comme nous le savons, pour les variables aléatoires indépendantes, donc,

"La variance de la somme des variables aléatoires indépendantes est égale à la somme de leurs variances." Ainsi, par exemple, la variance du montant pouvant être gagné avec un billet de loterie est égale à
Par conséquent, la dispersion des gains totaux de deux billets de loterie dans deux loteries différentes (indépendantes) sera la valeur de dispersion correspondante pour les billets de loterie indépendants sera
La variance de la somme des points lancés sur deux dés peut être obtenue à l’aide de la même formule, puisqu’il s’agit de la somme de deux variables aléatoires indépendantes. Nous avons
pour le bon cube ; donc, dans le cas d'un centre de masse déplacé
donc, si les deux cubes ont un centre de masse déplacé. Notez que dans ce dernier cas, la variance est plus grande, même si elle prend plus souvent une valeur moyenne de 7 que dans le cas des dés ordinaires. Si notre objectif est d’obtenir plus de sept chanceux, alors la variance n’est pas le meilleur indicateur de succès.
D'accord, nous avons établi comment calculer la variance. Mais nous n'avons pas encore répondu à la question de savoir pourquoi il est nécessaire de calculer la variance. Tout le monde le fait, mais pourquoi ? La raison principale est l'inégalité de Chebyshev, qui établit une propriété de dispersion importante :
(Cette inégalité diffère des inégalités de Chebyshev pour les sommes que nous avons rencontrées au chapitre 2.) Au niveau qualitatif, (8.17) affirme que la variable aléatoire X prend rarement des valeurs éloignées de sa moyenne si sa variance VX est petite. Preuve
la gestion est extraordinairement simple. Vraiment,

la division par complète la preuve.
Si nous désignons l'espérance mathématique par a et l'écart type par a et remplaçons dans (8.17) par alors la condition se transforme en donc, nous obtenons de (8.17)
Ainsi, X se situera dans - fois l'écart type de sa moyenne, sauf dans les cas où la probabilité ne dépasse pas. La variable aléatoire se situera dans 2a d'au moins 75 % des essais ; allant de à - au moins pour 99%. Ce sont des cas d'inégalité de Chebyshev.
Si vous lancez quelques dés une fois, la somme totale des points de tous les lancers sera presque toujours proche de. La raison en est la suivante : la variance des lancers indépendants sera La variance signifie l'écart type de tout.
Par conséquent, à partir de l’inégalité de Chebyshev, nous obtenons que la somme des points se situera entre
au moins pour 99 % de tous les lancers de dés corrects. Par exemple, le résultat d'un million de lancers avec une probabilité de plus de 99 % sera compris entre 6,976 millions et 7,024 millions.
En général, soit X toute variable aléatoire sur l'espace de probabilité Π ayant une espérance mathématique finie et un écart type fini une. On peut alors introduire en considération l'espace de probabilité Pn, dont les événements élémentaires sont des -séquences où each , et la probabilité est définie comme
Si l'on définit maintenant les variables aléatoires par la formule
alors la valeur
sera la somme de variables aléatoires indépendantes, qui correspond au processus de sommation des réalisations indépendantes de la valeur X sur P. L'espérance mathématique sera égale à et l'écart type - ; donc la valeur moyenne des réalisations,
![]()
variera de à dans au moins 99 % de la période. En d'autres termes, si vous en choisissez une assez grande, la moyenne arithmétique des tests indépendants sera presque toujours très proche de la valeur attendue (dans les manuels de théorie des probabilités, un théorème encore plus fort est prouvé, appelé la loi forte des grands nombres ; mais pour nous le simple corollaire de l'inégalité de Chebyshev, que nous venons de supprimer.)
Parfois, nous ne connaissons pas les caractéristiques de l’espace de probabilité, mais nous devons estimer l’espérance mathématique d’une variable aléatoire X à l’aide d’observations répétées de sa valeur. (Par exemple, nous pourrions vouloir connaître la température moyenne à midi en janvier à San Francisco ; ou nous pourrions vouloir connaître l'espérance de vie sur laquelle les agents d'assurance devraient baser leurs calculs.) Si nous disposons d'observations empiriques indépendantes, nous pouvons supposer que la la vraie espérance mathématique est approximativement égale
![]()
Vous pouvez également estimer la variance à l'aide de la formule
En regardant cette formule, vous pourriez penser qu’il y a une erreur typographique ; Il semblerait qu'elle devrait être là comme dans (8.19), puisque la vraie valeur de la dispersion est déterminée dans (8.15) à travers les valeurs attendues. Cependant, remplacer ici par permet d’obtenir une meilleure estimation, puisqu’il résulte de la définition (8.20) que
![]()
En voici la preuve :

(Dans ce calcul nous nous appuyons sur l'indépendance des observations lorsque nous remplaçons par )
En pratique, pour évaluer les résultats d'une expérience avec une variable aléatoire X, on calcule généralement la moyenne empirique et l'écart type empirique, puis on écrit la réponse sous la forme Voici, par exemple, les résultats d'un lancer de dés, probablement correct.