Cours "Séries de Fourier et leur application". où k est le numéro harmonique. La série de Fourier s'écrit

Dans de nombreux cas, la tâche consistant à obtenir (calculer) le spectre d'un signal ressemble à ceci. Il existe un CAN qui, avec une fréquence d'échantillonnage Fd, convertit un signal continu arrivant à son entrée pendant le temps T en échantillons numériques - N morceaux. Ensuite, le tableau d'échantillons est introduit dans un certain programme qui produit N/2 de certaines valeurs numériques (le programmeur qui volé sur Internet a écrit un programme, assure qu'il fait la transformée de Fourier).

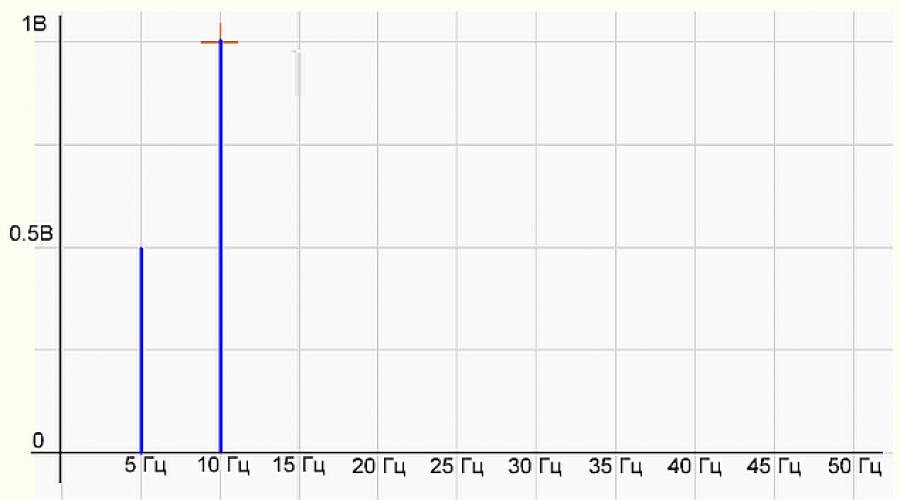
Pour vérifier si le programme fonctionne correctement, nous formerons un tableau d'échantillons comme la somme de deux sinusoïdes sin(10*2*pi*x)+0,5*sin(5*2*pi*x) et le glisserons dans le programme. . Le programme a dessiné les éléments suivants :

Fig.1 Graphique de la fonction temps du signal

Fig.2 Graphique du spectre du signal

Sur le graphique du spectre il y a deux bâtons (harmoniques) 5 Hz avec une amplitude de 0,5 V et 10 Hz avec une amplitude de 1 V, tout est comme dans la formule du signal d'origine. Tout va bien, bravo programmeur ! Le programme fonctionne correctement.

Cela signifie que si nous appliquons un signal réel provenant d'un mélange de deux sinusoïdes à l'entrée du CAN, nous obtiendrons un spectre similaire composé de deux harmoniques.

Au total, notre réel signal mesuré, dure 5 secondes, numérisé par l'ADC, c'est-à-dire représenté discret compte, a discret non périodique gamme.

D’un point de vue mathématique, combien d’erreurs y a-t-il dans cette phrase ?

Maintenant que les autorités ont décidé, nous avons décidé que 5 secondes, c'est trop long, mesurons le signal en 0,5 seconde.



Fig.3 Graphique de la fonction sin(10*2*pi*x)+0,5*sin(5*2*pi*x) pour une période de mesure de 0,5 sec

Fig.4 Spectre de fonctions

Quelque chose ne semble pas normal ! L'harmonique de 10 Hz est dessinée normalement, mais à la place du bâton de 5 Hz, plusieurs harmoniques étranges apparaissent. Nous regardons sur Internet ce qui se passe...

Eh bien, ils disent que vous devez ajouter des zéros à la fin de l'échantillon et le spectre sera dessiné normalement.

Fig.5 Ajout de zéros jusqu'à 5 secondes

Fig.6 Spectre reçu

Ce n'est toujours pas la même chose qu'à 5 secondes. Nous devrons traiter de la théorie. Allons à Wikipédia- source de connaissances.

2. Fonction continue et sa représentation en série de Fourier

Mathématiquement, notre signal d'une durée de T secondes est une fonction f(x) définie sur le segment (0, T) (X dans dans ce cas- temps). Une telle fonction peut toujours être représentée comme une somme de fonctions harmoniques (sinus ou cosinus) de la forme :

(1), où :

K - numéro de fonction trigonométrique (numéro de composant harmonique, numéro harmonique)
T - segment où la fonction est définie (durée du signal)
Ak est l'amplitude de la k-ième composante harmonique,
θk- phase initiale de la k-ième composante harmonique

Que signifie « représenter une fonction comme la somme d’une série » ? Cela signifie qu'en additionnant les valeurs des composantes harmoniques de la série de Fourier en chaque point, nous obtenons la valeur de notre fonction en ce point.

(Plus strictement, l'écart quadratique moyen de la série par rapport à la fonction f(x) tendra vers zéro, mais malgré la convergence quadratique moyenne, la série de Fourier d'une fonction, d'une manière générale, n'est pas obligée de y convergent ponctuellement. Voir https://ru.wikipedia.org/wiki/Fourier_Series.)

Cette série peut également s’écrire :

(2),
Où , k-ième complexe amplitude.

La relation entre les coefficients (1) et (3) est exprimée par les formules suivantes :

Notez que ces trois représentations de la série de Fourier sont complètement équivalentes. Parfois, lorsque l'on travaille avec des séries de Fourier, il est plus pratique d'utiliser les exposants de l'argument imaginaire au lieu des sinus et des cosinus, c'est-à-dire d'utiliser la transformée de Fourier pour forme complexe. Mais il nous convient d'utiliser la formule (1), où la série de Fourier est présentée comme une somme d'ondes cosinusoïdales avec les amplitudes et phases correspondantes. Quoi qu’il en soit, il est inexact de dire que la transformée de Fourier d’un signal réel aboutira à des amplitudes harmoniques complexes. Comme Wiki l'indique à juste titre, « La transformée de Fourier (ℱ) est une opération qui associe une fonction d'une variable réelle à une autre fonction, également une variable réelle. »

Total:
La base mathématique de l'analyse spectrale des signaux est la transformée de Fourier.

La transformée de Fourier permet de représenter une fonction continue f(x) (signal) définie sur le segment (0, T) comme la somme d'un nombre infini (série infinie) fonctions trigonométriques(sinus et/ou cosinus) avec certaines amplitudes et phases, également considérées sur le segment (0, T). Une telle série est appelée série de Fourier.

Notons encore quelques points dont la compréhension est nécessaire pour application correcte Transformations de Fourier pour l'analyse du signal. Si l'on considère la série de Fourier (la somme des sinusoïdes) sur tout l'axe X, on voit qu'en dehors du segment (0, T) la fonction représentée par la série de Fourier répétera périodiquement notre fonction.

Par exemple, dans le graphique de la figure 7, la fonction d'origine est définie sur le segment (-T\2, +T\2), et la série de Fourier représente fonction périodique, défini sur tout l'axe des x.

Cela se produit parce que les sinusoïdes elles-mêmes sont des fonctions périodiques et que, par conséquent, leur somme sera une fonction périodique.

Fig.7 Représentation d'une fonction originale non périodique par une série de Fourier

Ainsi:

Notre fonction originale est continue, non périodique, définie sur un certain segment de longueur T.
Le spectre de cette fonction est discret, c'est-à-dire qu'il se présente sous la forme d'une série infinie de composantes harmoniques - la série de Fourier.
En fait, la série de Fourier définit une certaine fonction périodique qui coïncide avec la nôtre sur le segment (0, T), mais pour nous cette périodicité n'est pas significative.

Les périodes des composantes harmoniques sont des multiples de la valeur du segment (0, T) sur lequel la fonction originale f(x) est définie. Autrement dit, les périodes harmoniques sont des multiples de la durée de la mesure du signal. Par exemple, la période de la première harmonique de la série de Fourier est égale à l'intervalle T sur lequel est définie la fonction f(x). La période de la deuxième harmonique de la série de Fourier est égale à l'intervalle T/2. Et ainsi de suite (voir Fig. 8).

Fig.8 Périodes (fréquences) des composantes harmoniques de la série de Fourier (ici T = 2π)

En conséquence, les fréquences des composantes harmoniques sont des multiples de 1/T. Autrement dit, les fréquences des composantes harmoniques Fk sont égales à Fk= k\T, où k va de 0 à ∞, par exemple k=0 F0=0 ; k=1 F1=1\T; k=2 F2=2\T; k=3 F3=3\T;… Fk= k\T (à fréquence nulle - composante constante).

Soit notre fonction originale un signal enregistré pendant T=1 sec. Alors la période de la première harmonique sera égale à la durée de notre signal T1=T=1 sec et la fréquence harmonique sera de 1 Hz. La période de la deuxième harmonique sera égale à la durée du signal divisée par 2 (T2=T/2=0,5 sec) et la fréquence sera de 2 Hz. Pour la troisième harmonique T3=T/3 sec et la fréquence est de 3 Hz. Et ainsi de suite.

Le pas entre les harmoniques dans ce cas est de 1 Hz.

Ainsi, un signal d'une durée de 1 seconde peut être décomposé en composantes harmoniques (obtention d'un spectre) avec une résolution en fréquence de 1 Hz.
Pour augmenter la résolution de 2 fois à 0,5 Hz, vous devez augmenter la durée de mesure de 2 fois - jusqu'à 2 secondes. Un signal d'une durée de 10 secondes peut être décomposé en composantes harmoniques (pour obtenir un spectre) avec une résolution en fréquence de 0,1 Hz. Il n’existe aucun autre moyen d’augmenter la résolution en fréquence.

Il existe un moyen d'augmenter artificiellement la durée d'un signal en ajoutant des zéros au tableau d'échantillons. Mais cela n’augmente pas la résolution en fréquence réelle.

3. Signaux discrets et transformée de Fourier discrète

Avec développement technologie digitale Les méthodes de stockage des données de mesure (signaux) ont également changé. Si auparavant un signal pouvait être enregistré sur un magnétophone et stocké sur bande sous forme analogique, les signaux sont désormais numérisés et stockés dans des fichiers dans la mémoire de l'ordinateur sous la forme d'un ensemble de nombres (échantillons).

Le schéma habituel pour mesurer et numériser un signal est le suivant.

Fig.9 Schéma du canal de mesure

Le signal du transducteur de mesure arrive à l'ADC pendant un temps T. Les échantillons de signal (échantillonnage) obtenus pendant le temps T sont transmis à l'ordinateur et stockés en mémoire.

Fig. 10 Signal numérisé - N échantillons reçus pendant le temps T

Quelles sont les exigences relatives aux paramètres de numérisation du signal ? Un appareil qui convertit l'entrée Signal analogique au code discret ( signal numérique) est appelé convertisseur analogique-numérique (ADC, anglais Analog-to-digital converter, ADC) (Wiki).

L'un des principaux paramètres de l'ADC est la fréquence d'échantillonnage maximale (ou taux d'échantillonnage, taux d'échantillonnage anglais) - le taux d'échantillonnage d'un signal continu dans le temps lors de son échantillonnage. Elle se mesure en hertz. ((Wiki))

Selon le théorème de Kotelnikov, si un signal continu a un spectre limité par la fréquence Fmax, alors il peut être reconstruit complètement et sans ambiguïté à partir de ses échantillons discrets prélevés à intervalles de temps. , c'est à dire. avec une fréquence Fd ≥ 2*Fmax, où Fd est la fréquence d'échantillonnage ; Fmax - fréquence maximale du spectre du signal. Autrement dit, la fréquence de numérisation du signal (fréquence d'échantillonnage ADC) doit être au moins 2 fois supérieure à la fréquence maximale du signal que l'on souhaite mesurer.

Que se passera-t-il si nous prélevons des échantillons avec une fréquence inférieure à celle requise par le théorème de Kotelnikov ?

Dans ce cas, il se produit l'effet « aliasing » (également connu sous le nom d'effet stroboscopique, effet moiré), dans lequel un signal haute fréquence, après numérisation, se transforme en un signal basse fréquence, qui n'existe pas en réalité. En figue. L'onde sinusoïdale haute fréquence 11 rouge est un signal réel. Une sinusoïde bleue d'une fréquence inférieure est un signal fictif qui apparaît du fait que pendant la période d'échantillonnage, plus d'une demi-période du signal haute fréquence a le temps de passer.

Riz. 11. L'apparition d'un faux signal basse fréquence à un taux d'échantillonnage insuffisamment élevé

Pour éviter l'effet de crénelage, un filtre anti-crénelage spécial est placé devant l'ADC - un filtre passe-bas (LPF), qui laisse passer les fréquences inférieures à la moitié de la fréquence d'échantillonnage de l'ADC et coupe les fréquences plus élevées.

Afin de calculer le spectre d'un signal à partir de ses échantillons discrets, la transformée de Fourier discrète (TFD) est utilisée. Notons encore une fois que le spectre d'un signal discret « par définition » est limité par la fréquence Fmax, qui est inférieure à la moitié de la fréquence d'échantillonnage Fd. Par conséquent, le spectre d'un signal discret peut être représenté par la somme d'un nombre fini d'harmoniques, contrairement à la somme infinie pour la série de Fourier d'un signal continu, dont le spectre peut être illimité. Selon le théorème de Kotelnikov, la fréquence maximale d'une harmonique doit être telle qu'elle représente au moins deux échantillons, donc le nombre d'harmoniques est égal à la moitié du nombre d'échantillons d'un signal discret. Autrement dit, s’il y a N échantillons dans l’échantillon, alors le nombre d’harmoniques dans le spectre sera égal à N/2.

Considérons maintenant la transformée de Fourier discrète (TFD).

Comparaison avec la série de Fourier

Nous voyons qu'ils coïncident, sauf que le temps dans la DFT est de nature discrète et que le nombre d'harmoniques est limité par N/2 - la moitié du nombre d'échantillons.

Les formules DFT sont écrites en variables entières sans dimension k, s, où k sont le nombre d'échantillons de signal, s est le nombre de composantes spectrales.
La valeur s indique le nombre d'oscillations harmoniques complètes sur la période T (durée de mesure du signal). La transformée de Fourier discrète est utilisée pour trouver les amplitudes et les phases des harmoniques à l'aide d'une méthode numérique, c'est-à-dire "sur l'ordinateur"

Revenons aux résultats obtenus au début. Comme mentionné ci-dessus, lors de l'expansion d'une fonction non périodique (notre signal) en une série de Fourier, la série de Fourier résultante correspond en fait à une fonction périodique de période T (Fig. 12).

Fig. 12 Fonction périodique f(x) avec période T0, avec période de mesure T>T0

Comme on peut le voir sur la figure 12, la fonction f(x) est périodique de période T0. Cependant, du fait que la durée de l'échantillon de mesure T ne coïncide pas avec la période de la fonction T0, la fonction obtenue sous forme de série de Fourier présente une discontinuité au point T. De ce fait, le spectre de cette fonction contiendra un grand nombre d'harmoniques haute fréquence. Si la durée de l'échantillon de mesure T coïncidait avec la période de la fonction T0, alors le spectre obtenu après transformée de Fourier ne contiendrait que la première harmonique (sinusoïde de période égale à la durée d'échantillonnage), puisque la fonction f(x) est une sinusoïde.

En d'autres termes, le programme DFT "ne sait pas" que notre signal est un "morceau de sinusoïde", mais essaie de représenter une fonction périodique sous la forme d'une série, qui présente une discontinuité due à l'incohérence des morceaux individuels de la sinusoïde.

De ce fait, des harmoniques apparaissent dans le spectre, qui doivent résumer la forme de la fonction, y compris cette discontinuité.

Ainsi, pour obtenir le spectre « correct » d’un signal qui est la somme de plusieurs sinusoïdes de différentes périodes, il faut que la période de mesure du signal contienne un nombre entier de périodes de chaque sinusoïde. En pratique, cette condition peut être remplie pour une durée de mesure du signal suffisamment longue.

Fig. 13 Exemple de fonction et de spectre du signal d'erreur cinématique de la boîte de vitesses

Avec une durée plus courte, l'image sera « pire » :

Fig. 14 Exemple de fonction et de spectre d'un signal de vibration du rotor

En pratique, il peut être difficile de comprendre où sont les « composantes réelles » et où sont les « artefacts » provoqués par les périodes non multiples des composantes et la durée d’échantillonnage du signal ou les « sauts et ruptures » dans la forme du signal. . Bien entendu, les mots « composants réels » et « artefacts » sont mis entre guillemets pour une raison. La présence de nombreuses harmoniques sur le graphique du spectre ne signifie pas que notre signal en est réellement « constitué ». Cela revient à penser que le nombre 7 « se compose » des nombres 3 et 4. Le nombre 7 peut être représenté comme la somme des nombres 3 et 4 – c’est exact.

Donc notre signal... ou plutôt même pas « notre signal », mais une fonction périodique composée de la répétition de notre signal (échantillonnage) peut être représentée comme une somme d'harmoniques (ondes sinusoïdales) avec certaines amplitudes et phases. Mais dans de nombreux cas importants pour la pratique (voir les figures ci-dessus), il est effectivement possible de relier les harmoniques obtenues dans le spectre à processus réels, qui sont de nature cyclique et apportent une contribution significative à la forme du signal.

Quelques résultats

1. Un signal réel mesuré d'une durée de T secondes, numérisé par un CAN, c'est-à-dire représenté par un ensemble d'échantillons discrets (N pièces), possède un spectre discret non périodique, représenté par un ensemble d'harmoniques (N/ 2 pièces).

2. Le signal est représenté par un ensemble de valeurs réelles et son spectre est représenté par un ensemble de valeurs réelles. Les fréquences harmoniques sont positives. Le fait qu’il soit plus pratique pour les mathématiciens de représenter le spectre sous une forme complexe en utilisant des fréquences négatives ne signifie pas que « c’est correct » et que « cela devrait toujours être fait ».

3. Un signal mesuré sur un intervalle de temps T est déterminé uniquement sur un intervalle de temps T. Ce qui s'est passé avant que nous commencions à mesurer le signal, et ce qui se passera après cela, est inconnu de la science. Et dans notre cas, ce n’est pas intéressant. La TFD d'un signal limité dans le temps donne son « vrai » spectre, dans le sens où, sous certaines conditions, elle permet de calculer l'amplitude et la fréquence de ses composantes.

Matériaux utilisés et autres matériaux utiles.

Introduction

Un cas particulier de séries fonctionnelles sont les séries trigonométriques. L'étude des séries trigonométriques a conduit au problème bien connu d'une corde sonore, sur lequel ont travaillé des mathématiciens comme Euler, d'Alembert, Fourier et d'autres.

Actuellement, les séries trigonométriques, ainsi que série de puissance, jouent un rôle important dans la science et la technologie.

1. Système trigonométrique de fonctions. Série de Fourier.

Définition. Séquence de fonctions

1, cosx, sinx, cos2x, sin2x, … , cosnx, sinnx, …

appelé système de fonctions trigonométriques.

Pour le système de fonctions trigonométriques, les égalités suivantes sont valables :

π ∫ cosnxdx=	π ∫ sinnxdx=	π ∫ cosnx sinmxdx = 0, (n ≥ 1),
−π	−π	−π
π ∫ cosnx cosmxdx = π ∫ sinnx sinmxdx = 0, (n ≠ m),
−π	−π
π ∫ cos2 nxdx = π ∫ sin2 nxdx = π , (n ≥ 1).
−π	−π

Ces égalités peuvent être facilement prouvées en utilisant formules connues trigonométrie:

	cos nx sinmx =						(sin(n + m )x − sin(n − m )x ),
	cos nx cosmx =						(cos(n + m )x + cos(n − m )x ),
	sinnx sinmx =					(cos(n − m )x − cos(n + m )x ).

	Totalité					égalités				appelé	orthogonalité
	système trigonométrique.
	Soit f(x) une fonction intégrable sur l'intervalle [-π ,π ] et
	un n=			∫ f (x) cosnxdx ,b n =				∫ f (x) sinnxdx, (n = 0,1,2,...).
			−π					−π
	Définition.					Gamme fonctionnelle
					+ ∑ (an cosnx + b n sinx ),
					n= 1

dans laquelle les coefficients a n , b n sont définis par les formules (2), est appelé

série trigonométrique Fonction de Fourier f(x) , et les coefficients eux-mêmes sont

Coefficients de Fourier.

Le fait que la série (3) soit une série de Fourier trigonométrique de la fonction f(x) s'écrit comme suit :

	f(x)		+ ∑ (an cosnx + b n sinx )
			n= 1

Chaque terme de la série (4) est appelé vibration harmonique. Dans un certain nombre de problèmes appliqués, il est nécessaire de représenter une fonction périodique sous la forme d'une série (4), c'est-à-dire sous la forme d'une somme d'oscillations harmoniques.

2. Développement en série de Fourier de fonctions périodiques de période 2π.

Définition. On dit que la fonction f(x) continu par morceaux sur le segment

Si f(x) est continue sur un intervalle sauf, peut-être, pour un nombre fini de points, en chacun desquels la fonction f(x) a des limites à droite et à gauche.

Formulons un théorème qui fournit des conditions suffisantes pour la convergence d'une série trigonométrique.

Théorème de Dirichlet. Soit une fonction périodique f(x) de période 2π satisfaisant les conditions :

1) f (x) et f ′ (x) sont continus par morceaux sur l'intervalle [-π ,π ] ;

2) si x=c est le point de discontinuité de la fonction f(x), alors

f (c )= 1 2 (f (c − 0)+ f (c + 0)).

Alors la série trigonométrique de Fourier de la fonction f(x) converge vers f(x), c'est-à-dire que l'égalité est vraie

	f(x)=		+ ∑ (an cosnx + b n sinnx ),
			n= 1

où les coefficients a n, b n sont déterminés par les formules (2).

Preuve. Laissez l'égalité (4) être vraie et laissez la série (4) admettre une intégration terme par terme. Trouvons les coefficients dans l'égalité (4). Pour ce faire, multipliez les deux côtés de l'égalité (4) par cosnx et intégrez-le dans la plage de -π à π ; du fait de l'orthogonalité du système trigonométrique, on obtient un n. De même, en multipliant par sinnx et en intégrant, on obtient b n.

3.Série de Fourier de fonctions paires et impaires.

Corollaire 1 (série de Fourier pour une fonction paire). Laisser même fonction f(x)

satisfait les conditions du théorème de Dirichlet.

		f(x)=					+ ∑ une n cosnx ,
							n= 1
					π ∫ cosnxdx , (n = 0,1,2,3,...).

Corollaire 2 (série de Fourier pour une fonction impaire). Laisser fonction impaire f(x) satisfait aux conditions du théorème de Dirichlet.

Ensuite, le développement suivant de la série de Fourier a lieu :

	f (x )= ∑ b n sinnx ,
					n= 1
					π ∫ f(x) sin nxdx.

Pour prouver les corollaires 1 et 2, nous utilisons le lemme suivant, géométriquement évident (l'intégrale est une aire).

Lemme. Soit deux fonctions intégrables sur l'intervalle [-a,a] : une fonction paire g(x) et une fonction impaire h(x).

Alors les égalités sont vraies

∫ une g(x) dx= 2 ∫ une g(x) dx,		∫ une h(x) dx= 0.
−une		−une

Exemple 1. Développez la fonction f(x)=x, (x [-π ,π ] en une série de Fourier.

Puisque la fonction est impaire, alors d'après les formules (8) et (7) nous aurons :

2π

n+12

bn=

∫0

x péché nxdx= −

∫0

xd cosnx=−

cosπ n = (− 1)

(− 1)

m+ 1

x = 2 ∑

sin nx ,x ]− π ,π [.

n= 1

Aux points x=±π la somme de cette série est nulle.

En fixant x = π 2 dans la série (9), nous obtenons une série conditionnellement convergente

(− 1)

m+ 1

= ∑

1 −

+ ...

2n+1

n= 0

Des exercices

1. Développez la fonction périodique f (x) de période 2π en une série de Fourier

0 ≤ x ≤ π,

f(x)=

−π ≤x<0.

2. Développez la fonction f (x) de période 2π en une série de Fourier

−π ≤x ≤0,

0 < x < π ,

f(x) = x

x = π.

f(x)=

−π ≤x<π ,

f(x)=

x = π.

f(x)=x.

			−π ≤x<0,
f(x)=			0 ≤ X ≤ π .
−1

7. Développez la fonction sur l'intervalle [0,π] en une série de Fourier trigonométrique en cosinus

	0 ≤x ≤
f(x)=

< x ≤ π .

8. Répartir sur un segment

			0 ≤x ≤
f(x)=
				< x ≤π .
π−x

f(x)=2x.

f(x) = ex.

Questions de test sur le sujet de la leçon :

1. Rappelez-vous la définition d'une série de Fourier.

2. Définir la convergence d'une série fonctionnelle de Fourier.

Conclusion.

Introduction.

La série de Fourier constitue une partie importante de la théorie des séries trigonométriques. La série de Fourier est apparue pour la première fois dans les travaux de J. Fourier (1807), consacrés à l'étude des problèmes de conduction thermique. Par la suite, les séries de Fourier se sont répandues en mathématiques théoriques et appliquées. Ainsi, lors de l'étude du thème «Équations de physique mathématique», les séries de Fourier sont utilisées pour trouver des solutions à l'équation de la chaleur, équation des ondes avec diverses conditions initiales et aux limites. La transformée de Fourier intégrale, appliquée à une large classe de fonctions, s'est également répandue.

En séparant les variables dans de nombreux problèmes de physique mathématique, en particulier dans les problèmes de valeurs limites de la théorie du potentiel pour une région cylindrique, on aboutit à la solution des équations dites de Bessel.

F. Bessel fut le premier à étudier systématiquement la solution d'équations de ce type, mais encore plus tôt elles furent rencontrées dans les travaux de D. Bernoulli, L. Euler, J. Lagrange.

1. Série de fonctions de Fourier avec n'importe quelle période 2L.

Les fonctions de n'importe quelle période 2L peuvent être étendues en une série de Fourier. Le théorème suivant est valable.

Théorème. Soit une fonction périodique f(x) de période 2L satisfaisant les conditions du théorème de Dirichlet sur l'intervalle [-L,L].

Alors sur l'intervalle [-L,L] il y a un développement en série de Fourier

πnx

π nx ),

f(x)=

∑ (un cos

n= 1

un n=

f(x)cos

π nx dx,

bn=

f(x)péché

π nx dx

L − ∫ L

L − ∫ L

(n = 0,1,2,...)

Preuve. Considérez la fonction

g(y)=f(

−π ≤y ≤π ,

auquel s'applique le théorème de Dirichlet. C'est pourquoi

g(y)=

+ ∑ (an cosny + b n sinny ),

n= 1

π ∫f (

) parce que nydy,

π∫

)péché nydy.

−π

−π

égalités (12)

remplacement x =

Obtenons le requis

égalités (10) et (11).

Commentaire. Si la fonction f(x) est paire sur l'intervalle [-L,L], alors sa

La série de Fourier ne contiendra que le terme libre a 2 0 et les cosinus, si

f(x) est une fonction impaire, alors sa série de Fourier ne contiendra que des sinus. Exemple 2. Développez la fonction f(x) de période 2 en une série de Fourier, qui

le segment [-1,1] est donné par la formule f(x)=| x| .

Puisque la fonction f(x)=| x|

Même, alors b n = 0,

2 ∫ 1

xdx = 1,

0, n = 2 m,

an = 2 ∫ xcos π nxdx=

((− 1)

− 1)=

N = 2m + 1.

Ainsi,

cosπ (2m + 1)x

XR.

(2m + 1)

m= 1

À x=0, la formule (14) donne :

π 2

+…

2. Série de Fourier de fonctions non périodiques.

Soit la fonction non périodique f(x) définie sur l'intervalle [-L,L]. Afin de l'étendre en une série trigonométrique, sur ce segment on construit

g(x)=f(x) à -L
	fonction non périodique		f(x) requis	introduire

Fourier sur l'intervalle ]0,L[. Pour ce faire, on construit une fonction périodique g(x) de période 2L

f(x),0< x < L ,g (x ) = f 1((x ),− L < x < 0.

Puisque la fonction f 1 (x) peut être choisie en un nombre incalculable

façons (tant que g(x) satisfait aux conditions du théorème de Dirichlet), alors nous obtenons un ensemble infini de séries de Fourier

pour la fonction g(x).

En particulier, la fonction g(x) peut être choisie paire ou impaire.

Supposons maintenant que la fonction non périodique f(x) soit définie sur un intervalle ]a,b[. Afin de présenter cette fonction

Série de Fourier, nous construisons une fonction périodique arbitraire f 1 (x) avec

période 2L≥ b-a, coïncidant sur l'intervalle ]a,b[ avec la fonction f(x), et nous la développons en une série de Fourier.

3. Forme complexe de la série de Fourier.

Transformons la série (10) et ses coefficients (11) à l'aide des formules d'Euler

(ω n = π L n )

cosωnx =	e iω n x+ e − iω n x		sinωnx =	e iω n x− e − iω n x

On obtient donc la série

			f (x) = ∑ cn ei ω n x
				n =−∞
	avec des chances
	cn=		∫L	f (x )e − i ω n x dx ,n = 0,± 1,± 2,...,
			−L

qui est appelée série de Fourier trigonométrique sous forme complexe

fonctions f(x) de période 2L.

La terminologie suivante est acceptée, notamment en génie électrique et en génie radio. Les expressions e i ω n x sont appelées harmoniques,

les nombres ω n sont appelés numéros d'onde fonctions f(x). Ensemble de vague

les numéros sont appelés spectre discret. Les coefficients (16) sont appelés amplitude complexe.

L'analyse spectrale traite de l'étude des propriétés des coefficients (16). Exemple 3. Trouver la série de Fourier trigonométrique sous forme complexe

fonctions f(x)=e ax , (a≠ 0), avec L=π.

Les formules (15) et (16) donnent :

shaπ

n ∑ =−∞

(− 1)e

un-dans

En passant à la série de Fourier habituelle, on obtient :

shaπ

2 shaπ

(− 1)n (a cosnx − n sinnx )

n= 1

En particulier, pour x=0 on aura :

(− 1)

2 ashaπ

n= 1

a+n

Des exercices

	Développez la fonction périodique f (x) de période 2π en une série de Fourier
			0 ≤ x ≤ π,
							x = π.
3. Développez en série de Fourier la fonction spécifiée dans l'intervalle [ − 1,1] par l'équation
4. Développez la fonction dans une série de Fourier			f(x)=
					−π ≤x<π ,
f(x)=
							x = π.

5. Développez la fonction en sinus dans l'intervalle [0,1]

f(x)=x.

6. Trouver les coefficients de Fourier d'une fonction série trigonométrique f(x)

			−π ≤x<0,
f(x)=			0 ≤ X ≤ π .
−1
7. Développez l'intervalle [0,π] en une série de Fourier trigonométrique en cosinus
			0 ≤x ≤
f(x)=

< x ≤ π .

8. Répartir sur un segment[ 0,π ] dans la série trigonométrique de Fourier en cosinus0 à 2

			0 ≤x ≤
f(x)=
				< x ≤π .
π−x

9. Dans l'intervalle [0,1] développez la fonction en une série de Fourier trigonométrique

f(x)=2x.

10. Dans l'intervalle [ − 1,1] développez la fonction en une série de Fourier trigonométrique

f(x) = ex.

Conclusion.

La conférence a examiné les séries de Fourier de fonctions périodiques sur différents intervalles. La transformée de Fourier est considérée et une solution à l'équation de Bessel, qui apparaît lors de la séparation de variables dans de nombreux problèmes de physique mathématique, est obtenue.

Introduction.

La conférence discute du cas limite de la série de Fourier, conduisant à l'intégrale de Fourier. Les formules de l'intégrale de Fourier sont écrites pour les fonctions paires et impaires. On note le rôle que joue l'intégrale de Fourier dans diverses applications. L'intégrale de Fourier est représentée sous une forme complexe, similaire à la représentation complexe de la série de Fourier.

Des formules pour la transformée et la transformée de Fourier inverse, les transformées de Fourier cosinus et sinus seront obtenues. Des informations sont fournies sur l'application de la transformée de Fourier à des problèmes de physique mathématique et de génie électrique.

1. Intégrale de Fourier comme cas limite de la série de Fourier

Soit la fonction f(x) définie sur un intervalle infini

]-∞ ,∞ [ et y est absolument intégrable, c'est-à-dire qu'il existe une intégrale convergente

∞ ∫ f(x)dx.

f(x)=

+ ∑ (an cosω n x + b n sinω n x ),

n= 1

un n=

∫ f (x) cosω n xdx ,b n =

∫ f(x)sin ω n xdx,

−L

−L

En substituant les coefficients (2) dans la série (1), on obtient :

f(x)=

∫ f(t)dt+

∑ ((∫ f (t) cosω n tdt ) cosω n x + (∫ f (t) sinω n tdt ) sinω n x ))

−L

Ln=1

−L

−L

Signalons sans preuve que comme L→ la formule (3) prend la forme

f(x)=

∫(∫

f (t) cosω tdt) cosω xd ω +

∫ (∫ f (t ) sinω tdt ) sinω xd ω .

0 −∞

L'expression de droite dans la formule (4) s'appelle Intégrale de Fourier pour la fonction f(x). L'égalité (4) est valable pour tous les points où la fonction est continue. Aux points de discontinuité, f(x) sur le côté gauche de la formule (4) doit être remplacé par

Séries de Fourier et leur application dans les technologies de communication

Le nom du paramètre	Signification
Sujet de l'article :	Séries de Fourier et leur application dans les technologies de communication
Rubrique (catégorie thématique)	Éducation

Décomposition d'un signal continu en séries orthogonales

Conférence 6. Canal continu

Critères de qualité de la restauration.

Les critères suivants existent :

1) Critère du plus grand écart

où : erreur de reconstruction admissible, - valeur maximale - erreur d'approximation actuelle.

Dans le même temps, il est certain que toute modification du signal d'origine, y compris les émissions à court terme, sera enregistrée.

2) Critère SKZ. où : - erreur d'approximation CS supplémentaire, - erreur d'approximation CS.

3) Critère intégral

La valeur moyenne maximale pour la période d'échantillonnage est déterminée.

4) Critère probabiliste

Le niveau admissible est défini, la valeur P est la probabilité que l'erreur d'approximation actuelle ne dépende pas d'une valeur spécifique.

Objectif du cours : familiarisation avec le canal continu

a) décomposition d'un signal continu en séries orthogonales ;

b) les séries de Fourier et leur application dans les technologies des communications ;

c) le théorème de Kotelnikov (théorème fondamental de Shannon) ;

d) capacité d'un canal continu ;

e) Modèle NKS.

En théorie de la communication, deux cas particuliers d'expansion de fonctions en séries orthogonales sont largement utilisés pour représenter des signaux : l'expansion en fonctions trigonométriques et l'expansion en fonctions de la forme sinx/x. Dans le premier cas, on obtient une représentation spectrale du signal sous forme d'une série de Fourier ordinaire, et dans le second cas, une représentation temporelle sous forme d'une série V.A. Kotelnikov.

La forme la plus simple d'expression d'un signal d'un point de vue pratique est une combinaison linéaire de quelques fonctions élémentaires

En général, le signal est une oscillation complexe, ce qui rend extrêmement important la représentation d'une fonction complexe. St), définir le signal à travers des fonctions simples.

Lors de l’étude de systèmes linéaires, cette représentation du signal est très pratique. Il permet de diviser la solution de nombreux problèmes en parties en utilisant le principe de superposition. Par exemple, pour déterminer le signal à la sortie d'un système linéaire, la réponse du système à chaque effet élémentaire ψ k (t) est calculée, puis les résultats multipliés par les coefficients correspondants a k ont ​​été facilement calculés et ne dépendaient pas du nombre des termes de la somme. Ces exigences sont pleinement satisfaites par un ensemble de fonctions orthogonales.

Fonctions ψ 1 (t), ψ 2 (t), . . . . , ψ n (t) . (6.2)

Les données sur un intervalle sont dites orthogonales,

si à. (6.3)

La base de l'analyse spectrale des signaux est la représentation des fonctions temporelles sous la forme d'une série de Fourier ou d'une intégrale. Tout signal périodique s(t) qui satisfait à la condition de Dirichlet doit être représenté sous forme de série dans des fonctions trigonométriques

La quantité a 0, exprimant la valeur moyenne du signal sur une période, est habituellement appelée composante constante. Il est calculé par la formule

La forme complexe d'écriture de la série de Fourier est très pratique

Ordre de grandeur Un k est une amplitude complexe, elle se trouve par la formule

Les relations (6.8) et (6.9) constituent une paire de transformées de Fourier discrètes. Il est à noter que la série de Fourier peut représenter non seulement un signal périodique, mais aussi tout signal de durée finie. Dans ce dernier cas, le signal St) est supposé s'étendre périodiquement sur tout l'axe du temps. Dans ce cas, l'égalité (6.4) ou (6.8) représente le signal uniquement dans l'intervalle de sa durée (- T/2,T/2). Un signal (ou bruit) aléatoire spécifié sur un intervalle (- T/2,T/2), doit également être représenté par une série de Fourier

Où un k Et b k sont des variables aléatoires (pour le bruit de fluctuation - aléatoire indépendant avec distribution normale).

Séries de Fourier et leur application dans les technologies de communication - concept et types. Classement et caractéristiques de la catégorie « Séries de Fourier et leur application dans les technologies de communication » 2017, 2018.

1

La capacité d'approcher les séries de Fourier dans le cas d'un signal linéaire est nécessaire pour construire des fonctions dans le cas d'éléments périodiques discontinus. La possibilité d'utiliser cette méthode pour les construire et les décomposer à l'aide de sommes finies de la série de Fourier est utilisée pour résoudre de nombreux problèmes de diverses sciences, telles que la physique, la sismologie, etc. Les processus des marées océaniques et de l'activité solaire sont considérés par la méthode de décomposition des processus oscillatoires et des fonctions décrites par ces transformations. Avec le développement de la technologie informatique, les séries de Fourier ont commencé à être utilisées pour des problèmes de plus en plus complexes, et grâce à cela, il est devenu possible d'utiliser ces transformations dans des sciences indirectes, comme la médecine et la chimie. La transformée de Fourier est décrite à la fois sous une forme réelle et complexe ; la deuxième distribution a permis de faire une percée dans l'exploration de l'espace. Le résultat de ce travail est l'application des séries de Fourier à la linéarisation d'une fonction discontinue et la sélection du nombre de coefficients de la série pour une imposition plus précise de la série sur la fonction. De plus, lors de l'utilisation du développement en série de Fourier, cette fonction cesse d'être discontinue et déjà à des valeurs suffisamment petites, une bonne approximation de la fonction utilisée est obtenue.

série de Fourier

Transformée de Fourier

spectre de phases.

1. Alasheyeva E.A., Rogova N.V. Méthode numérique pour résoudre le problème de l'électrodynamique dans l'approximation du fil mince. Science et paix. Revue scientifique internationale, n° 8(12), 2014. Volume 1. Volgograd. P.17-19.

2. Vorobyov N.N. Théorie des séries. Éd. Science, Rédaction principale de littérature physique et mathématique, M., 1979, -408 S.

3. Kalinina V.N., Pankin V.F. Statistiques mathématiques. - M. : Ecole Supérieure, 2001.

4. Série R. Edwards Fourier dans une présentation moderne. Éd. Monde. En 2 tomes. Tome 1. 1985. 362 p.

5. V.P. Sigorski Appareil mathématique d'ingénieur. Éd. 2ème stéréotype. "Techniques", 1997. – 768 p.

La représentation d'une fonction arbitraire avec une période spécifique sous la forme d'une série est appelée série de Fourier. Cette solution sous forme générale est appelée expansion sur une base orthogonale. L'expansion des fonctions de la série de Fourier est un outil assez puissant pour résoudre une variété de problèmes. Parce que Les propriétés de cette transformation lors de l'intégration, de la différenciation, ainsi que du déplacement d'une expression par argument et convolution sont bien connues et étudiées. Une personne qui n'est pas familière avec les mathématiques supérieures, ainsi qu'avec les travaux du scientifique français Fourier, ne comprendra probablement pas ce que sont ces « séries » et à quoi elles servent. Cette transformée de Fourier fait désormais partie intégrante de nos vies. Il est utilisé non seulement par les mathématiciens, mais aussi par les physiciens, les chimistes, les médecins, les astronomes, les sismologues, les océanographes et bien d'autres.

Les séries de Fourier sont utilisées pour résoudre de nombreux problèmes appliqués. La transformée de Fourier peut être réalisée à l'aide de méthodes analytiques, numériques et autres. Les processus tels que les marées océaniques et les ondes lumineuses jusqu'aux cycles d'activité solaire font référence à la méthode numérique de décomposition de tout processus oscillatoire en une série de Fourier. À l’aide de ces techniques mathématiques, vous pouvez analyser des fonctions, représentant tout processus oscillatoire comme une série de composants sinusoïdaux qui se déplacent du minimum au maximum et inversement. La transformée de Fourier est une fonction qui décrit la phase et l'amplitude des sinusoïdes correspondant à une fréquence spécifique. Cette transformation est utilisée pour résoudre des équations très complexes décrivant des processus dynamiques survenant sous l'influence de l'énergie thermique, lumineuse ou électrique. Aussi, les séries de Fourier permettent d'isoler des composantes constantes dans des signaux oscillatoires complexes, permettant d'interpréter correctement les observations expérimentales obtenues en médecine, chimie et astronomie.

Avec le développement de la technologie, c'est-à-dire L'avènement et le développement de l'ordinateur ont amené la transformée de Fourier à un nouveau niveau. Cette technique est solidement implantée dans presque tous les domaines scientifiques et technologiques. Un exemple est l’audio et la vidéo numériques. Ce qui est devenu une claire prise de conscience de la croissance du processus scientifique et de l’application des séries de Fourier. Ainsi, la série de Fourier sous une forme complexe a permis de faire une percée dans l'étude de l'espace. En outre, cela a influencé l'étude des matériaux semi-conducteurs et de la physique des plasmas, de l'acoustique des micro-ondes, de l'océanographie, du radar et de la sismologie.

Considérons le spectre de phase d'un signal périodique déterminé à partir de l'expression suivante :

où les symboles et désignent respectivement les parties imaginaire et réelle de la quantité entre crochets.

Si on le multiplie par une valeur constante réelle K, alors le développement en série de Fourier a la forme suivante :

De l'expression (1), il résulte que le spectre de Fourier de phase a les propriétés suivantes :

1) est fonction de , c'est-à-dire que contrairement au spectre de puissance, qui ne dépend pas de , il change à mesure que le signal se déplace le long de l'axe du temps ;

2) ne dépend pas de K, c'est-à-dire qu'il est invariant à l'amplification ou à l'atténuation du signal, alors que le spectre de puissance est fonction de K.

3) c'est-à-dire que c'est une fonction impaire de n.

Note. Compte tenu de l’interprétation géométrique des considérations ci-dessus, il peut être exprimé en termes de spectre de puissance et de spectre de phase comme suit :

Parce que le

puis de (2) et (3) il s'ensuit qu'il peut être reconstruit sans ambiguïté si les spectres d'amplitude (ou de puissance) et de phase sont connus.

Regardons un exemple. On nous a donné une fonction entre

Vue générale de la série de Fourier :

Remplaçons nos valeurs et obtenons :

Remplaçons nos valeurs et obtenons.

La série de Fourier s'écrit :

, où k est le numéro harmonique.

Les coefficients de Fourier pour cette série sont trouvés à l'aide des formules :

Les signaux périodiques sont représentés par une série de Fourier sous la forme :

, où est la fréquence fondamentale ;

Ici, les coefficients sont calculés à l'aide des formules :

Une autre forme d'écriture de la série de Fourier est souvent utilisée :

, Où:

- amplitude k les harmoniques ; - phase initiale

Pour faciliter les calculs, la série de Fourier s'écrit sous forme complexe :

Affichage graphique de l'heure et de la fréquence

Spectre d'un signal périodique

image temporaire

(F)

Image de fréquence ASF

Semblable au PSF, en tenant seulement compte du fait que les phases peuvent également être négatives.

Un tel spectre est dit discret ou linéaire, il est caractéristique d'un signal périodique.

Spectre d'une séquence d'impulsions rectangulaires

Considérez la disposition symétrique des impulsions

, où est le cycle de service.

Trouvons les points zéro du sinus :

Le premier point zéro est le plus important pour le spectre de la séquence d'impulsions rectangulaires.

Séquence ASF d'impulsions rectangulaires :

ω 1 ω 2 2π/t vous 4π/t vous

L'essentiel de l'énergie est véhiculé par les harmoniques situées de 0 au premier point zéro (environ 90 % de l'énergie). Cette région de fréquence, où 90 % de l'énergie du signal est concentrée, est appelée la largeur spectrale du signal (de fréquence).

Pour une impulsion rectangulaire, la largeur du spectre est .

Toute transmission de signal numérique nécessite plus de spectre qu’une simple transmission analogique.

Séquence PSF d'impulsions rectangulaires :

si soleil(x)>0, alors Ψk =0

si péché(x)<0, то Ψ k = π

L'influence de la durée et de la période d'impulsion sur le type de spectre

Si la durée diminue, la fréquence fondamentale ne changera pas, les points zéro se déplaceront vers la droite. Un plus grand nombre de composants atteignent le premier point zéro, où l'énergie principale est concentrée. Techniquement, ils constatent que le spectre s’élargit.

Si la durée de l'impulsion augmente, le spectre se rétrécit.

Si la période de répétition augmente, la fréquence fondamentale diminue. Si la période de répétition diminue, la fréquence fondamentale augmente.

Modification de la position ou de l'origine du pouls

Cela n’affecte pas l’ASF ; seul le spectre de phase change. Cela peut être reflété sur la base du théorème du retard :

Spectre de phase du signal décalé à N=4:

Le concept de circuits de calcul avec des signaux périodiques

Méthode de calcul:

1. Le spectre complexe du signal périodique est déterminé ;

2. Le spectre est évalué en laissant les harmoniques les plus significatives (premier critère : toutes celles qui sont inférieures à 0,1 de l'amplitude harmonique maximale sont coupées) ;

Les courants et les tensions de chaque composant sont calculés séparément. Vous pouvez utiliser une méthode de calcul complexe.

je 0 =0

La fonction non harmonique peut être estimée par sa valeur efficace, c'est-à-dire moyenne quadratique pour la période :

Le concept du spectre d'un signal non périodique

Les signaux non périodiques sont les plus importants car ils véhiculent des informations. Les signaux périodiques sont des signaux de service destinés à transmettre des informations et ne transportent pas de nouvelles informations. Dès lors, la question des spectres des signaux non périodiques se pose. Vous pouvez essayer de les obtenir en passant à la limite des signaux périodiques, en dirigeant la période vers l'infini (). Il reste un seul signal. Trouvons l'amplitude complexe du spectre d'un seul signal : à .

,

Un signal non périodique peut être divisé en une somme infinie de composantes harmoniques avec des amplitudes infiniment petites et différant en fréquence par des valeurs infinitésimales - C'est ce qu'on appelle un spectre continu d'un signal non périodique, et non discret. Pour les calculs, le concept d'amplitudes non complexes et de densité spectrale complexe d'amplitudes est utilisé - la valeur d'amplitude par unité de fréquence.

Il s'agit d'une transformée de Fourier directe (bidirectionnelle).