Méthode de coordonnées pour trouver l'angle entre des lignes droites. Méthode de coordonnées dans l'espace : formules et commentaires du tuteur

Méthode de coordonnées pour trouver l'angle entre des lignes droites. Méthode de coordonnées dans l'espace : formules et commentaires du tuteur
Méthode de coordonnées pour trouver l'angle entre des lignes droites. Méthode de coordonnées dans l'espace : formules et commentaires du tuteur
22.09.2019

Dans cet article, à l'aide de l'exemple de résolution du problème C2 de l'examen d'État unifié, la méthode de recherche à l'aide de la méthode des coordonnées est analysée. Rappelez-vous que les lignes droites sont asymétriques si elles ne se trouvent pas dans le même plan. En particulier, si une ligne se trouve dans un plan et que la deuxième ligne coupe ce plan en un point qui ne se trouve pas sur la première ligne, alors ces lignes se coupent (voir figure).

Trouver distances entre les lignes qui se croisent nécessaire:

  1. Tracez un plan passant par l’une des lignes sécantes et parallèle à l’autre ligne sécante.
  2. Déposez une perpendiculaire à partir de n’importe quel point de la deuxième ligne sur le plan résultant. La longueur de cette perpendiculaire sera la distance requise entre les lignes.

Analysons cet algorithme plus en détail à l'aide de l'exemple de résolution du problème C2 de l'examen d'État unifié en mathématiques.

Distance entre les lignes dans l'espace

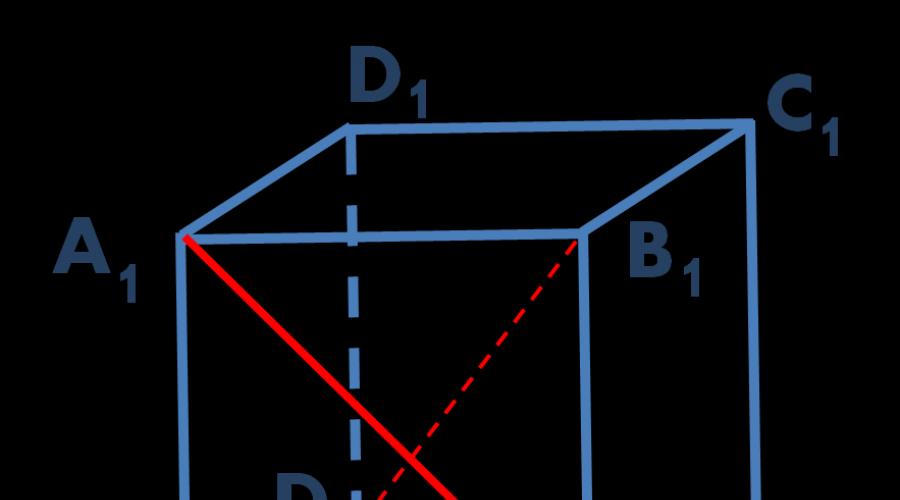
Tâche. Dans un cube unité ABCDA 1 B 1 C 1 D 1 trouver la distance entre les lignes B.A. 1 et D.B. 1 .

Riz. 1. Dessin pour la tâche

Solution. Par le milieu de la diagonale du cube D.B. 1 (point Ô) trace une droite parallèle à la droite UN 1 B. Points d'intersection de cette ligne avec les arêtes AVANT JC. Et UN 1 D 1 est noté en conséquence N Et M.. Droit MN se trouve dans un avion MNB 1 et parallèle à la ligne UN 1 B, qui ne se trouve pas dans ce plan. Cela signifie que la ligne droite UN 1 B parallèle au plan MNB 1 basé sur le parallélisme d’une droite et d’un plan (Fig. 2).

Riz. 2. La distance requise entre les lignes qui se croisent est égale à la distance entre n'importe quel point de la ligne sélectionnée et le plan représenté

Maintenant, nous recherchons la distance à partir d'un point sur la ligne UN 1 B planer MNB 1 . Cette distance, par définition, sera la distance requise entre les lignes de croisement.

Pour trouver cette distance, nous utiliserons la méthode des coordonnées. Introduisons un système de coordonnées cartésiennes rectangulaires pour que son origine coïncide avec le point B, axe Xétait dirigé le long du bord B.A., axe Oui- le long du bord AVANT JC., axe Z- le long du bord BB 1 (Fig. 3).

Riz. 3. Nous choisissons un système de coordonnées cartésiennes rectangulaires comme le montre la figure

Trouver l'équation du plan MNB 1 dans ce système de coordonnées. Pour ce faire, on détermine d'abord les coordonnées des points M., N Et B 1: Nous substituons les coordonnées résultantes dans l'équation générale de la droite et obtenons le système d'équations suivant :

De la deuxième équation du système nous obtenons de la troisième nous obtenons après quoi de la première nous obtenons Remplacez les valeurs obtenues dans l'équation générale de la droite :

On remarque que sinon l'avion MNB 1 passerait par l’origine. Divisons les deux côtés de cette équation par et nous obtenons :

La distance d'un point à un plan est déterminée par la formule.

Utiliser la méthode des coordonnées lors du calcul d'un angle

entre les avions

La plupart méthode générale trouver l'angleentre les plans - la méthode des coordonnées (utilisant parfois des vecteurs). Il peut être utilisé lorsque tous les autres ont été essayés. Mais il existe des situations dans lesquelles il est logique d'appliquer immédiatement la méthode des coordonnées, à savoir lorsque le système de coordonnées est naturellement lié au polyèdre spécifié dans l'énoncé du problème, c'est-à-dire Trois lignes perpendiculaires par paires sont clairement visibles, sur lesquelles les axes de coordonnées peuvent être spécifiés. De tels polyèdres sont cuboïde et une pyramide quadrangulaire régulière. Dans le premier cas, le système de coordonnées peut être spécifié par des arêtes s'étendant à partir d'un sommet (Fig. 1), dans le second - par la hauteur et les diagonales de la base (Fig. 2)

L'application de la méthode des coordonnées est la suivante.

Un système de coordonnées rectangulaires dans l'espace est introduit. Il est conseillé de l'introduire de manière « naturelle », c'est-à-dire de le « lier » à un trio de droites perpendiculaires deux à deux qui ont un point commun.

Pour chacun des plans dont l'angle est recherché, une équation est établie. Le moyen le plus simple de créer une telle équation est de connaître les coordonnées de trois points du plan qui ne se trouvent pas sur la même ligne.

Équation du plan dans vue générale ressemble à Hache + Par + Cz + D = 0.

Coefficients A, B, Les C dans cette équation sont les coordonnées du vecteur normal du plan (le vecteur perpendiculaire au plan). On détermine ensuite les longueurs et le produit scalaire des vecteurs normaux aux plans dont l'angle est recherché. Si les coordonnées de ces vecteurs(A 1, B 1 ; C 1) et (A 2 ; B 2 ; C 2 ), puis l'angle souhaitécalculé par la formule

Commentaire. Il faut se rappeler que l'angle entre les vecteurs (par opposition à l'angle entre les plans) peut être obtus, et pour éviter une éventuelle incertitude, le numérateur à droite de la formule contient un module.

Résolvez ce problème en utilisant la méthode des coordonnées.

Problème 1. Étant donné un cube ABCDA 1 B 1 C 1 D 1 . Le point K est le milieu du bord AD, le point L est le milieu du bord CD. Quel est l'angle entre les plans A ? 1 KL et A 1 AD ?

Solution . Soit l'origine du système de coordonnées au point UN, et les axes de coordonnées suivent les rayons AD, AB, AA 1 (Fig. 3). Supposons que le bord du cube soit égal à 2 (il est pratique de le diviser en deux). Puis les coordonnées des points A 1 , K, L sont les suivants : A 1 (0 ; 0 ; 2), K(1 ; 0 ; 0), L(2 ; 1 ; 0).

Riz. 3

Écrivons l'équation du plan Un 1 K L en général. Ensuite, nous y substituons les coordonnées des points sélectionnés de ce plan. On obtient un système de trois équations à quatre inconnues :

Exprimons les coefficients A, B, C à D et on arrive à l'équation

Diviser les deux parties en D (pourquoi D = 0 ?) puis en multipliant par -2, on obtient l'équation du plan A 1 KL : 2x - 2 y + z - 2 = 0. Alors le vecteur normal à ce plan a les coordonnées (2 : -2 ; 1). Équation plane Un 1 AD vaut : y=0, et les coordonnées du vecteur normal, par exemple (0 ; 2 : 0). D'après la formule ci-dessus pour le cosinus de l'angle entre plans, on obtient :

Dans le devoir C2 en mathématiques, vous devez le plus souvent résoudre un problème dans lequel vous devez déterminer :

  1. Distance entre deux points
  2. Distance d'un point à une ligne
  3. Distance du point au plan
  4. Distance entre les lignes qui se croisent
  5. Angle entre deux droites
  6. Angle entre une droite et un plan
  7. Angle entre les plans
Les tâches sont élémentaires si vous suivez l'algorithme de solution C2 et rappelez les bases propriétés trigonométriques, comme les propriétés des diagonales ou la surface d'un polyèdre. Les tâches de base vous aideront à mémoriser ces propriétés de base.

Passons maintenant directement aux algorithmes.

1. Pour déterminer la distance entre deux points A et B, nous utilisons l’une des deux méthodes suivantes :

  • Nous incluons AB dans un triangle et trouvons sa longueur comme côté du triangle
  • D'après la formule

De plus, la méthode des coordonnées, à mon avis, est la plus simple ; il suffit de déterminer soigneusement les coordonnées de chaque point.

2. Pour déterminer la distance d'un point à une ligne, calculez

  • comme la longueur d'un segment perpendiculaire, s'il est possible d'inclure ce segment dans un triangle comme l'une des hauteurs
en utilisant la méthode des coordonnées en utilisant des formules de calcul de la surface, dans lesquelles la distance requise sera la hauteur et

3. La distance d'un point à un plan est

  • la longueur de la perpendiculaire tombée de ce point sur le plan. Pour ce faire, nous construisons soigneusement une section perpendiculaire au plan et passant par point donné. La distance requise sera égale à la hauteur du nouveau polyèdre résultant.
  • Utiliser la méthode des coordonnées

L'équation se trouve en substituant les coordonnées de trois points appartenant à ce plan

  • Utiliser la méthode vectorielle
Pour ce faire, vous devez vous rappeler les règles d'addition et de soustraction de vecteurs, selon lesquelles le produit des vecteurs perpendiculaires est égal à zéro.
  • En utilisant la méthode du volume, s'il existe une pyramide ABCM, alors la distance du point M au plan contenant le triangle ABC est calculée par la formule
  • Utiliser la méthode des problèmes de référence, qui peuvent être visualisés
4. La distance entre les lignes qui se croisent peut être résolue en utilisant

4.1. Méthode de calcul étape par étape :

  • construire une perpendiculaire commune de deux lignes sécantes et trouver sa longueur ;
  • construire un plan contenant l'une des droites et parallèle à la seconde. Alors la distance requise sera égale à la distance du point à la droite construite dans le plan ;
  • joindre les données directement dans plans parallèles, en passant par ces lignes qui se croisent, trouvez la distance entre ces plans
  • construire un plan perpendiculaire à l'une de ces droites et construire une projection orthogonale de la deuxième droite

4.2. Méthode de coordonnées vectorielles

  • Trouver les coordonnées des extrémités d'un segment qui est une perpendiculaire commune à deux lignes sécantes
  • Trouver la distance entre deux points
4.3. Méthode vectorielle
On réduit le problème à déterminer la longueur d'un vecteur appartenant à une perpendiculaire qui est la perpendiculaire commune de deux droites obliques.

6. Angle entre une droite et un plan déterminé en l'incluant dans triangle rectangle comme l'un des coins pointus, ou par la méthode de coordination vectorielle

Nous verrons comment l'angle entre les plans est déterminé dans la prochaine leçon. Ces algorithmes de résolution de C2 contribuent à une compréhension globale de la méthode de résolution du problème. "Un magazine destiné aux écoliers et à leurs parents pour aider les écoliers." Lire la suite : http://education-club.ru/#ixzz2IXf5GOJU

7. Angle entre les plans(méthode géométrique)

  • 1. Trouvez la ligne droite le long de laquelle les plans se coupent.
  • 2. Sélectionnez un point sur cette ligne et tracez-y deux perpendiculaires situées dans ces plans. Ou dessinez un plan perpendiculaire à la ligne d'intersection des plans.
  • 3. Trouvez la fonction trigonométrique de l'angle formé par les perpendiculaires à la ligne d'intersection des plans. En règle générale, nous le faisons à travers un triangle qui inclut l'angle souhaité.
  • 4. Notez la valeur de l'angle dans votre réponse, ou fonction trigonométrique coin.

Angle entre les plans. Méthode de coordonnées. Tâche C2

Deux plans sécants forment deux paires d'angles dièdres égaux :

L'amplitude de l'angle dièdre est mesurée par l'amplitude de l'angle linéaire correspondant.

Pour construire un angle linéaire d'un angle dièdre, vous devez prendre un point arbitraire sur la ligne d'intersection des plans et, dans chaque plan, tracer un rayon jusqu'à ce point perpendiculaire à la ligne d'intersection des plans. L'angle formé par ces rayons est l'angle linéaire de l'angle dièdre :

La grandeur de l’angle entre les plans est la grandeur de l’angle inférieur au dièdre.

Soit nos plans définis par les équations :

Le cosinus de l'angle entre les plans se trouve par la formule suivante :

Dans la réponse, nous écrivons , puisque la valeur de l'angle entre les plans est la valeur du plus petit angle dièdre.

Dans le droit prisme quadrangulaire avec un côté de base de 12 et une hauteur de 21, on prend un point M sur le bord de telle sorte que . Le point K est pris sur le bord de telle sorte que . Trouvez l'angle entre l'avion et l'avion.

Faisons un dessin. Puisque nous utiliserons la méthode des coordonnées, nous introduirons immédiatement un système de coordonnées :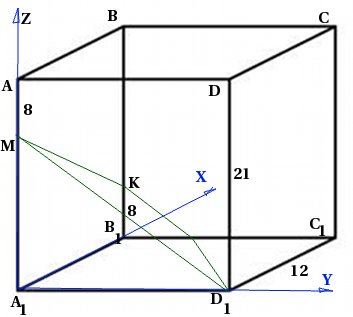

Nous sommes maintenant confrontés à la tâche d'écrire les équations du plan et du plan.

J'ai décrit un algorithme détaillé pour trouver l'équation d'un plan en utilisant trois points.

Après avoir trouvé les coefficients dans les équations du plan et du plan, nous les substituons dans la formule pour trouver le cosinus de l'angle entre les plans et trouver l'angle.

Je vous suggère de regarder une solution vidéo détaillée à ce problème :


Une autre tâche d'Inna Vladimirovna Feldman


Cours vidéo "Méthode de coordonnées pour résoudre les problèmes s-2"

Leçon 2 http://youtu.be/dKQWG8OZRGo
Leçon 3 http://youtu.be/ddgr0PnbFno
Leçon 4 http://youtu.be/n6yx2pQC0Lo
Leçon 5 http://youtu.be/JkWbxAw1YLI
Leçon 6 http://youtu.be/gybIqCMKBiI
leçon 7 http://youtu.be/_LpARpYxp5g
Leçon 8 http://youtu.be/XJhyZQoofD8

La méthode des coordonnées est très efficace et méthode universelle trouver des angles ou des distances entre des objets stéréométriques dans l'espace. Si votre professeur de mathématiques est hautement qualifié, il devrait le savoir. Sinon, je conseillerais de changer de tuteur pour la partie « C ». Ma préparation à l'examen d'État unifié en mathématiques C1-C6 comprend généralement une analyse des algorithmes et formules de base décrits ci-dessous.

Angle entre les lignes a et b

L'angle entre les lignes dans l'espace est l'angle entre toutes les lignes sécantes qui leur sont parallèles. Cet angle égal à l'angle entre les vecteurs directeurs de ces droites (ou le complète à 180 degrés).

Quel algorithme le professeur de mathématiques utilise-t-il pour trouver l’angle ?

1) Choisissez n'importe quel vecteur et ayant les directions des droites a et b (parallèles à elles).
2) On détermine les coordonnées des vecteurs à l'aide des coordonnées correspondantes de leurs débuts et fins (les coordonnées du début doivent être soustraites des coordonnées de la fin du vecteur).
3) Remplacez les coordonnées trouvées dans la formule :
. Pour trouver l’angle lui-même, vous devez trouver l’arc cosinus du résultat.

Normal au plan

Une normale à un plan est tout vecteur perpendiculaire à ce plan.
Comment retrouver la normale ? Pour trouver les coordonnées de la normale, il suffit de connaître les coordonnées de trois points quelconques M, N et K situés dans un plan donné. En utilisant ces coordonnées, nous trouvons les coordonnées des vecteurs et exigeons que les conditions et soient remplies. En assimilant le produit scalaire des vecteurs à zéro, nous composons un système d'équations à trois variables, à partir duquel nous pouvons trouver les coordonnées de la normale.

Note du professeur de mathématiques : Il n'est pas du tout nécessaire de résoudre complètement le système, car il suffit de sélectionner au moins une normale. Pour ce faire, vous pouvez remplacer n'importe laquelle de ses coordonnées inconnues par n'importe quel nombre (par exemple, un) et résoudre le système de deux équations avec les deux inconnues restantes. S'il n'y a pas de solutions, cela signifie que dans la famille des normales, il n'y a personne dont la valeur est un dans la variable sélectionnée. Ensuite, remplacez-en une par une autre variable (une autre coordonnée) et résolvez nouveau système. Si vous manquez à nouveau, votre normale en aura une à la dernière coordonnée, et elle se révélera elle-même parallèle à un plan de coordonnées (dans ce cas, il est facile à trouver sans système).

Supposons que l'on nous donne une droite et un plan avec les coordonnées du vecteur directeur et de la normale
L'angle entre la droite et le plan est calculé à l'aide de la formule suivante :

Soit et soit deux normales à ces avions. Alors le cosinus de l'angle entre les plans est égal au module du cosinus de l'angle entre les normales :

Équation d'un avion dans l'espace

Les points satisfaisant l'égalité forment un plan avec une normale. Le coefficient est responsable de l'ampleur de l'écart (décalage parallèle) entre deux plans avec la même normale donnée. Afin d'écrire l'équation d'un plan, vous devez d'abord trouver sa normale (comme décrit ci-dessus), puis substituer les coordonnées de n'importe quel point du plan ainsi que les coordonnées de la normale trouvée dans l'équation et trouver le coefficient.

Moyenne du protocole d'accord école polyvalente №13

Méthode de coordonnées


2008
Plan:


  1. Introduction


  3. L'essence de la méthode des coordonnées

  4. Systèmes de méthodes de coordonnées

  5. Formules de base de la méthode des coordonnées

  6. Problèmes de différents niveaux de complexité sur le thème « Méthode des coordonnées »
(avec des solutions détaillées)

  1. Conclusion

  2. Bibliographie

Introduction

Utilisé en géométrie diverses méthodes la résolution de problèmes est une méthode synthétique (purement géométrique), une méthode de transformation, une méthode vectorielle, une méthode de coordonnées et autres. Ils occupent différents postes au sein de l'école. La méthode principale est considérée comme synthétique et parmi les autres, la méthode des coordonnées occupe la position la plus élevée car elle est étroitement liée à l'algèbre. L'élégance de la méthode synthétique est obtenue à l'aide de l'intuition, de conjectures et de constructions supplémentaires. La méthode des coordonnées ne l'exige pas : la solution des problèmes est en grande partie algorithmique, ce qui simplifie dans la plupart des cas la recherche et la solution du problème lui-même.

Méthode de coordonnées- un moyen de déterminer la position d'un point ou d'un corps à l'aide de chiffres ou d'autres symboles.

Système de coordonnées- un ensemble de définitions qui implémente la méthode des coordonnées, c'est-à-dire un moyen de déterminer la position d'un point ou d'un corps à l'aide de chiffres ou d'autres symboles.

Donnant à la recherche géométrique un caractère algébrique, la méthode des coordonnées transfère le plus caractéristique importante algèbre - uniformité des façons de résoudre les problèmes. Si en arithmétique et en géométrie élémentaire il faut, en règle générale, rechercher un chemin de solution particulier pour chaque problème, alors en algèbre et en géométrie analytique les solutions s'effectuent selon un plan commun à tous les problèmes, facilement adaptable à n'importe quel problème. Le transfert de méthodes de résolution de problèmes caractéristiques de l'algèbre et donc très générales à la géométrie est l'intérêt principal de la méthode des coordonnées. Un autre avantage de la méthode des coordonnées est que son utilisation élimine le besoin de recourir à une représentation visuelle d'images spatiales complexes.

Objectifs de l'étude de la méthode des coordonnées

On peut souligner les objectifs suivants pour l'étude de la méthode des coordonnées dans un cours de géométrie scolaire :


  • donner aux étudiants méthode efficace résoudre des problèmes et prouver un certain nombre de théorèmes ;

  • montrer, à partir de cette méthode, le lien étroit entre l'algèbre et la géométrie ;

  • contribuer au développement de la culture informatique et graphique des étudiants.

L'essence de la méthode des coordonnées

L'essence de la méthode des coordonnées en tant que méthode de résolution de problèmes est qu'en spécifiant des figures avec des équations et en exprimant diverses relations géométriques en coordonnées, nous pouvons résoudre un problème géométrique en utilisant l'algèbre. À l’inverse, en utilisant les coordonnées, on peut interpréter géométriquement les relations et les faits algébriques et analytiques et ainsi appliquer la géométrie à la solution de problèmes algébriques.

La méthode des coordonnées est une méthode universelle.

Dans une relation cours scolaire En géométrie, on peut dire que dans certains cas, la méthode des coordonnées permet de construire des preuves et de résoudre de nombreux problèmes de manière plus rationnelle et plus belle que par des méthodes purement géométriques. La méthode des coordonnées est cependant associée à une complexité géométrique. Le même problème reçoit une représentation analytique différente en fonction d'un choix particulier de système de coordonnées. Et seule une expérience suffisante permet de choisir le système de coordonnées le plus approprié.


Systèmes de coordonnées :
1. Système de coordonnées rectangulaires (cartésiennes) (Descartes René (1596-1650))

Né à Turin dans une riche famille noble. Quelques jours plus tard, sa mère mourut de consomption ; sa nourrice sortit et lui sauva la vie. À l’âge de 8 ans, René est confié aux soins complets d’un des meilleurs collèges jésuites. Depuis son enfance, Descartes aimait résoudre des problèmes et tous ses temps libre se consacre à l'étude des mathématiques. Descartes a étudié la philosophie, les mathématiques, la physique, l'astronomie et la philologie. Descartes fut le premier à montrer comment les mathématiques pouvaient être utilisées pour visualiser et analyse mathematique pour une grande variété de phénomènes naturels et sociaux.

Les éléments suivants apparaissent pour la première fois dans ses œuvres :


  1. variables

  2. les lois strictes de la géométrie sont traduites en langage algébrique

  3. il a été proposé de représenter les liens entre les phénomènes naturels avec des lignes courbes et de les écrire dans des expressions algébriques

  4. Lettres latines de constantes et variables, ainsi que les désignations de diplômes
2.Système de coordonnées obliques diffère d'un rectangle en ce que ses axes ne sont pas perpendiculaires. Les coordonnées d'un point sont déterminées comme dans un système de coordonnées rectangulaires le long d'axes parallèles droits.

3. Système de coordonnées polaires . Les coordonnées polaires d'un point sont déterminées comme suit : un rayon numérique OX est spécifié sur le plan. Le début du rayon, le point O, est appelé pôle et l’axe OX est appelé axe polaire. Pour déterminer la position du point M dans le système de coordonnées polaires, indiquez la distance du pôle à ce point et la direction dans laquelle il se trouve. La distance d'un point à un pôle s'appelle le rayon polaire d'un point et est désignée par la lettre (prononcé « roh »).

La direction est définie par l'angle de rotation du faisceau OX au faisceau OM

Méthode de coordonnées

formules

Longueur d'un vecteur en fonction de ses coordonnées

Formule pour trouver les coordonnées du milieu d'un segment

Distance entre deux points

Équation d'un cercle,(centre du cercle
,rayon r)

Équation d'une droite
, étant donné que
(l'équation d'une droite dans un système de coordonnées rectangulaires est une équation du premier degré)

Chaque droite est donnée par une équation. Où nombres a,b,c sont déterminés pour chaque droite de manière unique à proportionnalité près (si on les multiplie par le même nombre
, alors l'équation résultante
définira la même ligne).

Distance du point
à une ligne droite m
,équivaut à

Distance du point
planer
, équivaut à

Dérivation de la formule
.

Laissons tomber le sujet
perpendiculaire AB au plan , donné par l'équation
.Laisser
- le point d'intersection de cette perpendiculaire avec le plan . Alors
- distance du point
planer .Puisque le vecteur est perpendiculaire au plan , il est colinéaire au vecteur
.Cela signifie que
,Si
, ou
,Si
, c'est
.Réécrivons cette égalité en coordonnées : .Mais le point
, C'est pourquoi
Et
=
.
(Théorème de Stewart)

Si le triangle ABC est donné et sur cette base, le point D , situé entre les points B et C, alors l'égalité est vraie :

Preuve:

Choisissons un système de coordonnées comme indiqué sur la figure.

Dans le système de coordonnées sélectionné, les sommets du triangle abc aura les coordonnées suivantes :

Hache 1 ;oui 1 ), B(x 2 ;0), C(0;0) et période ré(x 3 ;0) .

Calculons toutes les quantités incluses dans l'égalité :

Remplaçons toutes ces valeurs par côté gaucheégalité:

Q.E.D.

Tache 1. Trouver la distance du point A(-1,3,0) à l'avion , donné par l'équation x -3y -2z +5=0.

Solution. D'après la formule
on a:

.

Répondre:
.


Problème 2. Vecteurs Et mutuellement perpendiculaires, et le vecteur forme un angle de 60˚ avec chacun d’eux. Sachant que
, calculez le produit scalaire

Solution. En utilisant la propriété du produit scalaire, ouvrons les parenthèses :

=

De la définition du produit scalaire on obtient :
(parce que Et perpendiculaire);

Substitution de ces valeurs dans l'expression
=, on trouve le produit scalaire :
=0 – 50+9 12 -120=-62

Répondre:
=0 – 50+9 12 -120=-62
Problème 3.Étant donné un carré A B C D avec le côté UN . Déterminer la distance entre le milieu du segment SUIS , Où M. - milieu Soleil , et un point N sur le côté CD , en le divisant de sorte que CN:ND=3:1 .

Solution:


Choisissons un système de coordonnées comme indiqué sur la figure.

Puis les points M. Et N , selon la condition, aura les coordonnées :

respectivement.

Parce que E - milieu SUIS , alors ses coordonnées seront les suivantes :

Moyens, E .

Trouvons la distance entre les points E Et N :

Réponse : FR =


Problème 4Étant donné un cube ABCDA1B1C1D1 d'arêtes de longueur 1. Le point E est pris sur son arête latérale AA 1 de sorte que
.Le point F est pris sur l'arête BC de sorte que
Un plan est tracé passant par le centre du cube et les points E et F .Trouver la distance du sommet B au plan .

Solution.

Introduisons un système de coordonnées dont le centre est le sommet B. Alors
Trouvons l'équation du plan . Soit cette équation. remarquerez que ne passe pas par l'origine, donc
et l'équation peut être divisée par D ; on obtient l'équation suivante :
ou hache + par + cz +1=0

Pour déterminer les coefficients inconnus a, b et c, on substitue dans l'équation ax + par + cz +1=0 les coordonnées de trois points E, F et O qui satisfont à cette équation (puisque ces points se situent dans le plan ).On obtient un système d’équations :
Transformons le système en multipliant la première équation par 3, la deuxième par 4 et la troisième par -6 et en ajoutant la première équation avec la troisième que nous obtenons
, b=-4,
.Donc l’équation plane a la forme :

5x + 8y - 9z – 2 =0. Nous trouvons maintenant la distance du point B1(0,0,1) au plan
.

Répondre:
.


Problème 5.Base pyramide triangulaire SABC est un triangle équilatéral ABC dont le côté est égal à 4. On sait aussi que AS = BS =
, et CS=3.Trouvez l'aire de la sphère circonscrite à cette pyramide.