Comment résoudre des inégalités à deux racines. Comment résoudre les inégalités ? Comment résoudre les inégalités fractionnaires et quadratiques

Le maintien de votre vie privée est important pour nous. Pour cette raison, nous avons développé une politique de confidentialité qui décrit la manière dont nous utilisons et stockons vos informations. Veuillez consulter nos pratiques de confidentialité et faites-nous savoir si vous avez des questions.

Collecte et utilisation des informations personnelles

Les informations personnelles font référence aux données qui peuvent être utilisées pour identifier ou contacter une personne spécifique.

Il peut vous être demandé de fournir vos informations personnelles à tout moment lorsque vous nous contactez.

Vous trouverez ci-dessous quelques exemples des types d'informations personnelles que nous pouvons collecter et de la manière dont nous pouvons utiliser ces informations.

Quelles informations personnelles collectons-nous :

• Lorsque vous soumettez une demande sur le site, nous pouvons collecter diverses informations, notamment votre nom, numéro de téléphone, adresse E-mail etc.

Comment utilisons-nous vos informations personnelles:

• Collecté par nos soins informations personnelles nous permet de vous contacter et de vous informer des offres uniques, des promotions et d'autres événements et événements à venir.
• De temps en temps, nous pouvons utiliser vos informations personnelles pour envoyer des notifications et des communications importantes.
• Nous pouvons également utiliser des informations personnelles à des fins internes telles que l'audit, l'analyse des données et diverses études afin d'améliorer les services que nous proposons et de vous fournir des recommandations concernant nos services.
• Si vous participez à un tirage au sort, un concours ou une promotion similaire, nous pouvons utiliser les informations que vous fournissez pour administrer ces programmes.

Divulgation d'informations à des tiers

Nous ne divulguons pas les informations reçues de votre part à des tiers.

Des exceptions:

• Si nécessaire, conformément à la loi, procédure judiciaire, V procès, et/ou sur la base de demandes publiques ou de demandes de organismes gouvernementaux sur le territoire de la Fédération de Russie - divulguez vos informations personnelles. Nous pouvons également divulguer des informations vous concernant si nous déterminons qu'une telle divulgation est nécessaire ou appropriée à des fins de sécurité, d'application de la loi ou à d'autres fins de santé publique. cas importants.
• En cas de réorganisation, de fusion ou de vente, nous pouvons transférer les informations personnelles que nous collectons au tiers successeur concerné.

Protection des informations personnelles

Nous prenons des précautions - notamment administratives, techniques et physiques - pour protéger vos informations personnelles contre la perte, le vol et l'utilisation abusive, ainsi que contre l'accès, la divulgation, l'altération et la destruction non autorisés.

Respecter votre vie privée au niveau de l'entreprise

Pour garantir la sécurité de vos informations personnelles, nous communiquons les normes de confidentialité et de sécurité à nos employés et appliquons strictement les pratiques de confidentialité.

Inégalité est une expression avec, ≤ ou ≥. Par exemple, 3x - 5 Résoudre une inégalité signifie trouver toutes les valeurs des variables pour lesquelles l'inégalité est vraie. Chacun de ces nombres est une solution à l’inégalité, et l’ensemble de toutes ces solutions est son de nombreuses solutions. Les inégalités qui ont le même ensemble de solutions sont appelées inégalités équivalentes.

Inégalités linéaires

Les principes de résolution des inégalités sont similaires aux principes de résolution d’équations.

Principes pour résoudre les inégalités
Pour tout nombre réel a, b et c :
Le principe de l'addition des inégalités: Si un Principe de multiplication des inégalités: Si un 0 est vrai alors ac Si un bc est également vrai.
Des affirmations similaires s’appliquent également pour a ≤ b.

Lorsque les deux côtés d’une inégalité sont multipliés par un nombre négatif, il faut changer complètement le signe de l’inégalité.
Les inégalités de premier niveau, comme dans l’exemple 1 (ci-dessous), sont appelées inégalités linéaires.

Exemple 1 Résolvez chacune des inégalités suivantes. Dessinez ensuite l’ensemble des solutions.
a) 3x - 5 b) 13 - 7x ≥ 10x - 4
Solution
Tout nombre inférieur à 11/5 est une solution.
L’ensemble des solutions est (x|x
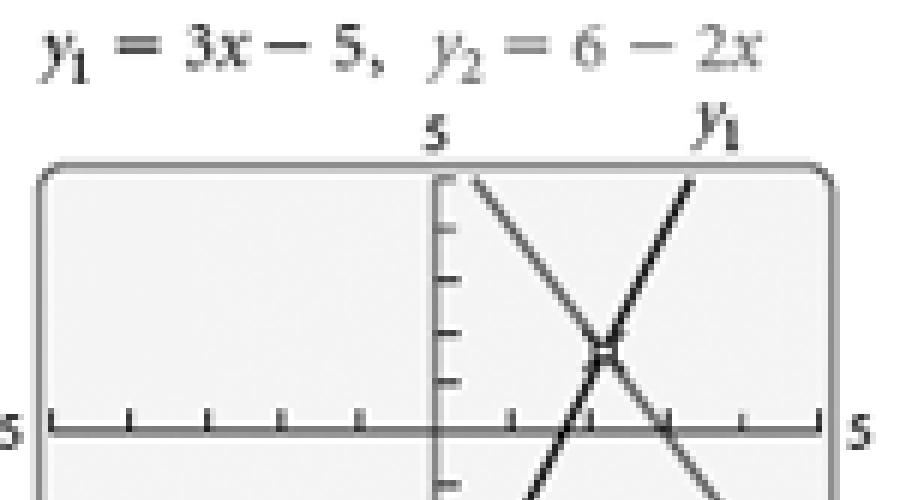
Pour vérifier, nous pouvons tracer un graphique de y 1 = 3x - 5 et y 2 = 6 - 2x. Alors il est clair que pour x
L'ensemble de solutions est (x|x ≤ 1), ou (-∞, 1]. Le graphique de l'ensemble de solutions est présenté ci-dessous.

Doubles inégalités

Quand deux inégalités sont reliées par un mot Et, ou, alors il se forme double inégalité. Double inégalité comme
-3 Et 2x + 5 ≤ 7
appelé connecté, parce qu'il utilise Et. Entrée -3 Les doubles inégalités peuvent être résolues en utilisant les principes d'addition et de multiplication des inégalités.

Exemple 2 Résoudre -3 Solution Nous avons

Ensemble de solutions (x|x ≤ -1 ou x > 3). Nous pouvons également écrire la solution en utilisant la notation par intervalles et le symbole de les associations ou incluant les deux ensembles : (-∞ -1] (3, ∞). Le graphique de l'ensemble de solutions est présenté ci-dessous.

Pour vérifier, traçons y 1 = 2x - 5, y 2 = -7 et y 3 = 1. Notez que pour (x|x ≤ -1 ou x > 3), y 1 ≤ y 2 ou oui 1 > oui 3 .

Inégalités en valeur absolue (module)

Les inégalités contiennent parfois des modules. Les propriétés suivantes sont utilisés pour les résoudre.
Pour un > 0 et expression algébrique X:
|x| |x| > a est équivalent à x ou x > a.
Déclarations similaires pour |x| ≤ une et |x| ≥ une.

Par exemple,
|x| |y| ≥ 1 équivaut à y ≤ -1 ou y ≥ 1 ;
et |2x + 3| ≤ 4 équivaut à -4 ≤ 2x + 3 ≤ 4.

Exemple 4 Résolvez chacune des inégalités suivantes. Représentez graphiquement l’ensemble des solutions.
une) |3x + 2| b) |5 - 2x| ≥ 1

Solution
une) |3x + 2|

L’ensemble de solutions est (x|-7/3
b) |5 - 2x| ≥ 1
L’ensemble de solutions est (x|x ≤ 2 ou x ≥ 3), ou (-∞, 2] .

Résumons ce que nous avons appris.
Disons qu'il faut résoudre le système d'inégalités : $\begin(cases)f_1 (x)>f_2 (x)\\g_1 (x)>g_2 (x)\end(cases)$.
Alors, l'intervalle ($x_1 ; x_2$) est la solution de la première inégalité.
L'intervalle ($y_1; y_2$) est la solution de la deuxième inégalité.
La solution d’un système d’inégalités est l’intersection des solutions de chaque inégalité.

Les systèmes d'inégalités peuvent comprendre non seulement des inégalités de premier ordre, mais également tout autre type d'inégalités.

Règles importantes pour résoudre les systèmes d'inégalités.
Si l’une des inégalités du système n’a pas de solution, alors le système tout entier n’a pas de solution.
Si l'une des inégalités est satisfaite pour n'importe quelle valeur de la variable, alors la solution du système sera la solution de l'autre inégalité.

Exemples.
Résoudre le système d'inégalités :$\begin(cases)x^2-16>0\\x^2-8x+12≤0 \end(cases)$
Solution.
Résolvons chaque inégalité séparément.
$x^2-16>0$.
$(x-4)(x+4)>0$.

Résolvons la deuxième inégalité.
$x^2-8x+12≤0$.
$(x-6)(x-2)≤0$.

La solution de l'inégalité est l'intervalle.
Traçons les deux intervalles sur la même ligne et trouvons l'intersection.
L'intersection des intervalles est le segment (4 ; 6).
Réponse : (4;6].

Résoudre le système d'inégalités.
a) $\begin(cases)3x+3>6\\2x^2+4x+4 b) $\begin(cases)3x+3>6\\2x^2+4x+4>0\end(cases )$.

Solution.
a) La première inégalité a une solution x>1.
Trouvons le discriminant de la deuxième inégalité.
$D=16-4 * 2 * 4=-16$. $D Rappelons la règle : lorsqu'une des inégalités n'a pas de solution, alors tout le système n'a pas de solution.
Réponse : Il n’y a pas de solutions.

B) La première inégalité a une solution x>1.
La deuxième inégalité est supérieure à zéro pour tout x. Alors la solution du système coïncide avec la solution de la première inégalité.
Réponse : x>1.

Problèmes sur les systèmes d'inégalités pour une solution indépendante

Résoudre des systèmes d’inégalités :
a) $\begin(cases)4x-5>11\\2x-12 b) $\begin(cases)-3x+1>5\\3x-11 c) $\begin(cases)x^2-25 d) $\begin(cases)x^2-16x+55>0\\x^2-17x+60≥0 \end(cases)$
e) $\begin(cases)x^2+36

Pour commencer, un peu de poésie pour avoir une idée du problème que résout la méthode des intervalles. Disons que nous devons résoudre l'inégalité suivante :

(x − 5)(x + 3) > 0

Quelles sont les options? La première chose qui vient à l’esprit de la plupart des étudiants est les règles « plus sur plus donne plus » et « moins sur moins donne plus ». Par conséquent, il suffit de considérer le cas où les deux parenthèses sont positives : x − 5 > 0 et x + 3 > 0. Ensuite, nous considérons également le cas où les deux parenthèses sont négatives : x − 5< 0 и x + 3 < 0. Таким образом, наше неравенство свелось к совокупности двух систем, которая, впрочем, легко решается:

Les étudiants plus avancés se souviendront (peut-être) qu'à gauche se trouve fonction quadratique, dont le graphique est une parabole. De plus, cette parabole coupe l'axe OX aux points x = 5 et x = −3. Pour la poursuite des travaux vous devez ouvrir les parenthèses. Nous avons:

x 2 − 2x − 15 > 0

Or, il est clair que les branches de la parabole sont dirigées vers le haut, car coefficient a = 1 > 0. Essayons de tracer un schéma de cette parabole :

La fonction est supérieure à zéro là où elle passe au-dessus de l'axe OX. Dans notre cas, ce sont les intervalles (−∞ −3) et (5 ; +∞) - c'est la réponse.

Attention : l'image montre exactement diagramme de fonction, pas son emploi du temps. Parce que pour un vrai graphique, il faut compter des coordonnées, calculer des déplacements et autres conneries dont nous n'avons absolument aucune utilité pour l'instant.

Pourquoi ces méthodes sont-elles inefficaces ?

Nous avons donc envisagé deux solutions à la même inégalité. Les deux se sont révélés assez encombrants. La première décision se pose : réfléchissez-y ! — un ensemble de systèmes d'inégalités. La deuxième solution n'est pas non plus particulièrement simple : vous devez vous souvenir du graphique de la parabole et d'un tas d'autres petits faits.

C'était une inégalité très simple. Il n'a que 2 multiplicateurs. Imaginez maintenant qu'il n'y aura pas 2, mais au moins 4 multiplicateurs. Par exemple :

(x − 7)(x − 1)(x + 4)(x + 9)< 0

Comment résoudre une telle inégalité ? Passer en revue toutes les combinaisons possibles d’avantages et d’inconvénients ? Oui, nous nous endormirons plus vite que trouvons une solution. Dessiner un graphique n'est pas non plus une option, car le comportement d'une telle fonction sur le plan de coordonnées n'est pas clair.

Pour de telles inégalités, un algorithme de solution spécial est nécessaire, que nous examinerons aujourd'hui.

Quelle est la méthode des intervalles

La méthode des intervalles est un algorithme spécial conçu pour résoudre des inégalités complexes de la forme f (x) > 0 et f (x)< 0. Алгоритм состоит из 4 шагов:

1. Résolvez l'équation f (x) = 0. Ainsi, au lieu d'une inégalité, nous obtenons une équation beaucoup plus simple à résoudre ;
2. Marquez toutes les racines obtenues sur la ligne de coordonnées. Ainsi, la ligne droite sera divisée en plusieurs intervalles ;
3. Découvrez le signe (plus ou moins) de la fonction f (x) sur l'intervalle le plus à droite. Pour ce faire, il suffit de substituer dans f (x) n'importe quel nombre qui se trouvera à droite de toutes les racines marquées ;
4. Marquez les panneaux aux intervalles restants. Pour ce faire, rappelez-vous simplement qu'en passant par chaque racine, le signe change.

C'est tout! Après cela, il ne reste plus qu'à noter les intervalles qui nous intéressent. Ils sont marqués du signe « + » si l'inégalité était de la forme f (x) > 0, ou du signe « - » si l'inégalité était de la forme f (x)< 0.

À première vue, il peut sembler que la méthode des intervalles soit une sorte de chose minuscule. Mais en pratique, tout sera très simple. Entraînez-vous un peu et tout deviendra clair. Jetez un œil aux exemples et voyez par vous-même :

Tâche. Résoudre l'inégalité :

(x − 2)(x + 7)< 0

Nous travaillons selon la méthode des intervalles. Étape 1 : remplacez l'inégalité par une équation et résolvez-la :

(x − 2)(x + 7) = 0

Le produit est nul si et seulement si au moins un des facteurs est nul :

x − 2 = 0 ⇒ x = 2 ;
x + 7 = 0 ⇒ x = −7.

Nous avons deux racines. Passons à l'étape 2 : marquez ces racines sur la ligne de coordonnées. Nous avons:

Maintenant étape 3 : trouvez le signe de la fonction sur l'intervalle le plus à droite (à droite du point marqué x = 2). Pour ce faire, vous devez prendre n'importe quel nombre supérieur au nombre x = 2. Par exemple, prenons x = 3 (mais personne n'interdit de prendre x = 4, x = 10 et même x = 10 000). On a:

f (x) = (x − 2)(x + 7);
x = 3 ;
f (3) = (3 − 2)(3 + 7) = 1 10 = 10 ;

Nous trouvons que f (3) = 10 > 0, nous mettons donc un signe plus dans l'intervalle le plus à droite.

Passons au dernier point : nous devons noter les signes sur les intervalles restants. Nous rappelons qu'en passant par chaque racine, le signe doit changer. Par exemple, à droite de la racine x = 2 il y a un plus (nous nous en sommes assurés à l'étape précédente), il doit donc y avoir un moins à gauche.

Ce moins s'étend sur tout l'intervalle (−7 ; 2), il y a donc un moins à droite de la racine x = −7. Par conséquent, à gauche de la racine x = −7 il y a un plus. Reste à marquer ces panneaux sur axe de coordonnées. Nous avons:

Revenons à l'inégalité originelle, qui avait la forme :

(x − 2)(x + 7)< 0

La fonction doit donc être inférieure à zéro. Cela signifie que nous nous intéressons au signe moins, qui n'apparaît que sur un seul intervalle : (−7 ; 2). Ce sera la réponse.

Tâche. Résoudre l'inégalité :

(x + 9)(x − 3)(1 − x )< 0

Étape 1 : assimiler côté gaucheà zéro :

(x + 9)(x − 3)(1 − x ) = 0;
x + 9 = 0 ⇒ x = −9 ;
x − 3 = 0 ⇒ x = 3 ;
1 − X = 0 ⇒ X = 1.

Rappel : le produit est égal à zéro lorsqu'au moins un des facteurs est égal à zéro. C’est pourquoi nous avons le droit d’assimiler chaque tranche à zéro.

Étape 2 : marquez toutes les racines sur la ligne de coordonnées :

Étape 3 : découvrez le signe de l'écart le plus à droite. On prend n'importe quel nombre supérieur à x = 1. Par exemple, on peut prendre x = 10. On a :

f (x) = (x + 9)(x − 3)(1 − x);
x = 10 ;
f (10) = (10 + 9)(10 − 3)(1 − 10) = 19 · 7 · (−9) = − 1197 ;
f (10) = −1197< 0.

Étape 4 : placement des panneaux restants. Nous rappelons qu'en passant par chaque racine, le signe change. En conséquence, notre image ressemblera à ceci :

C'est tout. Il ne reste plus qu'à écrire la réponse. Jetez un autre regard sur l’inégalité d’origine :

(x + 9)(x − 3)(1 − x )< 0

C'est une inégalité de la forme f(x)< 0, т.е. нас интересуют интервалы, отмеченные знаком минус. А именно:

x ∈ (−9 ; 1) ∪ (3 ; +∞)

C'est la réponse.

Une remarque sur les signes de fonction

La pratique montre que les plus grandes difficultés de la méthode des intervalles surviennent dans les deux dernières étapes, c'est-à-dire lors de la pose de panneaux. De nombreux étudiants commencent à se perdre : quels chiffres prendre et où placer les panneaux.

Pour enfin comprendre la méthode des intervalles, considérons deux observations sur lesquelles elle se base :

1. Une fonction continue change de signe uniquement à ces points où il est égal à zéro. De tels points divisent l'axe des coordonnées en morceaux au sein desquels le signe de la fonction ne change jamais. C'est pourquoi nous résolvons l'équation f (x) = 0 et marquons les racines trouvées sur la ligne droite. Les chiffres trouvés sont des points « limites » séparant le pour et le contre.
2. Pour connaître le signe d'une fonction sur n'importe quel intervalle, il suffit de substituer n'importe quel nombre de cet intervalle dans la fonction. Par exemple, pour l'intervalle (−5 ; 6) on a le droit de prendre x = −4, x = 0, x = 4 et même x = 1,29374 si on veut. Pourquoi c'est important? Oui, car le doute commence à ronger de nombreux étudiants. Par exemple, et si pour x = −4 nous obtenions un plus, et pour x = 0 nous obtenions un moins ? Mais rien de tel n’arrivera jamais. Tous les points d'un même intervalle donnent le même signe. Rappelez-vous ceci.

C'est tout ce que vous devez savoir sur la méthode des intervalles. Bien sûr, nous l'avons démonté version simplifiée. Il y en a plus inégalités complexes- non stricts, fractionnaires et à racines répétitives. Vous pouvez également utiliser la méthode des intervalles pour eux, mais il s'agit d'un sujet pour une grande leçon distincte.

J'aimerais maintenant examiner une technique avancée qui simplifie considérablement la méthode des intervalles. Plus précisément, la simplification n'affecte que la troisième étape : le calcul du signe sur le morceau le plus à droite de la ligne. Pour une raison quelconque, cette technique n'est pas enseignée dans les écoles (du moins personne ne me l'a expliqué). Mais en vain - car en fait cet algorithme est très simple.

Ainsi, le signe de la fonction se trouve sur la partie droite de la droite numérique. Cette pièce a la forme (a ; +∞), où a est la plus grande racine de l’équation f (x) = 0. Afin de ne pas vous épater, considérons un exemple précis :

(x − 1)(2 + x )(7 − x )< 0;
f (x) = (x − 1)(2 + x)(7 − x);
(x − 1)(2 + x)(7 − x) = 0;
x − 1 = 0 ⇒ x = 1 ;
2 + X = 0 ⇒ X = −2 ;
7 − X = 0 ⇒ X = 7 ;

Nous avons 3 racines. Listons-les par ordre croissant : x = −2, x = 1 et x = 7. Évidemment, la plus grande racine est x = 7.

Pour ceux qui trouvent plus facile de raisonner graphiquement, je marquerai ces racines sur la ligne de coordonnées. Voyons ce qui se passe:

Il faut trouver le signe de la fonction f (x) sur l'intervalle le plus à droite, c'est-à-dire à (7; +∞). Mais comme nous l'avons déjà noté, pour déterminer le signe, vous pouvez prendre n'importe quel nombre de cet intervalle. Par exemple, vous pouvez prendre x = 8, x = 150, etc. Et maintenant - la même technique qui n'est pas enseignée dans les écoles : prenons l'infini comme nombre. Plus précisément, plus l'infini, c'est à dire. +∞.

« Etes-vous défoncé ? Comment pouvez-vous substituer l’infini dans une fonction ? » - pourriez-vous demander. Mais réfléchissez-y : nous n’avons pas besoin de la valeur de la fonction elle-même, nous avons seulement besoin du signe. Ainsi, par exemple, les valeurs f (x) = −1 et f (x) = −938 740 576 215 signifient la même chose : la fonction sur un intervalle donné est négative. Il vous suffit donc de trouver le signe qui apparaît à l'infini, et non la valeur de la fonction.

En fait, remplacer l’infini est très simple. Revenons à notre fonction :

f (x) = (x − 1)(2 + x)(7 − x)

Imaginez que x est très grand nombre. Des milliards, voire des milliards. Voyons maintenant ce qui se passe dans chaque tranche.

Première parenthèse : (x − 1). Que se passe-t-il si vous soustrayez un d’un milliard ? Le résultat sera un nombre peu différent d’un milliard, et ce nombre sera positif. De même avec la deuxième parenthèse : (2 + x). Si vous ajoutez un milliard à deux, vous obtenez un milliard et des kopecks - c'est un nombre positif. Enfin, la troisième parenthèse : (7 − x ). Ici, il y aura moins un milliard, dont un morceau pathétique en forme de sept a été « rongé ». Ceux. le nombre obtenu ne différera pas beaucoup de moins un milliard - il sera négatif.

Il ne reste plus qu'à retrouver le signe de l'ensemble de l'œuvre. Puisque nous avons eu un plus dans les premières parenthèses et un moins dans la dernière, nous obtenons la construction suivante :

(+) · (+) · (−) = (−)

Le signe final est moins ! Et peu importe la valeur de la fonction elle-même. L'essentiel est que cette valeur soit négative, c'est-à-dire l'intervalle le plus à droite a un signe moins. Il ne reste plus qu'à réaliser la quatrième étape de la méthode des intervalles : disposer tous les signes. Nous avons:

L’inégalité initiale était :

(x − 1)(2 + x )(7 − x )< 0

Nous nous intéressons donc aux intervalles marqués d'un signe moins. Nous écrivons la réponse :

x ∈ (−2; 1) ∪ (7; +∞)

C'est toute l'astuce que je voulais vous raconter. En conclusion, voici une autre inégalité qui peut être résolue par la méthode des intervalles en utilisant l'infini. Pour raccourcir visuellement la solution, je n'écrirai pas de numéros d'étape ni de commentaires détaillés. Je n'écrirai que ce dont vous avez réellement besoin pour résoudre de vrais problèmes :

Tâche. Résoudre l'inégalité :

x (2x + 8)(x − 3) > 0

Nous remplaçons l'inégalité par une équation et la résolvons :

x (2x + 8)(x − 3) = 0 ;
x = 0 ;
2x + 8 = 0 ⇒ x = −4 ;
X − 3 = 0 ⇒ X = 3.

Nous marquons les trois racines sur la ligne de coordonnées (avec des signes à la fois) :

Il y a un plus sur le côté droit de l'axe des coordonnées, car la fonction ressemble à :

f (x) = x (2x + 8)(x − 3)

Et si nous substituons l'infini (par exemple, un milliard), nous obtenons trois parenthèses positives. Puisque l’expression originale doit être supérieure à zéro, nous ne nous intéressons qu’aux positifs. Il ne reste plus qu'à écrire la réponse :

x ∈ (−4; 0) ∪ (3; +∞)

Après avoir obtenu des premières informations sur les inégalités à variables, passons à la question de leur résolution. Nous analyserons la solution des inégalités linéaires à une variable et toutes les méthodes pour les résoudre avec des algorithmes et des exemples. Seules les équations linéaires à une variable seront considérées.

Yandex.RTB R-A-339285-1

Qu’est-ce que l’inégalité linéaire ?

Vous devez d’abord définir une équation linéaire et la comprendre vue générale et en quoi il sera différent des autres. Du cours scolaire, nous retenons qu'il n'y a pas de différence fondamentale entre les inégalités, il est donc nécessaire d'utiliser plusieurs définitions.

Définition 1

Inégalité linéaire avec une variable x est une inégalité de la forme a · x + b > 0, lorsqu'au lieu de > n'importe quel signe d'inégalité est utilisé< , ≤ , ≥ , а и b являются действительными числами, где a ≠ 0 .

Définition 2

Inégalités a x< c или a · x >c, avec x étant une variable et a et c étant des nombres, est appelé inégalités linéaires à une variable.

Puisque rien n'est dit sur la question de savoir si le coefficient peut être égal à 0, alors une inégalité stricte de la forme 0 x > c et 0 x< c может быть записано в виде нестрогого, а именно, a · x ≤ c , a · x ≥ c . Такое уравнение считается линейным.

Leurs différences sont :

• forme de notation a · x + b > 0 dans le premier, et a · x > c – dans le second ;
• l'admissibilité du coefficient a étant égale à zéro, a ≠ 0 - dans le premier, et a = 0 - dans le second.

On pense que les inégalités a · x + b > 0 et a · x > c sont équivalentes, car elles sont obtenues en transférant un terme d'une partie à une autre. Résoudre l'inégalité 0 x + 5 > 0 conduira au fait qu'elle devra être résolue, et le cas a = 0 ne fonctionnera pas.

Définition 3

On pense que les inégalités linéaires dans une variable x sont des inégalités de la forme une x + b< 0 , a · x + b >0, une x + b ≤ 0 Et une x + b ≥ 0, où a et b sont des nombres réels. Au lieu de x, il peut y avoir un nombre régulier.

D'après la règle, nous avons que 4 x − 1 > 0, 0 z + 2, 3 ≤ 0, - 2 3 x - 2< 0 являются примерами линейных неравенств. А неравенства такого плана, как 5 · x >7 , − 0 , 5 · y ≤ − 1 , 2 sont dits réductibles à linéaires.

Comment résoudre l'inégalité linéaire

La principale façon de résoudre de telles inégalités est d'utiliser des transformations équivalentes afin de trouver les inégalités élémentaires x< p (≤ , >, ≥) , p qui est un certain nombre, pour a ≠ 0, et de la forme a< p (≤ , >, ≥) pour a = 0.

Pour résoudre les inégalités dans une variable, vous pouvez utiliser la méthode des intervalles ou la représenter graphiquement. N'importe lequel d'entre eux peut être utilisé séparément.

Utiliser des transformations équivalentes

Pour résoudre une inégalité linéaire de la forme a x + b< 0 (≤ , >, ≥), il est nécessaire d’appliquer des transformations d’inégalité équivalentes. Le coefficient peut être nul ou non. Considérons les deux cas. Pour le savoir, vous devez respecter un schéma composé de 3 points : l'essence du processus, l'algorithme et la solution elle-même.

Définition 4

Algorithme de résolution d'inégalité linéaire une x + b< 0 (≤ , >, ≥) pour a ≠ 0

• le nombre b sera déplacé vers la droite de l'inégalité c signe opposé, ce qui nous permettra d'arriver à l'équivalent a x< − b (≤ , > , ≥) ;
• Les deux côtés de l’inégalité seront divisés par un nombre différent de 0. De plus, lorsque a est positif, le signe demeure ; lorsque a est négatif, il change en sens inverse.

Considérons l'application de cet algorithme pour résoudre des exemples.

Exemple 1

Résolvez l'inégalité de la forme 3 x + 12 ≤ 0.

Solution

Cette inégalité linéaire a a = 3 et b = 12. Cela signifie que le coefficient a de x n’est pas égal à zéro. Appliquons les algorithmes ci-dessus et résolvons-le.

Il faut déplacer le terme 12 vers une autre partie de l'inégalité et changer le signe devant lui. On obtient alors une inégalité de la forme 3 x ≤ − 12. Il faut diviser les deux parties par 3. Le signe ne changera pas puisque 3 est un nombre positif. On obtient que (3 x) : 3 ≤ (− 12) : 3, ce qui donne le résultat x ≤ − 4.

Une inégalité de la forme x ≤ − 4 est équivalente. Autrement dit, la solution pour 3 x + 12 ≤ 0 est tout nombre réel inférieur ou égal à 4. La réponse s'écrit sous la forme d'une inégalité x ≤ − 4, ou d'un intervalle numérique de la forme (− ∞, − 4].

L'ensemble de l'algorithme décrit ci-dessus s'écrit ainsi :

3 x + 12 ≤ 0 ; 3 x ≤ − 12 ; x ≤ − 4 .

Répondre: x ≤ − 4 ou (− ∞ , − 4 ] .

Exemple 2

Indiquez toutes les solutions disponibles à l’inégalité − 2, 7 · z > 0.

Solution

D'après la condition, nous voyons que le coefficient a pour z est égal à - 2,7 et que b est explicitement absent ou égal à zéro. Vous ne pouvez pas utiliser la première étape de l'algorithme, mais passer immédiatement à la seconde.

Nous divisons les deux côtés de l'équation par le nombre - 2, 7. Le nombre étant négatif, il faut inverser le signe de l’inégalité. Autrement dit, nous obtenons que (− 2, 7 z) : (− 2, 7)< 0: (− 2 , 7) , и дальше z < 0 .

Nous écrirons l’intégralité de l’algorithme dans forme abrégée:

− 2, 7 z > 0 ; z< 0 .

Répondre: z< 0 или (− ∞ , 0) .

Exemple 3

Résolvez l'inégalité - 5 x - 15 22 ≤ 0.

Solution

Par condition, on voit qu'il faut résoudre l'inégalité de coefficient a pour la variable x, qui est égale à - 5, avec le coefficient b, qui correspond à la fraction - 15 22. Il faut résoudre l'inégalité en suivant l'algorithme, c'est-à-dire : déplacer - 15 22 vers une autre partie de signe opposé, diviser les deux parties par - 5, changer le signe de l'inégalité :

5 x ≤ 15 22 ; - 5 x : - 5 ≥ 15 22 : - 5 x ≥ - 3 22

Lors de la dernière transition pour le côté droit, la règle de division numérique est utilisée avec différents signes 15 22 : - 5 = - 15 22 : 5, après quoi nous effectuons la division fraction communeà l'entier naturel - 15 22 : 5 = - 15 22 · 1 5 = - 15 · 1 22 · 5 = - 3 22 .

Répondre: x ≥ - 3 22 et [ - 3 22 + ∞) .

Considérons le cas où a = 0. Expression linéaire de la forme a x + b< 0 является неравенством 0 · x + b < 0 , где на рассмотрение берется неравенство вида b < 0 , после чего выясняется, оно верное или нет.

Tout est basé sur la détermination de la solution à l’inégalité. Pour toute valeur de x on obtient une inégalité numérique de la forme b< 0 , потому что при подстановке любого t вместо переменной x , тогда получаем 0 · t + b < 0 , где b < 0 . В случае, если оно верно, то для его решения подходит любое значение. Когда b < 0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.

Nous considérerons tous les jugements sous la forme d'un algorithme de résolution des inégalités linéaires 0 x + b< 0 (≤ , > , ≥) :

Définition 5

Inégalité numérique de la forme b< 0 (≤ , >, ≥) est vrai, alors l'inégalité d'origine a une solution pour n'importe quelle valeur, et elle est fausse lorsque l'inégalité d'origine n'a pas de solution.

Exemple 4

Résolvez l'inégalité 0 x + 7 > 0.

Solution

Cette inégalité linéaire 0 x + 7 > 0 peut prendre n'importe quelle valeur x. On obtient alors une inégalité de la forme 7 > 0. La dernière inégalité est considérée comme vraie, ce qui signifie que n’importe quel nombre peut être sa solution.

Répondre: intervalle (− ∞ , + ∞) .

Exemple 5

Trouver une solution à l'inégalité 0 x − 12, 7 ≥ 0.

Solution

En substituant la variable x par n'importe quel nombre, on obtient que l'inégalité prend la forme − 12, 7 ≥ 0. C'est incorrect. Autrement dit, 0 x − 12, 7 ≥ 0 n’a pas de solution.

Répondre: il n'y a pas de solutions.

Considérons la résolution d'inégalités linéaires où les deux coefficients sont égaux à zéro.

Exemple 6

Déterminez l’inégalité insoluble de 0 x + 0 > 0 et 0 x + 0 ≥ 0.

Solution

En substituant n'importe quel nombre au lieu de x, nous obtenons deux inégalités de la forme 0 > 0 et 0 ≥ 0. La première est incorrecte. Cela signifie que 0 x + 0 > 0 n’a pas de solutions et que 0 x + 0 ≥ 0 a un nombre infini de solutions, c’est-à-dire n’importe quel nombre.

Répondre: l'inégalité 0 x + 0 > 0 n'a pas de solutions, mais 0 x + 0 ≥ 0 a des solutions.

Cette méthode est discutée dans cours scolaire mathématiques. La méthode des intervalles est capable de résoudre différentes sortes inégalités, également linéaires.

La méthode des intervalles est utilisée pour les inégalités linéaires lorsque la valeur du coefficient x n'est pas égale à 0. Sinon, vous devrez calculer en utilisant une autre méthode.

Définition 6

La méthode des intervalles est la suivante :

• introduisant la fonction y = a · x + b ;
• rechercher des zéros pour diviser le domaine de définition en intervalles ;
• définition de signes pour leurs concepts sur les intervalles.

Assemblons un algorithme pour résoudre les équations linéaires a x + b< 0 (≤ , >, ≥) pour a ≠ 0 en utilisant la méthode des intervalles :

• trouver les zéros de la fonction y = a · x + b pour résoudre une équation de la forme a · x + b = 0 . Si a ≠ 0, alors la solution sera une racine unique, qui prendra la désignation x 0 ;
• construction d'une ligne de coordonnées avec l'image d'un point de coordonnée x 0, avec inégalité stricte le point est indiqué par un point crevé, ou s'il n'est pas strict, par un point peint ;
• déterminer les signes de la fonction y = a · x + b sur les intervalles ; pour cela il faut trouver les valeurs de la fonction en des points de l'intervalle ;
• résoudre une inégalité avec des signes > ou ≥ sur la ligne de coordonnées, en ajoutant un ombrage sur l'intervalle positif,< или ≤ над отрицательным промежутком.

Examinons plusieurs exemples de résolution d'inégalités linéaires à l'aide de la méthode des intervalles.

Exemple 6

Résolvez l'inégalité − 3 x + 12 > 0.

Solution

Il découle de l'algorithme qu'il faut d'abord trouver la racine de l'équation − 3 x + 12 = 0. Nous obtenons que − 3 · x = − 12 , x = 4 . Il est nécessaire de tracer une ligne de coordonnées où l'on marque le point 4. Elle sera crevée car l'inégalité est stricte. Considérez le dessin ci-dessous.

Il est nécessaire de déterminer les signes aux intervalles. Pour le déterminer sur l'intervalle (− ∞, 4), il faut calculer la fonction y = − 3 x + 12 en x = 3. De là, nous obtenons que − 3 3 + 12 = 3 > 0. Le signe sur l'intervalle est positif.

Nous déterminons le signe à partir de l'intervalle (4, + ∞), puis substituons la valeur x = 5. On a ça − 3 5 + 12 = − 3< 0 . Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.

Nous résolvons l'inégalité avec le signe > et l'ombrage est effectué sur l'intervalle positif. Considérez le dessin ci-dessous.

D'après le dessin, il est clair que la solution souhaitée a la forme (− ∞ , 4) ou x< 4 .

Répondre: (− ∞ , 4) ou x< 4 .

Pour comprendre comment représenter graphiquement, il faut considérer 4 inégalités linéaires à titre d'exemple : 0, 5 x − 1< 0 , 0 , 5 · x − 1 ≤ 0 , 0 , 5 · x − 1 >0 et 0, 5 x − 1 ≥ 0. Leurs solutions seront les valeurs de x< 2 , x ≤ 2 , x >2 et x ≥ 2. Pour ce faire, traçons un graphique fonction linéaire y = 0,5 x − 1 donné ci-dessous.

Il est clair que

Définition 7

• résoudre l'inégalité 0, 5 x − 1< 0 считается промежуток, где график функции y = 0 , 5 · x − 1 располагается ниже О х;
• la solution 0, 5 x − 1 ≤ 0 est considérée comme l'intervalle où la fonction y = 0, 5 x − 1 est inférieure à O x ou coïncide ;
• la solution 0, 5 · x − 1 > 0 est considérée comme un intervalle, la fonction est située au dessus de O x ;
• la solution 0, 5 · x − 1 ≥ 0 est considérée comme l'intervalle où le graphique au-dessus de O x ou coïncide.

Signification solution graphique Les inégalités consistent à trouver les intervalles qui doivent être représentés sur un graphique. Dans ce cas, nous constatons que le côté gauche a y = a · x + b, et le côté droit a y = 0 et coïncide avec O x.

Définition 8

Le graphique de la fonction y = a x + b est tracé :

• en résolvant l'inégalité a x + b< 0 определяется промежуток, где график изображен ниже О х;
• lors de la résolution de l'inégalité a · x + b ≤ 0, l'intervalle est déterminé là où le graphique est représenté sous l'axe O x ou coïncide ;
• lors de la résolution de l'inégalité a · x + b > 0, l'intervalle est déterminé là où le graphique est représenté au-dessus de O x ;
• Lors de la résolution de l'inégalité a · x + b ≥ 0, l'intervalle est déterminé là où le graphique est au-dessus de O x ou coïncide.

Exemple 7

Résolvez l'inégalité - 5 · x - 3 > 0 à l'aide d'un graphique.

Solution

Il est nécessaire de construire un graphique de la fonction linéaire - 5 · x - 3 > 0. Cette droite est décroissante car le coefficient de x est négatif. Pour déterminer les coordonnées du point de son intersection avec O x - 5 · x - 3 > 0, on obtient la valeur - 3 5. Représentons-le graphiquement.

En résolvant l'inégalité avec le signe >, vous devez alors faire attention à l'intervalle au-dessus de O x. Mettons en évidence la partie requise de l'avion en rouge et obtenons cela

L'espace requis est la partie O x rouge. Cela signifie que le rayon ouvert - ∞ , - 3 5 sera une solution à l'inégalité. Si par condition nous avions une inégalité non stricte, alors la valeur du point - 3 5 serait également une solution à l'inégalité. Et cela coïnciderait avec O x.

Répondre: - ∞ , - 3 5 ou x< - 3 5 .

La solution graphique est utilisée lorsque le côté gauche correspond à la fonction y = 0 x + b, c'est-à-dire y = b. Alors la droite sera parallèle à O x ou coïncidera en b = 0. Ces cas montrent que l’inégalité peut n’avoir aucune solution, ou que la solution peut être n’importe quel nombre.

Exemple 8

Déterminer à partir des inégalités 0 x + 7< = 0 , 0 · x + 0 ≥ 0 то, которое имеет хотя бы одно решение.

Solution

La représentation de y = 0 x + 7 est y = 7, alors un plan de coordonnées sera donné avec une droite parallèle à O x et située au dessus de O x. Donc 0 x + 7< = 0 решений не имеет, потому как нет промежутков.

Le graphique de la fonction y = 0 x + 0 est considéré comme y = 0, c'est-à-dire que la droite coïncide avec O x. Cela signifie que l’inégalité 0 x + 0 ≥ 0 a plusieurs solutions.

Répondre: La deuxième inégalité a une solution pour toute valeur de x.

Des inégalités qui se réduisent à linéarité

La solution aux inégalités peut se réduire à la solution équation linéaire, que l'on appelle des inégalités qui se réduisent à linéaires.

Ces inégalités ont été prises en compte dans le cours scolaire, car elles constituaient un cas particulier de résolution d'inégalités, ce qui conduisait à l'ouverture de parenthèses et à la réduction de termes similaires. Par exemple, considérons que 5 − 2 x > 0, 7 (x − 1) + 3 ≤ 4 x − 2 + x, x - 3 5 - 2 x + 1 > 2 7 x.

Les inégalités données ci-dessus sont toujours réduites à la forme d'une équation linéaire. Ensuite, les parenthèses sont ouvertes et des termes similaires sont donnés et transférés de Différents composants, en changeant le signe en l'opposé.

En réduisant l'inégalité 5 − 2 x > 0 à linéaire, on la représente de telle manière qu'elle ait la forme − 2 x + 5 > 0, et pour réduire la seconde on obtient que 7 (x − 1) + 3 ≤ 4 X − 2 + X . Il faut ouvrir les parenthèses, amener les termes similaires, déplacer tous les termes vers la gauche et amener les termes similaires. Cela ressemble à ceci :

7 x − 7 + 3 ≤ 4 x − 2 + x 7 x − 4 ≤ ​​​​​​5 x − 2 7 x − 4 − 5 x + 2 ≤ 0 2 x − 2 ≤ 0

Cela conduit à la solution d’une inégalité linéaire.

Ces inégalités sont considérées comme linéaires, puisqu'elles ont le même principe de solution, après quoi il est possible de les réduire à des inégalités élémentaires.

Pour résoudre ce type d’inégalité, il est nécessaire de la réduire à une inégalité linéaire. Cela devrait être fait de cette façon :

Définition 9

• parenthèses ouvertes;
• collecter les variables à gauche et les nombres à droite ;
• donner des termes similaires ;
• divisez les deux côtés par le coefficient de x.

Exemple 9

Résolvez l'inégalité 5 · (x + 3) + x ≤ 6 · (x − 3) + 1.

Solution

On ouvre les parenthèses, on obtient alors une inégalité de la forme 5 x + 15 + x ≤ 6 x − 18 + 1. Après réduction des termes similaires, nous obtenons que 6 x + 15 ≤ 6 x − 17. Après avoir déplacé les termes de gauche à droite, on trouve que 6 x + 15 − 6 x + 17 ≤ 0. Il existe donc une inégalité de la forme 32 ≤ 0 à partir de celle obtenue en calculant 0 x + 32 ≤ 0. On voit que l’inégalité est fausse, ce qui signifie que l’inégalité donnée par condition n’a pas de solution.

Répondre: pas de solutions.

Il convient de noter qu’il existe de nombreux autres types d’inégalités qui peuvent être réduites à des inégalités linéaires ou du type présenté ci-dessus. Par exemple, 5 2 x − 1 ≥ 1 est équation exponentielle, ce qui se réduit à une solution linéaire 2 x − 1 ≥ 0 . Ces cas seront pris en compte lors de la résolution d’inégalités de ce type.

Si vous remarquez une erreur dans le texte, veuillez la surligner et appuyer sur Ctrl+Entrée