Comment résoudre des équations logarithmiques et des inégalités. Inégalités logarithmiques complexes

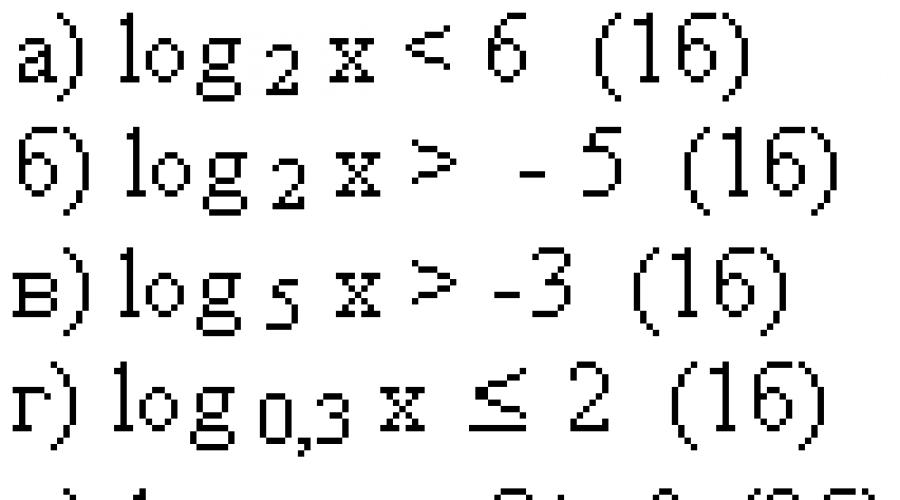
Comment résoudre des équations logarithmiques et des inégalités. Inégalités logarithmiques complexes
Comment résoudre des équations logarithmiques et des inégalités. Inégalités logarithmiques complexes
14.10.2019

Objectifs de la leçon:

Didactique:

  • Niveau 1 – apprendre à résoudre les inégalités logarithmiques les plus simples, en utilisant la définition d'un logarithme et les propriétés des logarithmes ;
  • Niveau 2 – résolvez les inégalités logarithmiques en choisissant votre propre méthode de solution ;
  • Niveau 3 – être capable d’appliquer ses connaissances et compétences dans des situations non standard.

Éducatif: développer la mémoire, l'attention, pensée logique, capacités de comparaison, capacité à généraliser et à tirer des conclusions

Éducatif: cultiver la précision, la responsabilité de la tâche accomplie et l’entraide.

Méthodes d'enseignement: verbal , visuel , pratique , recherche partielle , autonomie gouvernementale , contrôle.

Formes d'organisation activité cognitiveétudiants: frontal , individuel , travailler en équipe de deux.

Équipement: un ensemble de tâches de test, résumé de référence, des feuilles vierges pour les solutions.

Type de cours : apprendre du nouveau matériel.

Pendant les cours

1. Moment organisationnel. Le sujet et les objectifs du cours, le plan du cours sont annoncés : chaque élève reçoit une fiche d'évaluation, qu'il remplit pendant le cours ; pour chaque paire d'étudiants - les documents imprimés avec les tâches doivent être complétés par paires ; des feuilles de solutions vierges ; fiches supports : définition du logarithme ; graphique d'une fonction logarithmique, ses propriétés ; propriétés des logarithmes ; algorithme de solution inégalités logarithmiques.

Toutes les décisions après auto-évaluation sont soumises à l'enseignant.

Feuille de notes de l'élève

2. Actualisation des connaissances.

Consignes du professeur. Rappelez-vous la définition d'un logarithme, le graphique d'une fonction logarithmique et ses propriétés. Pour ce faire, lisez le texte aux pages 88-90, 98-101 du manuel « L'algèbre et les débuts de l'analyse 10-11 » édité par Sh.A Alimov, Yu.M Kolyagin et autres.

Les étudiants reçoivent des fiches sur lesquelles sont inscrites : la définition d'un logarithme ; montre un graphique d'une fonction logarithmique et de ses propriétés ; propriétés des logarithmes ; algorithme de résolution d'inégalités logarithmiques, un exemple de résolution d'une inégalité logarithmique qui se réduit à une inégalité quadratique.

3. Étudier du nouveau matériel.

La résolution des inégalités logarithmiques repose sur la monotonie de la fonction logarithmique.

Algorithme de résolution des inégalités logarithmiques :

A) Trouver le domaine de définition de l'inégalité (l'expression sublogarithmique est supérieure à zéro).
B) Représentez (si possible) les côtés gauche et droit de l’inégalité sous forme de logarithmes sur la même base.
C) Déterminer si le fonction logarithmique: si t>1, alors croissant ; si 0 1, puis décroissante.
D) Aller à plus inégalité simple(expressions sublogarithmiques), en tenant compte du fait que le signe d'inégalité restera si la fonction augmente, et changera si elle diminue.

Élément d'apprentissage n°1.

Objectif : consolider la solution aux inégalités logarithmiques les plus simples

Forme d'organisation de l'activité cognitive des élèves : travail individuel.

Tâches pour travail indépendant pendant 10 minutes. Pour chaque inégalité, il y a plusieurs réponses possibles ; vous devez choisir la bonne et la vérifier à l'aide de la clé.


CLÉ : 13321, nombre maximum de points – 6 points.

Élément d'apprentissage n°2.

Objectif : consolider la solution des inégalités logarithmiques en utilisant les propriétés des logarithmes.

Consignes du professeur. Rappelez-vous les propriétés de base des logarithmes. Pour ce faire, lisez le texte du manuel aux pp. 92, 103-104.

Tâches de travail indépendant pendant 10 minutes.

CLÉ : 2113, nombre maximum de points – 8 points.

Élément d'apprentissage n°3.

Objectif : étudier la solution des inégalités logarithmiques par la méthode de réduction au quadratique.

Consignes de l'enseignant : la méthode pour réduire une inégalité à une inégalité quadratique consiste à transformer l'inégalité sous une forme telle qu'une certaine fonction logarithmique soit désignée par une nouvelle variable, obtenant ainsi une inégalité quadratique par rapport à cette variable.

Utilisons la méthode des intervalles.

Vous avez réussi le premier niveau de maîtrise de la matière. Vous devrez maintenant choisir indépendamment une méthode de résolution d'équations logarithmiques, en utilisant toutes vos connaissances et capacités.

Élément d'apprentissage n°4.

Objectif : consolider la solution aux inégalités logarithmiques en choisissant indépendamment une méthode de solution rationnelle.

Tâches de travail indépendant pendant 10 minutes

Élément d'apprentissage n°5.

Consignes du professeur. Bien joué! Vous maîtrisez la résolution d’équations du deuxième niveau de complexité. L'objectif de vos travaux ultérieurs est d'appliquer vos connaissances et vos compétences dans des situations plus complexes et non standard.

Tâches pour une solution indépendante :

Consignes du professeur. C'est génial si vous avez terminé toute la tâche. Bien joué!

La note pour l'ensemble de la leçon dépend du nombre de points marqués pour tous les éléments pédagogiques :

  • si N ≥ 20, alors vous obtenez une note « 5 »,
  • pour 16 ≤ N ≤ 19 – note « 4 »,
  • pour 8 ≤ N ≤ 15 – note « 3 »,
  • en N< 8 выполнить работу над ошибками к следующему уроку (решения можно взять у учителя).

Remettre les épreuves d'évaluation à l'enseignant.

5. Devoirs: si vous n'avez pas obtenu plus de 15 points, travaillez sur vos erreurs (les solutions peuvent être prises auprès du professeur), si vous avez obtenu plus de 15 points, réalisez une tâche créative sur le thème « Inégalités logarithmiques ».

Avec eux se trouvent des logarithmes intérieurs.

Exemples:

\(\log_3⁡x≥\log_3⁡9\)
\(\log_3⁡ ((x^2-3))< \log_3⁡{(2x)}\)
\(\log_(x+1)⁡((x^2+3x-7))>2\)
\(\lg^2⁡((x+1))+10≤11 \lg⁡((x+1))\)

Comment résoudre les inégalités logarithmiques :

Nous devrions nous efforcer de réduire toute inégalité logarithmique à la forme \(\log_a⁡(f(x)) ˅ \log_a(⁡g(x))\) (le symbole \(˅\) signifie l'un des ). Ce type permet de s'affranchir des logarithmes et de leurs bases, en passant à l'inégalité des expressions sous logarithmes, c'est-à-dire à la forme \(f(x) ˅ g(x)\).

Mais lors de cette transition, il y a une subtilité très importante :
\(-\) si est un nombre et qu'il est supérieur à 1, le signe de l'inégalité reste le même pendant la transition,
\(-\) si la base est un nombre supérieur à 0 mais inférieur à 1 (se situe entre zéro et un), alors le signe d'inégalité devrait changer à l'opposé, c'est-à-dire

Exemples:

\(\log_2⁡((8-x))<1\)
ODZ : \(8-x>0\)
\(-x>-8\)
\(X<8\)

Solution:
\(\log\)\(_2\) \((8-x)<\log\)\(_2\) \({2}\)
\(8-x\)\(<\) \(2\)
\(8-2\(x>6\)
Réponse : \((6;8)\)

\(\log\)\(_(0,5⁡)\) \((2x-4)\)≥\(\log\)\(_(0,5)\) ⁡\(((x+ 1))\)
ODZ : \(\begin(cases)2x-4>0\\x+1 > 0\end(cases)\)
\(\begin(cases)2x>4\\x > -1\end(cases)\) \(\Leftrightarrow\) \(\begin(cases)x>2\\x > -1\end(cases) \) \(\Leftrightarrow\) \(x\in(2;\infty)\)

Solution:
\(2x-4\)\(≤\) \(x+1\)
\(2x-x≤4+1\)
\(x≤5\)
Réponse : \((2;5]\)

Très important! Dans toute inégalité, le passage de la forme \(\log_a(⁡f(x)) ˅ \log_a⁡(g(x))\) à la comparaison d'expressions sous logarithmes ne peut se faire que si :


Exemple . Résoudre l'inégalité : \(\log\)\(≤-1\)

Solution:

\(\enregistrer\) \(_(\frac(1)(3))⁡(\frac(3x-2)(2x-3))\)\(≤-1\)

Écrivons l'ODZ.

ODZ : \(\frac(3x-2)(2x-3)\) \(>0\)

\(⁡\frac(3x-2-3(2x-3))(2x-3)\)\(≥\) \(0\)

Nous ouvrons les supports et apportons .

\(⁡\frac(-3x+7)(2x-3)\) \(≥\) \(0\)

On multiplie l'inégalité par \(-1\), sans oublier d'inverser le signe de comparaison.

\(⁡\frac(3x-7)(2x-3)\) \(≤\) \(0\)

\(⁡\frac(3(x-\frac(7)(3)))(2(x-\frac(3)(2)))\)\(≤\) \(0\)

Construisons une droite numérique et marquons les points \(\frac(7)(3)\) et \(\frac(3)(2)\) dessus. Veuillez noter que le point est supprimé du dénominateur, malgré le fait que l'inégalité ne soit pas stricte. Le fait est que ce point ne sera pas une solution, puisque substitué à l’inégalité, il nous conduira à la division par zéro.


\(x∈(\)\(\frac(3)(2)\) \(;\)\(\frac(7)(3)]\)

Maintenant, nous traçons l'ODZ sur le même axe numérique et notons en réponse l'intervalle qui tombe dans l'ODZ.


Nous écrivons la réponse finale.

Répondre: \(x∈(\)\(\frac(3)(2)\) \(;\)\(\frac(7)(3)]\)

Exemple . Résoudre l'inégalité : \(\log^2_3⁡x-\log_3⁡x-2>0\)

Solution:

\(\log^2_3⁡x-\log_3⁡x-2>0\)

Écrivons l'ODZ.

ODZ : \(x>0\)

Passons à la solution.

Solution : \(\log^2_3⁡x-\log_3⁡x-2>0\)

Nous avons ici une inégalité logarithmique carrée typique. Faisons-le.

\(t=\log_3⁡x\)
\(t^2-t-2>0\)

Mise en page côté gauche inégalités sur .

\(D=1+8=9\)
\(t_1= \frac(1+3)(2)=2\)
\(t_2=\frac(1-3)(2)=-1\)
\((t+1)(t-2)>0\)

Nous devons maintenant revenir à la variable d'origine - x. Pour ce faire, allons à , qui a la même solution, et effectuons la substitution inverse.

\(\left[ \begin(rassemblé) t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3⁡x>2\\\log_3⁡x<-1 \end{gathered} \right.\)

Transformez \(2=\log_3⁡9\), \(-1=\log_3⁡\frac(1)(3)\).

\(\left[ \begin(rassemblé) \log_3⁡x>\log_39 \\ \log_3⁡x<\log_3\frac{1}{3} \end{gathered} \right.\)

Passons à la comparaison des arguments. Les bases des logarithmes sont supérieures à \(1\), donc le signe des inégalités ne change pas.

\(\left[ \begin(rassemblé) x>9 \\ x<\frac{1}{3} \end{gathered} \right.\)

Combinons la solution de l'inégalité et de l'ODZ en une seule figure.


Écrivons la réponse.

Répondre: \((0; \frac(1)(3))∪(9;∞)\)

Une inégalité est dite logarithmique si elle contient une fonction logarithmique.

Les méthodes de résolution des inégalités logarithmiques ne diffèrent pas de celles-ci, à l'exception de deux choses.

Premièrement, lorsqu'on passe de l'inégalité logarithmique à l'inégalité des fonctions sublogarithmiques, il faut suivre le signe de l'inégalité résultante. Il obéit à la règle suivante.

Si la base de la fonction logarithmique est supérieure à 1$, alors lors du passage de l'inégalité logarithmique à l'inégalité des fonctions sous-logarithmiques, le signe de l'inégalité est conservé, mais s'il est inférieur à 1$, alors il change à l'opposé .

Deuxièmement, la solution de toute inégalité est un intervalle, et, par conséquent, à la fin de la résolution de l'inégalité des fonctions sous-logarithmiques, il est nécessaire de créer un système de deux inégalités : la première inégalité de ce système sera l'inégalité des fonctions sous-logarithmiques, et le second sera l'intervalle du domaine de définition des fonctions logarithmiques incluses dans l'inégalité logarithmique.

Pratique.

Résolvons les inégalités :

1. $\log_(2)((x+3)) \geq 3.$

$D(y) : \x+3>0.$

$x \in (-3;+\infty)$

La base du logarithme est $2>1$, donc le signe ne change pas. En utilisant la définition du logarithme, on obtient :

$x+3 \geq 2^(3),$

$x \in )